Онлайн решение показательных уравнений онлайн с подробным решением: Решения показательных уравнений | Онлайн калькулятор

Уравнения онлайн. Решение показательных уравнений

Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.

Советую поступать немного по-другому. Почему? Писал об этом .

Предлагаю решать такие задания следующим образом:

1. Находим производную.
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).

В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать .

Рассмотрим примеры:

77422. Найдите наибольшее значение функции у=х 3 –3х+4 на отрезке [–2;0].

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = –1.

Вычисляем значения функции в точках –2, –1 и 0:

Наибольшее значение функции равно 6.

Ответ: 6

77425. Найдите наименьшее значение функции у = х 3 – 3х 2 + 2 на отрезке .

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 2.

Вычисляем значения функции в точках 1, 2 и 4:

Наименьшее значение функции равно –2.

Ответ: –2

77426. Найдите наибольшее значение функции у = х 3 – 6х 2 на отрезке [–3;3].

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 0.

Вычисляем значения функции в точках –3, 0 и 3:

Наименьшее значение функции равно 0.

Ответ: 0

77429. Найдите наименьшее значение функции у = х 3 – 2х 2 + х +3 на отрезке .

Найдём производную заданной функции:

3х 2 – 4х + 1 = 0

Получим корни: х 1 = 1 х 1 = 1/3.

Указанному в условии интервалу принадлежит только х = 1.

Найдём значения функции в точках 1 и 4:

Получили, что наименьшее значение функции равно 3.

Ответ: 3

77430. Найдите наибольшее значение функции у = х 3 + 2х 2 + х + 3 на отрезке [– 4; –1].

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х 2 + 4х + 1 = 0

Получим корни:

Указанному в условии интервалу принадлежит корень х = –1.

Находим значения функции в точках –4, –1, –1/3 и 1:

Получили, что наибольшее значение функции равно 3.

Ответ: 3

77433. Найдите наименьшее значение функции у = х 3 – х 2 – 40х +3 на отрезке .

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х 2 – 2х – 40 = 0

Получим корни:

Указанному в условии интервалу принадлежит корень х = 4.

Находим значения функции в точках 0 и 4:

Получили, что наименьшее значение функции равно –109.

Ответ: –109

Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).

77437. Найдите наименьшее значение функции у=7+12х–х 3 на отрезке [–2;2].

Подставляем точки от –2 до 2: Посмотреть решение

77434. Найдите наибольшее значение функции у=х 3 + 2х 2 – 4х + 4 на отрезке [–2;0].

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений. . Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.

Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения.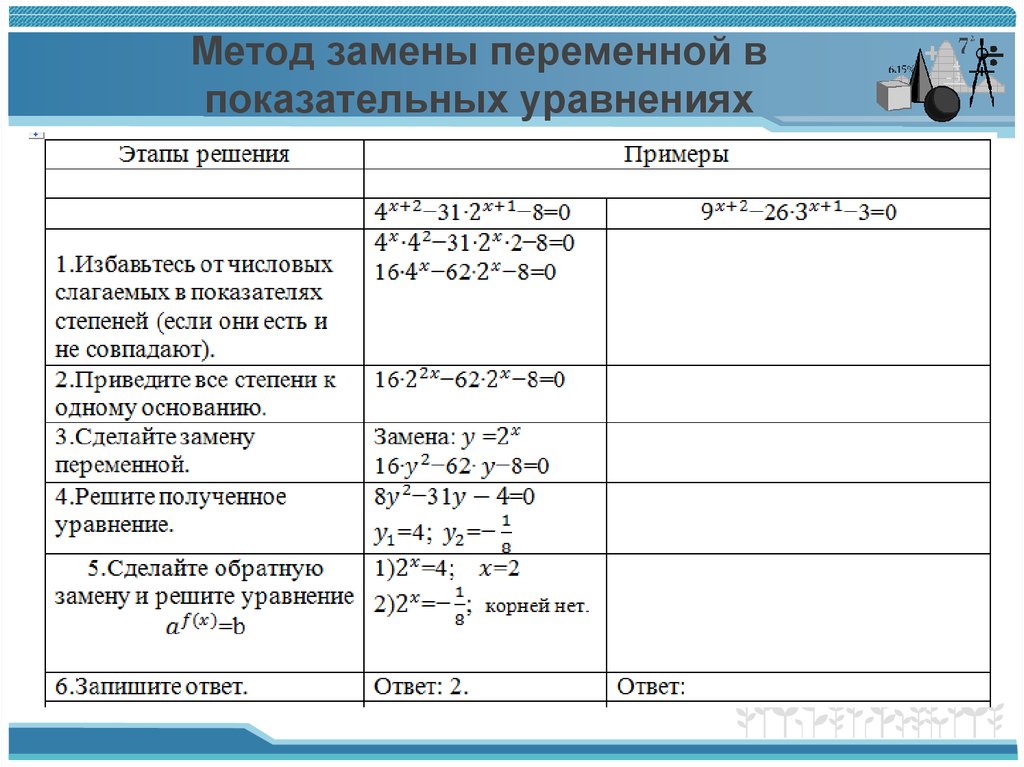 Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

=

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www. сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

Решение показательных уравнений. Примеры.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Что такое показательное уравнение ? Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся в показателях каких-то степеней. И только там! Это важно.

Вот вам примеры показательных уравнений :

3 х ·2 х = 8 х+3

Обратите внимание! В основаниях степеней (внизу) — только числа . В показателях степеней (вверху) — самые разнообразные выражения с иксом. Если, вдруг, в уравнении вылезет икс где-нибудь, кроме показателя, например:

это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Здесь мы будем разбираться с решением показательных уравнений в чистом виде.

Вообще-то, даже чистые показательные уравнения чётко решаются далеко не всегда. Но существуют определённые типы показательных уравнений, которые решать можно и нужно. Вот эти типы мы и рассмотрим.

Решение простейших показательных уравнений.

Для начала решим что-нибудь совсем элементарное. Например:

Даже безо всяких теорий, по простому подбору ясно, что х=2. Больше-то никак, верно!? Никакое другое значение икса не катит. А теперь глянем на запись решения этого хитрого показательного уравнения:

Что мы сделали? Мы, фактически, просто выкинули одинаковые основания (тройки). Совсем выкинули. И, что радует, попали в точку!

Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, эти числа можно убрать и приравнять показатели степеней. Математика позволяет. Остаётся дорешать куда более простое уравнение. Здорово, правда?)

Однако, запомним железно: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов. Скажем, в уравнениях:

2 х +2 х+1 = 2 3 , или

двойки убирать нельзя!

Ну вот, самое главное мы и освоили. Как переходить от злых показательных выражений к более простым уравнениям.

«Вот те раз!» — скажете вы. «Кто ж даст такой примитив на контрольных и экзаменах!?»

Вынужден согласиться. Никто не даст. Но теперь вы знаете, куда надо стремиться при решении замороченных примеров. Надо приводить его к виду, когда слева — справа стоит одно и то же число-основание. Дальше всё будет легче. Собственно, это и есть классика математики. Берём исходный пример и преобразовываем его к нужному нам виду. По правилам математики, разумеется.

Рассмотрим примеры, которые требуют некоторых дополнительных усилий для приведения их к простейшим. Назовём их простыми показательными уравнениями.

Решение простых показательных уравнений. Примеры.

При решении показательных уравнений, главные правила — действия со степенями. Без знаний этих действий ничего не получится.

К действиям со степенями надо добавить личную наблюдательность и смекалку. Нам требуются одинаковые числа-основания? Вот и ищем их в примере в явном или зашифрованном виде.

Посмотрим, как это делается на практике?

Пусть нам дан пример:

2 2х — 8 х+1 = 0

Первый зоркий взгляд — на основания. Они… Они разные! Два и восемь. Но впадать в уныние — рано. Самое время вспомнить, что

Двойка и восьмёрка — родственнички по степени.) Вполне можно записать:

8 х+1 = (2 3) х+1

Если вспомнить формулку из действий со степенями:

(а n) m = a nm ,

то вообще отлично получается:

8 х+1 = (2 3) х+1 = 2 3(х+1)

Исходный пример стал выглядеть вот так:

2 2х — 2 3(х+1) = 0

Переносим 2 3 (х+1) вправо (элементарных действий математики никто не отменял!), получаем:

2 2х = 2 3(х+1)

Вот, практически, и всё. Убираем основания:

Решаем этого монстра и получаем

Это правильный ответ.

В этом примере нас выручило знание степеней двойки. Мы опознали в восьмёрке зашифрованную двойку. Этот приём (шифровка общих оснований под разными числами) — очень популярный приём в показательных уравнениях! Да и в логарифмах тоже. Надо уметь узнавать в числах степени других чисел. Это крайне важно для решения показательных уравнений.

Дело в том, что возвести любое число в любую степень — не проблема. Перемножить, хоть на бумажке, да и всё. Например, возвести 3 в пятую степень сможет каждый. 243 получится, если таблицу умножения знаете.) Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот… Узнавать, какое число в какой степени скрывается за числом 243, или, скажем, 343… Здесь вам никакой калькулятор не поможет.

Степени некоторых чисел надо знать в лицо, да… Потренируемся?

Определить, какими степенями и каких чисел являются числа:

2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.

Ответы (в беспорядке, естественно!):

5 4 ; 2 10 ; 7 3 ; 3 5 ; 2 7 ; 10 2 ; 2 6 ; 3 3 ; 2 3 ; 2 1 ; 3 6 ; 2 9 ; 2 8 ; 6 3 ; 5 3 ; 3 4 ; 2 5 ; 4 4 ; 4 2 ; 2 3 ; 9 3 ; 4 5 ; 8 2 ; 4 3 ; 8 3 .

Если приглядеться, можно увидеть странный факт. Ответов существенно больше, чем заданий! Что ж, так бывает… Например, 2 6 , 4 3 , 8 2 — это всё 64.

Предположим, что вы приняли к сведению информацию о знакомстве с числами.) Напомню ещё, что для решения показательных уравнений применим весь запас математических знаний. В том числе и из младших-средних классов. Вы же не сразу в старшие классы пошли, верно?)

Например, при решении показательных уравнений очень часто помогает вынесение общего множителя за скобки (привет 7 классу!). Смотрим примерчик:

3 2х+4 -11·9 х = 210

И вновь, первый взгляд — на основания! Основания у степеней разные… Тройка и девятка. А нам хочется, чтобы были — одинаковые. Что ж, в этом случае желание вполне исполнимое!) Потому, что:

9 х = (3 2) х = 3 2х

По тем же правилам действий со степенями:

3 2х+4 = 3 2х ·3 4

Вот и отлично, можно записать:

3 2х ·3 4 — 11·3 2х = 210

Мы привели пример к одинаковым основаниям. И что дальше!? Тройки-то нельзя выкидывать… Тупик?

Вовсе нет. Запоминаем самое универсальное и мощное правило решения всех математических заданий:

Не знаешь, что нужно — делай, что можно!

Глядишь, всё и образуется).

Что в этом показательном уравнении можно сделать? Да в левой части прямо просится вынесение за скобки! Общий множитель 3 2х явно намекает на это. Попробуем, а дальше видно будет:

3 2х (3 4 — 11) = 210

3 4 — 11 = 81 — 11 = 70

Пример становится всё лучше и лучше!

Вспоминаем, что для ликвидации оснований нам необходима чистая степень, безо всяких коэффициентов. Нам число 70 мешает. Вот и делим обе части уравнения на 70, получаем:

Оп-па! Всё и наладилось!

Это окончательный ответ.

Случается, однако, что выруливание на одинаковые основания получается, а вот их ликвидация — никак. Такое бывает в показательных уравнениях другого типа. Освоим этот тип.

Замена переменной в решении показательных уравнений.

Примеры.

Решим уравнение:

4 х — 3·2 х +2 = 0

Сначала — как обычно. Переходим к одному основанию. К двойке.

4 х = (2 2) х = 2 2х

Получаем уравнение:

2 2х — 3·2 х +2 = 0

А вот тут и зависнем. Предыдущие приёмы не сработают, как ни крутись. Придётся доставать из арсенала ещё один могучий и универсальный способ. Называется он замена переменной.

Суть способа проста до удивления. Вместо одного сложного значка (в нашем случае — 2 х) пишем другой, попроще (например — t). Такая, казалось бы, бессмысленная замена приводит к потрясным результатам!) Просто всё становится ясным и понятным!

Итак, пусть

Тогда 2 2х = 2 х2 = (2 х) 2 = t 2

Заменяем в нашем уравнении все степени с иксами на t:

Ну что, осеняет?) Квадратные уравнения не забыли ещё? Решаем через дискриминант, получаем:

Тут, главное, не останавливаться, как бывает… Это ещё не ответ, нам икс нужен, а не t. Возвращаемся к иксам, т.е. делаем обратную замену. Сначала для t 1:

Стало быть,

Один корень нашли. Ищем второй, из t 2:

Гм… Слева 2 х, справа 1… Неувязочка? Да вовсе нет! Достаточно вспомнить (из действий со степенями, да…), что единичка — это любое число в нулевой степени. Любое. Какое надо, такое и поставим. Нам нужна двойка. Значит:

Вот теперь всё. Получили 2 корня:

Это ответ.

При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:

Из семёрки двойка через простую степень не получается. Не родственники они… Как тут быть? Кто-то, может и растеряется… А вот человек, который прочитал на этом сайте тему «Что такое логарифм?» , только скупо улыбнётся и запишет твёрдой рукой совершенно верный ответ:

Такого ответа в заданиях «В» на ЕГЭ быть не может. Там конкретное число требуется. А вот в заданиях «С» — запросто.

В этом уроке приведены примеры решения самых распространённых показательных уравнений. Выделим основное.

Практические советы:

1.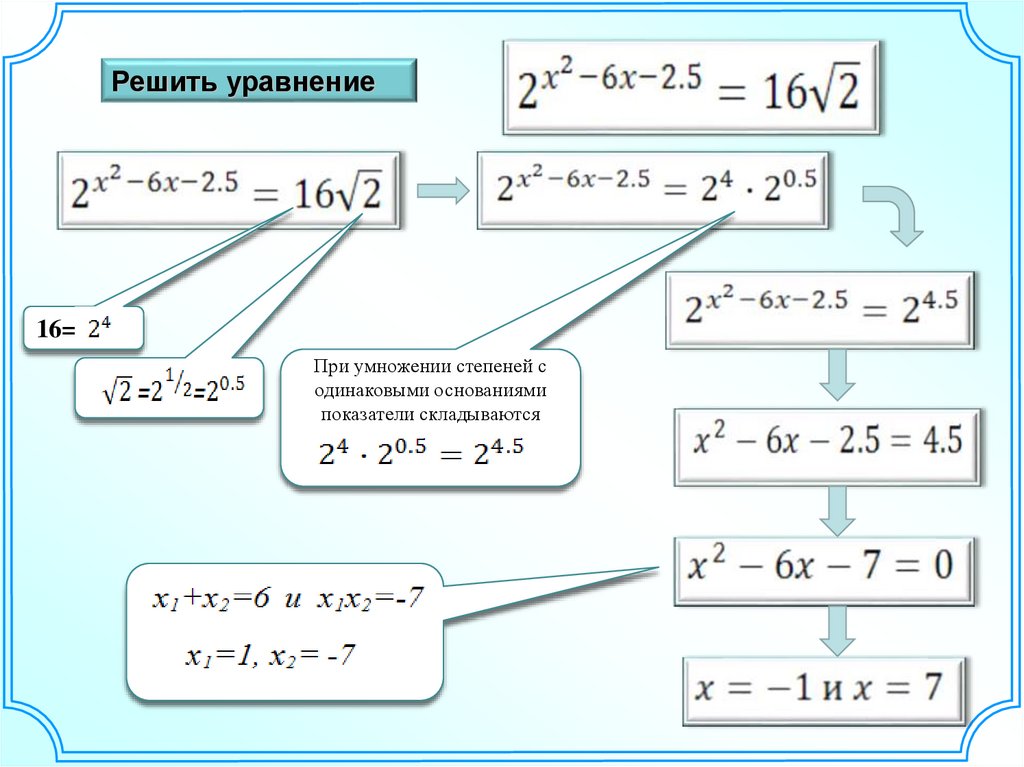 Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!

2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах — считаем.

3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего — квадратное. Или дробное, которое тоже сводится к квадратному.

4. Для успешного решения показательных уравнений надо степени некоторых чисел знать «в лицо».

Как обычно, в конце урока вам предлагается немного порешать.) Самостоятельно. От простого — к сложному.

Решить показательные уравнения:

Посложнее:

2 х+3 — 2 х+2 — 2 х = 48

9 х — 8·3 х = 9

2 х — 2 0,5х+1 — 8 = 0

Найти произведение корней:

2 3-х + 2 х = 9

Получилось?

Ну, тогда сложнейший пример (решается, правда, в уме. ..):

7 0.13х + 13 0,7х+1 + 2 0,5х+1 = -3

Что, уже интереснее? Тогда вот вам злой пример. Вполне тянет на повышенную трудность. Намекну, что в этом примере спасает смекалка и самое универсальное правило решения всех математических заданий.)

2 5х-1 · 3 3х-1 · 5 2х-1 = 720 х

Пример попроще, для отдыха):

9·2 х — 4·3 х = 0

И на десерт. Найти сумму корней уравнения:

х·3 х — 9х + 7·3 х — 63 = 0

Да-да! Это уравнение смешанного типа! Которые мы в этом уроке не рассматривали. А что их рассматривать, их решать надо!) Этого урока вполне достаточно для решения уравнения. Ну и, смекалка нужна… И да поможет вам седьмой класс (это подсказка!).

Ответы (в беспорядке, через точку с запятой):

1; 2; 3; 4; решений нет; 2; -2; -5; 4; 0.

Всё удачно? Отлично.

Есть проблемы? Не вопрос! В Особом разделе 555 все эти показательные уравнения решаются с подробными объяснениями. Что, зачем, и почему. Ну и, конечно, там имеется дополнительная ценная информация по работе со всякими показательными уравнениями. Не только с этими.)

Последний забавный вопрос на соображение. В этом уроке мы работали с показательными уравнениями. Почему я здесь ни слова не сказал про ОДЗ? В уравнениях — это очень важная штука, между прочим…

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.

Показательные уравнения — алгоритмы и примеры вычисления

Показательные уравнения, как и любые другие, требуют поиска неизвестной переменной. Особенность в том, что она или выражение с ней находится в показателе степени.

Содержание

• Основные понятия и свойства
• Примеры решения показательных уравнений
  • Задание 1
  • Задание 2
  • Задание 3
  • Задание 4
  • Задание 5
  • Задание 6

Основные понятия и свойства

В показательных уравнениях, которые часто называют степенными, в основании находятся исключительно числа. Переменная же есть только в показателе. 

Она может быть одна или являться частью выражения. Если она появляется в другом месте, приходится иметь дело с уравнениями смешанного типа.

Школьники знакомятся с простыми вычислениями уже в 7 классе, более сложные решают выпускники и студенты вузов. Если фигурирует несколько переменных и представлено больше одного уравнения, говорят об их системе. 

Тогда необходимо выразить одну неизвестную через другую и искать результат методом подстановки. Поэтому умение находить значения, в которые возводят натуральные числа, пригодится на долгие годы.

Изучаются также и показательные функции: она может быть восходящей и нисходящей, в зависимости от значения переменной или выражения.

Два типа:

При этом:

• 2 – основание, оно должно соответствовать двум условиям, а именно: быть больше нуля и отличаться от единицы;

• х – показатель.

Если вместо знака «=» используются обозначения «>», «<», «≥», «≤», говорят о показательных неравенствах. Остальные условия остаются неизменными.

Для решения необходимо опираться на следующие свойства и правила:

1. Любое положительное число, возведенное в степень, равную единице, равно самому себе, то есть 9¹ = 9. Если же возвести число в степень ноль, то результат всегда будет одинаковым, а именно, равным единице: 9⁰ = 1.

2. Если математическое выражение возводится в отрицательное значение, то его можно заменить дробью, где числитель – единица, а знаменатель первоначальное выражение, но уже в положительной степени. Числитель – значение, находящееся над чертой, знаменатель – под ней. Математически правило записывается в следующем виде: 

.

3. Чтобы возвести число в степень, нужно умножить его на себя такое количество раз, которое равно ее значению, то есть р⁵ = р·р·р·р·р.

4. Если нужно умножить два положительных числа, отличных от единицы и равных между собой, то нужно сложить их показатели и возвести в полученное значение основание: p⁵·p³= p⁵⁺³ = p⁸.

5. Когда требуется разделить одно число на другое, имеющие отличные показатели, нужно вычесть из одного другой и возвести в полученное значение неизменное основание: p⁹/p³= p^9-3 = p⁶.

6. Если необходимо возвести одну степень в другую, то нужно их перемножить. Само основание при этом остается без изменений. Его нужно возвести в полученное после арифметических действий значение: (p³)⁴ = p^3*4 = p¹².

Применение свойств и правил помогает упростить выражения, быстрее произвести вычисления и получить результат.

Примеры решения показательных уравнений

Закрепить материал помогут подробные объяснения при решении показательных уравнений. Разъяснения на практике помогут изучить сложные моменты и облегчат усвоение знаний.

Задание 1

Упростить и решить уравнение: 5^3x+14 = 5^7+2x

В обеих частях примера одинаковые основания, значит, можно приравнять математические выражения, находящиеся в показателе. В результате получится:

3х + 14 = 7 + 2х.

Путем переноса чисел в одну часть, а переменных в другую, не сложно решить пример. Главное, не забывать менять знак на противоположный, плюс на минус и наоборот:

3х – 2х = 7 – 14,

х = -7.

Ответ: -7.

Задание 2

Выполнить вычисление и найти х:

4^x+1 = 16,

4^x+1 = 4².

Основания обеих частей примера – 4, оно не меняется, следовательно, можно воспользоваться изученными свойствами и получить простейшее уравнение:

х + 1 = 2;

х = 2 — 1 = 1.

Ответ: 1.

Задание 3

Упростить и найти значение х:

Дроби в примере разные. Поэтому приравнять их показатели сразу не получится. Но стоит обратить внимание, что числитель одной равен знаменателю другой и наоборот. 

Чтобы решить, придется вспомнить о правиле возведения в отрицательную степень, когда выражение представляется в виде дроби. Значит, числитель можно поменять местами со знаменателем. 

В показателе при этом появится знак «минус»:

При равных основаниях приравниваются степени: -х = 2х + 3.

Далее придется выполнить простое задание, чтобы найти неизвестную переменную:

3х = -3;

х = -1

Ответ: -1. 

Задание 4

Вычислить: (3^x)² = 81.

Можно представить в следующем виде: (3^x)² = 3⁴.

Если воспользоваться изученными свойствами, получается: 3^2x = 3⁴.

Далее выполнить простые действия, чтобы получить результат:

2х = 4;

х = = 2;

Ответ: 2.

Задание 5

Решить уравнение: 5^x+1 + 7·5^x-2= 132.

Если воспользоваться свойством степеней, применяемых для умножения значений с одинаковым основанием, можно преобразовать уравнение. Общий множитель прежде всего нужно поставить за скобки, это правило регулярно применяется при решении:

5^x-2(5³ + 7) = 132;

5^x-2 * 132 = 132.

Если обе части уравнения разделить или умножить на одно и то же число, результат не изменится. В данном случае необходимо разделить на число 132. Это помогает избавиться от громоздких вычислений, удлиняющих ход решения:

5^x-2 = 1.

Далее необходимо вспомнить, что любое значение, возведенное в ноль, равно единице:

5^x-2 = 5⁰

Остается только приравнять показатели и решить элементарный пример:

х — 2 = 0,

х = 2.

Ответ: 2. 

Задание 6

Решить показательное уравнение √4^x = 16.

Квадратный корень можно заменить степенью 1/2. Получается, что 4 имеет показатель x/2.

Значит, уравнение преобразуются в следующее:

4^x/2 = 4².

А дальше необходимо действовать по уже проверенному и закрепленному методу:

x/2 = 2, x = 4.

Ответ: 4.

Чтобы быстро решать показательные уравнения, нужно знать свойства степеней и умело ими пользоваться на практике. Это позволит легко находить неизвестные переменные. Полученные знания обязательно пригодятся для вычисления более сложных задач.

Существуют онлайн калькуляторы, позволяющие легко и просто решить степенные уравнения. Требуется просто вписать их в ячейку и немного подождать, пока машина справится с подсчетами. Но гораздо интереснее самому произвести арифметические действия и получить верный результат. 

Интернет не всегда есть под рукой, а подобные примеры – основа решения более трудных задач, которые могут встретиться на экзамене ЕГЭ по математике. Например, логарифмических. Они могут содержать тригонометрические элементы и объемные алгебраические конструкции.

Предыдущая

МатематикаДеление на двузначное число — способы и примеры решений

Следующая

МатематикаПреобразование тригонометрических выражений — формулы и примеры вычислений

X2 0 решение. Калькулятор онлайн.Решение показательных уравнений

Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. Вы можете получить как общее решение уравнения, так и частное для указанных вами числовых значений коэффициентов. Для решения алгебраического уравнения на сайте достаточно корректно заполнить всего два поля: левую и правую части заданного уравнения. У алгебраических уравнений с переменными коэффициентами бесконечное количество решений, и задав определенные условия, из множества решений выбираются частные. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www. сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. n} \)

7) a n > 1, если a > 1, n > 0

8) a n 1, n
9) a n > a m , если 0

В практике часто используются функции вида y = a x , где a — заданное положительное число, x — переменная. Такие функции называют показательными . Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \(a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \(a \neq 1\), не имеет корней, если \(b \leq 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \(a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \(a \neq 1\) равны тогда и только тогда, когда равны их показатели. {x-2} = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \(3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1. Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Пример №1:

Решим методом подстановки

Решение системы уравнений методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y. Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Пример №2:

Решим методом почленного сложения (вычитания).

Решение системы уравнений методом сложения

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2

5y=32 | :5
y=6,4

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.

Как решать уравнения?

В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.

Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.

4. Все остальные.)

Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.

Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.

И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы.

Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.

Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?)

Тождественные преобразования уравнений.

В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.

Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.

Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.

Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.

Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.

Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:

Дело знакомое, переносим двойку вправо, и получаем:

На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:

х+2 — 2 = 3 — 2

Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….

Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа

Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.

Вот и всё.

Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)

Примеры тождественных преобразований уравнений. Основные проблемы.

Начнём с первого тождественного преобразования. Перенос влево-вправо.

Пример для младшеньких.)

Допустим, надо решить вот такое уравнение:

3-2х=5-3х

Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования. ) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:

3-2х+3х=5

Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:

-2х+3х=5-3

Остались сущие пустяки. Слева — привести подобные, справа — посчитать. Сразу получается ответ:

В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)

Пример для старшеньких.)

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Решение показательных уравнений через преобразования

Продолжаем разговор про решение показательных уравнений. Среди методов решения показательных уравнений есть метод решения уравнений через преобразования. При решении показательных уравнений этим методом используются практически все известные преобразования уравнений. Среди них можно выделить преобразования, характерные именно для показательных уравнений. С этого мы и начнем эту статью – составим список характерных преобразований показательных уравнений и приведем простейшие примеры их проведения. Дальше укажем основные направления проведения преобразований, которых следует придерживаться при решении показательных уравнений через преобразования, и рассмотрим несколько примеров с решениями.

Список характерных преобразований

Замена числа степенью

Преобразование, заключающееся в замене числа степенью, в основном используется для приведения показательного уравнения a^f(x)=b, a>0, a≠1, b>0 к виду a^f(x)=a^c, c – некоторое число, с целью дальнейшего его решения, например, методом уравнивания показателей. Приведем пример. Показательное уравнение 2^x=8 путем замены числа 8 степенью 2³ преобразовывается в уравнение 2^x=2³, что дает возможность уравнять показатели и получить решение x=3.

Здесь стоит особо подчеркнуть два частных случая:

• Число 1 всегда можно заменить нулевой степенью любого положительного числа, ведь a⁰=1 для любого a>0. Например, это преобразование позволяет осуществить переход от показательного уравнения 5^x−3=1 к уравнению 5^x−3=5⁰, что в дальнейшем позволяет уравнять показатели и получить решение.
• Любое положительное число a можно рассматривать как первую степень числа a, так как a=a¹. Например, показательное уравнение 2^x2−2·x=2 можно рассматривать как уравнение 2^x2−2·x=2¹, что полезно в плане его решения методом уравнивания показателей.

К началу страницы

Преобразования на базе свойств степеней

Очень характерными для показательных уравнений являются преобразования, базирующиеся на свойствах степеней. Давайте рассмотрим их.

Преобразование на базе свойств умножения и деления степеней с одинаковыми основаниями

Этим свойствам соответствуют равенства a^p·a^q=a^p+q и a^p:a^q=a^p−q, a, p и q – действительные числа, причем a>0. Первое равенство позволяет заменять произведения степеней с одинаковыми основаниями одной единственной степенью с суммой в показателе и обратно. На базе второго равенства можно частные степеней заменять одной степенью с разностью в показателе и наоборот. Рассмотрим это на примерах преобразования показательных уравнений.

Для примера возьмем показательное уравнение 2^x+1·2^x·2^x−5=2². В его левой части, очевидно, находится произведение степеней с одинаковыми основаниями, которое в силу свойства умножения степеней с одинаковыми основаниями можно заменить степенью 2^x+1+x+x−5. То есть, мы можем преобразовать показательное уравнение 2^x+1·2^x·2^x−5=2² к виду 2^x+1+x+x−5=2², который удобен для дальнейшего решения.

Теперь рассмотрим уравнение . Можно выполнить преобразование этого показательного уравнения, основываясь на свойстве деления степеней с одинаковыми основаниями. Указанное свойство позволяет заменить частное в левой части уравнения степенью 5^{2·x−1−(x−3)}. В результате проведения такого преобразования получается уравнение 5^{2·x−1−(x−3)}=5, которое легко решается через уравнивание показателей.

Наконец, возьмем показательное уравнение 2^x+1+5·2^x−2=13. Для его преобразования равенства a^p·a^q=a^p+q и a^p:a^q=a^p−q используются справа налево: . Дальше полученное уравнение легко преобразовывается в уравнение 2^x=2², решение которого тривиально.

Преобразования на базе свойств степени произведения и частного

Указанным свойствам отвечают равенства (a·b)^p=a^p·b^p и (a:b)^p=a^p:b^p, где a, p и q – действительные числа, причем a>0, b>0. Первое свойство позволяет заменять степень произведения произведением степеней и обратно, второе – степень частного частным степеней и обратно. Покажем, как преобразования, базирующиеся на этих свойствах степеней, используются при решении показательных уравнений.

Рассмотрим показательное уравнение 5·2^x−(2·5)^x=0. В данном случае мы имеем право провести преобразование, заключающееся в замене степени произведения (2·5)^x произведением степеней 2^x·5^x. Выполнив его, мы придем к уравнению 5·2^x−2^x·5^x=0, которое после вынесения за скобки общего множителя 2^x может быть решено методом разложения на множители.

Вот пример использования свойства степени произведения в обратную сторону: 2^x·3^x=6⁻², (2·3)^x=6⁻² и дальше 6^x=6⁻², x=−2.

Аналогично проводится решение показательных уравнений через преобразования, базирующиеся на свойстве степени частного. Например, это преобразование позволяет перейти от показательного уравнения к уравнению , после чего вынести общий множитель 2^x за скобки и решить уравнение методом разложения на множители. А показательное уравнение следует преобразовать к виду и дальше 6^x=6⁻², x=−2.

Преобразование на базе свойства степени в степени

Свойству степени в степени отвечает равенство (a^p)^q=a^p·q, где a, p и q – действительные числа, причем a>0. Покажем, как это свойство используется для преобразования показательных уравнений.

Обратимся к уравнению . В силу свойства степени в степени данное показательное уравнение можно преобразовать к виду 2^{2·3·(x−2)}=2^{(−1)·(1−x)}, что позволяет провести дальнейшее решение через уравнивание показателей.

Равенство (a^p)^q=a^p·q для преобразования показательных уравнений может применяться и справа налево. Например, преобразование показательного уравнения 3^2·x−4·3^x+3=0 к виду (3^x)²−4·3^x+3=0 позволяет вести дальнейшее решение методом введения новой переменной.

К началу страницы

Использование определения степени с отрицательным показателем

Из определения степени с отрицательным показателем следует, что , a>0. Этот результат при необходимости используется для преобразования показательных уравнений. Рассмотрим пример.

Возьмем показательное уравнение . Видно, что в его записи содержатся две степени, основания этих степеней одинаковые, а показатели отличаются знаком. В этой ситуации опора на определение степени с отрицательным показателем позволяет заменить выражение степенью 2^x2−4·x. Такое преобразование приводит исходное показательное уравнение к более простому в плане решения уравнению , в котором степени уже одинаковые. Дальнейшее решение не вызывает вопросов: , , , x²−4·x=5, x²−4·x−5=0, последнее квадратное уравнение имеет два корня −1 и 5. Они составляют решение исходного показательного уравнения.

К началу страницы

Замена корней степенями

Определение степени с дробным показателем дает нам соотношение , a≥0 (в частности, ), связывающее корень со степенью. Оно дает возможность преобразовывать показательные уравнения, осуществляя замену корней степенями. Это касается как числовых выражений с корнями, так и выражений с переменными. Покажем это на примерах.

Решение показательного уравнения требует преобразования числового выражения с корнем в степень . В результате проведения такого преобразования получается показательное уравнение , решение которого находится, например, через уравнивание показателей.

Аналогично проводится преобразование показательных уравнений, в которых под знаками радикалов находятся выражения с переменными. Так с опорой на равенство мы можем преобразовать показательное уравнение к виду . Ну а дальше напрашивается преобразование по свойству степени в степени, которое мы разбирали чуть выше.

К началу страницы

Деление обеих частей уравнения на одну и ту же степень

Решение уравнений в некоторых случаях проводится с использованием преобразования, заключающегося в делении обеих частей уравнения на одно и то же выражение. Деление обеих частей уравнения на одно и то же выражение используется и при решении показательных уравнений. В частности, ряд показательных уравнений решается через деление обеих частей уравнения на одну и ту же степень или произведение степеней. Известно, что деление обеих частей уравнения на одно и то же выражение является равносильным, если выражение, на которое производится деление, не обращается в нуль. Так как степень a^f(x) не обращается в нуль ни при каких значениях переменной, то деление обеих частей уравнения на одну и ту же степень или на произведение степеней является равносильным преобразованием уравнения. Рассмотрим примеры проведения указанного преобразования при решении показательных уравнений.

В основном через деление обеих частей уравнения на одну и ту же степень решаются показательные уравнения, однородные относительно каких-либо степеней (см. однородные уравнения). Например, — однородное показательное уравнение первой степени относительно степеней 3^x и 5^x. Его решение требует деления на любую из этих степеней. Так деление на 5^x дает равносильное показательное уравнение , решение которого легко находится через ряд следующих преобразований:

Показательное уравнение является однородным уравнением второй степени относительно степеней и . Его решение можно провести через деление обеих частей уравнения на степень или . Покажем его полное решение.

Пример

Решите уравнение

Смотреть решение

Деление обеих частей уравнения на одну и ту же степень позволяет решать не только однородные показательные уравнения. Например, через деление на степень 13^3·x+1 можно решить показательное уравнение 13^5·x−1·17^2·x−2=13^3·x+1.

А вот пример решения показательного уравнения через деление его обеих частей на произведение трех степеней, находящееся в правой части:

К началу страницы

Разложение чисел на простые множители

Довольно характерным преобразованием показательных уравнений является преобразование, состоящее в разложении чисел на простые множители. После него, как правило, следует преобразование, базирующееся на свойстве степени произведения. Проиллюстрируем сказанное примерами.

Допустим, нам потребовалось решить показательное уравнение 5·2^x−10^x=0. Решение можно начинать с разложения составного числа 10 на простые множители 2 и 5, то есть, переходить к уравнению 5·2^x−(2·5)^x=0

. Теперь следует применить свойство степени произведения: 5·2^x−2^x·5^x=0. Остается вынести за скобки общий множитель 2^x и решить полученное показательное уравнение методом разложения на множители.

Вот другое характерное показательное уравнение , решение которого связано с проведение преобразования, заключающегося в разложении числа на простые множители. Разложим число 504 на простые множители:

Значит, 504=2³·3²·7. Полученное разложение позволяет от исходного показательного уравнения перейти к уравнению , и дальше по свойству степени произведения — к уравнению , что то же самое . Полученное уравнение решается через деление его обеих частей на выражение, находящееся в правой части. Это уравнение мы решили в конце предыдущего пункта.

К началу страницы

Преобразование показательных уравнений с сопряженными выражениями

Стоит отдельно выделить группу показательных уравнений, в которых основаниями степеней с одинаковыми показателями являются сопряженные выражения. Вот пример показательного уравнения , которое является типичным представителем этой группы. Для решения подобных уравнений обычно находятся произведения степеней с сопряженными выражениями в основаниях, и полученные соотношения используются для преобразования уравнений. Например, в нашем случае

То есть, . Полученное равенство позволяет преобразовать исходное уравнение к виду . После этого остается провести деление обеих частей уравнения на степень (это преобразование мы разбирали выше), что дает очень простое равносильное уравнение 27=3^x−2.

Аналогично решается показательное уравнение . Оно в силу равенства может быть преобразовано к виду , и решено методом введения новой переменной. Вот его подробное решение.

К началу страницы

Выделение целой части из рациональной дроби

Выделение целой части из рациональной дроби сложно назвать часто используемым преобразованием по отношению к показательным уравнениям и уж тем более типичным и характерным. Но оно бывает полезно при решении показательных уравнений. Так что воспользуемся случаем лишний раз напомнить про него.

Например, выделение целых частей из рациональных дробей в показательном уравнении позволяет ввести новую переменную. Действительно, и , что позволяет преобразовать исходное показательное уравнение в уравнение , и дальше по свойствам степеней . Остается принять или и довести решение до конца.

К началу страницы

Направления проведения преобразований.

Примеры.

Выше мы рассмотрели самые основные и характерные преобразования показательных уравнений по отдельности, а также разобрали примеры их проведения. Но на практике при решении показательных уравнений обычно приходится проводить не одно какое-то преобразование, а серию последовательных преобразований. Естественно, при этом необходимо четко понимать, для чего проводится то или иное преобразование. Сейчас мы обозначим основные направления проведения преобразований, которых следует придерживаться при решении показательных уравнений.

Можно выделить три основных направления проведения преобразований показательных уравненийM:

• К одинаковым степеням.
• К одинаковым основаниям степеней.
• К одинаковым показателям степеней.

Придерживаясь указанных направлений, следует от исходного показательного уравнения продвигаться к уравнениям, для которых известен метод решения, то есть, к уравнениям a^f(x)=b, a^f(x)=a^c, a^f(x)=a^g(x), f(g(x))=0, f₁(g(x))=f₂(g(x)), f₁(x)·f₂(x)·…·f_n(x)=0 и др. Давайте разбираться с этим на конкретных примерах.

К одинаковым степеням

Стремление к одинаковым степеням, то есть, к степеням с одинаковыми основаниями и одинаковыми показателями, при решении показательных уравнений легко объяснимо – после получения одинаковых степеней появляется возможность привести уравнение к удобному для дальнейшего решения виду, ввести новую переменную или каким-либо другим способом продвинуться в решении. Приведем примеры.

Возьмем показательное уравнение 3^x+2+3^x+1+3^x=39. Очевидна возможность получить одинаковые степени 3^x. Реализовать ее позволяет свойство умножения степеней с одинаковыми основаниями. Это свойство позволяет преобразовать исходное показательное уравнение в уравнение 3^x·3²+3^x·3¹+3^x=39 с одинаковыми степенями 3^x. Дальше степень 3^x выносится за скобки как общий множитель, и уравнение приводится к простейшему показательному уравнению 3^x=3 с очевидным решением x=1.

Рассмотрим еще один пример. В показательном уравнении 49·7^2·x−50·7^x+1=0 тоже несложно получить одинаковые степени 7^x. Достичь этого позволяет опора на свойство степени в степени. По свойству степени в степени мы можем заменить 7^2·x выражением (7^x)², то есть, перейти к уравнению 49·(7^x)²−50·7^x+1=0. Это открывает путь к решению показательного уравнения через введение новой переменной 7^x=t.

К одинаковым основаниям

Когда нет возможности получить одинаковые степени или такая возможность не очевидна, то можно довольствоваться получением одинаковых оснований. Это тоже бывает полезно при решении показательных уравнений. Проиллюстрируем сказанное примерами.

Несложно заметить, что выражения, отвечающие частям показательного уравнения , можно преобразовать в степени с основаниями 3. Это позволяют сделать свойства степеней и связь между корнями и степенями с дробными показателями. Действительно, так как и , то исходное показательное уравнение можно преобразовать в уравнение , которое легко решается, например, методом уравнивания показателей.

Переход к одинаковым основаниям позволяет уменьшать количество степеней с разными основаниями, что часто неплохо продвигает в решении показательных уравнений. Например, в показательном уравнении (10^x)²+9·20^x−10·(2^x)²=0 три степени и у всех этих степеней различные основания. Представление степени 20^x в виде 10^x·2^x позволяет преобразовать исходное уравнение к виду (10^x)²+9·10^x·2^x−10·(2^x)²=0. При этом уменьшается количество степеней с различными основаниями с трех до двух, и получается показательное уравнение, однородное относительно степеней 10^x и 2^x, а для таких уравнений есть стандартный метод решения.

Аналогично, в показательном уравнении представление степени 504^x−2 в виде 504^x−2=2^3·x−6·3^2·x−4·7^x−2 уменьшает количество степеней с разными основаниями, и открывает дорогу к дальнейшему решению через деление обеих частей уравнения на 2^3·x−6·3^2·x−4·7^x−2.

К одинаковым показателям

Если нет возможности вести преобразования в сторону получения одинаковых степеней или хотя бы одинаковых оснований степеней, то стоит рассмотреть возможность продвижения к одинаковым показателям степеней. Это тоже может быть полезно в плане решения показательных уравнений. Приведем примеры.

Легко заметить, что показатели степеней в записи показательного уравнения 5^−3−x·13^3+x=1 различаются только знаками. В подобных случаях можно переходить к одинаковым показателям. В нашем случае степень 5^−3−x можно рассматривать как , ведь в силу свойства степени в степени . Это позволяет от исходного уравнения перейти к показательному уравнению , в записи которого степени имеют одинаковые показатели, что в свою очередь позволяет с опорой на свойство степени произведения перейти к простейшему показательному уравнению , и получить искомое решение.

Давайте разберем еще один пример. Возьмем показательное уравнение 2·3^2·x=9·2^x. Здесь можно осуществить переход к степеням с одинаковыми показателями, заменив 3^2·x на 9^x. Это преобразование дает уравнение 2·9^x=9·2^x, которое через деление обеих частей на 2^x приводится к простейшему показательному уравнению . Его решением является x=1.

X4 10×2 25 0 решить

Обновлено: 22.09.2022

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу. Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек.

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Реши уравнение x4−10×2+25=0
============================
x ⁴ -10x ² +25 =0 ;
(x ² -5) ² =0 ;
x² -5 = 0; * * * x² = 5 ⇒ x = ± √5. * * *
(x + √5)(x — √5) =0 ; * * * [ x = — √5 ; x = √5
x₁ = — √5 ;
x₂ = √5 .

ответ : .

Новые вопросы в Алгебра

между какими натуральными числами распаложенны следующие числа : а) корень из 35 в) корень из 5+20Пажалуйста срочно ​

3.Постройте график квадратичной функции у = х2 + 4х + 2 и опишите её свойства

Вы учитесь? Тогда данные сервисы должны вам помочь. Решение уравнений онлайн позволяет быть уверенным в правильности решения вашего уравнения.
В каждом из разделов приведены различные способы для помощи вам. Правила ввода уравнений указаны на соответствующих страницах, внимательно прочитайте их и у вас должно получиться.
Вообще этот калькулятор сделан только как вспомогательный инструмент. Вы должны сами научиться решать уравнения — это пригодится Вам в жизни (поможет по жизни мыслить логически в финансовых, экономических и инженерных вопросах).
Данный сервис позволяет проверить свои решения на правильность.

Разложим квадратные трехчлен в числителе и знаменателе по формуле ax² + bx + c = a(x — x₁)(x — x₂) (где x₁ и x₂ — это корни квадратного трехчлена).

Корень по теореме Виета равен 5.

Значит, x² — 10x + 25 = (х — 5)².

Корни по теореме Виета равны 6 и -2.

Значит, x² — 4x — 12 = (х — 6)(х + 2).

(x — 5)²/(x — 6)(х + 2) ≥ 0.

Числитель всегда больше нуля (квадрат числа всегда положителен), числитель может равняться нулю: х — 5 = 0; х = 5.

Знак неравенства ≥ 0, значит, знаменатель тоже больше (но не равен) нуля.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Читайте также:

  
• Маска от черных точек tony moly
  
• Doom 3 достижения
  
• Отключить пвп нью ворлд
  
• Dlc 15 датчик схема
  
• Верстак умельца conan exiles какой раб

Показательные уравнения — как решать? Примеры, свойства и определение

Определение показательного уравнения

Показательными называются уравнения, в которых переменная находится в показателе степени. Простейшее уравнение такого вида: a^х = b, где a > 0, a ≠ 1 и a^x = a^y.

Для решения даже простейших показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс тему «Свойства степенной функции» — советуем повторить ее перед тем, как читать дальнейший материал.

Показательной функцией называют такую: y = a^x, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже.

Важно знать

Показательная функция не может быть отрицательным числом, т. е. выражение у = a^x при а ≤ 0 корней не имеет.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут решать сложные показательные уравнения.

am · an	am+n
am:an	am-n
(a · b)n	an · bn
(a : b)n	an : bn
(an)m	an · m
a−n

Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.

Методы решения показательных уравнений

Самые короткие и простые показательные уравнения решаются легко при помощи свойств степеней. Например:

4^х = 64.

Требуется найти, в какую степень нужно возвести 4, чтобы получить 64.

4 · 4 · 4 = 64

4³ = 64

4^x = 4³

Х = 3

Но как решать показательные уравнения вот такого вида: ? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2.

Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени.

В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Приведение к одинаковому основанию

Весомую часть уравнений вида а^х = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общее основание.

Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются.

Пример 1

Рассмотрим еще одно показательное уравнение с корнем.

Мы знаем, что 64 и 8 являются степенями 2. Попробуем использовать это, и тогда 64² = 2¹², а 8 = 2³.

Ответ: .

Пример 2

В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую.

(0,5)^х2 · 4^х+1 = 64^-1

Найдем общее основание показательных функций:

0,5 = 1/2 = 2⁻¹

4 = 2²

64 = 2⁶

В результате у нас получается:

(2⁻¹)^х2 · (2²)^х+1 = (2⁶)⁻¹

2^−х2 · 2^2х+2 = 2⁻⁶

2^−х2+2х+2 = 2⁻⁶

−х² + 2х + 2 = −6

х²− 2х − 8 = 0

Ответ: x = −2; 4.

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): a^xb^x = (ab)^x.

Пример

5^2х−4 = 49^2−х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

5^2х−4 = 49^2−х

5^2х−4 = 7^4−2х

5^2х−4 = (1/7)^2х−4

35^2х−4 = 1

2х − 4 = 0

х = 2

Пример 2

2^х−2 = 5^2−х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2^х−2 = 1/5^х−2

Теперь умножим обе части на 5^2−х и придем к уравнению:

2^х−2 × 5^2−х = 1

10^х−2 = 1

10^х−2 = 10⁰

х − 2 = 0

х = 2

Замена переменной

Суть этого способа решения показательных уравнений проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить.

Пример

4^x— 2^x+1— 8 = 0

Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4^х = 2^2х, а 2^х+1 = 2 × 2^х.

2^2х — 2 × 2^х — 8 = 0

Что-то напоминает. 🤔 Если бы из этого выражения можно было волшебным образом убрать 2^х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2^х новой переменной — допустим, y.

Если 2^х = y, y > 0, то получается: у²— 2у — 8 = 0.

У такого уравнения есть два корня: у₁ = 4, у₂ = -2.

Проведем обратную замену: 2^х = 4 (подходит по ограничениям).

х = 2.

Ответ: х = 2.

Пример 2

25^х — 6 × 5^х + 5 = 0

Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5^х = у, y > 0.

у² — 6у + 5 = 0

Корни такого уравнения: 1 и 5.

Выполним обратную замену:

5^х = 1, значит х = 0.

5^х = 5, значит х = 1.

Ответ: x = 0; 1.

Вынесение общего множителя

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить.

Общий множитель — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки, чтобы упростить уравнение.

Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3^х+1 + 3^х — 3^х-2 = 35

Вынесем 3^3-x за скобки и получим:

3^х-2(3³ + 3² — 1) = 35

3^х-2 × 35 = 35

3^х-2 = 1

Поскольку 1 равно любое число в нулевой степени, мы можем записать:

3^х-2 = 3⁰

х — 2 = 0

х = 2

Ответ: х = 2.

Пример 2

5 × 3^-3х+1 + 3^-3х+2 = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3^-3х+2 = 3^-3х+1+1 = 3 · 3^-3х+1.

Теперь у нас есть общий множитель 3^-3х+1, который можно вынести за скобки, чтобы получить более простое уравнение:

3^-3х+1(5+3) = 24

8 · 3^-3х+1 = 24

3^-3х+1 = 3¹

-3х + 1 = 1

х = 0

Ответ: х = 0.

Решатель экспоненциального уравнения

Expression Equation Inequality Contact us Simplify Factor Expand GCF LCM Solve Graph System Решение График Система Математический решатель на вашем сайте Наших пользователей: Поздравляем и благодарим за это замечательное программное обеспечение. Это и сложно, и весело. Г-н Том Кэрол, Нью-Йорк Алгебратор был намного дешевле, чем традиционные репетиторы по алгебре, и позволял мне работать в своем темпе с каждой задачей. Если бы не алгебра, боюсь, я бы провалил урок по алгебре. Ты спасатель! Джефф Кастен, Мичиган Я использовал вашу систему, и она справилась со всеми проблемами, которые не удалось решить с помощью PAT. Я действительно впечатлен удобной для пользователя настройкой и возможностями вашей системы. Спасибо еще раз! Дженнифер, Огайо. Я несколько месяцев искал программу, которая помогла бы мне улучшить свои навыки в алгебре. Моим решением был Алгебратор, и теперь я могу рассказать вам, каково это быть отличником. Б.Ф., Вермонт Алгебратор — идеальный репетитор по алгебре. Он охватывает все, что вам нужно знать об алгебре, в простой и всеобъемлющей форме. Кэндис Мюррей, ИЛИ Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 18 июля 2010 г.: логарифмическая замена однородного дифференциального уравнения второго порядка примеров викторин о геометрии перестановки и комбинации — баскетбольная задача онлайн-викторина по математике KS4 несколько нелинейных уравнений Matlab Математика ks3 бесплатные вопросы Гленко, Техас, Алгебра 1, 2007 г., учебное пособие бесплатных загрузок уроков по математике в процентах онлайн одновременное уравнение формула времени бесплатные печатные тесты способностей планы уроков проценты gcse калькулятор преобразования десятичных знаков в дроби рациональных выражений НАЙТИ ЛЕГКО KS3 Mathematics Pack D: Pearson Publishing Level 6 ответы игры по алгебре для печати графические рабочие листы линейных уравнений алгебра квадратный корень помощь образец вопросника по математике для 11 класса Рабочий лист для пиццы английская сат. бумага ks3 бесплатно калькулятор добавления подкоренных выражений упрощение выражений с квадратными корнями онлайн ks3 sats документы тренировочные тесты dolciani решатель криптографической подстановки онлайн алгебраические суммы Упрощение уравнений рабочих листов для обучения расширению по математике Холт тест главы современной химии Фактор 9 ТИ 84 справочник по алгебре Структура и методическая книга 1 распечатайте практические упражнения извлечение квадратного корня алгебра 1 ответы glencoe понимание математики yr8 pi развернуть( калькулятор онлайн одновременные уравнения линейно-квадратичные Решения вероятностных задач для 9-го класса кс2 уравнения математические мелочи с ответами Бесплатная загрузка GMAT Онлайн-решатель Rational Expressions решатель наивысшего общего множителя «Matrix Intermediate» «Ключ ответов» скачать бесплатно базовые математические записи десятичные дроби бесплатные рабочие листы Калькулятор общего знаменателя Бесплатный рабочий лист по математике для четвертого класса Рабочие листы EQUATION одновременное уравнение решить уравнения с 3 переменными+TI расчет процента наклона и коэффициентов как находить корни многочленов 3-го порядка сложение/вычитание целых чисел как решить уравнения с тремя переменными с помощью графического калькулятора Наибольший общий делитель полиномов рабочий лист Решатель алгебры II неявное дифференцирование + решатель Практические вопросы по математике для 8 класса — площадь поверхности МАТЕМАТИКА Викторины ОБРАЗЦЫ как упростить калькулятор наименьших кратных одночленов Решатель 3 одновременных уравнений помощь с домашним заданием по алгебре тесты по математике 8 год перестановки и комбинации в повседневной жизни бесплатные пошаговые задачи по алгебре Калькулятор доли смеси вычислить НОД бесплатная алгебра 1 решение задач Алгебра Гленко 2 превратить дробь в проценты Тригонометрический вычислитель решатель числовой последовательности объединение рабочих листов и пересечение неравенств математика 11 класс факторизация онлайн Калькулятор сложения и вычитания подкоренных выражений Калькулятор химических уравнений балансировки математические мелочи с решениями и ответами mcdougal littell раздел викторина ответы бесплатный калькулятор решит ваши задачи по алгебре кто изобрел формулу пирога рабочий лист математического перевода Калькулятор радикальных форм бесплатные рабочие листы по математике модуль gcse 1 ti факторинг загрузки программы калькулятор математическое уравнение Калькулятор степени lcm алгебра кс3 Предыдущий Далее

Онлайн-решатель экспоненциального уравнения

алгебра вершинной формы	шага к решению квадратных уравнений с помощью факторизации и использования чисел	калькулятор знаменателя	бесплатное решение задач по алгебре шаг за шагом	упрощение выражений путем объединения рабочих листов похожих терминов
Прентис Холл математика алгебра 1 ответы бесплатно	Калькулятор метода обратной фольги	упростить квадратный корень √125	rudin руководство по раствору	год 10 тест по математике онлайн
Калькулятор коэффициента уравнения	Булева алгебра и математика+приложения Java	сколько стоит пирог?	перестановки и комбинации в статистике	метода решения вопросов о способностях любая электронная книга скачать бесплатно
Глава 7 Прямоугольные треугольники и тригонометрия Макдугал Литтел Миссури Эдишн Геометрия	изучение алгебры 2 выпускной	исследовательская задача по математике	Решатель уравнения балансировки	саксонская математическая алгебра 2
Макдугал Литтел: рабочая тетрадь по всемирной истории ответы	упрощение алгебраических выражений	Рабочий лист по алгебре для третьего класса	Trigo Tutorial Упражнение на сложный угол	листы вращения по математике
куб квадрат на ti 83	учебник алгебры Холта	Калькулятор сложного неравенства	расчет рационального выражения онлайн	МНЕ НУЖНА БЕСПЛАТНАЯ ВЕРСИЯ ДЛЯ ПЕЧАТИ РАБОЧЕЙ ТЕТРАДИ ПО МАТЕМАТИКЕ VII КЛАСС КЕМБРИДЖСКОЙ СИСТЕМЫ ДЛЯ ПРАКТИКИ
Образцы рабочих листов для вступительного теста по алгебре с отличием 2	комплексные числа шаг за шагом в ti 89 ti	бесплатные рабочие листы координатной плоскости	«Бесплатные экзаменационные работы 10 класса»	математика средней школы с блеском! книга c ответы
«Алгебра 1 Хоутон Миффлин» решения	ввод числа по основанию 2 в калькулятор	бесплатные рабочие листы для пиццы онлайн	как подключить кубический корень к калькулятору	решение дифференциального уравнения 2-го порядка (как экспоненциальное At)
Сгенерированный бесплатный рабочий лист, среднее значение, медиана, диапазон мод.	формула наклона квадратичной формулы	решить любую производную	настройка журнала изменений на TI 84	калькулятор неопределенного интеграла шаг за шагом
В чем разница между оценкой и упрощением выражения?	число в степень с переменной пример	как вычитать квадратные корни с помощью калькулятора переменных	решение нескольких уравнений с помощью Excel	«помощь студентам по алгебре»
бесплатных загрузок калькуляторов TI-84	Рабочие листы с уравнениями балансировки	ti 84 plus silver edition и метод алгебраической подстановки	Предварительный тест по алгебре по математике для 6-го класса	фактор трехчленов онлайн
факторинг квадратичный интерактивный	базовая алгебра	формула скорости изменения	калькулятор алгебры без глупостей онлайн	решение дифференциального уравнения второго порядка в Matlab
основные математические уравнения колледжа	математика	помощники по алгебре	Генератор тестов сложения и вычитания уравнений	сложные уравнения
поиск формы вершины из графа	СКАЧАТЬ БЕСПЛАТНО APTITUDE QUESTIONS	бесплатный калькулятор радикал онлайн	алгебра кс2 — уроки	исходный код java, парабола
балансировка математики	ti 89 десятичная дробь	Калькулятор упрощения алгебраических выражений	введите вопросы к математическим задачам и дайте мне ответы	образец вопроса о способностях, ответ
домен радикалов	концептуальная физика ответ 3-й	квадратичные задачи со словами	двучленное уравнение в ecxel	наибольший общий делитель ti-83
алгебраизатор 29,99	комбинации и перестановки печатные формы	решать комплексные числа	решать уравнения с дробями	математический рабочий лист полиномы gcf
порядок рациональных чисел от меньшего к большему	интерактивных уравнения, неравенства и функции для 7 класса	умножение на десятичные числа преобразование измерений	ПОЛИНОМ ДЛЯ РЕШЕНИЯ ДЛИННЫХ ДЕЛЕНИЙ	Вопросы о навыках JAVA
квадратичная формула в MATLAB	квадратный корень из дробей	интерактивных перестановки и комбинации для элементарного	преобразовать в таблицы уравнений	Рабочие листы по математике Отражение Вращение Перевод
бесплатные распечатки по математике для третьего класса	упрощенная радикальная форма	порядок от меньшего к большему	математика ks3 алгебра объяснение и задание	Разделение мономов бесплатные рабочие листы
преобразование смешанных числовых дробей в десятичные	как решать дроби на калькуляторе casio ti-83	ФЛОРИДА ПРЕДАЛГЕБРА КНИГА NLINE	действия по обогащению в умножении и делении целых чисел	Алгебра: Квадратный корень в квадрате.
определить квадратичное соотношение	алгебра 2 книга ответы	решатель области рациональных выражений	фольга 2 шага уравнений	Java-коды для проверки, является ли число простым или составным
учебник по бухгалтерскому учету скачать	упростить sqrt до степени	решение одновременных уравнений в mathcad	рабочий лист по ускорению в средней школе	Функция абсолютного значения уравнения диапазона области графа
история квадратных неравенств	печатных рабочих листа по алгебраическим уравнениям	решатель наименьших общих множителей	математическое стихотворение с математическими терминами для 7 класса	предварительная алгебра для чайников
(бесплатные печатные таблицы функций, пошаговый график)	бесплатное объяснение превращения процентов в десятичные дроби для 6-го класса по математике	печатных листа полиномиальной степени по алгебре	Численный анализ — перестановка и комбинация	рабочий лист квадратного корня бесплатно
предварительная алгебра с пиццей	образец теста gcse по математике	упростить квадратные радикалы	комбинированных рабочих листа и 3-й класс	математические мелочи
решающая алгебра — радикал в радикале	решение систем линейных уравнений с помощью графических рабочих листов	задача по математике для телефонных операторов	примеры задач на деление квадратных уравнений	рудин реальный и комплексный анализ
Рабочий лист операций с целыми числами	упрощение квадратных корней	Математика для 6 класса — руководство для учителя	рабочий лист переменных деления целых чисел	ti-83 plus факториальная программа разложения
Прейскуранты по математике для 3 класса	ответы на домашнее задание по саксонской алгебре 2	ответа в книге Техасская алгебра 1	Предварительные алгебраические уравнения	решение бинома в кубе
переменные и показатели	Научи меня логарифмам	рабочих листов кумон	ode45 matlab пример второго порядка	предварительная алгебра с ключом ответа на пиццу
процедура решения системы уравнений с двумя переменными	Калькуляторы решения распределительных свойств	обычные конверсионные игры	Генератор рабочих листов без вероятностей	решения нелинейных дифференциальных уравнений
вычитание переменных квадратных корней	как настроить калькулятор TI-83 для алгебры колледжа	математические задачки для проверки способностей+умножение	бесплатные практические задачи по алгебре среднего уровня	заполнить квадрат вопросы и ответы
упростить переменные	рабочий лист деления целых чисел	таблица дробей с наименьшими условиями	калькулятор производной +квадратный корень	учить алгебру в 9 классе
простая викторина по алгебре для 8 класса	эмулятор калькулятора ti 84 plus	онлайн заимствование и перенос дробей для 4 класса	Графические линейные уравнения Power Point	бесплатные рабочие листы с параллельными линиями
Сложение и вычитание дробей Рабочий лист 7 класс	решатель таблицы истинности ti 84	Геометрия McDougal Littell/Houghton Mifflin отвечает на радикалы	формула общего знаменателя	деятельность по факторингу решения квадратных уравнений
об алгебраических дробях в ежедневнике	Алгебра 8 класс	Power Points & Houghton & Math	выучить алгебру бесплатно	старый калькулятор алгебры онлайн
КВАДРАТИЧНОЕ УРАВНЕНИЕ	«Шпаргалка по умножению»	База бревна ти-89	как преобразовать целые числа в десятичные	РАБОЧАЯ ТЕТРАДЬ ДЛЯ ПРЕДВАРИТЕЛЬНОЙ АЛГЕБРЫ
Iowa Algebra Aptitude Test Practice	решение переменных дробями	РАБОЧАЯ ТЕТРАДЬ И РУКОВОДСТВО ПО АЛГЕБРЕ 2	как извлекать квадратные корни из дробей	Математика для 4 класса положительные и отрицательные числа
задачи по математике 9 класс алгебра 1	посторонний раствор ti 84	ti 83 плюс образ ПЗУ	Калькулятор квадратного корня переменной	Упрощение логарифмов алгебраических выражений: задачи
помощь по алгебре для учеников холла 2004	Рабочий лист обзора решения уравнений	умножение смешанного рабочего листа	5-9 математический лист Макгроу Хилл ответы	листы сложения и вычитания дробей
онлайн-тест по математике для девятого класса	алгебра для начинающих бесплатно	Основы физики 8-я загрузка	сбалансированные уравнения в математических рабочих листах	Вычитание отрицательных чисел из целых чисел
калькулятор вычитания квадратных корней с переменными	самый сложный математический расчет	очень сложных рабочих листа по алгебре бесплатно	показательная деятельность 4 класс	связь полиномиальной функции и ее абсолютного значения
деление многочленов с показателями	уравнения математические игры	Упростить алгебру	бесплатные распечатанные рабочие листы по математике для 7-го класса	Репетиторство по алгебре 2
Калькулятор факторизации PRIME TI	помогите решить рациональные выражения	Бесплатная печатная таблица наибольшего общего множителя	калькулятор рациональных выражений	как рассчитать с помощью графического калькулятора
учебники по алгебре Холта	метод наименьших квадратов на TI-83	скачать электронную книгу о концепциях и навыках Холта Макдугласа	квадратный корень с подкоренными выражениями	TI-83 находит вершину параболы
прентис, вкл. Обогащение 10-1 возведение прямоугольника в квадрат ответ	саксонские математические бумаги для печати	ответ для учебника по алгебре Гленко 1-й класс	Калькулятор наименьшего общего знаменателя	как зарегистрировать базу 2 ti 89
Факторизация машины квадратичных вычислений	рабочие листы квадратного неравенства	суммы алгебраического выражения	МНОЖЕСТВО КВАДРАТНЫХ КОРНЕЙ	рабочая тетрадь для студентов Prentice Hall
Рабочий лист пропорций	бесплатных математических ответа	как преобразовать смешанное число в десятичное	Рабочий лист матричного уравнения	термин от меньшего к большему
Калькулятор полиномов деления	сочетание сложения, вычитания, умножения и деления дробей	руководство по алгебратору	учебники по математике и ответы онлайн	алегебра средней школы
поиск уравнений онлайн	c тесты на знание языка	деление дробных показателей	логарифм для детей	изменить десятичное число на смешанное
задачи на разность частных	как десятичную дробь смешать	самая сложная математическая задача в мире	Калькулятор дифференциальных уравнений первого порядка	Калькулятор деления уравнений
книги по способностям для бесплатного скачивания	Калькулятор решения рациональных чисел	инструмент поиска общего знаменателя	рабочих листа коэффициента масштабирования	упрощенный логический калькулятор
бухгалтерские бесплатные книги	«преобразование формул» «алгебра»	упростить выражения с показателями путем деления	круговой график EOG вопросы	диапазон и распределение в алгебре
как превратить десятичную дробь в дробь	Тестовая практика по алгебре в Айове	решение экспоненциального дифференциального уравнения второго порядка	калькулятор дробей разные знаменатели	как сделать вход в ти-83
бесплатный рабочий лист по теореме Пифагора для специального образования	онлайн-книга по математике Прентис Холл (техасская алгебра 2)	абстрактная алгебра тупые решения	Калькулятор метода подстановки алгебры	матричные математические задачи исполнитель
простейшая десятичная форма	бесплатная шпаргалка по факторинговым полиномам	как складывать, вычитать и умножать дроби в предварительной алгебре	Алгебра 2 приложения для ti 84	Программа TI-84 plus silver edition для упрощения радикалов
Рабочие листы со свободными пропорциями для 6-го класса	бесплатных загружаемых рабочих листа по предварительной алгебре	алгебраические уравнения трехчленные	самые сложные математические задачи в мире я хочу на них ответить	Решатель алгебры неравенств
по алгебре что означает оценка вопроса	Дроби в порядке от наименьшего до наибольшего	ti 89 решение уравнения с несколькими переменными	Рабочий лист формы пересечения откосов	Фиолетовая математика для задач на перестановки 4-х классов
TI ​​92 plus Загрузка образа ПЗУ	обзор программного обеспечения по алгебре для колледжа	mathcad одновременные дифференциальные уравнения	как делать алгебру	как решить одновременное квадратное уравнение
как складывать дроби	дополнительная алгебра 2 практические задачи с отличием	как научить абсолютное значение	имулятор ti 84	Техасский Прентис Холл Учебное пособие по биологии Ответы
алгебраический решатель cd	формулы элементарной алгебры	Алгебратический калькулятор	Различия шестого и пятого изданий тригонометрии Маккега	упрощенная радикальная таблица
Алгебратор исключения Гаусса	mcdougal littel современная всемирная история ответы из книги	математические стратегии	дробные многошаговые словесные задачи	уравнения свободной балансировки
Макдугал Литтел Алгебра 2 кроссворд	упростить подкоренные выражения	Предварительная алгебра 8-го класса	умножение рациональных выражений, содержащих многочлены	калькулятор предварительной алгебры онлайн
Практика простых задач по алгебре	бесплатное решение задач по алгебре	Гр. 8 площадь круга рабочий лист	Уравнения 3-го порядка	точки построения рисунок
интерактивные игры для lcm	решение пар дифференциальных уравнений	Рабочие листы по математике	алгебра 1 вопросы для начинающих	скачать бесплатно документы ks2
вопросы по математике прямая линейная вариация	Комбинации математики для 6 класса	МАТЕМАТИКА ЧЕТВЕРТАЯ ГЛАВНАЯ КНИГА	вычисление степени корня на графическом калькуляторе	как разложить выражения 7 класс
Домашняя школа 5-го класса, тест на эог, рабочие листы для печати	шагов графического калькулятора	как рассчитать математический коэффициент роста	вводные исследования булевых алгебраических уравнений	математическая ЗАГАДКА С ОТВЕТОМ
дифференциальные уравнения Matlab второго порядка	Рабочий лист группировки вычитания	бесплатный онлайн калькулятор ответов на радикальные уравнения	10 класс алгебра	Формула простых процентов для 6 класса
как упростить корень	как посчитать на калькуляторе	алгебра 1 вопросы для начинающих	Предварительная алгебра с ответами Pizzazz	бесплатный онлайн калькулятор дробей смешанные числа
радикальные представители реальной жизни	как упрощать и делить квадратные корни	задачи с целыми положительными и отрицательными словами	от высшего к низшему по математике	как решить два уравнения с двумя неизвестными с помощью Solve на ti-89
Учебник по геометрии, Скотт, Форман и компания, издание для учителей UCSMP, ответы на главы 8-7	KS3 РАБОЧИЕ ТАБЛИЦЫ ПО МАТЕМАТИКЕ	составить уравнение для каждого графика	предварительная алгебра. . преобразование формул	TI-89 Неалгебраическая переменная
по какой формуле сложить дроби	Онлайн-поиск химических уравнений	Макдугал Литтел ОТВЕТЫ	год 9 целых чисел рабочий лист	математика* gcse печать рабочего листа
ответы по физике, обзор регентов Прентис Холл	калькулятор упрощенных выражений	пифагорейское тождество работало в комплексных числах	Практический лист Iowa Test для девятого класса	выражения квадратного корня
Рабочие листы по математике для 6-го класса с множественным выбором	Алгебраические уравнения, 5 класс, рабочие листы	тестовых вопросов и ответов на банковские способности в формате pdf	бесплатный предварительный тест по алгебре для печати 1	ключ ответа на освоение заданий по физике
Алгебра шлюза 2 модуль #5 видео	Квадратные уравнения могут быть решены путем построения графика, использования квадратной формулы, завершения квадрата и разложения на множители.	mcdougal littell сша история конспекты	квадратное уравнение с тремя переменными	Glencoe Math отвечает на вопросы по алгебре 2
упражнения + «решатель инженерных уравнений»	Промежуточный экзамен по алгебре	Линейные уравнения бесплатные веселые рабочие листы	я хочу сдать онлайн тест по математике, 8 класс	вершинная форма алгебры
ТАБЛИЦА ПРЕОБРАЗОВАНИЯ ШКОЛЬНЫХ ПОКАЗАТЕЛЕЙ ДЛЯ ПЕЧАТИ ДЛЯ ДОМАШНИХ ЗАДАНИЙ	математика для чайников	позволить графическому калькулятору решить задачу уравнения параболы	Рабочий лист одношаговых уравнений	код мастер-листа и перестановка
рабочая тетрадь по биологии ответы	метод алгебраического ящика	математическая задача со словами покажи свою работу	Что такое биологический словарь и рабочие листы бесплатно	вычисление знаменателя
правила построения графиков линейных уравнений	руководство по решениям современной абстрактной алгебры	Решение трехчленов	Алгебра среднего уровня для чайников	Иллинойс PSAE алгебра 1 рабочий лист ответы
свободное занятие делением и умножением дробей	сложение вычитание умножение целых чисел	Рабочий лист умножения деления дробей	рабочий лист деления десятичных дробей	сложение и вычитание квадратных корней
Калькулятор умножения переменных	линейные уравнения с десятичными знаками	онлайн-практика по математике, контрольные работы ks2	скачать Glencoe Math Books	glencoe/mcGraw-Hill Advanced Mathematical Concepts test ответы
смешанное число в процентах	учебные пособия по учету затрат	бесплатно скачать тест на пригодность	алгебраические правила факторинга	практические задания по математике И математика 6-го класса
бесплатный калькулятор для построения графиков линейных уравнений	тетради по алгебре для четвертого класса	заявки на сумму или разность кубов	решение алгебры y перехват	«коэффициент масштабирования» математические координаты
графических точек	решение зависящих от времени дифференциальных уравнений второго порядка	детские математические стихи	десятичная формула для 2/3	2004 г. Учебник по алгебре для учителей Prerentice Hall
бесплатные разминки перед алгеброй	решение алгебраических задач	ти-83 читерство	алгебра с пиццей 163 ответ	большой общий делитель многочленов
вопрос масштабирования по математике	Калькулятор факторизации квадратного уравнения	трудные математические игры для 6-го класса	образец углубленного теста по алгебре	решатель математических задач
Статистика GCSE — планы уроков	решить уравнение 3-го порядка с помощью ode45	Полиномиальный корень 6-й степени	квадратичный калькулятор в биномы	деление моих мономов
картинки полярного уравнения	алгебра с пиццей	Калькулятор наименьших кратных рациональных выражений	пошаговый метод общих кратных	бесплатная алгебра 1 решение задач
Бумага для практики по математике GCSE	ключи ответов на вопросы по навыкам glencoe	бесплатных математических рабочих листа по показателям	Решатель задач линейной алгебры. pdf	формула для x в квадрате плюс tx
умножение дробей с вычитанием переменных	бесплатное средство упрощения уравнений	радикальный десятичный калькулятор онлайн	правила сложения вычитания целых чисел	алгебра 2 трудный лист бесплатно
графические равенства бесплатные рабочие листы	УРАВНЕНИЕ ДЛЯ ВЫЧИСЛЕНИЯ ДИАМАТРА	искатель калькулятор квадратного корня	решатель разности частных	KS2 Рабочие листы с процентами
Prentice hall Книга по концептуальной физике ответы	рабочие листы по геометрии для 3 класса	Тест по математике ks3 бесплатно	БЕСПЛАТНАЯ ТАБЛИЦА АБСОЛЮТНЫХ ЦЕННОСТЕЙ	Рабочие листы по одновременным уравнениям gcse
электронные книги aptitude скачать бесплатно	равновесные значения Дифференциальное уравнение 2-го порядка	книга способностей онлайн	большой общий делитель JavaScript	как рассчитать математические комбинации
легкое решение уравнений	бесплатная практика Sollege алгебра графический подход	значение продукта ,разница. Математические листы с делением суммы	задачи на вычитание	РАБОЧИЙ ТАБЛИЦ УМНОЖЕНИЕ 2-1
Флорида Прентис Холл Математика Алгебра 2	многопараметрический графический калькулятор онлайн	бесплатные разминки по алгебре	перекрестное умножение для решения неравенства	формула для нахождения квадратного корня с помощью алгебры
чтение онлайн практика ЭОГ тест 8 класс	как получить систему уравнений с графиком	рабочий лист по десятичной дроби	как рассчитать вершину линейного уравнения	бесплатный рабочий лист по математике
рабочих листа по поиску медианы	эквивалентные выражения по алгебре, калькулятор	дроби с квадратными корнями	Тест дифференциальных способностей для пятиклассников	Лесник Пол отвечает
Подгонка нелинейного уравнения с несколькими переменными	Учебные листы по математике для 4 класса	алгебра два онлайн репетиторство	MATLAB наибольший общий делитель вектора	как настроить предварительную алгебру 9 класс
решение уравнений дробей на сложение и вычитание	радикалы дроби	решение линейной неоднородной оды	ti-92 решить линейное уравнение	сложение, вычитание, умножение и деление десятичных дробей примеры и рабочие листы
бесплатные решенияинструкции онлайн	Таблица тригонометрических значений дробей	комбинации и перестановки текстовые задачи рабочие листы	+методика обучения элементарной грамматике	Построение графика уравнения
фактор 9программа для ти-84	правила квадратных корней	клен Используйте систему уравнений, чтобы найти квадратичную функцию	радикалы и квадратики	как использовать экспоненты для детей, используя классную математику для детей
вычислить кубический корень ti 83	добавление на двух листах	Программы PRT TI-84	Меррилл учебник физики	триггерные уроки
бесплатных математических листа по вероятности	какая самая сложная математическая задача	Рабочий лист по математике для 9-го класса	детские математические балансирующие уравнения	Теория Пифагора расчетная программа бесплатно dowenloadin
Концептуальная+Физика+ответы 3-е издание	преобразовать уравнение в калькулятор координат	одновременные дифференциальные уравнения	Холт Физика ответы	бесплатно онлайн домашняя работа за 1 год распечатка
эмулятор калькулятора ti-84	планы уроков для первого класса	решение уравнений на сложение и вычитание	Калькулятор графика параболы	2 неизвестных в алгебраическом преобразовании
учебное пособие — основные тригонометрические тождества — glencoe	Двухшаговые задачи с уравнениями для печати	www. gr.tx 1math . ком	Математическое уравнение для преобразования десятичных чисел в дроби	формула для картинок на графическом калькуляторе

Как решать показательные уравнения с переменной в показателе степени. Шаг 1 просто…

Примеры экспоненциальных уравнений 9{\ красный {х+1}} = 512 $$

Как вы могли заметить, экспоненциальное уравнение — это особый тип уравнения. Это уравнение, в котором показатели степени являются $$ \red{ переменными}$$.

шагов для решения

Существуют различные виды показательных уравнений. Мы сосредоточимся на экспоненциальных уравнениях, которые имеют по одному члену в обеих частях. Эти уравнения можно разделить на 2 типа. 99 $$

Шаг 1

Игнорировать основания и просто установить степени равными друг другу

$$ х + 1 = 9 $$

Шаг 2

Решите для переменной

$$ х = 9 — 1 \\ х = \fbox { 8 } $$

Проверять 99 $$

Средство решения экспоненциальных уравнений

Введите любое показательное уравнение в решатель алгебры ниже:

Пример 2

Пример 3

9х $$

Шаг 1

Забудьте на минуту о показателях и сосредоточьтесь на основаниях:
Перепишите основания как степени общего основания. Сделайте это, спросив себя:

Ответ: обе степени числа 2

Шаг 2 9{\ красный 6} $$
$$ 64 = 64 $$

Пример с отрицательным показателем степени

В отличие от оснований часто используются отрицательные или дробные основания, как в примере ниже. Мы будем рассматривать эти задачи так же, как и любое другое показательное уравнение с разными основаниями — путем преобразования оснований, чтобы они были одинаковыми. 9х = 81$$

Шаг 1

Забудьте на минуту о показателях и сосредоточьтесь на основаниях:
Перепишите основания как степени общего основания. Спроси себя :

Вы можете использовать 3 или 9. Я буду использовать 9{2} $$

Шаг 4

Решите как показательное уравнение с одинаковыми основаниями

$$ х = 2 $$ 9{2x} = 64 $$

---

Забудьте на минуту о показателях и сосредоточьтесь на основаниях:
Перепишите основания как степени общего основания. Спроси себя :

Обе степени двойки и четвёрки. Вы можете использовать любое основание для решения этой задачи. Я буду использовать базу 4 9{\ синий 3} $$

На этот раз делать особо нечего 🙂

Шаг 4

Решите как показательное уравнение с одинаковыми основаниями

$$ 2х = 3 \\ х = \ гидроразрыва {3} {2} $$

Проблема 3

Решите экспоненциальное уравнение: $$ \left( \frac{1}{4} \right)^x = 32 $$

Шаг 1

Поскольку эти уравнения имеют разные основания, выполните шаги для разных оснований.

---

Забудьте на минуту о показателях и сосредоточьтесь на основаниях:
Перепишите основания как степени общего основания. Спроси себя : 95 \\ -2x = 5 \\ \frac{-2x}{-2} = \frac{5}{-2} \\ х = — \ гидроразрыва {5} {2} $$

9х-3 = 24 $$

Шаг 1

Перепишите это уравнение так, чтобы оно выглядело как другие, которые мы решали. Изолируйте экспоненциальное выражение следующим образом:

$$ \ влево ( \ гидроразрыва {1} {9х=27 $$

---

Забудьте на минуту о показателях и сосредоточьтесь на основаниях:
Перепишите основания как степени общего основания. Спроси себя :

Обе степени числа 3.

$ \\ \фракция 1 93 $$

Шаг 4

Решите как показательное уравнение с одинаковыми основаниями

$$ -2x = 3 \\ х = \ гидроразрыва {3} {-2} \\ х = -\фракция{3}{2} $$ 9{(3x -4)} -1 = 124 $$

Шаг 1

Перепишите это уравнение так, чтобы оно выглядело как другие, которые мы решали. {(3x -4)} = 125 $$ 93 $$

Шаг 4

Решите как показательное уравнение с одинаковыми основаниями

$$ -6x + 8 = 3 \\ -6x = -5 \\ х = \фракция{-5}{-6} \\ х = \ гидроразрыва {5} {6} $$

Лучшие бесплатные веб-сайты с калькулятором экспоненциальных уравнений

Рейтинги редакторов:

Рейтинги пользователей:

[Всего: 0 Среднее: 0]

Вот 5 лучших бесплатных веб-сайтов с калькулятором экспоненциальных уравнений . С помощью этих онлайн-калькуляторов вы можете мгновенно найти решения показательных уравнений.

Процесс поиска решения прост, все, что вам нужно сделать, это ввести уравнение, и эти калькуляторы рассчитают ответ за вас. Однако все эти экспоненциальные калькуляторы уравнений имеют некоторые ограничения. Некоторые ограничены характером экспоненциальных уравнений (поддерживаются только линейные экспоненциальные уравнения, а не квадратичные), а некоторые поддерживают только несколько функций.

Хотя эти онлайн-калькуляторы можно использовать бесплатно, для доступа к некоторым функциям требуется премиум-членство. Эти функции включают в себя: пошаговое решение, графическое представление уравнения и т.д. Keisan.Casio.com

Keisan.Casio.com  предлагает различные онлайн-инструменты расчета для образовательных и профессиональных целей. 9х .

Вы можете попробовать Keisan.Casio.com Экспоненциальное уравнение Калькулятор здесь .

WolframAlpha.com

WolframAlpha.com — еще один веб-сайт, который предлагает различные вычислительные инструменты в различных областях. Он имеет множество математических инструментов, которые помогут вам решить математические задачи. С помощью инструмента «Решение экспоненциальных уравнений » вы можете легко найти решение любого экспоненциального уравнения с числовыми основаниями.

Для этого введите числовые основания и их алгебраические показатели в поля ввода и нажмите « Отправить ». В новом всплывающем окне вы увидите ответ для вашего экспоненциального уравнения. Это дает вам возможность получить ответ либо в точной форме, либо в десятичной форме. А с членством Wolfram Alpha Pro вы также можете получить пошаговое решение вашего экспоненциального уравнения.

Попробуйте это  Калькулятор экспоненциального уравнения  здесь .

MathPapa.com

MathPapa  – это онлайн-калькулятор, который поможет вам разобраться в алгебре. Его Алгебра Калькулятор легко решает экспоненциальные уравнения и дает вам пошаговое решение с инструкциями для первых трех задач. Просто введите экспоненциальное уравнение в поле ввода и нажмите « Calculate It », чтобы получить пошаговое решение.

Как и в случае с Wolfram Alpha, вы можете получить пошаговое решение для каждого уравнения, подписавшись на один из их премиальных планов.

Решите экспоненциальные уравнения с MathPapa.com ‘s  Экспоненциальное уравнение  Калькулятор  здесь .

MathWay.com

MathWay.com  – это веб-сайт, созданный для помощи людям, решающим математические задачи. В разделе Тригонометрия он предлагает Экспоненциальное уравнение Калькулятор , где вы можете легко вычислить решение вашего показательного уравнения.

Этот калькулятор имеет уникальный интерфейс для современного молодого поколения, вдохновленный конверсией. Введите экспоненциальное уравнение и нажмите значок отправки. Он ответит вам ответом. Как и в других калькуляторах в этом списке, для получения пошаговых решений вместе с подробным объяснением вам потребуется премиум-подписка на MathWay .

Попробуйте это Экспоненциальное уравнение  Калькулятор  .

Symbolab.com

Symbolab.com  это еще один веб-сайт, который предлагает различные онлайн-инструменты, которые помогут вам решить практически любые математические задачи и вычисления. С помощью калькулятора экспоненциальных уравнений вы можете легко решать здесь экспоненциальные уравнения. Просто введите свои экспоненциальные уравнения и нажмите « Go », чтобы получить ответ. Он также показывает вам графическое представление вашего уравнения. Здесь вы также можете загрузить свой ответ в виде файла PDF на свой компьютер.

Если у вас есть другой ответ на уравнение, вы также можете проверить свой ответ здесь. Как и в MathPapa, вы можете увидеть пошаговое решение первых трех задач. После этого он просит обновить вашу учетную запись до премиум-класса, чтобы получить шаги решения.

Вы можете попробовать этот Калькулятор экспоненциального уравнения здесь .

Заключительные слова:

Все эти веб-сайты просты в использовании. Все эти калькуляторы очень похожи с точки зрения удобства использования и функциональности. Во время тестирования мне понравилось Symbolab больше всего. Причиной этого является его аккуратный и чистый интерфейс, а также возможность загрузки решения в формате PDF.

Решение показательных уравнений с помощью логарифмов

Из определения с помощью калькуляторов

Purplemath

Большинство показательных уравнений не решаются аккуратно; не будет способа преобразовать основания в одно и то же, например, преобразовать 4 и 8 в степень двойки. При решении этих более сложных уравнений вам придется использовать логарифмы.

Логарифмирование позволит нам воспользоваться правилом журнала, которое гласит, что силы внутри журнала могут быть вынесены вперед в виде множителей. Взяв логарифм экспоненты, мы можем затем переместить переменную (находящуюся в экспоненте, которая теперь находится внутри логарифма) вперед как множитель логарифма. Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее заполучить.

Например:

Содержание продолжается ниже

MathHelp.com

• Решить 2

  ^x = 30

Если бы это уравнение попросило меня «Решить 2 ^x = 32», то найти решение было бы легко, потому что я мог бы преобразовать 32 в 2 ⁵ , приравнять показатели степени и решить для « x = 5″. Но, в отличие от 32, 30 не является степенью числа 2, поэтому я не могу приравнять степени друг другу. Мне нужен другой способ добраться до x , потому что я не могу решить уравнение с переменной, плавающей над 2; Мне нужно, чтобы он вернулся на землю, где ему и место, где я могу его достать. И мне придется использовать логарифмы, чтобы уменьшить эту переменную.

При работе с уравнениями я могу делать с уравнением все, что захочу, при условии, что я делаю одно и то же с обеими сторонами. И, чтобы решить уравнение, я должен получить переменную сам по себе по одну сторону от знака «равно»; чтобы изолировать переменную, я должен «отменить» все, что было сделано с переменной.

В этом случае в показатель степени была помещена переменная x . Обратные (технически «обратные») экспоненты являются логарифмами, поэтому мне нужно отменить экспоненту, взяв логарифм обеих частей уравнения. Это полезно для меня из-за правила журнала, которое гласит, что показатели степени внутри журнала можно превратить в множители перед журналом:

log _b ( m ⁿ ) = n · log _б ( m ) ​​

Когда я беру логарифм обеих частей уравнения, я могу использовать любой логарифм, который мне нравится (логарифм по основанию 10, логарифм по основанию 2, натуральный логарифм и т. д.), но некоторые из них иногда более полезны чем другие. Поскольку основание в уравнении «2 ^x = 30» равно «2», я могу попробовать использовать логарифм по основанию 2:

log ₂ (2 ^x ) = log ₂ (30)

Любой журнал базы журнала возвращает значение 1, поэтому log ₂ (2) = 1. Тогда:

x · log ₂ (2) = log ₂ (30)

x (1) = log ₂ (30)

x = (30)

x =

1 (30)

x 9310 = (30)

x 9310 = (30)

x 9310 = (30)

.

Если вас попросят «найти решение», приведенный выше ответ должен быть приемлемым. Однако это значение, хотя и «точное», не будет очень полезным для текстовых задач (или в «реальной жизни»), если вам нужно числовое приближение.

Но мы не можем вычислить это выражение в наших калькуляторах в его нынешнем виде. Во-первых, нам нужно применить формулу замены базы, чтобы преобразовать выражение в нечто в базе, понятной нашим калькуляторам; а именно, натуральный бревно или обыкновенный бревно. Это преобразование выглядит так:

x = log ₂ (30)

= ln(30)/ln(2)

журнал» на английском языке. Аббревиатура произносится как «элл-энн» и пишется строчной буквой «L», за которой следует строчная «N». В названии функции нет «я» («глаз»)!

Что произойдет, если я просто буду использовать натуральный логарифм вместо логарифма с основанием два? Процесс был бы точно таким же, и окончательный ответ был бы эквивалентным.

2 ^x = 30

LN (2 ^x ) = LN (30)

x · ln (2) = LN (30)

x · ln (2) = Ln (30)

9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9263 9. . . )/ln(2)

В любом случае, я получаю один и тот же ответ, но в первую очередь использование натурального логарифма было проще и короче.

Примечание. Я мог бы использовать обычный (по основанию 10) журнал вместо естественного (то есть по основанию и ) журнала и все равно получить то же значение (при оценке в калькуляторе).

---

Поскольку в науке так часто используется натуральный логарифм, и поскольку это один из двух логарифмов, которые могут вычислить калькуляторы, я склонен брать натуральный логарифм обеих сторон при решении экспоненциальных уравнений. Это (обычно) не требуется, но часто более полезно, чем другие варианты.

---

Поскольку 212 не является степенью числа 5, то для решения этого уравнения мне придется использовать логи. Я мог бы взять логарифм по основанию 5 для каждой стороны, решить, а затем применить формулу изменения основания, но я думаю, что лучше просто использовать натуральный логарифм в первую очередь:

5 ^x = 212

LN (5 ^x ) = LN (212)

x · LN (5) = LN) 9966666666666666666666666666666666666666666 (212). )/ln(5)

…или около 3,328, округленное до трех знаков после запятой.

---

• Решить 10

  ^{2 x} = 52

Поскольку 52 не является степенью числа 10, мне придется использовать журналы, чтобы решить эту проблему. В этом конкретном случае, поскольку основание равно 10 и поскольку логарифм по основанию 10 можно сделать на калькуляторе, я буду использовать обычный логарифм вместо натурального логарифма для решения этого конкретного уравнения:

10 ^{2 x} = 52

log(10 ^{2 x} ) = log(52)

2 x · log (10) = log(52)

2 x (1) = log(52)

2 x = log(52)

x = ^log(52) / ₂

…или около 0,858, округленное до трех знаков после запятой.

---

• Решить 3(2

  ^{x +4} ) = 350

Прежде чем я смогу начать рассматривать экспоненту, мне сначала нужно избавиться от 3, поэтому я разделю это, чтобы получить:

2 ^{x +4} = ³⁵⁰ / ₃

Поскольку ³⁵⁰ / ₃ не является степенью числа 2, мне придется использовать логи. В данном случае я буду использовать натуральный логарифм:

…или около 2,866, округленное до трех знаков после запятой.

---

Примечание. Вы также можете решить вышеуказанное, используя правила экспоненты, чтобы разбить степень на 2:

2 ^{x +4} = (2 ^x ) (2 ⁴ ) = (2 ^x ) = (2 ^X ) = (2 ^X ). получаем:

(2 ^x )(16) = 350/3

2 ^x = 350/(3·16) = 175/24

9

. Вы получите ответ в виде:

x = ln(175/24)/ln(2)

Когда вы оцените это, вы получите тот же десятичный эквивалент, 2,866, в вашем калькуляторе. Не стесняйтесь быть гибкими!

---

URL: https://www.purplemath.com/modules/simpexpo2.htm

Страница 1 Страница 3

Экспоненциальные и логарифмические уравнения

Экспоненциальные и логарифмические уравнения

Графер Калькулятор Возврат Справка Точечная диаграмма

---

Содержание: Эта страница соответствует § 4. 4 (стр. 348) текста.

Предлагаемые проблемы из текста:

р. 355 #13,17,21,25,27,29,31,51,53,57,59,81,89

Экспоненциальные уравнения

Логарифмические уравнения

---

Экспоненциальные уравнения

Некоторые показательные уравнения можно решить, используя тот факт, что показательные функции взаимно однозначны. В других Другими словами, экспоненциальная функция не может принимать два разных значения одного и того же числа.

Пример 1.

3 ^х = 9

3 ^х = 3 ²

Функция f(x) = 3 ^x является взаимно однозначной, поэтому она не принимает два разных значения, равных 9, поэтому x должно быть равно 2.

х = 2

Уравнение в примере 1 было легко решить, потому что мы могли выразить 9 как степень числа 3. Однако часто необходимо использовать логарифм при решении показательного уравнения.

Пример 2.

е ^х = 20

Мы собираемся использовать тот факт, что натуральный логарифм является обратной экспоненциальной функцией, поэтому ln e ^x = x, по логарифмическому тождеству 1. Мы должны взять натуральный логарифм обеих частей уравнения.

ln e ^x = ln 20

Теперь левая часть упрощается до x, а правая часть представляет собой число. Это примерно 2,9957.

х = 2,9957

Упражнение 1 :

Используйте калькулятор, чтобы проверить ответ, который мы нашли для уравнения в примере 2.

Пример 3.

5 ^x = 16 Мы решим это уравнение двумя разными способами.

Первый подход: мы используем тот факт, что журнал ₅ 5 ^x = x (логарифмическая тождество 1 снова).

5 ^х = 16

журнал ₅ 5 ^x = журнал ₅ 16

х = журнал ₅ 16

x = ln 16 / ln 5 по формуле замены основания.

х = 1,7227 (приблизительно)

Второй подход: мы будем использовать натуральный логарифм и свойство 3.

5 ^x = 16 Возьмем натуральный логарифм обеих частей.

ряд 5 ^x = ряд 16

х пер. 5 = пер. 16

х = пер. 16 / пер. 5

х = 1,7227 (приблизительно)

Во втором подходе мы могли использовать любой логарифм. Второй подход — тот, который вы видите чаще всего. довольно часто.

Упражнение 2 :

Используйте калькулятор, чтобы проверить ответ, который мы нашли для уравнения в примере 3.

Уравнения, подобные приведенному в следующем примере, часто встречаются в приложениях.

Пример 4.

200 е ^{0,07 т} = 500

Сначала мы изолируем экспоненциальную часть, разделив обе части уравнения на 200.

е ^{0,07 т} = 2,5

Теперь возьмем натуральный логарифм обеих частей.

ln e ^{0,07 т} = ln 2,5

Левая часть упрощается до 0,07t по логарифмическому тождеству 1.

0,07t = ln 2,5

т = ln (2,5) / 0,07

т = 13,1 (приблизительно)

Упражнение 3 :

Решите следующие уравнения и проверьте ответы.

(а) 3 ^х = 10

(б) 150 е ^{0,05 т} = 350

Ответить

Вернуться к содержанию

Логарифмические уравнения

При решении экспоненциальных уравнений мы часто использовали логарифмическое тождество 1, потому что оно предполагает применение логарифмическая функция, чтобы «отменить» эффект экспоненциальной функции. При работе с логарифмическими уравнениями мы будем использовать логарифмическое тождество 2, где экспоненциальная функция применяется для «отмены» эффекта логарифмическая функция.

Пример 5.

2 log х = 12

Мы хотим изолировать журнал x, поэтому делим обе части на 2.

лог х = 6

Поскольку log — это логарифм по основанию 10, мы применяем экспоненциальную функцию по основанию 10 к обеим частям уравнения.

10 ^{журнал x} = 10 ⁶

По логарифмическому тождеству 2 левая часть упрощается до x.

х = 10 ⁶ = 1000000

Пример 6.

7 + 3 ln x = 15 Первый изолят ln x.

3 ln х = 8

ln х = 8/3

Теперь применим экспоненциальную функцию к обеим сторонам.

e ^{ln x} = e ^8/3

х = е ^8/3

Это точный ответ. Если вы используете калькулятор для вычисления этого выражения, вы получите приближение к ответу.

х примерно равно 14,39.

Упражнение 4 :

Проверьте ответы в примерах 5 и 6.

Пример 7.

пер (х + 4) + пер (х — 2) = пер 7

Сначала воспользуемся свойством 1 логарифмов, чтобы скомбинировать члены слева.

пер (х + 4)(х — 2) = пер 7

Теперь применим экспоненциальную функцию к обеим сторонам.

e ^{ln (x + 4)(x — 2)} = e ^{ln 7}

Логарифмическое тождество 2 позволяет нам упростить обе части.

(х + 4)(х — 2) = 7

х ² + 2х — 8 = 7

х ² + 2х — 15 = 0

(х — 3)(х + 5) = 0

х = 3 или х = -5

x = 3 проверки, для ln 7 + ln 1 = ln 7.

No related posts.