⊹ — Эрмитово сопряжение матрицы: U+22B9 hercon
U+22B9
Нажмите, чтобы скопировать и вставить символ
Техническая информация
| Название в Юникоде | Hermitian Conjugate Matrix |
| Номер в Юникоде | U+22B9 |
| HTML-код | ⊹ |
| CSS-код | \22B9 |
| Мнемоника | ⊹ |
| Раздел | Математические операторы |
| Версия Юникода: | 1. 1 (1993) |
Значение символа
Эрмитово сопряжение матрицы. Математические операторы.
Символ «Эрмитово сопряжение матрицы» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 22B9 |
| Простое изменение регистра | 22B9 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8A B9 | 226 138 185 | 14846649 | 11100010 10001010 10111001 |
| UTF-16BE | 22 B9 | 34 185 | 8889 | 00100010 10111001 |
| UTF-16LE | B9 22 | 185 34 | 47394 | 10111001 00100010 |
| UTF-32BE | 00 00 22 B9 | 0 0 34 185 | 8889 | 00000000 00000000 00100010 10111001 |
| UTF-32LE | B9 22 00 00 | 185 34 0 0 | 3106013184 | 10111001 00100010 00000000 00000000 |
Наборы с этим символом:
∑
Математические знаки
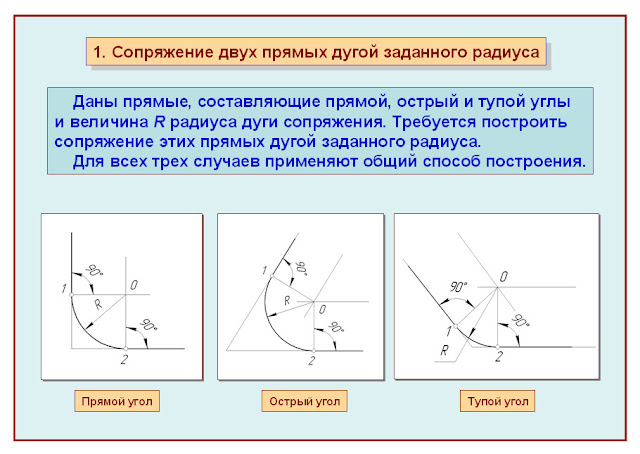
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит. Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Транспонирование уже обсуждалось выше: если , то . След Основная статья: След матрицы Для квадратной матрицы определен след: (иногда также обозначается как Sp или Spur). Является инвариантом ортогональных (унитарных) преобразований матрицы, соответствующих преобразованию матричного представления линейного оператора или билинейной (квадратичной) формы при соотвестствующем преобразовании векторного пространства (например, вращении). Определитель (детерминант) Основная статья: Определитель Перманент Основная статья: Перманент Линейные трансформации Основные статьи: Линейная трансформация, Трансформация матрицы Векторы представлены как матрица 2 x 2, образованная сторонами соответствующего единичного квадрата, трансформируемого в параллелограмм. Матрицы и их произведения выявляют их существенные особенности, когда это связано с линейными преобразованиями, так же известными, как линейные карты. Матрица A вещественных чисел размера m × n порождает линейное преобразование Для примера матрица 2×2 может быть рассмотрена при трансформации единичного квадрата в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d). Параллелограмм, показанный на рисунке справа получается путем умножения матрицы A на каждый вектор-столбец и . Эти векторы определяют вершины единицы площади. В следующей таблице показаны матрицы 2 × 2 вещественных чисел с соответствующими им линейными картами R2. Синим цветом обозначена исходная карта, а зеленым — трансформированная and shapes. Начало (0,0) обозначено черной точкой.
Связанные понятия Линейные комбинации В векторном пространстве линейной комбинацией векторов называется вектор где — коэффициенты разложения:
Это позволяет описать произведение матриц и терминах линейных комбинаций:
Линейная зависимость Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации. Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или где не все числа равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой. Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы. Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:
Ранг матрицы Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы. Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы. Свойства Матричные операции Сложение и вычитание допускается только для матриц одинакового размера. Существует нулевая матрица такая, что её прибавление к другой матрице A не изменяет A, то есть Все элементы нулевой матрицы равны нулю. Возводить в степень можно только квадратные матрицы.
, если обратная матрица существует. Примеры Основная статья: Список матриц ⇐ Предыдущая1234Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
..
Для комплексных матриц более употребительно эрмитово сопряжение: . С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.
Матрица A как говорят, представляет собой линейную карту f, и называется матрицей трансформирования f.
..квантовая механика — сопряжение оператора, примененного к функции
заданный вопрос
Изменено 8 лет, 6 месяцев назад
Просмотрено 3к раз
$\begingroup$
В разделе 6.3.1 следующего MIT Open Course Ware (PDF) (22-02, Introduction to Applied Nuclear Engineering) автор, профессор Паола Каппелларо, выводит уравнение Гейзенберга, используя определение ожидаемых значений, 9*$ такой, что $\phi=\hat H\psi$, но правая часть является оператором: производная еще ни к чему не применима.
Это уравнение само по себе просто не имеет смысла для меня.
Любая помощь по любому из этих двух вопросов будет принята с благодарностью!
- квантовая механика
- операторы
$\endgroup$
0
$\begingroup$
Ни левая, ни правая часть не являются собственно операторами, которые воздействуют на состояния и задают состояния. Они представляют собой форму операторов, которые действуют на состояния и дают комплексные числа. Мы называем такую вещь 9*$ где звездочка — это комплексное сопряжение, а умножение матриц — вектор-строка, а вектор-столбец — интегрирование.
$\endgroup$
4
$\begingroup$
В этом выводе я не понимаю двух вещей. Во-первых, полная производная по времени $\frac{d}{d t}$ превращается в частную производную по времени $\frac{\partial}{\partial t}$ внутри интеграла.
{x_1} \frac{\partial f(x ,t)}{\partial t} dx$$ См. ссылки на выводы и, по крайней мере, обратите внимание, что если сами пределы интегрирования равны 9*\шляпа{Н}$. Это меня смущает, поскольку $\hat{H}$ — это оператор Гамильтона, который содержит производную $x$.
{x_1} \frac{\partial f(x ,t)}{\partial t} dx$$
См. ссылки на выводы и, по крайней мере, обратите внимание, что если сами пределы интегрирования равны 9*\шляпа{Н}$. Это меня смущает, поскольку $\hat{H}$ — это оператор Гамильтона, который содержит производную $x$.Следуя ответу Робина Экмана, вы обнаружите, что часто бывает полезнее и поучительнее думать об этих выражениях, надев очки линейной алгебры, то есть думая об операторах как о самосопряженных матрицах, а не о дифференциальных операторах, действующих о функциях в декартовом базисе. Последнее становится очень уродливым, очень быстро, когда вы попадаете в трехмерный QM. Нотация Дирака (bra-ket) станет вашим лучшим другом, я обещаю. 9* g dx = <\hat{p}f|g>$$ Обратите внимание, что первый член должен быть равен нулю, учитывая, что волновые функции в КМ интегрируемы с квадратом или «нормализуемы», что требует, чтобы они стремились к нулю при $\pm \infty$.
[Пример источника: Griffiths Introduction to QM, section 3.
2.1]
$\endgroup$
5
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
квантовая механика — Является ли оператор комплексного сопряжения эрмитовым?
Задавать вопрос
Спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 3к раз
$\begingroup$
Интересно, может ли оператор комплексного сопряжения, определенный на волновой функции как 9\dagger$ должен быть сам $C$.