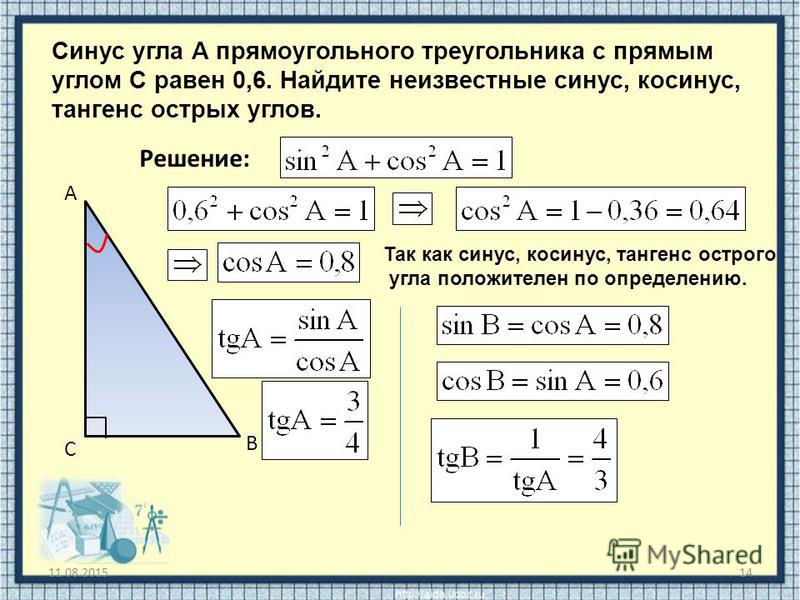
Как найти котангенс если известен синус?
Как найти котангенс если известен синус?
Тангенс это отношение синуса к косинусу: Tg(a)=Sin(a)/Cos(a). Котангенс это отношение косинуса к синусу: Ctg(a)=Cos(a)/Sin(a).
Как найти тангенс и котангенс?
Определения для числа: Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t, то есть, tg(t)=y/x. Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t, то есть, ctg(t)=x/y.
Как найти тангенс и котангенс на окружности?
Знаки тангенса и котангенса в квадрантах определяются с использованием уже известных знаков синуса и косинуса и основных тригонометрических тождеств: tg α = sin α cos α ; ctg α = cos α sin α .
Как найти тангенс на числовой окружности?
Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают tg t.
Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают ctg t. Получим, что: tg t = sin t cos t ; ctg t = cos t sin t .
Как найти тангенс по кругу?
п. Ось тангенсов это вертикальная касательная к числовой окружности в точке (1;0), на которой расположены тангенсы соответствующих углов. Построим горизонтальную касательную к числовой окружности в точке B(0;0). Продолжим луч OM до пересечения с касательной, обозначим точку пересечения E.
Как определить в какой четверти находится угол?
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох). Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2). Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи). Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Как определить в какой четверти находится график функции?
В первую четверть попадают точки, у которых обе координаты (x и y) больше нуля.
Во вторую: x 0; третью: x 0, y функции и соображаете в каких четвертях находится график.
Какой координатной четверти принадлежит угол 10 Радиан?
Ответ, проверенный экспертом Третья четверть. Darmaidayxx и 7 других пользователей посчитали ответ полезным!
Какой координатной четверти принадлежит угол Радиан?
α ∈ (180°; 270°) ⇒ III координатная четверть; α ∈ (270°; 360°) ⇒ IV координатная четверть.
Чем отличаются градусы в радианы?
360 градусов соответствует 2Пи радианам. 180 градусов – Пи радиан, 90 градусов – это Пи/2 радиан. Теперь вы знаете, что же такое написано на Тригонометрическом круге, что такое радианы и почему в круге 360 градусов. Если у вас есть другие версии, почему именно 360, пишите в комментариях.
Как переводить из градусов в радианы?
То есть, если известна величина угла в градусах, то умножив ее на пи и разделив на 180, получим величину этого угла в радианах.
Рассмотрим решение примера. Переведите 47 градусов в радианы. Согласно формуле перевода градусов в радианы, нам следует 47 умножить на пи и разделить на 180, получаем .
Как переводить числа из градусной меры в Радианную?
Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на π и разделить на 180. x x x x — значение угла в градусах; y — значение того же угла в радианах.
Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса. Синус, косинус и тангенс углов α и –α
Определение синуса, косинуса, тангенса и котангенса угла
План урока
- Введение понятий синуса, косинуса угла
- Частные случаи тригонометрических уравнений.
- Введение понятий тангенса, котангенса угла
- Таблица некоторых значений синуса, косинуса, тангенса, котангенса угла
- Решение задач на нахождение синуса, косинуса, тангенса угла, вычисление значений тригонометрических выражений, решение тригонометрических уравнений
Цели урока
- Знать определения синуса, косинуса, тангенса и котангенса угла, их некоторые табличные значения, решения частных случаев тригонометрических уравнений
- Уметь вычислять значения выражений, содержащих синус, косинус, тангенс или котангенс угла, решать тригонометрические уравнения типа sinx=0, sinx=±1, cosx=0, cosx=±1
Разминка
1.
2. Определите четверть, в которой расположена точка, полученная путем поворота точки (1; 0) на угол: 2π3, -4π3,-6270.
Что такое синус, косинус и тангенс угла вы уже знаете из курса геометрии, углы рассматривались от 00 до 1800. Введем определение синуса и косинуса для произвольного угла.
Рис. 1
Синусом угла α называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (Рис. 1). Обозначается sinα.
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (Рис. 1). Обозначается cosα.
Например, при повороте точки (1; 0) на угол π получается точка (–1; 0). Так как синус это ордината, а косинус — абсцисса, то sinπ=0, cosπ=-1.
Пример 1
Найти sin-π2 и cos-π2.
Решение
Так как при повороте на угол -π2 точка (1; 0) попадает в точку (0; –1), то sin-π2=-1, cos-π2=0.
Ответ: sin-π2=-1, cos-π2=0.
Радианную меру угла α можно рассматривать как действительное число, значит sinα и cosα являются числовыми выражениями. В уравнении sinx=a, где a∈R, x считается неизвестным.
Рис. 2
Решим уравнение cosx=0. Найдем все углы, косинус которых 0. У двух точек единичной окружности (0; 1)и (0; –1) абсциссы равны нулю (Рис. 2). Они получаются из точки (1; 0) путем поворота вокруг начала координат на углы π2,3π2,5π2,7π2и т. д., и на углы -π2,-3π2,-5π2,-7π2 и т. д.
Тогда cosx=0 при x=π2+πk, k∈Z. (1)
Аналогично, при помощи единичной окружности можно решить уравнения sinx=0, sinx=±1, cosx=±1.
Их называют частными случаями тригонометрических уравнений .
Приведем их решения.
sinx=0, x=πk, k∈Z.
(2)
sinx=1, x=π2+2πk, k∈Z. (3)
sinx=-1, x=-π2+2πk, k∈Z. (4)
cosx=1, x=2πk, k∈Z. (5)
cosx=-1, x=π+2πk, k∈Z. (6)
sinα и cosα определены для любого угла, а их значения находятся в промежутке [–1; 1].
Тангенсом угла α называется отношение синуса угла α к его косинусу. Обозначается tg α.
tg α=sinαcosα.
Котангенсом угла α называется отношение косинуса угла α к его синусу. Обозначается ctg α.
ctg α=cosαsinα.
Тангенс угла определен тогда, когда cosα≠0, т. е. α≠π2+πk, k∈Z. Котангенс угла определен когда sinα≠0, α≠πk, k∈Z.
Таблица некоторых значений синуса, косинуса, тангенса и котангенса
Пример 2
Найти все углы из промежутка [-2π; 2π], на которые нужно повернуть точку
А(1; 0), чтобы получить точку Aα, если:
а)sinα=32; б)cosα=-12.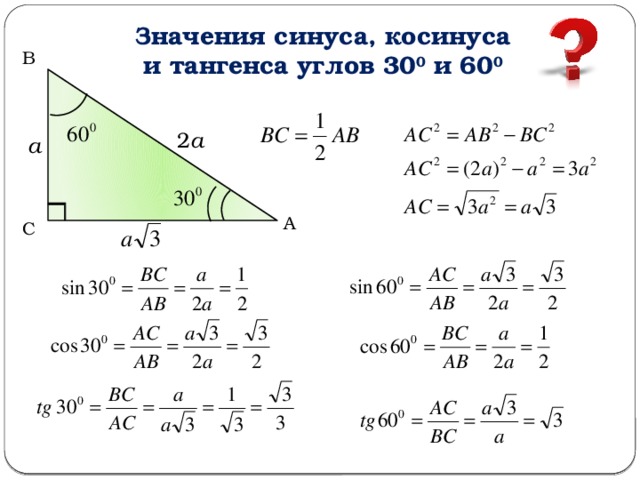
Решение
а) По определению синус угла это ордината точки. Ординату, равную 32, имеют две точки единичной окружности – В и С (Рис. 3). Точка С получена путем поворота точки А на угол α1=π3 или на угол α2=-2π+π3=-5π3. Точка В получена из А поворотом на α3=π-π3=2π3 или на угол α4=-π-π3=-4π3.
Рис. 3
б) Абсциссу, равную -12, имеют точки В и Е единичной окружности. С углами поворота точки
Ответ: а) π3,-5π3, 2π3,-4π3;
б) 2π3,-4π3, 4π3,-2π3.
Пример 3
Найти sinα, cosα, tgα, если:
а) α=-7π; б) α=5π2; в) α=19800.
Решение
а) Представим α в виде α=2πκ+β, k∈Z, β<2π, или, другими словами, выделим в α полные обороты окружности: α=-6π-π.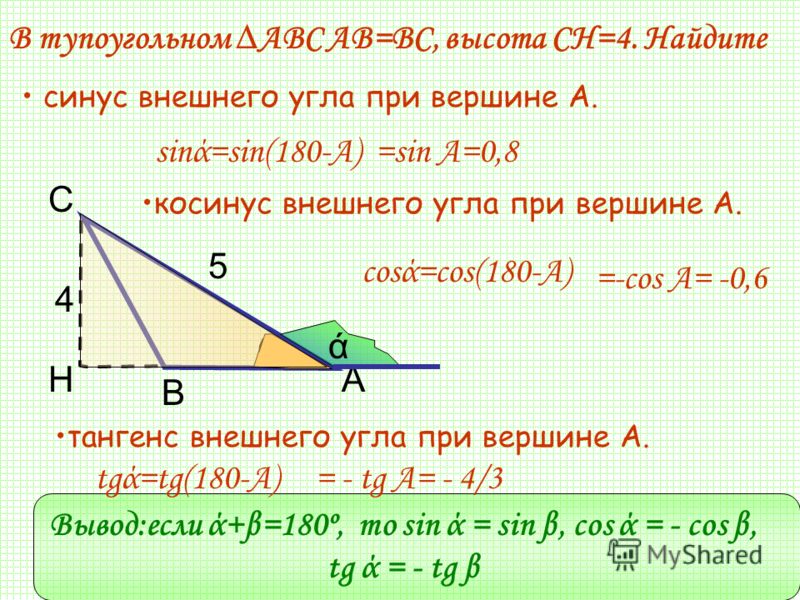
Значит, точка, полученная из точки A(1; 0) поворотом на угол -7π совпадает с точкой, полученной поворотом на -π, координаты которой (–1; 0). Тогда sinα=0, cosα=-1, tgα=sinαcosα=0.
б) α=5π2=2π+π2. Точка, полученная из начальной точки поворотом на 5π2 совпадает с точкой, полученной поворотом на π2. Она имеет координаты (0; 1). Значит, sinα=1, cosα=0, tgα не существует.
в) α=19800=5×3600+1800. Тогда sinα=0, cosα=-1, tgα=0.
Ответ:
а) sinα=0, cosα=-1, tgα=0;
б) sinα=1, cosα=0, tgα не существуют;
в) sinα=0, cosα=-1, tgα=0.
Пример 4
Вычислить:
а) sinπ3+cos-3π2;
б) cos-π+tgπ4.
Решение
а) Воспользуемся таблицей некоторых значений синуса, косинуса, тангенса и котангенса.
sinπ3+cos-3π2=32+0=32.
б) cos-π+tgπ4=-1+1=0.
Ответ: а) 32;
б) 0.
Пример 5
Решить уравнение:
а) 4cosx=-4;
б) sin3x=1;
в) cos2x+π3=1.
Решение
а) 4cosx=-4. Разделим обе части уравнения на 4: cosx=-1. Согласно уравнению (6) x=π+2πk, k∈Z.
б) sin3x=1. Воспользуемся уравнением (3): 3x=π2+2πk, k∈Z.
Выразим x из этого уравнения:
x=π6+2πk3, k∈Z.
в) cos2x+π3=1. По уравнению (5) имеем:
2x+π3=2πk, κ∈Z, 2x=-π3+2πk, k∈Z, x=-π6+πk, k∈Z.
Ответ: а) π+2πk, k∈Z;
б) π6+2πk3, k∈Z;
в) -π6+πk, k∈Z.
Упражнение 1
Найти все углы из промежутка [-2π; 2π], на которые нужно повернуть точку
А(1; 0), чтобы получить точку Аа, если:
а)sinα=-22; б)cosα=32.
Упражнение 2
Найти sinα, cosα, tgα, если:
а) α=5π; б) α=9π2; в) α=-12600.
Упражнение 3
Вычислить:
а)cosπ6-sin-π2;
б)sin-2π+cosπ4.
Упражнение 4
Решить уравнение:
а) 5sinx-5=0;
б) cos4x=1;
в) cos5x+π6=0.
Контрольные вопросы
1. Какая область допустимых значений переменной в выражении tg x?
2. Какая область допустимых значений переменной в выражении ctg x?
3. Как можно найти котангенс угла, если известен тангенс этого угла?
Ответы
Упражнение 1
а) -π4;-3π4;5π4;7π4; б)π6;-π6;11π6;-11π6.
Упражнение 2
а)sinα=0, cosα=-1, tg α=0;
б)sinα=1, cosα=0, tg α не существует;
в)sinα=0, cosα=-1, tg α=0.
Упражнение 3
а)32+1; б)22.
Упражнение 4
а)π2+2πk, k∈Z; б)πk2, k∈Z; в)π15+πk5, k∈Z.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Взаимные тождества — формулы, доказательство, примеры
LearnPracticeDownload
Взаимные тождества являются обратными величинами шести основных тригонометрических функций, а именно синуса, косинуса, тангенса, котангенса, секанса, косеканса.
Важно отметить, что взаимные тождества — это не то же самое, что обратные тригонометрические функции. Каждая фундаментальная тригонометрическая функция является обратной величиной другой тригонометрической функции. Например, косеканс — это обратная идентичность функции синуса.
В этой статье мы будем определять взаимные тождества, доказывать взаимные тождества и находить связь между ними с помощью решенных примеров.
| 1. | Что такое взаимные тождества? |
| 2. | Формулы взаимных тождеств |
| 3. | Доказательство взаимной идентичности |
| 4. | Связь взаимных тождеств |
| 5. | Часто задаваемые вопросы о взаимных тождествах |
Что такое взаимная идентичность?
Обратные величины шести основных тригонометрических функций (синус, косинус, тангенс, секанс, косеканс, котангенс) называются обратными тождествами.
Взаимные тождества являются важными тригонометрическими тождествами, которые используются для решения различных задач тригонометрии. Каждая тригонометрическая функция является обратной величиной другой тригонометрической функции. Функция синуса является обратной функцией косеканса и наоборот; функция косинуса является обратной функцией секущей и наоборот; функция котангенса является обратной функцией тангенса и наоборот.
Формулы взаимных тождеств
Взаимные тождества применяются в различных задачах тригонометрии для упрощения вычислений. Формулы шести основных взаимных тождеств таковы:
- sin x = 1/cosec x
- cos х = 1/сек х
- коричневый х = 1/детская кроватка х
- детская кроватка х = 1/загар х
- сек х = 1/cos х
- косек х = 1/sin х
Доказательство взаимной идентичности
Теперь, когда мы знаем взаимные тождества тригонометрии, давайте теперь докажем каждое из них, используя определение основных тригонометрических функций.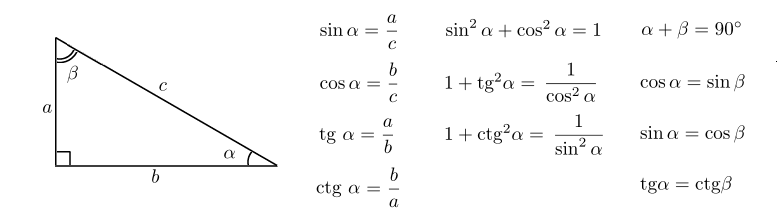
Во-первых, мы выведем обратное тождество функции синуса. Рассмотрим прямоугольный треугольник ABC с прямым углом при вершине C.
Мы знаем, что sin θ = перпендикуляр/гипотенуза = c/a и cosec θ = гипотенуза/перпендикуляр = a/c ⇒ sin θ является обратной величиной cosec θ, а cosec θ является обратной величиной sin θ. Аналогично докажем и другие взаимные тождества. cos θ = основание / гипотенуза = b / a и cosec θ = гипотенуза / основание = a / b ⇒ cos θ является обратной величиной sec θ, а sec θ является обратной величиной cos θ. тангенс θ = sin θ/cos θ и кроватка θ = cos θ/sin θ ⇒ тангенс θ является величиной, обратной величине кроватки θ, а кроватка θ является величиной, обратной величине тангенса θ. Следовательно, у нас есть
- sin θ является обратной величиной cosec θ
- cosec θ является обратной величиной sin θ
- cos θ является обратной величиной sec θ
- сек θ является обратной величиной cos θ
- tan θ является обратной величиной cot θ
- cot θ является обратной величиной tan θ
Связь взаимных тождеств
Поскольку мы знаем, что произведение числа и его обратного числа всегда равно единице, мы установили аналогичные отношения между обратными тождествами.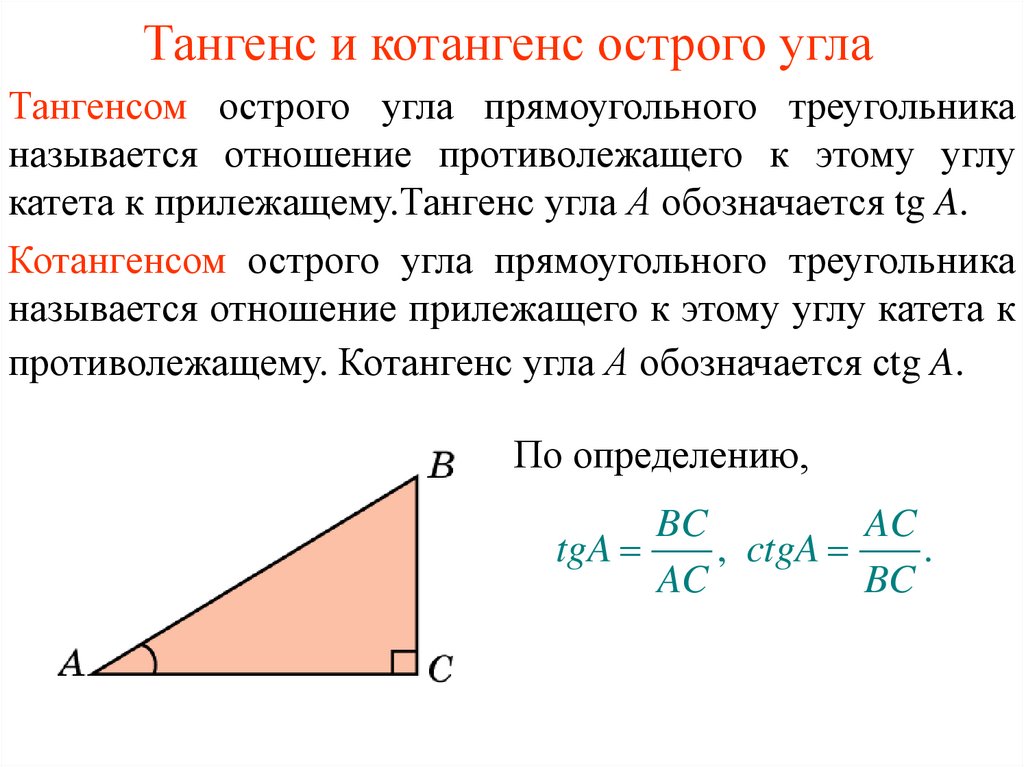
Произведение тригонометрической функции на обратную ей равно 1. Следовательно, имеем
- sin θ × cosec θ = 1
- cos θ × сек θ = 1
- загар θ × кроватка θ = 1
Приведенные выше уравнения устанавливают связь между обратными тождествами тригонометрии для любого угла θ и показывают, что произведение тригонометрической функции на ее обратную величину равно 1. величина, обратная cosec θ
Связанные темы по взаимным тождествам
- Обратные тригонометрические формулы
- Тригонометрические формулы
- Тригонометрическая таблица
- Тригонометрия
Взаимные тождества Примеры
Пример 1: Упростите выражение [cot x(sin x + tan x)/(cosec x + cot x)], используя взаимные тождества.
Решение: Мы запишем выражение [cot x (sin x + tan x)/(cosec x + cot x)] через sin x и cos x и воспользуемся взаимной тождественностью cosec x = 1/sin x
[cot x (sin x + tan x)/(cosec x + cot x)] = [(cos x/sin x)(sin x + (sin x/cos x))/((1/sin x) + (cos x/sin x))]
= (cos x + 1)(sin x)/(1 + cos x)
= sin x
Ответ: [cot x (sin x + tan x)/(cosec x + cot x)] = sin x
Пример 2: Определите значение sec x, если cos x = 3/7, используя взаимное тождество.
Решение: Мы знаем взаимное тождество sec x = 1/cos x
Итак, если cos x = 3/7, то sec x = 1/cos x = 1/(3/7) = 7/3
Ответ: сек х = 7/3
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Взаимные проблемы идентичности
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о взаимных тождествах
Что такое взаимные тождества в тригонометрии?
Обратные тождества шести фундаментальных тригонометрических функций (синус, косинус, тангенс, секанс, косеканс, котангенс) называются обратными тождествами. Функция синуса является обратной функцией косеканса и наоборот; функция косинуса является обратной функцией секущей и наоборот; функция котангенса является обратной функцией тангенса и наоборот.
Что такое шесть взаимных тождеств?
Формулы шести основных обратных тождеств:
- sin x = 1/cosec x
- cos х = 1/сек х
- коричневый х = 1/детская кроватка х
- детская кроватка х = 1/загар х
- сек х = 1/cos х
- косек х = 1/sin х
Какова обратная идентичность Cos x?
Обратное тождество cos x равно sec x, поскольку cos x = 1/sec x.