Если в параллелограмме: 1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник. 2) Если диагонали параллелограмма…

Содержание

Параллелограмм — тест с ответами

«По геометрии проверить знания учеников по пройденной теме можно с помощью тестов. На этой странице представлен тест по теме параллелограмм. Правильные варианты ответов выделены символом [+]. Обращаем ваше внимание что на решение теста отводится всего 20-30 минут, поэтому вы должны поторопиться, чтобы успеть выполнить задание полностью.

Чему равна наименьшая из сторон параллелограмма, если его периметр равен 36 см, а одна из сторон в два раза больше другой:
[+] а) 6 см
[-] б) 12 см
[-] в) 18 см

Если в параллелограмме ABCD угол А + угол В + угол D = 252°, тогда угол А равен:
[-] а) 90°
[+] б) 108°
[-] в) 72°

В параллелограмме ABCD диагональ АС со сторонами АВ и ВС образует углы 45° и 25° соответственно. Величина угла С равна:
[-] а) 45°
[-] б) 25°
[+] в) 70°

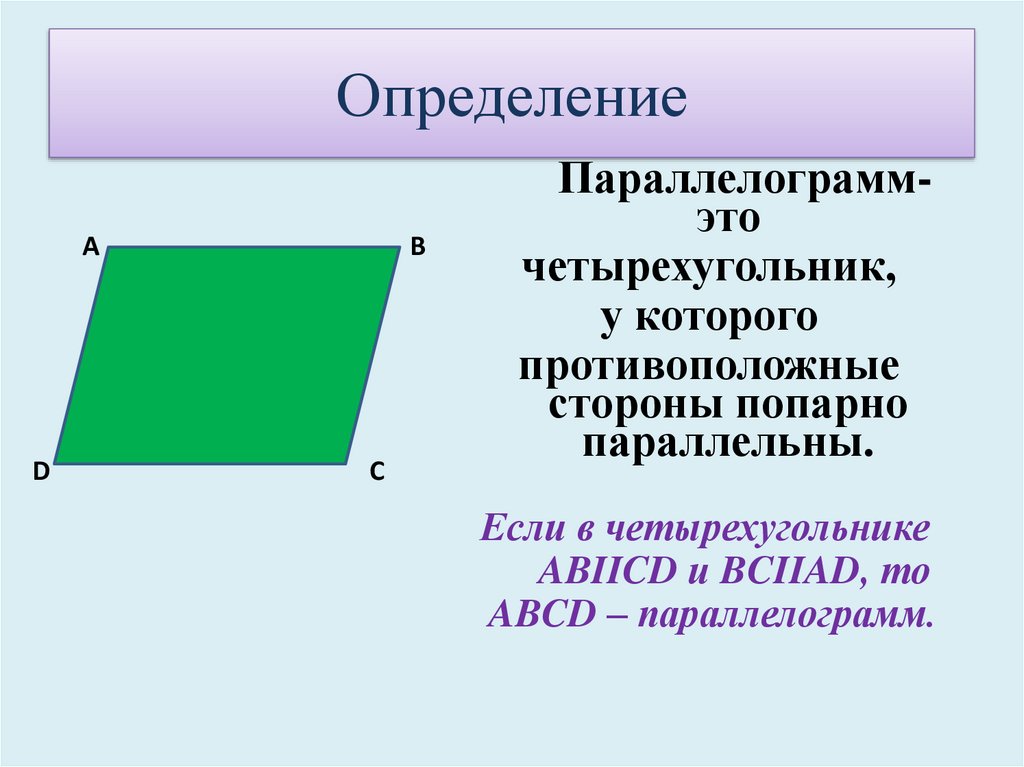
Четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых:
[+] а) параллелограмм
[-] б) ромб
[-] в) квадрат

Частным случаем параллелограмма является:
[-] а) треугольник
[-] б) сфера
[+] в) ромб

Частным случаем параллелограмма является:
[-] а) круг
[+] б) квадрат
[-] в) сфера

Частным случаем параллелограмма является:
[-] а) круг
[-] б) треугольник
[+] в) прямоугольник

Противолежащие стороны параллелограмма:
[+] а) равны
[-] б) не равны
[-] в) зависит от условий

Противолежащие углы параллелограмма:
[-] а) зависит от условий
[-] б) не равны
[+] в) равны

Сумма углов, прилежащих к одной стороне, равна:
[-] а) 90°
[+] б) 180°
[-] в) 45°

Точка пересечения диагоналей является … параллелограмма:
[+] а) центром симметрии
[-] б) сферой симметрии
[-] в) основой симметрии

Параллелограмм диагональю делится на два … треугольника:
[-] а) не равных
[+] б) равных
[-] в) оба варианта верны

Аффинное преобразование всегда переводит параллелограмм в:
[+] а) параллелограмм
[-] б) ромб
[-] в) круг

У четырёхугольника без самопересечений две противоположные стороны:
[-] а) только параллельны
[-] б) только равны
[+] в) одновременно равны и параллельны

У четырёхугольника без самопересечений все противоположные стороны попарно:
[+] а) равны
[-] б) параллельны
[-] в) оба варианта верны

Площадь параллелограмма равна произведению его основания:
[-] а) на одну из сторон
[+] б) на высоту
[-] в) оба варианта верны

Площадь параллелограмма равна произведению его сторон на … угла между ними:
[-] а) косинус
[-] б) тангенс
[+] в) синус

Средние линии параллелограмма пересекаются в точке пересечения:
[-] а) его высоты
[+] б) его диагоналей
[-] в) его основания

Одно из равенств в векторной алгебре и векторном анализе:
[-] а) природа параллелограмма
[-] б) свойство параллелограмма
[+] в) тождество параллелограмма

Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна:
[-] а) его периметру
[+] б) его полупериметру
[-] в) его основанию

В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Периметр параллелограмма равен:
[+] а) 34 см
[-] б) 30 см
[-] в) 38 см

В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует с диагональю BD угол 30°, АВ = 10 см. Необходимо найти периметр параллелограмма:
[-] а) 28 см
[+] б) 40 см
[-] в) 30 см

В параллелограмме ABCD биссектрисы углов B и D пересекают стороны AD и ВС в точках М и К соответственно так, что MD = 5 см, КС = 7 см. Необходимо найти периметр ABCD:
[-] а) 32 см
[-] б) 24 см
[+] в) 38 см

Периметр параллелограмма равен 32 см, а две из его сторон относятся как 3 : 1. Наибольшая из его сторон равна:
[-] а) 22 см
[+] б) 12 см
[-] в) 8 см

Если в параллелограмме ABCD угол А + угол В + угол С = 237°, тогда угол В равен:
[-] а) 79°
[-] б) 29°
[+] в) 123°

В параллелограмме ABCD диагональ BD со сторонами АВ и AD образует углы, равные соответственно 52° и 26°.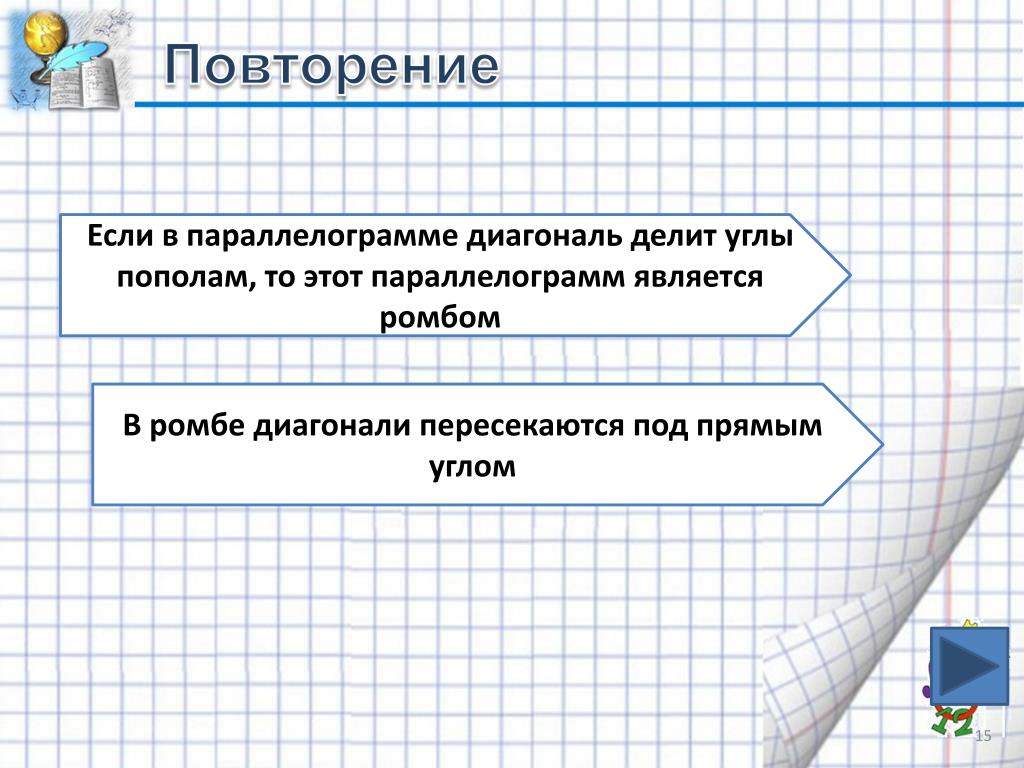 Величина угла В равна:
[-] а) 26°
[+] б) 78°
[-] в) 52°

В параллелограмме ABCD биссектриса угла В пересекает сторону AD в точке М так, что АМ = 8 см, MD = 4 см. Периметр параллелограмма равен:
[+] а) 40 см
[-] б) 12 см
[-] в) 24 см

В параллелограмме ABCD отрезки AC и BD являются:
[-] а) соседними сторонами
[-] б) противоположными сторонами
[+] в) диагоналями

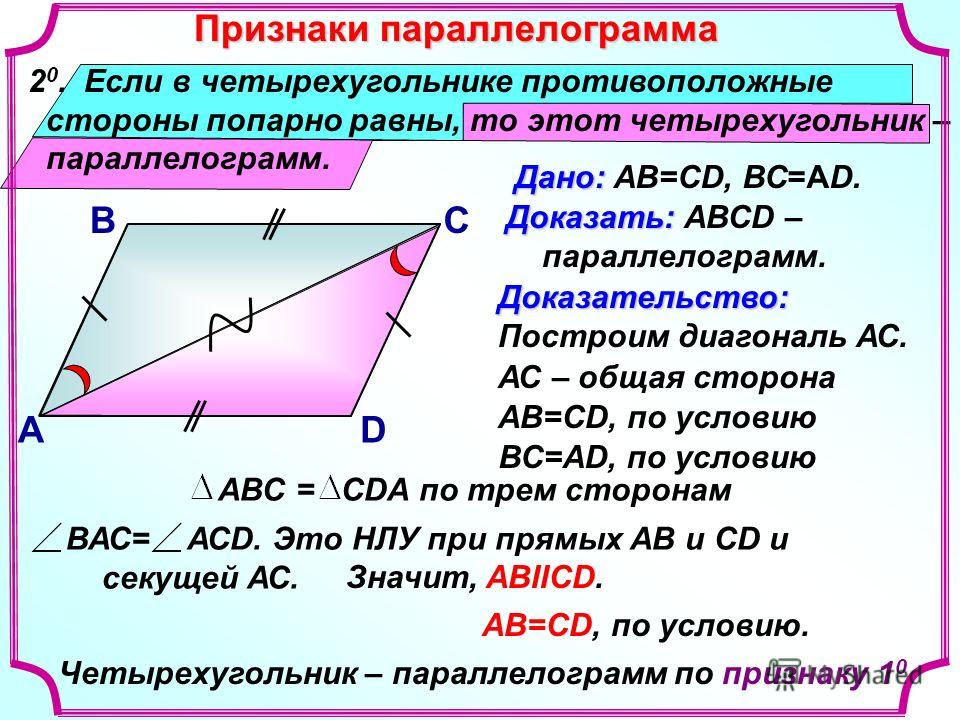
Дайте название следующему утверждению: в параллелограмме противоположные стороны равны:
[+] а) свойство параллелограмма
[-] б) определение параллелограмма
[-] в) признак параллелограмма

Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то это параллелограмм:
[-] а) свойство параллелограмма
[+] б) признак параллелограмма
[-] в) определение параллелограмма»

Открытый урок по геометрии в 8-м классе на тему «Параллелограмм, прямоугольник, ромб, квадрат»

org/Person»> Власова Валентина Ивановна

Разделы: Математика

Тема: «Параллелограмм, прямоугольник, ромб, квадрат»

Цель урока: Систематизировать, обобщить знания о четырех фигурах — параллелограмме, прямоугольнике, ромбе, квадрате, их свойствах, признаках.

Девиз урока:
«Математику уже затем учить надо, что она ум в порядок приводит.»
(М. В. Ломоносов).

План урока:

Загадки.
Беседа с классом по вопросам.
Работа по готовым чертежам (работа в парах).
Применение в жизни (сообщение).
Физкультминутка («истинно — ложно»).
Тест (2 варианта).
Домашнее задание: п. 45, 46, № 406, № 411, на оценку «5» № 412.
Самостоятельная работа
Итоги урока.

1. Загадки:

УЧИТЕЛЬ: Вспомним определения четырехугольников. В этих загадках используются их свойства. Я читаю загадку, а вы поднимаете карточку с верным ответом (у каждого ученика карточки: параллелограмм, квадрат, ромб, прямоугольник).

1. Знаете ли вы меня
Хочу проверить,
Любую площадь я могу измерить,
Ведь у меня четыре стороны
И все они между собой равны.
И у меня равны еще диагонали,
Углы мне они делят пополам, и ими
На части равные разбит я сам.
(Квадрат)

2. И у меня равны диагонали,
Хочу сказать я, хотя меня не называли,
И хоть я не зовусь квадратом
Он мне приходится родным братом.
(Прямоугольник)

3. Хоть стороны мои
Попарно и равны, и параллельны,
Все ж я в печали, что не равны мои диагонали,
Да и углы они не делят пополам
Но все ж, скажи, дружок, кто я?
(Параллелограмм)

4. Мои хотя и не равны диагонали,
По значимости всем я уступлю едва ли.
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам,
И очень важная фигура я, скажу я вам.
(Ромб)

(См. Приложение4)
По окончанию задания каждый учащийся оценивает себя сам, выставляется первая оценка в «Карточку самооценки» (см. Приложение1)

2. Беседа с классом по вопросам:

К какому виду четырехугольников относятся прямоугольник, ромб, квадрат?
Назовите свойства параллелограмма?
Назовите признаки параллелограмма?
Назовите особое свойства прямоугольника?
Назовите особое свойства ромба?
Назовите основные свойства квадрата?

3. Работа по готовым чертежам (работа в парах):
(См. Приложение5)
Задание: Указать вид четырехугольника на рисунках. Объяснить почему?

Двое учащихся выполняют это задание на откидной доске (работают в паре). Учитель проверяет задание, остальные учащиеся оценивают друг друга, выставляется вторая оценка в «Карточку самооценки» (см. Приложение1)

4. Применение в жизни. (Сообщение):

Параллелограмм дает определение прямоугольнику, ромбу. В жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жесткости проведена диагональ.

Прямоугольник несет красоту, стройность, четкость. Это стены домов, пол, потолок, грани карандашей.

Реечный домкрат для легковых автомобилей имеет форму ромба. Плиточники укладывают плитки в виде ромба, квадрата – из них получаются красивые узоры.

В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов. Их располагают на обожженном участке в шахматном порядке, так как кожа имеет свойство расти во всех направлениях, со временем промежутки между квадратами зарастают.

В сельском хозяйстве применяют квадратно – гнездовой способ посадки культур – урожай при этом лучше, этот способ хорош тем, что можно применять механизированную обработку.

В физике применяют параллелограмм при изучении разложения сил, при нахождении равнодействующей силы.

5. Физкультминутка («истинно — ложно»):

Учитель: Я скажу несколько предложений. Если предложение ложное, то вы встаете, если верное, то поднимаете руку.

Диагонали прямоугольника равны.
Все углы квадрата прямые.
Диагонали параллелограмма равны.
В ромбе все стороны равны.
Диагонали прямоугольника перпендикулярны.
В параллелограмме противоположные стороны равны.
Диагонали ромба равны.

6. Тест (2 варианта):

Вопросы, I вариант	Ответы
1. Любой прямоугольник является …	а) Ромбом б) Квадратом в) Параллелограммом
2. Если в четырехугольнике диагонали равны, взаимно перпендикулярны и имеют общую середину, то этот четырехугольник	а) Ромб б) Квадрат в) Прямоугольник
3. Ромб, у которого один угол прямой является	а) Квадратом б) Прямоугольником в) Параллелограммом
4. Какой четырехугольник не имеет собственно свойств, а обладает свойствами других четырехугольников?	а) Прямоугольник б) Ромб в) Квадрат
5. Если в параллелограмме диагонали равны, то этот параллелограмм	а) Ромб б) Прямоугольник в) Квадрат

1	2	3	4	5

Вопросы, II вариант	Ответы
1. Любой квадрат является …	а) Параллелограммом б) Прямоугольником в) Ромбом
2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм — …	а) Ромб б) Квадрат в) Нет правильного ответа
3. В ромбе…	а) Все углы равны б) Все стороны равны в) Диагонали равны
4. Параллелограмм, один из углов которого прямой является…	а) Прямоугольником б) Квадратом в) Ромбом
5. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник — …	а) Ромб б) Квадрат в) Нет правильного ответа

1	2	3	4	5

(см. Приложение2)

Результаты заносятся в таблицу, расположенную в конце теста, который содержит пять заданий. Выполнив тест, учащиеся обмениваются результатами, учитель называет правильные ответы. За верно выполненное задание – 1 балл.

Оценка заносится в « Карточку самооценки » (см. Приложение1).

Выставляется итоговая оценка по трем заданиям в «Карточку самооценки».
Учитель подводит итоги « Карточки самооценки ».

7. Домашнее задание: п. 45, 46, № 406, № 411, на оценку «5» № 412.

8. Самостоятельная работа (см. Приложение3)

I вариант:

Вычислить углы параллелограмма, если его углы, прилежащие к одной стороне, относятся как 2:7.
В ромбе периметр равен 24 см, один из углов 120°. Чему равна длина меньшей диагонали.
AEDF – параллелограмм. Доказать: ECFB – параллелограмм.

II вариант:

Вычислить углы параллелограмма, если его углы, прилежащие к одной стороне, относятся как 4:5.
В ромбе один из углов 120°, длина меньшей диагонали 5 см, найти периметр ромба.
ABDE – параллелограмм. Доказать: ACDF – параллелограмм.

Двое учащихся выполняют самостоятельную работу по вариантам на откидных досках. По окончанию работы ученики сверяют свои решения с доской.

9. Подведение итогов урока.

Рефлексия:

Если было хорошо у нас – улыбнись и покажи квадрат.
Если было скучно вам – покажи параллелограмм.
Если ждешь таких уроков – хлопни.
Если больше ничего не хочешь — топни.

Спасибо за внимание!

5.05.2010

Когда параллелограмм является прямоугольником?

Я думаю о параллелограмме, диагонали которого равны. Назовите этот параллелограмм.

Не все параллелограммы имеют равные диагонали. У ромбов диагонали не равны. У прямоугольников диагонали равны, как и у квадратов. Вы не можете заключить, что параллелограмм, о котором я думаю, является квадратом, потому что это было бы слишком ограничительно. При игре в «Назови этот четырехугольник» ваш ответ должен быть как можно более общим. Поскольку квадрат — это прямоугольник, а прямоугольник не обязательно должен быть квадратом, наиболее общий четырехугольник, который соответствует этому описанию, — это прямоугольник.

Теорема 16.5 : Если диагонали параллелограмма равны, то параллелограмм является прямоугольником.

На рис. 16.5 изображен параллелограмм ABCD с равными диагоналями ¯AC и ¯BD. Поскольку мы имеем дело с параллелограммом, вы знаете, что противоположные стороны конгруэнтны. Вы можете использовать постулат SSS, чтобы показать, что ACD ~= DBA. Используя CPOCTAC, мы можем показать A ~= D. Поскольку ABCD — параллелограмм, противоположные углы конгруэнтны, поэтому A ~= C и B ~= D.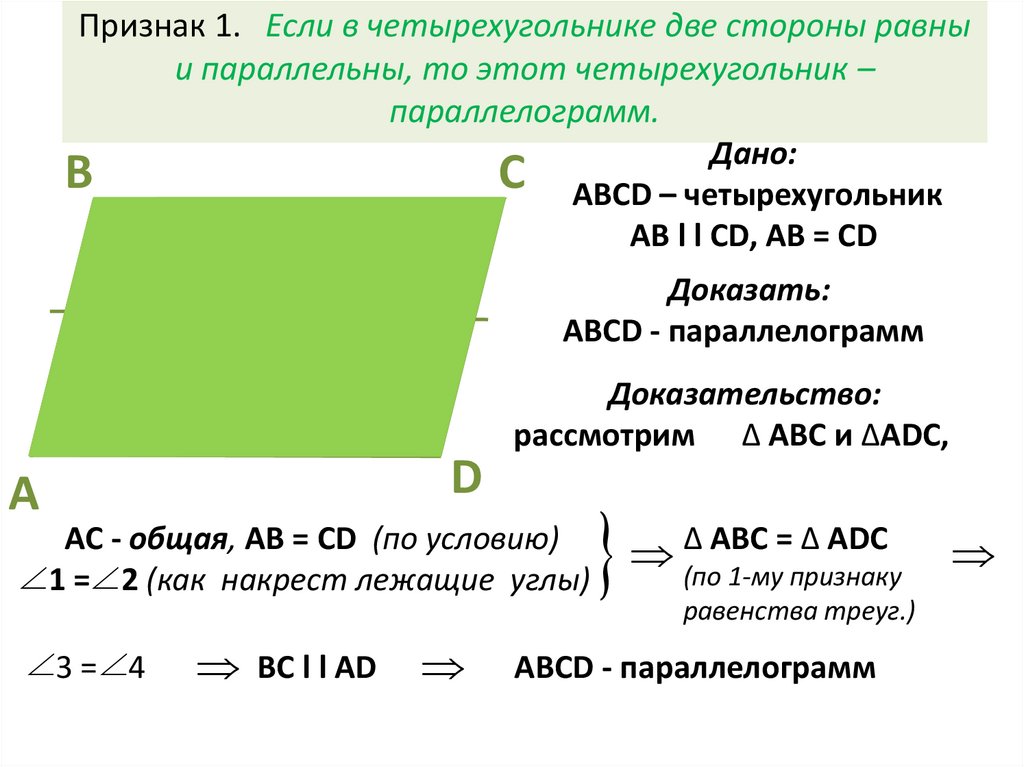 По транзитивному свойству ~= все четыре угла конгруэнтны. Поскольку внутренние углы четырехугольника в сумме составляют 360º, вы можете показать, что все четыре угла нашего параллелограмма прямые. Этого более чем достаточно, чтобы сделать ваш параллелограмм прямоугольником.

Рисунок 16.5 Параллелограмм ABCD с равными диагоналями ¯AC и ¯BD.

н.э.

	Заявления	Причины
1.	Параллелограмм ABCD с ¯AC ~= ¯BCD	Дано
2.	¯AB ~= ¯CD	Теорема 15.4
3.	¯ н.э. ~=	Рефлексивное свойство ~=
4.	АКД ~= ДБА	Постулат ССС
5.	А ~= Д	КПОКТАК
6.	А ~= С и В ~= D	Теорема 15.5
7.	мА = мКл и мБ = мД	Определение ~=
8.	мА + мБ + мКл + мД = 360º	Внутренние углы четырехугольника в сумме дают 360º
9.	мА + мА + мА + мА = 360º	Замена (шаги 7 и 8)
10.	мА = 90°	Алгебра
11.	А прямой угол	Определение прямого угла
12.	Параллелограмм ABCD является прямоугольником	Определение прямоугольника

Выдержки из Полное руководство идиота по геометрии © 2004 Denise Szecsei, Ph.D. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.

Геометрия: когда четырехугольник является параллелограммом?

В тренде

Вот факты и мелочи, о которых говорят люди.

Олимпийские боги и богини (их имена и силы)
Крупнейшие штаты США по площади
Текущие события на этой неделе: март 2023
Кристина Россетти: Иисус, люблю ли я Тебя?
10 самых больших водопадов в мире (самый высокий, самый широкий и самый объемный!)
Мировые религии: во что люди верят и где

Как проверить, образуют ли заданные точки параллелограмм?

Здесь мы увидим, как проверить, образуют ли заданные точки параллелограмм.

Чтобы доказать, что данные точки образуют параллелограмм, мы должны выполнить шаги, указанные ниже.

(i) Найдите длину всех сторон, используя формулу расстояния между двумя точками.

(ii) В параллелограмме длина противоположной стороны равна, а середины диагоналей равны.

Проверка того, образуют ли заданные точки параллелограмм.

Пример

Вопрос 1:

Проверить, являются ли заданные точки A (4, 6) и B (7, 7), C (10, 10) и D (7, 9) образует параллелограмм.

Решение:

Расстояние между двумя точками (x₁, y₁) и (x₂ , y₂)

√(x₂ — x₁)² + (y₂ — y₁)²

Четыре точки A (4,6) и B (7,7) и C (10,10) и D (7,9)

Длина AB :

Здесь x₁ = 4, y₁ = 6, x₂ = 7 и y₂ = 7 √(7-4)² + (7-6)²

= √(3)² + (1)²

= √9 + 1

= √10 единиц

Длина BC:

Здесь x₁ = 7, y₁ = 7, x₂ = 10 и y₂ = 10

= √(10-7)² + (10-7)²

= √(3)² + (3)²

= √9 + 9

= √18 единиц

Длина CD:

Здесь x₁ = 10, y₁ = 10, x₂ = 7 и y₂ =

= √ (7-10) ² + (9-10)²

= √(-3)² + (-1)²

= √9 + 1

= √10 единиц

, y₁ = 9, x₂ = 4 и y₂ = 6

= √(4-7)² + (6-9)²

= √(-3)² + (-3)²

= √9 + 9

= √0013 единиц

AB = √10 шт.

BC = √18 шт.

CD = √10 шт.

DA = √18 шт.

Длины противоположных сторон равны. Таким образом, данные вершины образуют параллелограмм.

Чтобы найти середины диагоналей, мы используем формулу

= (x ₁ + x ₂ )/2, (y ₁ + y ₂ )/2

Середина диагонали AC :

= (4+10)/2, (6+10)/2

= 14/2, 16/2

= (7, 8) ——-( 1)

Середина диагонали BD :

= (7+7)/2, (7+9)/2

= 14/2, 16/2

= (7, 8) ——-( 2)

Поскольку середины диагоналей равны, данные точки образуют параллелограмм.

Как проверить, образуют ли заданные точки параллелограмм — практические вопросы

(2) Проверить, образуют ли заданные точки A (3,-5) и B (-5,-4) и C (7,10) и D (15,9) параллелограмм. Решение

(3) Проверьте, образуют ли заданные точки A (-4,-3) и B (3,1) и C (3,6) и D (-4,2) параллелограмм.