производная / Вопросы о дифференцируемости функции / Математика
|
а. Можно ли утверждать, что произведение $%F(x) = f(x)g(x)$% не имеет производной в точке $%x_0$%, если функции $%f(x)$% и $%g(x)$% не имеют производной в этой точке? б. Что можно сказать о дифференцируемости функции $%F(x) = f(g(x))$% в точке $%x_0$%, если функция $%f(y)$% не имеет производной в точке $%g(x_0)$%, а функция $%g(x)$% имеет производную в точке $%x_0$%? дифференцируемость производная функции задан 9 Июл ’15 23:31 Можно также взять любую разрывную функцию $%f(x)$%, принимающую отличные от нуля значения, а в качестве второй функции взять $%g(x)=\frac1{f(x)}$%. Тогда произведение будет тождественно равно единице. Конкретный пример: $%f(x)=1$% при $%x\in\mathbb Q$%, и $%f(x)=-1$% при $%x\notin\mathbb Q$%. Обе функции окажутся всюду разрывными. б) Можно взять $%g(x)=0$% (тождественно), а в качестве $%f(x)$% взять любую «плохую» функцию (например, из предыдущего пункта). При этом $%F(x)=f(g(x))$% будет константой. Аналогичный пример строится, когда $%f(x)$% всюду дифференцируема, а $%g(x)$% любая: достаточно положить $%f(x)=0$% при всех $%x$%. ссылка отвечен 10 Июл ’15 0:46 falcao |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | ||
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92-3$.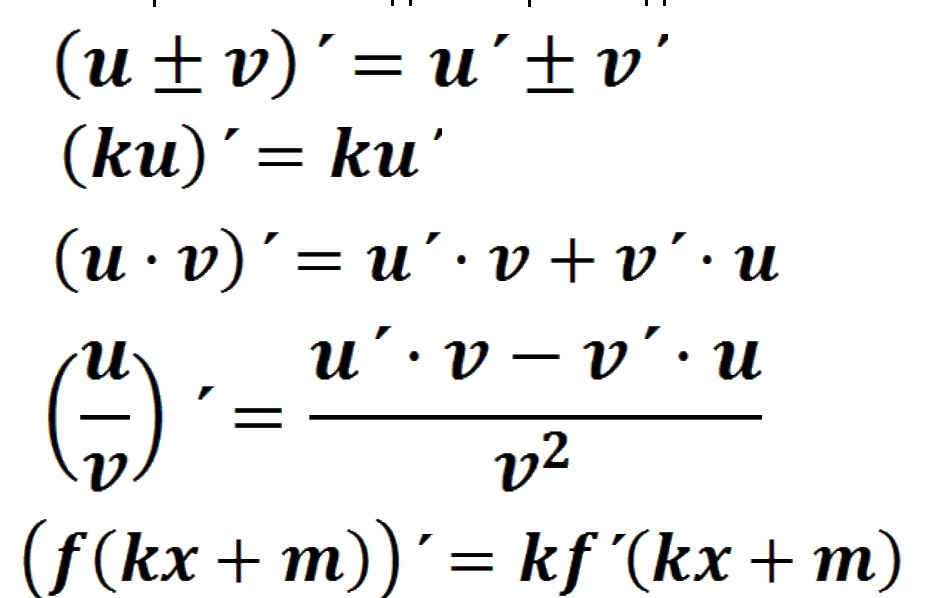 Даже не близко! Что пошло не так?
на самом деле ничего, кроме того, что догадка была неверной. Таким образом, производная от $f(x)g(x)$ НЕ так проста, как
$f'(x)g'(x)$. Наверняка есть какое-то правило для такой ситуации? Там
есть, и поучительно «открыть» его, пытаясь сделать
общий расчет даже не зная заранее ответа.
$$\выравнивание{
{d \ over dx} (& f (x) g (x)) = \ lim _ {\ Delta x \ to0} {f (x + \ Delta
x)g(x+\Delta x) — f(x)g(x)\over \Delta x}\cr
&=\lim_{\Delta x \to0} {f(x+\Delta
x)g(x+\Delta x)-f(x+\Delta x)g(x) + f(x+\Delta x)g(x)- f(x)g(x)\over
\Дельта х}\кр
&=\lim_{\Delta x \to0} {f(x+\Delta
x)g(x+\Delta x)-f(x+\Delta x)g(x)\over \Delta x} +
\lim_{\Delta x \to0} {f(x+\Delta x)g(x)- f(x)g(x)\over
\Дельта х}\кр
&=\lim_{\Delta x \to0} f(x+\Delta x){
g(x+\Delta x)-g(x)\over \Delta x} +
\lim_{\Delta x \to0} {f(x+\Delta x) — f(x)\over
\Дельта х}г(х)\кр
&=f(x)g'(x) + f'(x)g(x)\cr
}$$
Несколько пунктов здесь нуждаются в обсуждении. Сначала мы использовали стандартный
трюк, «добавь и вычти одно и то же», чтобы преобразовать то, что у нас было
в более полезную форму. Что нам действительно нужно знать, так это то, что $\ds \lim_{\Delta x\to 0}f(x+\Delta x)=f(x)$, или на языке раздел 2.5, что $f$ непрерывна в $х$. Мы уже знаем, что $f'(x)$ существует (или весь подход, запись производной от $fg$ через $f’$ и $g’$ не делает смысл). Оказывается, это означает, что $f$ также непрерывна. Вот Почему: $$ \выравнивание{ \lim_{\Delta x\to 0} f(x+\Delta x) &= \lim_{\Delta x\to 0} (f(x+\Delta х) -f(x) + f(x))\cr &= \lim_{\Delta x\to 0} {f(x+\Delta x) -f(x)\over \Delta x}\Delta x + \lim_{\Delta x\to 0} f(x)\cr &=f'(x)\cdot 0 + f(x) = f(x)\cr }$$ 92$. Нарисуйте функцию. Найдите уравнение касательной к кривой в точке $х=2$. Нарисуйте касательную в точке $x=2$. (отвечать) Пример 3. |
