Факториал n равен: Вычисление факториала. Решение задачи на Python

Чему равен факториал n 1? – Обзоры Вики

Факториалы чисел от 1 до 10 Таблица

n	Факториал числа n!	Значение
1	1!	1
2	2!	2
3	3!	6
4	4!	24

Аналогично, кто изобрел факториал? Одним из самых основных понятий перестановок и комбинаций является использование факториальной записи. Используя понятие факториалов, многие сложные вещи упрощаются. Использование! был начат Кристиан Крамп в 1808 году.

Как вычислить факториал n? Расчет факториала. Факториал n обозначается через n! и вычисляется целыми числами от 1 до n. Формула для n факториала: n! = п × (п — 1)!

Как факториалы используются в реальной жизни?

Это очень полезно, когда мы пытаемся подсчитайте, сколько существует различных заказов на вещи или сколько различных способов мы можем комбинировать вещи. Например, сколькими различными способами мы можем расположить n вещей? У нас есть n вариантов для первого.

тогда как работают факториалы? Проще говоря, факториальная функция говорит умножить все целые числа из выбранного числа на единицу. Говоря более математическим языком, факториал числа (n!) равен n(n-1). Например, если вы хотите вычислить факториал для четырех, вы должны написать: … = n*(n -1)!

Фактиарное сложение или умножение? да. Я предполагаю, что вы имеете в виду, поскольку факториал равен , аддитивный факториал будет . Число в таком виде называется треугольным числом, а формула проста.

Как объяснить факториалы?

факториал, в математике произведение всех положительных целых чисел, меньших или равных данному положительному целому числу и обозначаемое этим целым числом и восклицательным знаком.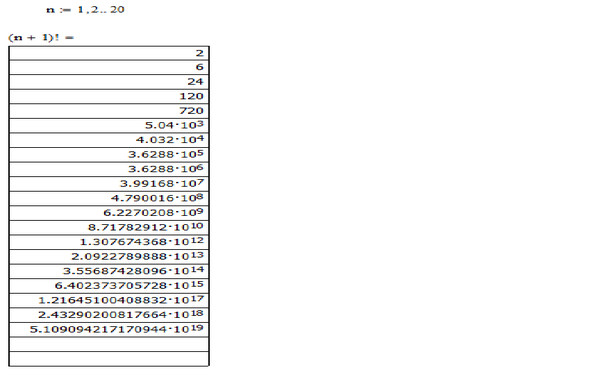 Таким образом, факториал семь записывается как 7!, что означает 1 × 2 × 3 × 4 × 5 × 6 × 7. Факториал ноль определяется как равный 1.

Что такое факториал числа 9? Ответ: Факториал числа 9 равен 362,880.

Что такое N в уравнении химии?

n = м/Мn — количество вещества, в молях, моль. m — масса вещества, в граммах, г. М – молярная масса вещества (масса одного моля вещества) в г моль-1.

Как переписать факториалы?

Сравните факториалы в числителе и знаменателе. Расширьте больший факториал так, чтобы он включал меньшие в последовательности. Сократите общие множители между числителем и знаменателем. Упростите дальше, умножив или разделив оставшиеся выражения.

Как решить 7 факториалов?

1. Чтобы получить 6!, умножьте 120 на 6, чтобы получить 720.
2. Чтобы получить 7!, умножьте 720 на 7, чтобы получить 5040.
3. И так далее.

Можно ли умножать факториалы? Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.

Как вы используете N в математике? В уравнении N представляет собой конкретное число, а не любое число. N + 9 = 12 означает, что N — это число, которое при добавлении к 9 должно дать ответ 12. Таким образом, N может быть только числом 3, потому что только 3 + 9 равно 12.

Для чего используются факториалы в математике?

Факториал — это операция умножения любого натурального числа на все натуральные числа, которые меньше его, что дает нам математическое определение n! … Наконец, факториал используется для вопросы, которые просят вас выяснить, сколькими способами вы можете расположить или заказать определенное количество вещей.

Что такое факториал и для чего он нужен? Факториальная функция (символ: !) говорит умножить все целые числа из выбранного нами числа на 1. Примеры: 4!

Как вы произносите n factorial?

Каково назначение факториала в математике? Факториал операция умножения любого натурального числа на все натуральные числа, которые меньше его, что дает нам математическое определение n! = п * (п — 1) * (п — 2) * (п — 3) …. Наконец, факториал используется для вопросов, в которых вас просят определить, сколькими способами можно упорядочить или упорядочить определенное количество вещей.

Как сложить два факториала?

Двойной факториал — формула и онлайн калькулятор для быстрого расчета

Использование двойного факториала может быть полезным при решении математических задач, которые требуют знания четности чисел. Он может также использоваться в комбинаторике и теории вероятностей для подсчета числа перестановок элементов множества.

Содержание:

1. калькулятор двойного факториала
2. что такое двойной факториал
3. формула двойного факториала
4. примеры нахождения двойного факториала
5. таблица двойных факториалов
6. примеры задач с использованием двойных факториалов

Что такое двойной факториал

Двойной факториал – это математическая операция, которая применяется к натуральным числам и обозначается как n!! (читается как «n двойной факториал«). Она представляет собой произведение всех чисел, меньших или равных n, с одинаковой четностью. Если n четное, то двойной факториал будет равен произведению всех четных чисел от 2 до n, а если n нечетное, то он будет равен произведению всех нечетных чисел от 1 до n.

Формула двойного факториала

{n!! = \begin{cases} n \cdot (n-1)…5\cdot3\cdot1 & \text{если } n>0 \; и \; нечётное \\ n \cdot (n-2)…6\cdot4\cdot2 & \text{если } n>0 \; и \; чётное \\ 1 & \text{если } n=-1, 0 \\ \end{cases}}

n — число, для которого рассчитывается двойной факториал

Примеры вычисления двойного факториала

Пример 1

Найдите двойной факториал 7.

Решение

Так как число 7 нечётное, то для нахождения двойного факториала 7 по формуле нам необходимо перемножить все нечетные числа от 7 до 1:

7!! = 7 x 5 x 3 x 1 = 105

Ответ: 7!! = 105

Полученный ответ легко проверить на калькуляторе .

Пример 2

Найдите двойной факториал 6.

Решение

Число 6 чётное, значит для нахождения двойного факториала 6 нам необходимо перемножить все четные числа от 6 до 2:

6!! = 6 x 4 x 2 = 48

Ответ: 6!! = 48

Проверим ответ с помощьюкалькулятора .

Таблица двойных факториалов

0!!	1
1!!	1
2!!	2
3!!	3
4!!	8
5!!	15
6!!	48
7!!	105
8!!	384
9!!	945
10!!	3840
11!!	10395
12!!	46080
13!!	135135
14!!	645120
15!!	2027025
16!!	10321920
17!!	34459425
18!!	185794560
19!!	654729075
20!!	3715891200
21!!	13749310575
22!!	81749606400
23!!	316234143225
24!!	1961990553600
25!!	7905853580625
26!!	51011754393600
27!!	213458046676875
28!!	1428329123020800
29!!	6190283353629375
30!!	42849873690624000
31!!	191898783962510625
32!!	1371195958099968000
33!!	6332659870762850625
34!!	46620662575398912000
35!!	221643095476699771875
36!!	1678343852714360832000
37!!	8200794532637891559375
38!!	63777066403145711616000
39!!	319830986772877770815625
40!!	2551082656125828464640000
41!!	13113070457687988603440625
42!!	107145471557284795514880000
43!!	563862029680583509947946875
44!!	4714400748520531002654720000
45!!	25373791335626257947657609375
46!!	216862434431944426122117120000
47!!	1192568192774434123539907640625
48!!	10409396852733332453861621760000
49!!	58435841445947272053455474390625
50!!	520469842636666622693081088000000

Надеемся, эта таблица будет полезна вам при решении задач, связанных с двойным факториалом.

Примеры задач на двойной факториал

Задача 1

Сколькими способами можно выбрать команду из 6 человек, если группа состоит из 10 человек, а в команде должно быть ровно 3 мужчины и 3 женщины?

Решение

Для решения этой задачи нужно вычислить количество способов выбрать 3 мужчин и 3 женщин из 5 мужчин и 5 женщин. Количество способов выбрать 3 мужчин из 5 равно 5!!, а количество способов выбрать 3 женщин из 5 равно 5!!. Таким образом, общее количество способов выбрать команду из 6 человек равно произведению двойных факториалов: 5!! × 5!! = 1200.

Ответ: 1200.

Задача 2

На факультете информатики 10 студентов, и они должны разбиться на 5 пар для выполнения лабораторных работ. Сколько существует различных комбинаций пар?

Решение

Для того, чтобы получить количество различных комбинаций пар, нужно вычислить двойной факториал от числа студентов (10!!), а затем поделить его на произведение двойных факториалов от числа студентов в каждой паре (2!!). 5 = (10 × 8 × 6 × 4 × 2) / (2 × 2 × 2 × 2 × 2) = 945

То есть, существует 945 различных комбинаций пар из 10 студентов.

Ответ: 945.

Задача 3

Сколько различных способов можно использовать, чтобы расставить 6 книг на 3 полках так, чтобы на каждой полке лежало хотя бы по одной книге?

Решение

Первую полку можно заполнить любой из 6 книг, вторую — любой из 5 оставшихся книг, а третью — любой из 4 оставшихся книг. Таким образом, количество способов расставить книги на полках равно произведению двойных факториалов: 6!! × 5!! × 4!! = 46080.

Ответ: 46080.

Задача 4

Сколько существует перестановок букв в слове «БАБУШКА»?

Решение

В слове «БАБУШКА» 2 буквы «Б», 2 буквы «У», 1 буква «А», 1 буква «Ш» и 1 буква «К». Количество перестановок букв в этом слове равно произведению двойных факториалов для каждой буквы: 2!! × 2!! × 1!! × 1!! × 1!! × 1!! = 8.

Ответ: 8.

Задача 5

Сколько существует способов разложить число 10 в сумму нечетных положительных целых чисел?

Решение

Число 10 можно разложить в сумму нечетных чисел следующим образом: 1 + 3 + 5 + 1. Количество способов разложить число 10 в сумму нечетных положительных целых чисел равно произведению двойных факториалов: 5!! × 3!! × 1!! = 15.

Ответ: 15.

Двойной факториал можно использовать для вычисления произведения чисел с определенной четностью. Например, произведение всех нечетных чисел от 1 до 15 равно 15!!, а произведение всех четных чисел от 2 до 14 равно 14!! (см. формулу факториала).

Таким образом, двойной факториал может быть использован в различных задачах, связанных с комбинаторикой, теорией вероятностей и математическим анализом. Он позволяет более эффективно решать задачи, связанные с четностью чисел и перестановками элементов множества.

4 способа найти факториал числа в Python | Автор Ramandeep Ladhar

Программа Python для нахождения факториала числа.

Факториальная программа на Python — одна из самых основных программ Python. Но есть много способов написать факториальную программу, что довольно запутанно. Вы согласны?

Очень важно понимать значение факториала и алгоритм факториала числа в Python.

Итак, приступим!

Математически факториал натурального числа n, обозначаемый n! является произведением всех положительных целых чисел, меньших или равных n . Другими словами, умножение числа от 1 до n даст значение факториала n.

Представляется восклицательным(!) знаком после числа, например n!.

Формула: n*(n-1)*(n-2)…..3*2*1

Пример : Значение факториала 6 равно 720 при использовании этой формулы.

6!= 6×5×4×3×2×1= 720

Прежде чем писать код на Python для факториальной программы, мы должны знать алгоритм этой программы. Итак, давайте разберемся с алгоритмом факторного кода.

1. Введите положительное число n.
2. Проверить, больше ли число или равно нулю.
3. Если число равно нулю, вернуть 1, иначе перейти к следующему шагу.
4. Сохранить факториал = 1
5. Теперь проверьте умножение факториала на n, т. е. (factorial×n) и уменьшить n на 1, т.е. (n-1) .
6. Проверьте, больше ли новое значение n 1, если оно истинно, затем повторите шаг 5.
7. Если предыдущее условие ложно, верните factorial .
8. Стоп.

Существует много способов написать программу Python для факториала числа. Давайте разберемся с этими способами

1. Факториальная программа на Python с использованием математического модуля

В этом методе мы должны импортировать математический модуль и использовать встроенную функцию факториала в Python. 9
import math ))

Ввод =10

  #Вывод 
  Введите число: 10 
 Факториал 10: 
 3628800 

Это основной метод записи факториала с использованием итерации. В этом мы будем использовать условие while, чтобы проверить, меньше ли переменная, чем равна заданному числу, чтобы обеспечить количество итераций для получения результата.

 #factorial программа с использованием цикла while 
 n= int(input("Введите число: ")) 
 fact = 1 
 a=1 
 while a <= n : 
 fact*=a 
 a+=1 
 print( «Фактор», «n», «IS», FACT) 

Вход = 20

  #Output 
  Введите номер: 20 
 ФАКТАРИИ 20 IS 24328176640000 

#NOTE: эта программа работать также для отрицательных и нулевых. В случае факториала 0 или отрицательного числа он вернет 1

Цикл for также используется для определения факториала в Python.

 #Программа факториала, использующая цикл for 
 n = int(input("Введите число: ")) 
 fact = 1 
 if n < 0: 
 print("Извините, факториал не существует для отрицательных чисел") 
 elif n == 0: 
 print("Факториал 0 равен 1") 
 else: 
 для i в диапазоне (1,n + 1): 
 fact = fact*i 
 print("Факториал",n, "есть",факт) 

У вас есть вопрос, что такое факториал числа 5? Если да. Давайте найдем факториал числа 5, используя эту факториальную программу.

Ввод= 5

 #Выход 
 Введите число: 5 
 Факториал 5 равен 120 

Рекурсия — это функция, вызывающая сама себя снова и снова. Рекурсию можно использовать для определения факториала числа с помощью функции определения Python.

 #Программа факториала, использующая recursiondef recur_fact (n): 
 if n==1: 
 return n 
 else: 
 return n*recur_fact(n-1)num= int(input("Введите число: "))if num< 0: 
 print("Извините, факториал отрицательного числа не существует") 
 elif num==0: 
 print("Факториал 0 равен 1") 
 else: 
 print("Факториал",num,"is", recur_fact(num)) 

Ввод = 30

  #Output 
  Введите число: 30 
 Факториал 30 равен 265252859812191058636308480000000 

В заключение, программа Factorial на python может быть создана разными способами. Но самым быстрым и эффективным с точки зрения времени является факторный код с использованием math.factorial(). Эта программа на Python для поиска факториала числа мне показалась лучшей.

Попробуйте сами коды и узнайте, какая факториальная программа на питоне вам больше подходит!

Ознакомьтесь с оригинальной статьей по адресу:

Программа факториала на Python — 4 способа — Cloud Punjabi

Факториал положительного целого числа n, обозначаемого буквой n! является произведением всех положительных целых чисел, меньших или равных n. Там…

cloudpunjabi.com

Больше контента на plainenglish.io . Подпишитесь на нашу бесплатный еженедельный информационный бюллетень . Получите эксклюзивный доступ к возможностям письма и советам в нашем сообществе Discord .

Факториал | Encyclopedia.

com

Гейл

просмотров обновлено 21 мая 2018

Число n! — это произведение 1×2×3×4×…× n, то есть произведение всех натуральных чисел от 1 до n, включая само n, где 1 — натуральное число. Он называется либо n-факториальным, либо факториальным n. Таким образом 5! это число 1×2×3×4×5, или 120,

В старых книгах иногда использовался символ In для факториала n, но в настоящее время стандартным символом является число, за которым следует восклицательный знак. В 1808 году французский математик Кристиан Крамп (1760–1826) впервые использовал обозначение n!.

Факториалы появляются во многих формулах статистики, вероятности, комбинаторики, исчисления, алгебры и других формул. Например, формула для количества перестановок n вещей, взятых по n за раз, это просто n!. Если певец выбирает восемь песен для своего концерта, эти песни могут быть представлены в 8!, или 40 320 различных порядках. Точно так же количество комбинаций n вещей r за раз равно n! разделить на произведение r!(n-r)!. Таким образом, количество различных рук, которые можно разыграть в бридже, равно 52! разделить на 13!39!. Это оказывается очень большим числом.

При использовании в сочетании с другими операциями, например, в формуле для комбинаций, функция факториала имеет приоритет перед сложением, вычитанием, отрицанием, умножением и делением, если только скобки не указывают на обратное. Таким образом, в выражении r!(n-r)! сначала выполняется вычитание из-за скобок; тогда р! и (р-н)! вычисляются; затем результаты умножаются.

Как н! определено, 0! без разницы. Однако во многих формулах, таких как приведенная выше, 0! может возникнуть. Если использовать эту формулу для вычисления количества комбинаций из 6 вещей по 6 одновременно, формула дает 6! разделить на 6!0!. Чтобы такие формулы работали, математики решили дать 0! значение 1. Когда это делается, получается 6!/6!, или 1, что, конечно же, равно количеству способов, которыми можно выбрать все шесть вещей.

При замене n все большими значениями значение n! увеличивается очень быстро. Десять факториалов больше трех миллионов и 70! выходит за рамки возможностей даже тех калькуляторов, которые могут представлять числа в экспоненциальном представлении.

Это не обязательно недостаток. В представлении ряда синус х, который равен х/1! — х3/3! + х5/5! -…, знаменатели становятся большими так быстро, что требуется очень мало членов ряда для вычисления хорошей десятичной аппроксимации для конкретного значения синуса x.

Научная энциклопедия Гейла

gale

просмотров обновлено 11 мая 2018 г.

---

Схема умножения положительного целого числа на следующее меньшее целое число часто встречается в математике. Найдите закономерность в следующих выражениях.

7 × 6 × 5 × 4 × 3 × 2 × 1

4 × 3 × 2 × 1

( n + 5) × ( n + 4) × ( n + 3) × ( н + 2) × ( n + 1) × n

Математический символ для этой цепочки множителей — знакомый восклицательный знак (!). Этот образец умножения целых чисел называется n факториалом и записывается как n ! Итак, начиная с наибольшего множителя, n, , факториальная схема выглядит следующим образом:

n ! = н ( н — 1)( н — 2)( н — 3)… (1).

Итак,

3! 3 × 2 × 1 = 6

5! 5 × 4 × 3 × 2 × 1 = 120 и 1! = 1.

Нулевой факториал (0!) произвольно определяется равным 1.

Большинство научных калькуляторов имеют ключ (например, x !), который можно использовать для нахождения значений факториала. По мере того, как n становится больше, значение его факториалов быстро увеличивается. Например, 13! составляет 6 227 020 800 человек.

Как используются факториалы

Во многих математических формулах используется факториальная запись, включая формулы для нахождения перестановок и комбинации . Например, количество перестановок n элементов, взятых n за раз, равно n !, а количество перестановок n элементов, взятых r за раз, равно .

Существует также задача, связанная с простыми и составными числами , в которой используется формула, содержащая факториал. Математики в течение многих лет ломали голову над вопросом, как простых чисел были распространены. Обратите внимание, что среди целых чисел меньше 20 есть восемь простых чисел (2, 3, 5, 7, 11, 13, 17 и 19). Но от 20 до 40 есть только четыре простых числа (23, 29, 31 и 37).

Никто еще не нашел формулы, которая будет генерировать все простые числа. Однако следующая последовательность даст строку из n последовательных составных чисел (числа, которые являются , а не простыми) для любого положительного целого числа n.

( n + 1)! + 2, ( н + 1)! + 3, ( н + 1)! + 4, ( н + 1)! + 5, ( н + 1)! + 6 и так далее до ( n + 1)! + ( н + 1).

Когда n равно 2, обратите внимание, что эта последовательность состоит только из двух членов:

( n + 1)! + 2, ( н + 1)! + ( n + 1)

что

(2 + 1)! + 2, (2 + 1)! + (2 + 1)

За первый срок (2 + 1)! + 2 равно 3! + 2 или (3 × 2 × 1) + 2, что дает значение 8. Второй член имеет значение 9.

Когда n = 2, эта последовательность дает два последовательных числа, которые являются , а не простыми числами: 8, 9. Когда n = 3, эта последовательность дает три последовательных числа, которые являются , а не простыми числами: 26, 27, 28. Это соотношение между значением n и количеством последовательных чисел, которые не являются простыми числами, продолжается в этой последовательности для любого целого значения числа для n. Для больших n, , таких как 300, можно найти последовательность из 300 составных чисел (то есть список из 300 последовательных чисел без простого числа в списке).

см. также Факторы; простые числа, головоломки; Перестановки и комбинации.

Люсия Маккей

Библиография

Стивенс, Ларри. Алгебра для совсем запутавшихся. New York: McGraw-Hill, 2000.

Математика McKay, Lucia

Гейл

просмотров обновлено 11 июня 2018 г.

Число n! есть произведение 1 × 2 × 3 × 4 ×… × n, то есть произведение всех натуральных чисел от 1 до n, включая само n, где 1 — натуральное число. Это называется либо «n факториал», либо «факториал n». Таким образом 5! это число 1 × 2 × 3 × 4 × 5, или 120,

В старых книгах иногда использовался символ In для факториала n, но цифра, за которой следует восклицательный знак , точка в настоящее время является стандартным символом.

Факториалы появляются во многих формулах статистики , вероятности, комбинаторики , исчисления , алгебры и в других местах. Например, формула для количества перестановок n вещей, взятых n в раз , это просто n!. Если певец выбирает восемь песен для своего концерта, эти песни могут быть представлены в 8!, или 40 320 различных порядках. Точно так же количество комбинаций n вещей r за раз равно n! разделить на произведение r!(n — r)!. Таким образом, количество различных рук, которые можно разыграть в бридже, равно 52! разделить на 13!39!.

Это оказывается очень большим числом.

При использовании в сочетании с другими операциями, как в формуле для комбинаций, факториал функция имеет приоритет над сложением , вычитанием , отрицанием, умножением и делением , если не используются круглые скобки, чтобы указать иное . Таким образом, в выражении r!(n — r)! сначала выполняется вычитание из-за скобок; тогда р! и (р — н)! вычисляются; затем результаты умножаются.

Как н! определено, 0! без разницы. Однако во многих формулах, таких как приведенная выше, 0! может возникнуть. Если использовать эту формулу для вычисления количества комбинаций из 6 вещей по 6 одновременно, формула дает 6! разделить на 6!0!. Чтобы такие формулы работали, математики решили дать 0! значение 1. Когда это делается, получается 6!/6!, или 1, что, конечно же, равно количеству способов, которыми можно выбрать все шесть вещей.

При замене n все большими значениями значение n! увеличивается очень быстро.

No related posts.