ОГЭ корни задания. Действия с корнями в заданиях ОГЭ. Извлечение корня. Урок 13. Алгебра 8 класс
12+
4 месяца назад
Математика от Баканчиковой265 подписчиков
Алгебра 8 класс. Какие задания с корнями предлагают на ОГЭ? Сегодня мы частично ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме «Извлечение корней», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам разбор 5 типовых заданий с корнями на ОГЭ. А чтобы Вы проверили свои знания по теме корни, то предложим Вам для самостоятельного решения несколько типовых заданий. Если у Вас появятся вопросы, то мы с удовольствием ответим на них. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:24 Упростить выражение: 2√2 * 5√3 * √6.
01:51 Упростить выражение: √( 15 * 32 * 30 ).
04:26 Упростить выражение: √(4 – 2√3) * √(4 + 2√3) – √2*√8.
05:43 Упростить выражение: 18/(2√3)² – (1/√2)².
06:54 Упростить выражение: √24 – (√3 – √2)².
09:58 Задания с ОГЭ для домашней работы.
Если Вы впервые на нашем канале или не смотрели предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Определения квадратного, кубического, корня n степени. Компоненты корня. Чтение и запись корней. Извлечение корня. Урок 2. Алгебра 8 класс. https://rutube.ru/video/a1f135d897a31e096d939bdbf95588ba/
Рациональные, иррациональные и действительные или вещественные числа. Извлечение корня. Урок 4. Алгебра 8 класс. https://rutube.ru/video/03d750dd166b7b3d86b839af1748588d/
Действия с корнями в формулах разности кубов и суммы кубов. Извлечение корня. Урок 12. Алгебра 8 класс. https://rutube.ru/video/4e9b2bbf0b0c96dfe64973fdfa06c825/
Действия с корнями в формуле разности квадратов. Извлечение корня. Урок 11. Алгебра 8 класс. https://rutube.ru/video/ddb2f58361d3df94db9c99da6a124b20/
Действия с корнями в формулах квадрата суммы и квадрата разности. Извлечение корня. Урок 10. Алгебра 8 класс. https://youtu.
Квадратные корни — Математика — Уроки
Тема урока: «Свойства арифметического квадратного корня»
Цели урока:
Создать условия для обобщения и контроля учащимися знаний и умений по изученной теме.
Способствовать развитию самостоятельности и познавательного интереса школьников.
Содействовать воспитанию организованности, формированию навыков здорового образа жизни.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: презентация, тестовые задания, карточки к самостоятельной работе, кружочки красные, зелёные, синие.
Ход урока:
Организационный момент. 3 мин
Сегодня у нас не совсем обычный урок, к нам пришли гости. Давайте, улыбнемся друг другу и начнем наш урок. Прежде всего, примите правильную осанку: опустите плечи, соедините лопатки, поднимите подбородок и старайтесь соблюдать правильное положение в течение урока. Откройте тетради, запишите число и тему урока «Свойства арифметического квадратного корня». (Слайд 1)
Послушайте стихотворение-загадку:
Он есть у дерева, цветка,
Он есть у уравнений,
И знак особый – радикал –
С ним связан, вне сомнений.
Заданий многих он итог,
И с этим мы не спорим,
Надеемся, что каждый смог
Ответить: это … (корень)
Ребята, сегодня у нас последний урок по теме: «Свойства арифметического квадратного корня». Какие цели каждый для себя поставит на сегодняшний урок? (Слайд 2)
(повторить, обобщить и привести в систему изученный материал )
И наш урок будет проходить под девизом: «Покоряет вершины тот, кто к ним стремится». (Слайд 3)
Вершин на нашем уроке – 5, и каждый должен вложить свои усилия, чтобы покорить эти вершины.
Систематизация теоретического материала. ( Первая вершина – «Теоретическая») 3 мин
(Слайды 4,5)
а) Блиц-опрос ( закончите предложение)
1. Арифметическим квадратным корнем из числа а, называется (неотрицательное число, квадрат которого равен а.)
2. Знак называется (радикал)
3. Число а называется ( подкоренным выражением)
4.
Выражениене имеет смысла ( при а )
5. Сколько имеет корней уравнение х2 = а, если:
а 0 ( два корня х = , х = —)
а = 0 ( один корень х = 0)
а
6. Корень из произведений неотрицательных множителей равен ( произведению корней из этих множителей)
7. Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен ( корню из числителя, деленному на корень из знаменателя)
8.Чему равен ( )
б) Запишем последние три свойства на доске
= · , а ≥ 0, b ≥ 0
= , а ≥ 0, b 0
=
Фронтальная работа с классом. ( Вторая вершина – «Историческая») 5 мин
Всегда интересно знать имя ученого-математика, который ввел новое понятие, либо доказал теорему, либо придумал новый математический символ. Выполнив задания, выясним имя и фамилию великого математика, который в первым ввел знак корня.
Найдите значение выражения (Слайд 6) (записываем только ответы)
=5 × =24 = 0,28 = 24 = | =24 × =6 = 0,5 = 5 = 3 |
Закончили? Поставьте буквы около того примера, ответ которой соответствует этой букве
(Слайд 7)
24 | 3 | 6 | 5 | 0,5 | 0,28 | |
д | е | т | к | р | а | н |
5 24 0,28 24 6\7 24 6 0,5 5 3
Р е н е д е к а р т
Рене Декарт (1596-1650) французский дворянин, Воин, математик, философ, физиолог, мыслитель.
В 1637г ввел знак корня, которым пользуемся мы. (Слайд 8)
4. Самостоятельная работа (Третья вершина – «Самостоятельная») 5 мин
На карточках, которые лежат у каждого из вас на столе, зашифрованы слова .Вы можете их разгадать, выполнив задание.
Карточка 1 | Карточка 2 | Карточка 3 | Карточка 4 | ||
Карточка 5 | Карточка 6 | Карточка 7 | |||
Ё | С | Г | У | Е | А | Ш | Ц | Ж | Л | З | Д | И | О | Р | К | Т | М |
2 | 72 | 12 | 8 | 1,1 | 9 | 24 | 7 | 35 | -0,1 | 1 | 3,6 | 16 | 18 | 0,1 | 0,2 | 17 | 95 |
На доске запишите получившиеся слова : Сердце, уши , рот , легкие, глаза, кожа, мозг.
Привал 3 мин
( привал – остановка в пути для отдыха в походе, путешествии, во время которого также рассказывают разные истории и т. д.)
Я тоже хочу вам поведать такую притчу:
Продавец табака расхваливает на ярмарке свой товар: «Покупайте табак, прекрасный табак! Мой табак не простой, а с секретом. От моего табака стариком не будешь, собака не укусит, вор в дом не залезет.»
Один парень купил немного табака и начал расспрашивать продавца:
– А почему стариком не буду?
– Потому что до старости не доживёшь.
– А почему собака не укусит?
– Так с палкой ведь будешь ходить.
– А почему вор в дом не залезет?
– Потому что всю ночь будешь кашлять.
(Слайд 9)
Таким образом, мы видим: при курении ухудшается внешность, теряется зрение и слух, повышается раздражительность, из-за быстрой утомляемости резко ухудшается успеваемость.
Какие выводы вы сделаете для себя?
(Беречь здоровье, избавляться от вредных привычек, правильно питаться) Если нет дурных привычек, так подумайте стоит ли их заводить?
5.
Физкультурная пауза: (Слайд 10) 2 мин
Буратино потянулся,
Раз – нагнулся, два – нагнулся.
Руки в стороны развел,
Ключик видно не нашел.
Чтобы ключик нам достать,
Нужно на носочки встать.
Работа с учебником (Четвертая вершина)
Открыли 88 страницу учебника. №396. (Слайд 11) 5 мин
Пятая вершина – «Тестовая» 10 мин
Найти значение выражения: -2( )2 А. 9,6 Б. 0 В. 0,38 Г. 2,4 Вычислите: (2 )2 + (-3 )2 А. 42 Б. 18 В. 60 Г. 6 Найти значение выражения: 0,5 + 3 А. 62,93 Б. 0 В. 8,2 Г. 1 Найти значение выражения: — 0,5 ( )2 А. Вычислите значение выражения: А. 0 Б. 0,7 В.1 Г.0,1 | Найти значение выражения: -2( )2 А. 8,75 Б. 0,1 В. 0,28 Г. 3,6 Вычислите: (3 )2 + (-2 )2 А. 47 Б. 8 В. 70 Г. 16 Найти значение выражения: 0,5 + 3 А. 0 Б. 58,61 В. 8,1 Г. 1 Найти значение выражения: — 0,5 ( )2 А. 7 Б. 121 В. 6 Г. 0 Вычислите значение выражения: А. 0 Б. 1 В. 0,3 Г. 0,1 |
141 Б. 9. В. 6 Г. 0Ключ к тесту (Слайд 12)
Самопроверка
1 | 2 | 3 | 4 | 5 |
Б | А | В | В | Г |
Если правильно решено 5 заданий – ставим 5, за 4 задания – 4, за 3 задания – 3
7.
Домашнее задание (Слайд 13) №476 а,б; №478 а,в; №481 а,г,ж
8. Подведение итогов урока
а) рефлексия
Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал сегодня?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал сегодня?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием. А я принимал участие в строительстве храма.
— Ребята, кто работал так, как первый человек, поднимите синие кружочки.
-Кто работал как второй человек, поднимите зелёные кружочки?
— Кто принимал участие в строительстве храма, поднимите красные кружочки.
б) выставление отметок за урок
Спасибо за урок. Пусть у вас будет всегда хорошее настроение. .
(Слайд 14)
Поиски математических корней, 1870-1940 гг.
Поиски математических корней, 1870-1940 гг.
И. Граттан-Гиннесс
Мягкая обложка
ISBN: 9780691058580
130,00 долларов США / 109,00 фунтов стерлингов электронная книга
ISBN: 9781400824045 Доступно как
EPUB или PDF
$91,00/£76,30 130,00 $ / 109,00 £
Shipping to:
Choose CountryUnited StatesCanadaUnited KingdomAfghanistanAland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua And BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia And HerzegovinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCabo VerdeCambodiaCameroonCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCongo, Democratic RepublicCook IslandsCosta RicaCote D’IvoireCroatiaCubaCuraçao CyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland Islands (Мальвинские острова)Фарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные ТерриторииГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГваделупаГуамГватемалаГуэр nseyGuineaGuinea-BissauGuyanaHaitiHeard Island & Mcdonald IslandsHoly See (Vatican City State)HondurasHong KongHungaryIcelandIndiaIndonesiaIran, Islamic Republic OfIraqIrelandIsle Of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKoreaKorea People’ Republic OfKuwaitKyrgyzstanLao People’s Democratic RepublicLatviaLebanonLesothoLiberiaLibyan Arab JamahiriyaLiechtenstein LithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesia, Federated States OfMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinian Territory, OccupiedPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarReunionRomaniaRussian FederationRwandaSaint BarthelemySaint HelenaSaint Китс и НевисСент-ЛюсияСент-МартинСен-Пьер и Микелон Saint Vincent And GrenadinesSamoaSan MarinoSao Tome And PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part) SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia And Sandwich Isl.
Выберите тип электронной книги: EPUBPDF
добавить в корзину добавить в корзинуОб электронных книгах и аудио
Электронная книга в формате PDF должна быть прочитана в нашем мобильном приложении, доступном для телефонов или планшетов Android/iOS. Приложение для настольного компьютера, позволяющее читать PDF-файлы, в настоящее время находится в стадии разработки.
Мы обновим наш Страница часто задаваемых вопросов , когда она станет доступной.Узнайте больше об электронных книгах и аудио от Princeton University Press.
Поддержите свой местный независимый книжный магазин.
- Соединенные Штаты
- Канада
- Великобритания
- Европа
Мы обновим наш Страница часто задаваемых вопросов , когда она станет доступной.Математика
- I. Граттан-Гиннесс
Мягкая обложка
электронная книга
Купить это- Скачать обложку
Хотя о философии Бертрана Рассела и несколько о его логике написано много книг, И.
Граттан-Гиннесс написал первую всестороннюю историю математической основы, содержания и влияния математической логики и философии математики, разработанных Расселом вместе с А.Н. Уайтхед в их Принципы математики (1910-1913).
?
Эта окончательная история критического периода в математике включает подробные отчеты о двух основных факторах, повлиявших на Рассела примерно в 1900 году: теории множеств Кантора и математической логике Пеано и его последователей. Представлены существенные обзоры многих связанных тем и рисунков конца девятнадцатого века: основы математического анализа под Вейерштрассом; создание алгебраической логики Де Морганом, Булем, Пирсом, Шредером и Джевонсом; вклад Дедекинда и Фреге; феноменология Гуссерля; и теория доказательств Гильберта. Многоликая история приема записана до 1940, включая подъем логики в Польше и влияние на философов Венского кружка Карнапа и Гёделя. Сильная американская тема проходит через всю историю, начиная с математика Э. Х.
Grattan-Guinness опирается на около пятидесяти коллекций рукописей, включая архивы Рассела, а также множество оригинальных обзоров. Библиография насчитывает около 1,900 предметов, выявив множество первичных материалов.
Написано для математиков, логиков, историков и философов — «особенно для тех, кто интересуется историческим взаимодействием между этими дисциплинами» — в этом авторитетном отчете рассказывается важная история с самой забытой точки зрения. Уайтхед и Рассел надеялись показать, что (большая часть) математики выразима в рамках их логики; они потерпели неудачу по-разному, но окончательной альтернативной позиции не появилось ни тогда, ни после.
Награды и признание
- Айвор Граттан-Гиннесс, обладатель медали и премии Кеннета О. Мэя за вклад в историю математики, присужденной Международной комиссией по истории математики
И.
Граттан-Гиннесс — профессор истории математики и логики Миддлсекского университета. Основатель журнала History and Philosophy of Logic и бывший президент Британского общества истории математики, он является автором или редактором множества книг, в том числе The Norton History of Mathematics, Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, и Convolutions in French Mathematics, 1800-1840.
«Очень интересный и ценный отчет Граттан-Гиннеса о переплетении развития логики и смежных областей математики… между 1870 и 1940 годами представляет собой значительно переработанный анализ истории того периода… [Его] книга важно, потому что он дает то, чего недоставало: полное описание периода с первичной математической точки зрения». —Джеймс В. Ван Эвра, Исида
«Я не знаю сравнительно всестороннего рассмотрения истории этого важного периода в современной логике. синтез и мастерский обзор, которые дает эта работа.
Хотя большинство людей признают математику основной движущей силой развития современной логики, влияние математики на математику и из нее в значительной степени игнорируется или сводится к минимуму. The Search for Mathematical Roots служит проводником в этой непростой математической дебри». — Альберт К. Льюис, главный редактор журнала The History of Mathematics from Antiquity to Present
обзор истории попыток прийти к пониманию математической логики и ее отношения к математике в период 1870-1940 гг. Учитывая богатые детали и включение недооцененных личностей, которые заслуживают большей известности, это особенно важная и полезная книга», — Джозеф Добен, автор Джордж Кантор: его математика и философия бесконечности
- Удовольствие от математики
Ганс Радемахер и Отто Теплиц - Анри Пуанкаре
Джереми Грей - Призрак Платона
Джереми Грей - История доказательств
Джон Стиллвелл - Игры для вашего разума
Джейсон Розенхаус
Оставайтесь на связи, чтобы быть в курсе последних книг, идей и специальных предложений.
Оставайтесь на связи, чтобы быть в курсе последних новостей о книгах.
Гребень павлина: неевропейские корни математики Джордж Гевергезе Джозеф
1 сентября 2012 г. Проблема европоцентризма сильно преувеличена, особенно когда речь идет об истории математики, но я думаю, нападки на нее — это простой способ заставить людей думать о вас как о искушенном и храбром человеке.
Если Джозеф намеревался, как он неоднократно заявлял, показать, что неевропейцы внесли гораздо больший вклад в современную математику, чем принято считать, он потерпел неудачу. Если он просто хотел показать, что люди за пределами Европы и исламского мира также имели очень сложные математические традиции, я даже не уверен, что ему это удалось.
Большая проблема, похоже, заключается в том, что Джозеф был побужден к написанию этой книги не знаниями (либо знаниями, которые у него уже были и которыми он хотел поделиться, либо просто любовью к погоне за знаниями), а злобой.
Он охватывает много тем, с которыми я не очень хорошо знаком, но в тех областях, где у меня есть возможность обвинить его в чуши, он показывает себя более чем готовым позволить себе вольности с правдой.
Особенно вопиющим примером (который, как я понимаю, является его хобби) является школа Кералы, которой он не просто приписывает независимое открытие некоторых умных понятий в протоисчислении и бесконечных рядах (что, вероятно, уже слишком щедры; есть веские основания полагать, что они получили довольно много помощи от исламских ученых), но на самом деле он несет ответственность за все достижения Ньютона и Лейбница несколько десятилетий спустя, которые, как он утверждает, имели доступ к работе Керальской школы через миссионеров-иезуитов, чему нет абсолютно никаких доказательств и во что не верит ни один заслуживающий доверия историк.
Керала, кстати, также является местом рождения Джозефа. Не то чтобы я предлагаю предвзятость или что-то в этом роде.
Впрочем, эта чушь характерна для всей книги; когда факты не согласуются с вами, просто обратитесь к «сложному пониманию» этих фактов или прямо сфабрикуйте их.
Добавьте изрядное количество снисходительного расизма, направленного против большинства людей, которых вы утверждаете, что защищаете (египтян, месоамериканцев, китайцев), и вуаля! у вас есть книга, за которую вы, очевидно, можете взять 27 евро.
Ортодоксия, которую она призвана бросить вызов, — это усталое соломенное чучело, и Джозеф ничего не делает для опровержения стереотипа об индийских исторических ревизионистах как о завистливых мракобесах и мелких культурных релятивистах.
- история математика
3 марта 2015 г.
Эта книга у меня уже много лет. Время от времени я пролистывал ее и хранил под рукой, потому что интересовался многочисленными историями происхождения математики. В противовес другому обзору здесь автор не выдвигает тезис о европейском наследии математики из других мест и не прославляет индийских математиков. Он предполагает, что могут быть некоторые пути такого рода, но они явно являются свободными гипотезами.
В основном он фокусируется на математике, и в конце концов мы добираемся до реального наследования нашей доминирующей десятичной системы.
Лучше всего для меня работали чередующиеся исторические отрывки с довольно четким изложением, обычно рядом с современной алгеброй, какого-то древнего метода выполнения вычислений. Это было очень интересно для меня, чтобы работать. Я ожидаю вернуться к некоторым математикам в книге здесь и там, чтобы решить больше проблем, которые он предлагает читателю решить.
Это очень беспристрастная книга. Там, где у автора нет времени углубиться в тему, он предлагает другие пути в тексте. Я приму его предложение.
15 апреля 2016 г.
Эта книга поможет вам двигаться вперед! Здесь есть главы, в которых будет сравниваться математика египтян и месопотамцев, а также сравнение индусов и китайцев. Я бы сказал, что это также зависит от того, какая культура вас интересует: вас интересует повторяющийся тип или вас больше интересует «широко распространенная» математическая история
23 июня 2017 г.
Это отличная книга. Особенно с исторической точки зрения, как математические концепции развивались в разных цивилизациях в одно и то же время. Это также дает возрождение многим цивилизациям, забытым под влиянием европоцентризма. Это интересная перспектива изучать историю в стороне от математики. То, как идеи путешествовали из Африки, Ближнего Востока, Индии, Китая и наоборот, также свидетельствует о том, насколько взаимосвязанной была научная сеть даже тогда.
Что касается критических замечаний, то, если рассматривать это как сокровище исторической математики, критиковать особо нечего. Возможно, европейцы воспримут некоторые аспекты европоцентричного подхода к математике как личную атаку. Но это не так. Эта книга нацелена на изучение неевропейской математики. Так что было бы хорошо, если бы кто-то продолжал читать, помня об этом заголовке.
Ханна
148 отзывов1 подписчик
27 декабря 2013 г.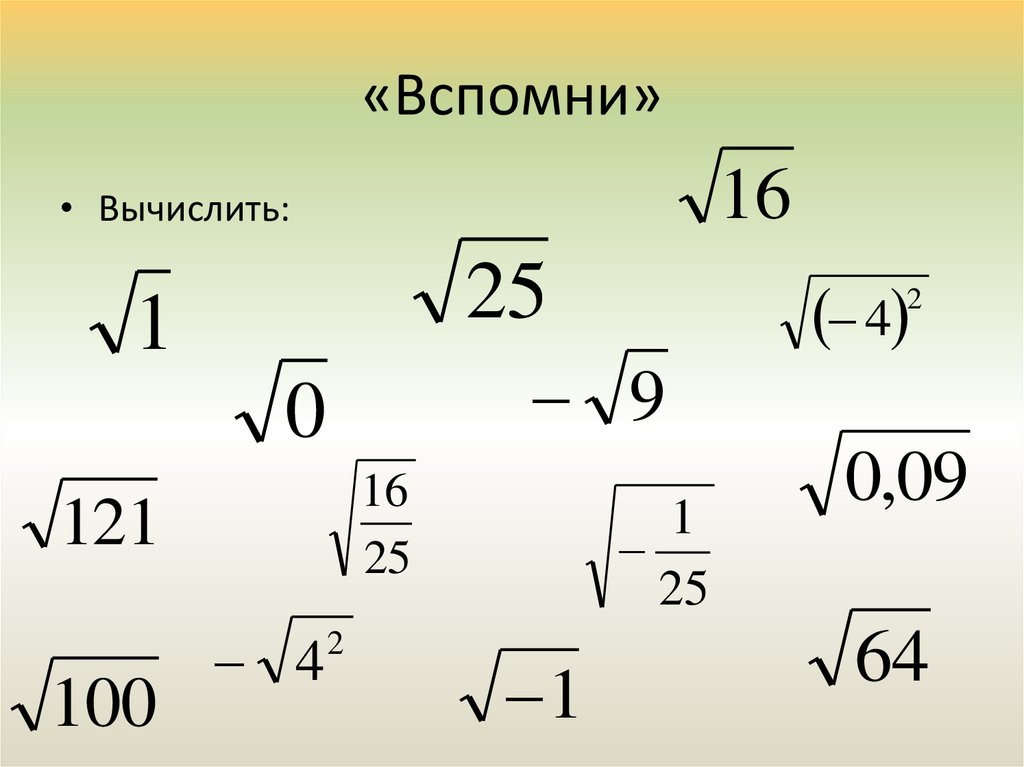
наши учебники. Было действительно интересно узнать о различных исторических корнях математики, которые обычно не обсуждаются. Частично было трудно понять, но большую часть можно было прочитать. Особенно мне понравились его диаграммы, изображающие взаимосвязи между влиянием цивилизаций на развитие математики.
- книги-я-читаю-в-колледже
29 ноября 2020 г.
Это важная книга по истории математики, но, к сожалению, она полезна скорее как справочник, чем как читаемый рассказ.
Джозеф излагает ясным и хорошо задокументированным аргументом, какой вклад в развитие современной математики внесли культуры Египта, древней Месопотамии, Китая, Индии и исламского мира. Его аргумент действует как поправка к европоцентристскому взгляду на то, что вся осмысленная математика возникла благодаря трудам греков. Как будто между греческим творчеством и европейским Ренессансом не произошло ничего существенного и все развитие исходило из европейских умов.
Предоставив этот ценный сборник математических достижений из других частей мира и честно изучив передачу этих идей из культур, в которых они возникли, Джозеф создал очень ценную работу.
К сожалению, текст сухой и утилитарный, хотя мог бы быть более увлекательным. Кажется, что здесь достаточно места для более сильного писателя, чтобы взять любое количество изложенных здесь историй, чтобы создать убедительное повествование, которого заслуживает великая история математических открытий и изобретений.
- история математика
17 мая 2021
Немного запутанный, большую часть времени он больше похож на учебник по математике, чем на историю. Что меня беспокоит, так это то, что это, кажется, написано с единственной целью убедить евроцентричных математиков в том, что небелые люди *занимались* математикой. Любой, кто изучал историю за пределами Европы, знает, что почти в каждой культуре в истории были математика, счет и организационные системы, которые требовали счета и, во многих случаях, приложений счета.
С этой точки зрения кажется очевидным, что греческие/европейские математики поэтому только компилировали методы и стратегии других культур и создавали теоремы и доказательства на основе тысячелетнего опыта таких мест, как Египет, Индия и Китай.
Тем не менее, в этой книге прекрасно освещены оригинальные методы вычислений и проведены параллели с их алгебраическими кузенами. Он также отлично справляется с контекстуализацией социальных и культурных требований к древним математическим методам (например,… египтяне изобрели дроби для справедливого распределения ресурсов и оплаты). Если вы похожи на меня и определенно не изучали историю математики в колледже, это поможет вам быстро узнать о происхождении и современных приложениях!
Майкл
80 отзывов8 подписчиков
17 ноября 2019 г.Для книги по истории математики не так много исторического или математического контекста.
Я читал 2-е издание, где послесловие «Размышлений» было написано гораздо лучше, чем тело.
Судя только по оглавлению, третье издание, кажется, было переписано, поэтому, возможно, оно читается лучше.
6 декабря 2021 г.
Моя лучшая подруга прислала мне эту книгу, и я так рада, что она это сделала. Я просмотрел кучу документальных фильмов о Ньютоне и нашел несколько странных вещей:
— почему он уничтожил работу для своих доказательств исчисления и как он ее открыл. Это было традицией еще во времена Кеплера до него сохранить работу, чтобы показать другим процесс открытия и разжечь дискуссию
— почему он ждал 40 лет, чтобы опубликовать полные работы (через год после смерти Крюка)… Я знаю мертвецов не спорьте, а почему сразу не опубликовать?
— как этот удивительный человек чуть за двадцать открыл все это всего за один год и больше ничего в области математики за свою долгую жизнь? Кажется странным бросать все ради алхимии/религии
— что содержится в его записных книжках, которые были куплены на аукционе Кейнсом и другим человеком, передавшим их государству Израиль
— насколько храбро с его стороны провести тест, проткнув себе глаз иглой, а затем записав результаты эксперимент.
Мне кажется, что это очень жестокая форма пытки, которую можно применять к заключенным во имя «науки» и которая проводится не просто скучающим 20-летним студентом колледжа
— как это люди, которые изобрели арабские цифры, алгебра, число ноль и т. д. просто прекратились после падения Османской империи, и внезапно люди, которые были настолько плохи в астрономии/навигации, что думали, что Северная Америка — это Азия, что им потребовались столетия, чтобы принять ноль после того, как они познакомились с ним (Китай приняли ее почти так, как о ней слышали), и изобрели римские цифры (по крайней мере, мы все можем согласиться с тем, что это устаревшая система счисления для математики) внезапно заполучили этого гения в свои 20, у которого появилось несколько отличных идей, когда ему на голову упало яблоко.
Эта книга помогает показать доказательство, которое, я уверен, многие проигнорируют, как парень, который дал ей 1 звезду. Ну ладно… математика принадлежит всем, это действительно не имеет значения, но довольно грустно видеть, как некоторые люди настолько обеспокоены правдой истории, которая представлена таким образом, что (на этот раз) не имеет предвзятого отношения к людям.
сегодня у власти.
Давайте просто наслаждаться математикой и стремиться к истине. Ничто другое не имеет значения.
Ardyth
639 отзывов50 подписчиков
Отложен как «заброшенный»
19 февраля 2022 г.Больше учебник по математике, чем текст по истории. Не совсем то, что я искал, поэтому я отложил его в сторону.
Хорошая новость заключается в том, что многое из того, что я здесь прочитал, также обсуждается (и в более удобном для непрофессионалов стиле) в книге «Как не ошибиться: сила математического мышления». Предложенная Джозефом диаграмма культурного обмена нова для меня, хотя идеи, которые она предлагает, — нет.
Гребень павлина на данный момент тридцать лет, и я могу с некоторой уверенностью сказать (будучи в то время старшеклассником), что его вступительные залпы были справедливы: он был прав, что неевропейская математика не упоминалась в моем двенадцатилетнем школьном обучении.