Факториал суммы: «Существует ли аналог факториала, но для суммы? » — Яндекс Кью

Содержание

из области математики — Хочу все знать!

Germany.ru → Форумы → Архив Досок→ Хочу все знать!

из области математики

378 1 2 все

shevtsovaсвой человек16.08.07 11:16

16.08.07 11:16

Последний раз изменено 16.08.07 11:22 (shevtsova)

1+2+3+…+n-1+n=n!
забыла формулу

golma1злая мачеха16.08.07 11:26

NEW 16.08.07 11:26

в ответ shevtsova 16.08.07 11:16

n!=1*2*3*…*(n-1)*n

EvilSpiritкоренной житель16.08.07 11:30

NEW 16.08.07 11:30

в ответ shevtsova 16.08.07 11:16

это называется Факториал (если я правильно понял «n!»)
только это не сумма, а перемножение предшествующих чисел

GANDJUBASГанджубас16. 2 + n)/2

юлия 24.02.86знакомое лицо16.08.07 12:08

NEW 16.08.07 12:08

в ответ GANDJUBAS 16.08.07 11:35

ой,как стыдно.я вообще это не помню,расскажите
пожалуйста,что за формула.спасибо

прохладянинпрохожий16.08.07 12:15

NEW 16.08.07 12:15

в ответ юлия 24.02.86 16.08.07 12:08

Формула «Суммы n-первых членов арифметической прогрессии»
В виде «1+2+3+…+n = (n+1)*n/2» была предложена Карлом Гауссом в довольно таки юном возрасте. Если не ошибаюсь, было тогда ему 8 лет от роду.

юлия 24.02.86знакомое лицо16.08.07 12:22

NEW 16.08.07 12:22

в ответ прохладянин 16.08.07 12:15

спасибо!!!

GANDJUBASГанджубас16. 08.07 12:30

NEW 16.08.07 12:30

в ответ юлия 24.02.86 16.08.07 12:08

http://www.courier.com.ru/kvant/kv0406dvorianinov.htm

shevtsovaсвой человек16.08.07 13:16

NEW 16.08.07 13:16

в ответ GANDJUBAS 16.08.07 11:35

надо же, я думала, что сумма — это факториал, а как тогда сумма называется.
За формулу спасибо.

юлия 24.02.86знакомое лицо

16.08.07 13:21

NEW 16.08.07 13:21

в ответ GANDJUBAS 16.08.07 12:30

мамочка,как все сложно,когда голова пару лет не работала

#10

GANDJUBASГанджубас16.08.07 13:35

NEW 16.08.07 13:35

в ответ shevtsova 16. 08.07 13:16

На сколько мне известно специального названия у этой суммы нет. Говорят «Сумма натуралных чисел от и до», «Сумма арифметической прогрессии» и т.д.

#11

ShooTermodicus18.08.07 19:14

NEW 18.08.07 19:14

в ответ EvilSpirit 16.08.07 11:30

В ответ на:

это называется Факториал (если я правильно понял «n!»)

только это не сумма, а перемножение предшествующих чисел

Вообще то,факториал — это произведение всех целых чисел от 1 до n включительно.

#12

fuedor2003знакомое лицо20.08.07 09:59

NEW 20.08.07 09:59

в ответ ShooTer 18.08.07 19:14

В ответ на:

произведение всех целых чисел от 1 до n включительно.

произведение натуральных чисел до n включительно, так лаконичней и тем самым сгущает плотность мысли
в Вики тоже исправил

#13

ShooTermodicus20. 08.07 10:05

NEW 20.08.07 10:05

в ответ fuedor2003 20.08.07 09:59

Думаю, что вы не правы.
Это все таки произведение натуральных чисел именно от единицы до какого-либо данного натурального числа n, т. е. 1╥2╥3╥… ╥n; обозначается n!. Например, 5! = 1╥2╥3╥4╥5 и так далее…
То есть, берем натуральные числа именно с 1, а не с 2, не 3-ех…
П.С. Исправьте вики, что бы откат не делали

#14

fuedor2003знакомое лицо20.08.07 10:11

NEW 20.08.07 10:11

в ответ ShooTer 20.08.07 10:05

попробуйте снова выразить мысль: в чем я не прав?
может, конечно, я не выспался…

#15

ShooTermodicus20.08.07 10:28

fuedor2003знакомое лицо20.08.07 10:36

NEW 20.

08.07 10:36

в ответ ShooTer 20.08.07 10:28

итак
Вы пишите: «произведение всех целых чисел от 1 до n включительно»
я пишу:»произведение натуральных чисел до n включительно»
если Вы не видите идентичности написаного — это не мои проблемы
ввиду той же самой идентичности будем считать Вас неправыми в Вашем утверждении о моей якобы неправоте

#17

fuedor2003знакомое лицо20.08.07 10:42

NEW 20.08.07 10:42

в ответ fuedor2003 20.08.07 10:36

ха, вот Вам и стороннее док-во идентичности написанного
с русской вики можно тыркнуть в английскую — там увидите кальку про «произведение всех целых чисел от 1 до n включительно»
ежели тыркнуть в немецкую — там увидите кальку про «произведение натуральных чисел до n включительно»

если еще не доходит, повторю: «Вы неправы (безаппеляционны), когда говорите, что я не прав»

#18

ShooTermodicus20. 08.07 10:49

NEW 20.08.07 10:49

в ответ fuedor2003 20.08.07 10:36

Как вы видите сами, есть большая разница между произведением всех чисел и просто произведением. Так как в вашем случае не указывается, конкретная величина чисел — не понятно, сколько их именно. В моем же случае, мы имеем конкретный диапазон чисел.

#19

ShooTermodicus20.08.07 10:57

NEW 20.08.07 10:57

в ответ fuedor2003 20.08.07 10:42

Если мне мои знания не изменяют, то натуральные числа в немецком понимании тоже самое, что и целые числа в русском.

Далее, заметьте, что используется слово включительно, которое указывает на диапазон чисел, который отсутствует в вашем утверждении.

#20

Значение, Определение, Предложения . Что такое факториал

Онлайн-переводчик
Грамматика
Видео уроки
Учебники
Лексика
Специалистам
Английский для туристов
Рефераты
Тесты
Диалоги
Английские словари
Статьи
Биографии
Обратная связь
О проекте

Варианты | Примеры | Склонение / спряжение

Значение Викисловарь

Значение Википедия

Источник: Викисловарь

Факториа́л натурального числа n (лат. {n}}}
.

Источник: Википедия

Предложения со словом «факториал»

Сумма N в интервале от нуля до бесконечности… лямбда в степени N делить на факториал N умножить на сумму при V в интервале от нуля до бесконечности умножить на -1 в степени V.
Таким образом, факториал является подходящим кандидатом для арифметики произвольной точности.
Помимо неотрицательных целых чисел, факториал также может быть определен для нецелых значений, но это требует более продвинутых инструментов математического анализа.
Для больших значений аргумента факториал можно аппроксимировать через Интеграл функции дигаммы, используя представление непрерывной дроби.
Поправочный коэффициент пересчета — это факториал числа частиц.
Большинство калькуляторов используют научную нотацию с 2-значными десятичными экспонентами, и самый большой факториал, который подходит, составляет тогда 69!
Сходимость этого ряда к 1 можно видеть из того факта, что его частные суммы меньше единицы на обратный факториал.
В этом случае 42 называется получателем сообщений, а факториал — селектором сообщений.
Мы можем заменить факториал гамма-функцией, чтобы распространить любую такую формулу на комплексные числа.
Другие результаты
Числитель содержит фактор р по определению факториала.
Ряд Тейлора √1 + x с x = 1 и с использованием двойного факториала n!
При реализации без запоминания каждый вызов факториала верхнего уровня включает совокупную стоимость шагов 2-6, пропорциональную начальному значению n. .
способы перестановки букв-распространенная трактовка факториала как числа уникальных перестановок.

Для этого нужно придать смысл биномиальным коэффициентам с произвольным верхним индексом, чего нельзя сделать с помощью обычной формулы с факториалами.
Формула утверждает, что число эйлеровых контуров в орграфе является произведением факториалов определенной степени и числа корневых древостоев.
Тем не менее, обычно считается наиболее естественным способом распространить значения факториалов на сложную функцию.
Хотя последовательность факториалов начинается с жестких чисел в базе 10, не все факториалы являются жесткими числами.
Число возможных ранжирований равно факториалу от общего числа ограничений, что дает основание для термина факториальная типология.
Эта функция может вычислять гораздо большие факториалы, такие как 120!
В 1677 году Фабиан Стедман описал факториалы как применяемые для изменения звона, музыкального искусства, включающего в себя звон многих настроенных колоколов.
Хотя факторная функция имеет свои корни в комбинаторике, формулы, включающие факториалы, встречаются во многих областях математики.
Кроме того, функция pi удовлетворяет той же рекуррентности, что и факториалы, но при каждом комплексном значении z, где она определена.
Как и в случае с базой 10, не все факториалы являются жесткими числами в базе 12. После 7!
Факториальная операция встречается во многих областях математики, особенно в комбинаторике, алгебре и математическом анализе.
Факториальная функция также может быть расширена до нецелочисленных аргументов, сохраняя при этом свои наиболее важные свойства путем определения x!
Интересная вещь в числе 7, что это не только простое факториальное число…
После 1800-х годов Кристиан Крамп продвигал факториальную нотацию во время своих исследований обобщенной факториальной функции, которая применялась к нецелым числам.
Подход Тагучи обеспечивает более полную информацию о взаимодействии, чем типичные фракционные факториальные конструкции, утверждают его сторонники.

Словосочетания

На данной странице приводится толкование (значение) слова «факториал», а также синонимы, антонимы и предложения в которых содержится слово «факториал». Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование слова «факториал», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу качеству значения слова «факториал», просим написать нам в разделе «Обратная связь».

Рекурсия в Python

Сумма чисел от 1 до n

Если бы я хотел узнать сумму чисел от 1 до n, где n — натуральное число, я мог бы посчитать вручную 1 + 2 + 3 + 4 + … + (несколько часов спустя) + n. А можно просто написать цикл for:

n = 0
for i in range (1, n+1):
    n += i

Или использовать рекурсию:

def recursion(n):
	if n == 1:
		return 1
	return n + recursion(n - 1)

У рекурсии есть несколько преимуществ в сравнении с первыми двумя методами. Рекурсия занимает меньше времени, чем выписывание 1 + 2 + 3 на сумму от 1 до 3.

Для recusion(4) рекурсия может работать в обратную сторону:

Вызов функций: (4 -> 4 + 3 -> 4 + 3 + 2 -> 4 + 3 + 2 + 1 -> 10)

Принимая во внимание, что цикл [for] работает строго вперед: (1 -> 1 + 2 -> 1 + 2 + 3 -> 1 + 2 + 3 + 4 -> 10). Иногда рекурсивное решение проще, чем итеративное решение. Это очевидно при реализации обращения связанного списка.

Как и когда происходит рекурсия

Рекурсия появляется когда вызов функции повторно вызывает ту же функцию до завершения первоначального вызова функции. Например, рассмотрим известное математическое выражение x! (т.е. факториал). Факториал определяется для всех неотрицательных целых чисел следующим образом:

Если число равно 0, то будет 1.

В противном случае ответом будет то, что число умножается на факториал на единицу меньше этого числа.

В Python наивная реализация факториала может быть определена как функция следующим образом:

def factorial(n):
	if n == 0:
		return 1
	else:
		return n * factorial(n - 1)

Иногда функции рекурсии трудно понять, поэтому давайте рассмотрим поэтапно.

Рассмотрим выражение factorial(3). Эта и все остальные вызовы функций создают новую среду. Среда представляет собой таблицу, которая сопоставляет идентификаторы (например, n, factorial, print и т. д.) с их соответствующими значениями.

В любой момент времени вы можете получить доступ к текущей среде с помощью locals(). В первом вызове функции единственная локальная переменная, которая определяется n = 3.Поэтому locals() будет показывать {"n": 3}. Так как n == 3, возвращаемое значение становится n * factorial(n - 1).

На следующем этапе ситуация может немного запутаться. Глядя на наше новое выражение, мы уже знаем, что такое n. Однако мы еще не знаем, что такое factorial(n - 1).

Во-первых, n - 1 принимает значение 2.Затем 2 передаётся factorial как значение для n. Поскольку это новый вызов функции, создаётся вторая среда для хранения нового n.

Пусть A — первое окружение, а B — второе окружение. A всё ещё существует и равен {"n": 3} , однако B (что равно {"n": 2}) является текущей средой.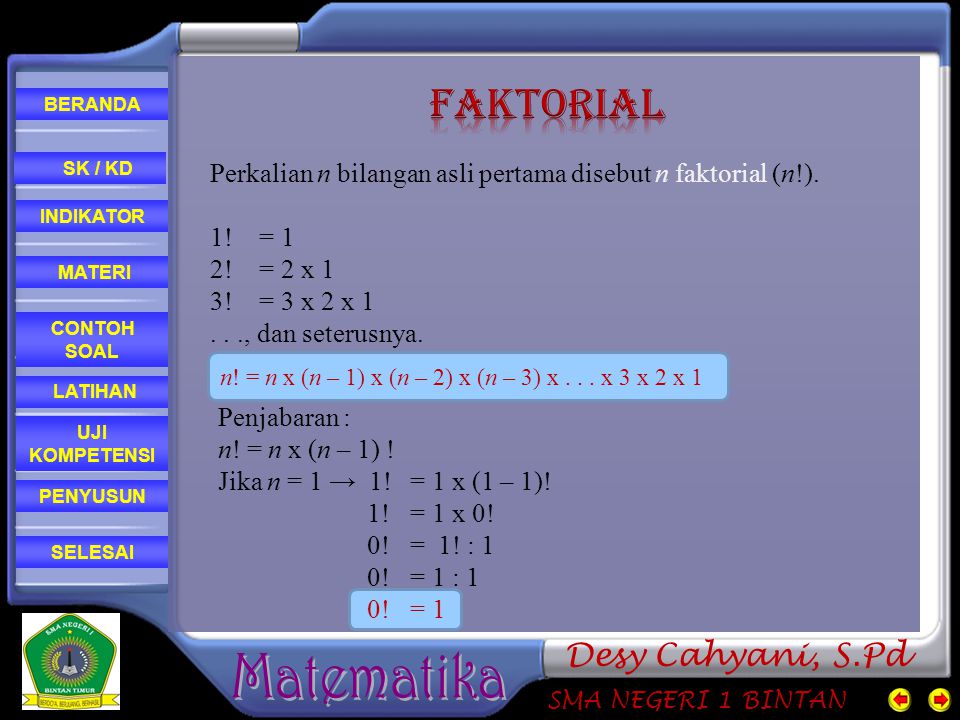 Если посмотреть на тело функции, возвращаемое значение, опять же, n * factorial(n - 1).

Не определяя это выражение, заменим его на исходное выражение return. Делая это, мы мысленно отбрасываем B, поэтому не забудьте заменить n соответственно (т.е. ссылки на B n заменены на n - 1) который использует A n ). Теперь исходное обратное выражение становится n * ((n - 1) * factorial((n - 1) - 1)). Подумайте, почему так?

Теперь давайте определим factorial((n - 1) - 1)). Так как A n == 3, мы пропускаем 1 через factorial. Поэтому мы создаем новую среду C, которая равна {"n": 1}. Мы снова возвращаем значение n * factorial(n - 1). Итак, заменим исходный factorial((n - 1) - 1)) выражения return аналогично тому, как раньше мы скорректировали исходное выражение return. Исходное выражение теперь n * ((n - 1) * ((n - 2) * factorial((n - 2) - 1))).

Почти закончили. Теперь нам нужно оценить factorial((n - 2) - 1). На этот раз мы пропустим через 0. Следовательно, должно получиться 1.

Теперь давайте проведём нашу последнюю замену. Исходное выражение return теперь n * ((n - 1) * ((n - 2) * 1)). Напомню, что исходное выражение возврата оценивается под A , выражение становится 3 * ((3 - 1) * ((3 - 2) * 1)). Здесь получается 6.

Чтобы убедиться, что это правильный ответ, вспомните, что 3! == 3 * 2 * 1 == 6. Прежде чем читать дальше, убедитесь, что вы полностью понимаете концепцию среды и то, как они применяются к рекурсии.

Утверждение, if n == 0: return 1, называется базовым случаем. Потому что это не рекурсия. Базовый случай необходим, без него вы столкнетесь с бесконечной рекурсией. С учетом сказанного, если у вас есть хотя бы один базовый случай, у вас может быть столько случаев, сколько вы хотите. Например, можно записать факториал таким образом:

def factorial(n):
	if n == 0:
    	return 1
    elif n == 1:
    	return 1
   	else:
    	return n * factorial(n - 1)

У вас может также быть несколько случаев рекурсии, но мы не будем вдаваться в подробности, потому что это редкий случай, и его трудно мысленно обрабатывать.

Вы также можете иметь «параллельные» рекурсивные вызовы функций. Например, рассмотрим последовательность Фибоначчи, которая определяется следующим образом:

Если число равно 0, то ответ равен 0.
Если число равно 1, то ответ равен 1.

В противном случае ответ представляет собой сумму двух предыдущих чисел Фибоначчи.

Мы можем определить это следующим образом:

def fib(n):
    if n == 0 or n == 1:
        return n
    else:
        return fib(n - 2) + fib(n - 1)

Я не буду разбирать эту функцию также тщательно, как и с factorial(3), но окончательное значение возврата fib(5) эквивалентно следующему (синтаксически недействительному) выражению:

(
  fib((n - 2) - 2)
  +
  (
    fib(((n - 2) - 1) - 2)
    +
    fib(((n - 2) - 1) - 1)
  )
)
+
(
  (
    fib(((n - 1) - 2) - 2)
    +
    fib(((n - 1) - 2) - 1)
  )
  +
  (
    fib(((n - 1) - 1) - 2)
    +
    (
      fib((((n - 1) - 1) - 1) - 2)
      +
      fib((((n - 1) - 1) - 1) - 1)
    )
  )
)

Решением (1 + (0 + 1)) + ((0 + 1) + (1 + (0 + 1))) будет 5.

Теперь давайте рассмотрим еще несколько терминов:

Tail call — это просто вызов рекурсивной функции, который является последней операцией и должна быть выполнена перед возвратом значения. Чтобы было понятно, return foo(n - 1) — это хвост вызова, но return foo(n - 1) + 1 не является (поскольку операция сложения будет последней операцией).

Оптимизация хвоста вызова (TCO или tail cost optimization) — это способ автоматического сокращения рекурсии в рекурсивных функциях.

Устранение хвоста вызова (TCE или tail cost elimination) — это сокращение хвостового вызова до выражения, которое может быть оценено без рекурсии. TCE — это тип TCO.

Оптимизация хвоста вызова может пригодиться по нескольким причинам:

Интерпретатор может снизить объём памяти, занятый средами. Поскольку ни у кого нет неограниченной памяти, чрезмерные рекурсивные вызовы функций приведут к переполнению стека.

Интерпретатор может уменьшить количество переключателей кадров стека.

В Python нет TCO по нескольким причинам, поэтому для обхода этого ограничения можно использовать другие методы. Выбор используемого метода зависит от варианта использования. Интуитивно понятно, что factorial и fib можно относительно легко преобразовать в итеративный код следующим образом:

def factorial(n):
    product = 1
    while n > 1:
        product *= n
        n -= 1
    return product

def fib(n):
    a, b = 0, 1
    while n > 0:
        a, b = b, a + b
        n -= 1
    return a

Обычно это самый эффективный способ устранения рекурсии вручную, но для более сложных функций может быть трудно.

Другим полезным инструментом является декодер lru_cache, который можно использовать для уменьшения количества лишних вычислений.

Теперь вы знаете, как избежать рекурсии в Python, но когда её нужно использовать? Ответ «не часто». Все рекурсивные функции могут быть реализованы итеративно. Это просто вопрос, как именно сделать. Однако есть редкие случаи, когда можно использовать рекурсию. Рекурсия распространена в Python, когда ожидаемые вводы не вызовут значительного количества вызовов рекурсивных функций.

Если вы интересуетесь рекурсией, стоит изучить функциональные языки, такие как Scheme или Haskell. На таких языках рекурсия намного полезней.

Хотя приведённый выше пример последовательности Фибоначчи, хорошо показывает, как применять определение в python и позже использовать кэш lru, при этом он имеет неэффективное время работы, из-за того, что выполняет 2 рекурсивных вызова. Количество вызовов функции растет экспоненциально до n.

В таком случае лучше использовать линейную рекурсию:

def fib(n):
    if n <= 1:
        return (n,0)
    else:
        (a, b) = fib(n - 1)
        return (a + b, a)

Но у этого примера есть проблема в возвращении пары числе вместо одного. Это показывает, что не всегда стоит использовать рекурсию.

Исследование дерева с рекурсией

Допустим, у нас есть такое дерево:

root
- A
  - AA
  - AB
- B
  - BA
  - BB
    - BBA

Если мы хотим перечислить все имена элементов, мы можем сделать это с помощью простого цикла for. У нас есть функция get_name(), которая возвращает строку с именем узла, функция get_children(), которая возвращает список всех подузлов данного узла в дереве, и функция get_root() для получить корневой узел.

root = get_root(tree)
for node in get_children(root):
    print(get_name(node))
    for child in get_children(node):
        print(get_name(child))
        for grand_child in get_children(child):
            print(get_name(grand_child))
# Выводит: A, AA, AB, B, BA, BB, BBA

Этот код работает хорошо и быстро, но что если под-узлы получили свои под-узлы? И эти под-узлы могут иметь больше под-узлов … Что если вы не знаете заранее, сколько их будет? Решением этой проблемы будет использование рекурсии.

def list_tree_names(node):
    for child in get_children(node):
        print(get_name(child))
        list_tree_names(node=child)
list_tree_names(node=get_root(tree))
# Выводит: A, AA, AB, B, BA, BB, BBA

Возможно, вы не хотите вывести, а вернуть список всех имён узлов. Это можно сделать с помощью передачи прокручиваемого списка в качестве параметра.

def list_tree_names(node, lst=[]):
    for child in get_children(node):
        lst.append(get_name(child))
        list_tree_names(node=child, lst=lst)
    return lst

list_tree_names(node=get_root(tree))
# returns ['A', 'AA', 'AB', 'B', 'BA', 'BB', 'BBA']

Увеличение максимальной глубины рекурсии

Существует предел глубины возможной рекурсии, который зависит от реализации Python. Когда предел достигнут, возникает исключение RuntimeError:

RuntimeError: Maximum Recursion Depth Exceeded

Пример программы, которая может вызвать такую ошибку:

def cursing(depth):
  try:
    cursing(depth + 1) # actually, re-cursing
  except RuntimeError as RE:
    print('I recursed {} times!'.format(depth))
cursing(0)
# Out: I recursed 1083 times!

Можно изменить предел глубины рекурсии с помощью

sys.setrecursionlimit(limit)

Чтобы проверить текущие параметры лимита, нужно запустить:

sys. getrecursionlimit()

Если запустить тот же метод выше с новым пределом, мы получаем

sys.setrecursionlimit(2000)
cursing(0)
# Out: I recursed 1997 times!

В Python 3.5 ошибка стала называться RecursionError, которая является производной от RuntimeError.

Хвостовая рекурсия — как не надо делать

Хвостовая рекурсия — частный случай рекурсии, при котором любой рекурсивный вызов является последней операцией перед возвратом из функции.

Вот пример обратного отсчета, написанного с использованием хвостовой рекурсии:

def countdown(n):
    if n == 0:
        print("Blastoff!")
    else:
        print(n)
        countdown(n-1)

Любое вычисление, которое может быть выполнено с использованием итерации, также может быть выполнено с использованием рекурсии. Вот версия find_max, написанная с использованием хвостовой рекурсии:

def find_max(seq, max_so_far):
    if not seq:
        return max_so_far
    if max_so_far < seq[0]:
        return find_max(seq[1:], seq[0])
    else:
        return find_max(seq[1:], max_so_far)

Хвостовую рекурсию лучше не использовать, поскольку компилятор Python не обрабатывает оптимизацию для хвостовых рекурсивных вызовов. В таких случаях рекурсивное решение использует больше системных ресурсов, чем итеративное.

Оптимизация хвостовой рекурсии с помощью интроспекции стека

По умолчанию рекурсивный стек Python не превышает 1000 кадров. Это ограничение можно изменить, установив sys.setrecursionlimit(15000) который быстрее, однако этот метод потребляет больше памяти. Вместо этого мы также можем решить проблему рекурсии хвоста, используя интроспекцию стека.

#!/usr/bin/env python2.4
# Эта программа показыает работу декоратора, который производит оптимизацию хвостового вызова. Он делает это, вызывая исключение, если оно является его прародителем, и перехватывает исключения, чтобы вызвать стек.
import sys
class TailRecurseException:
  def __init__(self, args, kwargs):
  	self.args = args
    self.kwargs = kwargs
# Эта программа показыает работу декоратора, который производит
# оптимизацию хвостового вызова. Он делает это, вызывая исключение, если
# оно является его прародителем, и перехватывает исключения, чтобы
# подделать оптимизацию хвоста Эта функция не работает, если функция
# декоратора возвращается без хвоста. 
def tail_call_optimized(g):
  def func(*args, **kwargs):
    f = sys._getframe()
    if f.f_back and f.f_back.f_back \
        and f.f_back.f_back.f_code == f.f_code:
      raise TailRecurseException(args, kwargs)
    else:
      while 1:
        try:
          return g(*args, **kwargs)
        except TailRecurseException as e:
            args = e.args
            kwargs = e.kwargs
  func.__doc__ = g.__doc__
  return func

Чтобы оптимизировать рекурсивные функции, мы можем использовать декоратор @tail_call_optimized для вызова нашей функции. Вот несколько примеров общей рекурсии с использованием декоратора, описанного выше:

Факториальный пример:

#  "calculate a factorial"
@tail_call_optimized
def factorial(n, acc=1):
  if n == 0:
    return acc
  return factorial(n-1, n*acc)
print(factorial(10000))
# печатает очень большое число
# и не достигает лимита рекурсии.

Пример Фибоначчи:
@tail_call_optimized
def fib(i, current = 0, next = 1):
  if i == 0:
    return current
  else:
    return fib(i - 1, next, current + next)
print(fib(10000))
# также выводит большое число,
# но не доходит до лимита рекурсии

Чтобы выйти из рекурсии, нужно ввести команду stopCondition.

Исходная переменная должна быть передана рекурсивной функции, чтобы сохранить её.

Приятная факторная сумма из Франции — думайте о своих решениях

Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.

Опубликовано 4 октября 2021 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .

Эта задача адаптирована из задачи, заданной на ежегодном национальном экзамене по математике во Франции. Оцените бесконечный ряд:

1/2! + 2/3! + 3/4! + …

Как обычно, смотрите видео для решения.

Хорошая сумма из Франции. Решается тремя способами

Или продолжайте читать.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.

.
.

.
.
.
.
М
И
Н
Д
.
Д
О
У
Р
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на хорошую факториальную сумму из Франции

(Практически все посты расшифровываются быстро после того, как я делаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки/ошибки, и я исправлю их, спасибо).

Когда я увидел задачу, я решил ее с помощью математической индукции. Затем я исследовал методы и нашел пост на Quora с решениями, использующими телескопическую сумму и степенной ряд. Я представлю все три способа, так как всегда полезно знать разные методы решения проблем.

Метод 1: математическая индукция

Рассмотрим частичную сумму:

S ( n ) = 1/2! + 2/3! + 3/4! + … + n /( n + 1)!

Мы можем вычислить некоторые значения, чтобы установить закономерность:

S (1) = 1/2! = 1/2 = 1 – 1/2!
С (2) = С (1) + 2/3! = 1/2 + 2/6 = 5/6 = 1 – 1/3!
С (3) = С (2) + 3/4! = 5/6 + 3/24 = 23/24 = 1 – 1/4!

Из вычислений мы можем предположить, что формула частичной суммы выглядит следующим образом:

S ( n ) = 1 – 1/( n + 1)!

Докажем это по индукции. Мы установили базовые случаи n = 1, 2, 3. Предположим теперь, что формула верна для некоторого n = k , и мы покажем, что если S ( k ) верно, то S ( k + 1) верно.

S ( k + 1)
= S ( k ) + ( k + 1)/( k + 2)!

По предположению индукции имеем S ( k ) = 1 – 1/( k + 1)!, поэтому можно упростить:

S ( к ) + ( к + 1)/( к + 2)!
= 1 – 1/( к + 1)! + ( к + 1)/( к + 2)!

Теперь умножим второй член на ( k + 2)/( k + 2) и упростим:

1 – ( k + 2)/[( k + 1)!( к + 2)] + ( к + 1)/( к + 2)!
= 1 – (k + 2)/(k + 2)! + ( к + 1)/( к + 2)!
= 1 – 1/( к + 2)!

Это подтверждает второй шаг индукции, и, таким образом, формула индукции верна.

Тогда мы имеем бесконечный ряд S — предел S ( n ), поскольку n стремится к бесконечности. С 1/( n + 2)! n уйдет в 0, как

S = 1 – 0 = 1

Таким образом, бесконечный ряд имеет значение, равное 1.

Метод 2: телескопическая сумма

Начнем снова с рассмотрения частичной суммы.

S ( n ) = 1/2! + 2/3! + 3/4! + … + n /( n + 1)!

Теперь мы перепишем каждый член суммы, используя прием добавления и вычитания 1 из числителя.

к /( к + 1)!
= (k + 1 – 1)/(k + 1)!
= (k + 1)/(k + 1)! – 1/( к + 1)!
= 1/ к ! – 1/( к + 1)!

Мы можем применить эту формулу к каждому члену в сумме, чтобы получить:

S ( n )
= 1/2! + 2/3! + 3/4! + … + n /( n + 1)!
= 1/1! – 1/2! + 1/2! – 1/3! + 1/3! – 1/4! + … + 1/ n ! – 1/( n + 1)!
= 1/1! + (-1/2! + 1/2!) + (-1/3! + 1/3!) + (-1/4! + 1/4!) + … + (-1/ n ! + 1/ n !) – 1/( n + 1)!
= 1/1! – 1/( n + 1)!
= 1 – 1/( n + 1)!

Таким образом, мы имеем ту же частичную сумму, что и в методе 1. Затем мы используем предел, поскольку n стремится к бесконечности, чтобы сделать вывод, что сумма бесконечного ряда равна 1.

Метод 3: степенной ряд

Поскольку сумма включает знаменатели с возрастающими значениями факториальной функции, мы можем думать о степенном ряду для экспоненциальной функции.

e ^х = 1 + х /1! + x ² /2! + x ³ /3! + x ⁴ /4! + …

Мы как-то хотим получить бесконечный ряд с общим членом k /( k + 1)!. Для этого мы разделим обе стороны на x , а затем возьмем производную от обеих сторон.

и ^х / х = 1/ х + 1/1! + х /2! + x ² /3! + х ³/4! + …

Now we take the derivative of each side to get:

( x e ^x – e ^x )/ x ² = -1/ x ² + 0 + 1/2! + 2 х /3! + 3 x ² /4! + …

Затем подставим x = 1.

( e ¹ – e ¹ )/1 ² = -1/1 + 1/1 + 1/1! + 2/3! + 3 x ² /4! + …
0 = -1 + 1/2! + 2/3! + 3/4! + …
0 = -1 + S
S = 1

Таким образом, бесконечный ряд имеет значение, равное 1 — какой невероятный способ решения этой задачи!

Выражаем особую благодарность в этом месяце:

Майклу Анвари
Роберту Зарнке
Фионе Харпер
Кайлу
Джамалу Джексону
Майку Робертсону

Спасибо всем подписчикам на Patreon!

№ по каталогу

Я узнал о методах 2 и 3 на Quora
https://www.quora.com/What-is-sum-of-the-series-1-2-+2-3-+3-4-+- to-infinity

МОИ КНИГИ

Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

Рейтинги книг указаны с января 2022 года. 0002

Думайте о своих решениях представляет собой сборник из 5 книг:

(1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов в логике, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать обдуманные решения и преодолевать предубеждения
(4) Лучшие приемы ментальной математики
(5) Умножение чисел путем рисования линий

Радость теории игр показывает, как можно использовать математику, чтобы перехитрить ваш конкурс. (рейтинг 4,2/5 звезд по 224 отзывам)

40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (оценка 4/5 звезд в 24 обзорах)

Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4,2/5 звезд в 76 обзорах)

Умножение чисел путем рисования линий Эта книга является справочным пособием для моего видео, которое набрало более 1 миллиона просмотров по геометрическому методу умножения чисел. (оценка 4,3/5 звезд в 30 обзорах)

Размышляйте над головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.

Математические головоломки, том 2 — продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)

Math Puzzles Volume 3 — третья книга в серии. (оценка 4,2/5 звезд по 22 отзывам)

KINDLE UNLIMITED

Преподаватели и студенты со всего мира часто пишут мне о книгах по электронной почте. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.

В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited. Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)

ТОВАРЫ

Возьмите кружку, футболку и многое другое на официальном сайте товаров: Следите за своими решениями в Teespring .

13.3.1: Вычисление суммы квадратов для факторного дисперсионного анализа Сводная таблица

Последнее обновление
Сохранить как PDF

Идентификатор страницы
22138

Мишель Ойя
Колледж Тафт

Вам должно быть интересно, как рассчитать дисперсионный анализ 2×2. Мы еще не обсуждали это. Мы только показали вам, что вам не нужно делать это, когда план представляет собой план с повторяющимися измерениями 2×2 (обратите внимание, что это особый случай).

Сейчас мы рассмотрим несколько примеров расчета таблицы ANOVA для планов 2×2. Мы начнем с межсубъектного дисперсионного анализа для планов 2×2. По сути, мы делаем то же самое, что и раньше (в других дисперсионных анализах), и единственная новая вещь — показать, как вычислить эффект взаимодействия.

Помните, что логика дисперсионного анализа заключается в разделении дисперсии на разные части. Формула SS для межсубъектного дисперсионного анализа 2×2 выглядит следующим образом:

\[SS_\text{Всего} = SS_\text{Эффект IV1} + SS_\text{Эффект IV2} + SS_\text{Эффект IV1xIV2} + SS_ \text{Error} \nonumber \]

В следующих разделах мы используем таблицы, чтобы показать расчет каждой SS. Мы используем тот же пример, что и раньше, за исключением того, что мы превращаем его в межсубъектный план 9.0563 . Теперь в каждом состоянии есть 5 разных предметов, всего 20 предметов. В результате мы удаляем столбец Subjects.

Мы вычисляем общее среднее (среднее значение всех оценок). Затем мы вычисляем разницу между каждой оценкой и средним значением. Мы возводим в квадрат разницу оценок и суммируем их. Это \(SS_\text{Total}\), указанное в нижней желтой строке.

Нам нужно рассчитать СС для основного эффекта отвлечения внимания. Мы вычисляем общее среднее (среднее значение всех оценок). Затем мы вычисляем средние значения для двух условий отвлечения внимания. Затем мы относимся к каждому показателю так, как если бы он был средним значением для соответствующего состояния отвлечения внимания. Мы находим различия между средним значением каждого состояния отвлечения внимания и общим средним значением. Затем мы возводим различия и суммируем их. Это \(SS_\text{Отвлечение}\), указанное в нижней желтой строке.

На эти таблицы есть на что посмотреть! Обратите внимание, что мы сначала нашли среднее значение (8,95). Затем мы нашли среднее значение для всех показателей в условиях отсутствия отвлекающих факторов (столбцы A и C), которое составило 11,1. Все оценки разницы для состояния отсутствия отвлечения составляют 11,1–8,95 = 2,15. Мы также нашли среднее значение баллов в состоянии отвлечения внимания (столбцы B и D), которое составило 6,8. Итак, все оценки разницы равны 6,8-8,95 = -2,15. Помните, что средние значения являются точкой равновесия в данных, поэтому оценки разницы составляют +2,15 и -2,15. Среднее значение 8,95 находится между двумя средними условиями (11.1 и 6.8) с разницей в 2,15.

Нам нужно вычислить СС для основного эффекта вознаграждения. Мы вычисляем общее среднее (среднее значение всех оценок). Затем мы вычисляем средние значения для двух условий вознаграждения. Затем мы рассматриваем каждую оценку, как если бы она была средним значением для соответствующего условия вознаграждения. Мы находим различия между средним значением каждого условия вознаграждения и общим средним значением. Затем мы возводим различия и суммируем их. Это \(SS_\text{Reward}\), указанное в нижней желтой строке.

Теперь мы рассматриваем каждую оценку отсутствия вознаграждения как среднее значение условия отсутствия вознаграждения (6.6) и вычитаем его из общего среднего (8,95), чтобы получить -2,35. Затем мы рассматриваем каждую оценку вознаграждения как среднее значение условия вознаграждения (11.3) и вычитаем его из общего среднего (8,95), чтобы получить +2,35. Затем мы возводим различия и суммируем их.

Нам нужно вычислить SS для эффекта взаимодействия между отвлечением и вознаграждением. Это новая вещь, которую мы делаем в ANOVA с более чем одним IV. Как рассчитать вариацию, объясняемую взаимодействием?

Суть вопроса примерно такая. Делают ли индивидуальные средние для каждого из четырех условий что-то немного отличное от групповых средних для обеих независимых переменных?

Например, рассмотрим общее среднее для всех оценок в группе без вознаграждения, мы обнаружили, что оно равно 6,6 Теперь, было ли среднее значение для каждой группы без вознаграждения во всем дизайне равным 6,6? Например, в группе без отвлечения было ли среднее значение для столбца А (условие отсутствия вознаграждения в этой группе) также 6,6? Ответ нет, было 9.6. Как насчет отвлекающей группы? Было ли среднее значение условия вознаграждения в группе отвлечения (столбец B) 6,6? Нет, было 3,6. Среднее значение 9,6 и 3,6 равно 6,6. Если бы не было намека на взаимодействие, мы могли бы ожидать, что средства для условия вознаграждения на обоих уровнях группы отвлечения были бы одинаковыми, они оба были бы равны 6,6. Однако при взаимодействии средства для группы вознаграждения будут зависеть от уровней группы из другого IV. В этом случае похоже, что есть взаимодействие, потому что средства отличаются от 6.6, они 9.6 и 3.6 для условий отсутствия отвлечения внимания и отвлечения внимания. Это дополнительная дисперсия, которая не объясняется средним значением условия вознаграждения. Мы хотим зафиксировать эту дополнительную дисперсию и суммировать ее. Тогда у нас будет мера доли дисперсии, обусловленной взаимодействием условий вознаграждения и отвлечения.

Вот что мы сделаем. Мы найдем четыре средства условия. Затем мы увидим, сколько дополнительных вариаций, которые они объясняют вне группы, означают вознаграждение и отвлечение. Для этого мы рассматриваем каждую оценку как среднее условие для этой оценки. Затем мы вычитаем среднее значение для группы отвлечения и среднее значение для группы вознаграждения, а затем прибавляем общее среднее. Это дает нам уникальную вариацию, которая возникает из-за взаимодействия. Можно также сказать, что мы вычитаем среднее значение каждого условия из общего среднего, а затем прибавляем обратно среднее отвлечение и среднее вознаграждение, что будет равносильно тому же результату и, возможно, будет иметь больше смысла.

Вот формула, описывающая процесс для каждой оценки:

\[\bar{X}_\text{условие} -\bar{X}_\text{IV1} — \bar{X}_\text {IV2} + \bar{X}_\text{Grand Mean} \nonumber \]

Или мы могли бы написать так:

\[\bar{X}_\text{условие} — \bar{X }_\text{Grand Mean} + \bar{X}_\text{IV1} + \bar{X}_\text{IV2} \nonumber \]

Когда вы смотрите на следующую таблицу, мы применяем эту формулу к подсчету каждой из оценок различий. Затем мы возводим в квадрат оценки различий и суммируем их, чтобы получить \(SS_\text{Взаимодействие}\), что указано в нижней желтой строке.

Последнее, что нам нужно найти, это ошибку SS. Мы можем это решить, потому что все остальное мы нашли в этой формуле:

\[SS_\text{Всего} = SS_\text{Эффект IV1} + SS_\text{Эффект IV2} + SS_\text{Эффект IV1xIV2} + SS_ \text{Error} \nonumber \]

Несмотря на то, что этот учебник предназначен для пошагового объяснения, мы полагаем, что вы устали от наблюдения за тем, как мы работаем с дисперсионным анализом 2×2 вручную. Ты и я оба, изготовление этих столов было большой работой. Мы уже показали вам, как вычислить SS для ошибки, поэтому мы не будем приводить здесь полный пример. Вместо этого мы находим ошибку SS, используя уже полученные числа.

\[ \begin{align*} SS_\text{Ошибка} &= SS_\text{Всего} — SS_\text{Эффект IV1} — SS_\text{Эффект IV2} — SS_\text{Эффект IV1xIV2} \\ [4pt] & = 242,95 — 92,45 — 110,45 — 14,45 \\[4pt] &= 25,6 \end{align*}\]

СКО, чтобы мы могли вычислить три \(F\)-значения. Вместо этого, если мы правильно вычислили \(SS\)es, они должны быть такими же, как если бы мы использовали R для расчета \(SS\)es. Давайте заставим R выполнить работу, а затем сравним, чтобы проверить нашу работу.

библиотека (xtable)
А <- с(10,8,11,9,10) #nD_nR
В <- с(5,4,3,4,2) #D_nR
С <- с(12,13,14,11,13) #nD_R
D <- c(9,8,10,11,12) #D_R
Number_spotted <- c(A, B, C, D)
Отвлечение <- rep(rep(c("Не отвлекать", "Отвлекать"), каждый=5),2)
Награда <- rep(c("Без награды","Награда"),каждый=10)
Отвлечение <- as. factor(Отвлечение)
Награда <- as.factor(Награда)
all_df <- data.frame(Отвлечение, Вознаграждение, Number_spotted)
aov_summary <- summary(aov(Number_spotted~Distraction*Reward, all_df))
вязать:: кабель (xtable (aov_summary))

	Df	Сумма кв	Среднеквадратичное значение	F-значение	Пр(>F)
Отвлечение	1	92,45	92,45	57,78125	0,0000011
Вознаграждение	1	110,45	110,45	69. 03125	0,0000003
Отвлечение:Награда	1	14,45	14,45	9.03125	0,0083879
Остатки	16	25.60	1,60	нет данных	нет данных

Беглый просмотр столбца Сумма Квадрат показывает, что мы правильно выполнили свою работу вручную. Поздравляем нас! Обратите внимание, что это не те результаты, которые были у нас ранее с повторными измерениями ANOVA. Мы провели план между субъектами, поэтому у нас не было возможности дальнейшего разделения ошибки SS на часть из-за вариаций субъекта и оставшуюся часть. Мы также получили степень свободы в члене ошибки. Оказывается, с этим конкретным набором данных мы находим p-значения менее 0,05 для всех эффектов (основные эффекты и взаимодействие, которое было не менее 0,05 с использованием тех же данных, но рассматривая его как план с повторными измерениями)

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Мишель Оджа
Лицензия
СС BY-SA
Версия лицензии
4,0
Показать оглавление
да
Включено
да
Теги
1. источник[1]-статистика-17400
2. источник[1]-stats-7945

Нахождение суммы последовательных целых чисел Диапазон (Microsoft Excel)

Обратите внимание: Эта статья написана для пользователей следующих версий Microsoft Excel: 97, 2000, 2002 и 2003. Если вы используете более позднюю версию (Excel 2007 или более позднюю), этот совет может вам не подойти . Чтобы просмотреть версию этого совета, написанную специально для более поздних версий Excel, щелкните здесь: Нахождение суммы диапазона последовательных целых чисел.

Аллена Вятта
(последнее обновление: 20 августа 2020 г.)

Excel включает функцию рабочего листа FACT, которая возвращает факториал значения. (Факториал числа X является результатом умножения 1 * 2 * 3... * X.) Сабиш интересуется, существует ли аналогичная функция, которая вернет сумму значений (1 + 2 + 3... + X) вместо результата значений.

В Excel нет такой встроенной функции, но быстрая математическая формула поможет. Надлежащая терминология для обозначения этого типа суммы — «треугольное число». Это происходит от того, что если сумма была представлена предметами, то их всегда можно было расположить в виде треугольника. Например, если у вас есть 5 объектов в нижнем ряду, 4 в следующем, 3, три в третьем, 2 в четвертом и 1 в верхнем ряду, у вас есть треугольник. Суммирование количества объектов (5 + 4 + 3 + 2 + 1) — это то, что Сабиш хочет сделать.

Ответ на эту проблему можно выразить в виде математической формулы, которая, как сообщается, была открыта Карлом Фридрихом Гауссом. (Что является источником другого названия этого типа числа: сумма Гаусса.) Обратите внимание, что сумма противоположных строк в приведенном выше примере всегда одинакова: 5 + 1 совпадает с 4 + 2. Это верно независимо количества рядов; если было 100 строк, то 100 +1 — это тот же результат, что и 99 + 2, 98 + 3, 97 + 4 и т. д. В итоге вы получите 50 «пар» чисел, равных на 1 больше, чем верхний предел ваш диапазон.

Результатом всего этого — без особых объяснений — является то, что вы можете найти треугольное число для любого положительного значения (где вы начинаете с 1 и заканчиваете на X) следующим образом:

=Х*(Х+1)/2

Таким образом, если у вас есть число в ячейке A1 и вы хотите узнать сумму диапазона от 1 до этого числа, вы можете использовать эту формулу:

=А1*(А1+1)/2

Эта формула обеспечивает простой способ определения требуемой суммы без необходимости использования макроса.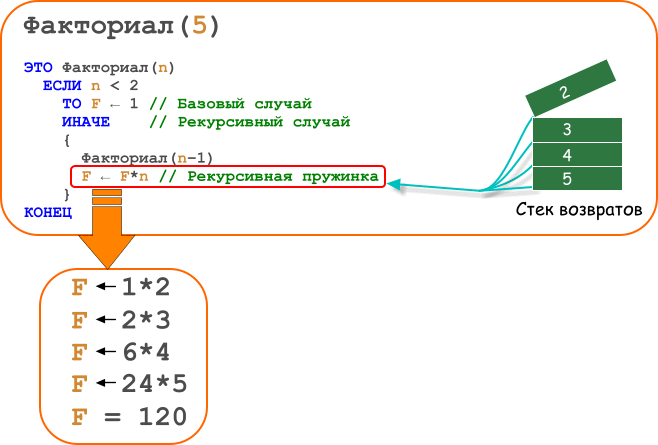

ExcelTips — ваш источник экономичного обучения работе с Microsoft Excel. Этот совет (9997) относится к Microsoft Excel 97, 2000, 2002 и 2003. Вы можете найти версию этого совета для ленточного интерфейса Excel (Excel 2007 и более поздних версий) здесь: Нахождение суммы диапазона последовательных целых чисел .

Биография автора

Allen Wyatt

На его счету более 50 научно-популярных книг и множество журнальных статей. Аллен Вятт является всемирно признанным автором. Он является президентом Sharon Parq Associates, компании, предоставляющей компьютерные и издательские услуги. Узнать больше об Аллене...

Успешно запрограммировать в Excel! Имя Джона Уокенбаха является синонимом мастерства в расшифровке сложных технических вопросов. В этом всеобъемлющем руководстве «Г-н Электронная таблица» показывает, как максимально использовать возможности Excel, используя профессиональные советы по разработке приложений для работы с электронными таблицами из его личной книжной полки. Ознакомьтесь с Excel 2013 Power Programming with VBA уже сегодня!

БЕСПЛАТНАЯ УСЛУГА: Получайте такие советы каждую неделю в ExcelTips, бесплатный информационный бюллетень о продуктивности. Введите свой адрес и нажмите «Подписаться».

Просмотреть последний информационный бюллетень.

(Ваш адрес электронной почты никому никогда не передается.)

Этот сайт

Есть версия Excel, которая использует интерфейс меню (Excel 97, Excel 2000, Excel 2002 или Excel 2003)? Этот сайт для вас! Если вы использовать более позднюю версию Excel, посетите наш ExcelTips Сайт с упором на ленточный интерфейс.