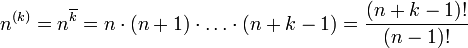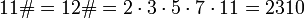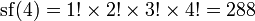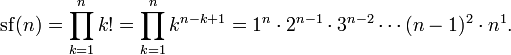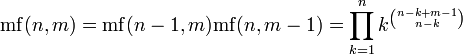Факториал — это… Что такое Факториал?
Факториа́л числа n (лат. factorialis — действующий, производящий умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:
Например:
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так:
- 1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, … (последовательность A000142 в OEIS)
Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.
Связь с гамма-функцией
 Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента.Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при
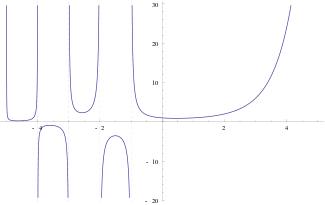 Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
- 100! ≈ 9,33×10157;
- 1000! ≈ 4,02×102567;
- 10 000! ≈ 2,85×1035 659.
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
Таким образом,
где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.
Другие свойства
- Для натурального числа n
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
По определению полагают 0!! = 1.
Последовательность значений n!! начинается так:
- 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … (последовательность A006882 в OEIS).
Кратный факториал
m-Кратный факториал числа
Пусть число n представимо в виде где Тогда[1]
Двойной факториал является частным случаем m-кратного факториала для m = 2.
Кратный факториал связан с гамма-функцией следующим соотношением[2]:
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал даёт число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Праймориал или примориал (англ. primorial) числа n обозначается n# и определяется как произведение всех простых чисел, не превышающих n. Например,
- 11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310.
Последовательность праймориалов (включая ) начинается так:
- 1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … (последовательность A002110 в OEIS).
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен
(поскольку устоявшегося обозначения нет, используется функциональное).
В общем
Последовательность суперфакториалов чисел n⩾0 начинается так:
- 1, 1, 2, 12, 288, 34 560, 24 883 200, … (последовательность A000178 в OEIS).
Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел
- 1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000 … (последовательность A055462 в OEIS)
Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть
где для и
Субфакториал
Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.
Ссылки
См. также
Примечания
- ↑ «Энциклопедия для детей» Аванта+. Математика.
- ↑ wolframalpha.com.
Факториал натурального числа n: как вычислить, формула
Факториал натурального числа n пишется как n! и считается как произведение всех натуральных чисел от 1 до n (включительно).Для n>0:
n! = 1 * 2 * 3 * 4 … * n
Для n=0:
0! = 1
Формула для определения факториала

Примеры:
1! = 1
2! = 1*2 = 2
3! = 1*2*3 = 6
4! = 1*2*3*4 = 24
5! = 1*2*3*4*5 = 120
Рекуррентная формула факториала

Примеры:
5! = 5*(5-1)! = 5×4! = 5×24 = 120
7! = 7*(7-1)! = 7×6! = 5×720 = 5040
Формула Стирлинга
Используется для приблизительного нахождения факториала.

Пример:

Таблица факториалов
| Число n | Факториал n! |
| 0 | 1 |
| 1 | |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 3,991680×107 |
| 12 | 4,790016×108 |
| 13 | 6,227021×109 |
| 14 | 8,717829×1010 |
| 15 | 1,307674×1012 |
| 16 | 2,092279×1013 |
| 17 | 3,556874×1014 |
| 18 | 6,402374×1015 |
| 19 | 1,216451×1017 |
| 20 | 2,432902×1018 |
microexcel.ru
Факториал, перестановки | Александр Будников
Комбинаторика – это, как и намекает само название, раздел математики, изучающий различные наборы или комбинации каких-либо объектов (элементов) – чисел, предметов, букв в словах и прочего. Очень интересный раздел.) Но по тем или иным причинам сложный для восприятия. Почему? Потому, что в нём сплошь и рядом фигурируют более сложные для визуального восприятия термины и обозначения. Если символы 10, 2, 3/4 и даже , или log25 нам визуально понятны, т.е. мы можем их как-то «пощупать», то с обозначениями типа 15!, P9, , начинаются проблемы. Кроме того, в большинстве учебников эта тема излагается довольно сухо и затруднительно для восприятия. Надеюсь, данный материал хотя бы немного поможет решить эти проблемы и комбинаторика вам понравится.)
С комбинаторными задачами ежедневно сталкивается каждый из нас. Когда утром мы принимаем решение, как одеться, мы комбинируем те или иные виды одежды. Когда готовим салат, мы комбинируем ингредиенты. От того, какая комбинация продуктов выбрана, зависит результат – вкусно или невкусно. Правда, вопросами вкуса занимается уже не математика, а кулинария, но тем не менее.) Когда, играем «в слова», составляя маленькие словечки из одного длинного, мы комбинируем буквы. Когда открываем кодовый замок или набираем номер телефона, то комбинируем цифры.) Завуч школы составляет расписания уроков, комбинируя предметы. Футбольные команды на Чемпионате Мира или Европы распределяют по группам, образуя комбинации. И так далее.)
Комбинаторные задачи люди решали ещё в глубокой древности (магические квадраты, шахматы), а настоящий расцвет комбинаторики пришёлся на VI–VII века, во время широкого распространения азартных игр (карты, игральные кости), когда игрокам приходилось продумывать различные ходы и тем самым фактически также решать комбинаторные задачи.) Вместе с комбинаторикой в это же время зародился и другой раздел математики – теория вероятностей. Эти два раздела – очень близкие родственники и идут рука об руку.) И при изучении теории вероятностей мы не раз будем сталкиваться с задачами комбинаторики.
И начнём мы изучение комбинаторики с такого краеугольного понятия, как факториал.
Что такое факториал?
Красивое слово «факториал», но многих пугает и ставит в тупик. А зря. В настоящем уроке мы разберёмся и хорошенько поработаем с этим несложным понятием.) Это слово происходит от латинского «factorialis», что означает «умножающий». И неспроста: в основе вычисления любого факториала стоит обыкновенное умножение.)) Итак, что же такое факториал.
Возьмём какое-нибудь натуральное число n. Совершенно произвольное: хотим 2, хотим 10, — какое угодно, лишь бы натуральное.) Так вот, факториал натурального числа n – это произведение всех натуральных чисел от 1 до n включительно. Обозначается вот так: n! То есть,
Чтобы не расписывать каждый раз это длинное произведение, просто придумали краткое обозначение. 🙂 Читается немного непривычно: «эн факториал» (а не наоборот «факториал эн», как может показаться).
И всё! Например,
Улавливаете идею?)) Отлично! Тогда считаем примеры:
Ответы (в беспорядке): 30; 0,1; 144; 6; 720; 2; 5040.
Всё получилось? Прекрасно! Считать факториалы и решать простейшие примеры с ними уже умеем. Идём дальше. 🙂
Свойства факториала
Рассмотрим не очень понятное с точки зрения определения факториала выражение 0! Так уж в математике договорились, что
Да-да! Такое вот интересное равенство. Что от единицы, что от нуля факториал один и тот же – единичка.)) Пока примем это равенство за догму, а вот почему это именно так, будет ясно чуть позже, на примерах.))
Следующие два очень похожих свойства:
Доказываются они элементарно. Прямо по смыслу факториала.)
Эти две формулки позволяют, во-первых, легко считать факториал текущего натурального числа через факториал предыдущего числа. Или следующего через текущий.) Такие формулы в математике называются рекуррентными.
Во-вторых, с помощью этих формул можно упрощать и считать некоторые хитрые выражения с факториалами. Типа таких.
Вычислить:
Как действовать будем? Последовательно перемножать все натуральные числа от 1 до 1999 и от 1 до 2000? Это одуреешь! А вот по свойствам пример решается буквально в одну строчку:
Или так:
Или такое задание. Упростить:
Снова работаем прямо по свойствам:
Зачем нужны факториалы и откуда они появились? Ну, зачем нужны – вопрос философский. В математике просто так, чисто для красоты, ничего не бывает.)) На самом деле приложений у факториала великое множество. Это и бином Ньютона, и теория вероятностей, и ряды, и формула Тейлора, и даже знаменитое число e, которое представляет собой вот такую интересную бесконечную сумму:
Чем больше задаётся n, тем большее число слагаемых в сумме и тем ближе будет эта сумма к числу e. А в пределе при она станет равна в точности числу e. 🙂 Но об этом удивительном числе мы поговорим в соответствующей теме. А здесь у нас – факториалы и комбинаторика.)
Откуда же они взялись? Они взялись как раз из комбинаторики, с изучения наборов элементов.) Простейшим таким набором является перестановка без повторений. С неё и начнём. 🙂
Перестановка без повторений
Пусть в нашем распоряжении имеются два различных объекта. Или элемента. Совершенно любые. Два яблока (красное и зелёное), две конфеты (шоколадная и карамель), две книги, две цифры, две буквы – всего чего угодно. Лишь бы они были различными.) Назовём их A и B соответственно.
Что можно с ними делать? Если это конфеты, то их, конечно, можно съесть.)) Мы же пока потерпим и будем их располагать в различном порядке.
Каждое такое расположение называется перестановкой без повторений. Почему «без повторений»? Потому, что все элементы, участвующие в перестановке, различны. Это мы пока что для простоты так решили. Есть ещё перестановка с повторениями, где некоторые элементы могут быть одинаковыми. Но такие перестановки чуть сложнее. О них – позже.)
Итак, если рассматривается два различных элемента, то возможны такие варианты:
AB, BA.
Всего два варианта, т.е. две перестановки. Негусто.)
А теперь добавим к нашему набору ещё один элемент C. В этом случае перестановок станет уже шесть:
ABC, ACB, BAC, BCA, CAB, CBA.
Идём дальше. Добавляем ещё один элемент D.
Перестановки из четырёх элементов будем строить так. Сначала на первое место поставим элемент A. При этом оставшиеся три элемента можно переставить, как нам уже известно, шестью способами:
Значит, число перестановок с первым элементом A равно 6.
Но та же самая история будет получаться, если мы на первое место поставим любой из этих четырёх элементов. Они же равноправны и каждый заслуживает оказаться на первом месте.) Значит, общее число перестановок из четырёх элементов будет равно . Вот они:
Итак, подытожим: перестановкой из n элементов называется любой упорядоченный набор из этих n элементов.
Слово «упорядоченный» здесь является ключевым: каждая перестановка различается только порядком элементов, а сами элементы в наборе остаются прежними.
Осталось только выяснить, чему равно количество таких перестановок из любого числа элементов: мы ведь не мазохисты, чтобы каждый раз выписывать все различные варианты и их подсчитывать. 🙂 Для 4-х элементов мы получили 24 перестановки – это уже довольно много для наглядного восприятия. А если элементов 10? Или 100? Хорошо бы сконструировать формулу, которая одним махом подсчитывала бы число всех таких перестановок для любого числа элементов. И такая формула есть! Сейчас мы её выведем.) Но для начала сформулируем одно очень важное во всей комбинаторике вспомогательное правило, называемое правилом произведения.
Правило произведения: если в наборе имеется n различных вариантов выбора первого элемента и для каждого из них есть m различных вариантов выбора второго элемента, то всего можно составить n·m различных пар из этих элементов.
А теперь, пусть теперь имеется набор из n различных элементов
,
где, естественно, . Нам нужно подсчитать число всех возможных перестановок из элементов этого набора. Рассуждаем точно так же.)) На первое место можно поставить любой из этих n элементов. Это значит, что число способов выбрать первый элемент равно n.
Теперь представим, что первый элемент у нас выбран (n способами, как мы помним). Сколько невыбранных элементов осталось в наборе? Правильно, n-1. 🙂 Это значит, что второй элемент можно выбрать уже только n-1 способами. Третий — n-2 способами (т.к. 2 элемента уже выбраны). И так далее, k-й элемент можно выбрать n-(k-1) способами, предпоследний – двумя способами, а последний элемент – только одним способом, так как все остальные элементы так или иначе уже выбраны. 🙂
Что ж, теперь конструируем формулу.
Итак, число способов выбрать первый элемент из набора равно n. На каждый из этих n способов приходится по n-1 способу выбрать второй. Это значит, что общее число способов выбрать 1-й и 2-й элементы, в соответствии с правилом произведения, будет равно n(n-1). Далее, на каждый из них, в свою очередь, приходится по n-2 способа выбрать третий элемент. Значит, три элемента можно выбрать уже n(n-1)(n-2) способами. И так далее:
4 элемента — способами,
k элементов способами,
n элементов способами.
Значит, n элементов можно выбрать (или в нашем случае расположить) способами.
Число таких способов обозначается так: Pn. Читается: «пэ из эн». От французского «Permutation — перестановка». В переводе на русский означает: «перестановка из n элементов».
Значит,
А теперь посмотрим на выражение , стоящее в правой части формулы. Ничего не напоминает? А если переписать справа налево, вот так?
Ну, конечно! Факториал, собственной персоной. 🙂 Теперь можно кратко записать:
Значит, число всех возможных перестановок из n различных элементов равно n!.
В этом и состоит основной практический смысл факториала.))
Теперь мы с лёгкостью можем ответить на многие вопросы, связанные с комбинациями и перестановками.)
Сколькими способами можно разместить на полке 7 разных книг?
P7 = 7! = 1·2·3·4·5·6·7 = 5040 способами.)
Сколькими способами можно составить расписание (на один день) из 6 разных предметов?
P6 = 6! = 1·2·3·4·5·6 = 720 способами.
Сколькими способами можно расставить в колонну 12 человек?
Не вопрос! P12 = 12! = 1·2·3·…·12 = 479001600 способами. 🙂
Здорово, правда?
На тему перестановок есть одна очень известная задача-шутка:
Однажды 8 приятелей зашли в ресторан, в котором стоял большой круглый стол, и долго спорили между собой, как им лучше сесть вокруг этого стола. Спорили-спорили, пока, наконец, хозяин ресторана не предложил им сделку: «Что же вы спорите-то? Голодным всё равно никто из вас не останется 🙂 Сядьте для начала хоть как-нибудь! Хорошенько запомните сегодняшнюю рассадку. Затем приходите завтра и садитесь уже по-другому. На следующий день приходите и садитесь опять по-новому! И так далее… Как только вы переберёте все возможные варианты рассадки и настанет черёд сесть снова так, как сегодня, — то так уж и быть, обещаю вас кормить в своём ресторане бесплатно!» Кто останется в выигрыше – хозяин или посетители? 🙂
Что ж, считаем число всех возможных вариантов рассадки. В нашем случае это число перестановок из 8 элементов:
P8 = 8! = 40320 способов.
Пусть в году у нас 365 дней (високосные для простоты учитывать не будем). Значит, даже с учётом этого допущения, число лет, которое потребуется, чтобы перепробовать все возможные способы посадки, составит:
Более 110 лет! То есть, даже если наших героев в колясках привезут в ресторан их мамы прямо из роддома, то получить свои бесплатные обеды они смогут только в возрасте очень преклонных долгожителей. Если, конечно, все восемь доживут до такого возраста.))
Всё потому, что факториал – ооочень быстро возрастающая функция! Смотрите сами:
Кстати сказать, как с точки зрения перестановок выглядят равенства и 1! = 1? А вот как: из пустого набора (0 элементов) мы можем составить только одну перестановку – пустой набор. 🙂 Так же, как и из набора, состоящего всего из одного элемента, мы тоже можем составить лишь одну перестановку – сам же этот элемент.
Всё понятно с перестановками? Отлично, тогда делаем задания.)
Задание 1
Вычислите:
а) P3 б) P5
в) P9😛8 г) P2000😛1999
Задание 2
Верно ли, что
Задание 3
Сколько различных четырёхзначных чисел можно составить
а) из цифр 1, 2, 3, 4
б) из цифр 0, 5, 6, 7?
Подсказка к пункту б): число не может начинаться с цифры 0!
Задание 4
Слова и фразы с переставленными буквами называются анаграммами. Сколько анаграмм можно составить из слова «гипотенуза»?
Задание 5
Сколько пятизначных чисел, делящихся на 4, можно составить, меняя местами цифры в числе 61135?
Подсказка: вспомнить признак делимости на 4 (по двум последним цифрам)!
Ответы в беспорядке: 2000; 3628800; 9; 24; 120; 18; 12; 6.
Ну как, всё получилось! Поздравляю! Уровень 1 пройден, переходим на следующий. Называется «Размещения без повторений.«
Двойной факториал — это… Что такое Двойной факториал?
Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:
 .
.
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.
Иногда словом «факториал» неформально называют восклицательный знак.
Свойства
Комбинаторное определение
В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества {A,B,C,D} можно линейно упорядочить 4!=24 способами:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
- n! = Γ(n + 1)
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при 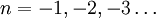 .
.
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые в степени
Таким образом,
 ,
,
где произведение берется по всем простым числам.
Другие свойства
- x!2 > xx > x! > = x, при x>1
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
По определению полагают 0!! = 1.
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал дает число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Примориал (англ. Primorial) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,
Последовательность праймориалов начинается так:
- 2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)
Суперфакториалы
Основная статья: Большие числа
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)
В общем
Последовательность суперфакториалов начинается (с n = 0) с
- 1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)
Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0) равны:
- 1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)
Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал n — произведение первых n (m − 1)-уровневых факториалов, то есть
где 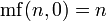 для n > 0 и
для n > 0 и 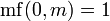 .
.
Субфакториал
Субфакториал 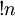 определяется как количество беспорядков порядка
определяется как количество беспорядков порядка 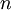 , то есть перестановок
, то есть перестановок 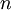 -элементного множества без неподвижных точек.
-элементного множества без неподвижных точек.
Ссылки
См. также
Wikimedia Foundation. 2010.
Формулы для факториалов
Факториал
Формулы для факториалов — это формулы определения конкретных значений факториала.
Определение 1
Под факториалом числа понимается результат произведения всех натуральных неотрицательных чисел, начиная с единицы и до основания факториала.
Термин факториал числа – это математический оператор, но применяется в самых разных научных дисциплинах, таких как комбинаторика, функциональный анализ, теория чисел.
Рисунок 1. Факториал. Автор24 — интернет-биржа студенческих работ
Формула вычисления
Для вычисления факториала конкретного числового выражения, надо найти произведение чисел, начиная от единицы, и заканчивая заданным числом. Исходя из этого, операцию нахождения факториала, возможно определить так:
$n! = 1 • 2 •… • n$, здесь $n$ – это целое не отрицательное числовое значение. Стандартным обозначением факториала является знак восклицания.
Главные факториальные особенности:
- $0! = 1$;
- $n! = n • (n – 1)!$;
- $n!^2 ≥ n^n ≥ n! ≥ n$.
Выражение под номером два определяется термином рекурсия, а сам факториал выступает как элементарная рекурсивная функция. Рекурсивная функция находит широкое распространение в теории алгоритмов и при создании программных приложений для компьютеров, так как большинство алгоритмических структур и программных процедур обладают рекурсивным наполнением.
Готовые работы на аналогичную тему
Вычислить факториал многоразрядных чисел возможно путём применения формулы Стирлинга, дающей, правда, не точный результат, хотя погрешность достаточно мала. Эту формулу можно представить следующим образом:
$n! = (n/e)^n • √(2 • π • n) • (1 + 1/(12 • n) + 1/(288 • n^2) + …)$
$ln (n!) = (n + 1/2) • ln n – n + ln √(2 • π)$,
здесь
- $e$ – является основанием натурального логарифма, его числовое значение примерно равно 2,71828…;
- $π$ – постоянная (отношение длины окружности к диаметру), в числовом выражении равняется примерно 3,14.
Используется ещё и такое определение формулы Стирлинга:
$n! ≈ √(2 • π • n) • (n/e)^n$.
Есть, так же, разные обобщённые формулировки факториала. К примеру, удвоенный, m – кратный, растущий, уменьшающийся. Удвоенный факториал имеет обозначение !! и равняется произведению натуральных чисел в диапазоне от единицы до выбранного числового значения, но только тех, которые обладают такой же чётностью. Пример: $6!! = 2 • 4 • 6$.
M – кратный факториал является разновидностью двойного факториала для всех положительных чисел m:
для $n = mk$ – выполняется условие $n!…!! = ∏ (m • I – r)$, здесь $r$ – целочисленный набор от нуля до $m –1$, $I$ – входит в числовое подмножество от единицы до $k$.
факториал — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | факториа́л | факториа́лы |
| Р. | факториа́ла | факториа́лов |
| Д. | факториа́лу | факториа́лам |
| В. | факториа́л | факториа́лы |
| Тв. | факториа́лом | факториа́лами |
| Пр. | факториа́ле | факториа́лах |
фак-то-ри-а́л
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).
Корень: -фактор-; суффиксы: -и-ал [Тихонов, 1996].
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. произведение всех натуральных чисел от единицы до данного числа включительно ◆ Заметим мимоходом, что использование обозначений для факториалов и то, что в дальнейшем мы будем пользоваться некоторыми рассмотрениями, относящимися к конечным разностям, не выводит нас, по нашему мнению, за пределы наиболее простых положений алгебры. М. В. Остроградский, «Об одном вопросе, касающемся вероятностей извлечения», 1846 г. (цитата из Национального корпуса русского языка, см. Список литературы) ◆ В немашинной математике иногда встречаются примеры определения функции через саму себя (классический пример ― факториал). В. А. Успенский, «Математическая логика в вычислительных науках и вычислительной практике», 2002 г. (цитата из Национального корпуса русского языка, см. Список литературы)
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
- произведение
Гипонимы[править]
- суперфакториал, субфакториал, гиперфакториал
Родственные слова[править]
Этимология[править]
Происходит от англ. factorial (с 1816 г.), из factor «делающий, производящий; создатель, виновник», из facere «делать, производить» (восходит к праиндоевр. *dhe- «девать, делать»)
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
факториал
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. факториал (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
факториал
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. факториал (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
факториал
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. факториал (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Субфакториал — это… Что такое Субфакториал?
Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (т. н. Задача о письмах).
Явная формула
Субфакториал можно вычислить с помощью принципа включения-исключения:
Другие формулы
Таблица значений
- !1 = 0
- !2 = 1
- !3 = 2
- !4 = 9
- !5 = 44
- !6 = 265
- !7 = 1 854
- !8 = 14 833
- !9 = 133 496
- !10 = 1 334 961
- !11 = 14 684 570
- !12 = 176 214 841
- !13 = 2 290 792 932
- !14 = 32 071 101 049
- !15 = 481 066 515 734
- !16 = 7 697 064 251 745
- !17 = 130 850 092 279 664
- !18 = 2 355 301 661 033 953
- !19 = 44 750 731 559 645 106
- !20 = 895 014 631 192 902 121
- !21 = 18 795 307 255 050 944 540
последовательность A000166 в OEIS
Свойства
- где и . Начальные члены последовательности :
- 1, 1, 3, 11, 53, 309, 2119, … (последовательность A000255 в OEIS)
- Число 148349 равно сумме субфакториалов своих цифр (аналог факториона):
- (найдено J. S. Madachy, 1979)
- Субфакториал иногда допускается в математических играх типа получения различных результатов из определённых цифр (например, известна игра Четыре четвёрки, где равенство !4 = 9 может принести пользу).
Факториалы
Факториалы

Факториалы очень простые вещи. Это просто продукты, обозначенные восклицательным знаком. Например, «четырехфакториал» записывается как «4!» и означает 1234 = 24. В общем, n ! («энн факториал») означает произведение всех целых чисел от 1 до № ; то есть n ! = 123… № .
(для различных причин, 0! определяется равным 1, не 0. Запомните это сейчас: 0! = 1.)
Многие (большинство?) Калькуляторов может оценить факториалы для вас. Например, команда факториала доступно в меню «вероятность» на одном из моих калькуляторов:
Ищите «!» кнопку или обратитесь к руководству пользователя.
- Упростить 12! Авторские права Элизабет Стапель 2004-2011 Все права защищены
12! = 1234 … О, черт с этим. Где мой калькулятор …?
12! = 4700
Когда начинаешь делать комбинации, перестановки и вероятность, вы будете упрощать выражения, которые имеют факториалы в числителях и знаменателях.Например:
- Упростите следующее:
Я могу сделать это в своем калькуляторе:
Я также могу работать с определение факториала:
В любом случае 6! 4! = 30
Обратите внимание, как я смог отмените кучу цифр в предыдущей задаче.Это потому что того, как определяются факториалы, и это свойство может упростить вашу работу много.
- Упростите следующее:
Сразу могу отменить от факторов 1 через 14 это будет общим для обоих 17! и 14 !. Тогда я могу упростить то, что осталось получить:
Обратите внимание, как я сократил то, что я должен был написать, оставив пробел («многоточие» или тройной период) посередине.Этот процесс отмены и пропуска станет удобным позже. (как в исчислении, где вы будете часто использовать эту технику), особенно когда вы имеете дело с выражениями, которые ваш калькулятор не может обработать. Например:
- Упростите следующее:
Мой калькулятор не может оценить это для меня, поскольку я имею дело с переменными, а не числами.Больной придется упростить это вручную. Для этого я выпишу факториалы, используя достаточное количество факторов, чтобы получить то, что можно компенсировать. Мышление вернуться к «числам» задачи со словами, последовательные целые числа разделены на одну единицу, поэтому множители в произведении ( n + 2)! имеют вид:
Вернувшись перечень факторов до « n 1 «, я создал список факторов, которые можно свести на нет:
Обратите внимание на то, как я обращался что отмена.Я достаточно расширил факториальные выражения, чтобы смог увидеть, где я могу отменить повторяющиеся факторы. Хотя у меня было понятия не имею, что n может быть, я все еще могу отменить. Сохраните эту технику в своем мозгу, потому что даже если он вам сейчас не нужен, вам почти наверняка понадобится это позже.
Для информации о поиске количество нулей в конце факториала (например, «Сколько нулей находятся в конце 23! после умножения? »), посмотрите на эту заметку.
Верх | Вернуться к индексу
Цитируйте эту статью как: | Стапель, Елизавета.
«Факториалы». Purplemath . Доступно по номеру |
факториалов, перестановок и комбинаций | Ресурсы Wyzant
Факториалы
Факториал обозначается знаком (!) . Когда мы встречаем n! (известный как ‘n факториал’) мы говорим, что факториал — это произведение всех целых чисел между 1 и n , где n всегда должно быть положительным.
Например
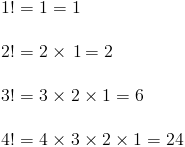
0! — частный случай факториала.

Это особенное, потому что нет положительных чисел меньше нуля, и мы определили факториал как произведение чисел от n до 1. Мы говорим, что 0! = 1, заявив что произведение без чисел равно 1. Рассуждения и математика, лежащие в основе этого сложно и выходит за рамки этой страницы, поэтому давайте просто примем 0! как равный к 1.
Это математически верно и позволяет нам переопределить n! следующим образом:
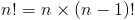
Например
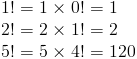
Вышеупомянутое позволяет нам манипулировать факториалами и разбивать их, что полезно в комбинациях и перестановках.
Полезные факториальные свойства
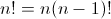
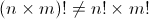
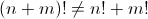

Важно помнить два последних свойства. Факториальный знак НЕ распределяет через сложение и вычитание.
Перестановки и комбинации
И перестановки, и комбинации в математике относятся к различным способам организации заданный набор переменных.Перестановки не строги, когда дело доходит до порядка вещей, пока есть Комбинации.
Например; учитывая буквы abc
Перестановки перечислены ниже.
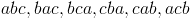
С другой стороны, комбинации считаются разными, все вышеперечисленное считается то же самое, поскольку у них одинаковые буквы, только расположенные по-разному.В других слова, в сочетании, вы не можете просто переставить одни и те же буквы, а затем заявить чтобы получилось совсем другое сочетание. Комбинации делаются по-разному: abc , мы можем составить ряд комбинаций, взяв группы букв в один раз, т.е.
В группах по 1 получаем

В группах по 2 человека получаем
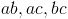
В группах по 3 человека получаем
Из вышесказанного вы должны увидеть, что Комбинации предназначены для определения того, сколько способов вы можете комбинировать различные элементы данного объекта.
Обозначения для комбинаций даны как
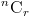
что означает количество комбинаций из n элементов, занимающих r элементов при время
Например
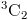
означает найти количество способов, которыми можно объединить 3 элемента, принимая 2 за раз, и из в предыдущем примере мы видели, что это 3.
Другой пример, иллюстрирующий это, выглядит следующим образом:
Даны четыре буквы abcd найти
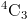
решение:
Помните, что порядок не имеет значения, когда речь идет о комбинациях, например, bcd то же самое, что и dbc , то же самое, что и cdb
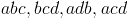
другими словами,
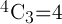
Комбинации также обычно обозначают как
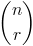
и рассматриваемый в приведенном выше примере можно было бы задать как
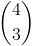
Поэтому важно помнить, что
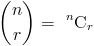
Теперь, когда мы увидели, что такое комбинации, давайте перейдем к соотнесению факториалов и комбинации.
Комбинированная функция может быть определена с использованием факториалов следующим образом:
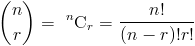
Мы можем доказать, что это правда, на предыдущем примере;
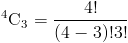
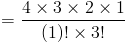
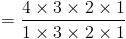
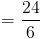
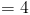
это тот же ответ, который мы получили раньше.
Вернемся к перестановкам, которые мы определили выше и также видели пример. Перестановки обозначаются следующими
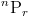
что означает количество перестановок n элементов, взятых r элементов на время.
Например; учитывая 3 буквы abc найти
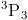
решение:
Помните, что повторение разрешено в перестановках, в отличие от комбинаций;
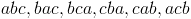
что означает, что есть 6 способов, другими словами
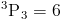
Функция перестановки также может использовать факториалы:

Мы можем доказать сказанное выше на предыдущем примере.
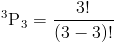


Это тот же ответ, что и раньше.
Если вы внимательно посмотрите на формулы для комбинаций и перестановок, вы сможет увидеть, что эти два значения могут быть выражены друг относительно друга, т. е.
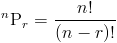
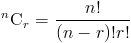
из вышеизложенного можно вывести следующие отношения:
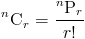
Сказанное выше можно доказать, подставив формулу для перестановок в уравнение

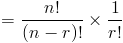

Что, как мы уже видели, является формулой комбинаций.
Примеры факториалов, перестановок и комбинаций
Пример 1
Оцените следующее без использования калькулятора
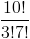
Шаг 1
Мы видели, что относительно большое число (например, 10 в этом примере) может быть разбито вниз в продукт факториалов, т.е.
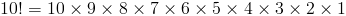
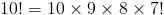
Шаг 2
Мы можем использовать приведенное выше, чтобы оценить выражение как

Шаг 3
С 7! появляется как в числителе, так и в знаменателе, мы можем перейти к отмене это из


Шаг 4
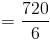
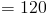
Пример 2
Оцените следующее

Шаг 1
Мы уже определили комбинацию обозначений выше как:

Шаг 2
Следовательно, мы можем просто подставить в приведенную выше формулу
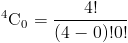
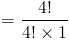
Шаг 3
Числитель и знаменатель равны, поэтому мы можем просто сократить их как

Пример 3
Оцените следующее выражение
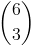
Шаг 1
Обозначения выше не должны быть такими уж незнакомыми, если вы просмотрели страницу всю эту страницу.Мы видели это

Отсюда следует, что
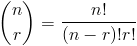
Шаг 2
Как и в предыдущем примере, мы можем просто подставить и решить
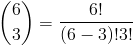
Шаг 3
но верно и следующее
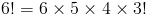
и мы можем быстро увидеть, что
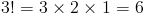
Шаг 4
И поэтому мы можем заменить вышеприведенное, чтобы упростить вычисления

Вычеркивая равные члены в числителе и знаменателе, получаем
= 5 х 4 = 20
Пример 4
Вычислите следующие
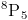
Шаг 1
Обозначения, использованные выше, являются обозначениями перестановок и означают следующее:
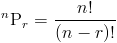
Шаг 2
Таким образом, мы можем подставить переменную, чтобы получить:

Шаг 3
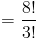
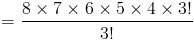
Шаг 4
3! отменяется, чтобы оставить следующее выражение
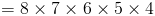
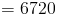
Викторина по факториалам, перестановкам и комбинациям
1.Насколько разными способами вы можете выбрать комитет из 5 человек из группы из 20 человек?Приведенный выше вопрос спрашивает, сколькими способами вы можете выбрать 5 вещей из 20, который, по сути, спрашивает, сколько комбинаций из 5 вещей вы можете выбрать из пул из 20 вещей т.е.
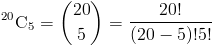
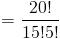
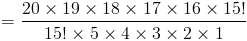

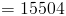
15504
2.Если вы подбросите монету 10 раз, возможны 1024 (или 2 10 ) возможных исходов. У скольких из этих исходов есть 6 хвостов?Когда вы подбрасываете монету один раз, есть два возможных исхода; голова или хвост. Если вы подбрасываете монету более одного раза, выходы появляются в комбинациях орлов и решки: например: если вы дважды подбросите монету, вы получите; 2 головы, или 2 хвоста, или голова и хвост, или хвост и голова.Другими словами, мы ищем для комбинаций! Поэтому вопрос задает

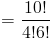
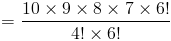
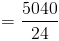
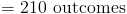
210
3. Сколько разных способов можно расположить буквы слова? КОМБИНАЦИИ ?Этот вопрос действительно прост, уловка состоит в том, чтобы игнорировать вводящий в заблуждение выбор словосочетания.Этот вопрос касается перестановок, поскольку нас попросили расположите буквы без какого-либо порядка.
Все, что нам нужно сделать, это подсчитать количество букв в слове «КОМБИНАЦИИ».



47
00
3b.Сколько разных способов можно расположить буквы слова? КОМБИНАЦИИ с первыми тремя буквами как BAN ?Этот вопрос аналогичен приведенному выше, нам все еще задают перестановки (расположение) букв слова «КОМБИНАЦИИ». Единственная разница здесь заключается в том, что нас спросили, чтобы первые 3 буквы всех различных перестановок должен быть «ЗАПРЕТ».
Так как же нам с этим справиться?
Решение состоит в том, чтобы вычесть количество букв, положение которых постоянное, и затем переставьте оставшиеся буквы:
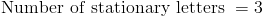
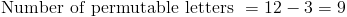
Поэтому количество различных способов расстановки букв в «КОМБИНАЦИЯХ» с BAN в качестве первой буквы:

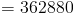
362880
.Функциядля факториала в Python
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Факторинг и факториалы | Потерянное письмо Гёделя и P = NP
Вычисление факториальной функции fast breaks factoring
Адриан-Мари Лежандр был одним из величайших теоретиков числа века. Он доказал целый ряд потрясающих результатов. Интересно, что он подумает о приложениях и последствиях своей работы более века спустя. Одним из его великих открытий является формула дублирования для гамма-функции .Гамма-функция,, — это функция, определенная для всех комплексных чисел, которая согласуется с факториальной функцией для натуральных чисел. В некотором смысле вы должны думать о гамма-функции как о обобщении факториальной функции. Факториальная функция, конечно, определяется для натуральных чисел как:
Точное соотношение между ними таково: вы можете спросить, почему, а нет? Здесь есть интересная история, но я не тот, кто ее рассказывает, так что нам придется просто принять ее.См. Подробности у наших друзей в Википедии.
Так что же такое формула дублирования и почему она связана с факторингом? Я объясню. Формула такая: для всего комплекса
Обоснование того, что это называется «Формулой дублирования», состоит в том, что левая часть — это почти «дублирование». За исключением формулы, у двух вхождений гамма-функции одно и то же значение. Отсюда и название «Формула дублирования». Однако две гамма-функции оцениваются с немного разными значениями: одна at и одна at.Эта небольшая разница, на мой взгляд, не является точным дублированием: возможно, ее следует называть «формулой почти дублирования». Думаю, это имя не было бы таким крутым и захватывающим.
Итак, какова связь между формулой дублирования и факторингом? Вскоре мы увидим, что если формула представляет собой формулу дублирования действительных , то мы могли бы использовать полиномиальное время. Таким образом, Лежандр почти открыл формулу, которая могла бы быстро разложить на множители, сломала бы современные криптосистемы, основанные на факторинге, такие как RSA, и в целом дала бы огромный результат.Увы, есть что маленькое, но критичное. Он почти не промахивается. Как говорил агент Максвелл Смарт в старом телешоу «Get Smart», « пропустили на ». Точнее, если бы формула была
для некоторой константы и некоторого полинома от, то факторизация будет простой. Остальная часть этого поста — объяснение того, почему это правда.
Факторинг с факториалами
Одно из любопытных свойств — народная теорема об арифметической сложности.Скажем, функция имеет арифметическую сложность при условии, что есть арифметическая схема, выполняющая пошаговые вычисления. Как обычно, арифметическая схема начинается с переменных и значения, затем на каждом шаге она выполняет одну из основных арифметических операций с парой предыдущих значений. Ответ — это, конечно, последнее вычисленное значение.
Одно из основных предположений современной криптографии состоит в том, что факторизация целых чисел сложна. Для криптографии обычно требуется менее общее предположение: предположим, что для случайных простых чисел в диапазоне.Тогда его сложно найти и из только что предоставленного достаточно большого размера. Обратите внимание, что часто на простые числа накладываются дополнительные ограничения, но они не влияют на наше обсуждение.
Под «жестким» мы можем понимать, что не существует алгоритма с полиномиальным временем или даже что нет схемы с полиномиальным размером. Это предположение связано с множеством проблем. Во-первых, проблема факторинга заключается в том, что он вряд ли будет NP-полным. Во-вторых, лучшие алгоритмы факторинга — «субэкспоненциальные».Например, приблизительное время работы сита числового поля:
где находится о. (В показателе степени есть несколько меньших членов, но это главный член.) Таким образом, если бы факторинг был NP-трудным, это имело бы ужасные последствия для теории сложности. В другом посте я расскажу о допущении факторинга. А пока я просто замечу, что на конференции несколько лет назад Ави Виджерсон говорил об использовании факторингового допущения, а Майкл Рабин говорил о возможностях того, что факторинг может быть простым.
Я, как и многие другие, нахожу эту проблему чрезвычайно интересной. В этом посте я хочу указать на старую, но интересную связь между факторингом и факториалами. В следующих статьях я расскажу о лучших текущих подходах к факторингу и возможности улучшения методов в будущем. А пока мы сосредоточимся на связи с факториальной функцией. Вот народная теорема:
Теорема 1 Если можно вычислить с помощью прямолинейного арифметического вычисления по шагам, то факторизация имеет схемы полиномиального размера.
Мы сформулировали теорему как неоднородный результат. Если вам нужна равномерная оценка, вам нужно сделать более сильное предположение, что арифметическая схема для однородна.
Доказательство этой народной теоремы простое. Предположим, вы хотите разложить на множители какое-то ненулевое число, которое является составным. Для любого числа определите число как. (Как обычно, это наибольший общий делитель (НОД) и.) Мы утверждаем, что он обладает следующим ключевым свойством: либо или, либо является собственным делителем.Это следует непосредственно из определения gcd.
Теперь мы будем использовать эту функцию и двоичный поиск, чтобы получить правильный коэффициент. Когда у нас есть такой фактор, мы можем получить все факторы, снова применив этот метод. Бинарный поиск работает следующим образом: установить и. Обратите внимание, что интервал имеет следующее свойство: and that. Последнее следует, поскольку не может быть; таким образом, если он меньше, чем у нас есть соответствующий коэффициент. В общем, у нас всегда будет интервал, чтобы и.
Предположим, у нас есть такой интервал.Мы утверждаем, что не может быть равным. Предположим от противного. Из этого следует, что и. Таким образом, должно равняться, что невозможно. Так . Позвольте быть числом, которое ближе всего к средней точке между и Проверьте, является ли правильный коэффициент. Если это не так, то есть только два случая. Во первых, это gcd. В этом случае переходите к интервалу. Во втором случае gcd есть, в этом случае переходим в интервал. Поскольку этот процесс в конечном итоге останавливается, он должен найти правильный коэффициент.
Не хватает одного, но критического момента.Мы не можем позволить себе вычислить факториалы, использованные в описанной выше процедуре. Они будут слишком большими. Итак, мы просто используем арифметическую схему для выполнения всех вышеперечисленных вычислений, но делаем их все по модулю. Ключевым моментом является то, что это не меняет никаких расчетов НОД. Это зависит от того же простого факта, что и.
В чем сложность факториалов
Итак, в чем сложность вычислений. Поскольку в настоящее время факторинг считается сложной задачей, очевидно, что это трудно вычислить.Но действительно ли это сложно?
Вспомним формулу дублирования:
Если вместо этого формула была
, тогда был бы быстрый алгоритм для факториала. Тогда мы сможем фактор. Позвольте быть стоимость вычислений. Тогда такое уравнение даст
Это подразумевает быстрый метод вычислений.
Представьте себе, что где — рациональная функция, а каждый — экспоненциальный член. Это член формы, где и являются многочленами.Если бы это было правдой, то было бы легко вычислить. Обратите внимание, что это остается верным, даже если тождество верно только для плотного подмножества натуральных чисел. Это должно удовлетворять свойству, что для каждого существует не более того.
Даже больше. Предположим, что это функция, так что
для натуральных чисел. Тогда будет достаточно быстрого вычисления этой функции. Обратите внимание: суть этого обобщения заключается в том, что вы не можете использовать какой-то простой аргумент роста, чтобы показать, что не существует настоящей формулы формулы дублирования — по крайней мере, я ее не вижу.
Открытые задачи
Можем ли мы доказать, что не может удовлетворить ни одно такое уравнение? Я думаю, что это может быть сложно, но, безусловно, было бы интересно получить такой результат. Хотя это не было бы общей нижней границей факторинга, отсутствие реальной «формулы дублирования», по крайней мере, показало бы, что нет простого способа разложения. С другой стороны, отсутствие такой нижней границы показывает, как мало мы знаем о факторинге. Те, кто считает, что факторинг — это сложный процесс, должны быть обеспокоены тем, что мы даже не можем исключить возможность существования такого метода факторинга.
Другое направление будет обсуждаться в следующем посте. Подход состоит в том, чтобы смотреть не на факториальную функцию прямо, а косвенно через полином. Рассмотрим полином, определенный для каждого. Если мы можем вычислить этот многочлен пошагово, то очевидно, что мы можем вычислить пошагово: просто установите. Однако предположим в более общем смысле, что это многочлен с различными целыми корнями. Если мы можем эффективно выполнять быстрые вычисления, сможем ли мы по-прежнему быстро учитывать фактор? Ответ — да, при мягких условиях на отдельных корнях.Подробнее об этом в будущем.
Нравится:
Нравится Загрузка …

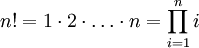 .
.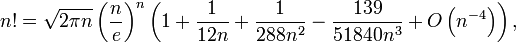
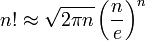
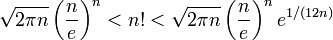
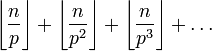
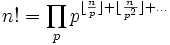 ,
,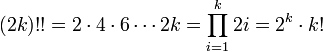
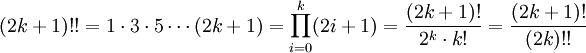
![(n)_k = n^{\underline{k}} = n^{[k]}= n\cdot (n-1)\cdot \ldots\cdot (n-k+1) = \frac{n!}{(n-k)!}](/800/600/https/dic.academic.ru/pictures/wiki/files/101/e47e3d43334ce21275b80d2fe438cc68.png)