Бесплатный STL файл Геометрические фигуры 3D・Идея 3D-печати для скачивания・Cults
Звезда
Бесплатно
Снежинка
Бесплатно
Брелок-молния
Бесплатно
Лучшие файлы для 3D-принтеров в категории Разное
STAR WARS CITIZEN HELMET , FALLOUT , STEAMPUNK , HALLOWEEN
13,06 €
Industrial Spur Gearbox / Gear Reducer (Cutaway version)
Бесплатно
Face Changing Halloween Pumpkin
Бесплатно
Домик для птиц, птичий домик, гнездо для птиц «Zen Bird House
5 €
Lada Niva
11,68 €
Paddle Boat
Бесплатно
XYZ 20mm Hollow Calibration Cube (Single Color / Dual Color)
Бесплатно
Крышки бинокулярных объективов 48 мм и 38 мм OD для гибкой нити
Бесплатно
Бестселлеры категории Разное
СФЕРИЧЕСКИЙ НОЧНИК MARIO BROS ЛИТОФАН
SlingHAMMER — повторяющийся арбалетный пистолет для 6 мм 8 мм 10 мм или 12 мм стальных шариков
12,50 €
Единорог — Волшебная лошадь с гибкой артикуляцией (печать на месте, без опор)
2 €
Держатель для ручки Gengar
1,50 €
Чаризард — покемон с гибкой артикуляцией (печать на месте, без опор)
3 €
ЛУМАЛЕ СУПЕР МАРИО БРАЗЕРС_ЛУМА_НИНТЕНДО
2,51 € -50%
1,25 €
Волк — Flexi Articulated Animal (печать на месте, без опор)
2,50 €
BoltHAMMER — повторяющийся арбалетный пистолет с быстросменным магазином
12,50 €
Планка Gremlin 640 мм FPV
0,90 €
Nuke — 3D-печатная электрическая укулеле
5,40 €
Тороидальный пропеллер для подвесных моторов Mercury, Yamaha, Mariner, Tohatsu 9.
 9-20HP (готов к 3d печати)
9-20HP (готов к 3d печати)9 €
Гиарадос — шарнирный морской змей
1,50 €
Лиса — гибкое шарнирное животное (печать на месте, без опор)
2 €
Кролик — Flexi Articulated Animal (печать на месте, без опор)
2 €Чармандер — покемон с гибкой артикуляцией (печать на месте, без опор)
2 €
Артикулированный Оникс
1,50 €
💖 Вы хотите поддержать Cults?
Вам нравятся Cults и вы хотите помочь нам продолжить наш путь самостоятельно? Обратите внимание, что мы — маленькая команда из 3 человек, поэтому поддержать нас в поддержании деятельности и создании будущих разработок очень просто. Вот 4 решения, доступные для всех:
РЕКЛАМА: Отключайте блокировщик баннеров AdBlock и кликайте на наши рекламные баннеры.

АФФИЛИАЦИЯ: Совершайте покупки онлайн, переходя по нашим партнерским ссылкам здесь Amazon.
ДОНАТЫ: Если хотите, то можно сделать пожертвование через Ko-Fi здесь 💜.
ПРИГЛАШЕНИЕ ДРУЗЕЙ: Приглашайте своих друзей, откройте для себя платформу и великолепные 3D-файлы, которыми делится сообщество!
Набор геометрических фигур – 3D модель
Набор геометрических фигур – 3D модель
200.00 ₽
Формат файла: STL.
Наличие ошибок: не обнаружено.
Количество товара Набор геометрических фигур – 3D модель
Описание
Общая информация
Макет набора геометрических фигур. Модель предназначена для получения физического макета на 3D-принтере.
Размер файла – 6,09 МБ.
Формат – STL.
Габаритные размеры модели – 190 мм х 110 мм х 237 мм.
Оплата и скачивание
Оплату товара можно совершить банковской картой или через счет для юридических лиц, оформив заказ на сайте.
 Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте.
Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте.Обращаем внимание, что покупка модели с целью перепродажи запрещена. Studia3D является зарегистрированной торговой маркой, которая следит за своими авторскими правами!
Где можно применить 3D-модель?
Во-первых, эта модель разрабатывалась для 3D-принтера. Если купить эту 3D-модель, то можно будет распечатать скачанный файл на 3D-принтере. Распечатанная модель может пригодиться для использования в макетном деле или как сувенир. Во-вторых, эту модель можно использовать для любого станка с ЧПУ, потому что принципы разработки 3D-моделей для 3D-принтера и других станков с ЧПУ существенно не различаются. Точно также эту модели можно использовать для фрезеровки. В-третьих, эту модель можно использовать для реализации проектов по 3D-моделированию. Например, использовать её можно в программе 3Ds MAX или аналогичном ПО.
 В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.
В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.Проверка модели
Все модели проходят качественную проверку на соответствие требованиям и внутреннему регламенту. Прежде всего, в моделях полностью сшита полигональная сетка. Кроме того, модель едина и не допускает несколько составных частей. Количество полигонов оптимально подобрано под особенности модели. Модель не содержит инвертированные нормали. Модель пригодна к масштабированию. Проверяйте габаритные размеры перед использованием модели. После этого для проверки моделей мы используем несколько профессиональных программ: Netfabb, Materialise и Meshmixer. В результате детальная проверка позволяет нашим клиентам использовать 3D-модели для любых задач без дополнительных негативных вопросов. Нам нравится дарить только лучшее качество, потому что его используют для больших проектов!
Отзывы (0)
Только зарегистрированные клиенты, купившие данный товар, могут публиковать отзывы.

Больше предложений
Больше никаких предложений по этому товару!
Вопросы
Общие вопросы
Запросов пока нет.
Сопутствующие товары
Трехмерные фигуры (трехмерные фигуры)
Что такое трехмерные фигуры?
В геометрии трехмерная форма может быть определена как твердая фигура или объект или форма, имеющая три измерения: длину, ширину и высоту . В отличие от двухмерных фигур, трехмерные фигуры имеют высоту, которая совпадает с толщиной или глубиной. Трехмерность также записывается как 3D, и, следовательно, эти фигуры также обычно называют 3D-формами. Все трехмерные фигуры занимают пространство, которое измеряется объемом .
В трехмерных фигурах трехмерность означает трехмерность. Размеры обычно можно рассматривать как измерения в направлении. Длину, ширину и глубину можно считать размерами.
Связанные игры
История трехмерных фигур
Все трехмерные фигуры имеют три измерения: длину, ширину и высоту . Формы выглядят по-разному с разных сторон. Все 2D-формы измеряются только по длине и ширине. Аристотель говорил, что двумерные формы — это линии, а не фигуры или тела. Они всегда описываются как продолжение линий или областей, ограниченных линиями. И наоборот, трехмерные фигуры имеют объем.
По соглашению первые три измерения представлены в виде пространственных измерений x-y-z. Ширина, высота и глубина — это их имена.
Связанные рабочие листы
Примеры трехмерных фигур
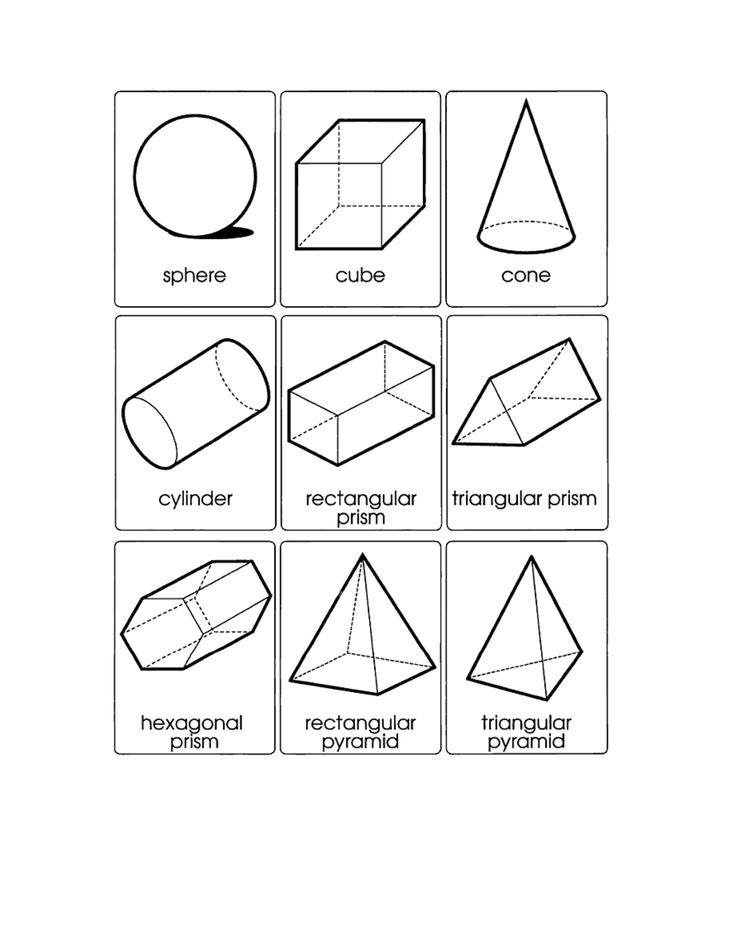
Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные фигуры, которые мы видим вокруг себя.
Реальные примеры трехмерных фигур
Трехмерные фигуры можно увидеть повсюду вокруг нас. Мы можем видеть кубик в кубике Рубика и кубике, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в морковке и рожке мороженого, цилиндр в ведерке и бочка вокруг нас.
Ниже перечислены некоторые примеры трехмерных фигур из реальной жизни:
- Конус: Дорожные конусы и кепки на день рождения имеют конусообразную форму.
- Треугольная призма: Палатка имеет форму треугольной призмы.
- Квадратная пирамида: Пирамида Гизы в Египте имеет форму квадратной пирамиды.
- Прямоугольная призма: Коробки, такие как коробки для обуви и коробки для хлопьев, имеют форму прямоугольных призм.
Атрибуты трехмерных фигур
У трехмерной фигуры есть три атрибута: грань, ребро и вершина. Давайте подробно разберемся с трехмерными формами и их свойствами.
Лицо: Каждая отдельная поверхность, плоская или изогнутая, трехмерной фигуры называется ее гранью.
Край: Линия, где встречаются две грани трехмерных фигур, называется его краем.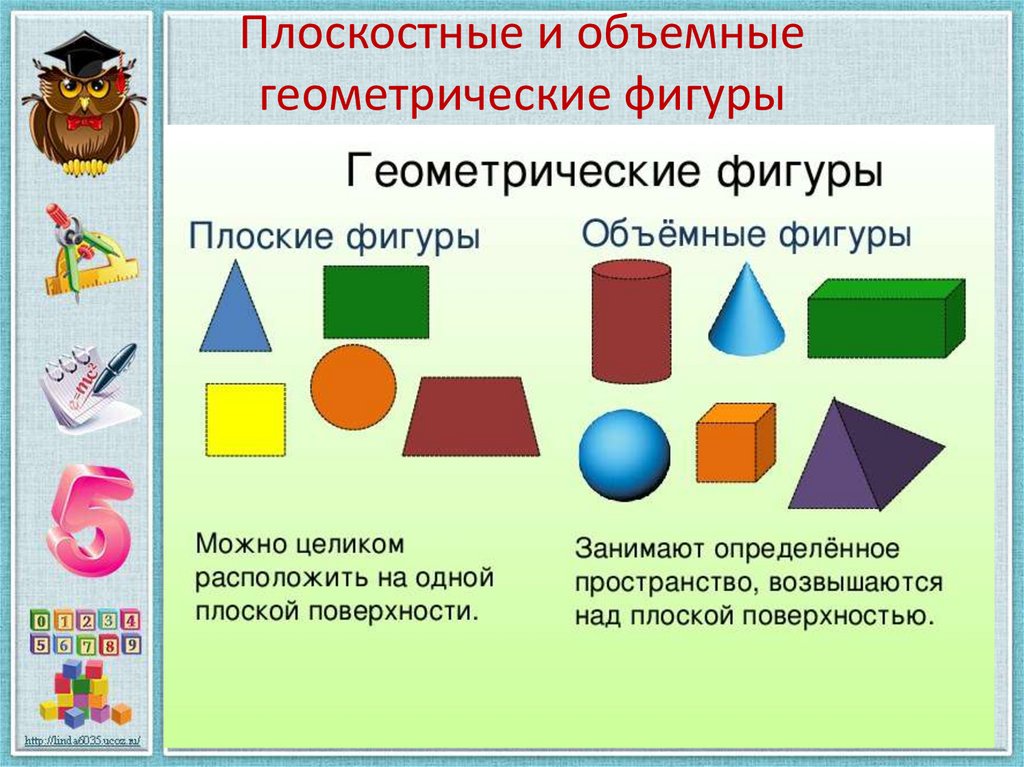
Вершина : Каждый угол, где встречаются три грани трехмерных фигур, называется его вершиной. Вершины — это множественное число от вершины.
Список трехмерных фигур
Вот список названий трехмерных фигур с их изображениями и атрибутами.
СфераВсе точки сферы находятся на одинаковом расстоянии от ее центра. Земля чем-то похожа на нее, за исключением одного: когда вы смотрите на нее издалека, она выглядит как сфера, но если вы смотрите на нее вблизи, она не совсем круглая. Сфера имеет несколько характеристик:
- Она идеально симметрична и имеет форму шара.
- Помимо радиуса, диаметра, длины окружности, объема и площади, у него также есть длина.
- Расстояние от центра до каждой точки на поверхности сферы одинаково.
- На одной грани не найдены ни ребра, ни вершины.
- Поскольку у него нет плоской грани, это не многогранник.
Куб и прямоугольный параллелепипед — это большие блоки. Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные.
Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные.
Цилиндр имеет две круглые поверхности на обоих концах и одну изогнутую поверхность по всей длине. Он имеет высоту и радиус. Высота цилиндра перпендикулярна его поверхности сверху вниз. Ниже приведены некоторые основные характеристики цилиндров:
- Поверхность цилиндра изогнута.
- Форма снизу вверх остается неизменной.
- Два одинаковых конца формируют трехмерную форму объекта. Концы могут быть круглыми или овальными.
- У прямого цилиндра центры круглых оснований расположены на одной линии, а у наклонного цилиндра центры оснований расположены на разных линиях.
Формула трехмерных фигур
Сеть трехмерных форм
Сеть — это узор, полученный путем плоской разбивки поверхности трехмерной фигуры, показывающей каждую грань фигуры .
3D-фигуры могут иметь более одного шаблона цепей. Ниже показаны названия нескольких 3D-форм и их сетей:
Ниже показаны названия нескольких 3D-форм и их сетей:
Интересные факты :
Все трехмерные фигуры состоят из двумерных фигур.
Разница между 2D- и 3D-фигурами
Давайте различать 2D- и 3D-формы, разбираясь в двухмерных и трехмерных формах и их свойствах.
Решенные примеры трехмерных фигур
Пример 1: Что из следующего является трехмерной фигурой?
Конус Квадрат Сфера Кубоид Цилиндр Параллелограмм
Решение:
Конус Сфера Кубоид Цилиндр
Пример 2. Укажите, являются ли следующие верными или 6 6
5 .- Трехмерная форма имеет 3 измерения.
- Трехмерные фигуры также называются плоскими.
- Трехмерные фигуры занимают пространство.
- Все трехмерные фигуры имеют плоские грани.
Решение:
- Правда
- Ложь.
 Трехмерные формы также называют объемными формами.
Трехмерные формы также называют объемными формами. - Правда
- Ложь. Сфера представляет собой трехмерную форму без плоской грани.
Пример 3: Заполните таблицу атрибутами перечисленных трехмерных фигур.
Решение:
Пример 4: Сопоставьте объект с его формой.
Решение:
- (a) – (iii)
- (б) – (и)
- (в) – (iv)
- (г) – (ii)
Пример 5: Вычислите площадь поверхности прямоугольного параллелепипеда шириной 4 единицы, длиной 3 единицы и высотой 5 единиц.
Решение:
Дан кубоид, имеющий три единицы длины, четыре единицы ширины и пять единиц высоты.
Площадь поверхности прямоугольного параллелепипеда $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ квадратных единиц
$= 2 \times (\text{lw} + \text {белая} + \text{левая})$
$= 2[(3 х 4) + (4 х 5) + (3 х 5)]$
$= 2(12 + 20 + 15)$
$= 2(47)$
$= 94$ квадратных единиц
Следовательно, площадь поверхности данного прямоугольного параллелепипеда равна 94 квадратных единиц.
Пример 6: Джейн любит пить молоко из цилиндрического стакана. Ее стакан имеет 15 единиц высоты и 3 единицы радиуса основания. Сколько молока она может налить в стакан?
Решение:
Учитывая, что высота стакана 15 единиц, а радиус основания 3 единицы. 92$
Таким образом, Джейн может налить в свой стакан приблизительно 424 кубических единицы молока.
Практические задачи трехмерных фигур
1
Какая фигура имеет две плоские грани и одну изогнутую?
Цилиндр
Сфера
Конус
Куб
Правильный ответ: Цилиндр
Цилиндр имеет две плоские грани, которые имеют форму круга, и одну изогнутую грань.
2
Сколько квадратных фигур имеет сетка куба?
4
6
8
10
Правильный ответ: 6
Куб имеет 6 граней, которые являются квадратами. Итак, в сетке куба будет 6 квадратных фигур.
3
Что из следующего не имеет ребра?
Конус
Цилиндр
Куб
Сфера
Правильный ответ: Сфера
Сфера имеет одну сторону. Так что у него нет края.
4
Какая из данных фигур НЕ является трехмерной?
Трапеция
Призма
Пирамида
Куб
Правильный ответ: Трапеция
Трапеция — это двумерная фигура с четырьмя сторонами, одна пара противоположных сторон которых параллельна друг другу, а две другие стороны не параллельны.
5
Как называется пересечение двух граней объемной фигуры?
Вершина
Сторона
Грань
Ребро
Правильный ответ: Ребро
Ребра — это отрезки, соединяющие две грани. Грани куба пересекаются по линиям, называемым ребрами. Фигуры с несколькими ребрами называются сплошными фигурами. Пересечение нескольких плоскостей называется вершиной.
6
Трехмерные геометрические фигуры называются ________.
фигуры
тела
грани
многоугольники
Правильный ответ: тела
Трехмерные геометрические фигуры называются телами.
7
Что такое в математике сплошная заостренная фигура, соединенная с вершиной изогнутой поверхностью с плоским круглым основанием?
Конус
Сфера
Цилиндр
Пирамида
Правильный ответ: Конус
Конусы представляют собой трехмерные тела, состоящие из круглого основания, соединенного с одной точкой (называемой вершиной) изогнутыми сторонами. В качестве альтернативы вы можете думать о конусе как о круглой пирамиде.
Часто задаваемые вопросы о трехмерных фигурах
Какие существуют типы трехмерных фигур?
Куб, прямоугольный параллелепипед, цилиндр, сфера, конус, призма и пирамиды.
Каковы атрибуты трехмерных фигур?
Трехмерные фигуры имеют 3 измерения — длину, ширину и глубину. В результате этих размеров эти формы имеют атрибуты граней, ребер и вершин.
Что такое ребро?
Ребро — это линия, на которой сходятся две грани трехмерной формы.
Например, у куба 12 ребер.
Что такое вершины?
Вершины — это углы, в которых сходятся три грани. Например, прямоугольный параллелепипед имеет 8 вершин.
Какая польза от объема трехмерной формы?
Объем помогает найти пространство, занимаемое данной фигурой.
Из скольких квадратов состоит кубическая сеть?
Кубическая сеть состоит из шести квадратов.
Трехмерные фигуры | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые формы с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
Подробнее о работе с полигонами см. на нашей странице Свойства полигонов .
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются по количеству ребер, граней и вершин, которые они имеют, а также по тому, имеют ли все их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновые тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.

См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, имеющий два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. стороны призмы параллелограммы — четырехгранные фигуры с двумя парами сторон одинаковой длины.
Антипризмы похожи на обычные тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание в виде любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре основания, т.0005 Правая пирамида
Кроме того, пирамида может иметь вершину прямо в центре основания, т.0005 Правая пирамида
Более сложные многогранники
Существует множество других типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух разных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут включать по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Распространенные трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
Площадь поверхности
На нашей странице Вычисление площади объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы определяете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение — длина и ширина квадрата по определению одинаковы.
Таким образом, одна грань этого куба равна 10 × 10 см = 100 см 2 . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Чтобы вычислить площадь поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала вычислите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Для расчета площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.
Возможно, вам придется измерить стороны по отдельности.
Диаграммы сетей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о схемах сети см. нашу страницу 3D-формы и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.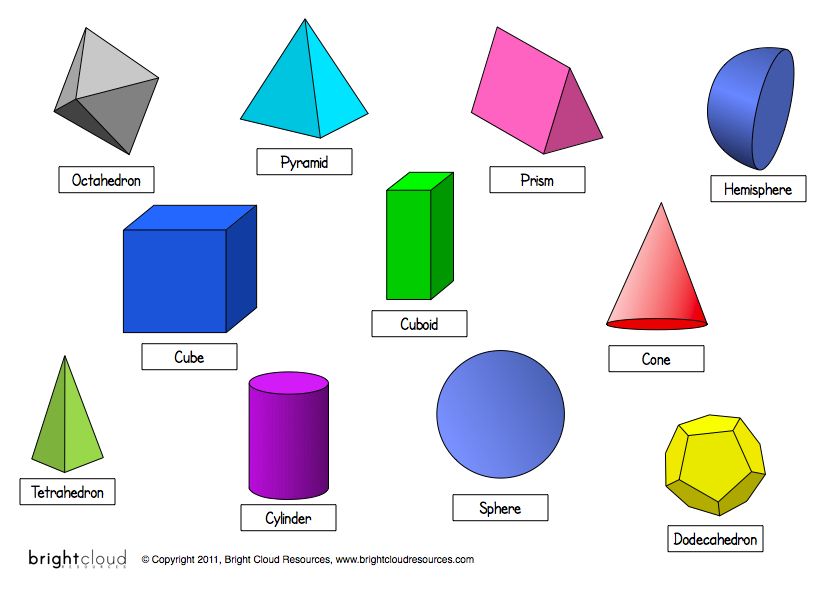
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0009
Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем суммирования площадей кругов и стороны:
157 + 314 = 471см 2
Пример:
Радиус = 5см 0 Длина наклона
Конус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонной части, можно найти по следующей формуле:
π (пи) × радиус × длина наклона.
В нашем примере расчет равен 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади боковой поверхности, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр — расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (Большой радиус) = 20 см
r (Малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература из раздела «Навыки, которые вам нужны»
«Понимание геометрии»
Часть «Руководства по навыкам, которые вам необходимы»
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Заполнение твердого тела: Объем
Для трехмерных фигур вам также может понадобиться знать, какой объем они имеют.

 Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте.
Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте. В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.
В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.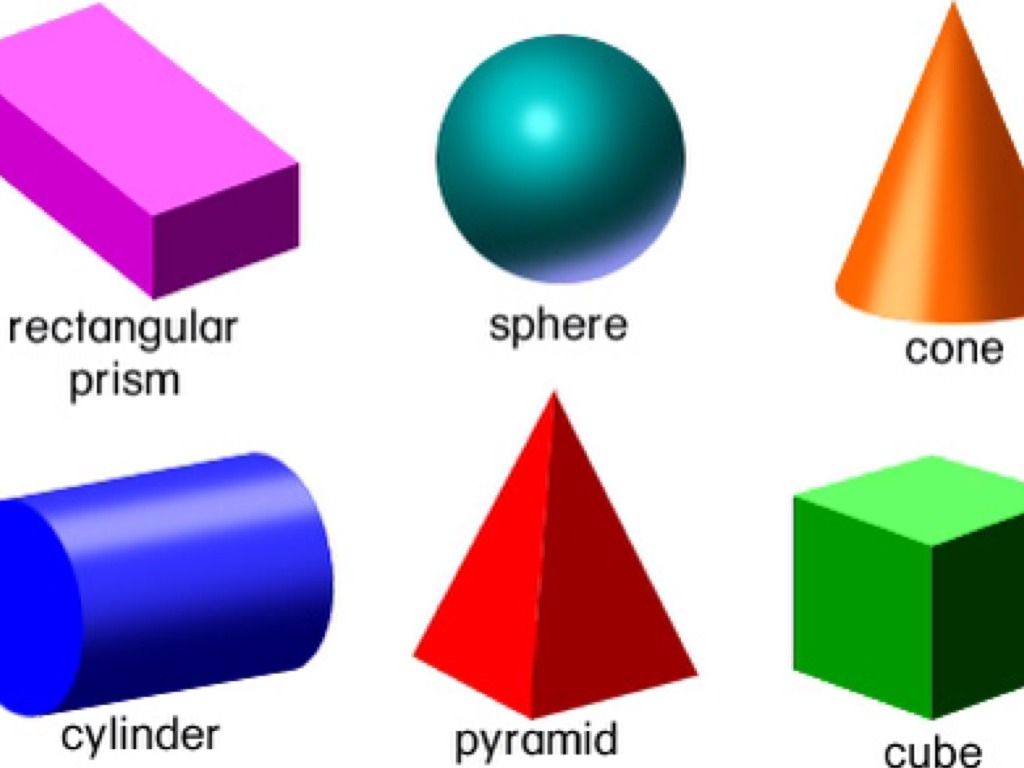
 Трехмерные формы также называют объемными формами.
Трехмерные формы также называют объемными формами.