Фигуры ограниченные двумя линиями: Вопросы»Вычислить площадь фигуры ограниченной линиями|Поступи в ВУЗ

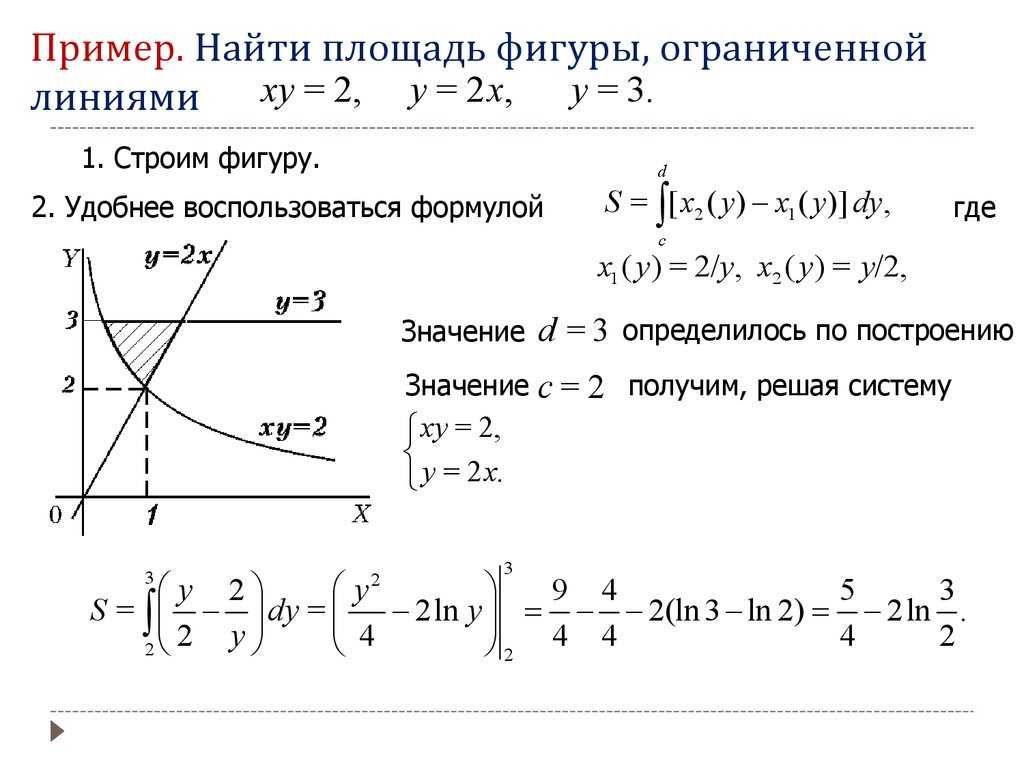
Найти площадь фигуры ограниченной линиями с примерами решения

Содержание:

1. Внешние, внутренние и граничные точки плоских множеств
2. Квадрируемые области.

Внешние, внутренние и граничные точки плоских множеств

Выше мы неоднократно использовали понятие площади плоской фигуры, опираясь на его интуитивное толкование. В этом параграфе мы дадим определение понятия площади плоской фигуры, установим свойства площадей и опишем класс фигур, имеющих площадь. Для этого введем несколько понятий, относящихся к плоским фигурам, т. е. к множествам, состоящим из точек плоскости.

Напомним, что открытым кругом с центром и радиусов называют множество точек плоскости, расстояние которых от точки а меньше . Любой открытый круг с центром называют окрестностью точки .

Пусть на плоскости задано некоторое множество . Назовем точку этого множества внутренней, если существует окрестность этой точки, целиком содержащаяся в . Точку плоскости называют внешней точкой для этого множества, если у нее есть окрестность, не содержащая ни одной точки множества . Наконец, точки плоскости, не являющиеся ни внутренними, ни внешними для множества , называют граничными точками этого множества. Граничные точки могут как принадлежать множеству , так и не принадлежать ему. Совокупность граничных точек множества образует границу этого множества. Если все граничные точки множества принадлежат этому множеству, то его называют замкнутым, а если ни одна граничная точка не принадлежит множеству то его называют открытым.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

На рисунке 20 изображен квадрат. Точка является внутренней для этого квадрата, точка — внешней, а точка — граничной. Граница квадрата состоит из отрезков и .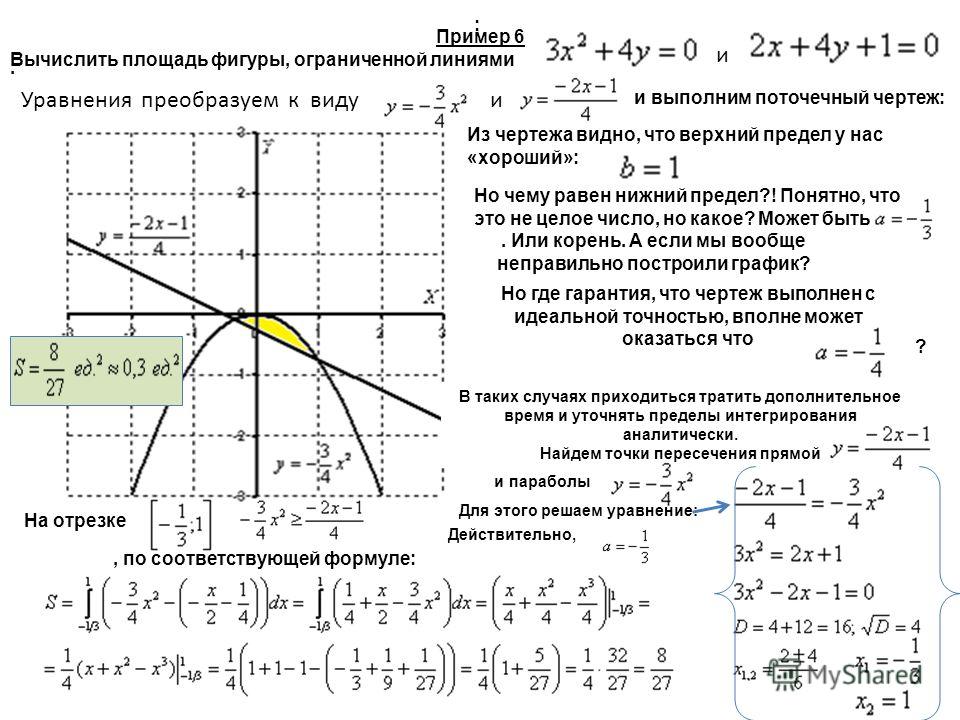

В дальнейшем будем говорить, что фигуры F и G налегают друг на друга, если у них есть хоть одна общая внутренняя точка (рис. 21).

Если фигура F является объединением попарно не налегающих с друг на друга фигур то говорят, что F разбита на 1 фигуры при этом не исключается, что некоторые из них имеют общие граничные точки (рис. 22).

Квадрируемые области.

Перейдем к определению понятия площади. Выберем на плоскости прямоугольную декартову систему координат . Назовем прямоугольник допустимым, если его стороны параллельны осям координат, причем не будем исключать и вырожденные прямоугольники, т. е. прямоугольники, у которых длина одной или обеих сторон равна нулю.

Подмножество F плоскости, которое можно разбить на конечное число допустимых прямоугольников, назовем ступенчатой фигурой (рис. 23). Очевидно, что объединение и пересечение двух ступенчатых фигур являются ступенчатыми фигурами.

Назовем площадью допустимого прямоугольника F произведение длин его сторон:

При этом площадь вырожденного прямоугольника равна нулю. Очевидно, что если прямоугольник разбит на два прямоугольника (рис. 24), то площадь всего прямоугольника равна сумме площадей его частей:

Вообще, если прямоугольник F разбит на конечное число прямоугольников то

Кроме того, если прямоугольник получается из прямоугольника F параллельным переносом, то .

Отметим, что квадрат со стороной, равной 1, имеет площадь, равную 1.

Определим далее площадь ступенчатой фигуры. Пусть ступенчатая фигура F разбита на прямоугольники .

Положим тогда

Одна и та же ступенчатая фигура может разбиваться на прямоугольники различными способами. Легко доказать, что ее площадь не зависит от способа разбиения.

Возможно вам будут полезны данные страницы:

Вычисление пределов

Свойства пределов функции

Равномерное распределение

Признак Даламбера: пример решения

Мы определили функцию на множестве ступенчатых фигур. Она обладает следующими свойствами:

• а) Если ступенчатые фигуры и не имеют общих внутренних точек, то
• б) Если ступенчатая фигура получается из ступенчатой фигуры параллельным переносом, то

Предоставляем читателю доказать эти утверждения.

Из свойства а), в частности, следует, что если и — ступенчатые фигуры и , то . В самом деле, если присоединить к граничные точки, то получится ступенчатая фигура , не налегающая на и такая, что . Значит,

Совокупность ступенчатых фигур не охватывает таких фигур, как, например, треугольник, параллелограмм общего вида, круг, эллипс. Даже повернутый прямоугольник уже не является ступенчатой фигурой (стороны ступенчатой фигуры параллельны осям координат). Поэтому надо распространить понятие площади на более широкий класс фигур.

Возьмем на плоскости фигуру и поставим ей в соответствие два числовых множества.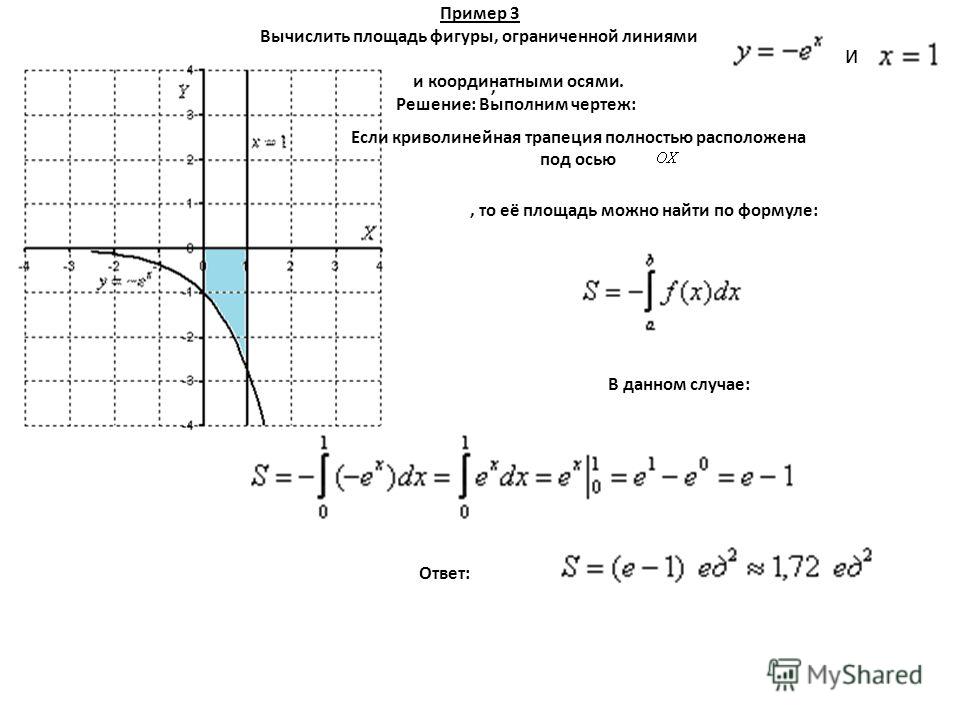 Множество состоит из площадей ступенчатых фигур, все точки которых принадлежат фигуре , а множество — из площадей ступенчатых фигур, содержащих фигуру . Очевидно, что множество расположено слева от множества . Поэтому существует хотя бы одно число, разделяющее эти множества.

Введем следующее определение.

Определение. Фигура называется квадрируемой (имеющей площадь), если соответствующие ей числовые множества разделяются единственным числом. Это единственное число , разделяющее и , назовем площадью фигуры .

Применяя критерий единственности разделяющего числа, получаем необходимое и достаточное условие квадрируемости фигуры :

Для того чтобы фигура была квадрируемой, необходимо и достаточно, чтобы для любого нашлись такие ступенчатые фигуры и , что , причем

Отметим, что граница фигуры лежит в области, заключенной между границами ступенчатых фигур и . Эта область сама является ступенчатой фигурой (рис. 25). Поэтому указанное условие можно сформулировать и так:

Для того чтобы фигура была квадрируемой, необходимо и достаточно, чтобы для любого границу фигуры можно было заключить в ступенчатую фигуру, площадь которой меньше .

Отметим следующее достаточное условие квадрируемости.

Теорема 1. Для того чтобы фигура была квадрируемой, достаточно, чтобы ее граница состояла из конечного числа дуг , являющихся графиками непрерывных функций или

Доказательство. Покажем сначала, что дугу , можно заключить в ступенчатую фигуру, имеющую сколь угодно малую площадь. Зададим . Так как функция непрерывна на отрезке , найдется разбиение этого отрезка такое, что для любого выполняется неравенство

где — соответственно наименьшее и наибольшее значения функции на отрезке (см. выше, с. 61). Но тогда дуга целиком содержится в объединении прямоугольников, имеющих основания и высоты (рис. 26). Общая площадь этих прямоугольников не превосходит числа

Объединение этих прямоугольников образует ступенчатую фигуру, содержащую дугу Г и имеющую площадь, меньшую, чем .

Поскольку граница фигуры состоит из конечного числа таких дуг, ее тоже можно накрыть ступенчатой фигурой сколь угодно малой площади, и потому область квадрируема.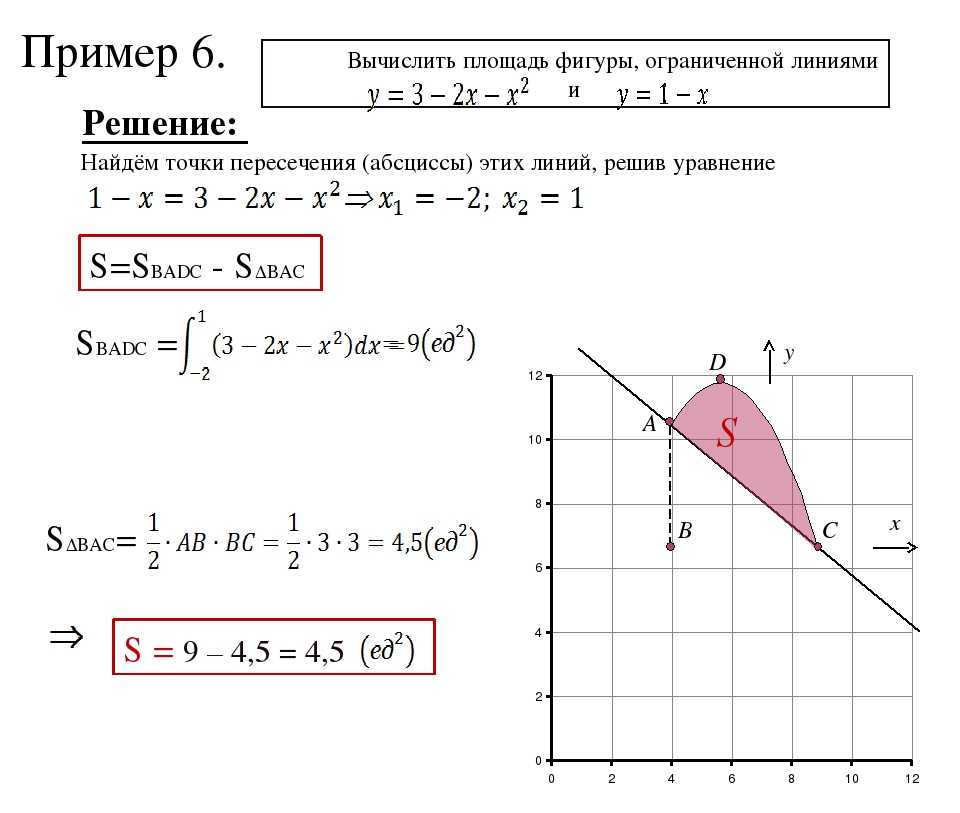

Например, круг квадрируем, так как его граница состоит из двух дуг, задаваемых уравнениями и, а эти функции непрерывны.

Иногда оказывается полезным следующее достаточное условие квадрируемости фигур.

Теорема 2. Если для любого найдутся такие квадрируемые фигуры и , что и , то фигура тоже квадрируема. Доказательство. Зададим и выберем такие квадрируемые фигуры и , что и .

Так как и квадрируемы, то найдутся такие ступенчатые фигуры и , что , причем

и

Но тогда и

Это и доказывает квадрируемость .

Свойства площадей квадрируемых фигур*.

Покажем, что площади квадрируемых фигур обладают свойствами, похожими на свойства площадей ступенчатых фигур. Сначала докажем следующее утверждение:

а) Пусть квадрируемые фигуры и не имеют общих внутренних точек и . Тогда фигура тоже квадрируема, причем ее площадь равна сумме площадей фигур и :

В самом деле, из квадрируемости фигур и вытекает, что для любого существуют такие ступенчатые фигуры , что , причем

Положим и . Тогда — ступенчатая фигура, содержащаяся в , а — ступенчатая фигура, содержащая . При этом фигуры и не имеют общих внутренних точек (рис. 27), и потому

Фигуры и могут иметь общие внутренние точки (рис. 28), а потому можно утверждать лишь, что

Отсюда следует, что

Итак, для любого нашлись ступенчатые фигуры и такие, что , причем . Поэтому фигура квадрируема.

Из неравенств и вытекает, что

С другой стороны,

а потому в силу соотношений (2) и (3)

Мы видим, что числа и разделяют одни и те же множества . При этом, как было показано, для любого найдутся такие что

Поэтому указанные множества могут разделяться лишь одним числом. Это и доказывает соотношение (1).

Доказанное свойство называют аддитивностью площади.

Второе свойство площадей состоит в том, что площадь квадрируемой фигуры не изменяется при параллельном переносе. Это следует из того, что при этом переносе каждая внутренняя ступенчатая фигура для переходит во внутреннюю ступенчатую

фигуру для образа фигуры , и то же самое верно для внешних ступенчатых фигур.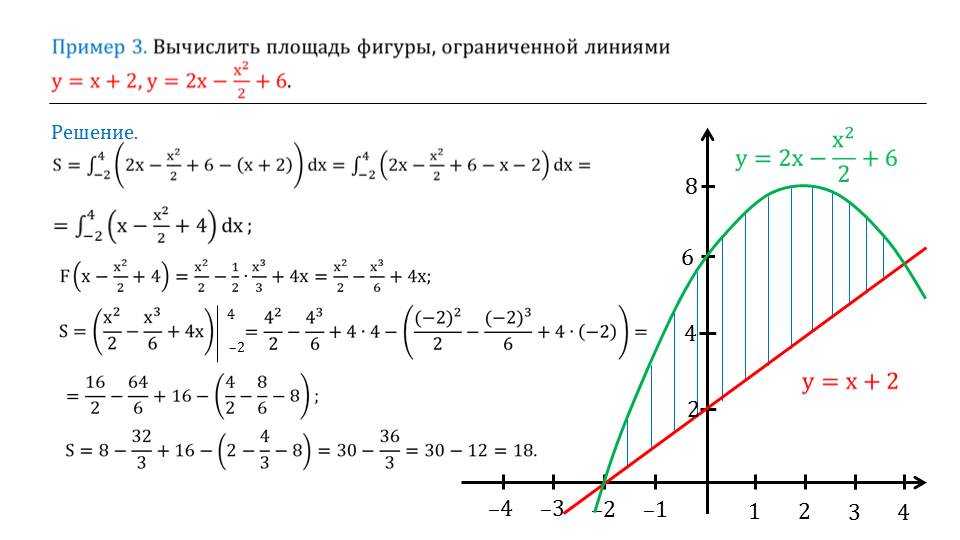 Но это значит, что при параллельном переносе не изменяются ни множество ни множество , а потому неизменным остается и разделяющее их число, т. е. площадь фигуры.

Недостатком данного выше определения площади является то, что оно связано с выбором системы координат на плоскости. Мы доказали лишь, что площадь не изменяется (инвариантна) при параллельных переносах, но не доказали такого же утверждения относительно других перемещений (симметрий, поворотов и т. д.). Справедливо более общее утверждение:

б) Если фигура квадрируема и — конгруэнтная ей фигура, то тоже квадрируема, причем

В курсе геометрии доказывают, что любое перемещение является композицией осевых симметрий. Поэтому достаточно доказать наше утверждение для случая, когда получается из с помощью осевой симметрии.

Рассмотрим сначала случай, когда — прямоугольник, одна из сторон которого параллельна оси симметрии (рис. 29). В этом случае образ этого прямоугольника может быть получен из не только с помощью осевой симметрии, но и с помощью параллельного переноса.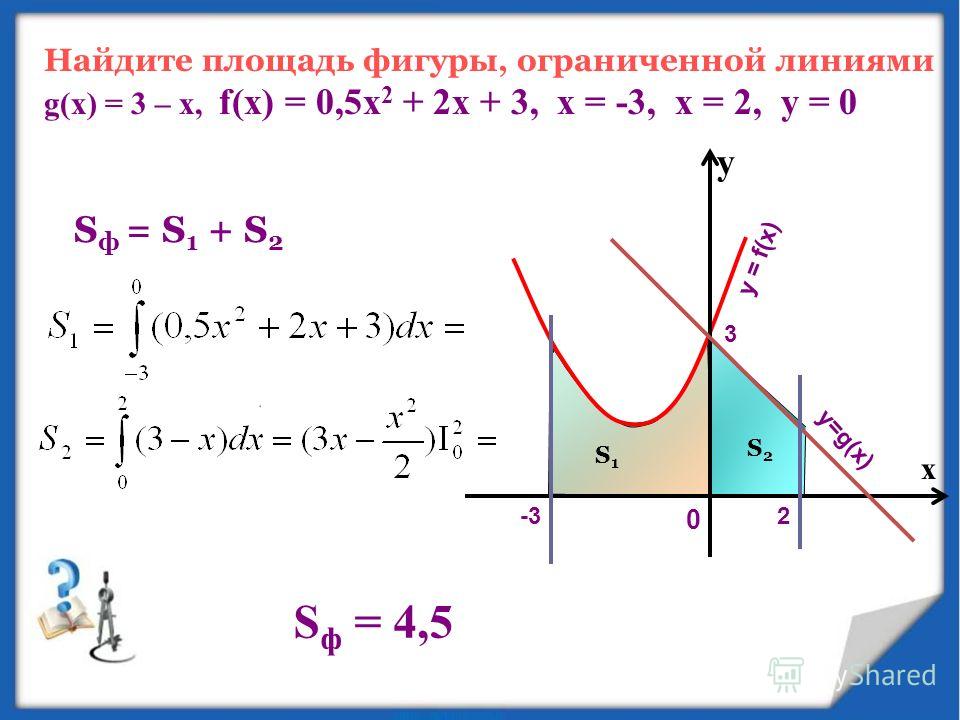 Поэтому. Но любую квадрируемую фигуру можно с любой степенью точности заменить фигурой, состоящей из прямоугольников, одна из сторон которых параллельна оси симметрии. Применяя доказанное утверждение для каждого из этих прямоугольников и складывая полученные равенства, убеждаемся, что равенство верно для любых квадрируемых фигур.

Мы доказали, что в классе квадрируемых фигур площадь обладает следующими свойствами:

1°. Для любой фигуры ее площадь — неотрицательное число (неотрицательность площади).

2°. Площади конгруэнтных фигур равны (инвариантность площади относительно перемещений).

3°. Если фигуры и не имеют общих внутренних точек, то

(аддитивность площади).

4°. Площадь единичного квадрата равна единице (условие нормировки).

Можно доказать, что условия 1°— 4° однозначно определяют площадь в классе квадрируемых фигур. Это позволяет понятию площади дать аксиоматическое определение, сказав, что на совокупности фигур определено понятие площади, если на задана числовая функция , удовлетворяющая условиям 4° (при этом, разумеется, требуется, чтобы совокупность вместе с двумя не налегающими друг на друга фигурами содержала их объединение).

4. Вычисление площади плоской фигуры в декартовых координатах. Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция неотрицательна на отрезке и непрерывна, на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

Доказательство.

Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в п. 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

где — площадь внутренней ступенчатой фигуры,

—площадь внешней ступенчатой фигуры. С другой стороны, по определению интеграла можно записать:

Таким образом, числа и разделяют одни и те же числовые множества:

Но, как было показано при изучении определенного интеграла,

эти множества разделяются лишь одним числом, и потому

Теорема доказана.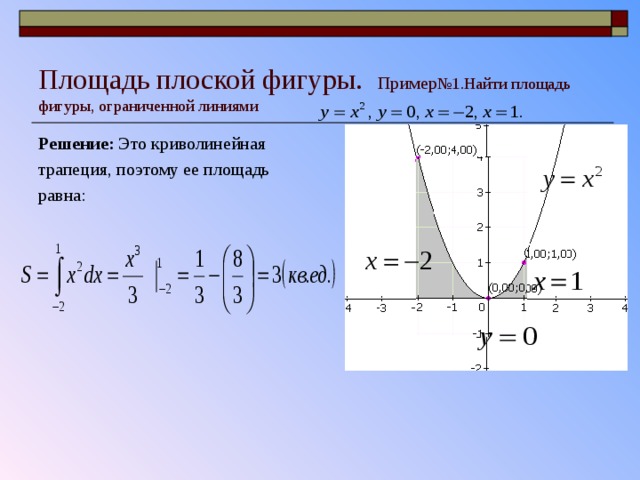

Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции ,а слева и справа прямыми (рис. 30), то ее площадь выражается формулой

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .

Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше

. Но . Значит,

Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Примеры с решением

Пример 1.

Найдем площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).

Решение:

Имеем: 2

Пример 2.

Вычислим площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).

Решение:

Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

Пример 3.

Найдем площадь фигуры, ограниченной графиками функций (рис. 35).

Решение:

Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника :

Пример 4.

Вычислим площадь фигуры, ограниченной петлей кривой .

Решение:

Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис.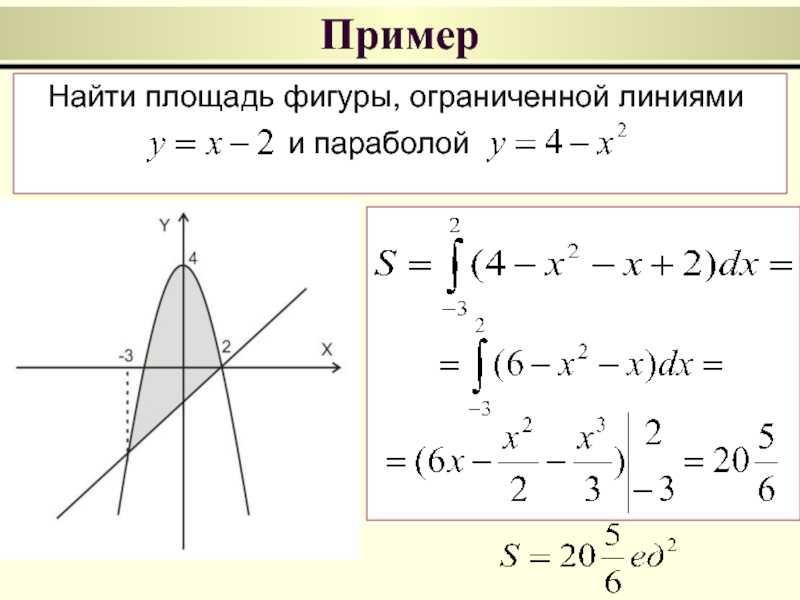 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Записав уравнение кривой в виде найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:

Воспользовавшись формулой № 40 таблицы (см. Приложение 1) при , получим:

Тогда

Значит,

Методическая разработка занятия по дисциплине «Математика» для технических специальностей колледжа тема «Вычисление площадей плоских фигур» — Информио

Дисциплина: Математика

Вид занятия: урок

Тип урока: комбинированный

 

Цель урока: Научить вычислять площади плоских фигур с помощью определенного интеграла.

 

Задачи:

Образовательные:

Знать алгоритм вычисления площади плоской фигуры.

Уметь вычислять площади плоских фигур с помощью определенного интеграла.

Развивающие:

Формировать элементы творческого математического мышления.

Развивать интерес студентов к решению задач, к творчеству.

Воспитывающие:

Ответственность за выполняемую работу.

Интерес к изучаемому предмету.

 

Оборудование:

Карточки для повторения темы «Определенный интеграл и его геометрический смысл»

Мультимедийная презентация темы «Применение определенного интеграла для вычисления площадей плоских фигур»

Карточки для контроля знаний по теме «Применение определенного интеграла для вычисления площадей плоских фигур»

 

Оформление доски:

На доске записана тема, план работы по теме.

ТЕМА «ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР» План: 1. Устный счет. 2. Основные случаи расположения плоских фигур. 3. Алгоритм решения задачи на вычисление площади. 4. Решение упражнений. 5. Проверка первичного усвоения знаний.

 

ХОД УРОКА

 

1. Организационный момент. Приветствие. Сообщение цели и плана урока.

2. Проверка домашнего задания: /приложение 1/

2.1. Индивидуальная работа по карточкам  — три студента;

2.2.  Актуализация знаний:

a) устный счет,

b) фронтальный опрос:

— Дать определение криволинейной трапеции.

— Как называется формула 

— Как называется число b?

— Как называется число a?

— Как называется, F(b),F(a)?

— Назовите формулу для вычисления площади плоской фигуры, ограниченной неотрицательной функцией на отрезке [а; b].

— Назовите формулу для вычисления площади плоской фигуры, ограниченной функцией, принимающей отрицательные значения на отрезке [a; b].

 

3. Основные способы расположения плоских фигур. (Записать формулы для вычисления площади к каждому варианту)

 

4. Алгоритм решения задачи:

1) Изобразить схематичный график заданных функций.

2) Найти пределы интегрирования.

3) Выяснить, какой формулой удобно воспользоваться в данном случае.

4) Вычислить площадь заданной фигуры.

 

5. Решение упражнений:

1) Вычислить площадь фигуры, ограниченной линиями:  

2) Придумать условие задачи по рисунку.

3) Вычислить площадь фигуры, изображенной в системе координат.

4) Решить задачи с  вычислением пределов интегрирования.

5) Вычислить площадь фигуры, ограниченной линиями:

 

6. Самостоятельная работа.

Вычислить площадь фигуры, ограниченной графиками функций:

 

7. Домашняя работа дифференцированного характера (с пояснением).

1) Стр. 212 – 218 учебного пособия Практические занятия по математике /Н.В. Богомолов/

2) Вычислить площадь фигуры, ограниченной графиками функций:

 

Подведение итога урока:

1) Алгоритм решения задачи.

2) Выставление оценок с учетом самоанализа своей деятельности на уроке.

3) Сообщение темы следующего занятия (Объем тела вращения)

Приложение 1 /проверка домашней работы/

Решение:

Карточки:                  

Ответы на вопросы:

1) Криволинейной трапецией называется фигура, ограниченная кривой Y=f(x), осью Ох и двумя прямыми х = a и х = b, где a < x < b ,  f(x )> 0.

2)      

3) Число «b» называется верхним пределом интегрирования.

4) Число «a» называется нижним пределом интегрирования.

5) F(b) и F(a)  называется первообразной в заданной точке.

6) Формулу для вычисления площади плоской фигуры, ограниченной неотрицательной функцией .

7) Формула для вычисления площади плоской фигуры, ограниченной функцией :

 

Литература

1. Богомолов Н.В. Практические занятия по математике: Учеб. пособие для средних проф. учеб. заведений/Н.В. Богомолов. – 10-е изд., перераб. – М.: Высш. шк., 2009. – 495 с.

2. Богомолов Н.В. Математика: учеб. Для ссузов/ Н.В. Богомолов, П.И. Самойленко. – 6-е изд., стереотип. – М. : Дрофа, 2009. – 395, [5] c. : ил.

3. Сергиенко Л.Ю., Самойленко П.И. Планирование учебного процесса по математике: Учеб. – метод. пособие для преподавателей сред. спец. учеб. заведений. – М.: Высш. шк., 1987. – 424 с.: ил.

3$, и пусть $p(x)=18-3x$ — прямая, касательная к графику $f(x)$. Пусть $R$ — область, ограниченная осью $x$ и графиком $f(x)$; и $S$ — область, ограниченная осью $x$, прямой $p(x)$ и графиком $f(x)$. Найдите площадь $S$.

Итак, я нашел площадь $R$, используя интеграл $f(x)$ от 0 до 4, так как это $x$-отрезки, которые равны 64/3, но теперь я не знаю, что я мог сделать, чтобы использовать, чтобы найти площадь $S$ после этого.

• исчисление
• интеграция 93)dx=\frac{95}{12}. $$

  $\endgroup$

  4

  Зарегистрируйтесь или войдите в систему

  Зарегистрируйтесь с помощью Google

  Зарегистрироваться через Facebook

  Зарегистрируйтесь, используя электронную почту и пароль

  Опубликовать как гость

  Электронная почта

  Требуется, но не отображается

  Опубликовать как гость

  Электронная почта

  Требуется, но не отображается

  Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

  .

  геометрия — Область между дугой и линией

  спросил 5 лет, 3 месяца назад

  Изменено 5 лет, 3 месяца назад

  Просмотрено 482 раза

  $\begingroup$

  Я работаю над проблемой уже несколько дней. Это была задача на лекции по тригонометрии. Мне удалось найти уравнение для радиуса, но я не смог его решить. 92} \конец{выравнивание*} Однако я не смог решить это уравнение. Любая помощь будет оценена по достоинству. Я также могу визуализировать математический подход, включающий нахождение площади между двумя кривыми, но я хочу решить его элементарным способом, если это возможно.

  • геометрия
  • окружности
  • длина дуги

  $\endgroup$

  3

  $\begingroup$

  Как прокомментировал ангривиан, задача сводится к следующему: найти ноль $$f(\theta)=\frac \theta {\sin\left(\frac\theta 2\right)}- 2.

  No related posts.