3. Поверхности второго порядка
3.1. Общее уравнение второго порядка
Пусть в пространстве задана прямоугольная система координат OXYZ. Общим уравнением второго порядка (уравнением второй степени) относительно X,Y,Z называется уравнение вида
a11x2 + a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a14x+2a24y+2a34z+a44=0, (23)
где aij(i,j=1,2,3,4) – некоторые фиксированные числа (коэффициенты данного уравнения). Значения коэффициентов могут быть любыми, но при условии, что , , , , , одновременно не обращаются в нуль.
Поверхность второго
порядка есть геометрическое место
точек пространства, декартовы координаты
которых удовлетворяют уравнению (23). В
зависимости от коэффициентов в уравнении
(23) поверхности второго порядка бывают
вырожденными и невырожденными.
Приведем примеры вырожденных поверхностей второго порядка.
Пример 1. Пара пересекающихся плоскостей: , здесь =1, =-1, остальные коэффициенты равны нулю. Представим уравнение в виде (а) х = 0 или (б) х — 2у = 0. Уравнение х = 0 – координатная плоскость УОZ, уравнение х – 2у = 0 задает плоскость, проходящую через ось OZ. По этой оси обе плоскости пересекаются.
Пример 2. Пара параллельных плоскостей: =1, , остальные коэффициенты =0. Представим уравнение в виде или . Плоскость является координатной ZОУ, плоскость параллельна ей.
Пример 3. Единственная точка: . Уравнению удовлетворяет единственная точка – начало координат.
Пример 4. Пустое множество: . Очевидно, ни одна точка пространства не удовлетворяет этому уравнению.
В дальнейшем мы
подробно рассмотрим невырожденные
поверхности второго порядка, к ним
относятся эллипсоид, гиперболоид,
параболоид, конус и цилиндры.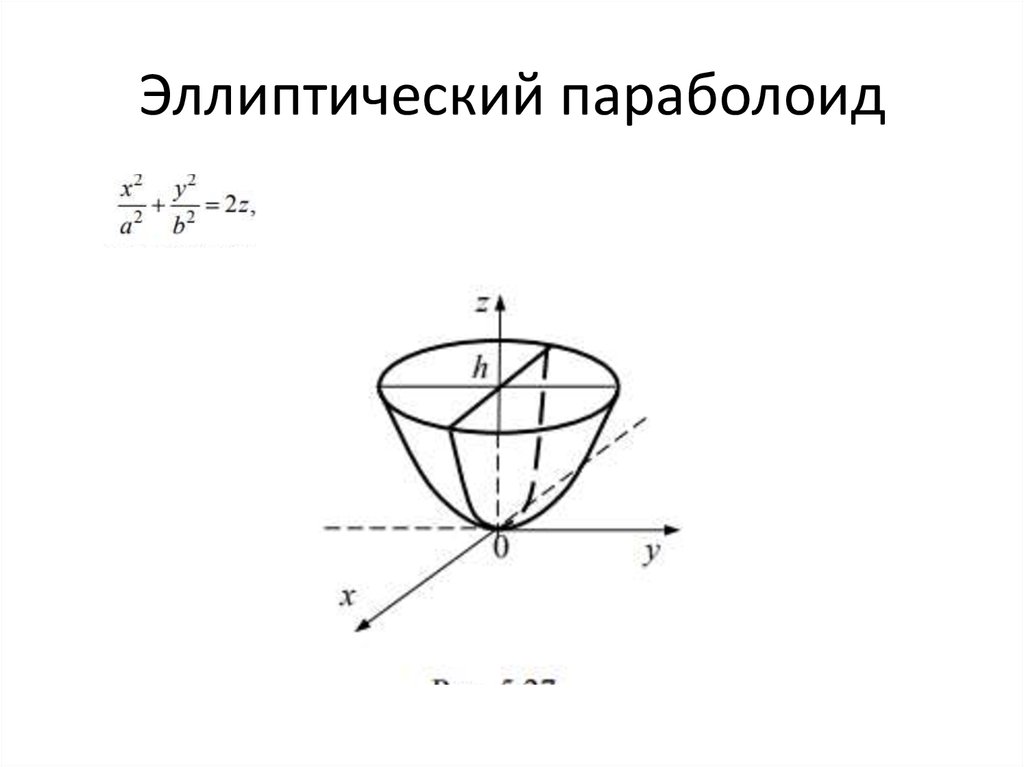
В левую часть уравнения (23) входит функция трех переменных
,
которая называется квадратичной формой от переменных ,,, а матрица
называется матрицей квадратичной формы. Она симметрична, т.к. совпадают коэффициенты, расположенные симметрично относительно главной диагонали. Определитель этой матрицы играет важную роль при определении типа поверхности, заданной общим уравнением.
Кроме того, левая часть уравнения (23) содержит линейную функцию трех переменных
.
3.2. Канонические уравнения второго порядка
Можно выбрать
такую систему координат ОХУZ,
в которой уравнение поверхности имеет
«наиболее простой» вид: в квадратичной
форме отсутствуют члены с произведением
координат, а линейная форма содержит лишь константу.
Такое уравнение поверхности второго порядка называется каноническим уравнением этой поверхности.
Перечислим канонические уравнения поверхностей, которые мы далее будем изучать. А затем, по этим уравнениям определим форму некоторых поверхностей, используя для этого так называемый «метод параллельных сечений».
Канонические уравнения поверхностей второго порядка:
— эллипсоид
— однополостный гиперболоид
— двуполостный гиперболоид
— эллиптический параболоид
— гиперболический параболоид
— конус
— эллиптический цилиндр
— гиперболический цилиндр
— параболический цилиндр
Мы уже говорили,
что введением соответствующей системы
координат (преобразованием исходной)
общее уравнение второго порядка можно
привести к каноническому виду.
В данном
пособии мы не ставим задачи рассмотрения
этих преобразований. Отметим лишь, что
в некоторых случаях простым выделением
полного квадрата (преобразованием
параллельного сдвига) общее уравнение
поверхности может быть приведено к
каноническому виду.
Так, уравнение
можно упростить следующим образом:
или
.
Отсюда
.
Как и в плоском случае, преобразованием координат (параллельным сдвигом)
получим каноническое уравнение эллипсоида в системе координат
.
Кривые второго порядка — парабола,гипербола,эллипс,окружность
Примеры решенийДискриминант Интегралы онлайн Пределы онлайн Производная онлайн Ряд ТейлораРешение уравненийМетод матриц Обратная матрица Умножение матриц
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0
где коэффициенты A,B,C одновременно не равны нулю.
Линии, определяемые такими уравнениями, называются кривыми второго порядка.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным центром, называются центральными.
Координаты центра S(x0 ; y0) линии определяются из системы:
Обозначим через .
При Δ≠0 кривая второго порядка будет центральной.
Причем, при Δ>0 уравнение является уравнением эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа).
При Δ<0 уравнение является уравнением гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых).
При Δ=0 линия второго порядка не является центральной. Такие уравнения называются уравнениями параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа
Классификация кривых второго порядка:
- Эллипс
- Окружность
- Гипербола
- Парабола
Для гиперболы: продолжение отраженного луча света, исходящего из одного фокуса гиперболы, попадает во второй фокус.
Для параболы: лучи света, исходящие из фокуса параболы, после зеркального отражения от нее образуют пучок лучей, параллельных ее фокальной оси.
Уравнение в полярных координатах.
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы имеет вид:
где φ,ρ — полярные координаты произвольной точки линии, p –параметр, ε — эксцентриситет.
При этом полярная система координат выбрана следующим образом: полюс находится в фокусе, полярная ось направлена в сторону, противоположную ближайшей к этому фокусу директрисы.
В частности, при ε=0, получим уравнение окружности в полярных координатах:
ρ=R
Приведение кривой второго порядка к каноническому виду
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
14.6: Реакции второго порядка — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24268
Простейший вид реакции второго порядка — это реакция, скорость которой пропорциональна квадрату концентрации одного реагента.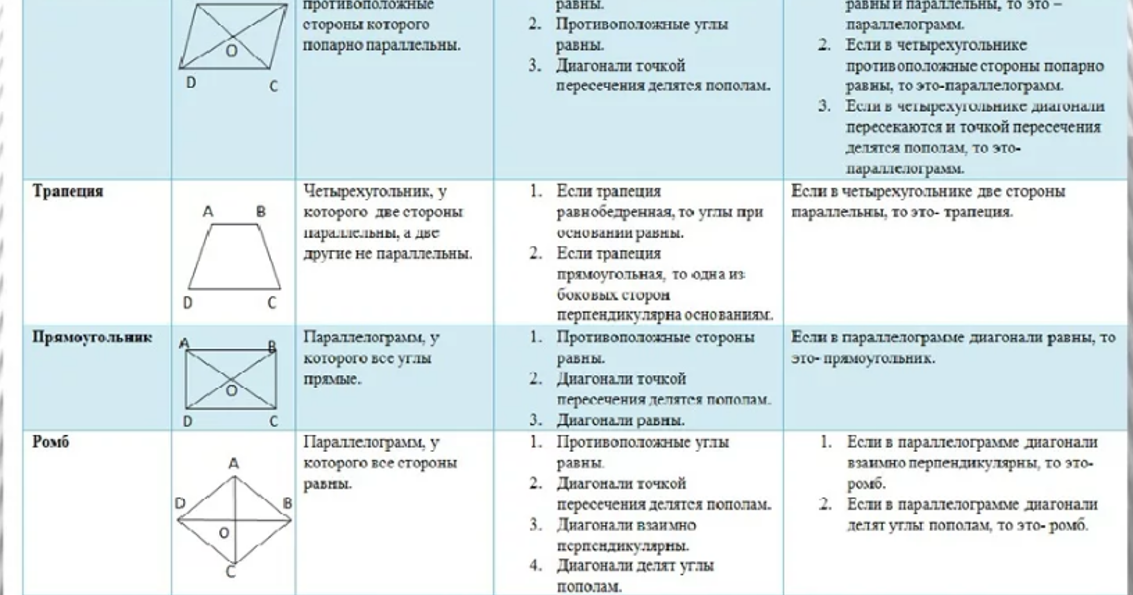
Как правило, они имеют форму 2A → продукты. Второй тип реакции второго порядка имеет скорость реакции, которая пропорциональна произведению концентраций двух реагентов. Такие реакции обычно имеют форму A + B → продукты. Примером первого является реакция димеризации, в которой две меньшие молекулы, каждая из которых называется мономером, объединяются, образуя более крупную молекулу (димер). 92 \метка{14.4.8}\]
Следовательно, удвоение концентрации А увеличивает скорость реакции в четыре раза. Чтобы единицами измерения скорости реакции были моли на литр в секунду (М/с), единицы константы скорости второго порядка должны быть обратными (M -1 · с -1 ). Поскольку единицы молярности выражаются как моль/л, единица константы скорости также может быть записана как л (моль·с).
Для реакции 2А → продукты следующий интегральный закон скорости описывает концентрацию реагента в данный момент времени:
\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt \label{14.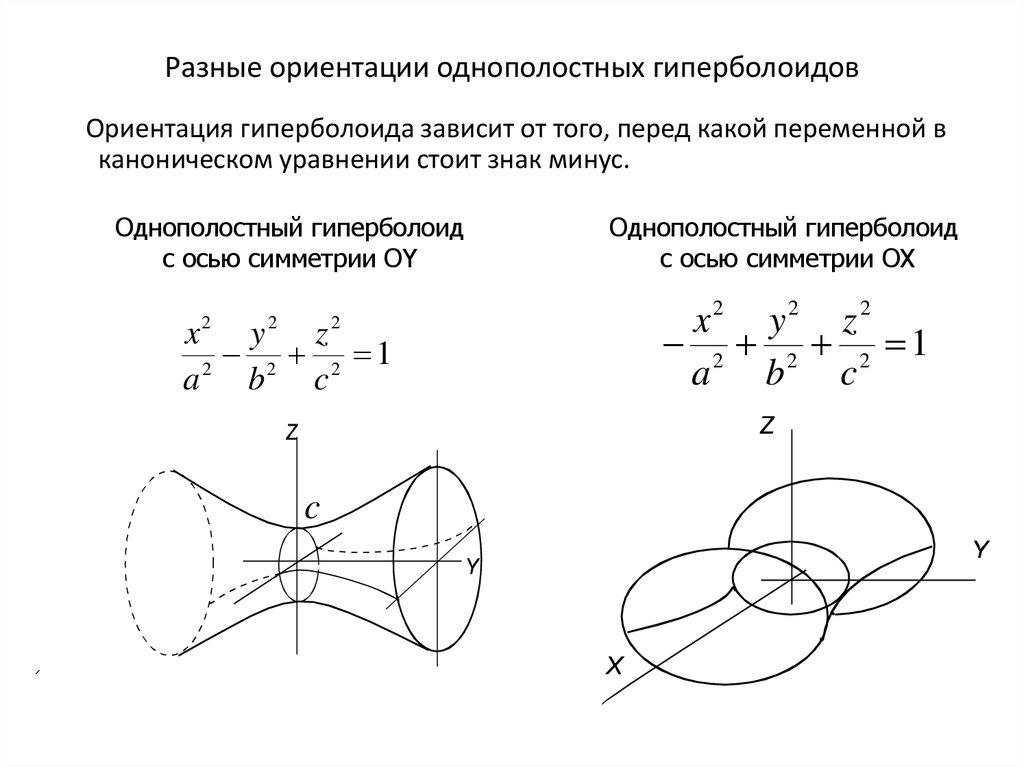
Поскольку уравнение \(\ref{14.4.9}\) имеет форму алгебраического уравнения для прямой линии, y = m x + b , где y = 1/[A] и b = 1/[A] 0 , график зависимости 1/[A] от t для простой реакции второго порядка представляет собой прямую линию с наклоном k и точкой пересечения 1/[A ] 0 .
Примечание
Реакции второго порядка обычно имеют вид 2А → продукты или А + В → продукты.
Распространены простые реакции второго порядка. Помимо реакций димеризации, двумя другими примерами являются разложение NO 2 до NO и O 2 и разложение HI до I 2 и H 2 . Большинство примеров включают простые неорганические молекулы, но есть и органические примеры. Мы можем следить за ходом реакции, описанной в следующем абзаце, наблюдая за уменьшением интенсивности красного цвета реакционной смеси.
Многие циклические органические соединения, содержащие две углерод-углеродные двойные связи, вступают в реакцию димеризации с образованием сложных структур.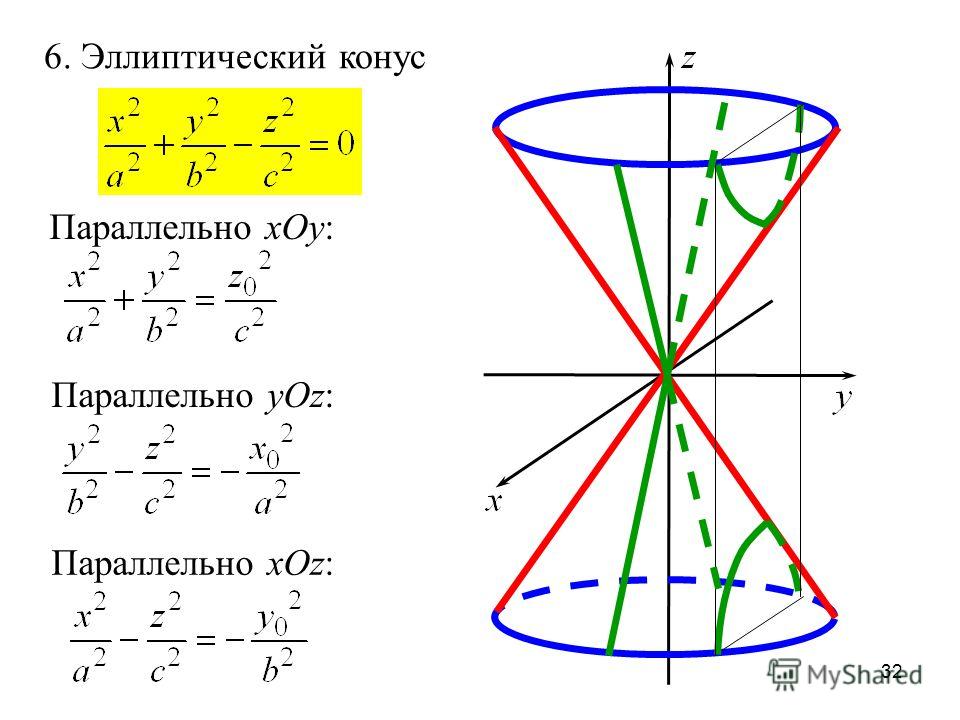
Один пример выглядит следующим образом:
Для простоты мы будем называть этот реагент и продукт соответственно «мономер» и «димер». Систематическое название мономера — 2,5-диметил-3,4-дифенилциклопентадиенон. Систематическое название димера — это название мономера, за которым следует слово «димер». Поскольку мономеры одинаковы, общее уравнение для этой реакции: 2А → продукт. Эта реакция представляет собой важный класс органических реакций, используемых в фармацевтической промышленности для получения сложных углеродных скелетов для синтеза лекарств. Подобно реакциям первого порядка, изученным ранее, ее можно анализировать с использованием дифференциального закона скорости (уравнение \(\ref{14.4.8}\)) или интегрированного закона скорости (уравнение \(\ref{14.4.9).}\)).
| Время (мин) | [Мономер] (М) | Мгновенная скорость (М/мин) |
|---|---|---|
| 10 | 0,0044 | 8,0 × 10 −5 |
| 26 | 0,0034 | 5,0 × 10 −5 |
| 44 | 0,0027 | 3,1 × 10 −5 |
| 70 | 0,0020 | 1,8 × 10 −5 |
| 120 | 0,0014 | 8,0 × 10 −6 |
Для определения дифференциального закона скорости реакции необходимы данные о том, как изменяется скорость реакции в зависимости от концентрации мономера, которые приведены в таблице \(\PageIndex{1}\).
{-1}&=k\end{align}\]
Мы также можем определить порядок реакции, используя интегральный закон скорости. Для этого мы используем снижение концентрации мономера в зависимости от времени для одной реакции, представленное в части (а) на рисунке \(\PageIndex{2}\). Измерения показывают, что концентрация мономера (исходно 5,4 · 10 -3 М) уменьшается с увеличением времени. Этот график также показывает, что скорость реакции плавно уменьшается с увеличением времени. Согласно интегральному закону скорости для реакции второго порядка, график зависимости 1/[мономер] от t должен быть прямой линией, как показано в части (b) на рисунке \(\PageIndex{7}\). Любая пара точек на линии может быть использована для расчета наклона, который является константой скорости второго порядка. В этом примере k = 4,1 M -1 · мин -1 , что согласуется с результатом, полученным с использованием дифференциального уравнения скорости. Хотя в этом примере стехиометрический коэффициент совпадает с порядком реакции, это не всегда так.
Порядок реакции всегда должен определяться экспериментально.
Для двух или более реакций одного порядка реакция с наибольшей константой скорости является самой быстрой. Однако, поскольку единицы констант скорости для реакций нулевого, первого и второго порядка различны, мы не можем сравнивать величины констант скорости для реакций разного порядка.
Пример \(\PageIndex{1}\)
При высоких температурах диоксид азота разлагается на оксид азота и кислород.
\[\mathrm{2NO_2(g)}\xrightarrow{\Delta}\mathrm{2NO(g)}+\mathrm{O_2(g)}\]
Экспериментальные данные для реакции при 300°C и четырех начальные концентрации NO 2 приведены в следующей таблице:
| Эксперимент | [№ 2 ] 0 (М) | Начальная скорость (М/с) |
| 1 | 0,015 | 1,22 × 10 −4 |
| 2 | 0,010 | 5,40 × 10 −5 |
| 3 | 0,0080 | 3,46 × 10 −5 |
| 4 | 0,0050 | 1,35 × 10 −5 |
Определите порядок реакции и константу скорости.
Дано: сбалансированное химическое уравнение, начальные концентрации и начальные скорости
Запрошено: порядок и константа скорости реакции соответствующие изменения исходных концентраций. Определите, характерны ли изменения для реакций нулевого, первого или второго порядка.
Раствор
A Мы можем определить порядок реакции по диоксиду азота, сравнив изменения концентрации NO 2 с соответствующими скоростями реакции. Сравнение экспериментов 2 и 4, например, показывает, что удвоение концентрации увеличивает скорость реакции в четыре раза [(5,40 × 10 -5 ) ÷ (1,35 × 10 -5 ) = 4,0], что означает, что скорость реакции пропорциональна [NO 2 ] 2 . Точно так же сравнение экспериментов 1 и 4 показывает, что увеличение концентрации втрое увеличивает скорость реакции в 9 раз, что снова указывает на то, что скорость реакции пропорциональна [NO 2 ] 2 .
Такое поведение характерно для реакции второго порядка.
B У нас есть ставка = k [NO 2 ] 9{-1}}&=k\конец{выравнивание}\)
Упражнение \(\PageIndex{1}\)
Когда в атмосфере образуется высокореактивное вещество HO 2 , одна важная реакция, которая затем удаляет его из атмосферы, выглядит следующим образом:
\[2HO_{2(g )} \rightarrow H_2O_{2(г)} + O_{2(г)} \nonumber\]
Кинетика этой реакции изучалась в лаборатории, некоторые данные по начальной скорости при 25°C приведены в следующую таблицу:
| Эксперимент | [ГО 2 ] 0 (М) | Начальная скорость (М/с) |
| 1 | 1,1 × 10 −8 | 1,7 × 10 −7 |
| 2 | 2,5 × 10 −8 | 8,8 × 10 −7 |
| 3 | 3,4 × 10 −8 | 1,6 × 10 −6 |
| 4 | 5,0 × 10 −8 | 3,5 × 10 −6 |
Определите порядок реакции и константу скорости.
Ответ второй заказ в HO 2 ; k = 1,4 × 10 9 M −1 · с −1
Примечание
Если график зависимости концентрации реагента от времени равен не линейный, но график зависимости 1/концентрация реакции от времени линейный, тогда реакция второго порядка.
Пример \(\PageIndex{2}\)
Если колбу, изначально содержащую 0,056 М NO 2 , нагреть до 300°C, какой будет концентрация NO 2 через 1,0 ч? Через какое время концентрация NO 2 уменьшится до 10% от начальной концентрации? Используйте интегральный закон скорости для реакции второго порядка (Уравнение \(\ref{14.4.9}\)) и константа скорости, рассчитанная выше.
Дано: сбалансированное химическое уравнение, константа скорости, интервал времени и начальная концентрация
Запрошено: конечная концентрация и время, необходимое для достижения заданной концентрации t и [A] 0 , используйте интегральный закон скорости для реакции второго порядка для расчета [A]. 2\textrm{s}=5,0\ textrm{ мин} \нон номер\]
NO 2 очень быстро разлагается; в этих условиях реакция завершается на 90% всего за 5,0 мин.
Упражнение \(\PageIndex{2}\)
В предыдущем упражнении вы рассчитали константу скорости разложения HO 2 как k = 1,4 × 10 9 M −1 · с −1 . Эта высокая константа скорости означает, что HO 2 быстро разлагается в условиях реакции, указанных в задаче. На самом деле НО 9Молекула 0052 2 настолько реакционноспособна, что ее практически невозможно получить в высоких концентрациях. Для образца HO 2 с концентрацией 0,0010 М рассчитайте концентрацию HO 2 , которая остается через 1,0 ч при 25°C. Сколько времени потребуется для разложения 90% HO 2 ? Используйте интегрированный закон скорости для реакции второго порядка (уравнение \(\ref{14.4.9}\)) и константу скорости, рассчитанную в упражнении в примере \(\PageIndex{3}\).
Ответ 2,0 × 10 −13 М; 6,4 × 10 −6 с
В дополнение к простой реакции второго порядка и закону скорости, которые мы только что описали, другая очень распространенная реакция второго порядка имеет общую форму \(A + B \rightarrow products\), в которой реакция имеет первый порядок в \( А\) и первый порядок в \(В\). Дифференциальный закон скорости этой реакции выглядит следующим образом:
\[\textrm{rate}=-\dfrac{\Delta[\textrm A]}{\Delta t}=-\dfrac{\Delta[\textrm B]}{\Delta t}=k[\textrm A ][\textrm B] \label{14.4.10}\]
Поскольку реакция имеет первый порядок как по А, так и по В, общий порядок реакции равен 2. (Интегральный закон скорости для этой реакции довольно сложен, поэтому мы не будем его описывать.) Мы можем распознать реакции второго порядка. такого рода, потому что скорость реакции пропорциональна концентрации каждого реагента.
Уравнение интегрального закона скорости второго порядка: https://youtu. be/hMSgk2Rm2xA
14.6: Second-Order Reactions распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.
- Теги
Мышление второго порядка: что умные люди используют, чтобы превзойти
Ментальные модели|Время чтения: 3 минуты
Великие ментальные модели.
Вещи не всегда такие, какими кажутся. Часто, решая одну проблему, мы в конечном итоге непреднамеренно создаем другую, еще более серьезную. Лучший способ изучить долгосрочные последствия наших решений — использовать мышление второго порядка.
Часто бывает легче определить, когда люди не учитывали должным образом воздействие второго и последующих порядков. Например, рассмотрим страну, которая, желая вдохновить на смену режима в другой стране, финансирует и предоставляет оружие группе «умеренных повстанцев». Только получается, что те умеренные повстанцы станут могущественными и потом будут десятилетиями воевать со страной-спонсором. Упс.
«Отказ от учета последствий второго и третьего порядка является причиной многих мучительно плохих решений, и это особенно опасно, когда первый худший вариант подтверждает ваши собственные предубеждения. Никогда не хватайтесь за первый доступный вариант, каким бы хорошим он ни казался, пока вы не зададите вопросы и не изучите его».
— Рэй Далио
Способность продумывать проблемы до второго, третьего и n-го порядка — или то, что мы для краткости будем называть мышлением второго порядка, — это мощный инструмент, который перегружает ваше мышление.
Мышление второго порядка.
Мышление первого уровня упрощенно и поверхностно, и почти каждый может это сделать (плохой знак для всего, что связано с попыткой превосходства). Все, что нужно мыслителю первого уровня, — это мнение о будущем, например: «Перспективы для компании благоприятны, что означает, что акции будут расти». Мышление второго уровня глубокое, сложное и запутанное.
Мышление первого порядка быстро и легко. Это происходит, когда мы ищем что-то, что решает только насущную проблему, не задумываясь о последствиях. Например, вы можете думать об этом так, как будто я голоден, поэтому давайте съем плитку шоколада.
Мышление второго порядка более обдуманно. Это мышление с точки зрения взаимодействия и времени, понимание того, что, несмотря на наши намерения, наше вмешательство часто причиняет вред. Мыслители второго порядка задают себе вопрос: «А потом что?» Это означает думать о последствиях многократного поедания плитки шоколада, когда вы голодны, и использовать это для обоснования своего решения. Если вы сделаете это, вы, скорее всего, съедите что-нибудь полезное.
Мышление первого уровня похоже. Все приходят к одним и тем же выводам. Здесь все становится интереснее. Путь к тому, чтобы перехитрить людей, не может исходить из мышления первого порядка. Это должно исходить из мышления второго порядка. Необычайная производительность достигается за счет того, что вы видите то, чего не видят другие люди.
Улучшение вашей способности мыслить
Вот три способа, которые вы можете использовать, чтобы применить мышление второго порядка на практике уже сегодня.
- Всегда спрашивайте себя: «А что потом?»
- Думай во времени — Как выглядят последствия через 10 минут? 10 месяцев? 10 лет? 1
- Создайте шаблоны, подобные второму изображению выше, с последствиями 1-го, 2-го и 3-го порядка.
Определите свое решение, обдумайте и запишите последствия. Если вы будете регулярно просматривать их, вы сможете откалибровать свое мышление. - (бонус) Если вы используете это, чтобы обдумывать бизнес-решения, спросите себя, как важные части экосистемы могут отреагировать. Как к этому отнесутся сотрудники? Что, скорее всего, сделают мои конкуренты? Что насчет моих поставщиков? А регуляторы? Часто ответ будет незначительным или никаким, но вы хотите понять немедленные и второстепенные последствия, прежде чем принимать решение.
Многие необычные вещи в жизни являются результатом вещей, которые являются отрицательными первого порядка, положительными второго порядка. Так что только потому, что вещи выглядят так, будто они не приносят немедленной отдачи, не означает, что это так. Все это означает, что у вас будет меньше конкурентов, если последствия второго и третьего порядка будут положительными, потому что каждый, кто думает в первом порядке, не будет думать до конца.