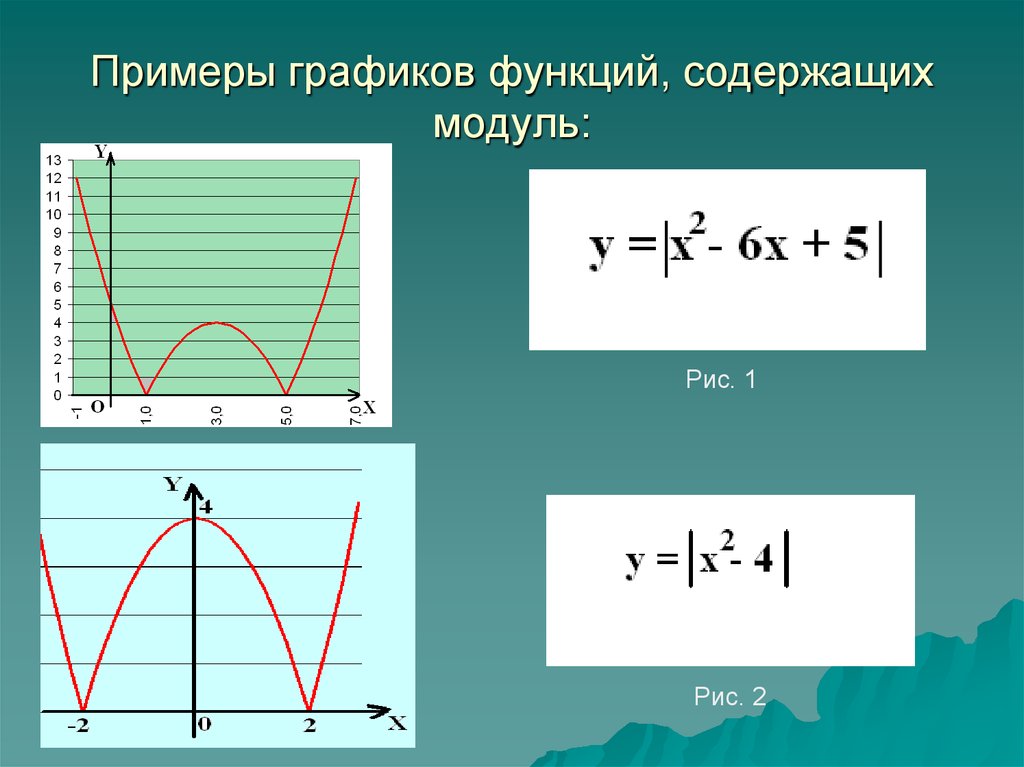
Графики линейной функции, содержащей модуль
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Графики линейной функции, содержащей модуль.
2. I. Графики функций вида y = |kx+b|
Для построения графика функции y=|kx+b|надо сохранить ту часть графика функции
y=kx+b, точки которой находятся на оси Ох
или выше этой оси, и симметрично отразить
относительно оси Ох ту часть графика
функции y=kx+b, которая расположена
ниже оси Ох.
3. Построение графика
y1
у х 3
2
1. Построим
график функции
1
у х 3
2
х
0
4
у
-3
-1
2. Выполним
необходимые
преобразования
графика линейной
функции
0
x
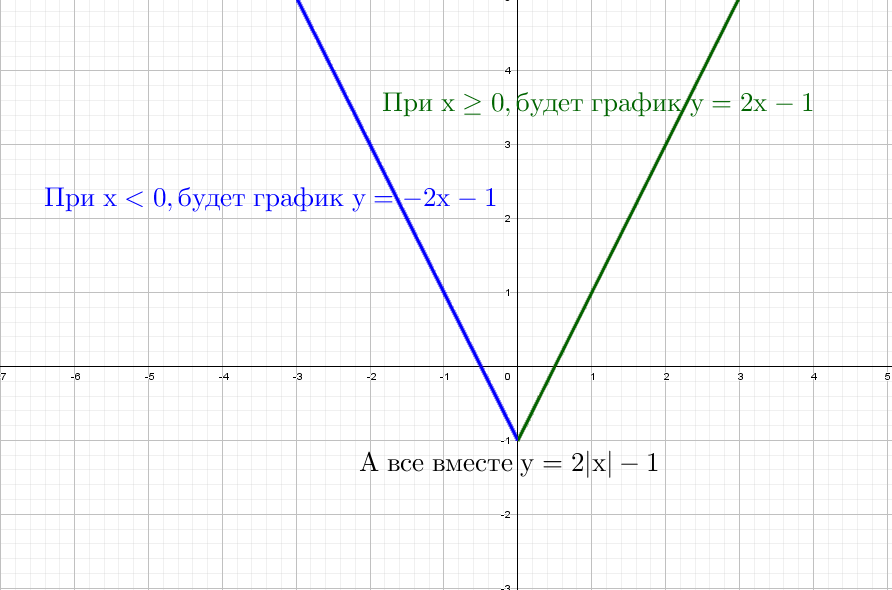
4. II. Графики функций вида y= k|x|+b
Для построения графика функцииy= k|x|+b надо сохранить ту часть
графика функции y=kx+b, точки которой
находятся на оси Оу или справа от неё, и
симметрично отразить эту часть
относительно оси Оу.
5. Построение графика функции
у 3 x 2y
1. Построить
график функции
у 3х 2
х
0
2
у
-2
4
x
0
2. Выполним
необходимые
преобразования
графика линейной
функции
6. Устная работа
y3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6
7. Устная работа
yУкажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1.
у х 33
1
№ 2. у х 3
3
№3. у
1
х 3
3
8. Устная работа
yНа рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5
9. Устная работа
y3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6
10. Устная работа
yУкажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3
11. Устная работа
yНа рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5
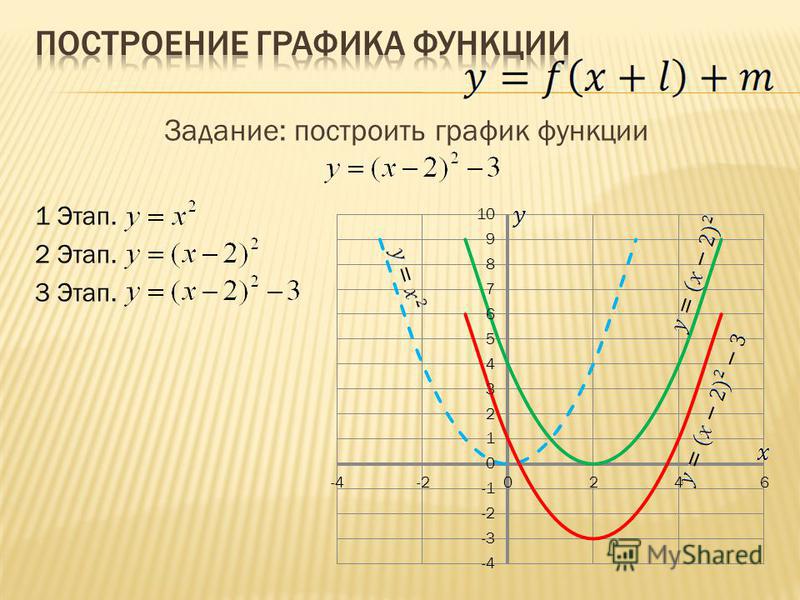
12. Построение графика функции
1у
х 2
1
2
1
1.
у х 22. у х 2
2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
Первый вариант выполняет построения №1, второй вариант — №2.
13. Проверка работы I варианта
1у х 2
2
х
0
4
у
-2
0
у
1
х 2
2
1
у х 2
2
y
x
0
1
14. Проверка работы II варианта
1у х 2
2
х
0
4
у
-2
0
1
у х 2
2
1
у х 2
2
y
x
0 1
Исследуйте число решений
у 2 х 2 4х 24
2
b
уравнения
y
у 2х 4 2
y b
у 2х 4 2
Горизонтальная
прямая, проходящая
через точку с
ординатой b.
Ответ: если b<0, то уравнение не имеет корней; если
b=0, то уравнение имеет два корня; если 0<b<2, то
уравнение имеет четыре корня; если b=2, то
уравнение
имеет
три корня;
если
то
уравнение
Если
Если
Если
0<b<2,
b>2
b<0,
уравнение
то
то
уравнение
уравнение
имеет
корней
имеет
дваb>2,
корня
четыре
не
имеет.
корня.
Если
Если
b=2,
b=0,
то
то
уравнение
уравнение
имеет
имеет
три
два
корня.
корня.
имеет два корня.
x
16. При каком значении b уравнение имеет единственное решение
При каком значении b уравнение 3х 6 2 х bимеет единственное решение
1. у 3х 6
y
2. у 2 х b
Ответ: при
b>-3
исходное
уравнение
имеет
единственно
е решение.
x
-3
18. Домашнее задание
у 2х 4y
1
0
1
x
English Русский Правила
График функций
График функций позволяет учащемуся выбрать функцию и настроить две точки на четырехквадрантной сетке. Учащийся может настроить пунктирную линию асимптоты для экспоненциальных и логарифмических графиков. Автор элемента определяет количество ячеек в симметричной сетке, значения осей и заголовки, функциональные возможности, к которым точки могут привязываться, и функции, которые может выбирать учащийся.
Чтобы создать элемент диаграммы функций, нажмите «Создать элемент», а затем перейдите на вкладку «Элементы». В разделе «Ответные взаимодействия» щелкните знак «плюс» рядом с меткой «График функций» на левой панели.
Обратите внимание, что в настоящее время режим предварительного просмотра не будет отражать никакие введенные значения или выборки. Используйте кнопку предварительного просмотра TN8, чтобы увидеть точное представление элемента.
Сетка
В этом разделе модуля «График функций» автор элемента определяет настройки сетки графика. Значения сетки и приращения шкалы настраиваются. Масштаб четырехквадрантной сетки по умолчанию меняется от -5 до 5 по осям x и y .
Общие
Эти настройки позволяют определить размер четырехквадрантной сетки. Вы можете определить количество ячеек в вертикальном столбце сетки (Вниз) и количество ячеек в горизонтальном ряду сетки (Поперек). Количество ячеек включает оба квадранта, которые имеют одну и ту же ось.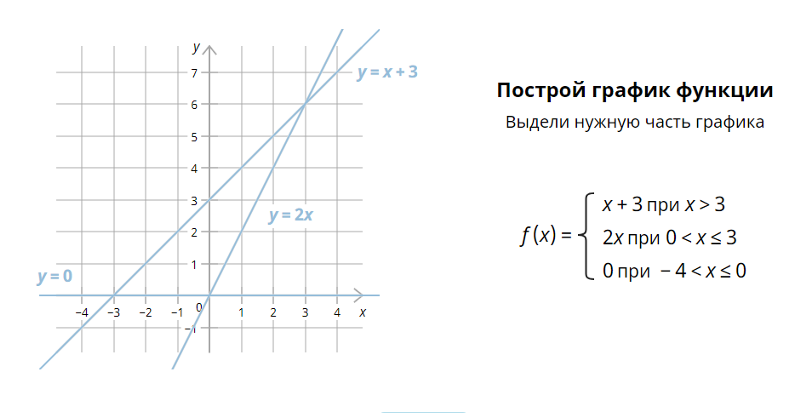
X — и Y — Подразделы осей
Приращение масштаба — это положительное целое или десятичное число, представляющее разницу в значениях между каждой вертикальной или горизонтальной линией сетки. Например, при шаге масштаба 5 создаются линии сетки с метками 0, 5, 10 и т. д. Значение шага масштаба по умолчанию для каждой оси равно 1. В этом поле должно быть указано значение для использования предварительного просмотра TN8.
Максимальное значение — наибольшее значение по каждой оси; самое правое значение на оси x и самое верхнее значение на оси y . Он генерируется автоматически с использованием значений, введенных в поле «Количество ячеек вниз и поперек» и «Приращение масштаба». Эти значения необходимо ввести для расчета и отображения наибольшего значения.
Правильные ответы
В этом разделе модуля Function Graph автор элемента вводит информацию о правильном ответе.
Правильная функция
В этом подразделе автор элемента выбирает одну правильную функцию.
В зависимости от выбранной функции появятся или исчезнут дополнительные поля для ввода правильной информации об ответе.
Инструкции по уравнению
Инструкции по уравнению закрыты по умолчанию. Щелкните стрелку, чтобы увидеть примеры уравнений, а также правила правильного ввода уравнений.
Уравнение
Введите уравнение для правильной функции в формате, описанном в разделе инструкции по уравнению. Все точки, нанесенные учащимся, должны соответствовать определенному уравнению, чтобы ответ считался правильным. Для просмотра элемента в предварительном просмотре TN8 необходимо ввести уравнение.
Значения графика
Все значения графика следует вводить с тем же значением десятичного разряда, которое фиксирует предварительный просмотр TN8. Вам не нужно включать конечные нули. Лучший способ получить это — просмотреть элемент в предварительном просмотре TN8, разместить точки в правильных местах и нажать «Получить счет».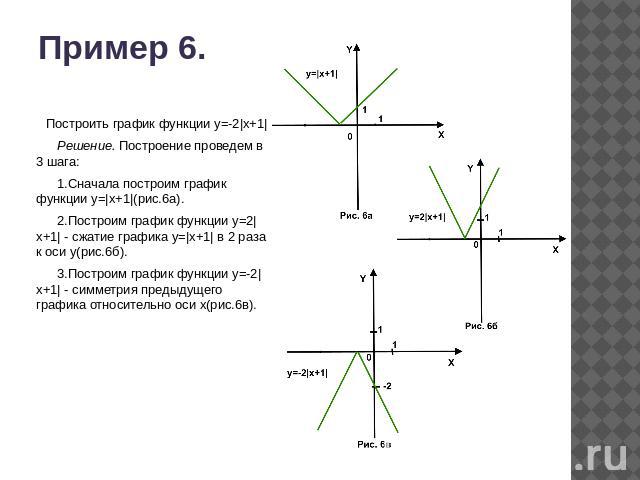
Скопируйте числа, которые вы видите в переменной RESPONSE (или RESPONSE_A, RESPONSE_B и т. д.), в соответствующее поле.
Значение асимптоты : Если правильная функция является экспоненциальной или логарифмической, автор элемента должен ввести значение асимптоты. Это значение y по оси асимптоты экспоненциальной функции является значением по оси X асимптоты логарифмической функции. Он может быть положительным или отрицательным, а также десятичным. Вам не нужно включать x= или y= перед значением, и интерфейс не позволит вам это сделать.
Среднее значение : Если правильной функцией является тангенс/котангенс или синус/косинус, автор элемента должен ввести среднее значение. Средняя линия – это среднее значение y значение максимума и значение y минимума функции. Это может быть положительное или отрицательное число, а также десятичное число. Вам не нужно включать x= или y= перед значением, и интерфейс не позволит вам это сделать.
Значение квартального периода : Если правильной функцией является тангенс/котангенс или синус/косинус, автор элемента должен ввести значение квартального периода. Квартальный период — это абсолютное значение разницы между значением x средней точки и значением x значение соседнего максимума или значение x соседнего минимума. Это может быть положительное или отрицательное число, а также десятичное число. Вам не нужно включать x= или y= перед значением, и интерфейс не позволит вам это сделать.
Точка вершины. Если правильным значением функции является абсолютное или квадратичное значение, автор элемента должен ввести координаты x и y для точки вершины функции. Они могут быть положительными или отрицательными, а также десятичными.
Образец правильных координат
Автор элемента должен предоставить координаты x и y для двух точек.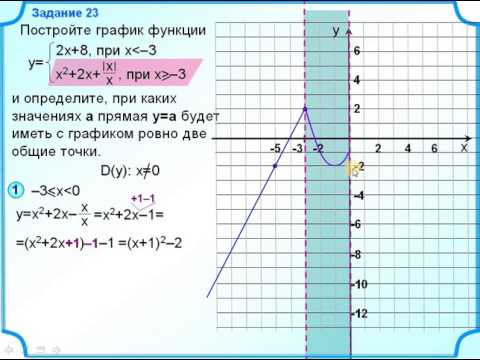
Это делается для того, чтобы публикация могла подтвердить правильность правильного ответа.
График функции
Ваш браузер либо не поддерживает Javascript, либо вы отключили его. Чтобы использовать Mentimeter, обязательно включите Javascript. Как включить Javascript?
Шаблоны/Образование/Математика
Этот шаблон Mentimeter можно использовать как продолжение после применения модуля «Понятие функции», но он также работает сам по себе. Шаблон уточняет, как функции могут быть визуализированы и поняты с помощью графического представления. Шаблон разработан в первую очередь как введение, но его также можно использовать в середине или в качестве подкрепления в конце тематического блока, связанного с линейными функциями.
Как пользоваться шаблоном
Ученикам нужны карандаши и бумага для ответа на некоторые вопросы презентации.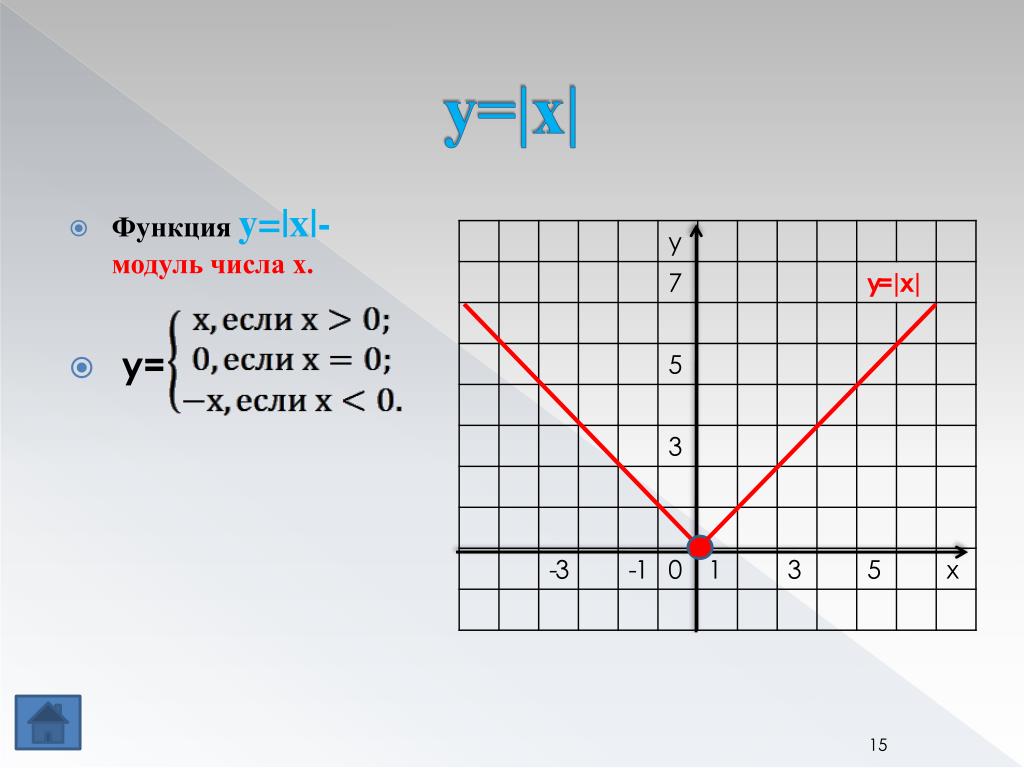
Ниже приведены некоторые идеи о том, как должны использоваться слайды, но не стесняйтесь использовать шаблон по своему усмотрению. В каждый раздел этой страницы включена цель и другая информация, которая может быть полезна вам как учителю. Общая идея относительно всех слайдов заключается в том, что учащиеся должны работать по модели «Думай, пари, делись» (TPS). При реализации TPS учащиеся должны сначала ответить на вопрос индивидуально, затем обсудить в парах (или группах по три человека), а затем обсудить в классе. В качестве заключительного замечания. Содержимое слайдов предназначено в первую очередь для развития понимания учащимися математических концепций, а не процедурного «ноу-хау». Поэтому обсуждения и вопросы учащихся являются центральной частью использования презентации, где ваш опыт как учителя играет центральную роль в прояснении неправильных представлений и ведении дискуссий в классе.
Теоретическая основа
Функция определяется как понятие порога.
Это означает, что он преображает — однажды выученный, он открывает новые способы понимания концепции, и его невозможно забыть. Непонимание концепции функции помешает учащемуся в дальнейшем получить глубокое математическое понимание.
Студенты иногда делают концептуальные ошибки при интерпретации графических представлений функций. Чтобы по-настоящему правильно понять график, учащиеся могут извлечь выгоду из продуманного дизайна обучающего программного обеспечения в сочетании с более глубокими математическими знаниями. Таким образом, этот шаблон может облегчить понимание функций, представленных графами, но требует некоторых математических знаний, чтобы связать возможности обучения с содержанием шаблона и желаемыми результатами.
Слайд 1 — График функции: Познакомить с темой лекции. Например, вы могли бы упомянуть, что графическое представление функции занимает центральное место в математике.
Слайд 2.
Слайд 3 — Критерии успеха: Представьте «критерии успеха» для урока с проблемой, которая будет повторно рассмотрена и решена в конце урока. Идея здесь состоит в том, чтобы сделать обучение видимым, чтобы учащиеся могли сами убедиться, что они действительно чему-то научились.
Слайд 4. По мнению учащихся, график — это…: Пусть учащиеся индивидуально напишут, как они понимают понятие графика. Это может помочь прояснить возможные заблуждения.
Слайд 5 – Куда бы вы хотели положить банан?: Учащиеся должны понять, что банан следует размещать в определенном положении в зависимости от соотношения между осью Y и осью X для разминки.
Слайд 6 – Где бы вы хотели разместить арбуз?: Учащиеся получают еще одну возможность попрактиковаться в идее размещения арбуза в определенном положении в зависимости от соотношения между осью Y и осью X.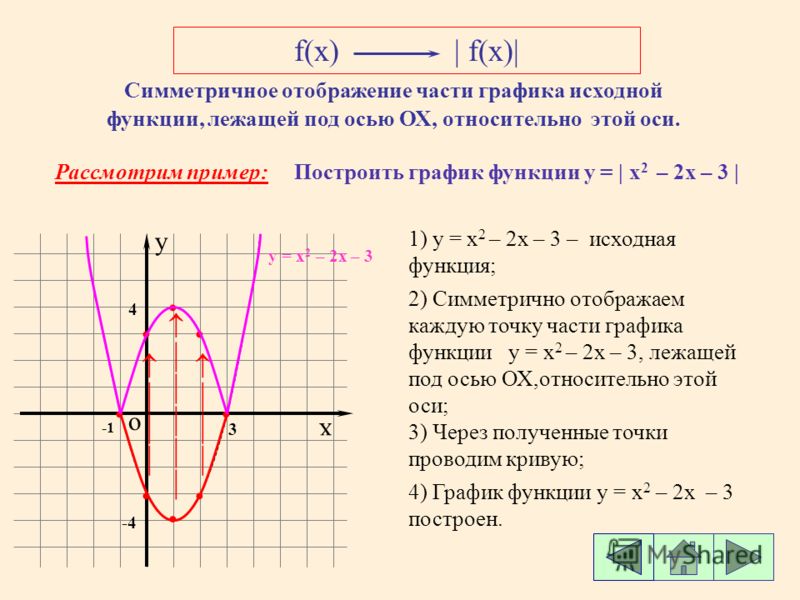
Слайд 7 — Где находится сокровище?: Мысль здесь состоит в том, чтобы вызвать чувство «ага» в понимании необходимости единого математического языка. В частности, точки в системе координат x-y задаются в виде (x, y) (а не (y, x)).
Слайд 8 – Где расположены точки?: Учащиеся получают возможность закрепить понимание (x,y)-представления с помощью точек.
Слайд 9 — Функциональная машина, которая принимает x:s и дает y:s: Это ключевой слайд. Слайд основан на предыдущем модуле («Концепция функции») и связывает «метафору-машину-функция» с графическим представлением.
Слайд 10. В какое значение преобразуются числа -4 и 2 с помощью функциональной машины?: Это ключевой слайд. Идея здесь состоит в том, чтобы укрепить интуицию из предыдущего слайда, в частности, что функция может быть представлена и визуализирована с помощью графика.
Слайд 11: Какова функция машины?: Это ключевой слайд. Идея здесь состоит в том, чтобы усилить два предыдущих слайда, в частности, чтобы функцию можно было представить и визуализировать с помощью графика.
Слайд 12: Возьмите предыдущую функцию f(x)=0,5x+1 и вставьте x=1…: Идея здесь состоит в том, чтобы усилить связь между функцией и ее графиком. Идея здесь состоит в том, чтобы понять, что определенный ввод (по оси x) для функции дает определенный результат (f(x)=y по оси y) и что это справедливо для любого x.
Слайд 14: Каков наклон этого графика?: Здесь понятие (рост/спад) усиливается для лучшего понимания m-значения.
Слайд 15: Каков наклон двух графиков?: Здесь мы вводим отрицательный наклон. Идея здесь состоит в том, что учащийся получит представление о проблемах, связанных с применением концепции (подъем / бег) к отрицательному уклону.
Слайд 16: Каковы функции двух линий?: Применяя формулу (подъем/бег), учащийся должен сформулировать функции.
Слайд 17: Формальное выражение линейной функции: «Введение» в формальное определение линейной функции. Попробуйте сообщить учащимся, что функция зависит только от одной переменной (x) и что m-значение и b-значение являются константами.
Слайд 18: Изменение значений m и b линейной функции: видео, показывающее, что происходит с функцией в визуальном представлении при изменении констант m и b.
Слайд 19: Напишите три точки пересечения по оси y для графиков: Идея здесь состоит в том, чтобы развить понимание значения b или, другими словами, точек пересечения по оси y.