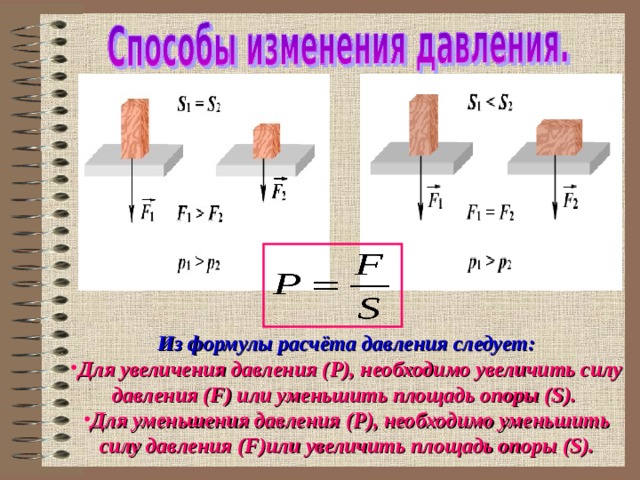
Формула давления в физике
Содержание:
- Определение и формула давления
- Среднее давление
- Давление идеального газа
- Гидростатическое давление
- Единицы измерения давления
- Примеры решения задач
Определение и формула давления
Определение
Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы, которая действует на участок поверхности тела площади $\Delta S$ к размеру данной площади при $\Delta S \rightarrow 0$ . Обозначается давление буквой p. Тогда математической записью определения давления станет формула:
$$p=\lim _{\Delta S \rightarrow 0} \frac{\Delta F_{n}}{\Delta S}=\frac{d F_{n}}{d S}$$
Выражение (1) определяет давление в точке.
Среднее давление
Средним давлением на поверхность называют величину:
$$\langle p\rangle=\frac{F_{n}}{S}(2)$$
где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
$$H=\frac{1}{2}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$$
R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно p0=105 Па, плотность морской воды равна $\rho$=1,03•103 кг/м3
Решение. {5}$ (Па)
{5}$ (Па)
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом $\alpha$ к нормали плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
За время $\Delta t$ о стенку ударяется масса воды равная:
$$m=l S \rho=v \Delta t S \rho$$
где S — поперечное сечение струи, $\rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F \Delta t=m \Delta v \rightarrow F=\frac{m \Delta v}{\Delta t}(2.2)$$
где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
 {2}$
{2}$Читать дальше: Формула закона Ома.
Простая физика — EASY-PHYSIC
Кто подзабыл формулы — тому сюда. Еще очень удобно открыть статью с формулами в соседнем окне, чтобы они были перед глазами.
1. Найдите площадь параллелограмма, если две его стороны равны 14 и 12, а угол между ними равен 30°.
По формуле площади параллелограмма через длины его сторон и синус угла между ними:
2. Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на .
Для того, чтобы найти площадь, необходимо знать сторону. Нам дан периметр, и, поскольку все стороны равны, найдем длину стороны: . Теперь воспользуемся формулой площади равностороннего треугольника: . Разделим на и запишем ответ: 25.
Однако, формулу площади равностороннего треугольника не все помнят. Как же решить эту задачу без формулы? Проведем высоту треугольника из вершины к основанию. Так как треугольник равносторонний, то высота его будет и медианой, и разделит основание пополам:
Так как треугольник равносторонний, то высота его будет и медианой, и разделит основание пополам:
Имеем прямоугольный треугольник с гипотенузой 10 и катетом 5. По теореме Пифагора находим высоту:
Теперь по общеизвестной формуле площади треугольника находим: . В ответ записываем результат, разделенный на .
Ответ: 25.
3. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на .
Можем найти высоту треугольника и основание, воспользовавшись определением косинуса и синуса, и затем площадь. Также нам известны две боковые стороны и угол между ними, поэтому можем воспользоваться формулой . Решим задачу обоими способами: ,
, здесь b — половина основания.
Находим площадь: .
Теперь вторым способом:
Ответ:
4. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.
Найдите площадь треугольника.
Второй способ из предыдущей задачи — единственный для этой задачи:
Ответ: 75.
5. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
Для того, чтобы найти площадь, нужна вторая сторона. Ее можно найти по теореме Пифагора:
Найдем площадь:
Ответ: 48.
6. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Как известно, диагонали ромба перпендикулярны друг другу и точкой пересечения делятся пополам. Поэтому треугольник АВС прямоугольный, его гипотенуза 5, один из катетов 3. Второй катет можем найти по теореме Пифагора: . Значит, диагонали ромба — 6 и 8, а зная их, найдем площадь:
Ответ: 24.
7. Периметр ромба равен 24, а косинус одного из углов равен . Найдите площадь ромба.
Здесь воспользуемся формулой для отыскания площади параллелограмма по двум сторонам и синусу угла между ними: . Но у нас имеется косинус, а не синус. Найдем синус из основного тригонометрического тождества:
Но у нас имеется косинус, а не синус. Найдем синус из основного тригонометрического тождества:
.
Все стороны ромба равны, найдем их, зная периметр:
Площадь ромба:
Ответ: 12.
8. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на .
В этой задаче нас хотят запутать, задав в условии основание треугольника. На самом деле совершенно неважно, каково его основание, так как треугольник равнобедренный, и нам известны боковые стороны и угол между ними, значит, можем воспользоваться формулой площади по двум сторонам и углу между ними:
Делим результат на и записываем ответ:
Ответ: 25
9. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на .
Найдем вторую сторону четырехугольника, чтобы потом определить площадь. Воспользуемся определением синуса, так как ищем мы противолежащий катет:
Площадь равна:
Есть другой путь решения этой задачи, если сообразить, что угол между диагоналями равен . Тогда площадь можем отыскать так:
Делим нашу найденную площадь на , и записываем ответ: 25.
10. Радиус круга равен 3, а длина ограничивающей его окружности равна .Найдите площадь круга. В ответ запишите площадь, деленную на .
Если дан радиус круга, то мы без проблем определим его площадь и без знания длины окружности, верно?
.
Делим результат на , получаем 9 и записываем это число в ответ.
11. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен . Найдите площадь трапеции, если её основания равны 6 и 9.
Найдем высоту трапеции. Катет, лежащий против угла в , вдвое меньше гипотенузы, поэтому высота равна 2,5.
Определяем площадь:
Ответ: 18,75
12. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
Полупериметр прямоугольника равен 46. Полупериметр — это сумма длинной и короткой сторон. Их отношение равно 3:20, то есть три части и двадцать частей. Тогда одна часть: . Тогда длинная сторона — 40 (), а короткая — 6. Площадь прямоугольника
Ответ: 240.
13. Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.
Тут годится единственная формула — это формула Герона: . Раз треугольник равнобедренный, значит, можно их найти: . p — половина периметра: .
Считаем площадь: .
Ответ: 2688.
Давление — это сила на единицу площади Рон Куртус
SfC Home > Physics > Force >
Рон Куртус
Давление — это сила на объект, распространяющийся на площадь поверхности .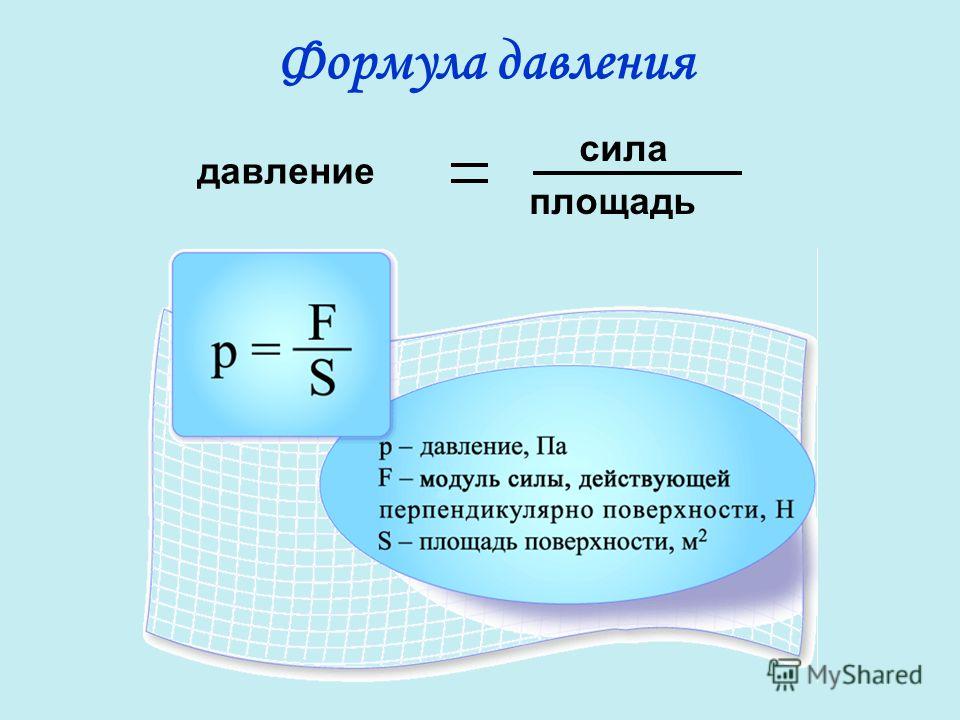
Уравнение давления представляет собой силу, деленную на площадь, на которую действует сила. Хотя это измерение является простым, когда твердое тело давит на твердое тело, в случае, когда твердое тело давит на жидкость или газ, требуется, чтобы жидкость была заключена в контейнер.
Сила также может создаваться весом объекта.
У вас могут возникнуть следующие вопросы:
- Каково давление, когда одно твердое тело давит на другое твердое тело?
- Что происходит, когда твердое тело давит на замкнутую жидкость?
- Что происходит, когда сила исходит от гравитации?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Давление твердого тела на твердое тело
Когда вы прикладываете силу к твердому объекту, давление определяется как приложенная сила, деленная на площадь приложения. Уравнение давления:
П = Ф/А
где
- P давление
- F приложенная сила
- A — площадь поверхности, на которую действует сила
- F/A равно F , разделенному на A
Например, если вы давите на объект рукой с силой 20 фунтов, а площадь вашей руки составляет 10 квадратных дюймов, то оказываемое вами давление составляет 20/10 = 2 фунта на квадратный дюйм.
Давление равно силе, деленной на площадь
Вы можете видеть, что для данной силы, чем меньше площадь поверхности, тем больше давление. Если вы используете большую площадь, вы распределяете силу, и давление (или сила на единицу площади) становится меньше.
Твердое давление на замкнутую жидкость
Когда жидкость или газ заключены в контейнере или цилиндре, вы можете создать давление, приложив усилие с помощью цельного поршня. Давление, создаваемое в цилиндре, равно приложенной силе, деленной на площадь поршня: P = Ф/Д .
В замкнутой жидкости, если пренебречь действием гравитации на жидкость, давление одинаково во всем сосуде, оказывая одинаковое давление на все стенки. В случае с велосипедным насосом давление, создаваемое внутри насоса, будет передаваться по шлангу в велосипедную шину. Но воздух по-прежнему замкнут.
Давление в жидкости действует во всех направлениях
Увеличение силы увеличивает давление внутри цилиндра.
Вызвано гравитацией
Поскольку вес объекта является силой, вызванной гравитацией, мы можем подставить вес в уравнение давления. Таким образом, давление ( P ), вызванное весом ( W ) объекта, равно весу, деленному на площадь ( A ), к которой приложен вес.
П = В/Д
Если положить на пол твердый предмет, давление на пол в области контакта равно весу предмета, деленному на площадь пола.
Давление равно весу, деленному на площадь
Пример с обувью
Хороший пример того, как сила на небольшой площади может привести к очень высокому давлению, можно увидеть в женской обуви с высокими каблуками с шипами. Эти типы обуви могут повредить некоторые полы из-за очень высокого давления на пол в области пятки.
Средняя обувь распределяет вес человека на 20 квадратных дюймов. Таким образом, человек весом 100 фунтов прикладывает к полу 100/20 = 5 фунтов на квадратный дюйм.
Так как площадь каблука-шпильки составляет всего 0,25 квадратных дюйма, человек весом 100 фунтов будет прикладывать 100/0,25 = 400 фунтов на квадратный дюйм к полу в районе пятки! В некоторых случаях этого достаточно, чтобы повредить пол.
Жидкий груз
Если вы поместите жидкость в сосуд, вес этой жидкости будет давить на дно сосуда подобно весу твердого предмета. Давление на дно сосуда было бы таким же, как если бы вес был из твердого тела:P = W/A .
Единственная разница в том, что давление в жидкости распространяется во всех направлениях. Так что давление по бокам внизу будет одинаковым.
Газы и жидкости испытывают давление из-за своего веса в каждой точке жидкости.
Резюме
Давление — это сила, действующая на объект, распределенная по площади поверхности. Уравнение для давления: P = F/A . Давление можно измерить, когда твердое тело давит на твердое тело, но в случае, когда твердое тело давит на жидкость или газ, требуется, чтобы жидкость была заключена в контейнер. Сила также может быть создана весом объекта.
Сила также может быть создана весом объекта.
Положите давление на себя на Excel
Ресурсы и ссылки
Рон Куртус. Условия
Веб -сайты
Ресурсы для физики
Книги
(УВЕДОМЛЕНИЕ: УВЕДОМЛЕНИЕ: УВЕДОМЛЕНИЕ ШКОЛА ДРУГА От 9011.
(УВЕРЕНИЕ: УВЕДОМЛЕНИЕ: УВЕДОМЛЕНИЕ ШКОЛА ДРУГА СРЕДНЯ 9011 ОТМЯ. покупки книг)
Книги с самым высоким рейтингом по физике силы
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
pressure.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа чемпионов
Темы по физике
Давление — это сила на единицу площади
Объяснение урока: соотношение силы, давления и площади
В этом объяснении мы узнаем, как использовать формулу давления 𝑝=𝐹𝐴 для расчета
давления, создаваемые силами, действующими на площади.
Сила является векторной величиной, поэтому сила может быть представлена стрелкой. Такая стрелка может быть нарисована толстой или тонкой линией.
Толщина или тонкость линии не имеет физического значения; только длина линии и ее направление соответствуют свойства силы (ее величина и направление).
Идеальная линия, используемая для обозначения силы, не имеет толщины, только длину. Такая линия, конечно, не будет видна на диаграмме.
Если считать, что стрелка, представляющая силу, имеет толщину, это приводит к ошибочному представлению о том, что сила, действующая на поверхность воздействует на некоторую область, как показано желтой областью на следующем рисунке.
Правильнее думать о кончике стрелки, действующей на поверхность, как показано ниже.
Кончик стрелки — точка; имеет нулевую площадь. Следовательно, сила действует в одной точке, а не на площади.
Представление о силе, действующей на точку, знакомо. Рассмотрим однородный куб, покоящийся на горизонтальной поверхности. Нет ничего необычного в том,
опишите вес куба как действующий в точке в центре грани куба, соприкасающейся с поверхностью.
Нет ничего необычного в том,
опишите вес куба как действующий в точке в центре грани куба, соприкасающейся с поверхностью.
Однако, если эту модель веса куба как силы понимать буквально, то во всех точках обращенной вниз грани куба, отличного от его центра, никакая сила не действовала бы.
В этом случае сила не будет действовать в точке, показанной в центре красного креста на следующем рисунке.
Объект на поверхности в положении центра красного креста, тем не менее, будет иметь силу, действующую на него в реальности. Ан объект под любой точкой на нижней поверхности коробки будет иметь некоторую силу, действующую на него из-за контакта с коробкой.
Когда мы хотим смоделировать силу, действующую на площадь, а не на точку, мы не можем использовать силы, действующие в отдельных точках. Мы должны вместо этого рассмотрим поверхность, для которой силы действуют в каждой точке поверхности.
Когда силы действуют в каждой точке поверхности, можно определить величину, являющуюся результатом действующих сил. Это количество
называется давлением.
Это количество
называется давлением.
Зависимость между силой, давлением и площадью визуально представлена на следующем рисунке. Силы действуют в каждой точке по прямоугольной площади (не все эти силы показаны). Сила в каждой точке одинакова.
Мы видим, что направление действия сил перпендикулярно обеим сторонам прямоугольника. Для производства давление, силы должны действовать перпендикулярно площади. Если силы действуют параллельно площади, то давление не создается.
На следующем рисунке показано поперечное сечение площади. Поперечное сечение площади – это длина. Силы действуют в каждый точку по длине (не все эти силы показаны). Сила в каждой точке одинакова.
Существует математическая связь между давлением на площадь и силой, действующей перпендикулярно всем сторонам области.
Связь: давление на площадь и сила, действующая перпендикулярно площади
Давление 𝑝 на площадь 𝐴 определяется выражением
𝑝=𝐹𝐴,
где 𝐹 — сила, действующая перпендикулярно всем сторонам площадки.
Если 𝐹 имеет единицу измерения ньютоны и 𝐴 имеет единицу квадратных метров, то 𝑝 имеет единицу измерения паскали (Па). Это означает, что 1=11.ПаН·м
Давление часто указывается в килопаскалях (кПа), где 1 кПа = 1 000 Па.
Когда мы рассматриваем формулу 𝑝=𝐹𝐴, мы можем видеть, что для фиксированного значения 𝑝, чем больше значение 𝐴, тем меньше значение из 𝐹 должен создавать давление 𝑝. Соответственно, меньшее значение 𝐴 соответствует большему значению 𝐹, необходимому для получения фиксированного значения 𝑝.
Мы видели, что силы давления имеют направление. Область, на которую действует давление, можно считать имеющей направление по сравнению с силами.
Показывая прямоугольную область, мы видим, что направление, в котором действуют силы, перпендикулярно обеим сторонам прямоугольник.
Тогда мы можем рассматривать как силу 𝐹, так и площадь 𝐴 как векторные величины. Это
случае, даже если площадь является скалярной величиной, когда она не связана с направлением силы. Отношение площади к силе
то, что перпендикулярно площади, меняет способ использования площади количества.
Это
случае, даже если площадь является скалярной величиной, когда она не связана с направлением силы. Отношение площади к силе
то, что перпендикулярно площади, меняет способ использования площади количества.
Соотнося силу, площадь и давление, мы видим, что умножение площади, перпендикулярной силе, на давление дает сила: 𝐴𝑝=𝐹.
Поскольку и сила, и площадь рассматриваются как векторные величины, когда они соотносятся таким образом, мы видим, что давление должно быть скаляром. количество. Это тот случай, когда умножение векторной величины на скалярную дает другую векторную величину.
Тогда мы можем выразить связь между силой, давлением и перпендикулярной площадью как ⃑𝐴𝑝=⃑𝐹.
Другой способ понять взаимосвязь между силой и давлением — сделать силой предмет формулы. Мы можем сделать это, умножив формулу на 𝐴: 𝑝×𝐴=𝐹𝐴×𝐴=𝐹.
Это дает нам 𝑝𝐴=𝐹.
Рассматривая формулу таким образом, мы можем сказать, что давление 𝑝 на площадь 𝐴 связано
с силой 𝐹, действующей в каждой точке этой области. Все силы действуют перпендикулярно площади.
Все силы действуют перпендикулярно площади.
Отношение визуально представлено на следующем рисунке, где снова длина представляет собой поперечное сечение площади.
Используя соотношение между силой, давлением и площадью, мы можем визуально представить изменение площади при фиксированном давлении. Это показано на следующем рисунке, на котором одинаковое давление действует на две разные области.
Мы видим, что сила, связанная с давлением, обратно пропорциональна площади.
Давление может действовать как на жидкости, так и на твердые объекты. Когда на жидкость действует давление, направление сил, действующих в жидкость может идти по разным направлениям.
На следующем рисунке показано, что увеличение давления на верхнюю часть емкости с водой может привести к тому, что сторона емкости разрыв.
Мы видим, что направление силы на стенке контейнера не совпадает с направлением силы из-за давления сверху
контейнер. Итак, мы видим, что давление не обязательно должно действовать в направлении силы, производящей давление.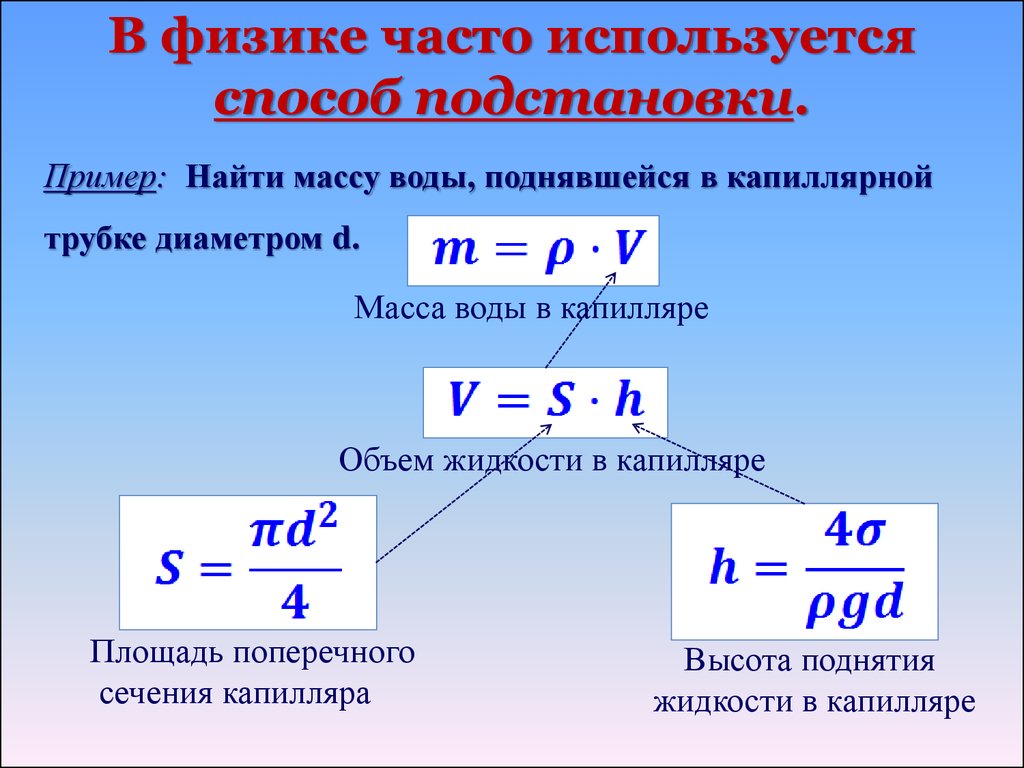 Мы не можем
тогда, вообще говоря, определите направление давления. Это означает, что давление считается скалярной величиной.
Мы не можем
тогда, вообще говоря, определите направление давления. Это означает, что давление считается скалярной величиной.
Теперь рассмотрим пример определения давления.
Пример 1: Определение давления
Какое давление создается 100 Н сила, приложенная к площади 2,5 м 2 ?
Ответ
Давление можно определить по формуле 𝑝=𝐹𝐴.
Подставляя значения в вопросе, получаем 𝑝=1002,5=40/=40,НмНмПа
Теперь рассмотрим пример определения силы по давлению.
Пример 2. Определение силы с помощью давления
Давление в 400 Па прикладывается к площади 2,5 м 2 . Какая сила производит это давление?
Ответ
Мы можем изменить формулу 𝑝=𝐹𝐴 сделать 𝐹 предметом.
Мы можем сделать это, умножив формулу на 𝐴: 𝑝×𝐴=𝐹𝐴×𝐴=𝐹.
Это дает нам 𝐹=𝑝𝐴.
Подставляя значения в вопросе, получаем
𝐹=400×2,5=1000⋅=1000. PamPamN
PamPamN
Давайте теперь рассмотрим пример определения площади с помощью давления.
Пример 3. Определение площади с помощью давления
Давление в 75 Па создается 3 сила Н. На какую площадь создается давление?
Ответ
Мы можем изменить формулу 𝑝=𝐹𝐴 сделать 𝐴 предметом.
Мы можем сделать это, сначала умножив формулу на 𝐴: 𝑝×𝐴=𝐹𝐴×𝐴=𝐹.
Это дает нам 𝐹=𝑝𝐴.
Затем формула делится на 𝑝: 𝐹𝑝=𝑝𝐴𝑝=𝐴𝐴=𝐹𝑝.
Подставляя значения в вопросе, получаем 𝐴=300075=40/=40.NPaNPam
Давайте теперь рассмотрим пример, в котором вес представляет собой силу, действующую на площадь.
Пример 4: Определение давления по весу
Диван массой 125 кг имеет основание площадью 2,5 м 2 . Какое давление оказывает диван на землю под ним?
Ответ
Давление можно определить по формуле 𝑝=𝐹𝐴.
Действующая сила равна весу дивана. Вес дивана указан
𝐹=𝑚𝑔,
где 𝑚 — масса дивана, а 𝑔 — ускорение свободного падения или силы тяжести.
напряженность поля. Значение 𝐹 определяется выражением
𝐹=125×9,8/𝐹=125×9,8/𝐹=1225.kgmskgNkgN
Вес дивана указан
𝐹=𝑚𝑔,
где 𝑚 — масса дивана, а 𝑔 — ускорение свободного падения или силы тяжести.
напряженность поля. Значение 𝐹 определяется выражением
𝐹=125×9,8/𝐹=125×9,8/𝐹=1225.kgmskgNkgN
Подставляя значения в вопросе, получаем 𝑝=12252,5=490/=490,НмНмПа
Давайте теперь рассмотрим пример, в котором площадь, на которую создается давление, должна быть определена, чтобы найти вес объект, поддерживаемый в этой области.
Пример 5: Определение веса при заданном давлении
Пустой резервуар для воды имеет прямоугольное основание с длиной сторон 1,2 м. и 2,3 м. Вес бака оказывает давление 350 Па к поверхности, на которую он опирается. Каков вес танка?
Ответ
Вес бака – это сила, действующая на него. Мы можем представить силу как 𝐹.
Мы можем изменить формулу 𝑝=𝐹𝐴 сделать 𝐹 предметом.
Мы можем сделать это, умножив формулу на 𝐴:
𝑝×𝐴=𝐹𝐴×𝐴=𝐹.