Площади фигур — формулы.
2014-07-25 | Автор: Анна
Вспоминаем формулы для вычисления площадей фигур!
Формулы площадей фигур
| Треугольник общего вида. a, b, c — стороны, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности |  |   |
| Прямоугольный треугольник. a, b — катеты, с — гипотенуза, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности |  |  |
| Правильный треугольник |  |  |
| Прямоугольник. a,b — стороны, d — диагонали. |  |  |
| Квадрат. |  |  |
| Параллелограмм. a,b — стороны, d — диагонали, h — высота |  |  |
| Ромб. a — сторона, d — диагональ, h — высота |  |  |
| Трапеция. a,b — основания, h — высота, d — диагонали. |  |  |
| Круг. |  |  |
| Элементы круга. |  |  |
| Правильный n-угольник |  |  |
Все формулы по школьной физике
Площади
l – длинна
b — высота, ширина.
Площадь круга:
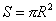
Кинематика.
Равномерное движение:
a = 0
V = S/t
Ускоренное движение:
a > 0
a = (V – V0 )/ t
S = S0 + V0t ± (at2 )/2
a = (V2 – V0
2 )/ 2SПоследовательный ряд нечетных чисел:
— ую:
просто:
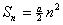
Движение под углом к горизонту.
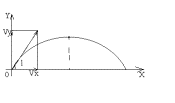
Скорость по оси ОХ:
Скорость по оси ОУ:
Максимальное время подъема:
tполн = 2t
Расстояние :
S = Vx tполн.
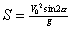
Максимальная высота:
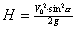
Движение тела, брошенного горизонтально:
; 
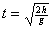Динамика.
F = ma
P = mg
Fтр. = -mN
F = -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x – удлинение.
k – кооф. растяжения.
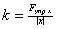
<l = l – l0
<l – абсолют. удлинение пружины.
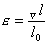
ε -относит. удлинение.
l0 –
начальная длинна 
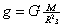
Работа и энергия.
; 
; 
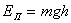
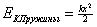
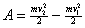
Движение по окр-ти.
; 
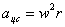
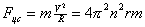
w — угловая скорость.[рад/с]
v -линейная скорость.
n — частота обращения. [об./мин.]
T – период обращения. [время]
Угловая скорость. Период
обращения.
; 
; 
; 
; 
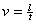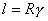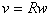
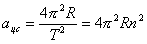
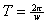Для случаев, когда n = [обороты]
; 
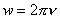
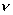— частота [1/с = 1 Гц]
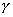— угол.
l – длинна дуги.
Импульс.
;
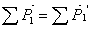
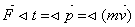
Не упругое вз-вие.
до: после: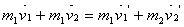 
в проекции на ось х:
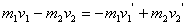
Упругое соударение.
до вз-я: после:
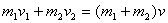
в проекции на ось х:
Реактивное движение:
в проекции на ось х: (вверх)
║
0 изначально.
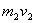— импульс газов
Импульс силы.
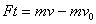
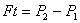
Механика жидкостей и газов.
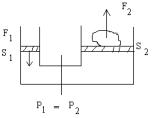
Давление. Закон Паскаля.
-//- жидкости на дно сосуда.
; F – сила давления
S – поверхность[1Па = 1Н/1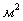
]
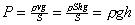
h – высота уровня жидкости.
Сообщающиеся сосуды.
; 
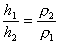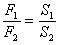
Архимедова сила. Атм. давление
; 
; 
/
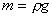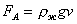
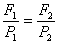
вытесненной жидкости цилиндром.
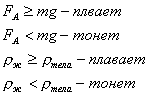
Закон Гука. Растягив. сила.
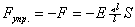
l –первоначальная длинна стержня
Δl –абсолютное удлинение
S –площадь поперечного сеч.
E –кооф. пропорцион., модуль Юнга, модуль упругости.
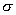— напряженность
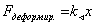-закон Гука
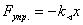
КПД машин.
; [1дж/1с = 1 Вт]
Колебания и волны. Звук.
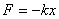
F – возвращающая сила
k – постоянная возвращающ.
x – смещение
Маятник.
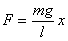;l – длинна маятника
Математический маятник – точка, подвешенная на невесомой и нерастяжимой нити.
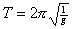
Пружинный маятник:
; 
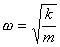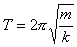
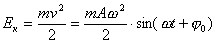
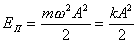
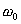— циклическая частота колебаний
Фаза колебаний.
— угловая скорость
— угол поворота
Скорость распространения волн
; 
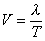Электромагнитные колебания.
; 
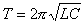
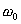— собственна частота колебаний в контуре
; 
; 
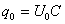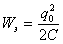
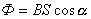
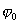— фаза колебаний
— амплитуда тока
С – скорость в ваакуме
n – абс. показатель преломления среды
Молекулярно-кинетическая
теория
; 
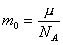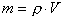
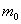— масса молекулы
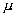— молярная масса
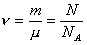; N – число
молекул.
Теплоемкость тела.
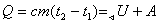
с – теплоемкость тела
U – внутренняя энергия
А – работа
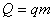
q – теплота сгорания
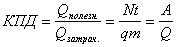
!!! Бывает наоборот!
Линейное расширение твердых тел.
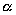— кооф. линейного расширен.
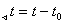— интервал температур.
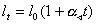
Объемное расширение твердых тел.
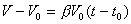
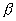— кооф. объемного расш. тел.
Свойства газов.
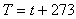
T = const – изотермический
P = const – изобарический
V = const – изохорический
Главный газовый закон:
Закон Менделеева – Клаперона
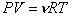
— концентрация молекул
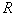= 8.31 Дж/моль*К
— кол-во в-ва.
; 
; 
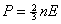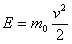
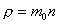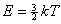
k = 1.38*10^-23 Дж/К
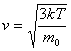
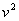— среднеквадратичная ск-ть
— средняя кинетич. энергия движ. мол-лы.
КПД тепловой машины.
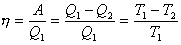
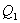— кол-во теплоты, получ. рабочим телом от нагрев.
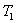— t холод.
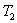— нагреват.
Электричество и магнетизм.
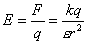[В/м] ; 
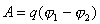
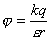
Эквипотенциальные пов-ти.
; 
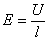l – расстояние
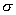— поверхностная плотность заряда
Закон Кулона
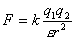; [Н]
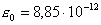Ф/м
\ эл. постоянная
Электроемкость. Конденсаторы.
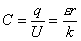
[Дж]
W – Энергия
Электроемкость плоского:
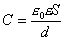
Шара: 
Параллельное подключение конденсаторов:
Последовательное подключение:
Постоянный электрический ток.
; 
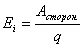
; i – плотность тока
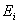— Электродвиж. сила
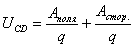[В]
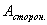— работа, совершенная сторонними силами
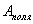— сила эл. поля
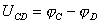
Закон Ома для участка цепи.
; 
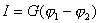
G — кооф. пропрциональности проводника(его проводимость)
; 
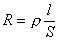
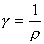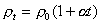
— удельная проводимость.
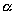— температурный кооф. сопр.
— удельное
сопротивление
[1 град. ^ -1]
постоянная:
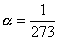
Последовательное и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной цепи:
Последоват. соед. батарей:
; 
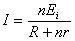n – кол-во батарей
Параллельное соед. батарей:
; 
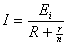Работа при перемещении эл. заряда в эл. поле. Потенциал.
; 
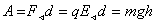
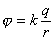
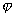— потенциал эл. поля
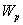— потенциальная энергия заряда в поле.
Работа и мощность эл. тока:
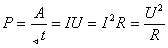
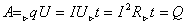
Напряжение.
Магнитное поле
; 
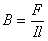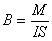
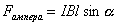
При расположении проводника с током под углом альфа к вектору В.
B – магнитная индукция
I — сила тока
l – длинна проводника
M – макс. момент сил
S – площадь рамки
Сила Лоуренца
; 
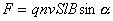
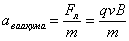
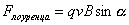
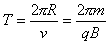
n – концентр. свободных частиц
v –скорость упор. движ.
S –площадь поперечного сечения проводника
Магнитная прониуаемость.
; 
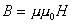
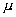— магнитная прониц. среды
H- напряженность магнитного поля.
Электромагнитная индукция
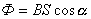[Вб]
; 
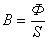
Ф – магнитный поток
; 
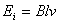
Самоиндукция.
; 
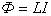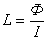[Гн]
; 
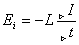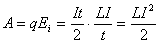
; W — энергия
Магнитная рамка.
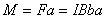
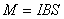
b,a – стороны рамки
S — площадь рамки
Электроны.
; 
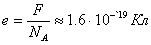
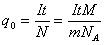
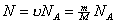
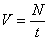
Электролиты
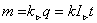
Оптика
Закон преломления
; 
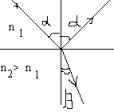
— ваакум
; 
; 
;
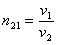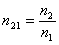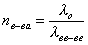
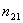— относит. показатель преломления.
— скорости света во 2-й и первой средах.
Линзы
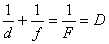
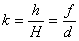
d –расстояние предмета от линзы
f –расстояние от изображения до предмета
F – фокус
D –Оптическая сила линзы [диоптрии]
k — увеличение линзы
Квантовая физика
; 
; 
; 
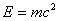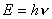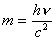
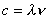
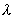— длинна волны излучения
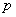— импульс фотона
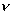— частота излучения
В магнитно-преломляющих средах:
В однородно прозрачной среде:
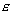— относит. диэликтрич. проницаемость среды
— относит. магнитная проницаемость среды.
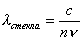
n – постоянная
Уравнение Эйнштейна.
; 
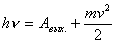А – работа выхода электрона из в-ва
Фотоэффект.
Для того, чтобы фотоэффект имел место, необходимо что бы энергия кванта света была больше работы выхода. Предельное значение частоты, при которой еще наблюдается фотоэффект, наз. красной границей фотоэффекта.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://ilib.ru/
Дата добавления: 30.07.2003
Формула Пика
Как определить площадь сложной фигуры? Если она нарисована на клетчатой бумаге, и невырождена -площадь ее ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга – то удобно воспользоваться формулой Пика.
Если обозначить: В – количество целочисленных точек внутри этой фигуры, Г – количество целочисленных точек на ее границе, S – площадь фигуры, то
S=В+Г/2-1
Рассмотрим следующую фигуру:
Формула Пика – определение числа узлов внутри и на границе фигуры.
Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие: В=12, Г=4. Определим теперь площадь по формуле: S=В+Г/2-1=12+2-1=13.
Давайте проверим правильность наших расчетов, тем более, что здесь это просто: рассчитаем площадь квадрата, обведенного красным, и вычтем площади цветных треугольников:
Вычисление площади при помощи отрезания “лишнего”
Тогда площадь квадрата Sкв=36, площадь голубого треугольника 6, площадь зеленого – 2, площадь фиолетового 15.
Площадь белого треугольника тогда: S=36-6-15-2=13.
Рассмотрим такую фигуру:
Еще один пример определения площади сложной фигуры с помощью формулы Пика
Для нее S=В+Г/2-1=4+3-1=6.
Проверим:
Отрежем лишнее
Тогда площадь прямоугольника Sпр=20, площадь голубого треугольника 5, площадь зеленого – 4, площадь фиолетового 5.
Площадь искомой фигуры тогда: S=20-5-4-5=6.
Третья фигура:
Еще один пример работы с формулой Пика
Для нее S=В+Г/2-1=4+4-1=7.
Проверим: площадь треугольников, составляющих нашу фигуру: голубого – 4, зеленого – 1, оранжевого – 2. Сумма их площадей S=4+1+2=7.
Расчет площади с помощью разрезания фигуры
Еще две фигуры:
Узлы решетки внутри и на границе фигуры
Площадь первой: S=10+2-1=11,
Узлы решетки внутри и на границе
второй – S=10+5-1=14.
Проверить правильность расчета их площадей вы можете самостоятельно.
Формулы площади поверхности тел
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Содержание статьи:
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
Sбок = ph=pl
р — периметр основания;
h — высота;
l — боковое ребро.
Формула площади поверхности куба
Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.
Sбок = 4a2
Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.
P = 6a2
а — ребро куба.
Формула площади поверхности пирамиды
1) Правильная пирамида:
Sбок = 1/2pA
p — периметр основания;
A — апофема.
Sбок = S/cos φ
S — площадь основания;
φ — угол между боковой гранью и основанием пирамиды.
Sбок = Sгр n
Sгр — площадь одной боковой грани;
n — количество боковых граней пирамиды.
2) Правильная усеченная пирамида:
Sбок = 1/2(p1 + p2)A
p1 ,p2 — периметры оснований;
A — апофема.
Р = Sбок + S1 + S2
Р — площадь полной поверхности правильной усеченной пирамиды;
Sбок — площадь боковой поверхности правильной усеченной пирамиды;
S1 + S2 — площади оснований.
Формула площади поверхности цилиндра
Sбок = 2πrh = πdh
P = 2πr2+2πrh = 2π(r+h)
P — площадь полной поверхности цилиндра;
r — радиус цилиндра;
d — диаметр цилиндра;
h — высота цилиндра.
Формула площади поверхности конуса
1) Прямой круговой конус:
Sбок = πrl = 1/2 πdl
P = πr2 + πrl= πr(r+l)
P — площадь полной поверхности конуса;
r -радиус конуса;
d -диаметр конуса;
l — образующая конуса.
2) Усеченный прямой круговой конус:
Sбок = πl(r1 + r2) = 1/2πl(d1 + d2)
P = πl(r1 + r2) + π(r1 + r2)
P — площадь полной поверхности усеченного конуса;
r1, r2 — радиусы оснований усеченного конуса;
d1, d2 — диаметры оснований усеченного конуса;
l — образующая усеченного конуса.
Формула площади поверхности шара (сферы)
Шар — тело, созданное вращением полукруга вокруг диаметра.
Сфера — поверхность шара.
P = 4πR2 = πD2
Формула площади поверхности сферического сегмента
Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.
Sсф. сегм. = 2πRh = π(a2 + h2)
Формула площади поверхности шарового сегмента
Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.
Sшар. сегм. = π(2Rh+a2)=π(h2+2a2)
R — радиус шара;
D — диаметр шара;
h — высота сегмента;
a — радиус основания сегмента.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Физические величины | Формулы и расчеты онлайн
Физические законы выражаются в виде математических соотношений между физическими величинами. Под последними понимают измеряемые характеристики (свойства) физических объектов (предметов, состояний, процессов).
Каждая физическая величина представляет собой произведение численного значения на единицу измерения.
Например:
\[ время = 5 · секунд \]
Только одного численного значения недостаточно для характеристики физической величины. Поэтому никогда нельзя опускать соответствующую единицу измерения.
Основные физические величины
В Физике, в международной системе единиц (СИ) применяются следующие 7 семь основных физических величин: Длина, Время, Масса, Температура, Сила тока, Количество вещества, Сила света.
Производные физические величины
С помощью основных величин можно получить другие величины либо используя выражения для законов природы, либо путем целесообразного определения через умножение или деление основных величин.
Например:
\[ Скорость = \frac{Путь}{Время} \] \[ Работа = Сила · Путь \] \[ Плотность = \frac{Масса}{Объем} \] \[ Заряд = Сила тока · Время \]
и т.д.
В международной системе (СИ), все единицы кроме основных, представляют собой произведения степеней основных единиц, не содержащие численных коэффициентов, или, иначе говоря, образуются когерентно из основных единиц. Другие единицы являются некогерентными и поэтому не входят в систему СИ.
Пример: Ватт (Вт) — когерентная единица мощности, она выведена без численного коэффициента
\[ 1 Вт = 1 кг · \frac{м^2}{с^2} \]
Киловатт (кВт) — некогерентная единица мощности, она выведена с помощью численного коэффициента
\[ 1 Вт = 10^3 кг · \frac{м^2}{с^2} \]
В помощь студенту
Физические величины |
стр. 363 |
|---|
Формулы площади поверхности и формулы объема 3D-фигур
Формулы площади поверхности и формулы объема снова и снова появляются в расчетах и домашних заданиях. Давление — это сила на площадь, а плотность — это масса на объем. Это всего лишь два простых типа вычислений, в которых используются эти формулы. Это краткий список распространенных геометрических фигур и формул их площади поверхности и формулы объема.
Формула площади поверхности сферы и Формула объема сферы
Сфера — это сплошная фигура, каждая точка на поверхности которой равноудалена от центра сферы.Это расстояние представляет собой радиус r сферы.
Площадь поверхности = 4πr 2
Объем = 4 ⁄ 3 πr 3
Формула площади поверхности призмы и формула объема призмы
Призма имеет геометрическую форму фигура, состоящая из стопки одинаковых базовых фигур, уложенных друг на друга на глубину d. Эта призма представляет собой призму, образованную стопкой треугольников.
Площадь поверхности призмы = 2 × (Площадь базовой формы) + (Периметр базовой формы) × (d)
Объем призмы = (Площадь базовой формы) × d
До найдите площадь и периметр базовой формы, ознакомьтесь с формулами площади и формулами периметра.
Формула площади поверхности коробки и формула объема коробки
Коробку можно представить как стопку прямоугольников длиной L и шириной W, сложенных друг на друга на глубину D.
Площадь поверхности коробки = Сумма площадей каждой стороны коробки, или
Площадь поверхности коробки = 2 (Д × Ш) + 2 (Д × Г) + 2 (Ш × Г)
Объем коробки = Д × Ш × Г
Формула площади поверхности куба и формула объема куба
Куб — это коробка особого случая, в которой все стороны имеют одинаковую длину.
Площадь поверхности куба = 6a 2
Объем куба = a 3
Формула площади поверхности цилиндра и формула объема цилиндра
A
цилиндр представляет собой призму, в которой основной формой является круг.
Площадь поверхности цилиндра = 2πr 2 + 2πrh
Объем цилиндра = πr 2 ч
Формула площади поверхности пирамиды и формула объема пирамиды
пирамида — это твердая форма, состоящая из многоугольного основания и треугольных граней, пересекающихся в общей точке над основанием.Показанная здесь пирамида представляет собой прямоугольную пирамиду. Для вычисления площади поверхности и объема пирамиды необходимы два важных измерения. Первый — это высота пирамиды (h). Это расстояние от основания до точки, где встречаются треугольные грани. Второй — это высота отдельных треугольников лица.
Площадь поверхности пирамиды = (сумма площадей каждой грани) + (площадь основания)
Объем пирамиды = 1 ⁄ 3 A × h
Для пирамид с одинаковые грани треугольников
Площадь поверхности пирамиды = ( 1 ⁄ 2 × Периметр формы основания × s) + (Площадь формы основания)
Объем пирамиды = 1 ⁄ 3 A × h
Если основание пирамиды — квадрат (a = b), то
Площадь квадратной пирамиды = a 2 + √3 (a 2 )
Объем квадратной пирамиды = √5 (a 3 /6)
Формула площади поверхности конуса и формула объема конуса
Конус представляет собой пирамиду с круглым основанием с радиусом r и высота h.Длину стороны s можно найти с помощью теоремы Пифагора.
с 2 = r 2 + h 2
или
s = √ (r 2 + h 2 )
Площадь конуса = πr 2 + πrs
Объем конуса = 1 ⁄ 3 (πr 2 ч)
.Физические уравнения и формулы — манекены
- Образование
- Наука
- Физика
- Физические уравнения и формулы
Стивен Хольцнер
Часть физики I Для чайников шпаргалка
Физика наполнена уравнениями и формулами, которые имеют дело с угловым движением, двигателями Карно, жидкостями, силами, моментами инерции, линейным движением, простым гармоническим движением, термодинамикой и работа и энергия.
Вот список некоторых важных физических формул и уравнений, которые нужно держать под рукой, отсортированный по темам, чтобы вам не приходилось искать их.
Угловое перемещение
Уравнения углового движения актуальны везде, где есть вращательные движения вокруг оси. Когда объект повернулся на угол θ с угловой скоростью ω и угловым ускорением α , вы можете использовать эти уравнения, чтобы связать эти значения вместе.
Для измерения угла необходимо использовать радианы. Кроме того, если вы знаете, что расстояние от оси составляет r, , тогда вы можете рассчитать пройденное линейное расстояние, с , скорость, v , центростремительное ускорение, a c и силу , F c . Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Двигатели Карно
Тепловой двигатель забирает тепло, Q h , от высокотемпературного источника при температуре T h и перемещает его в низкотемпературный сток (температура T c ) со скоростью Q c и, в процессе выполнения механической работы, W . (Этот процесс можно повернуть вспять, чтобы можно было выполнять работу по перемещению тепла в обратном направлении — тепловой насос.) Объем выполненной работы, пропорциональный количеству тепла, отобранного от источника тепла, является КПД двигателя. Двигатель Карно обратим и имеет максимально возможный КПД, определяемый следующими уравнениями. Эквивалент эффективности теплового насоса — это коэффициент полезного действия.
Жидкости
Объем, В , жидкости с массой, м , имеет плотность, ρ . Сила, F , по площади, A , вызывает давление, P .Давление жидкости на глубине х зависит от плотности и гравитационной постоянной г . Объекты, погруженные в жидкость, вызывающую массу веса, W вода смещено , создают направленную вверх силу плавучести, F плавучесть . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью, v , через площадь поперечного сечения A , является постоянным.Уравнение Бернулли связывает давление и скорость жидкости.
Силы
Масса, м , ускоряется со скоростью a за счет силы, F , действующей. Силы трения, F F , пропорциональны нормальной силе между материалами, F N , с коэффициентом трения μ. Две массы, м 1 и м 2 , разделенные расстоянием, r , притягиваются друг к другу с помощью силы тяжести, определяемой следующими уравнениями, пропорционально гравитационная постоянная G :
Моменты инерции
Вращательный эквивалент массы — инерция, I , , которая зависит от того, как масса объекта распределяется в пространстве.Здесь показаны моменты инерции для различных форм:
Диск, вращающийся вокруг своего центра:
Полый цилиндр, вращающийся вокруг своего центра: I = mr 2
Полая сфера, вращающаяся вокруг своей оси:
Обруч, вращающийся вокруг своего центра: I = mr 2
Точечная масса, вращающаяся по радиусу r: I = mr 2
Прямоугольник, вращающийся вокруг оси вдоль одного края, при этом длина другого края имеет длину r :
Прямоугольник, вращающийся вокруг оси, параллельной одному краю и проходящей через центр, где длина другого края составляет r :
Стержень, вращающийся вокруг оси, перпендикулярной ему, и через его центр:
Стержень, вращающийся вокруг перпендикулярной ему оси и через один конец:
Цельный цилиндр, вращающийся вокруг оси вдоль своей центральной линии:
Кинетическая энергия вращающегося тела с моментом инерции I и угловой скоростью ω :
Угловой момент вращающегося тела с моментом инерции I и угловой скоростью ω :
Линейное движение
Когда объект в позиции x движется со скоростью, v , и ускорением, a, , что приводит к смещению, s , каждый из этих компонентов связан следующими уравнениями:
Простое гармоническое движение
Определенные виды силы приводят к периодическому движению, при котором объект повторяет свое движение с периодом T , имеющим угловую частоту ω, и амплитуду A .Одним из примеров такой силы является пружина с жесткостью пружины k . Положение, x , скорость, v , и ускорение, a, объекта, совершающего простое гармоническое движение, можно выразить как синусы и косинусы.
Термодинамика
Случайные колебательные и вращательные движения молекул, составляющих объект вещества, обладают энергией; эта энергия называется тепловой энергией. Когда тепловая энергия перемещается из одного места в другое, это называется тепла, Q .Когда объект получает некоторое количество тепла, его температура, T , повышается.
Кельвина ( K ), Цельсия ( C ) и Фаренгейта (F ) — это температурные шкалы. Вы можете использовать эти формулы для преобразования одной шкалы температуры в другую:
Тепло, необходимое для изменения температуры массы, m , увеличивается с постоянной пропорциональностью, c , называется удельной теплоемкостью . В бруске материала с площадью поперечного сечения A , длиной L и разницей температур на концах ΔT существует тепловой поток с течением времени, t , , определяемый формулой эти формулы:
Давление P и объем V , n моль идеального газа при температуре T определяются по этой формуле, где R — газовая постоянная:
В идеальном газе средняя энергия каждой молекулы KE avg , пропорциональна температуре с постоянной Больцмана k :
Работа и энергия
Когда сила, F , перемещает объект на расстояние, s , которое находится под углом Θ , затем работа, W , выполнена.Импульс, p , является произведением массы m , и скорости v . Энергия, которую объект имеет за счет своего движения, называется KE .
Об авторе книги
Стивен Хольцнер, доктор философии, работал редактором журнала PC Magazine и работал на факультете Массачусетского технологического института и Корнельского университета. Он написал Physics II for Dummies , Physics Essentials for Dummies , and Quantum Physics For Dummies .
,Формула площади поверхности
Здесь мы предлагаем вам исчерпывающий список формул площади поверхности для некоторых распространенных трехмерных фигур, таких как куб, цилиндр, прямоугольная призма, сфера, правый круговой конус и правая квадратная пирамида.Куб:
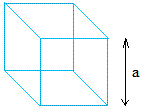
Площадь поверхности = 6 × a 2
Правый круговой цилиндр:
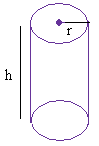
Площадь поверхности = 2 × pi × r 2 + 2 × pi × r × h
pi = 3.14
h — высота
r — радиус
Прямоугольная призма:
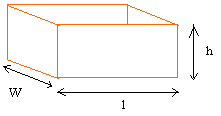
Площадь поверхности = 2 × l × w + 2 × l × h + 2 × w × h
l — длина
w — ширина
h — высота
Сфера:
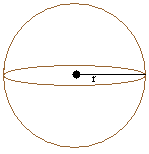
Площадь поверхности = 4 × pi × r 2
pi = 3,14
r — радиус
Правый круговой конус:
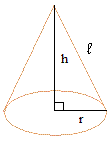
Площадь поверхности = pi × r 2 + pi × r × (√ (h 2 + r 2 ))
pi = 3.14
r — радиус
h — высота
l — наклонная высота
Правая квадратная пирамида:
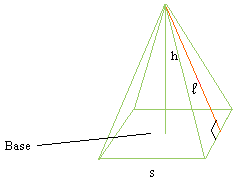
Площадь поверхности = s 2 + 2 × s × l
s — длина основания
h — высота
l — наклонная высота
Пара примеров, показывающих, как использовать формулу площади поверхности для решения некоторых задач.
Пример №1.
Найдите площадь поверхности куба, если длина одной стороны равна 5 см.
Формула для определения площади поверхности куба: 6a 2
6a 2 = 6 × a 2 = 6 × 5 2 = 6 × 25 = 150
Площадь поверхности куб 150 см 2
Пример №2.
Размеры прямоугольной призмы указаны ниже.
Длина равна 5 см
Ширина равна 6 см
Высота равна 3 см
Найдите площадь поверхности прямоугольной призмы.
Формула, которую следует использовать для определения площади поверхности прямоугольной призмы, как уже было показано выше: 2 × l × w + 2 × l × h + 2 × w × h
2 × 5 × 6 + 2 × 5 × 3 + 2 × 6 × 3
2 × 30 + 2 × 15 + 2 × 18
60 + 30 + 36
90 + 36
126
Площадь поверхности прямоугольной призмы 126 см 2
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
,Формула частоты
Частота — это количество циклов в единице времени. «Циклы» могут быть движениями чего-либо с периодическим движением, например пружины, маятника, чего-то вращения или волны. Частота равна 1, деленному на период, который представляет собой время, необходимое для одного цикла.
Производной единицей измерения частоты в системе СИ является герц, названный в честь Генриха Рудольфа Герца (символ hz). Один Гц — это один цикл в секунду.
f = частота, количество циклов в единицу времени
T = период, время, необходимое для одного цикла
N = количество циклов
t = количество времени
Формула частоты Вопросы:
1) Длинный маятник занимает 5.00 с для завершения одного цикла вперед-назад. Какая частота движения маятника?
Ответ: Для завершения одного цикла маятнику требуется 5,00 с , поэтому это его период T. Частоту можно найти с помощью уравнения:
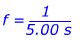
f = 0,20 цикла / с
Частота маятника 0,20 цикл / с . Единицы циклов / с часто обозначаются как «Герцы» с символом «Гц».Итак, частота этого маятника также может быть указана как 0,20 Гц.
2) Тахометр в автомобиле измеряет количество оборотов шин в минуту (обороты и циклы — это одно и то же). Автомобиль движется с постоянной скоростью, а тахометр показывает 2400 оборотов в минуту. Какова частота пробуксовки шин, измеренная в циклах в секунду? Какой период в секундах?
Ответ: Количество циклов (оборотов), которое необходимо учитывать, составляет 2400 . Это количество циклов, которые происходят за одну минуту, что равно 60 секундам.Итак, частота может быть найдена с помощью уравнения:
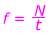
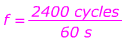
f = 40 циклов / с
Частота вращения шин составляет 40 циклов / с , что также можно записать как 40 Гц. Чтобы найти период из этого, измените уравнение, которое связывает период и частоту:
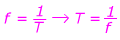
T = 0,025 с
Период вращения шин составляет 0,025 секунд.
.