Все формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
, , — стороны треугольника
— полупериметр
— центр окружности
Формула радиуса описанной окружности треугольника ( R ) :
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
— сторона треугольника
— высота
— радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
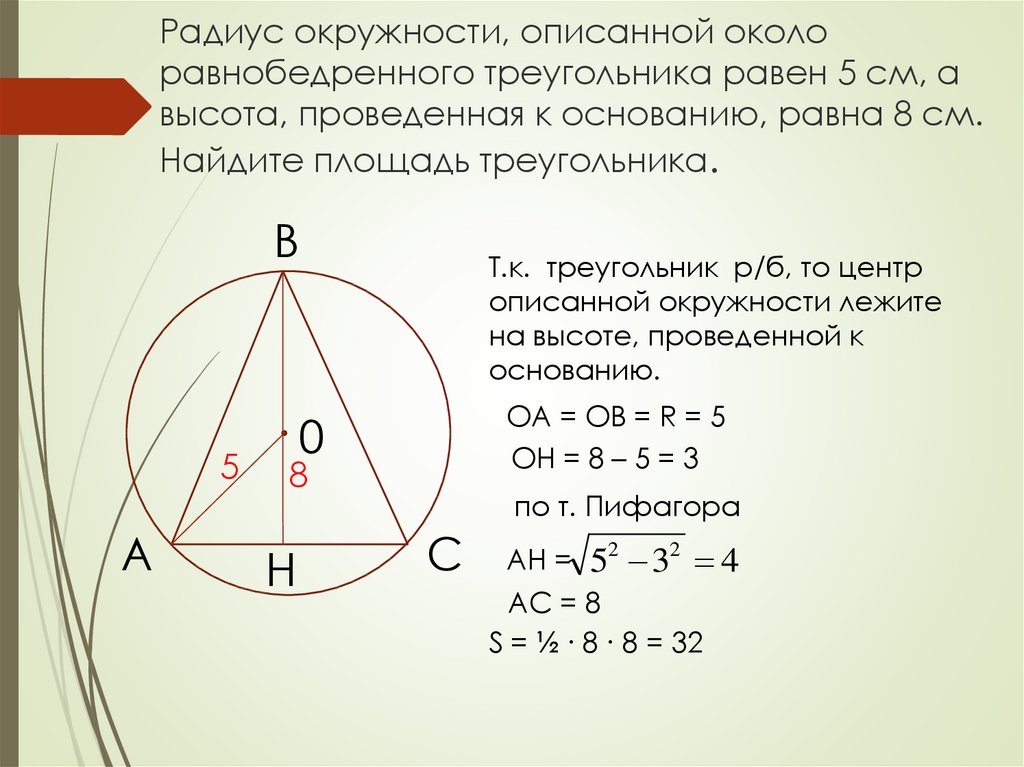
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
p — полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
a — сторона квадрата
d — диагональ
Формула радиуса описанной окружности квадрата (R):
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
Формула радиуса описанной окружности прямоугольника (R):
Радиус описанной окружности правильного многоугольника
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
Радиус описанной окружности правильного шестиугольника
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника ( R):
Равномерное движение по окружности 11 класс онлайн-подготовка на Ростелеком Лицей
Величины, входящие в уравнения кинематики равномерного движения по окружности
В уравнения кинематики равномерного движения по окружности входят следующие понятия:
1. T (период) – время одного полного оборота.
T (период) – время одного полного оборота.
2. – частота обращения.
Частота и период – обратно пропорциональные величины:
3. R – радиус окружности, по которому движется тело
4. – линейная скорость (скорость вдоль траектории). Так как за время, равное периоду, тело проходит путь, равный длине окружности, то:
5. – угловая скорость. Она равна отношению угла поворота за все время периода ко времени одного полного оборота.
Линейная скорость связана с угловой следующим соотношением:
6. Если происходит равномерное движение по окружности, то это не означает, что оно не имеет ускорения. Скорость по величине не меняется, но по направлению скорость меняется все время. Поэтому нормальное ускорение, которое характеризует быстроту изменения направления скорости, в данном случае называется центростремительным (направлено к центру окружности) и вычисляется по следующим формулам:
Задача 1 (определение линейной скорости)
Найти линейную скорость точки при движении по окружности радиусом 1 м при угловой скорости . Варианты ответа: 1. ; 2. ; 3. ; 4. .
Варианты ответа: 1. ; 2. ; 3. ; 4. .
Дано: ;
Найти:
Решение
Линейная скорость находится по следующей формуле:
Ответ: 3. .
Задача 2 (определение периода вращения)
Найти период вращения вала при частоте 60 оборотов в минуту. Варианты ответа: 1. ; 2. ; 3. ; 4. .
Дано:
Найти:
Решение
Частота равна 60 оборотов в минуту, а минута – это 60 секунд, следовательно, за 60 секунд выполняется 60 оборотов, а за одну секунду выполняется один оборот. Одна секунда и есть искомый период вращения.
Ответ: 3. .
Задача 3 (определение отношения линейных скоростей)
Длина минутной стрелки часов в 1,5 раза больше длины часовой стрелки. Во сколько раз скорость конца минутной стрелки больше скорости конца часовой? Варианты ответа: 1. 12; 2. 18; 3. 24; 4. 36.
Дано: ;
Найти:
Решение
Скорость при движении по окружности вычисляется по формуле:
Следовательно:
Ответ: 2. 18.
Задача 4 (определение радиуса)
Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 4 раза больше линейной скорости точки, лежащей на 0,9 м ближе к оси колеса.
Дано: ; (см. Рис. 1)
Найти: R
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображено колесо. Точка A лежит на ободе, точка B ближе к оси колеса на
При вращении колеса общей кинематической величиной для всех точек является угловая скорость (все точки двигаются с одной и той же угловой скоростью).
Следовательно, линейная скорость точки A равна:
Линейная скорость точки B равна:
Поэтому, если:
то:
Ответ: .
Задача 5 (определение линейной скорости и центростремительного ускорения)
Найти скорость и ускорение Исаакиевского собора, обусловленные вращением Земли.
Дано: – радиус Земли; Исаакиевский собор находится в Санкт-Петербурге, который находится на северной широты ; – время обращения Земли вокруг своей оси (см. Рис. 2).
Найти: ;
Решение
Рис. 2. Иллюстрация к задаче
Исаакиевский собор вместе с Землей совершает движение по окружности, радиус которой равен:
Следовательно, скорость Исаакиевского собора будет равна отношению длины этой окружности к периоду:
Подставим в это выражение известные значения:
Центростремительное ускорение вычисляется по формуле:
Подставим в это выражение известные значения:
Ответ: ; .
Список литературы
- Г. Я. Мякишев, Б. Б. Буховцев, Н. Н.

- А. П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О. Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А. В. Перышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В. А., Демидова М. Ю., Никифоров Г. Г., Ханнанов Н. К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «eduspb.com» (Источник)
- Интернет-портал «abramova.vitut.ru» (Источник)
- Интернет-портал «bambookes.ru» (Источник)
Домашнее задание
- Упражнение 5 (1,2) стр. 52 – Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы).
- Автомобиль движется по дороге со скоростью 72 км/час.
 Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки.
Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки. - Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
вращательная кинематика — Как я могу рассчитать радиус круга, созданного вращающимся телом с линейной скоростью?
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 710 раз
$\begingroup$
У меня есть объект, движущийся с линейной скоростью V. Он также вращается вокруг оси, перпендикулярной V, со скоростью z/t, где z — угол в радианах. Как я могу рассчитать радиус круга, который создаст его движение?
- вращательная кинематика
$\endgroup$
$\begingroup$
Мгновенное Центр вращения
Вращающееся тело с вектором угловой скорости ${\boldsymbol \omega} = \pmatrix{\omega_x & \omega_y & \omega_z}$ имеет присоединенную к нему точку A . Эта точка в некоторый момент времени имеет линейную скорость ${\boldsymbol v} = \pmatrix{v_x & v_y & v_z}$.
Эта точка в некоторый момент времени имеет линейную скорость ${\boldsymbol v} = \pmatrix{v_x & v_y & v_z}$.
Тело вращается вокруг оси, расположенной относительно 92$.
Вышеприведенное предполагает, что ${\boldsymbol \omega}\cdot {\boldsymbol v} =0$, что очевидно, поскольку ${\boldsymbol v} = -{\boldsymbol \omega} \times {\boldsymbol r}$ .
Related Posts
- Почему мы представляем ось вращения, используя векторную запись
- Центр задачи мгновенного вращения
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Определение радиуса круга и калькулятор
Определение радиуса круга и калькулятор — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Предметный указатель
1. Линия из центра круга в точку на круге.
Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет оставаться радиусом круга.
Радиус круга — это длина линии от центра до любой точки на его краю. Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). На рисунке выше перетащите оранжевую точку и убедитесь, что радиус всегда постоянен в любой точке окружности.
Иногда слово «радиус» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисовать радиус круга».
В более позднем смысле это длина линии, поэтому его называют «радиусом круга 1,7 сантиметра».
Если вы знаете диаметр
Учитывая диаметр круга, радиус равен половине диаметра: где:D диаметр круга
Если вы знаете длину окружности
Если известна длина окружности, то радиус можно найти по формулегде:
C это длина окружности
π это Пи, приблизительно 3,142
Если вы знаете район
Если известна площадь круга, радиус можно найти по формуле, где:
A – площадь круга
π – число Пи, примерно 3,142.
Калькулятор
| Радиус | прозрачный | |
| Диаметр | очистить | |
| Зона | прозрачный | |
| Окружность | прозрачный | |
Используйте калькулятор выше, чтобы рассчитать свойства круга.
Введите любое отдельное значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.
Точно так же, если вы введете область, радиус, необходимый для получения этой области, будет рассчитан вместе с диаметром и окружностью.
Связанные предметы
Диаметр Это «ширина» круга. Диаметр в два раза больше радиуса. См диаметр круга
Окружность Окружность — это расстояние вокруг края круга. Видеть Окружность круга для получения дополнительной информации.
Что попробовать
- На рисунке выше нажмите «Сброс» и перетащите оранжевую точку. Обратите внимание, что радиус имеет одинаковую длину в любой точке окружности.
- Щелкните «показать диаметр». Перетащите любую оранжевую точку на концах линии диаметра. Обратите внимание, что радиус всегда равен половине диаметра.
- Снимите флажок «фиксированный размер». Повторите вышеописанное и обратите внимание, что радиус всегда равен половине диаметра независимо от размера круга.

Другие темы кружка
Общий
- Определение окружности
- Радиус окружности
- Диаметр окружности
- Длина окружности
- Части круга (схема)
- Определение полукруга
- Касательная
- Секанс
- Аккорд
- Теорема о пересекающихся хордах
- Теорема о пересекающихся секущих длинах
- Теорема о пересекающихся секущих углах
- Площадь круга
- Концентрические окружности
- Кольцо
- Площадь кольца
- Сектор круга
- Площадь сектора круга
- Сегмент круга
- Площадь сегмента окружности (данный центральный угол)
- Площадь сегмента круга (данная высота сегмента)
Уравнения окружности
- Основное уравнение окружности (центр в начале координат)
- Общее уравнение окружности (центр в любом месте)
- Параметрическое уравнение окружности
Уголки по окружности
- Угол вписанный
- Центральный уголок
- Теорема центрального угла
Дуги
- Дуга
- Длина дуги
- Измеритель угла дуги
- Смежные дуги
- Большая/малая дуги
- Перехваченная дуга
- Сектор круга
- Радиус дуги или сегмента при заданной высоте/ширине
- Стрела — высота дуги или сегмента
(C) 2011 Copyright Math Open Reference.


 Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки.
Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки.