Степенная функция, ее свойства и график
Вы знакомы с функциями y=x, y=x2, y=x3, y=1/xи т. д. Все эти функции являются частными случаями степенной функции, т. е. функцииy=xp, где p — заданное действительное число. Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значенияхx иp имеет смысл степеньxp. Перейдем к подобному рассмотрению различных случаев в зависимости от показателя степениp.
Показатель p=2n -четное натуральное число.
В этом случае степенная функция y=x2n, гдеn— натуральное число, обладает следующими
свойствами:
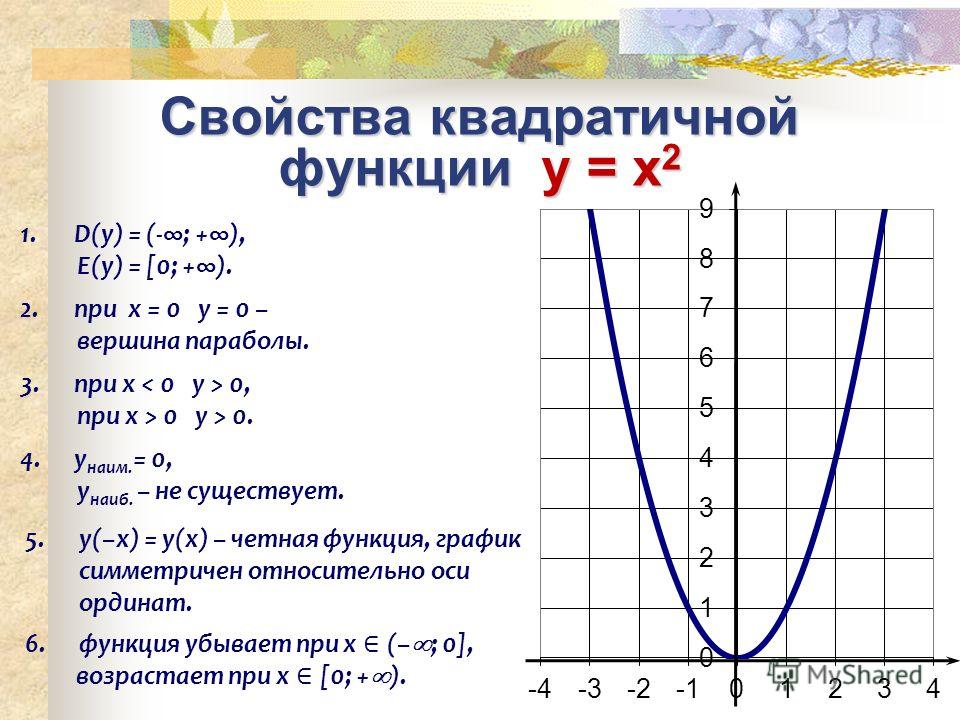
область определения — все действительные числа, т.
множество значений — неотрицательные числа, т. е. y больше или равно 0;
функция y=x2n четная, так какx2n=(-x)2n
функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.
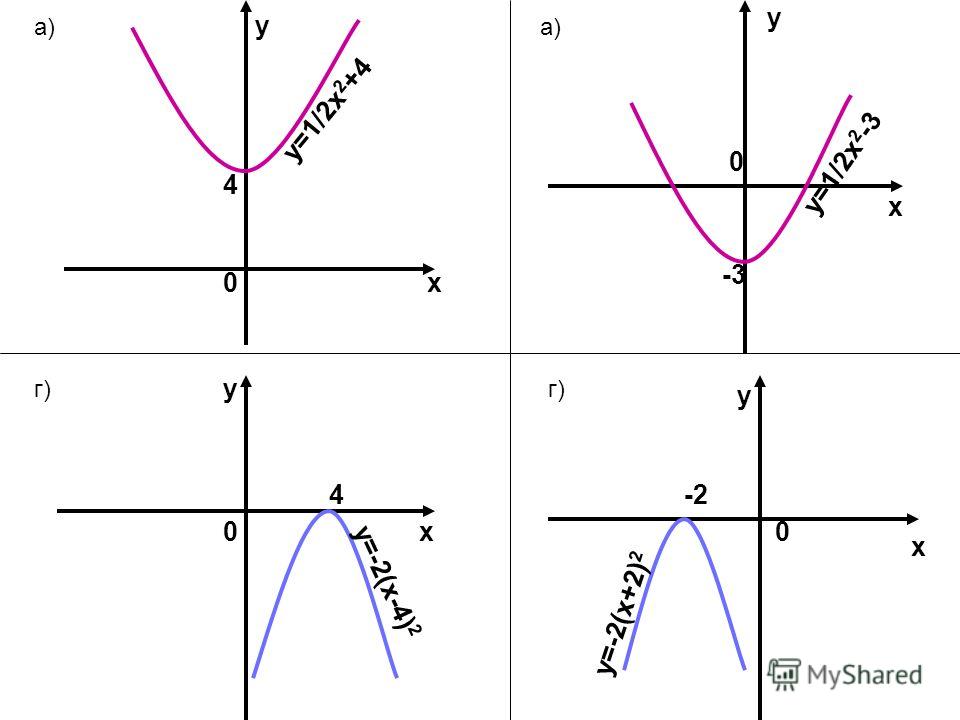
График функции y=x2n имеет такой же вид, как например график функцииy=x4.
2. Показатель p=2n-1— нечетное натуральное число В этом случае степенная функцияy=x2n-1 , где натуральное число, обладает следующими свойствами:
область определения — множество R;
множество значений — множество R;
функция y=x2n-1нечетная, так как (-x)2n-1=x2n-1;
функция является возрастающей на всей действительной оси.
График функции y=x2n-1имеет такой же вид, как, например, график функцииy=x3.
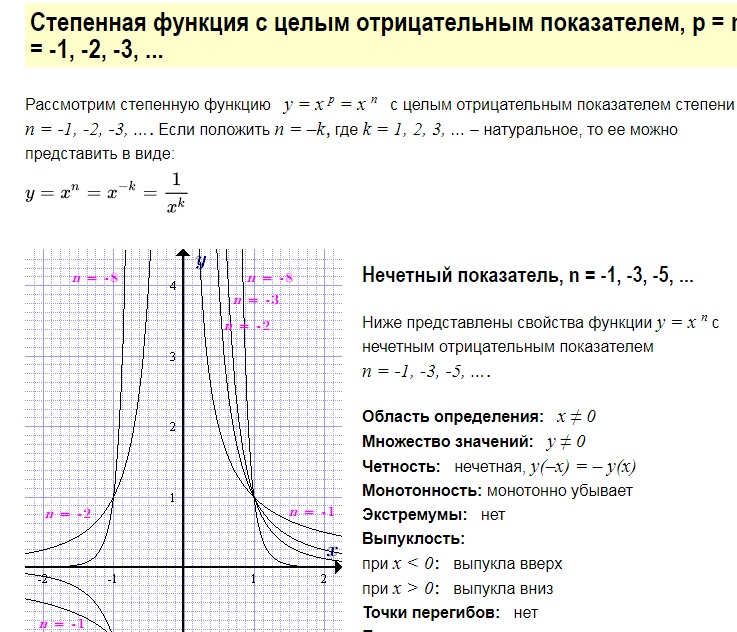
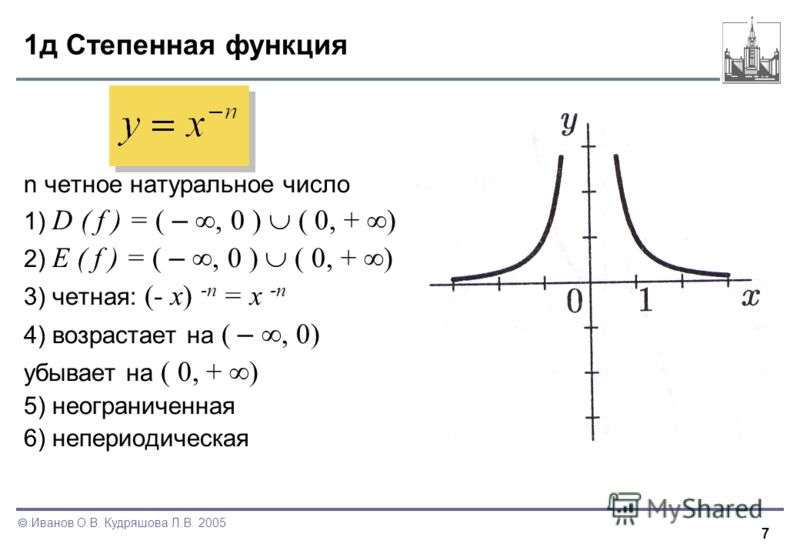
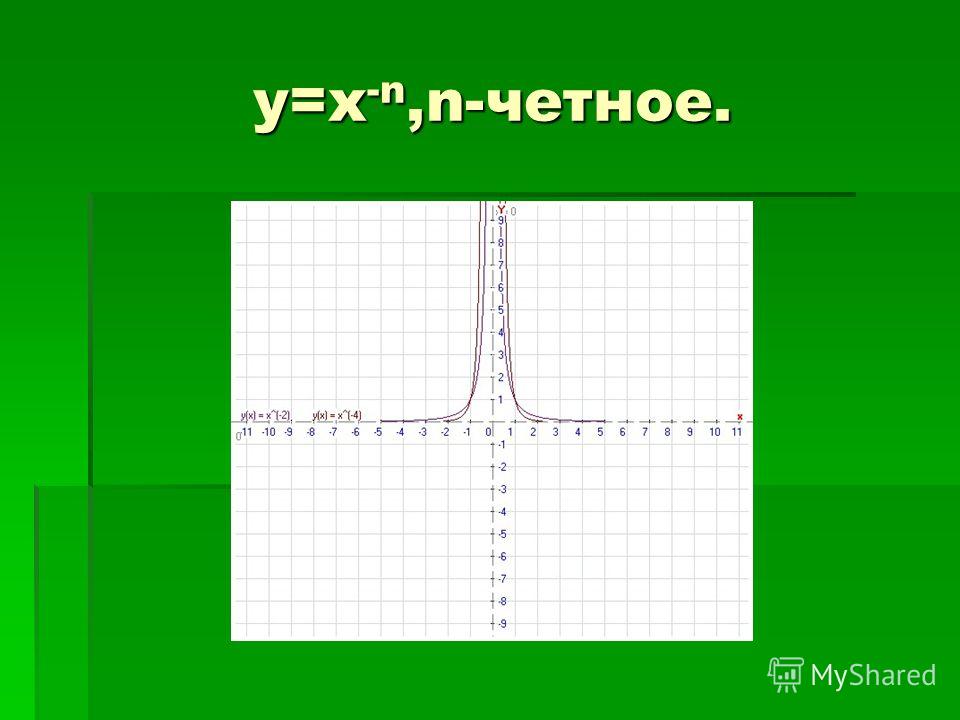
3.Показатель p=-2n, гдеn — натуральное число.
В этом случае степенная функция y=x-2n=1/x2n обладает следующими свойствами:
область определения — множество R, кроме x=0;
множество значений — положительные числа y>0;
функция y=1/x2nчетная, так как1/(-x)2n=1/x
функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.
График функции y=1/x2nимеет
такой же вид, как, например, график
функции y=1/x2.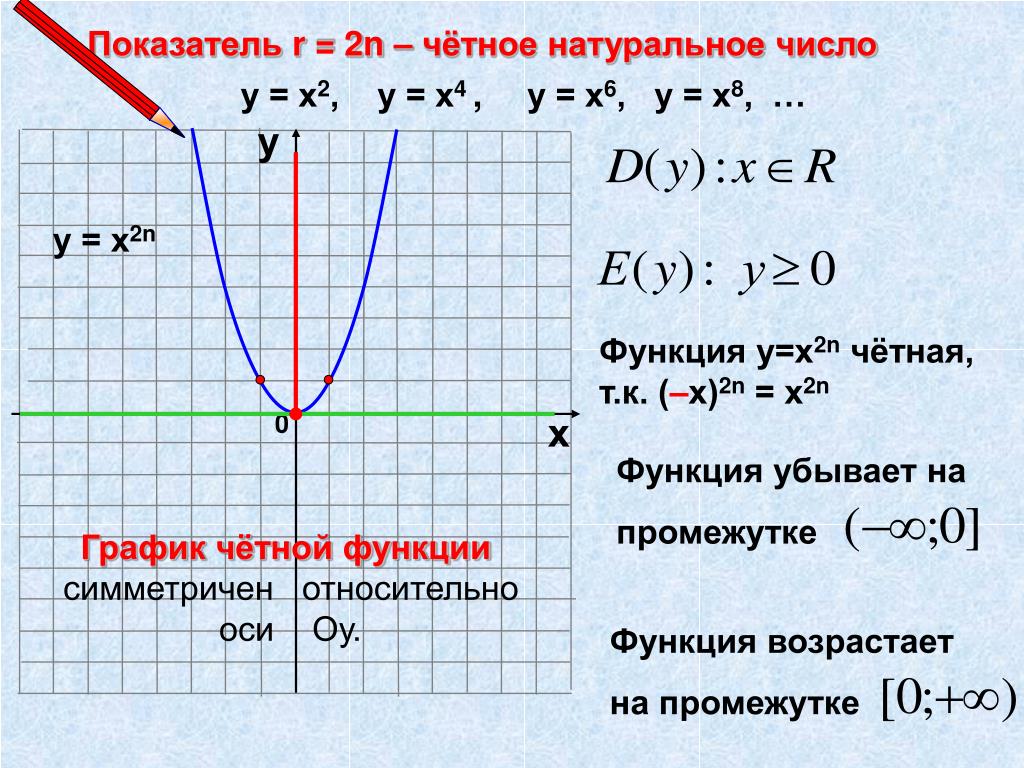
4.Показатель p=-(2n-1), гдеn— натуральное число. В этом случае степенная функцияy=x-(2n-1)обладает следующими свойствами:
область определения — множество R, кроме x=0;
множество значений — множество R, кроме y=0;
функция y=x-(2n-1)нечетная, так как (-x)-(2n-1)=-x-(2n-1);
функция является убывающей на промежутках x<0иx>0.
График функции y=x-(2n-1)имеет такой же вид, как, например, график функцииy=1/x3.
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции,
их свойства и графики.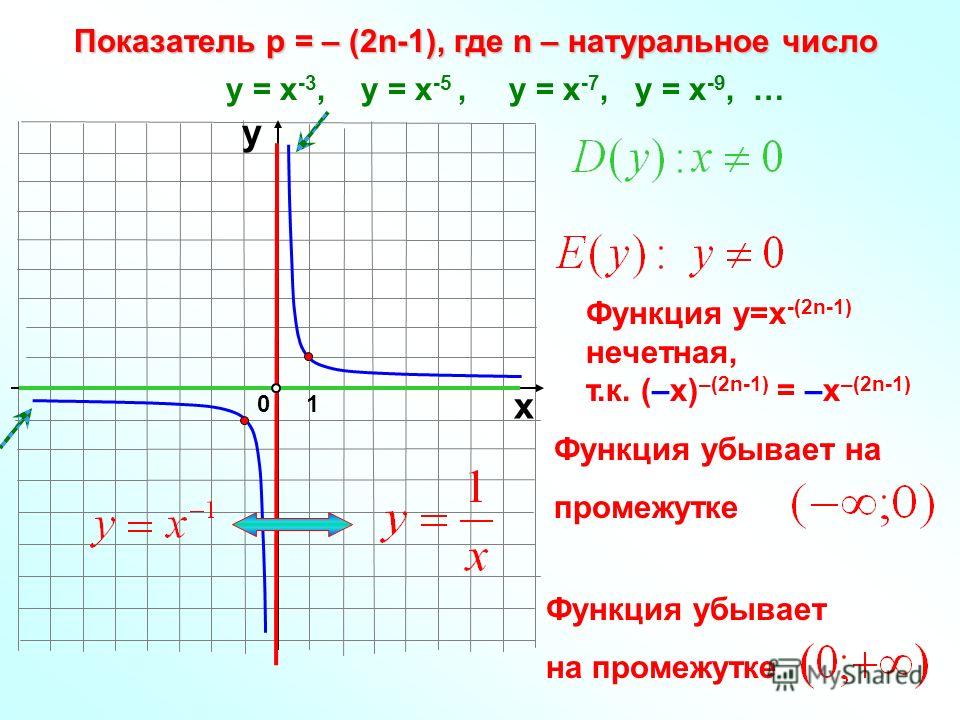
Обра́тные
тригонометри́ческие фу́нкции (круговые
функции, аркфункции) — математические
функции,
являющиеся обратными к тригонометрическим
функциям.
Функция arcsin
График функции .
Арксинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
[Править]Свойства функции arcsin
[Править]Получение функции arcsin
Дана
функция На
всей своей области
определения она
является кусочно-монотонной,
и, значит, обратное соответствие функцией
не является. Поэтому мы рассмотрим
отрезок, на котором она строго возрастает
и принимает все значения области
значений — .
Так как для функции на
интервале каждому
значению аргумента соответствует
единственное значение функции, то на
этом отрезке существует обратная
функция график
которой симметричен графику функции на
отрезке относительно
прямой
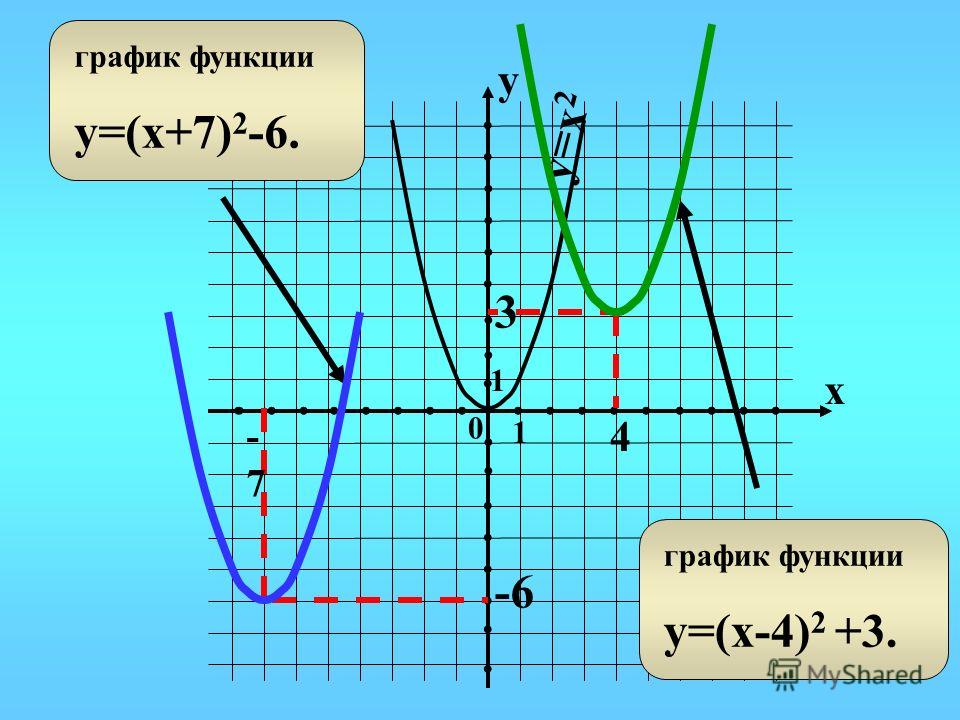
Степенные функции, их свойства и графики
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Степенные функции,
их свойства и
графики
Степенными функциями
называются функции вида
у = хr, где r – заданное
рациональное число
y
у = х2
у = х4
у = х6
-1 0 1 2
x
Показатель r = 2n – чётное натуральное число
Показатель r = 2n – чётное натуральное число
у = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
у = х2n
Е ( y) : у 0
0
График чётной функции
симметричен относительно
оси Оу.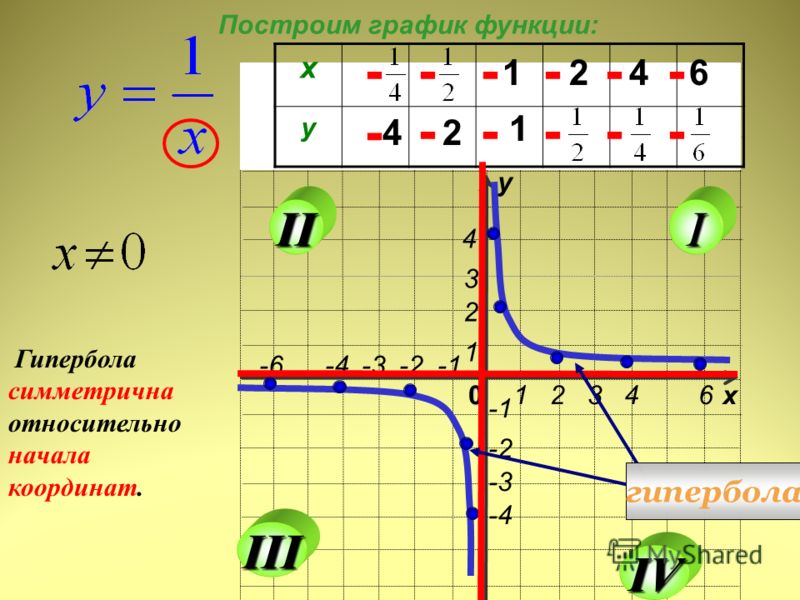
х
Функция у=х2n чётная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке
[0; )
нечётное
натуральное число
y
у = х3
у = х5
у = х7
-1 0 1 2
x
Показатель r = 2n-1 – нечётное натуральное число
у = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
х
Функция возрастает
на промежутке ;
График нечётной
функции симметричен
относительно начала
координат – точки О.
Показатель r — целое
отрицательное нечётное
число
y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x
Показатель r = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
( 2 n 1)
Функция у=х-(2n-1)
нечётная,
–(2n-1) = –х–(2n-1)
т.к.
(–х)
х
1
y
1
х
2 n 1
Функция убывает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
y
у = х-2
у = х-4
у = х-6
-1 0 1 2
Показатель r –целое отрицательное
чётное число
x
Показатель r = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2 n
1
1
y 2n
х
х
Функция у=х2n чётная,
т.
к. (–х)-2n = х-2nФункция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
y
у = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x
Показатель r – положительное дробное число,
0<r<1
Показатель r – положительное дробное число, 0 < 1r < 1
у
у = х0,3,
у = х0,7, у = х0,12,
у х3 …
D( y ) : x 0
у х
r
Е ( y) : у 0
Функция возрастает на
0
1
х промежутке
[0; )
y
у = х3,1
у = х1,5
D( y ) : x 0
Е ( y) : у 0
-1 0 1 2
Функция возрастает на
промежутке [0; )
число, r >1
x
y
у = х-1,3
у = х-2,3
у = х-3,8
у = х-0,3
-1 0 1 2
Показатель r – отрицательное
дробное число, r < 0
x
Показатель r – отрицательное дробное число 1
у
у=
х-1,3,
у=
х-0,7,
у=
х-2,12,
у х
3
…
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )
Графическое лото.
у
у
1
у
2
у
4
3
1
1
1
0
-1 0
у
1
х
х
1
у
5
1
1) у = х-0,7
6) у = х3,14
х
0
2) у = х-7
7) у = х8
0
1
у
1
1
х
у
6
1
1
0
-1 0
х
3) у = х
8) у = 1
0
х
1
1
7
1
х
4) у = х7
9) у = х-6
9
0
5) у = х0,6
8
1
х
у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции у х
лежит выше (ниже) графика
функции у = х.
у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у х
sin 450
лежит выше (ниже) графика
Пользуясь рисунком, найти промежутки, на которых
1
график функции
лежит выше (ниже) графика
у х
функции у = х.
у
0
1
х
Преобразования
графиков
степенных функций
Как построить график функции
y = f(x + l),
если известен график функции
y = f(x)
y
у = х-4
-1 0 1 2
у = (х – 2)-4
x
Как построить график функции
y = f(x) + m,
если известен график функции
y = f(x)
y
-1 0 1 2
у = х– 4 – 3
x
Как построить график функции
y = f(x + l) + m,
если известен график функции
y = f(x)
y
у = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x
y
у = (х-2)– 3– 1
у = х-3
-1 0 1 2
x
y
у = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x
Найдём производную функции:
Пример 1.
1
1
2 3
а ) у 3х ; у 3 х 3 х 2х 3 ;
3
4
4
11
11
4
б ) у 7х 7 ; у 7 х 7 7 х 7 4х 7 ;
7
5
3
5
5
в ) у 8(6х 5)8 ; у 8 6х 5 8 8 6 96х 5) 8
8
2
3
2
3
3
8
30(6х 5) .
При этом было использовано правило дифференцирования
( f (ax b )) af (ax b ).
Исследуем функцию
Пример 2.
3
1
2
y x 2 2x 2
3
На монотонность и экстремумы и
построим её график.
1. Найдём производную функции:
1
1
1
2
2 3 12
1 2
x 1
2
2
y x 2x x 2 x x x 1
2
3
3 2
x2
3
2
1
2
2. Функция существует при х ≥ 0, производная существует при х>0.
Поэтому критических точек у функции нет. Стационарную точку
x 1
0 , откуда х=1.
найдём из условия y 0 или
1
x2
3. Очевидно, что при х (0;1], значение у’≤0 и функция у(х) убывает
на этом промежутке. При х [1;+∞) значение у’≥0 и функция у(х)
возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
у min
2
4
2
3
3
Исследуем функцию
Пример 2.
3
1
2
y x 2 2x 2
3
На монотонность и экстремумы и
построим её график.
1. Найдём производную функции:
1
1
1
2
2 3 12
1 2
x 1
2
2
y x 2x x 2 x x x 1
2
3
3 2
x2
3
2
1
2
2.
Функция существует при х ≥ 0, производная существует при х>0.Поэтому критических точек у функции нет. Стационарную точку
x 1
0 , откуда х=1.
найдём из условия y 0 или
1
x2
3. Очевидно, что при х (0;1], значение у’≤0 и функция у(х) убывает
на этом промежутке. При х [1;+∞) значение у’≥0 и функция у(х)
возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
у min
2
4
2
3
3
English Русский Правила
{2n+1},$$, где $n\in\Bbb N$ — инъективная функция. Вернее, мне нужно доказать, что функция числа в нечетном показателе инъективна.
Я пытался доказать это с помощью противоречия, предполагая, что существует 2 разных значения $x$ для одного и того же $y$, но потом я застрял.
Мы будем очень признательны за любую помощь!
- доказательство-объяснение
$\endgroup$
2
9{2n+1} \подразумевает 1 = \frac{x}{y} $$
так как число $1$ имеет ровно один действительный корень $2n+1$st.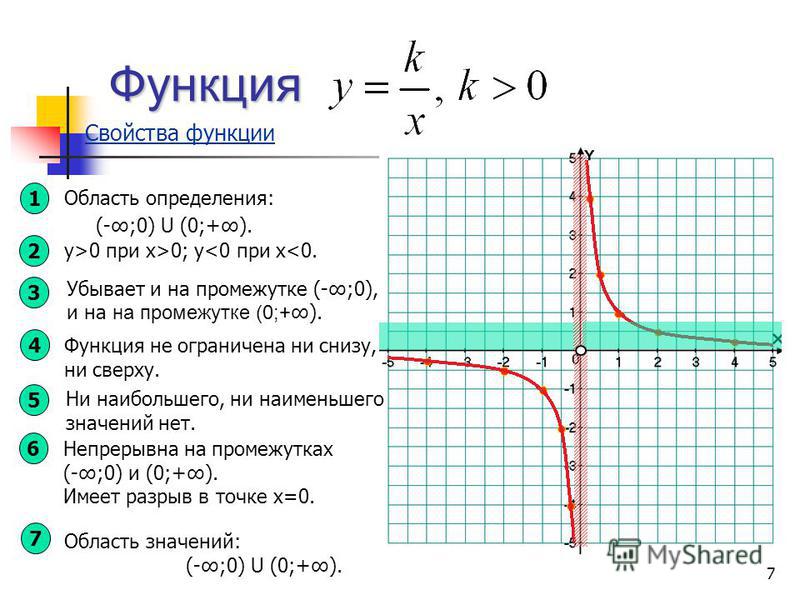
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 9п — 1)$
Задавать вопрос
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 125 раз
$\begingroup$
У меня вопрос.