Физические основы механики
Как известно, бывают величины скалярные, не имеющие направления, а бывают векторные, которым кроме величины приписывается некое направление. Время — величина скалярная, а положение в пространстве надо задавать векторами. Недостаточно сказать, что лекция состоится в 860 км от Таллинна. Этой информации не хватит, чтобы узнать, где именно: в Москве или, скажем, в Копенгагене. Отсюда ясно, что векторы должны играть важную роль в физике. Недаром векторное исчисление получило современный вид именно благодаря работам физиков (Дж. Гиббс). Кроме длины и направления, для векторов определяются операция умножения вектора на действительное число и операция сложения векторов, то есть задается векторная алгебра.
Использование векторного исчисления удобно тем, что многие соотношения получаются в общем компактном виде и без особого труда могут быть трансформированы в соответствующие соотношения для любой системы координат. Соотношения между векторами остаются неизменными при смене начала отсчета или выборе иной системы координат. В этом разделе мы напомним некоторые правила векторной алгебры. Занимаясь сейчас физикой, мы не стремимся к точным математическим доказательствам.
В этом разделе мы напомним некоторые правила векторной алгебры. Занимаясь сейчас физикой, мы не стремимся к точным математическим доказательствам.
Пусть нам дана какая-то декартова прямоугольная система координат. Любой вектор A можно задать тремя компонентами — проекциями вектора на оси , , .В дальнейшем мы используем обе общепринятых записи векторов, выделяя соответствующую букву жирным шрифтом, либо ставя над ней вектор:
Модулем вектора А (или его длиной) называется число:
Длина вектора не меняется при поворотах системы координат.
Произведение вектора А на число является вектором
проекции которого определяются как
Отсюда следует, во-первых, что длина вектора B равна длине вектора A, умноженной на абсолютное значение числа
Во-вторых, векторы A и A коллинеарны и имеют одно направление, если >0, и противоположное, если <0.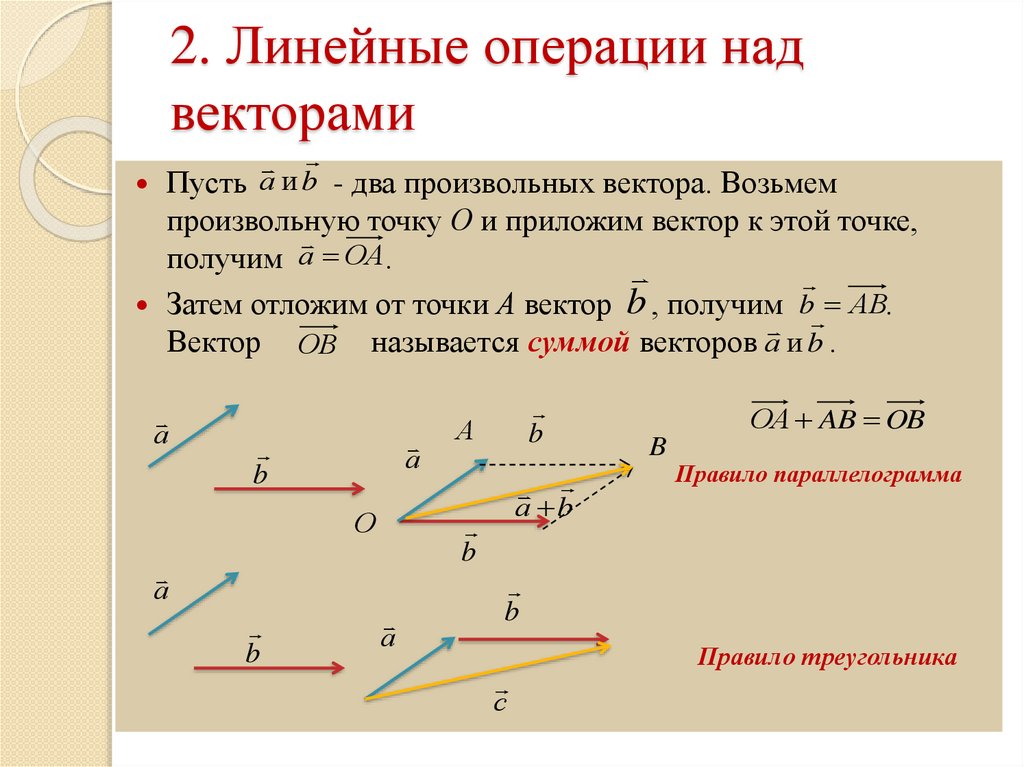
Суммой двух векторов A и B называется вектор с
чьи компоненты определяются как сумма компонент слагаемых
Отсюда следует геометрическое представление суммы векторов — правило параллелограмма либо правило треугольника (рис. 1.12).
Рис. 1.12. Сложение двух векторов
Аналогично для вычитания векторов
где
Правило вычитания векторов иллюстрируется на рис. 1.13.
Рис. 1.13. Вычитание векторов
Единичный вектор n — это вектор с длиной, равной единице
Единичный вектор nA в направлении какого-то вектора а равен
Особую роль играют единичные векторы вдоль положительных направлений осей , , системы координат.
Единичные векторы вдоль положительных направлений осей , , системы координат
называются ортами.Совокупность ортов состовляет базис данной системы координат.
Иногда оси маркируются цифрами (1,2,3 ) или индексами соответствия осям (x,y,z) обозначают так
или
Любой вектор а можно представить в виде разложения по базису
На рис. 1.14 показано разложение вектора вдоль координатных осей
Рис. 1.14. Разложение вектора вдоль координатных осей
Скалярное произведение двух векторов а и b — это число, равное сумме произведений одноименных проекций векторов — сомножителей
Отсюда следует, что скалярное произведение вектора на самого себя равно квадрату длины вектора
Второе следствие: скалярное произведение коммутативно, то есть
Справедливо также соотношение
Скалярное произведение не зависит от поворотов системы координат. Можно систему повернуть так, чтобы оба вектора лежали в плоскости и ось была направлена вдоль вектора а. В этой повернутой системе координат векторы-сомножители имеют следующие проекции:
Поэтому скалярное произведение может быть также представлено в виде
Здесь — угол между векторами а и b.
Если векторы ортогональны, то есть
то скалярное произведение равно нулю:
Обратно: если скалярное произведение равно нулю, то либо один из сомножителей — вектор нулевой длины, либо они ортогональны.
Рис. 1.15. Скалярное произведение
Приведем пример использования скалярного произведения (рис. 1.16). Пусть
Возведем в квадрат обе части равенства:
Это — так называемая теорема косинусов; в частном случае прямоугольного треугольника из нее следует теорема Пифагора.
Рис. 1.16. Теорема косинусов
Векторное произведение двух векторов а и b — это вектор с, чьи компоненты равны
Отсюда следует, что разложение векторного произведения по базису может быть представлено в виде определителя
(1.5.1)
Для обозначения векторного произведения используется либо косой крест между сомножителями, либо помещение разделенных запятой (запятая необязательна, если и без неё ясно, где кончается первый сомножитель и начинается второй) сомножителей в квадратные скобки.
Видно также, что в векторном произведении важен порядок сомножителей
Справедливо соотношение
Чтобы понять, куда направлено векторное произведение и чему равна его длина, снова повернем систему координат так, чтобы плоскость осей совпала с плоскостью векторов а и b и ось была направлена вдоль вектора а. Тогда
Подставляя эти значения в определитель (1.5.1) для векторного произведения, получаем
Это значит, что длина векторного произведения равна
и оно ортогонально обоим сомножителям а и b, причем направление его определяется по правилу правого винта.
Если правый винт вращается от первого вектора — сомножителя ко второму по кратчайшему пути, то этот винт перемещается по направлению их векторного произведения.
Применение правила буравчика иллюстрируется на рис. 1.17.
Рис. 1.17. Правило буравчика для определения направления векторного произведения
Видео 1. 2. Правое и левое вращение. Векторное произведение векторов
2. Правое и левое вращение. Векторное произведение векторов
Если сомножители векторного произведения коллинеарны (, ; = 0), то векторное произведение равно нулю. Обратно, из равенства нулю векторного произведения вытекает, что либо векторы — сомножители коллинеарны, либо один из векторов равен нулю.
Операция деления на вектор не определена.
Производная вектора a — это вектор, чьи компоненты равны производным от соответствующих компонент вектора а.
Пусть, например, вектор а зависит от времени t. Тогда
Производные от скалярного и векторного произведений выглядят обычным образом:
Подчеркнем, что в выражении для производной векторного произведения необходимо сохранять исходный порядок сомножителей.
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 54–59 (§ 7, п.п.9–11 и задачи 1–4): о векторных и скалярных величинах в физике.
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 44–48 (§ 6): о смысле производной и интеграла в физических приложениях.
Векторы.Действия над векторами. — Физика
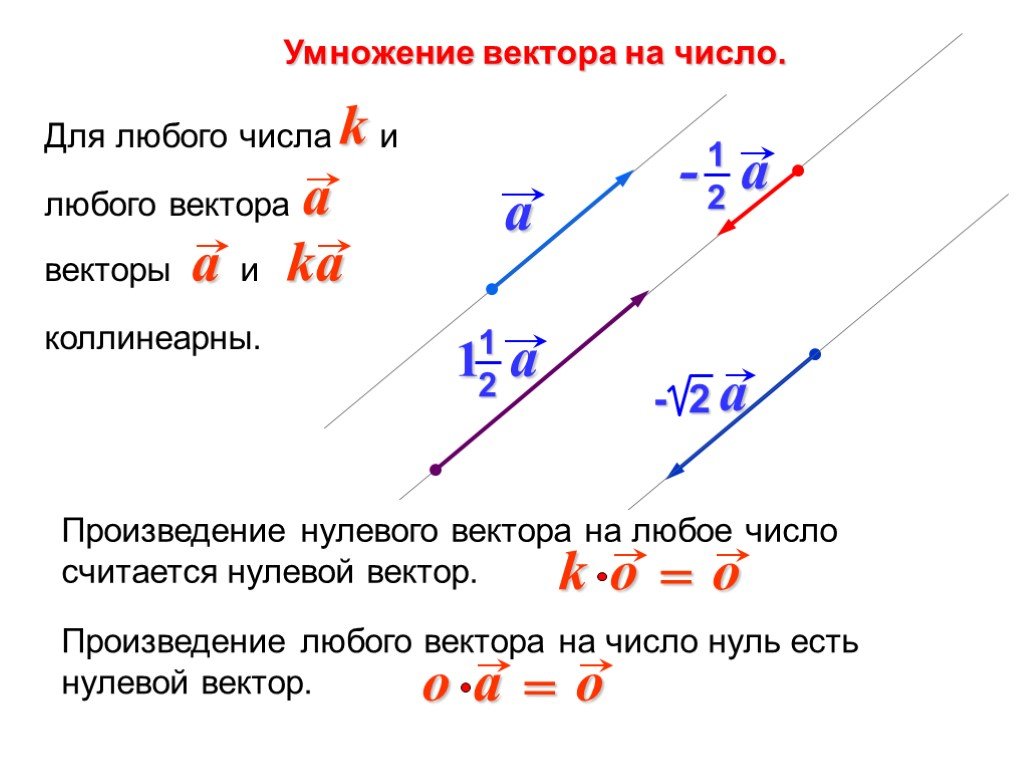
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»? А в самом деле, что такое векторы и зачем они? Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей». Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными. Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с2. Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины. Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной: Вот другой пример. Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила. Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль. Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов. А вот понятие равенства для векторов есть. Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината. Здесь в скобках записаны координаты вектора — по x и по y. Если координаты вектора заданы, его длина находится по формуле Сложение векторовДля сложения векторов есть два способа. 1. Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и . Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю. 2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и . По тому же правилу можно сложить и несколько векторов. Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F. При сложении векторов и получаем: Вычитание векторовВектор направлен противоположно вектору . Длины векторов и равны. Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора . Умножение вектора на числоПри умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля. Скалярное произведение векторовВекторы можно умножать не только на числа, но и друг на друга. Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Если векторы перпендикулярны, их скалярное произведение равно нулю. Из формулы для скалярного произведения можно найти угол между векторами: Эта формула особенно удобна в стереометрии. |
Умножение векторов — Гиперучебник по физике
[закрыть]
умножение скаляра на вектор
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным. Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, полярный форм-вектор…
r = r r̂ + θ θ̂
умножить на скаляр a равно…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр является дистрибутивным.
a ( A + B ) = a A + a B
Следовательно, прямоугольный форм-вектор…
r = x х + у х
умножить на скаляр а это…
a r = ax î + ау
скалярное произведение
Геометрически скалярное произведение двух векторов равно единице, умноженной на проекцию второго на первый.
Символ, используемый для обозначения этой операции, представляет собой небольшую точку средней высоты (·), откуда и произошло название «точечный продукт». Поскольку этот продукт имеет только величину, он также известен как 9.0087 скалярное произведение .
A · B = AB cos θ
Скалярный продукт является распределительным…
A · ( B + C ) = A · B + A · C 9001 0
и коммутативный…
А · Б = Б · А
Поскольку проекция вектора на самого себя оставляет его величину неизменной, скалярное произведение любого вектора на самого себя равно квадрату величины этого вектора.
А · А = AA cos 0° = А 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора с самим собой равно единице. Кроме того, поскольку вектор не имеет перпендикулярной к себе проекции, скалярное произведение любого единичного вектора на любой другой равно нулю.
(1) )(1)(cos 0°) = 1 (1) )(1)(cos 90°) = 0Используя эти знания, мы можем вывести формулу скалярного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, но он состоит в основном из членов, равных нулю.
| А · В = | ( А x î + A y х + A z k̂ ) · ( B x 9001 2 х + | |||||||||||
| А · Б = | А x î | · | В x î | + | А x î | · | Б у х | + | А x î | · | B z k̂ | |
| + | А у х | · | В x î | + | А у х | · | Б у х | + | А у х | · | B z k̂ | |
| + | А z к̂ | · | В x О | + | А z к̂ | · | Б у х | + | А z к̂ | · | B z k̂ | |
| А · В = | A x B x + A y B y + A z B z | |||||||||||
Таким образом, скалярное произведение двух векторов равно сумме произведений их параллельных компонентов. Отсюда мы можем вывести теорему Пифагора для трех измерений.
Отсюда мы можем вывести теорему Пифагора для трех измерений.
A · A = AA cos 0° = A x A x + A у А у + А z А z
А 2 = А x 2 + А y 2 + А z 2
перекрестное произведение
Геометрически перекрестное произведение двух векторов представляет собой площадь параллелограмма между ними.
Символ, используемый для обозначения этой операции, представляет собой большой диагональный крест (×), откуда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как число 9.0087 векторный продукт .
A × B = AB sin θ n̂
Вектор n̂ (n hat) представляет собой единичный вектор, перпендикулярный плоскости, образованной двумя векторами.
Перекрестное произведение является распределительным…
A × ( B + C ) = ( A × B ) + ( А × С )
, но не коммутативный…
А × В = — В × А
Изменение порядка перекрестного умножения на противоположное меняет направление произведения.
Поскольку два одинаковых вектора образуют вырожденный параллелограмм без площади, то векторное произведение любого вектора на самого себя равно нулю…
А × А = 0
Применение этого следствия к единичным векторам означает, что векторное произведение любого единичного вектора с самим собой равно нулю.
Следует отметить, что векторное произведение любого единичного вектора на любой другой будет иметь модуль, равный единице. (В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение равно не коммутативный, важен порядок операций.
(В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение равно не коммутативный, важен порядок операций.
- Держите правую руку горизонтально, большой палец должен быть перпендикулярен остальным. Ни в коем случае не сгибайте большой палец.
- Укажите пальцем в направлении первого вектора.
- Расположите ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
- Теперь ваш большой палец указывает в направлении векторного произведения.
A правая система координат , которая является обычной системой координат, используемой в физике и математике, является той, в которой любое циклическое произведение трех координатных осей положительно, а любое антициклическое произведение отрицательно. Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр.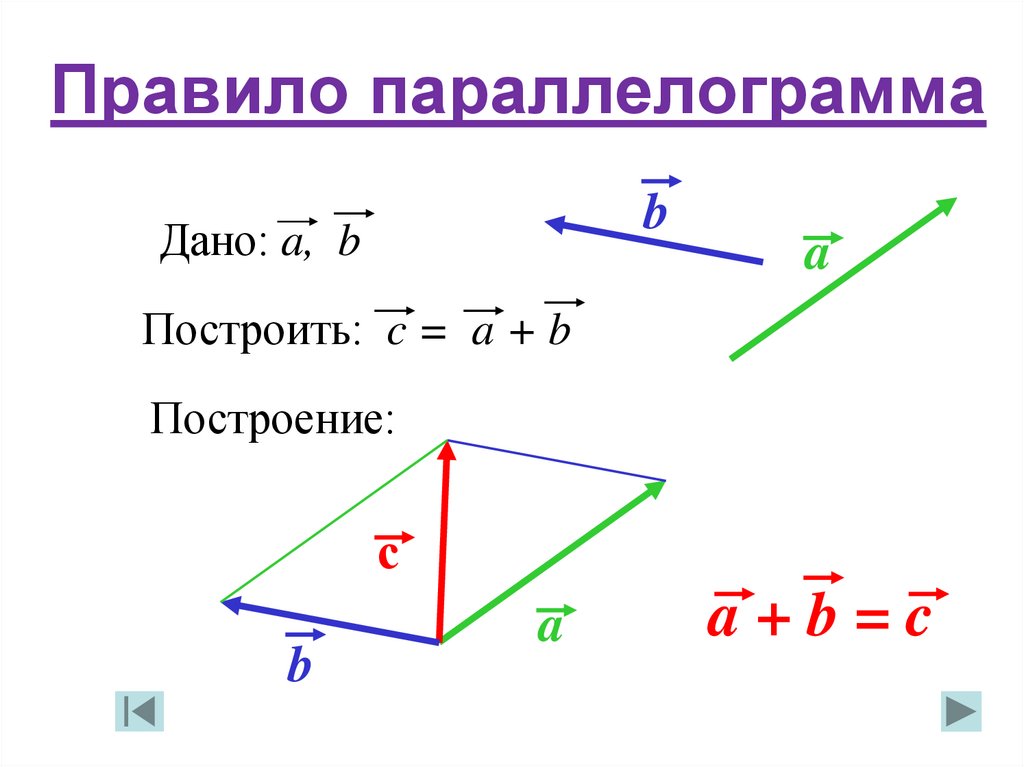 Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно , циклическому и положительному. Любой продукт, который работает в противоположном направлении, является антициклическим и отрицательным.
Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно , циклическому и положительному. Любой продукт, который работает в противоположном направлении, является антициклическим и отрицательным.
| Перекрестное произведение циклической пары единичных векторов равно положительному . | Перекрестное произведение антициклической пары |
Используя эти знания, мы можем вывести формулу векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто он будет ужасным беспорядком, и это так!
А × В = ( А х х + А х х + А х k̂ ) × ( B x î + B y ĵ + B z k̂ )
Произведение двух трехчленов состоит из девяти членов.
| А × В | = | А x î | × | В x î | + | А x î | × | Б у х | + | А x î | × | B z k̂ |
| + | А у х | × | В x î | + | А у х | × | Б у х | + | А у х | × | B z k̂ | |
| + | A z k̂ | × | В x î | + | А z к̂ | × | Б у х | + | А z к̂ | B z k̂ |
Три из них равны нулю. Устраните их.
Устраните их.
| А × Б | = | A x B y k̂ | − | А х В z х |
| − | A y B x k̂ | + | A y B z î | |
| + | А z B x х | − | A z B y î |
Сгруппируйте термины по единичному вектору и фактору.
A × B = ( A y B z − A z B y 9019 1 ) î
Есть более простой способ написать это. Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой представляет собой единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор. Символически…
Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой представляет собой единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор. Символически…
| А × В = | или | — | к̂ |
| А x | А у | А z | |
| В x | Б у | Б г |
Расширение определителя 3×3 по его первой строке — это первый шаг. Это дает нам три определителя 2×2.
| А × В = | А у | А z | î — | А x | А z | х + | А x | А у | к̂ |
| Б у | Б г | В x | Б г | В x | Б у |
Эти определители 2×2 можно быстро найти. Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители.
Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители.
A × B = ( A y B z − A z B y ) î
Векторное произведение векторов
Векторное произведение векторовВекторное произведение и скалярное произведение — два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Величину векторного произведения двух векторов можно получить, взяв произведение величин векторов на синус угла ( и направление определяется по правилу правой руки. , что несколько более компактно можно сформулировать в виде определителя. | Индекс Векторные понятия Приложения | ||
| Назад |
Векторное произведение компактно записывается в виде определителя, который для случая 3×3 имеет удобную процедуру вычисления: После того, как вы познакомитесь со схемой вычисления определителя, это удобный способ восстановить развернутую форму: | Индекс Векторные понятия | ||
| Назад |
Вы можете ввести значения в любое из полей ниже. | Индекс Векторные понятия | ||
| Назад |
Геометрически векторное произведение полезно как метод построения вектора, перпендикулярного плоскости, если у вас есть два вектора на плоскости. Физически появляется при расчете крутящего момента и при расчете магнитной силы на подвижном заряде. | Индекс Векторные понятия | ||
| Назад |
Направление векторного произведения можно визуализировать с помощью правила правой руки. |



 Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.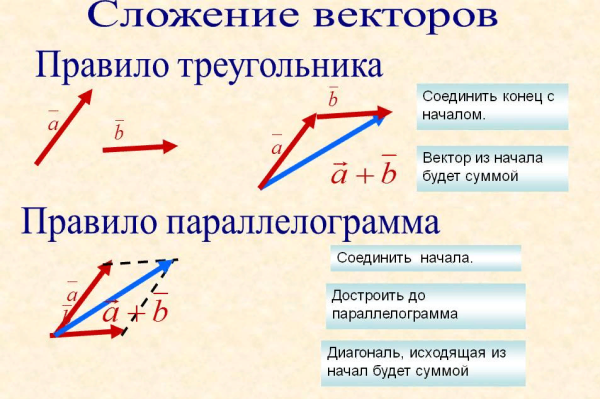 Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения: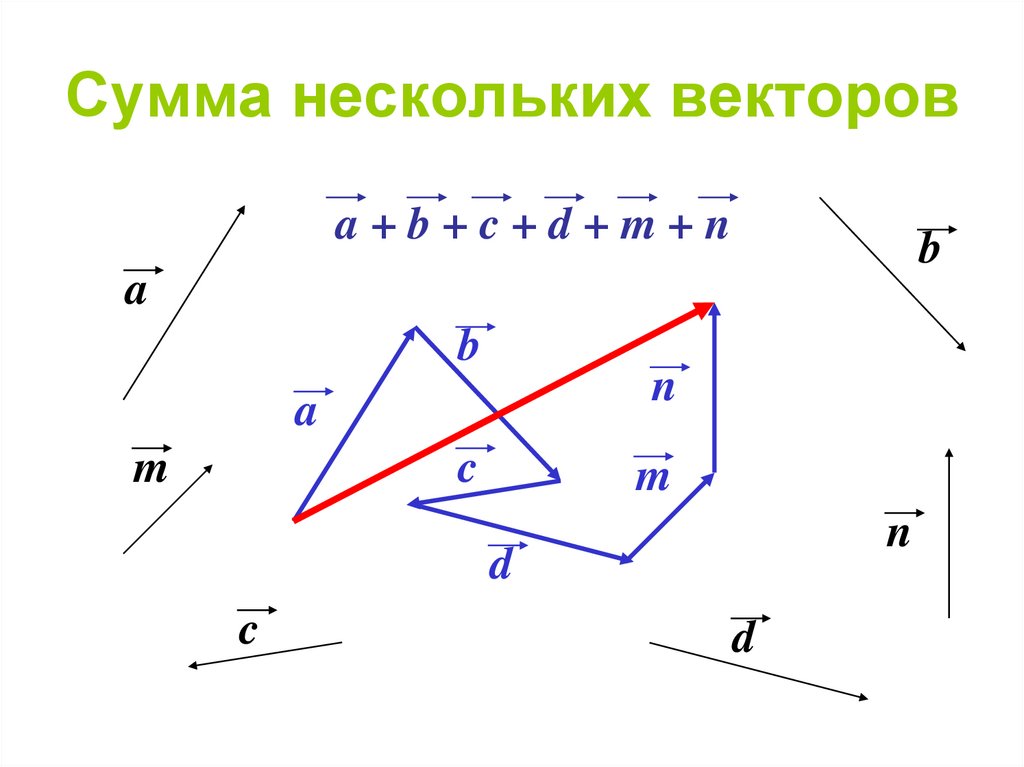 Если векторы выразить через единичные векторы i, j и k в направлениях x, y и z, то векторное произведение можно выразить в довольно громоздкой форме:
Если векторы выразить через единичные векторы i, j и k в направлениях x, y и z, то векторное произведение можно выразить в довольно громоздкой форме: Затем щелкните символ векторного произведения или угла.
Затем щелкните символ векторного произведения или угла.