Формула бинома ньютона примеры решения: 11. Бином Ньютона

Бином Ньютона — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

2. Содержание.

1) Понятие бинома Ньютона.
2) Свойства бинома и биномиальных
коэффициентов.
3) Примеры решения задач по теме
«Бином Ньютона».
4) Выход.

3. Понятие бинома Ньютона.

Биномом Ньютона называют разложение
вида:
(a b) n Cn0 a nb 0 Cn1 a n 1b1 Cn2 a n 2b 2 … Cnm a n mb m … Cnn a 0b n
n(n 1) n 2 2
n!
a na b
a b . ..
a n mb m … b n , где m n
2!
( n m) ! m !
Но, строго говоря, всю формулу нельзя назвать биномом,
так как «бином» переводится как «двучлен». Кроме того,
формула разложения была известна еще до Ньютона, Исаак
Ньютон распространил это разложение на случай n<0 и n –
дробного.
Цель изучения бинома Ньютона – упрощение
вычислительных действий.
n
n 1 1
( a b )n C n0 a n b 0 C n1 a n 1b 1 C n2 a n 2 b 2 … C nm a n m b m … C nn a 0 b n
a n na n 1b 1
n( n 1 ) n 2 2
n!
a b …
a n m b m … b n , где m n
2!
( n m )! m !
Компоненты формулы «бином
Ньютона»:
правая часть формулы – разложение
бинома;
С n0 ; С n1 ; … С nn – биномиальные коэффициенты, их
можно получить с помощью
треугольника Паскаля (пользуясь
операцией сложения).
общий член разложения бинома n-й
степени Tm 1 C nm a n m b m , m 0 ,1,2 ,…n
где Т – член разложения; – порядковый номер члена
разложения.
К содержанию.

5. Свойства бинома и биномиальных коэффициентов.

С С 1
Число всех членов разложения на единицу
больше показателя степени бинома, то есть
равно (n+l).
Сумма показателей степеней a и b каждого
члена разложения равна показателю степени
бинома, то есть n.
Биномиальные коэффициенты членов
разложения, равноотстоящих от концов
разложения, равны между собой: С m C n m
n
n
(правило симметрии).
0
n
n
n

Сумма биномиальных коэффициентов
n
всех членов разложения равна 2 .
Сумма биномиальных коэффициентов,
n 1
стоящих на нечетных местах, равна2
сумме биномиальных коэффициентов,
стоящих на четных местах и равна
.
0
2
4
1
3
5
n 1
С n С n С n … С n С n С n … 2
m
m
m 1
С
C
C
Правило Паскаля: n
n 1
n 1 .

Любой биномиальный коэффициент,
начиная со второго, равен
произведению предшествующего
биномиального коэффициента и
дроби n ( m 1 ) .
m
С C
m
n
m 1
n
n ( m 1)
m
К содержанию.

8. Примеры решения задач по теме «Бином Ньютона».

18
Пример 1
3 1
В биномиальном разложении x x 3
найти член разложения, не содержащий
х.
Решение:
Tm 1 C
m
18
x
3 18 m
m
1
m
54 3 m 3 m
m
54 6 m
C18 x
3 C18 x
x
Так как в разложении мы ищем член не
содержащий х, то 54 6 m 0 m 9 .
T9 1
18!
10 11 12 13 14 15 16 17 18
C
48620
( 18 9 )! 9!
2 3 4 5 6 7 8 9
9
18
Пример 2
Доказать, что при любом натуральном n
n
число 4 15n 1 делится на 9.
Доказательство:
1 способ:
4 n ( 3 1 )n 3 n C nn 1 3 n 1 C nn 2 3 n 2 … C n2 3 2 C n1 3 1 1
4 n 15n 1 3n Cnn 1 3n 1 Cnn 2 3n 2 … Cn2 32 Cn1 31 1 15n 1
n(n 1) n 3
n(n 1) 1
3 3n 1 n 3n 2
3 …
3 6n
2
2
n(n 1) n 4
n(n 1) 0
n 2
n 3
3 3 3 n 3
3 …
3 2n : 9
2
2
2 способ:
Начнем рассматривать бином в общем
виде:
n( n 1 ) n 2
n( n 1 ) 2
x . ..
x n x 1
2
2
n( n 1 ) n 4
n( n 1 ) 0
x 2 x n 2 n x n 3
x …
x n x 1 A x2 n x 1
2 2
( x 1 )n x n n x n 1
обозначим выражение в скобках за А
Тогда
4n 15n 1 (3 1) n 15n 1 A 32 n 3 1 15n 1 9 A 18n 9( A 2n) : 9
К содержанию.
Выход.

English     Русский Правила

5. Треугольник Паскаля. Бином Ньютона

Составим таблицу значений для n,m = 0, 1, 2, 3, 4, 5, 6, 7.

n m	0	1	2	3	4	5	6	7
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1

Эту таблицу можно неограниченно продолжать вниз и вправо. Она называется треугольником Паскаля. Еще удобнее ее записывать в виде равнобедренного треугольника.

							1
						1		1
					1		2		1
				1		3		3		1
			1		4		6		4		1
		1		5		10		10		5		1
	1		6		15		20		15		6		1
1		7		21		35		35		21		7		1

Такой треугольник Паскаля обладает свойством: каждое число равно сумме двух чисел, стоящих над ним, поэтому таблицу можно без труда продолжать вниз, не прибегая к вычислению числа сочетаний.

Нам знакомы формулы:

(a + b)¹ = a + b;

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a

2b + 3ab² + b³.

Легко заметить, что коэффициенты в правых частях этих формул взяты из соответствующих строк треугольника Паскаля. Оказывается, при любом натуральном n справедлива формула

, (4.4)

которая называется формулой Ньютона в честь английского физика и математика Исаака Ньютона. Правую часть формулы (4.4) называют разложением степени бинома. По этой же формуле вычисляется (а–b)ⁿ, полагая (а – b)ⁿ = (a +(–b))ⁿ. В этом случае второе слагаемое будет со знаком минус, далее знаки чередуются.

Пример 14. Записать разложение 4-й степени бинома (а + b)⁴.

Решение. Коэффициенты разложения берем из 4-й строки треугольника Паскаля и используем формулу Ньютона:

(а + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Пример 15. Записать разложение (2m –3n)⁵.

Решение. Используем 5-ю строку треугольника Паскаля.

(2m –3n)⁵ = (2m)⁵– 5(2m)⁴3n + 10(2m)³(3n)² –10(2m)²(3n)³ + 5(2m)(3n)⁴–

– (3n)⁵ = 32m⁵ – 240m⁴n + 720m³n² – 1080m²n³ + 810mn⁴ – 243n⁵.

Пример 16. Вычислить без калькулятора:

.

Решение. Сначала возведем в четвертую степень двучлен.

. Поэтому

. Ответ: 7.

Биномиальная теорема для разложения многочленов. Формула, примеры и практические задачи

Биномиальная теорема устанавливает формулу для выражения степеней сумм. Самый краткий вариант этой формулы показано сразу ниже.

Исаак Ньютон написал обобщенную форму биномиальной теоремы. Однако в течение довольно долгого времени Треугольник Паскаля был хорошо известен как способ расширения биномов. (Как ни странно, Паскаль 17 века был не первым, кто узнал о треугольнике Паскаля)

Калькулятор биномиальной теоремы

Пристальный взгляд на биномиальную теорему

Самый простой способ понять биномиальную теорему — сначала просто взглянуть на приведенную ниже схему полиномиальных разложений.

• (х + у) ² = х ² + 2ху + у ²
• (x + y) ³ = x ³ + 3x ² y + 3xy ² + y ³
• (х + у) ⁴ = х ⁴ + 4х ³ у + 6х ² у ² + 4ху ³ + у

  500014 4 ⁴

Биномиальная теорема

Формула

Обобщенная формула для приведенного выше шаблона известна как биномиальная теорема

Практика Задачи

Биномиальная теорема

Проблема 1

Используйте формулу биномиальной теоремы для определения четвертого члена в разложении (y − 1) ⁷

Проблема 2

Используйте формулу биномиальной теоремы для определения одиннадцатого члена в разложении (2a − 2) ¹²

Проблема 3

Используйте формулу биномиальной теоремы, чтобы определить четвертый член в разложении

9{n} $$ всегда равно n + 1. Следовательно, когда n — четное число, то количество термов равно (n + 1), что является нечетным числом.

Когда количество членов нечетно, то в разложении есть средний член, в котором показатели показателей a и b подобные.

Только в (a) и (d) есть термины, в которых показатели степени факторов одинаковы.

Проблема 5 9{9} $$: 1, 9, 36, 84$$ и 126$$.

Не раскрывая бином, определите коэффициенты при остальных членах.

У бинома есть два свойства, которые могут помочь нам определить коэффициенты остальных членов.

1. Переменные m и n не имеют числовых коэффициентов. Итак, данные числа являются результатом вычисления формула коэффициентов для каждого члена.
2. Степень бинома равна 9. Следовательно, количество членов равно 9 + 1 = 10.

Теперь у нас есть коэффициенты первых пяти членов. По биномиальной формуле, когда число членов четно, тогда коэффициенты каждых двух слагаемых, находящихся на одинаковом расстоянии от середины слагаемых, одинаковы. Таким образом, начиная слева, коэффициенты для всех членов будут следующими: 9{2} $$

Треугольник Паскаля (еще один способ расширения биномов)

Биномиальная теорема: формула, правила и использование

Полиномиальные выражения ежедневно используются для выполнения простых или более сложных математических операций в службах прогнозов погоды, инженерных науках и статистике. Но как вычислить полиномиальное выражение, когда индексы очень велики, а вычисления долгие и утомительные? Здесь на помощь приходит биномиальная теорема.

Эта статья расскажет о биномиальной теореме, ее формуле и о том, для чего она используется. Затем биномиальная теорема также будет применяться в примерах для решения биномиальных разложений.

Что такое формула биномиальной теоремы?

Биномиальная теорема позволяет нам разложить выражение формы (x+y)n в полиномиальную сумму, содержащую члены x и y. Общая формула биномиального выражения:

(x+y)n=n0xny0+n1xn-1y1+n2xn-2y2+…+nn-1x1yn-1+nnx0yn.

, который можно упростить до следующего.

Биномиальная формула выглядит следующим образом:

(x+y)n=∑k=0nnkxn-kyk,

, где n и k — целые числа.

В приведенном выше выражении ∑k=0n обозначает сумму всех членов, начиная с k = 0 и заканчивая k = n.

Обратите внимание, что здесь x и y можно поменять местами, поэтому биномиальную теорему также можно записать как

(x+y)n=∑k=0nnkxkyn-k

, и это даст те же результаты, что и выше.

Обозначение nk может обозначаться как «n выбирает k» и дает число, называемое биномиальным коэффициентом, которое представляет собой количество различных комбинаций упорядочения k объектов из общего числа n объектов.

Биномиальный коэффициент (n выбирает k или Ckn) определяется как,

,

где «!» означает факториал.

Факториал означает произведение целого числа на все целые числа под ним. Для целого числа n мы можем выразить факториал n как

n!=n×(n-1)×(n-2)×…×1.

Например, для 5 выберите 3, у нас будет

.

Какое доказательство биномиальной теоремы?

Биномиальную теорему можно доказать несколькими способами, но мы сосредоточимся на комбинаторном доказательстве.

Любое выражение в форме (x+y)n может быть записано как

(x+y)n=(x+y)×(x+y)×…×(x+y),

всего с n продуктами.

После раскрытия и удаления скобок каждый член имеет вид xn-kyk для некоторого произвольного k в диапазоне от 0 до n.

Коэффициент этого члена должен быть количеством способов выбрать k значений y из n значений (x+y). Следовательно, коэффициент xn-kyk равен nk и

(x+y)n=∑k=0nnkxn-kyk.

Как выполнить биномиальное разложение?

Чтобы понять, как расширить биномиальное разложение, рассмотрим пример.

Допустим, мы хотим расширить . В этом случае n = 4 и k будет варьироваться от 0 до 4. Используя формулу биномиальной теоремы, мы можем написать:

.

Теперь мы можем использовать уравнение для биномиального коэффициента, чтобы найти все постоянные члены в этом выражении. Для первого члена 4 выбираем 0 (4C ₀ ), имеем:

.

Повторяя это для всех 5 коэффициентов, мы получаем биномиальные коэффициенты ⁴ C ₀ = 1, ⁴ C ₁ = 4, ⁴ C 904 395 2 ₃ = 4 и ⁴ C ₄ = 1 по порядку.

Следовательно, наше выражение для биномиального разложения упрощается до:

.

Обратите внимание, что y также можно заменить любым числом.

Примеры биномиальной теоремы

Биномиальную теорему также можно использовать для нахождения конкретного члена биномиального разложения. Для этого вам не нужно выполнять все расширение, а потребуется только найти один термин.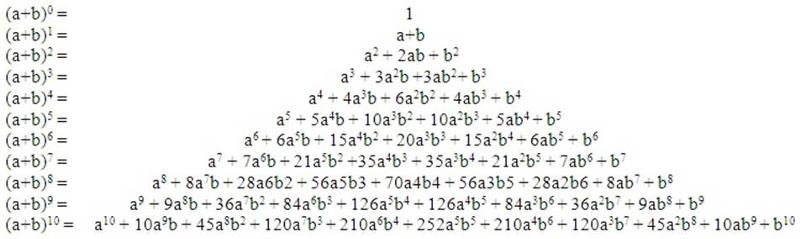 Давайте посмотрим на пример, чтобы увидеть, как это можно сделать.

Найдите коэффициент x4 в разложении (2x+1)6.

Решение

Вспомним биномиальную теорему,

.

Заметим, что в нашем случае n = 6, x = 2x и y = 1.

Нам нужно найти член, в котором степень x равна 4.

Это будет, когда xn-2=x6-2= х4. Таким образом, член, который мы рассматриваем в формуле, — это третий член

n2xn-2y2.

Заменив n = 6, y = 1 и x = 2x, мы получим

62(2x)412.

Чтобы найти биномиальный коэффициент, мы используем

nk=n!k!(n-k)!=6!2!(4!)=6×5×4×3×2×12×1×4×3×2×1=15.

Таким образом, искомый член равен 15×(2x)4×12=240×4. Поскольку вопрос касается коэффициента члена x4, ответ будет просто 240.

Развернуть (x2+3)5.

Решение

В этом случае мы имеем x=x2,y=3andn=5.

Используя биномиальную формулу, мы можем расширить это число до

(x2+3)5=50(x ² )530+51(x2)431+52(x2)332+53(x2)233+54( х2)134+55(х2)035.