Формула cos 2a: Cos^2a-cos2a =? ответ и объяснить как его получили

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28 Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )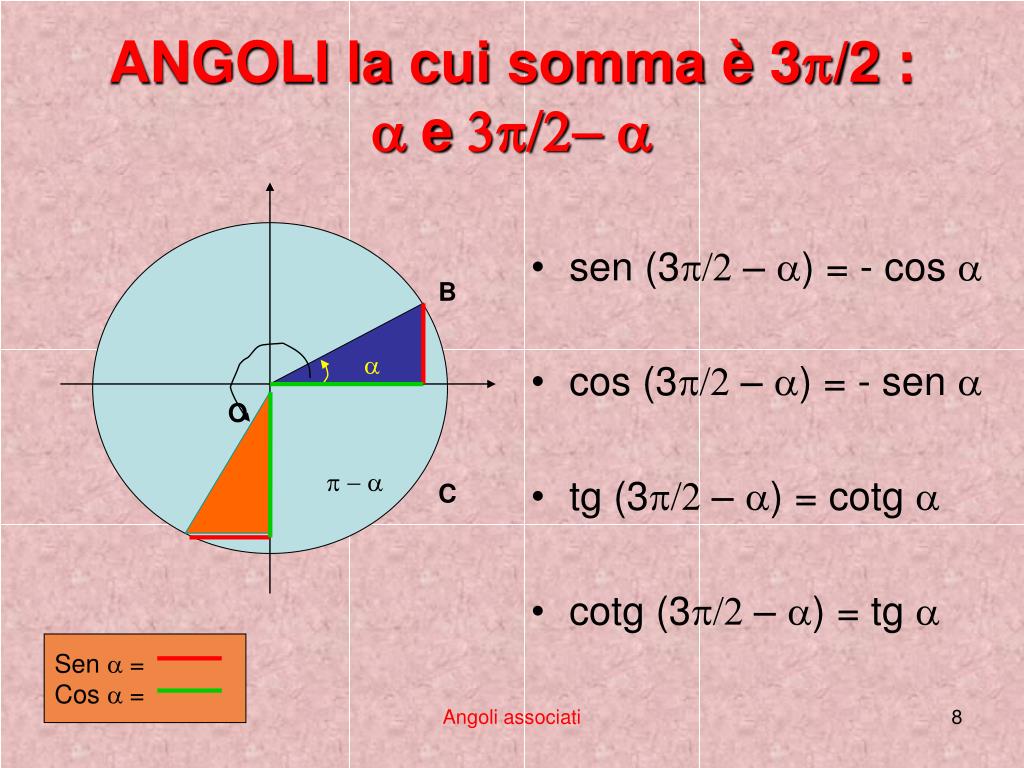
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )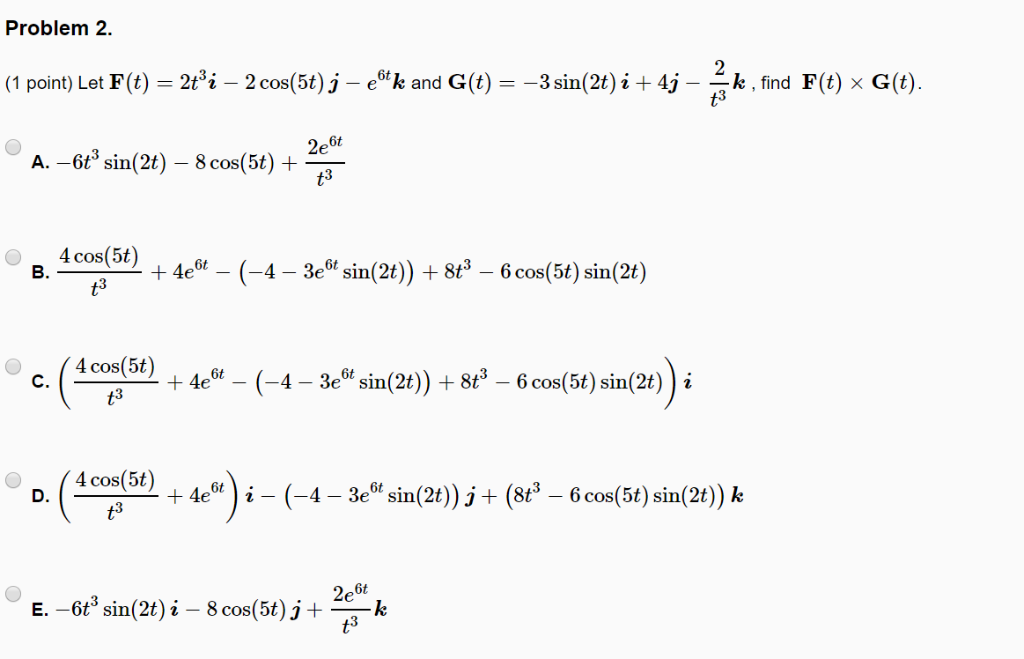
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значение
cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )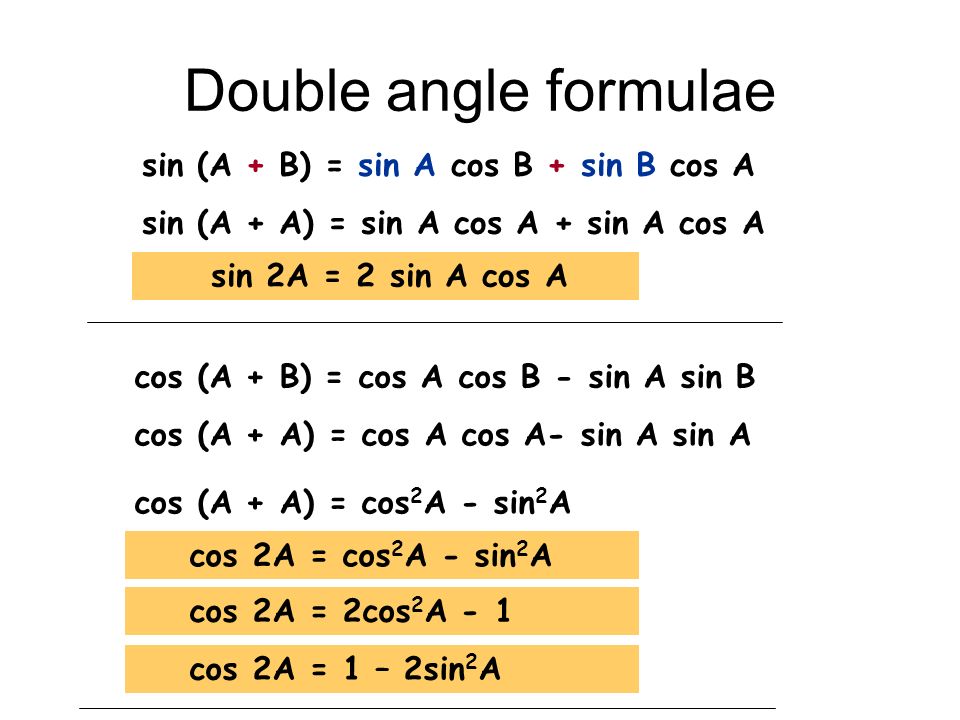
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значение
arcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87
Найти точное значение		sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град.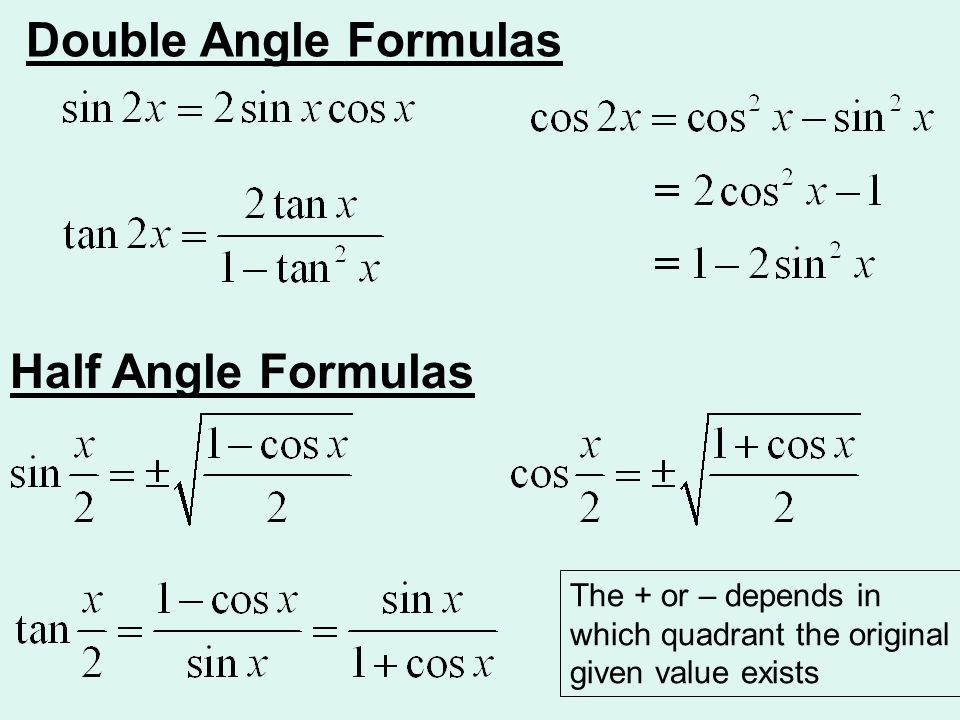 2a помогите вывести из этой формулы cos

Ответы

cos = tg2a/1         (по-моему)

19. 11.13

Валентина

19. 11.13

Михаил Александров
Читать ответы

Марина

Читать ответы

SpartanDav
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

От каната длинной 27 м отрезали третью частью. Сколько метров каната отрезали?Сколько метров каната осталось?Реши задачу двумя способами. Первый способ: 27:3=9 отрезали, 27-9=18 осталось

Решено

В3. Найдите площадь трапеции вершины которой имеют координаты (1;1),(10;1),(8;7),(5;7).?

Решено

Найдите значения х,при которых значения…

tg(2x-pi/4)=(корень из 3)/3

Тригонометрия

Пользуйтесь нашим приложением

Доказательство формулы cos(2x) | cos(2A) Идентичность

  • Математические сомнения
  • Тригонометрия
  • Формулы
  • Двойной уголок
  • Косинус

Тождество двойного угла cos — это математическая формула в тригонометрии, используемая для расширения функций cos, содержащих двойной угол. Например, если тета ($\theta$) — это угол прямоугольного треугольника, то косинус двойного угла записывается как $\cos{(2θ)}$. Математически он расширяется следующим образом.

92{\theta}$

Пришло время узнать, как формула cos двойного угла выводится в математической форме в тригонометрии с помощью геометрии.

Строительство

Косус двойного угла можно получить в тригонометрии, построив прямоугольный треугольник с двойным углом. Выполните следующие шаги, чтобы получить необходимый треугольник.

  1. Угол $\small \Delta FDE$ делится пополам прямой, проведенной из точки $\small D$ в сторону $\small \overline{EF}$, и пересекает сторону $\small \overline{EF }$ в точке $\small G$. Два угла равны, и каждый угол обозначается $x$.
  2. Проведите перпендикуляр к стороне $\small \overline{DG}$ из точки $\small G$ в сторону стороны $\small \overline{DE}$ и пересечь ее со стороной $\small \overline{DE}$ в точке $\маленький Н$.
  3. Теперь проведите перпендикуляр к стороне $\small \overline{DF}$ из точки $\small H$. Он пересекает сторону $\small \overline{DG}$ в точке $\small I$, а также перпендикулярно пересекает сторону $\small \overline{DF}$ в точке $\small J$.
  4. Из точки $\small G$ проведите перпендикуляр к стороне $\small \overline{HJ}$, который делит сторону $\small \overline{HJ}$ в точке $\small K$.

Прямоугольный треугольник построен геометрически с двойным углом и используется для математического нахождения разложения функции cos двойного угла в тригонометрической форме.

Выражение косинуса двойного угла

Угол $\Delta FDE$ равен $2x$ и является двойным углом. Геометрически треугольники $\Delta FDE$ и $\Delta JDH$ подобны. Значит, угол $\Delta JDH$ также равен $2x$.

Согласно $\Delta JDH$, запишите косинус двойного угла в форме отношения. $\overline{DJ}$ — смежная сторона (основание), а $\overline{DH}$ — гипотенуза в этом треугольнике.

$\cos{2x} = \dfrac{DJ}{DH}$

На самом деле сторона $\overline{HJ}$ делит сторону $\overline{DF}$ на две стороны $\overline{DJ} $ и $\overline{JF}$.

$DF \,=\, DJ + JF$

$\имеет DJ = DF \,–\, JF$

Следовательно, длину стороны $\overline{DJ}$ можно записать как вычитание длины стороны $\overline{DF}$ от стороны $\overline{JF}$.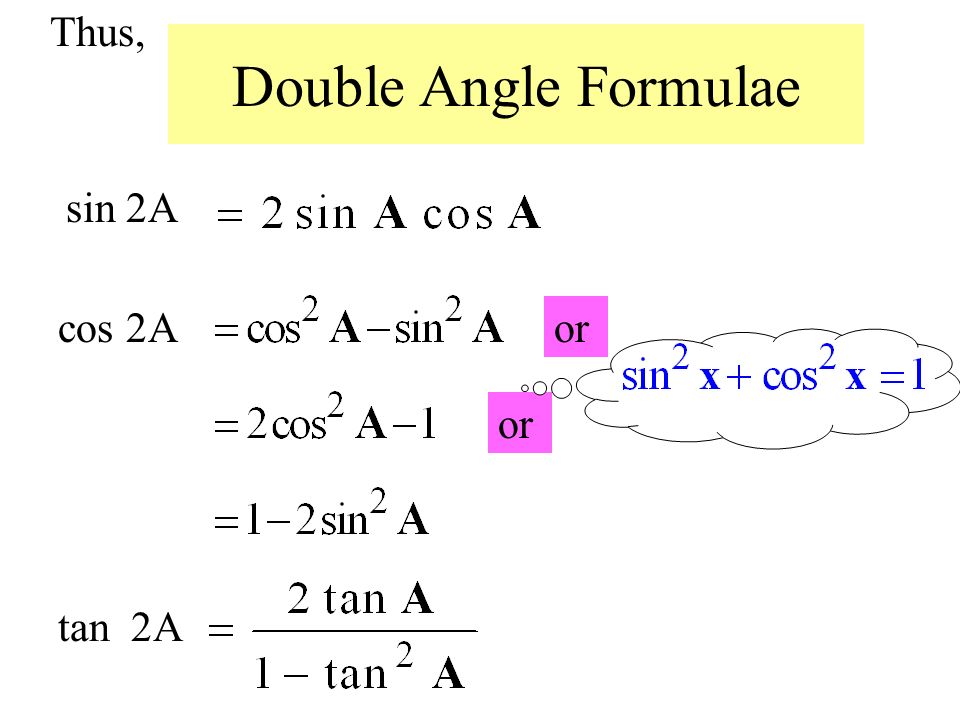

$\ подразумевает \cos{2x}$ $\,=\,$ $\dfrac{DF-JF}{DH}$

$\ подразумевает \cos{2x}$ $\,=\,$ $\ dfrac{DF}{DH}-\dfrac{JF}{DH}$

Сторона $\overline{KG}$ параллельна стороне $\overline{JF}$. Точно так же стороны $\overline{HJ}$ и $\overline{EF}$ также являются параллельными прямыми. Следовательно, длины сторон $\overline{KG}$ и $\overline{JF}$ геометрически равны.

$JF = KG$

Следовательно, длину стороны $\overline{JF}$ можно заменить на длину стороны $\overline{KG}$ в разложении $\cos{(2x) }$ функция.

$\ подразумевает \cos{2x}$ $\,=\,$ $\dfrac{DF}{DH}-\dfrac{KG}{DH}$

Преобразование сторон в тригонометрические функции

Функция двойного угла cos расширена с точки зрения сторон. Итак, пришло время преобразовать их в тригонометрические функции.

$\overline{DF}$ — смежная сторона $\Delta FDG$, угол которой равен $x$. Связь между ними можно записать следующим образом.

$\cos{x} \,=\, \dfrac{DF}{DG}$

$\имплицит DF = {DG}\cos{x}$

Подставить длину стороны $\overline{ DF}$ равным ему значением в разложении $\cos{2x}$.

$\ подразумевает \cos{2x}$ $\,=\,$ $\dfrac{{DG}\cos{x}}{DH}-\dfrac{KG}{DH}$

$\ подразумевает \ cos{2x}$ $\,=\,$ $\dfrac{DG}{DH} \times \cos{x}$ $-$ $\dfrac{KG}{DH}$

$\overline{DG} $ и $\overline{DH}$ — смежные катет и гипотенуза $\Delta GDH$. Отношение их может быть представлено функцией косинуса.

$\cos{x} \,=\, \dfrac{DG}{DH}$

Теперь заменим отношение длин сторон $\overline{DG}$ и $\overline{DH}$ в расширение cos двойного угла. 92{x}-\dfrac{KG}{DH}$

Таким же образом попробуем преобразовать оставшееся соотношение в тригонометрическом виде.

$\overline{KG}$ является стороной $\Delta KHG$, но угол этого прямоугольного треугольника неизвестен. Таким образом, продолжение вывода $\cos{(2x)}$ разложения невозможно, пока это препятствие не будет преодолено.

Найдите неизвестный угол треугольника

$\overline{KG}$ и $\overline{DF}$ — две параллельные прямые, а $\overline{DG}$ — их пересечение. $\угол FDG$ и $\угол KGD$ являются альтернативными внутренними углами и геометрически равны, но $\угол GDF$ равен $x$.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *