Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке.
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.
Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.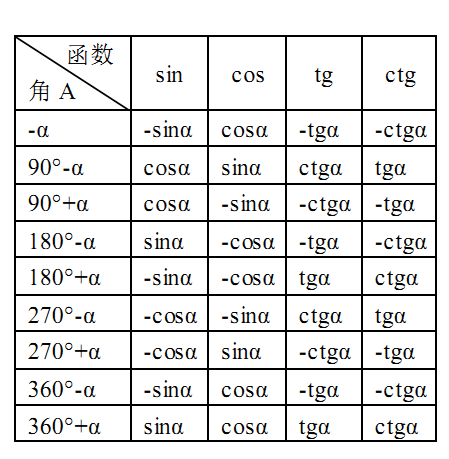
Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.
Здесь приведены знаки для трех отношений в четырех квадрантах.
Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.
Отношения в четырех квадрантах
Отношения для различных углов
Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.
В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
and
cos(A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разницы
Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.
Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
Отношения с помощью четырех секторов
Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.
«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.
Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах.
Пифагор в тригонометрии
Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.
Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos2 A + sin2 A = 1. Это выражение всегда истинно для любого значения A.
Немного о том, как это было записано. Cos2 A означает (cos A)2. Если вы написали это как cos A2, уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.
A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол. Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A.
Умножение углов
Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.
Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.
Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.
На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.
УМНОЖЕНИЕ УГЛОВ Производные от формул суммы
УМНОЖЕНИЕ УГЛОВ Соотношения для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами.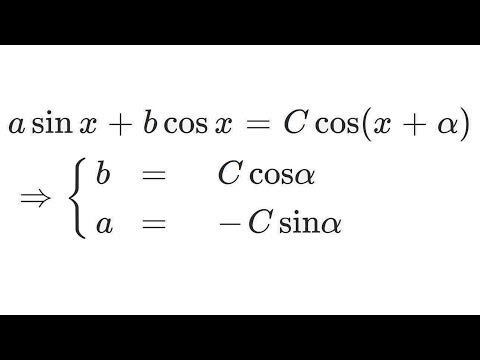 Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.
Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.
Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.
Углы в окружности
Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.
Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.
В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.
Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.
Угол в центре в два раза больше чем угол на окружности
Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.
Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.
Определения
Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Вопросы и задачи
1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.
2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?
3. Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.
5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.
6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.
7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.
8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.
9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.
11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.
12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.
14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.
15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.
16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор.
Приведите приближенные значения из таблицы или используя калькулятор.
Вывод тригонометрических функций и разностных формул
Знания о старшей школе почти забыты. Некоторое время назад формула суммы сумм была получена заново. Взять запись здесь
| 0X01 Вывод тригонометрической формулы |
Формула двух сумм
sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)
cot(A+B)=(cotAcotB-1)/(cotB+cotA) cot(A-B)=(cotAcotB+1)/(cotB-cotA)
Формула двойного угла
tan2A=2tanA/(1-tan2A) cot2A=(cot2A-1)/2cota
cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a
sinα+sin(α+2π/n)+sin(α+2π2/n)+sin(α+2π3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π2/n)+cos(α+2π3 / n) + … + cos [α + 2π * (n-1) / n] = 0 и
sin2(α)+sin2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
Формула четырехкратного угла:
sin4A=-4*(cosAsinA(2*sinA^2-1))
cos4A=1+(-8*cosA2+8*cosA4)
tan4A=(4tanA-4tanA3)/(1-6*tanA2+tanA^4)
Пятикратное общее:
sin5A=16sinA5-20sinA3+5sinA
cos5A=16cosA5-20cosA3+5cosA
tan5A=tanA*(5-10tanA2+tanA4)/(1-10tanA2+5*tanA4)
Шестикратный генерал:
sin6A=2*(cosAsinA(2sinA+1)(2sinA-1)(-3+4*sinA^2))
cos6A=((-1+2cosA2)*(16*cosA4-16cosA^2+1))
tan6A=(-6tanA+20tanA3-6*tanA5)/(-1+15*tanA2-15*tanA4+tanA^6)
Семикратный генерал:
sin7A=-(sinA*(56sinA2-112*sinA4-7+64sinA^6))
cos7A=(cosA*(56cosA2-112*cosA4+64cosA^6-7))
tan7A=tanA*(-7+35tanA2-21*tanA4+tanA6)/(-1+21*tanA2-35tanA4+7*tanA6)
Восьмикратное общее:
sin8A=-8*(cosAsinA(2sinA2-1)*(-8*sinA2+8sinA^4+1))
cos8A=1+(160cosA4-256*cosA6+128cosA8-32*cosA2)
tan8A=-8tanA(-1+7tanA2-7*tanA4+tanA6)/(1-28*tanA2+70tanA4-28*tanA6+tanA^8)
Девятикратное общее:
sin9A=(sinA*(-3+4sinA2)*(64*sinA6-96sinA4+36*sinA2-3))
cos9A=(cosA*(-3+4cosA2)*(64*cosA6-96cosA4+36*cosA2-3))
tan9A=tanA*(9-84tanA2+126*tanA4-36tanA6+tanA8)/(1-36tanA2+126*tanA4-84tanA6+9*tanA8)
В десять раз больше:
sin10A=2*(cosAsinA(4sinA2+2*sinA-1)*(4*sinA2-2sinA-1)(-20sinA2+5+16*sinA4))
cos10A=((-1+2cosA2)*(256*cosA8-512cosA6+304*cosA4-48*cosA^2+1))
tan10A=-2tanA(5-60tanA2+126*tanA4-60tanA6+5*tanA8)/(-1+45tanA2-210*tanA4+210tanA6-45*tanA8+tanA^10)
· Универсальная формула:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan2(α/2)]/[1+tan2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
Половина формулы
sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)
cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)
tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))
cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))
Сумма разницы продукта
2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)
2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)
sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)
tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB
cotA+cotBsin(A+B)/sinAsinB -cotA+cotBsin(A+B)/sinAsinB
Первые русские термины и
1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n2
2+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n^2=n(n+1)(2n+1)/6
13+23+33+43+53+63+…n3=(n(n+1)/2)2 12+23+34+45+56+67+…+n(n+1)=n(n+1)(n+2)/3
Теорема синуса a / sinA = b / sinB = c / sinC = 2R Примечание: где R — радиус описанной окружности треугольника
Теорема косинуса b2 = a2 + c2-2accosB Примечание: угол B — это угол между ребром a и c
Умножение и факторизация a2-b2 = (a + b) (a-b) a3 + b3 = (a + b) (a2-ab + b2) a3-b3 = (a-b (a2 + ab + b2)
Неравенство треугольника | a + b | ≤ | a | + | b | | a-b | ≤ | a | + | b | | a | ≤b <=> — b≤a≤b
|a-b|≥|a|-|b| -|a|≤a≤|a|
| 0X02 sin( α \alpha α+ β \beta β) Выведение |
Справочная статья
Вывод тригонометрических функций и разностных формул
Формула тригонометрической функции
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.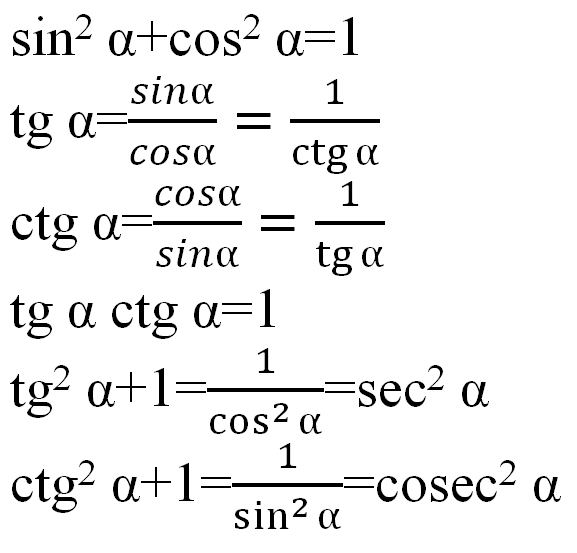 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.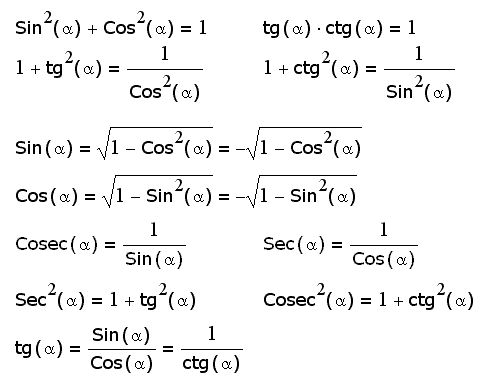 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 14 из 15Следующая ⇒
Тригонометрические формулы суммы и разности двух углов
Тригонометрические формулы двойного угла
Формулы понижения степени
Тригонометрические формулы произведения
Формулы суммы и разности тригонометрических функций sinα + sinβ= 2sin ∙cos ; sinα – sinβ = 2sin ∙cos ; cosα + cosβ = 2cos ∙cos ; cosα – cosβ = –2sin ∙sin . Формулы приведения Формул приведения много, а точнее 32. И все формулы надо знать. К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения. Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет. 1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»: , π, , 2πи острого угла α, а в правой части аргумент α. 2. В правой части знак перед функцией либо «плюс», либо «минус». Мнемоническое правило Достаточно задать себе два вопроса: 1. Меняется ли функция на кофункцию? Ответ: Если в формуле присутствуют углы или — это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет». 2. Какой знак надо поставить в правой части формулы? Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части. Например, sin( + α). 1) «Меняется функция или нет?» — угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит в правой части будет cosα. 2) «Знак?» Угол ( + α) попадает в IV четверть.Синус вIV четвертиимеет знак «минус». Значит, в правой части ставим знак «минус». Итак, получили формулу, sin( + α) = –cosα. Тригонометрический круг Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц. Сколько полезного на этом рисунке! 1. 2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси x, а значение синуса — на оси y. 3. И синус, и косинус принимают значения от –1 до 1. Тригонометрический круг: 1. Значение тангенса угла α тоже легко найти — поделив sinα на cosα. А чтобы найти котангенс — наоборот, косинус делим на синус. 2. Знаки синуса, косинуса, тангенса и котангенса. 3. Синус — функция нечётная, косинус — чётная. 4. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2π. Графики тригонометрических функций На рисунках приведены графики тригонометрических функций: y = sinx, y = cosx, y = tgx, y= ctgx. 1. График функции y = sinx 2. График функции y = cosx 3. 4. График функции y = ctgx
Площади плоских фигур Большинство планиметрических задач на экзамене заканчиваются словами «найти площадь…». В 99% таких задач работать в итоге придется с самыми простыми известными плоскими фигурами, а именно находить площадь треугольников, четырехугольников и окружности. На этом занятии мы рассмотрим и повторим все основные формулы нахождения площадей, а также обратим внимание на частные случаи, которые могут существенно облегчить задачу. Цель урока ― обобщить и систематизировать знания, умения и навыки по нахождению площадей плоских фигур. Сначала мы систематизируем и обобщим знания и умения по теме, затем вы должны будете выполнить несколько типов заданий, которые помогут закрепить материал и легко справиться с задачами такого типа на экзамене.
Треугольник Существует пять основных формул нахождения площади произвольного треугольника: S = ⋅ a ⋅ h,где a ― сторона треугольника, h ― высота, проведенная к этой стороне. S = ∙ a ∙ b ∙ sinγ, где a, b ― стороны треугольника, γ ― величина угла между ними. S = (формула Герона), где a, b, c ― стороны треугольника, p ― полупериметр треугольника. S = r ∙ p, где r ― радиус вписанной окружности, p ― полупериметр треугольника. S = , где a, b, c ― стороны треугольника, R ― радиус описанной окружности. Как следствия из этих формул, можно отметить следующие частные случаи:
Пример: Найдите площадь треугольника, если известны три его стороны: 5, 9, 12. Решение: Прежде всего определяемся с подходящей формулой нахождения площади. S = , P = = = 13. S = = = 4√26. Ответ: 4√26.
Параллелограмм S = a ∙ h, где a ― сторона параллелограмма, h ― высота, проведенная к этой стороне. S = a ∙ b ∙ sinγ, где a, b ― стороны параллелограмма, γ ― величина угла между ними. Как следствия из этих формул, можно отметить следующие частные случаи:
Пример: Стороны параллелограмма равны 1 и √3, а его площадь равна 1,5. Чему равен тупой угол, образованный его сторонами? Решение: Даны стороны и площадь, найти необходимо угол. 1.5 = 1√3 ∙ sinγ ⇔ sinγ = . Тогда γ =60 или 120. Но в задаче требуется найти тупой угол ⇒ γ = 120. Ответ: 120.
Трапеция S = ∙ h,где a, b ― основания трапеции, h ― высота трапеции. Пример: Вычислите среднюю линию трапеции, если ее высота 6 см, а площадь 36 см2. Решение: Зная площадь и высоту трапеции, можем найти полусумму ее оснований, а это и есть средняя линия: S = ∙ h ⇔ 36 = ∙ 6 ⇔ = 6. Ответ: 6 см.
⇐ Предыдущая6789101112131415Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 876; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Технологическая карта открытого урока по алгебре 10 класс «Основные формулы для синуса и косинуса» | Учебно-методический материал по алгебре (10 класс):
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
«Основные формулы для sina и cosa»
выполнил: учитель математики КГКОУ
«Вечерняя школа №1»
Вигель Сергей Давыдович
Рубцовск 2021
Предмет: алгебра.
Тема урока: Основные формулы для sina и cosa.
Тип урока: урок изучения и первичного закрепления нового знания.
Планируемые результаты:
Личностные:
-умение проверять себя;
-умение давать оценку своим действиям;
Метапредметные:
-познавательные — уметь вести самостоятельный поиск информации об основных формулах для sina и cosa;
-регулятивные — уметь ставить цели нахождения тригонометрических формул, поэтапно планировать эту работу, вести самоконтроль;
-коммуникативные — уметь работать в парах или группах; устно и письменно строить свое высказывание (как читать формулы sina и cosa).
Предметные:
— изучить основные формулы для sina и cosa;
— применять при решении задач;
— точно и грамотно выражать свои мысли с математической терминологией и символикой (sin;cos).
Дидактические средства: Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений/С.М. Никольский и др. / –9-е изд., – М.: Просвещение, 2021.; раздаточный материал; презентация «Тригонометрия в других науках».
Оборудование: компьютер и экран.
Образовательная цель: изучение основных формул для sina и cosa.
Развивающая цель: применение основных формул для sina и cosa при решении задач.
Воспитательная цель: желание самостоятельно добывать знания, выработка культуры общения.
Формы организации познавательной деятельности: фронтальная, индивидуальная и групповая работа обучающихся.
Методы обучения: репродуктивный, частично-поисковый.
- Основная таблица.
Этапы урока (в соответствии со структурой учебной деятельности) | Планируемая деятельность учащихся | Деятельность учителя | Развиваемые (формируемые) учебные действия | |
предметные | универсальные | |||
1. | 1. Приветствуют учителя. Обучающиеся внимательно слушают предлагаемую учителем информацию. 2.Вспоминают. Объясняют что такое синус и косинус угла 3. Находят синус 90 градусов и косинус 90 градусов 4. Испытывают затруднения в нахождении значения косинуса угла, если известно значение синуса угла | 1. Приветствует учащихся. Сл.1Приводит несколько интересных фактов о тригонометрии (приложение 1) 2.Предлагает вспомнить — что называется синусом и косинусом угла (приложение 1). 3.Предлагает найти синус 90 градусов и косинус 90 градусов (приложение 1). 4. Просит найти значение косинуса угла, если известно значение синуса угла (приложение 1). | осознавать значимость использования тригонометрии | Регулятивные УУД:осознание учащимися того, что уже усвоено и что ещё подлежит усвоению Познавательные УУД: видеть проблему, осознавать возникшие трудности; Коммуникативные УУД: участвовать в коллективном обсуждении проблемы, интересоваться чужим мнением и высказывать свое собственное; Личностные УУД:осознавать неполноту знаний, проявлять интерес к новому содержанию. |
2. Определение темы урока. Постановка цели урока. (Целеполагание) Планирование деятельности. (10 мин) | 1.Формулируют варианты темы и в окончательном варианте записывают в тетради. 2.Предлагают варианты, испытывают затруднения. 3. Заполняют колонки «Знаю» по высказанным мнениям (и ошибочные тоже). 4.Высказывают свои пожелания. 5. Участвуют в заполнении колонки «Хочу узнать». 6.Формулируют отдельные положения цели. После этого в окончательном варианте записывают цель урока. | 1. Просит выдвинуть предположение о теме урока. После этого тему Сл.2 урока выводит на экран и предлагает ее записать. 2. Предлагает поделиться своими знаниями об основных тригонометрических формулах синуса и косинуса. 3. Предлагает систематизи- ровать работу в виде таблицы. (таблица: «Знаю», «Хочу узнать», «Узнал») и заполнить колонку «Знаю» (Приложение 2) 4. 5. Просит записать свои предложения в колонке «Хочу узнать». Сл.3 (Приложение 2) 6. Предлагает внимательно посмотреть на заполнен-ную колонку «Хочу узнать» и сформулировать цель урока . Сл.4 (Приложение 2) | умение правильно применять основные тригонометрические формулы синуса и косинуса при решении задач | Регулятивные УУД: определять тему, цели учебной деятельности, осуществлять планирование, принимать предложенный способ решения проблемы; предвосхищать результат и уровень усвоения; Познавательные УУД:самостоятельно выделять и формулировать познавательной цели; выдвигать гипотезы, выделять материал, который будет использован в исследовании; устанавливать причинно-следственные связи; Коммуникативные УУД: уметь слушать и вступать в диалог; участвовать в коллективном обсуждении проблем, с достаточной полнотой и точностью выражать свои мысли. Личностные УУД: осознавать личностную значимость владения методами научного познания. |
3. Практический этап. Реализация плана. Изучение нового материала (15 мин) | 1. Визуально просматривают презентацию. Ведут самостоятельно записи в колонке «Узнал». 2.Самостоятельно знакомятся с новой темой. Задают друг другу вопросы, отвечают. Ведут самостоятельно записи в колонке «Узнал». | 1. Сл.5-8 Предлагает просмотреть презентацию «Тригонометрия в других науках» с использованием ПК, подготовленную учащимся и записать в колонке «Узнал» новою информацию. 2. Раздает учащимся раздаточные материалы и предлагает самостоятельно изучить новую тему. Делит на две группы и предлагает перекрестный опрос. Сл.9 Сл.10 | формулировать определение основных формул для синуса и косинуса | Регулятивные УУД: контролировать, корректировать, оценивать полученные знания; Познавательные УУД: поиск и выделение необходимой информации; закрепить общеучебные и логические умения и навыки, умение структурировать знания. Коммуникативные УУД: уметь сформулировать вопрос |
4.Контроль. Оценивание. Рефлексия. Постановка домашнего задания. ( 10 мин.) | 1.Решают самостоятельную работу. 2. Проверяют свои самостоятельные работы и выставляют себе оценки сравнивая свои ответы с правильными ответами, предложенными учителем. 3. Проверяют правильность решения самостоятельной работы и оценивания соседа. 4. Отвечают на вопрос о достижении цели урока. 5. Учащиеся заполняют листы самоконтроля 6.Записывают домашнее задание. | 1. Давайте проведем небольшую самостоятельную работу по материалам урока. Сл. 11 2.Предлагает самостоятельно проверить результаты самостоятельной работы и поставить себе оценку по пятибалльной шкале. Сл.12 (приложение 2) 3. Предлагает поменяться работами с соседом по парте и проверить правильность решения теста и оценивания 4. 5. Предлагает письменно ответить на вопросы бланка рефлексии. Сл.13 (приложение 3) 6.Благодарит за работу над презентацией и на уроке. Подводит итог по работе с таблицей. Выводит домашнее задание на экран (параграф, номера задач). Сл.14 | Закрепить знания нового математического понятия «основные формулы для синуса и косинуса» | Регулятивные УУД: самоконтроль, саморегуляция. Оценка степени достижения цели; Познавательные УУД: контроль и оценка процесса и результатов деятельности. Коммуникативные УУД: уметь с достаточной полнотой и точностью выражать свои мысли . Личностные УУД: выполнять саморегулирование |
Приложение 1.
1) Мотивационно-целевой этап (5 мин)
(Приветствие; проверка готовности к уроку).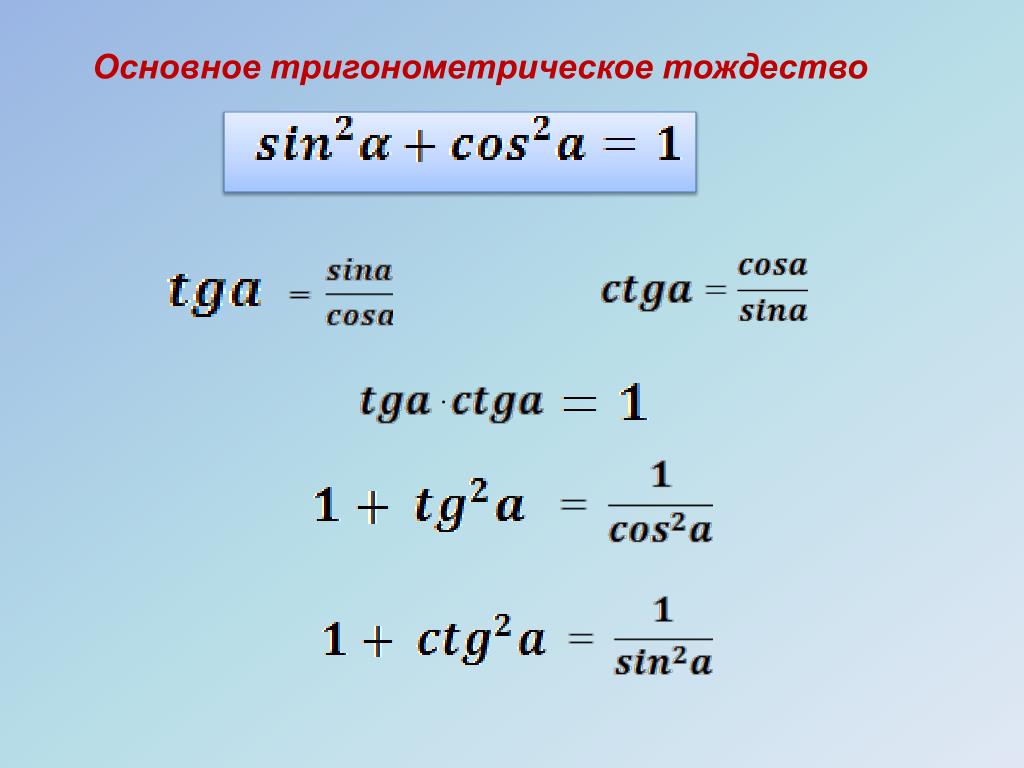
Учитель (У): Здравствуйте. Урок начну с мнемонического правила «тригонометрия в ладони»
Очень часто требуется знать наизусть значения cos, sin для углов 0°, 30°, 45°, 60°, 90°. Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки.
Правило: Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30°, 45°, 60°. Подставляя вместо n, 0, 1, 2, 3, 4, получаем значения sin, для углов 0°, 30°, 45°, 60°, 90°. Для cos отсчет происходит в обратном порядке.
Что называется синусом и косинусом угла?
Синус угла а-число равное ординате точки единичной окружности, соответствующей углу а.
Косинус угла а- число равное абсциссе точки единичной окружности, соответствующей углу а.
Чему равен синус и косинус 90 градусов?
Синус 90 градусов равен-1, Косинус 90 градусов равен-0.
Дано: sinα=0,8
Найти: cosa
Приложение 2.
2) Определение темы урока. Постановка цели урока. (Целеполагание). Планирование деятельности. (10 мин)
ЦЕЛЬ:
Знаю | Хочу узнать | Узнал |
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО МАТЕРИАЛАМ УРОКА.
Проверьте правильность ответов и поставьте себе оценку:
Ф. И. О.____________________________________________ ОЦЕНКА ___________
4) Контроль. Оценивание. Рефлексия. Постановка домашнего задания.(10 мин) Приложение 3
Оценивание. Рефлексия. Постановка домашнего задания.(10 мин) Приложение 3
РЕФЛЕКСИЯ
Ф. И. О.____________________________________________ КЛАСС ___________
На уроке я работал | активно / пассивно |
Своей работой на уроке | доволен / не доволен |
Урок для меня показался | коротким /длинным |
За урок я | не устал / устал |
Мое настроение стало | лучше / хуже |
Материал урока мне был | понятен / не понятен полезен / бесполезен интересен / скучен |
(Учащиеся записывают домашнее задание). Спасибо за урок, До свидания.
Спасибо за урок, До свидания.
Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным.
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
График. Поcтроение углов в Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева. График. Положительные и отрицательные
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 Решение: График. Нахождение всех углов по Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o — 45 o = 315o .
Пример 2 Найти все углы между 0o и 360o , тангенс которых равен 1, 327. Решение: Из рис ниже Θ = arctg1,327= 53o . Построение синусоиды и косинусоиды Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая — это ТS, а горизонтальная — ОS.
График. Из определения тригонометрических функций
Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева. Синусоидальные и косинусоидальные графики
Периодические функции и период Амплитуда Пример 3. Решение: Пример 4. Решение: График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o. Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже. В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α. Пример 5.
Решение: Пример 6. Решение: Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то Пример 7. Решение: Пример 8. Решение Пример 9. График. v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад. | ||||||||
Дополнительная информация от TehTab.ru: | ||||||||
Формула Sin Cos — Тригонометрия Формула Sin Cos, решенные примеры и часто задаваемые вопросы
Мы знаем, что часть математики, называемая тригонометрией, является частью математики, которая имеет дело с треугольниками. Тригонометрия — это часть математики, которая имеет дело с отношениями между тремя сторонами и тремя углами. Тригонометрия помогает нам найти оставшиеся стороны и углы треугольника, если известны некоторые из его сторон и углов. Эта задача решается с помощью некоторых отношений сторон треугольника к его острым углам. Эти соотношения острых углов называются основными тригонометрическими соотношениями. В этой статье давайте изучим различные тригонометрические формулы sin cos и основные тригонометрические отношения.
В этой статье давайте изучим различные тригонометрические формулы sin cos и основные тригонометрические отношения.
Основные формулы тригонометрических соотношений
Существует шесть основных тригонометрических соотношений для прямоугольного треугольника. Это Sin, Cos, Tan, Cosec, Sec, Cot, что означает синус, косеканс, тангенс, косеканс, секанс соответственно. Sin и Cos — это основные коэффициенты триггера, которые говорят о форме прямоугольного треугольника.
Прямоугольный треугольник — это треугольник, в котором один из углов — прямой, т. е. равен 900. Гипотенуза прямоугольного треугольника — это наибольшая сторона, которая является стороной, противоположной прямому углу. . Прилегающая сторона – это сторона, которая лежит между определяемым углом и прямым углом. Противоположная сторона противоположна определяемому углу..
(Изображение будет загружено в ближайшее время)
В любом прямоугольном треугольнике, для любого угла:
Синус угла (sin A) = длина противоположной стороны / длина гипотенузы
Косинус угла (cos A) = длина прилежащей стороны / длина гипотенузы
Тангенс угла (tan A) = длина противолежащей стороны / длина прилежащей сторона
Косеканс угла (косек A) = длина гипотенузы / длина противоположной стороны
Секанс угла (сек A) = длина гипотенузы / длина прилежащей стороны
Котангенс угла (cot A) = длина прилежащей стороны / длина противоположная сторона
Взаимные тригонометрические идентичности
Взаимные идентичности приведены как:
COSEC A = 1/SIN A
SEC A = 1/COS A
SEC A = 1/COS A
SEC A = 1/COS A
COT A = 1/COS A
SEC A = 1/COS A
SIN A = 1/COSEC A
COS A = 1/SEC A
TAN A = 1/COT A
SEC A = 1/COS A
СЕД A /тан А
Основные тригонометрические идентичности для SIN дать название каждой стороне прямоугольного треугольника.
 Давайте изучим основные формулы sin и cos.
Давайте изучим основные формулы sin и cos.Если A + B = 180°, то:
sin(A) = sin(B)
cos(A) = -cos(B)
Если A + B = 90° :
sin(A) = cos(B)
cos(A) = sin(B)
Формулы половинного угла
Sin (A/2)= ± \[\sqrt{\ frac{1−CosA}{2}}\]
Если A/2 находится в первом или втором квадранте, результат будет положительным.
Если A/2 находится в третьем или четвертом квадранте, результат будет отрицательным.
Cos(A/2) = ±1 \[\sqrt{\frac{1+CosA}{2}}\]
Если A/2 находится в первом или четвертом квадранте, то будет положительный.

Если A/2 находится во втором или третьем квадранте, результат будет отрицательным.
Двойной и тройной угол Формулы
SIN 2A = 2SIN A COS A
COS 2A = COS2A- SIN2A = 2 COS2A- 1 = SIN2A
SIN 3A = 3SIIN A- 4- 40003
SIN 3SIIN A- 3SIIN A- 4. Sin3A
Cos 3A = 4 Cos3A – 3CosA
Sin4A = (3/8)−(1/2)cos(2A)+(1/8)cos(4A)
Sin2A = 1–Cos(2A) / 2
Cos2A = 1+Cos(2A) / 2
Cos4A = 9001 – 6cos2A sin2A + sin4A
Сумма и разность углов
S 9 (06 S) A).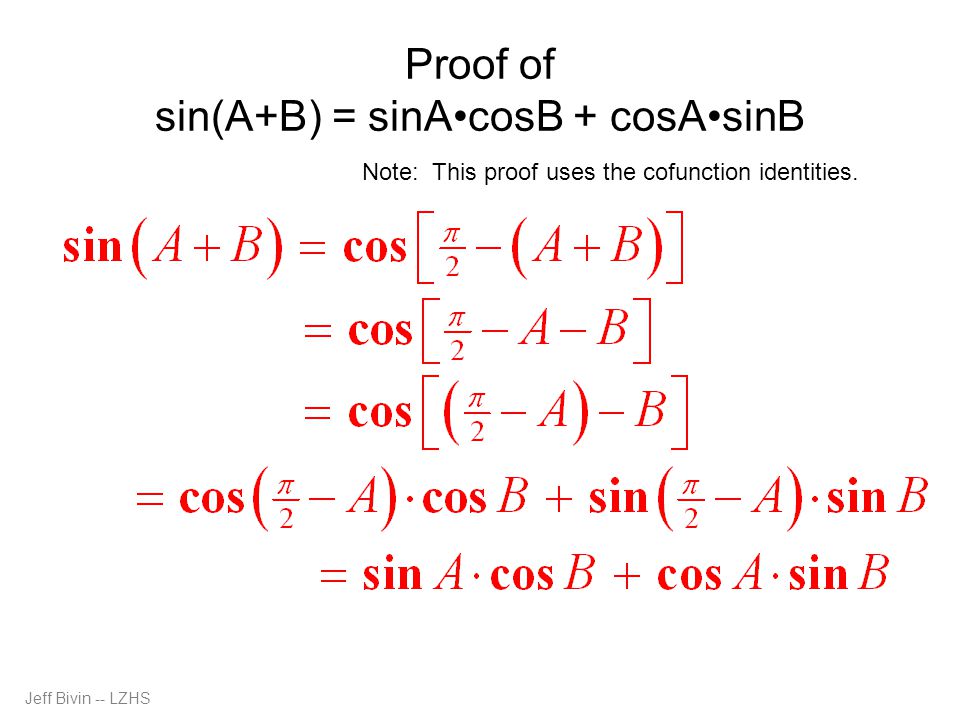 cos(B) + cos(A)sin(B)
cos(B) + cos(A)sin(B)Sin(A−B) = sin(A)⋅cos(B)−cos(A)⋅sin(B)
Cos(A+B) = cos(A)⋅cos(B)−sin(A)⋅sin(B)
Cos(A−B) = cos(A)⋅cos(B)+sin(A )⋅sin(B)
Sin(A+B+C) = senA⋅cosB⋅cosC+cosA⋅sin⋅cosC+cosA⋅cosB⋅sinC−sinA⋅sinB⋅sinC
Cos(A + B +C) = cos A Cos B Cos C- cos Asin Bsin C – sin Acos Bsin C – sin A sin B cos C
Sin A + Sin B = 2Sin(A+ B)/2 Cos(A−B)/2
Sin A – Sin B = 2Sin(A−B)/2Cos(A+B)/2
Cos A + Cos B = 2Cos(A +B)/2 Cos(A−B)/2
Cos A – Cos B = -2Sin(A+B)/2 Sin(A−B)/2
Примеры решения
Пример 1 : Найдите длину стороны x на диаграмме ниже:
(Изображение будет загружено в ближайшее время)
Решение: угол равен 600.
Гипотенуза = 13 см
прилежащая сторона = x см 60) = x / 13
, следовательно, x = 13 × cos(60) = 6,5
, следовательно, длина стороны x равна 6,5 см.
Изучите формулу Sin Cos с Веданту
Математика – это искусство, это наука и исследование качества, структуры, пространства и изменения любого объекта. Математики ищут закономерности, формулируют новые предположения и устанавливают истину путем строгой дедукции из правильно выбранных аксиом и определений.
Это наука о числах, количествах и формах, способах их измерения и отношениях между ними. Со знанием математики вы действительно можете изучать науку, которая вращается вокруг чисел, форм и закономерностей, того, как вещи можно считать, как организованы определенные вещи. Этот раздел математики с алфавитами обычно называют алгеброй, и в математике есть намного больше.
Когда вы строите дом или любое здание, измеряя длину, ширину и углы, оценивая стоимость проекта и объединяя все это вместе, это несколько примеров, которые показывают, насколько важна математика для выполнения строительных проектов. Куда бы вы ни шли за продуктами или покупали какие-либо вещи, вы рассчитываете цену за единицу, взвешиваете продукты, вычисляете процентные скидки и оцениваете окончательную стоимость, вы используете Math, чтобы упростить процесс покупок. Таким образом, эти основные понятия действительно полезно запомнить, чтобы эффективно и легко выполнять повседневную деятельность.
Куда бы вы ни шли за продуктами или покупали какие-либо вещи, вы рассчитываете цену за единицу, взвешиваете продукты, вычисляете процентные скидки и оцениваете окончательную стоимость, вы используете Math, чтобы упростить процесс покупок. Таким образом, эти основные понятия действительно полезно запомнить, чтобы эффективно и легко выполнять повседневную деятельность.
Грех — это термин, равный стороне, противоположной углу, на который вы проводите функции, над гипотенузой, которая является самой длинной стороной в треугольнике. Cos примыкает по гипотенузе. И тангенс противоположен соседнему, что означает, что тангенс — это sin/cos.
Формулы Sin Cos всегда основаны на сторонах данного прямоугольного треугольника. Sin и Cos являются основными тригонометрическими функциями наряду с функциями тангенса в тригонометрии, которая является частью математики. Синус любого измеряемого угла равен отношению противолежащего катета к гипотенузе, тогда как косинус угла равен отношению прилежащего катета к гипотенузе.
Доказательство формул двойного и половинного угла.
Доказательство формулы произведения и суммы
Продукты в сумме
| а) | sin cos β | = | ½[грех ( + β) + грех ( — β)] |
| б) | косинус β | = | ½[sin ( + β) − sin ( − β)] |
| в) | cos cos β | = | ½[cos ( + β) + cos ( − β)] |
| г) | sin sin β | = | -½[потому что ( + β) — потому что ( — β)] |
Доказательство
Эти формулы также получены из формул суммы и разности. Чтобы вывести (а), напишите
| грех (+β) | = | sin cos β + cos sin β |
| sin ( − β) | = | sin cos β − cos sin β |
и добавить по вертикали. Последние термины в каждой строке будут отменены:
Последние термины в каждой строке будут отменены:
грех ( + β ) + грех ( — β ) = 2 грех потому что β .
Следовательно, при смене сторон
2 sin cos β = sin ( + β ) + sin (- β ),
так что
sin cos β = ½ [sin ( + β ) + sin (- β )].
Это тождество (а)).
Формула (b) выводится точно таким же образом, только вместо сложения вычитается sin ( − β ) из sin ( + β ).
Формулы (c) и (d) получены аналогично. Чтобы вывести (c), напишите
cos ( + β ) = cos cos β − sin sin β ,
cos (- β ) = cos cos β + sin sin β ,
и доп. Чтобы получить (d), вычтите.
Выведем (d). При вычитании первые члены справа сокращаются. У нас будет
cos ( + β ) − cos ( − β ) = −2 sin sin β .
Следовательно, при решении вопроса о грехе sin β ,
sin sin β = −½[cos ( + β ) − cos ( − β )].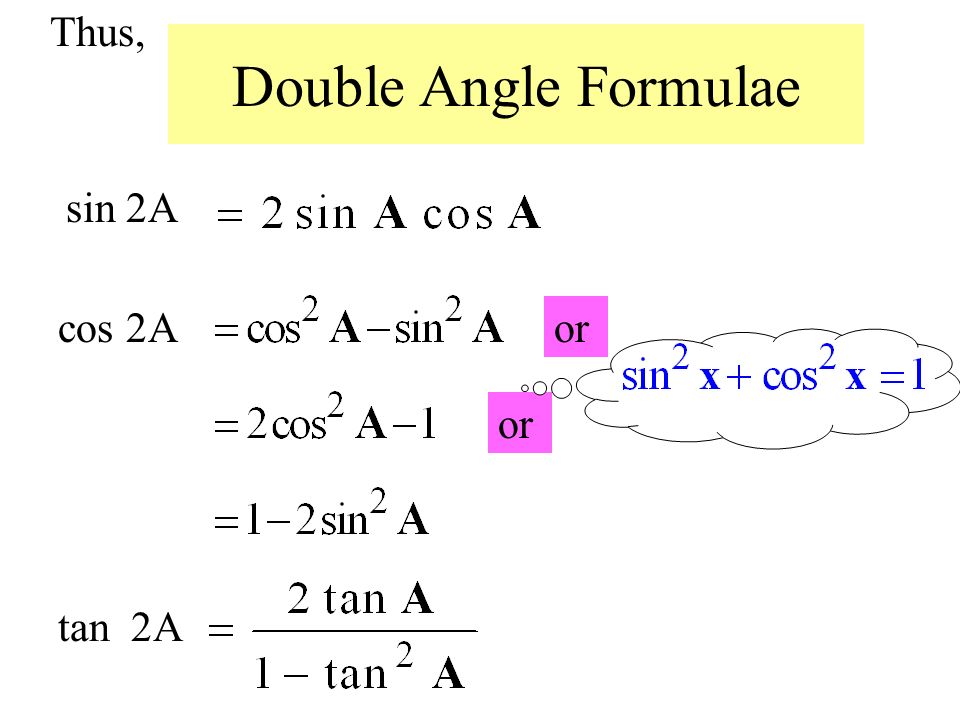
Суммы как произведения
| д) | грех А + грех В | = | 2 sin ½ ( A + B ) cos ½ ( A − B ) |
| е) | грех А − грех В | = | 2 sin ½ ( A − B ) cos ½ ( A + B ) |
| г) | cos A + cos B | = | 2 cos ½ ( A + B ) cos ½ ( A − B ) |
| ч) | соз А − соз В | = | −2 sin ½ ( A + B ) sin ½ ( A − B ) |
Доказательство
Формулы (e), (f), (g), (h) получены из (a), (b), (c), (d) соответственно; то есть (e) происходит от (a), (f) происходит от (b) и так далее.
Чтобы получить (е), поменяйте стороны в (а):
½ [sin ( + β ) + sin (- β )] = sin cos β ,
так что
грех ( + β ) + грех ( — β ) = 2 грех потому что β . . . . . . (1)
Теперь поставь
| + β | = | А | ||||
| и | ||||||
| − β | = | Б. . . . . . . . . . . . . . . .(2) | ||||
Левая часть строки (1) становится
.грех А + грех Б.
Теперь это левая часть (е), что мы и пытаемся доказать.
Чтобы завершить правую часть строки (1), решите одновременные уравнения (2) для и β .
При их добавлении 2 = A + B,
так что
90 240 = ½ (А + В).
Если вычесть эти два уравнения, 2 β = A − B,
так что
β = ½ (А — В).
В правой части строки (1) подставьте эти выражения для и β . Строка (1) становится
.sin A + sin B = 2 sin ½ (A + B) cos ½ (A − B).
Это тождество (е).
Читать следующим образом:
«sin A + sin B равен удвоенному синусу половины их суммы, умноженному на
, умноженному на косинус половины их разности».
Тождества (f), (g) и (h) получаются точно таким же образом из (b), (c) и (d) соответственно.
Тригонометрические тождества
Содержание | Дом
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Тригонометрические и геометрические преобразования, Sin(A + B), Sin(A
Список всех тригонометрических тождеств (формул)
Соотношения суммы углов
Как показали примеры, иногда нам нужны углы, отличные от 0, 30, 45, 60 и 90 градусов. В этой главе вам нужно усвоить две вещи:
В этой главе вам нужно усвоить две вещи:
1. Sin(A + B) не равен sin A + sin B . Это не работает, как удаление скобок в алгебре.
2. Формула, чему равен sin(A + B).
Во-первых, чтобы показать, что удаление скобок не «работает». Здесь: сделайте A 30 градусов и B 45 градусов.
Грех 30 равен 0,5. Грех 45 равен 0,7071. Добавление двух равно 1,2071.
Вы знаете, что никакой синус (или косинус) не может быть больше 1. Почему? отношение имеет гипотенузу в качестве знаменателя. Максимум, что может быть в числителе, равно знаменателю. Синус или косинус никогда не могут быть больше 1, поэтому значение 1,2071 должно быть неправильным.
Требуемый синус, косинус или тангенс целого угла (A + B)
Нахождение греха(А+В)
Самый простой способ найти sin(A + B) использует показанную здесь геометрическую конструкцию. Большой угол (А + В) состоит из двух меньших, А и В. Построение (1) показывает, что противолежащая сторона состоит из двух частей. Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).
Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Заштрихованный угол А, потому что линия на его верхней стороне параллельна базовой линии. Подобные прямоугольные треугольники с углом A показывают, что верхний угол, отмеченный A, также равен исходному A. Верхняя часть противоположного (6) на самом длинном из этого заштрихованного треугольника равна cos A. Противоположный угол на главной гипотенузе (7) есть sin B. Поскольку сторона, отмеченная как «противоположная» (7), находится как в числителе, так и в знаменателе, когда cos A и sin B умножаются вместе, cos A sin B является верхней частью исходной противоположности — для (A + B) — деленная на главную гипотенузу (8).
Теперь соберите все вместе (9). Sin(A + B) — это две противоположные части, разделенные гипотенузой (9). Поместив это в форму триггера:
sin(A + B) = sin A cos B + cos A sin B
Нахождение cos(A + B)
Очень похожая конструкция находит формулу косинуса угла, составленного из двух сложенных углов.
Используя ту же конструкцию (1), обратите внимание, что соседняя сторона представляет собой полную базовую линию (для cos A), часть которой вычитается справа. Каждая часть должна использовать один и тот же знаменатель, гипотенузу треугольника (A + B).
Полная базовая линия, разделенная разделительной линией между углами A и E, равна cos A (2). Эта разделительная линия, разделенная гипотенузой треугольника (A + B), равна cos B (3). Таким образом, полное основание, деленное на гипотенузу, равно произведению cos A и cos B (4).
Теперь о той части, которую нужно вычесть. Заштрихованная часть (5) представляет собой грех A, который, умноженный на заштрихованную часть (6), представляет собой грех E, который дает другой необходимый вам кусок (7). Вычитание дает cos(A + B) (8), так что нужная нам формула:
Вычитание дает cos(A + B) (8), так что нужная нам формула:
cos(A + B) = cos A cos B — sin A sin B
Поиск загара (A + B)
Полный геометрический вывод формулы для tan(A + B) сложен. Самый простой способ — вывести его из двух формул, которые вы уже сделали. Тангенс любого угла равен синусу, деленному на косинус. Используя этот факт, tan(A + B) = sin(A + B)/cos(A + B). Таким образом, что делает это, но вы можете расширить это до:
$\tan(A + B) = \frac{\sin\ A \cos\ B + \cos\ A\ \sin\ B}{\cos\ A \cos\ B — \sin\ A\ \sin\ Б}$
Разделить верх и низ на cos A и cos B, что превращает все члены в касательные, что дает:
$\tan(A + B) = \frac{\tan\ A + \tan\ B}{1 — \tan\ A\ \tan\ B}$
Передаточные числа для 75 градусов
Покажите отношения для синуса, косинуса и тангенса, подставив их в формулу суммы, а затем приведя результат к его простейшей форме, прежде чем оценивать сурды. После выполнения основных замен в каждом случае черновая работа заключается в штриховке — показать, как результат приводится к простейшему для оценки виду.
Если вы используете свой карманный калькулятор для вычислений, вероятно, не будет никакой разницы, упростите ли вы сначала выражения или просто проработаете его! Все зависит от калькулятора: что-то имеет значение, что-то нет!
Отношения углов больше 90 градусов
До сих пор рассматривались соотношения острых углов (от 0 до 90 градусов). Другие треугольники с тупыми углами (более 90 градусов) в более поздних задачах могут превысить 180 градусов. Для упрощения классификации углов по величине их делят на квадранты.
Квадрант — это четверть круга. Поскольку круг обычно делится на 360 градусов, квадранты называются сегментами по 90 градусов. 0-90 градусов — это 1-й квадрант, 90-180 — 2-й, 180-270 — 3-й и 270-360 — 4-й.
Рисование линий для представления границ квадрантов, с 0 или 360 по горизонтали вправо, 90 по вертикали вверх, 180 по горизонтали влево и 270 по вертикали вниз. Теперь используйте этот метод для построения графиков.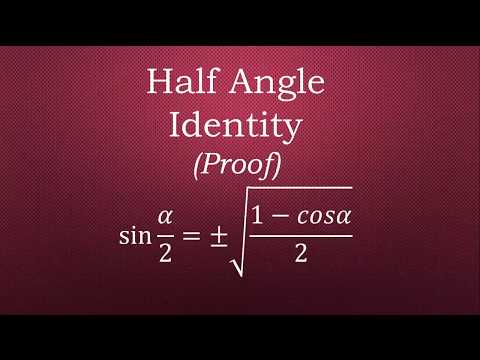
Постепенно увеличивающиеся углы определяются вращающимся вектором, начиная с нуля и вращаясь против часовой стрелки. Горизонтальные элементы равны x: положительный справа, отрицательный слева. Вертикальные элементы равны y. положительный вверх, отрицательный вниз. Вращающийся вектор равен r. Итак, синус угла равен y/r, косинус x/r и тангенс y/x. Вектор r всегда положителен. Итак, знак отношений может быть цифрой для различных квадрантов.
Здесь знаки трех отношений сведены в таблицу для четырех квадрантов. Также как эквивалентный угол в первом квадранте «переключается», когда вектор переходит из одного квадранта в другой. В первом квадранте стороны были определены в соотношениях для синуса, косинуса и тангенса. Когда вы двигаетесь к большим углам в оставшихся квадрантах, противоположная сторона всегда является вертикалью (y). То, что называлось соседним, всегда является горизонталью (х). Гипотенуза всегда является вращающимся вектором (r). Вы начнете видеть закономерность в том, как меняются эти тригонометрические отношения углов.
Соотношения в четырех квадрантах
Коэффициенты разности углов
Теперь у вас есть два способа получить формулы для разностных углов. Во-первых, используйте геометрическую конструкцию, такую как та, которая использовалась для суммы углов, перевернув ее так, чтобы (A — B) был угол B, вычтенный из угла A.
В рассуждениях, аналогичных тем, которые использовались для суммы углов, здесь несколько сокращенно представлены формулы синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
а также
cos(A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разности
Второй способ нахождения формулы разности углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных квадрантов отрицательные углы из 1-го квадранта окажутся в 4-м квадранте. Выполнение этой замены приводит к тем же результатам, которые были получены геометрически в предыдущем разделе.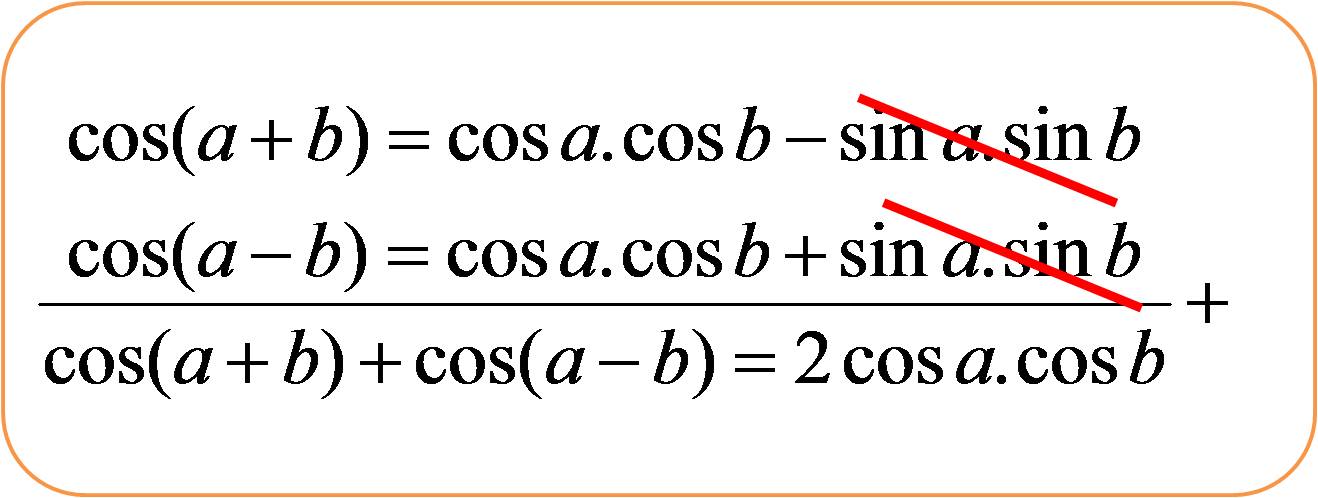
Нахождение формулы тангенса следует тому же методу, либо путем подстановки в формулы синуса и косинуса, либо, более непосредственно, путем преобразования tan(-B) = — tan B. В любом случае вы получите:
$\tan(A — B) = \frac{\tan\ A — \tan\ B}{1 + \tan\ A\ \tan\ B}$
Соотношения по четырем квадрантам
Вы можете вывести еще несколько отношений с помощью формул суммы и разности. Вы уже делали соотношения для 75 градусов. Теперь сделайте это для 15 градусов. Эти формулы дают соотношения для углов с интервалом в 15 градусов в четырех квадрантах. Разложив их на все 360 градусов, вы можете увидеть, как меняются эти три соотношения по мере того, как вектор проходит через четыре квадранта.
И синус, и косинус «колеблются» вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов одна относительно другой. Этот факт становится важным позже.
Тангенс начинается как синусоида, но быстро достигает бесконечности при 90 градусах. Зашкаливая в положительную сторону, она «заходит» с отрицательной стороны на другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы это видите). При 270 градусах он повторяет то, что делал при 9.0 градусов.
Зашкаливая в положительную сторону, она «заходит» с отрицательной стороны на другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы это видите). При 270 градусах он повторяет то, что делал при 9.0 градусов.
Пифагор в тригонометрии
Формулу часто можно упростить, как это было обнаружено, путем вывода формул тангенса из формул синуса и косинуса и замены слагаемых, использующих одно отношение, на слагаемые, использующие другое отношение. При этом очень удобна теорема Пифагора, выраженная в тригонометрических соотношениях.
Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1 единицу. Тогда одна из других сторон будет иметь длину sin A, а другая — cos A. Отсюда теорема Пифагора показывает, что: cos 2 A + sin 2 A = 1. Это утверждение верно всегда для любого значения A.
Немного о том, как это написано.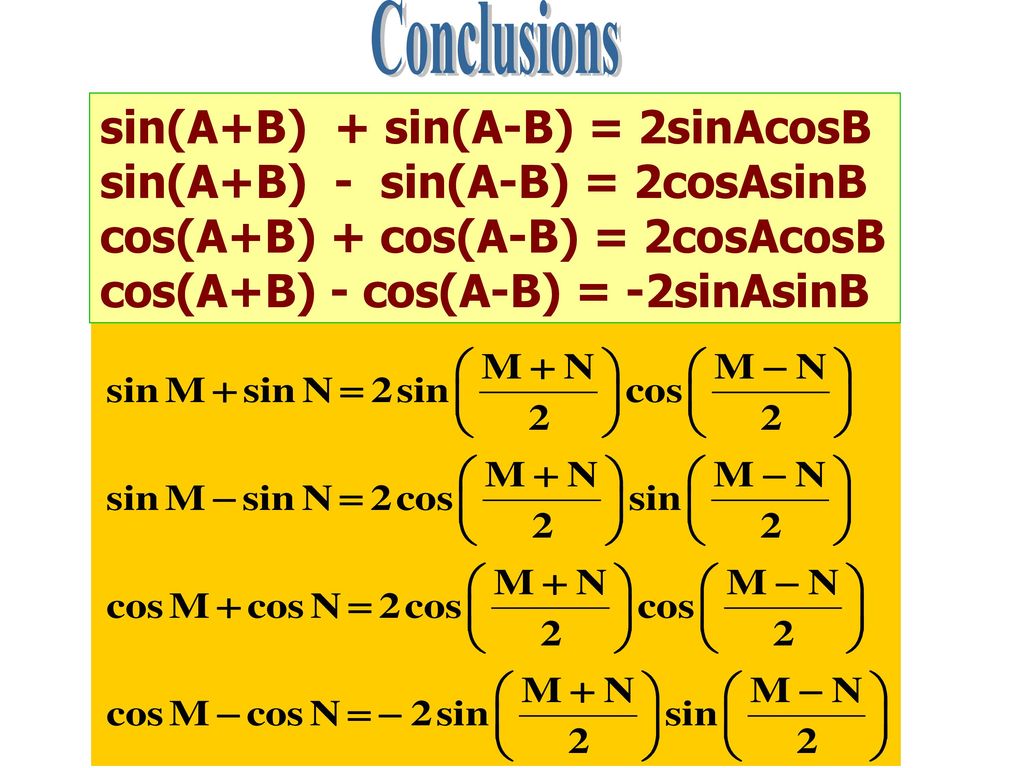 Cos 2 A означает (cos A) 2 . Если бы вы написали это потому, что A 2 , уравнение означало бы что-то другое. A — это число в некотором угловом представлении, представляющее угол. 2 будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, поэтому этот термин не подходит для использования. Имеется в виду квадрат синуса или косинуса угла, а не сам угол.
Cos 2 A означает (cos A) 2 . Если бы вы написали это потому, что A 2 , уравнение означало бы что-то другое. A — это число в некотором угловом представлении, представляющее угол. 2 будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, поэтому этот термин не подходит для использования. Имеется в виду квадрат синуса или косинуса угла, а не сам угол.
Формулу Пифагора можно транспонировать. Например, две другие формы:
cos 2 A = 1 — sin 2 A и sin 2 = 1 — cos 2 A.
Несколько углов
Формулы суммы, наряду с теоремой Пифагора, используются для углов, которые являются 2, 3 или более точными кратными любому исходному углу. Здесь приведите формулы для 2А и 3А. Тот же метод используется далее в частях 3 и 4 этой книги.
Формула суммы работает независимо от того, одинаковы оба угла или различны: sin(A + B) или sin(A + A). Однако sin(A + A) на самом деле является sin 2A. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.
Однако sin(A + A) на самом деле является sin 2A. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.
Сходным образом,
cos 2A = cos A cos A — sin A sin A,
, что также можно записать:cos 2A = cos 2 A — sin 2 A.
Используя теорему Пифагора, измените это на: 92 А}$Теперь тройной угол (3А) используется только для того, чтобы показать, как получаются дополнительные кратные.
По сути, это так же просто, как написать 3A = 2A + A и повторно применить формулы суммы. Но затем, чтобы получить результирующую формулу в работоспособном виде, вам нужно заменить часть 2А, чтобы получить все в терминах отношений для простого угла А.
Проработайте три деривации, показанные здесь. Вы можете видеть, что для 4 А и более (в частях 3 и 4 этой книги) все будет сложнее.
НЕСКОЛЬКО УГЛОВ Получено из формул суммы
НЕСКОЛЬКО УГЛОВ Коэффициенты для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур.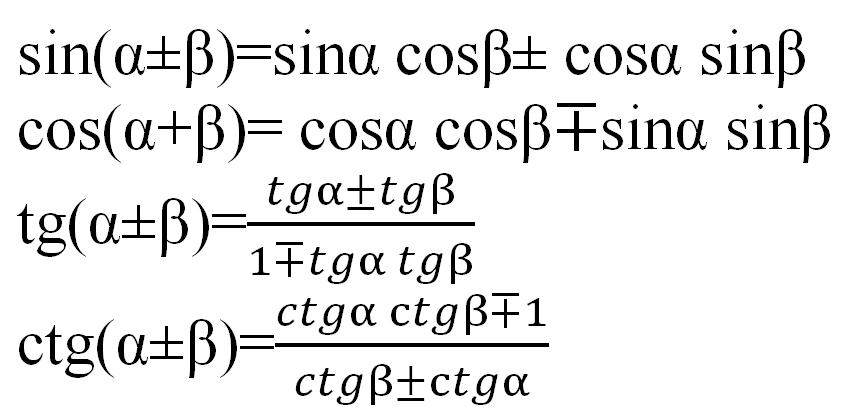 Равнобедренный треугольник имеет несколько иное применение. Но факт, на котором основаны эти употребления, заключается в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр из третьего угла (не из равных) на третью сторону (не из равных) делит эту третью сторону пополам. То есть делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
Равнобедренный треугольник имеет несколько иное применение. Но факт, на котором основаны эти употребления, заключается в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр из третьего угла (не из равных) на третью сторону (не из равных) делит эту третью сторону пополам. То есть делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
При равнобедренных треугольниках любой треугольник, кроме прямоугольного, можно разделить на три смежных равнобедренных треугольника, разделив каждую сторону на две равные части и возведя перпендикуляры из точек бисекции. Там, где встречаются любые два из этих биссектриссирующих перпендикуляров, если провести линии к углам исходного треугольника, эти три линии должны быть равны, потому что две из них образуют стороны равнобедренного треугольника. Значит, перпендикуляр с третьей стороны исходного треугольника тоже должен пересечься в той же точке.
Это утверждение верно, как мы покажем здесь, независимо от того, является ли исходный треугольник остроугольным или тупоугольным. Отличие тупоугольного треугольника в том, что точка встречи находится вне исходного треугольника, а не внутри.
Что делает прямоугольный треугольник? Перпендикуляры из середины гипотенузы к двум другим сторонам разделят эти две стороны пополам — вы получите два из трех! Место встречи находится на гипотенузе.
Углы в окружности 906:30
Основное свойство круга состоит в том, что его центр находится на одинаковом расстоянии от каждой точки окружности. Это равное расстояние является радиусом окружности.
Если вы начертите любой треугольник внутри круга, перпендикуляры из середины его сторон встретятся в центре круга, а радиусы из углов треугольника разделят его на три равнобедренных треугольника.
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике, A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A + B, один угол B + C и один угол A + C. Три угла в сумме составляют 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
Три угла в сумме составляют 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Из-за факта, выведенного в предыдущем абзаце, 180 — 2A должно быть таким же, как, например, 2B + 2C.
Рассмотрим углы, противоположные той части круга, против которой прилегает верхняя левая сторона треугольника. Угол в центре равен 2B + 2C, как только что выведено. Угол при окружности равен B + C. «Вы обнаружите, что для любого сегмента круга угол в центре всегда вдвое больше угла при окружности.
Приведенное выше доказательство приводит к интересному факту об углах в окружностях. Вместо того, чтобы отождествлять углы со стороной треугольника, используйте дугу (часть окружности) окружности. Важен угол, который соответствует дуге в центре. Часть окружности окружности, определяемая углом при центре, называется хордой окружности.
Угол в центре в два раза больше угла на окружности
Любой угол, нарисованный относительно окружности с использованием этой хорды в качестве окончания линий, ограничивающих угол, должен составлять только половину угла в центре. Таким образом, все углы в окружности, опирающиеся на одну и ту же хорду, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.
Таким образом, все углы в окружности, опирающиеся на одну и ту же хорду, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.
Частным случаем является полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол при окружности полукруга равен ровно 90 градусов (прямой угол). Любой треугольник в полуокружности является прямоугольным треугольником.
Определения
Выше мы часто использовали углы, которые в сумме составляют либо прямой угол (90 градусов), либо два прямых угла (180 градусов). Когда два угла в сумме составляют 180 градусов (два прямых угла), они называются дополнительными . Когда два угла в сумме составляют 90 градусов (один прямой угол), они называются дополнительными .
Вопросы и проблемы 906:30
1. Синус угла А равен 0,8, а синус угла В равен 0,6. Из различных соотношений, полученных к настоящему времени, найдите следующее: тангенс А, тангенс В, грех(А + В), соз (А + В), грех (А — В), соз (А — В), тангенс (А + B) и tan(A — B), без использования таблиц или триггерных кнопок калькулятора.
2. На экваторе радиус Земли составляет 4000 миль. Углы вокруг экватора измеряются в меридианах долготы с линией с севера на юг, проходящей через Гринвич, Англия, в качестве нулевой точки отсчета. Для наблюдения за Луной используются два места: одно — гора Кения на экваторе в 37,5° к востоку от Гринвича; другой — Суматра, на экваторе, в 100,5 восточной долготы. Как далеко друг от друга находятся эти два места, измеряемые воображаемой прямой линией, проходящей через Землю?
3. Если бы из точек наблюдения, рассматриваемых в вопросе 2, велись горизонтальные наблюдения (на восток от первой и строго на запад от второй), под каким углом пересеклись бы линии визирования?
4. В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении высота линии прямой видимости с центром на спутнике составляет 58 градусов над горизонталью в восточном направлении. На Суматре высота составляет 58 градусов над горизонтом, в западном направлении. Как далеко находится спутник? Используйте расстояние между точками, рассчитанное в вопросе 2.
5. Косинус определенного угла ровно в два раза больше синуса того же угла. Чему равен тангенс этого угла? Для этого вопроса вам не нужны ни таблицы, ни калькулятор.
6. Синус определенного угла ровно 0,28. Найдите косинус и тангенс без таблиц или функций триггера на вашем калькуляторе.
7. Синус некоторого угла равен 0,6. Найдите синус удвоенного и умноженного на этот угол втрое.
8. Найдите синус и косинус угла ровно в два раза больше, чем в вопросе 7.
9. Используя 15 градусов в качестве единицы угла и формулы для отношений 2А и ?>А, найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов в качестве единицы измерения угла, найдите значения синусов 60 и 90 градусов.
11. Используя 45 градусов в качестве единичного угла, найдите значения тангенсов 90 и 135 градусов.
12. Используя 60 градусов в качестве единицы угла, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов в качестве единицы угла, найдите значения косинусов 180 и 270 градусов.
14. Используя формулы тангенса для нескольких углов и таблицы, найдите тангенсы для трех углов, умноженных на 29, 31, 59 и 61 градус. Учитывайте изменения знака между тремя умножениями на 29 и 31 градус и между 59 и 61 градусом.
15. Синус угла равен 0,96. Найдите синус и косинус удвоенного угла.
16. Задача приводит к алгебраическому выражению вида 8cos 2 A + cos A = 3. Найдите cos A и укажите, в каком квадранте находится угол, представляющий каждое решение. Дайте приблизительные значения из таблиц или вашего калькулятора.
Тригонометрия
Тригонометрические тождества (формулы)
Что такое cosA * cosB?
cosA + cosB = 2 cos . ( А + В . 2 .
Посмотреть полный ответ на cuemath.com
Что такое формула cosA cosB?
Cos a Cos b — это тригонометрическая формула, используемая в тригонометрии. Формула Cos a cos b определяется выражением cos a cos b = (1/2) [cos (a + b) + cos (a — b)]. Мы используем формулу cos a cos b, чтобы найти значение произведения косинуса двух разных углов.
Мы используем формулу cos a cos b, чтобы найти значение произведения косинуса двух разных углов.
Посмотреть полный ответ на cuemath.com
Чему равно cosA cosB?
Формула Cos A — Cos B может применяться для представления разности косинусов углов A и B в форме произведения синуса (A + B) и синуса (A — B), используя формулу Cos A — Cos B. = 2 sin ½ (A + B) sin ½ (B — A).
Посмотреть полный ответ на cuemath.com
Что такое cosA плюс cosB?
Сумма Cos A + Cos B в формуле произведения в тригонометрии для углов A и B задается как, Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B) Здесь A и B — углы, а (A + B) и (A — B) — их сложные углы.
Посмотреть полный ответ на cuemath.com
Что означает cosB в математике?
Следовательно, cos B равно a/c. Другими словами, косинус угла прямоугольного треугольника равен прилежащему катету, деленному на гипотенузу: cos = adj hyp.
Просмотреть полный ответ на webspace.ship.edu
Как выучить тригонометрические формулы в тригонометрии || AB И CD ТЕХНИКА ЗАПОМИНАНИЯ ФОРМУЛ
Что такое sinA * cosA?
SinA CosA является произведением тригонометрических функций синуса и косинуса. Мы знаем тригонометрическую идентичность sin2A, которая определяется выражением sin2A = 2 sinA cosA. Итак, мы можем использовать эту формулу, чтобы вывести формулу sinA cosA. Эту формулу можно записать как sinA cosA = sin2A/2.
Посмотреть полный ответ на cuemath.com
Что такое Sinacosb?
sinacosb = 1 2 [sin(a + b) + sin(a − b)], cosacosb = 1 2 [cos(a + b) + cos(a − b)], sinasinb = 1 2 [cos(a − b ) − cos(a + b)]. Эти тождества полезны при интеграции и вычислении преобразований Лапласа.
Эти тождества полезны при интеграции и вычислении преобразований Лапласа.
Посмотреть полный ответ на math.sjsu.edu
Является ли Cos ab )= cos ba?
Ну, так как косинус — четная функция, мы имеем cos(A−B)=cos(B−A), так что формула та же самая.
Посмотреть полный ответ на math.stackexchange.com
Какова формула 2SinASinB?
Формула для 2SinASinB: 2SinASinB = cos(A — B) — cos(A + B). Мы можем вывести формулу 2SinASinB, используя формулы суммы углов и разности углов функции косинуса. Он используется для упрощения тригонометрических выражений и вычисления интегралов и производных тригонометрических функций.
Посмотреть полный ответ на cuemath.com
Что такое cosA cosA?
COSA — это аббревиатура, которая может означать: «Круги поддержки и подотчетности» — группы добровольцев под профессиональным надзором, которые поддерживают сексуальных преступников по мере их реинтеграции в общество после освобождения из-под стражи.
Посмотреть полный ответ на en.wikipedia.org
Что такое sinA cosB cosA sinB?
= cosA cosB − sinA sinB cos(A − B) = cosA cosB + sinA sinB sin2 A + cos2 A = 1, sin 2A = 2 sinA cosA cos 2A = 2 cos2 A − 1=1 − 2 sin2 A 2 sinA cosB = sin(A + B) + sin(A − B) 2 cosA sinB = sin(A + B) − sin(A − B)
Посмотреть полный ответ на macs.hw.ac.uk
Какова ценность Cos Pi?
Значение cos pi равно -1. Cos pi также можно выразить с помощью эквивалента заданного угла (пи) в градусах (180°). Поскольку функция косинуса является периодической функцией, мы можем представить cos pi как cos pi = cos (pi + n × 2pi), n ∈ Z.
Посмотреть полный ответ на cuemath.com
Какова формула 2 cosA cosB?
Формула 2cosacosb: 2 cos A cos B = cos (A + B) + cos (A – B). Эта формула преобразует произведение двух функций cos в сумму двух других функций cos. Например: 2 cos (2x) cos (2y) = cos (2x + 2y) + cos (2x — 2y)
Посмотреть полный ответ на cuemath.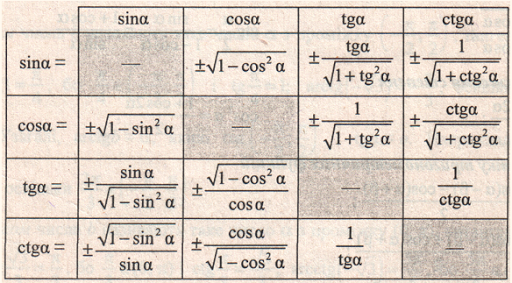 com
com
Какова формула cosA?
Формулы косинуса с использованием закона косинусов
Закон косинусов используется для нахождения недостающих сторон/углов в непрямоугольном треугольнике. Рассмотрим треугольник ABC, в котором AB = c, BC = a и CA = b. Формулы косинуса с использованием закона косинусов: cos A = (b 2 + с 2 — а 2 ) / (2bc)
Посмотреть полный ответ на cuemath.com
Какова формула преобразования?
Трансформация расширения
Вертикальное растяжение определяется уравнением y = a.f(x). Если a > 1, функция растягивается относительно оси y. Если a < 1, функция сжимается по оси y. Горизонтальное растяжение определяется выражением y = f.
Посмотреть полный ответ на cuemath.com
Что такое 2sina CosA?
2 sin a cos a — это тригонометрическая формула, равная синусу угла 2a, т. е. она задается формулой 2 sin a cos a = sin 2a. Это одно из важных тригонометрических тождеств, которое используется для решения различных тригонометрических и интегральных задач.
Это одно из важных тригонометрических тождеств, которое используется для решения различных тригонометрических и интегральных задач.
Посмотреть полный ответ на cuemath.com
Что такое Sina CosA и tanA?
Ответ: SinA равен стороне, противоположной углу А (сторона а), деленной на гипотенузу треугольника (сторона с). CosA равен стороне, прилежащей к углу A, деленной на гипотенузу и. tanA — это синус, деленный на косинус, и, следовательно, это сторона, противоположная углу, деленная на прилежащую сторону.
Посмотреть полный ответ на brainly.in
Что такое Sinasinb?
Формула Sina Sinb используется для определения произведения функции синуса для углов a и b по отдельности. Формула sina sinb представляет собой половину разности косинусов разности и суммы углов a и b, то есть sina sinb = (1/2)[cos(a — b) — cos(a + b)].
Посмотреть полный ответ на cuemath.com
Что такое тригонометрические тождества?
Это синус, косинус, тангенс, косеканс, секанс и котангенс. Все эти тригонометрические соотношения определяются с использованием сторон прямоугольного треугольника, таких как прилежащая сторона, противоположная сторона и сторона гипотенузы. Все фундаментальные тригонометрические тождества выводятся из шести тригонометрических соотношений.
Все эти тригонометрические соотношения определяются с использованием сторон прямоугольного треугольника, таких как прилежащая сторона, противоположная сторона и сторона гипотенузы. Все фундаментальные тригонометрические тождества выводятся из шести тригонометрических соотношений.
Посмотреть полный ответ на byjus.com
Является ли Cos (- π )= Cosπ?
π составляет 180º, и, используя тождество cos(-θ) = cos (θ), значения cos (π) и cos (-π) равны.
Посмотреть полный ответ на cuemath.com
Каково значение раскладушки пи?
Значение cot pi не определено. Кот пи радианы в градусах записывается как кроватка ((π) × 180°/π), т. е. кроватка (180°).
Посмотреть полный ответ на cuemath.com
Как найти COS 180?
Значение cos 180 градусов равно -1. Cos 180 градусов в радианах записывается как cos (180° × π/180°), т. е. cos (π) или cos (3,141592…).
…
Мы можем использовать тригонометрические тождества для представления cos 180° как
Посмотреть полный ответ на cuemath.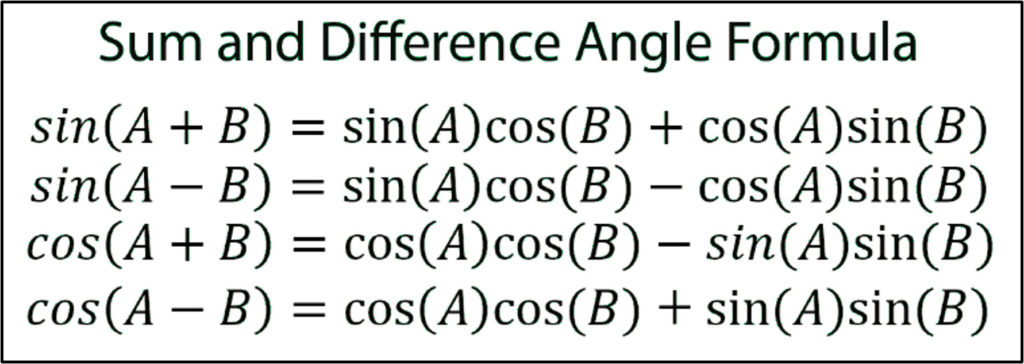 com
com
Как преобразовать COS в sin ?
909:00 Обычно для любого угла θ cos θ = sin (90° – θ). cos θ = sin (π/2 – θ).Посмотреть полный ответ на www2.clarku.edu
← Предыдущий вопрос
Когда вышла Series 6?
Следующий вопрос →
Что такое 2 контролируемые переменные?
Формула для синуса cosb?
Вопрос задан: д-р Келси Эйхманн, доктор философии
Оценка: 4,9/5 (41 голос)
2 sinA cosB = sin(A + B) + sin(A − B) Примечание: sin2 A — это обозначение, используемое для (sinA)2. Точно так же cos2 A означает (cosA)2 и так далее.
Какова формула cosA cosB sinA sinB?
= cosA cosB + sinA sinB sin2 A + cos2 A = 1, sin 2A = 2 sinA cosA cos 2A = 2 cos2 A − 1=1 − 2 sin2 A 2 sinA cosB = sin(A + B) + sin (A − B) 2 cosA sinB = sin(A + B) − sin(A − B)
Сколько будет cosA, умноженное на cosB?
cosA + cosB = 2 cos . ( A + B. 2. )
( A + B. 2. )
Что такое sinA * cosA?
sinA×cosA= 1/2 ×sin2A .
Что такое формула sin3x?
Пояснение: Согласно тригонометрическому тождеству имеем. sin 3x = 3sin x — 4sin 3 x . При перестановке 4 sin 3 x = 3sinx — sin 3x.
Как выучить тригонометрические формулы в тригонометрии || МЕТОДИКА ЗАПОМИНАНИЯ ФОРМУЛ AB И CD
Найдено 32 связанных вопроса
Каково значение sinA * cosA?
Значение sinA и cosA всегда меньше 1 .
Что такое sinA * SINB?
sina sinb = 1 . 2 (cos(a − b) − cos(a + b))
2 (cos(a − b) − cos(a + b))
Какова формула tan AB?
Tan(a — b) — одно из важных тригонометрических тождеств, также называемое формулой вычитания тангенса в тригонометрии. Tan(a — b) может быть задан как tan (a — b) = (tan a — tan b)/(1 + tan a·tan b) , где «a» и «b» — углы.
Что такое формула sin2x?
Формула Sin 2x: 2sinxcosx .
Какова формула cos2x?
Что такое формула cos 2x? Его можно выразить с помощью различных тригонометрических функций, таких как синус, косинус и тангенс. Его можно выразить так: cos 2x = cos 2 x — sin 2 x .
Какова формула cos3x?
Тригонометрическая формула для cos 3x: cos 3x = 4 cos 3 x — 3 cos x .
Что такое Cosa cosa?
Из Википедии, свободной энциклопедии. COSA — это аббревиатура, которая может означать: Круги поддержки и подотчетности — это группы волонтеров под профессиональным надзором для поддержки лиц, совершивших преступления на сексуальной почве, по мере их реинтеграции в общество после освобождения из заключения.
Чему равен tan AB?
tan(A + B) = (sin A cos B + cos A sin B) / (cos A cos B − sin A sin B) (50) tan(A + B) = (tan A + tan B) / (1 − загар A загар B) Теперь, если заменить B на −B, получится формула для tan(A − B).
Является ли грех AB СинА ГрехомБ?
Ответ проверен экспертом
Следовательно, Sin(A+B) = SinA+SinB , когда либо A равно 0°, либо B равно 0°.
Является ли CosA sinA равным Cot A?
Ответ: ДА . Согласно уравнениям тригонометрии, отношение синуса угла к косинусу того же угла равно тангенсу угла. Кроме того, котангенс угла обратно пропорционален тангенсу того же угла.
Почему CosA и sinA меньше 1?
В общем, значение sinA, а также CosA всегда меньше 1, потому что оно восходит к определению (одному из многих), что для прямоугольного треугольника синус представляет собой противоположную сторону, деленную на гипотенузу . Из-за этого сторона всегда ≤ гипотенузы, отношение должно быть ≤ 1.
Является ли sinA CosA тем же, что и tanA?
Ответ: Да , правильно.
Какова формула 2SINXCOSX?
ИСПОЛЬЗОВАНИЕ ФОРМУЛЫ 2SINXCOSX = SIN2X — YouTube.
Какова формула sin4x?
Пример:- sin 4x = sin2 (2x) = 2sin2xcos2x=4sinxcosxcos2x.
Как расширить грех АВ?
Разложение sin(a + b) задается как sin (a + b) = sin a cos b + cos a sin b.
Аналогичные вопросы
- 31 Равен ли sin cosb?
- 36Что такое sina по-английски?
- 26Были ли Синатра и Кросби друзьями?
- 26Синатраа вышла из Overwatch?
- 17Что такое sina по-английски?
- 38Когда следует принимать синарест?
- 22 Были ли Фрэнк Синатра и Элвис друзьями?
- 34Прощает ли Бог все грехи?
- 21 Гора Синай и гора Хорив — одно и то же?
- 36Кто такие синины барабаны?
Реклама
Популярные вопросы
- 15Кто проводит юзабилити-тестирование?
- 42Что из следующего лучше всего описывает оскольчатый перелом?
- 28Какой класс приема?
- 37Почему Онтарио — лучшее место для жизни?
- 41Что такое холинергический агонист?
- 38Какая работа была центральным элементом выставки 1889 г.
 парижская экспозиция?
парижская экспозиция? - 20Как соевое молоко влияет на организм?
- 43Жили долго и счастливо?
- 16Откуда взялась двусмысленность?
- 41Когда рагуза стала дубровником?
Таблицы математических формул
1. Десятичные множители
| 10 1 | дека (да) | 10 -1 | деци (д) |
| 10 2 | гекто (ч) | 10 -2 | санти (с) |
| 10 3 | килограмм (к) | 10 -3 | милли (м) |
| 10 6 | мега (М) | 10 -6 | микро (ты) |
| 10 9 | гига (G) | 10 -9 | нано (сущ. ) ) |
| 10 12 | тера (Т) | 10 -12 | пико (р) |
| 10 15 | пета (П) | 10 -15 | фемто (ф) |
| 10 18 | экза (Э) | 10 -18 | атто (а) |
2.
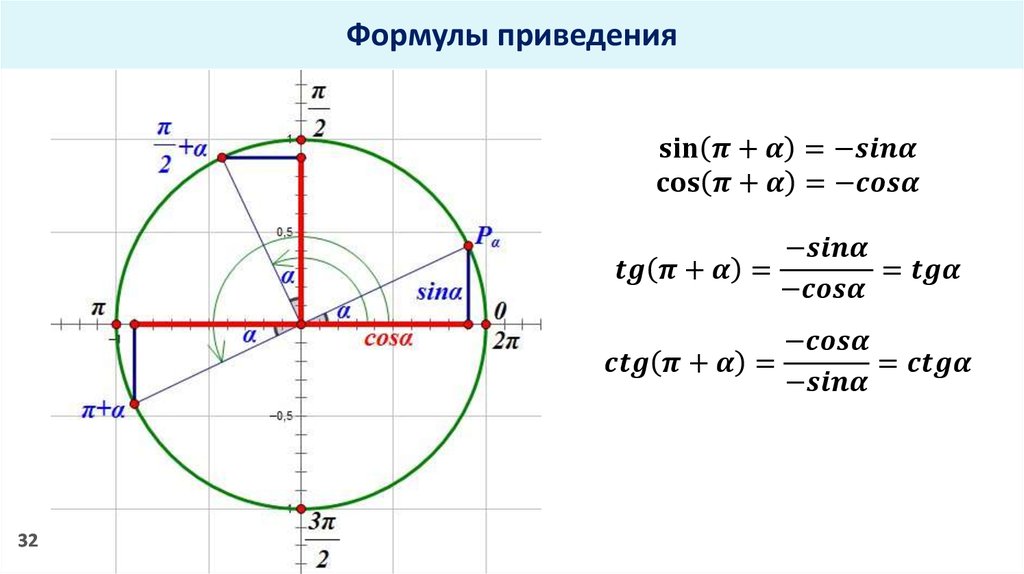 Серия
СерияСерия Маклорена.
1. e x = 1 + x + x 2 / 2! + … + х н / н! + … для всех х
2. sin x = x — x 3 / 3! + х 5 / 5! — х 7 /7! + .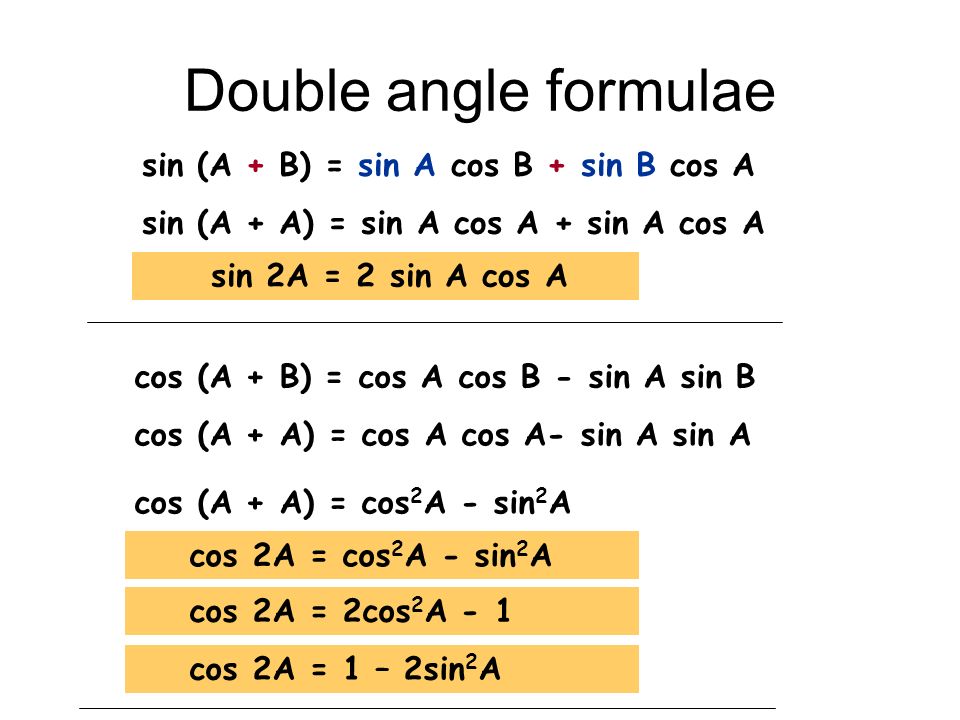 .. для всех х
.. для всех х
3. cos x = 1 — x 2 / 2! + х 4 / 4! — х 6 /6! + … для всех х
4. ln(1 + x) = x — x 2 / 2 + x 3 / 3 -… + (-1) n+1 x n / n + .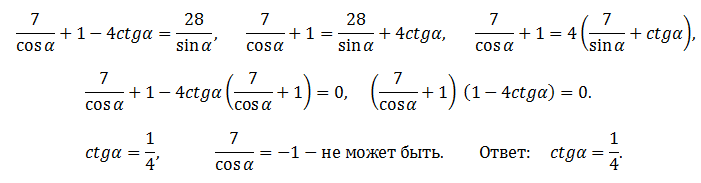 .. для (-1 < x ≤ 1)
.. для (-1 < x ≤ 1)
5. tan x = x + (1/3) x 3 + (2/15) x 5 + (17/315) x 7 + … для (-π/2 < x < п/2)
6. arcsin x = x + (1/2) x 3 / 3 + (1,3/2,4) x 5 / 5 + (1,3,5/2,4,6) x 7 / 7 + .. , для (-1 < x < 1)
7. arctan x = x — x 3 / 3 + x 5 / 5 — . .. для (-1 < x < 1)
.. для (-1 < x < 1)
8. sinx x = x + x 3 /3! + х 5 / 5! + х 7 / 7! + … для всех х
9. кош х = х + х 2 / 2! + х 4 / 4! + х 6 / 6! + … для всех х
10. arcsinh x = x — (1/2) x 3 / 3 + (1,3/2,4) x 5 / 5 — (1,3,5/2,4,6) x 7 / 7 + . . , для (-1 < x < 1)
. , для (-1 < x < 1)
11. 1 / (1 — x) = 1 + x + x 2 + x 3 + … для (-1 < x < 1)
Арифметический ряд.
12. Sn = a + (a + d) + (a + 2d)+…+(a + [n -1] d) = (n/2)[первый член + последний член] = (n/2 )[а + (а + [n — 1] d) = n (a + [n — 1] d)
Геометрический ряд.
13. Sn = a + a r + a r 2 + a r 3 +. ..+ a r n-1 = a (1 — r n )/(1 — r)
..+ a r n-1 = a (1 — r n )/(1 — r)
Целочисленный ряд.
14. 1 + 2 + 3 + … + n = (1 / 2) n (n + 1)
15. 1 2 + 2 2 + 3 2 + … + п 2 = (1 / 6) п (п + 1) (2п + 1)
15. 1 3 + 2 3 + 3 3 + … + n 3 = [ (1 / 2) n (n + 1) ] 2
1 3 + 2 3 + 3 3 + … + n 3 = [ (1 / 2) n (n + 1) ] 2
, 3. Мутации и Комбинации.
1. n факториал = n ! = п. (п — 1). (п — 2)… 2.1
2. Перестановки n объектов, взятых r в момент времени:
3.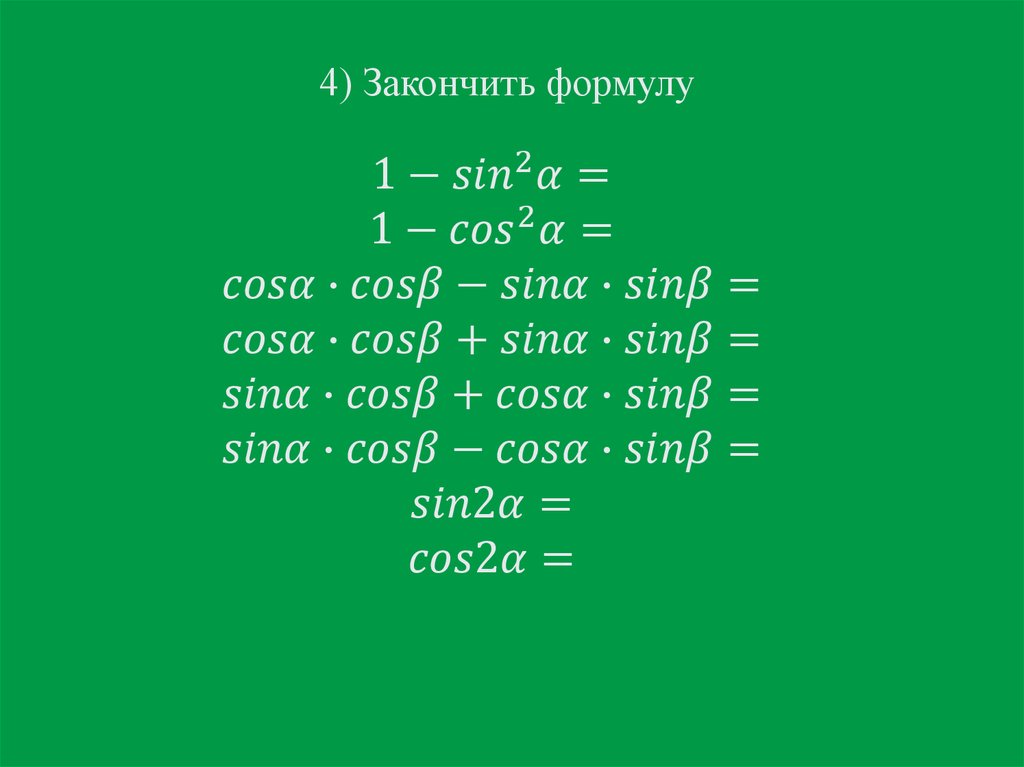 Комбинации n объектов, взятых r в момент времени:
Комбинации n объектов, взятых r в момент времени:
4. Биномиальное разложение (формула).
1. Если n — натуральное число, мы можем разложить (x + y) n следующим образом.
(x + y) n = n C 0 x n + n C 1 x n — 1 y + n C 2 x n — 2 y 2 + . .. + n C n y n
.. + n C n y n
Общий термин n C r определяется выражением
5. Тригонометрические формулы.
Формулы суммы/разности углов.
1. cos(A + B) = cos A cos B — sin A sin B
2. cos(A — B) = cos A cos B + sin A sin B
3. sin(A + B) = sin A cos B + cos A sin B
4. sin(A — B) = sin A cos B — cos A sin B
5. tan(A + B) = [ tan A + tan B ] / [ 1 — tan A tan B]
6. tan(A — B) = [ tan A — tan B ] / [ 1 + tan A tan B]
tan(A — B) = [ tan A — tan B ] / [ 1 + tan A tan B]
Сумма/разность формул тригонометрических функций.
7. sin A + sin B = 2 sin [ (A + B) / 2 ] cos [ (A — B) / 2 ]
8. sin A — sin B = 2 потому что [ (A + B) / 2 ] sin [ (A — B) / 2 ]
9. cos A + cos B = 2 cos [ (A + B) / 2 ] cos [ (A — B) / 2 ]
10. cos A — cos B = — 2 sin [ (A + B) / 2 ] sin [ (A — B) / 2 ]
Произведение формул тригонометрических функций.
11. 2 sin A cos B = sin (A + B) + sin (A — B)
12. 2 cos A sin B = sin (A + B) — sin (A — B)
13. 2 cos A cos B = cos (A + B) + cos (A — B)
14. 2 sin A sin B = — cos (A + B) + cos (A — B)
Формулы множественных углов.

15. sin 2A = 2 sin A cos A
16. cos 2A = cos 2 A — sin 2 A = 2 cos 2 A — 1 = 1 — 2 sin 2 A
17. sin 3A = 3 sin A — 4 sin 3 A
18. cos 3A = 4 cos 3 A — 3 cos A
Формулы для снижения мощности.



 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
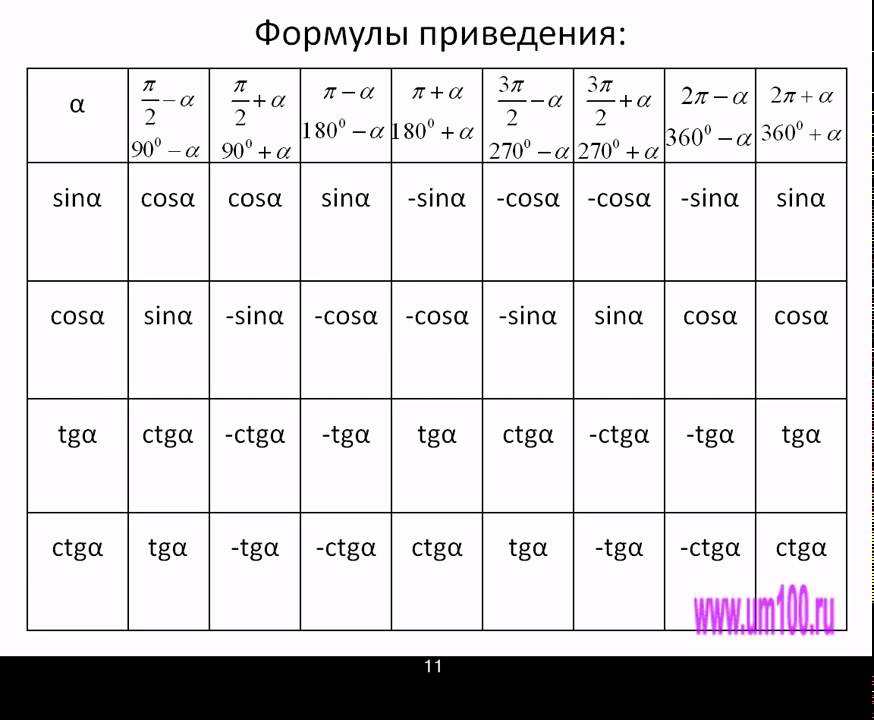

 Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан.
Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан. График функции y = tgx
График функции y = tgx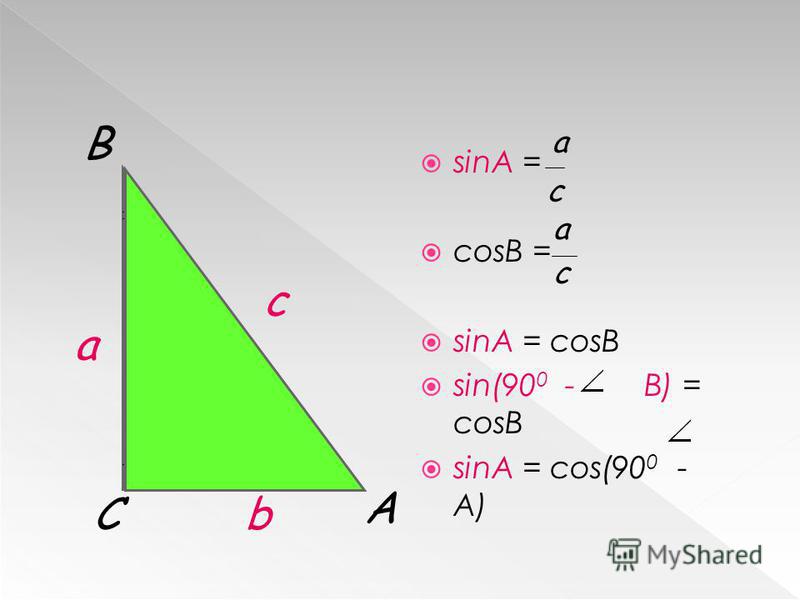
 Есть ли среди пяти основных форму та, в которой мы используем три стороны? Да, это формула Герона. Тогда:
Есть ли среди пяти основных форму та, в которой мы используем три стороны? Да, это формула Герона. Тогда: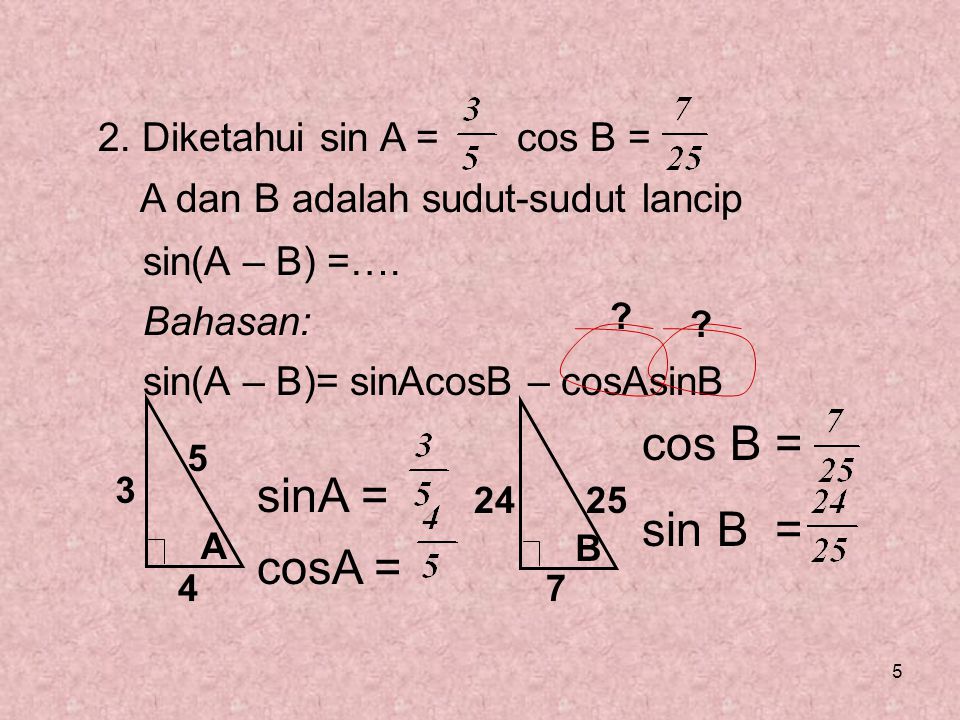 Подходящая формула: S = a∙ b ∙ sinγ. Подставим данные из условия задачи:
Подходящая формула: S = a∙ b ∙ sinγ. Подставим данные из условия задачи: su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.) Создание благоприятной атмосферы на уроке. Мотивация учащихся. (5мин)
Создание благоприятной атмосферы на уроке. Мотивация учащихся. (5мин)
 Предлагает ответить на вопрос: «А что бы вы хотели узнать об основных формулах для синуса и косинуса?»
Предлагает ответить на вопрос: «А что бы вы хотели узнать об основных формулах для синуса и косинуса?»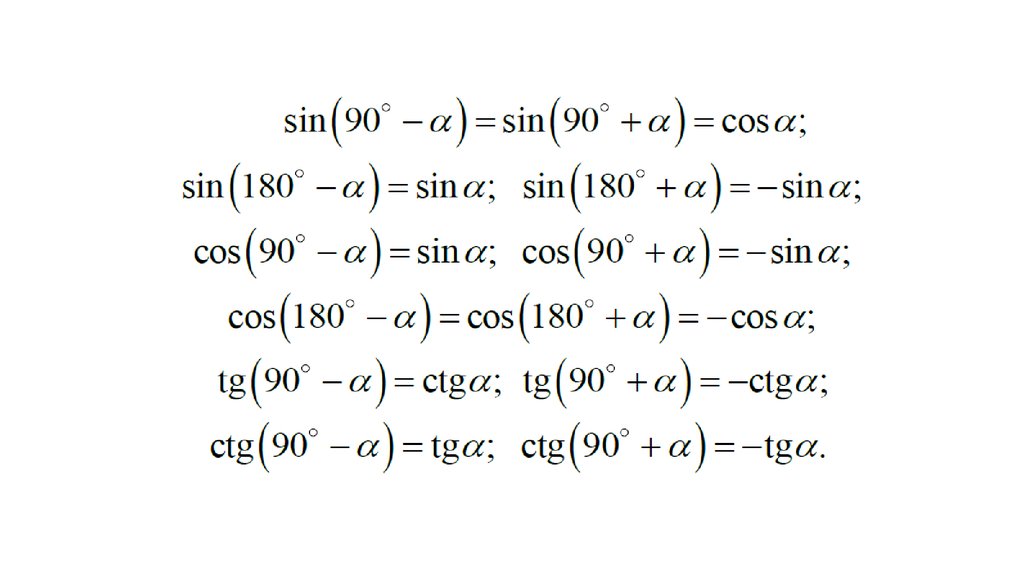
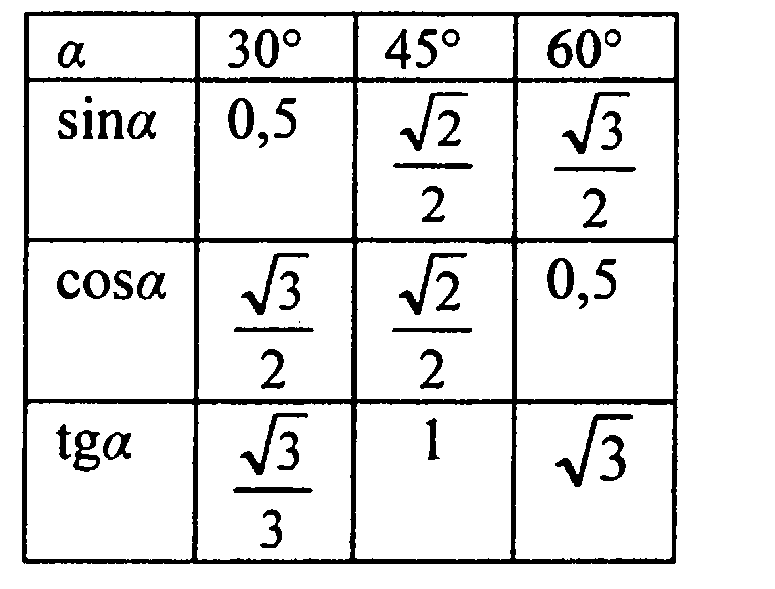
 Предлагает подвести итоги работы в таблице. «Знаю», «Хочу узнать», «Узнал». — Итак, давайте вернёмся к теме и целям нашего занятия. Назовите их. — Достигли ли поставленной цели?
Предлагает подвести итоги работы в таблице. «Знаю», «Хочу узнать», «Узнал». — Итак, давайте вернёмся к теме и целям нашего занятия. Назовите их. — Достигли ли поставленной цели?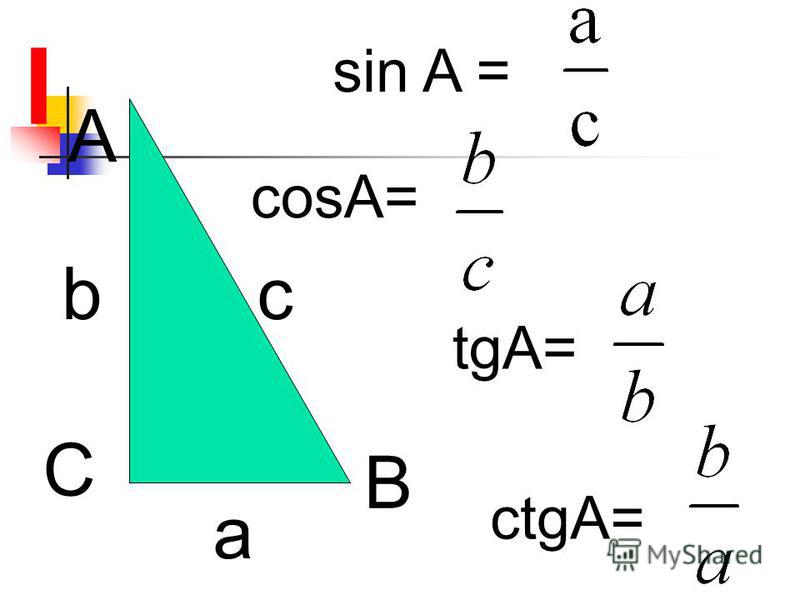 Фазовый угол. Сдвиг по фазе.
Фазовый угол. Сдвиг по фазе.
 Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
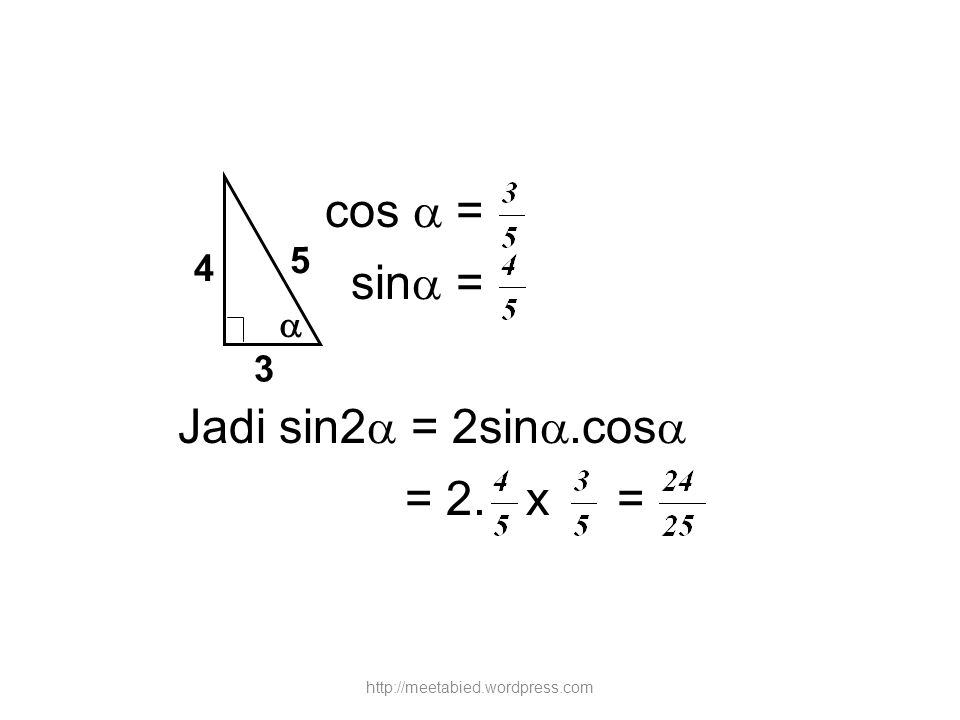

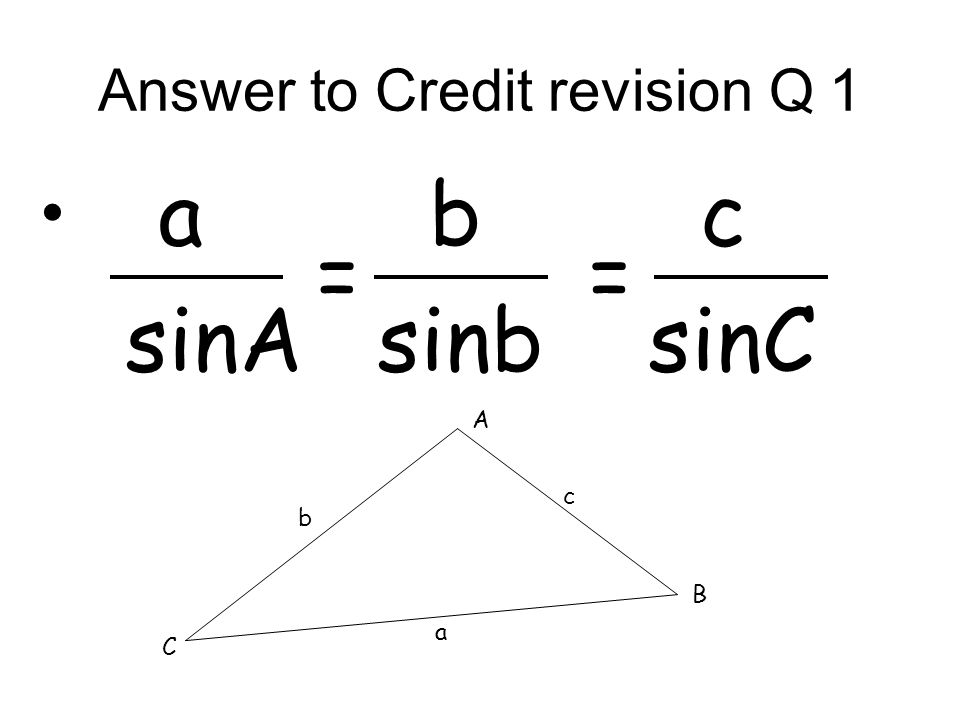 Построение синусоиды.
Построение синусоиды.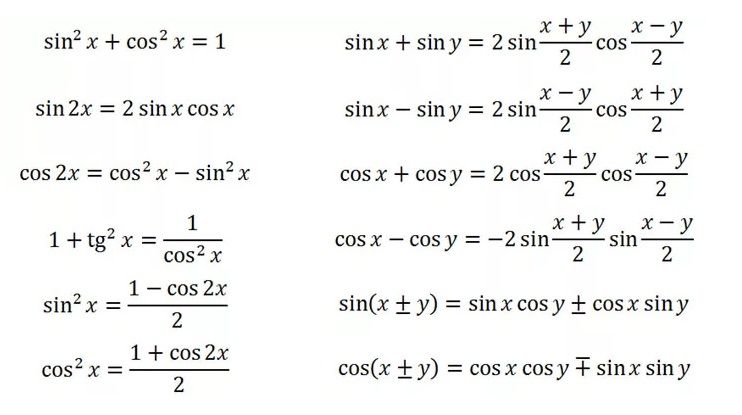


 y=sin(A-60o) (синусоида).
y=sin(A-60o) (синусоида).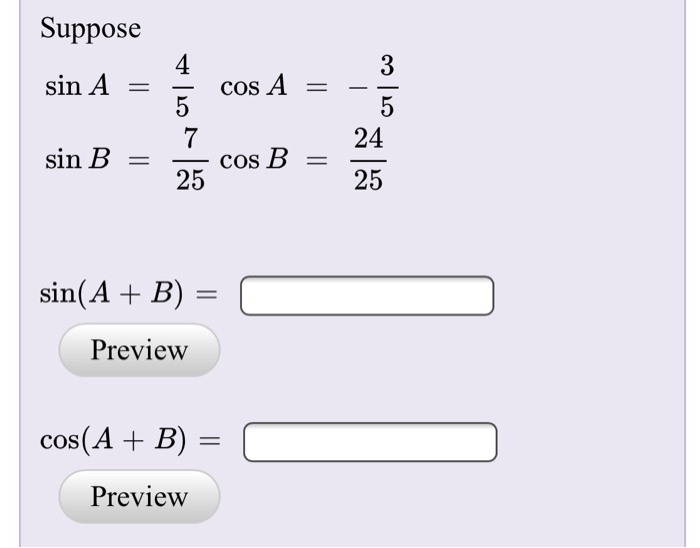
 слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.

 Колебательный механизм
Колебательный механизм
 парижская экспозиция?
парижская экспозиция?