Площадь ⚠️ параллелограмма, построенного на векторах
Содержание:
- Как определить площадь параллелограмма, построенного на векторах
- Что такое модуль векторного произведения
- Как рассчитать площадь обычного параллелограмма
- Пример решения задачи в трехмерном пространстве
- Пример решения в двухмерном пространстве
Содержание
- Как определить площадь параллелограмма, построенного на векторах
- Что такое модуль векторного произведения
- Как рассчитать площадь обычного параллелограмма
- Пример решения задачи в трехмерном пространстве
- Пример решения в двухмерном пространстве
Как определить площадь параллелограмма, построенного на векторах
Определение
Площадь параллелограмма, построенного на векторах, определяется как произведение их длин на синус угла между ними.
Если по условию задачи даны длины этих векторов, то вычисление площади параллелограмм не вызывает затруднений. Для этого необходимо воспользоваться формулой:
\( S=\left|a\right|\times\left|b\right|\times\sin\beta\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что такое модуль векторного произведения
Векторным произведением некоторых векторов m и n является третий вектор p.
\(\overline p\;=\left|\overline m\right|\times\left|\overline n\right|\\\)
Определение
Модуль векторного произведения, то есть скаляр вектора p определяется как произведение модулей векторов m и n, на синус лежащего между ними угла α. Это определение записывается математическим языком так:
\(\left|p\right|=\left|m\right|\times\left|n\right|\times\sin\alpha\\\)
Все три эти вектора образуют правую тройку.
Допустим, вектора заданы координатами:
\(\overline m=\left\{x_1;y_1;z_1\right\}\\\)
\(\overline n=\left\{x_2;y_2;z_2\right\}\\\)
В декартовой системе координат их произведение можно будет вычислить по формуле:
\(\left[m\times n\right]=\left\{y_1\times z_2-y_2\times z_1;z\times x_2-z_2\times x_1;x_2\times y_2-x_2\times y_1\right\}\\\)
Примечание
В этом виде запомнить формулу достаточно сложно. Значительно проще представить ее в другой форме:
\(\left[m\times n\right]=\begin{vmatrix}i&j&k\\x_1&y_1&z_1\\x_2&y_2&z_2\end{vmatrix}\\\\\\\)
Как рассчитать площадь обычного параллелограмма
Пример
Рассмотрим еще один пример. Дан параллелограмм с длиной сторон a – 5 см, b – 6 см и углом между ними равным 30^0\\\\\\. 0=30\times\frac12=15\\\\\\\)
0=30\times\frac12=15\\\\\\\)
Таким образом, площадь данного параллелограмма равна 15 квадратным сантиметрам.
Пример решения задачи в трехмерном пространстве
Пример
Даны два вектора, а и b, имеющие в декартовой системе следующие координаты:
\(\left\{4,\;2,\;6\right\}\\\\\\\)
\(\left\{4,\;8,\;11\right\}\\\\\\\)
Требуется найти площадь, образуемого ими параллелограмма.
Для решения требуется найти векторное произведение заданных векторов:
\(\left[a\times b\right]=\begin{vmatrix}i&j&k\\4&2&6\\4&8&11\end{vmatrix}=i\begin{vmatrix}2&6\\8&11\end{vmatrix}-j\begin{vmatrix}4&6\\4&11\end{vmatrix}+k\begin{vmatrix}4&2\\4&8\end{vmatrix}=i\left(2\times11-48\right)-j\left(44-24\right)+k\left(32-8\right)=-26i-20j+24k=\left\{-26;-20;24\right\}\\\\\\\)
Для полученного отрезка, имеющего направление, найдем модульное значение. Оно и будет площадью параллелограмма, построенного на векторах а и b. 2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)
2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)
После извлечения квадратного корня получаем, что площадь параллелограмма равна 40,64.
Пример решения в двухмерном пространстве
Пример
Вычислить площадь параллелограмма, заданного векторами a и b. Их координаты:
\(\left\{4;\;5\right\}\\\\\\\)
\(\left\{-7;\;8\right\}\\\\\\\)
Оба эти вектора лежат в одной плоскости. Поэтому третью их координату принимаем за 0. Тогда площадь данного параллелограмма будет равна:
\(S=\sqrt{32+35}=\sqrt{67}\approx8.2\\\\\\\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Даны два вектора найти площадь параллелограмма. Векторное произведение векторов. Смешанное произведение векторов
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7).
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
- Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.
 5.
5. - В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
На данном уроке мы рассмотрим ещё две операции с векторами:
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах.
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор.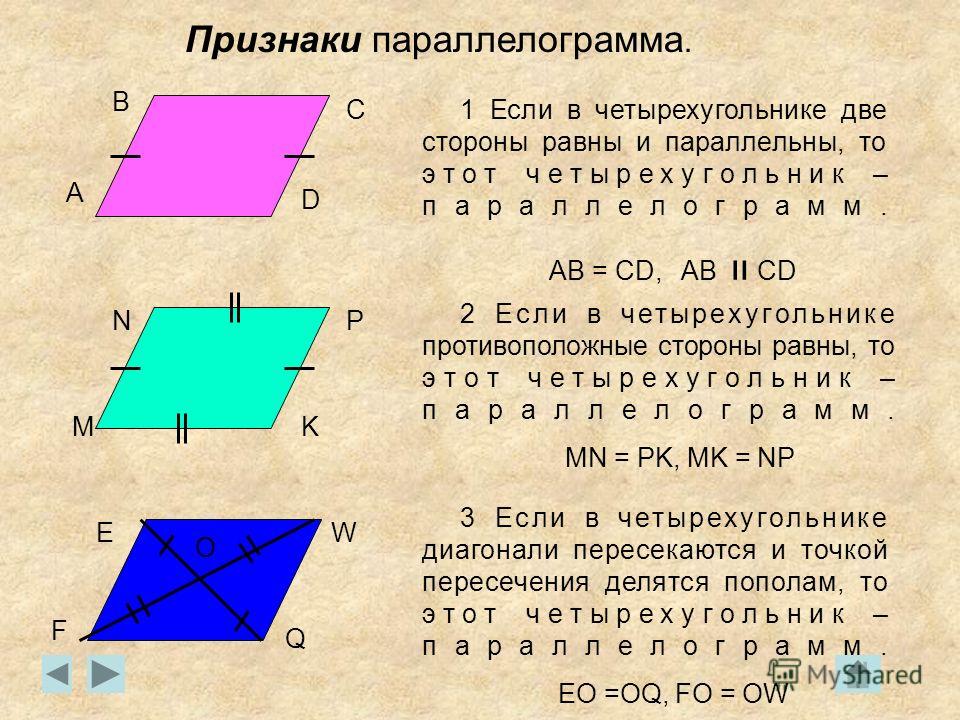 Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а».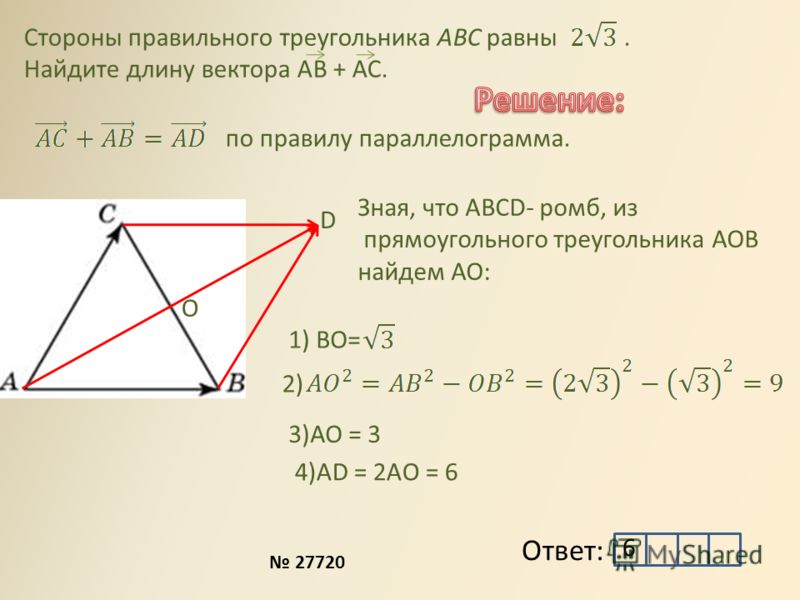 Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе .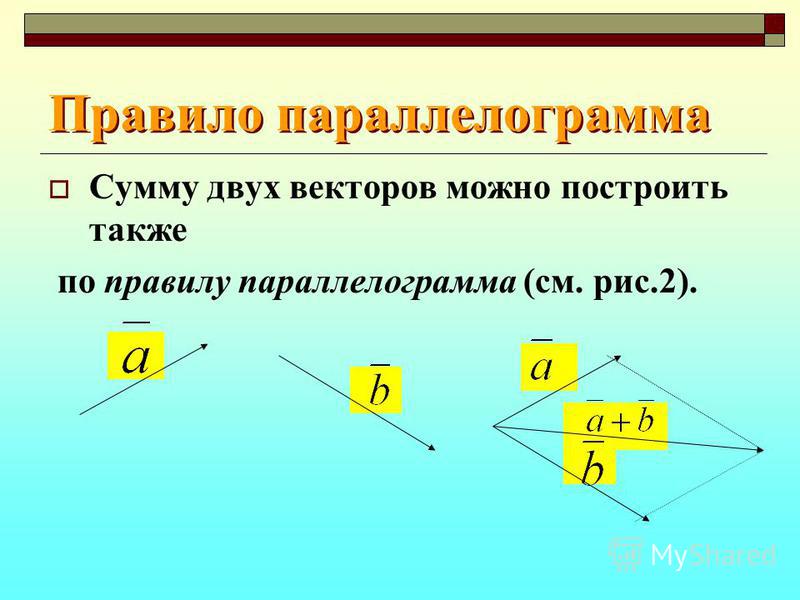 Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони.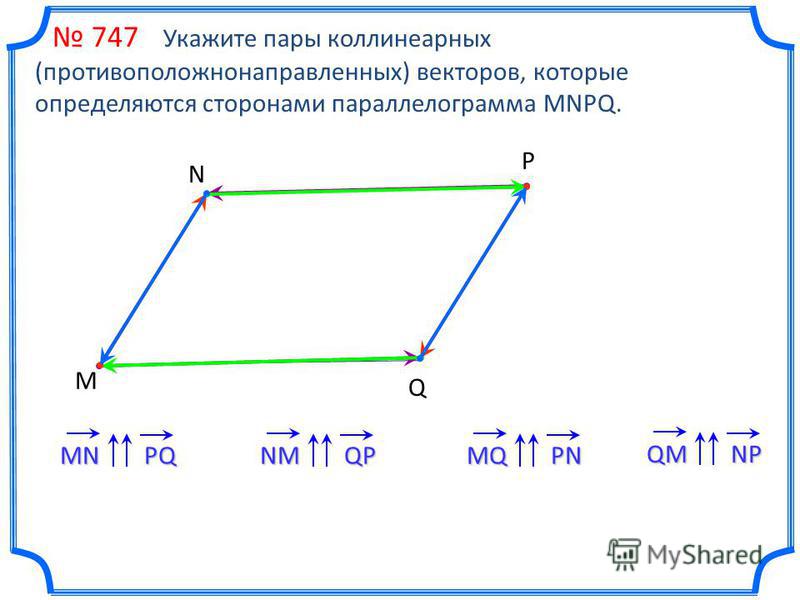 В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .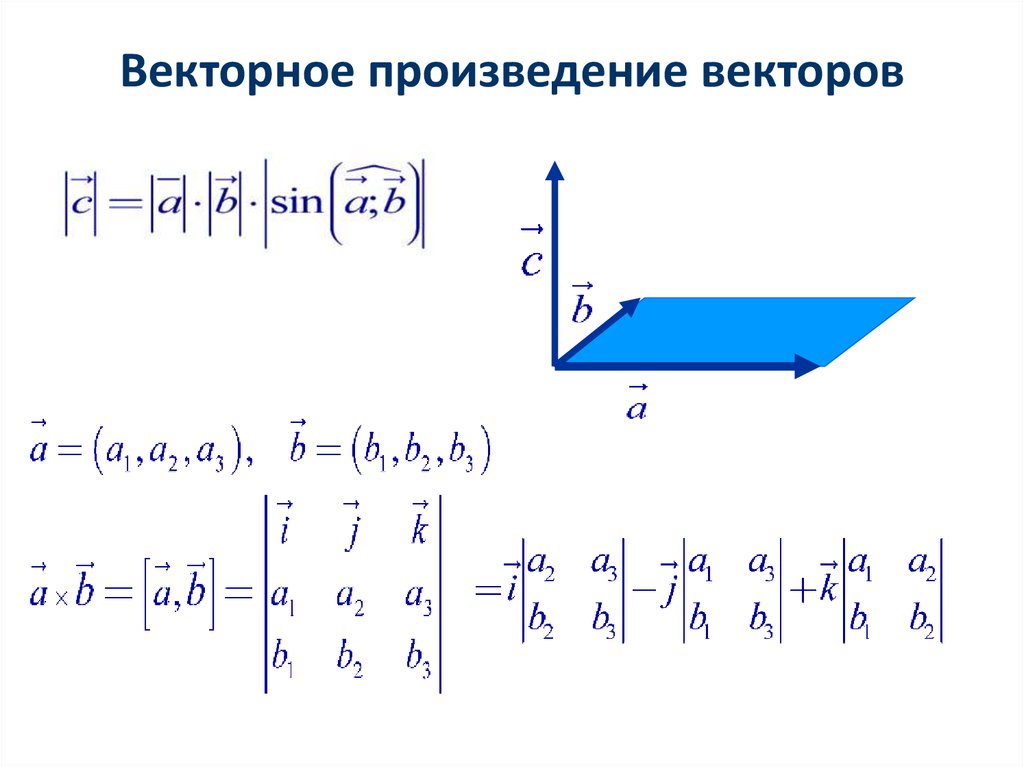
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.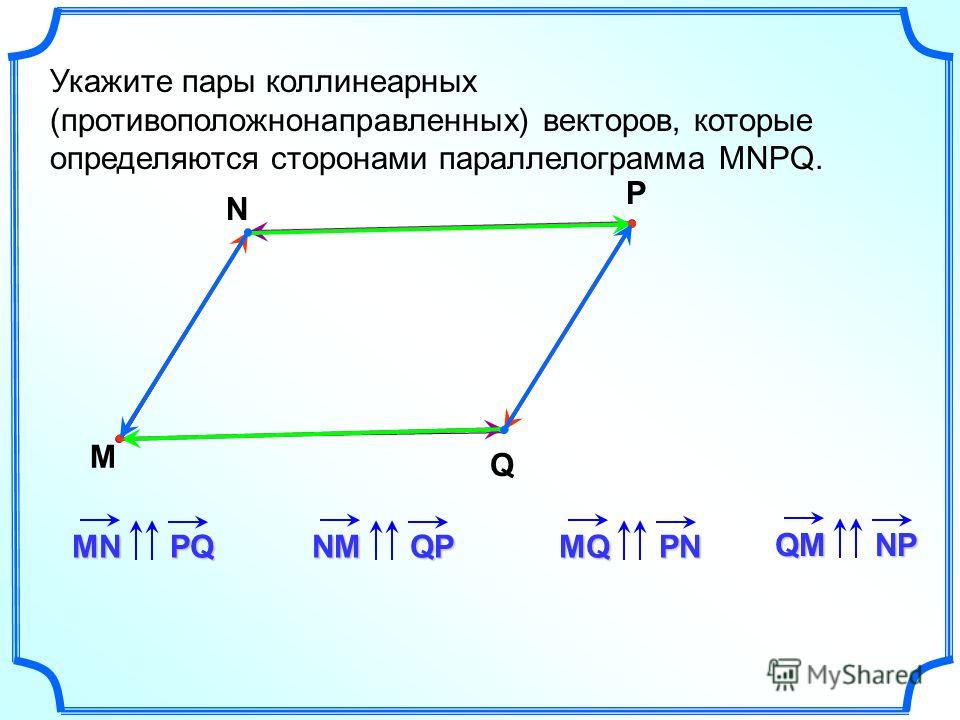
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма с вершинами в точках. Векторное произведение векторов.
 Смешанное произведение векторов
Смешанное произведение векторовПлощадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор.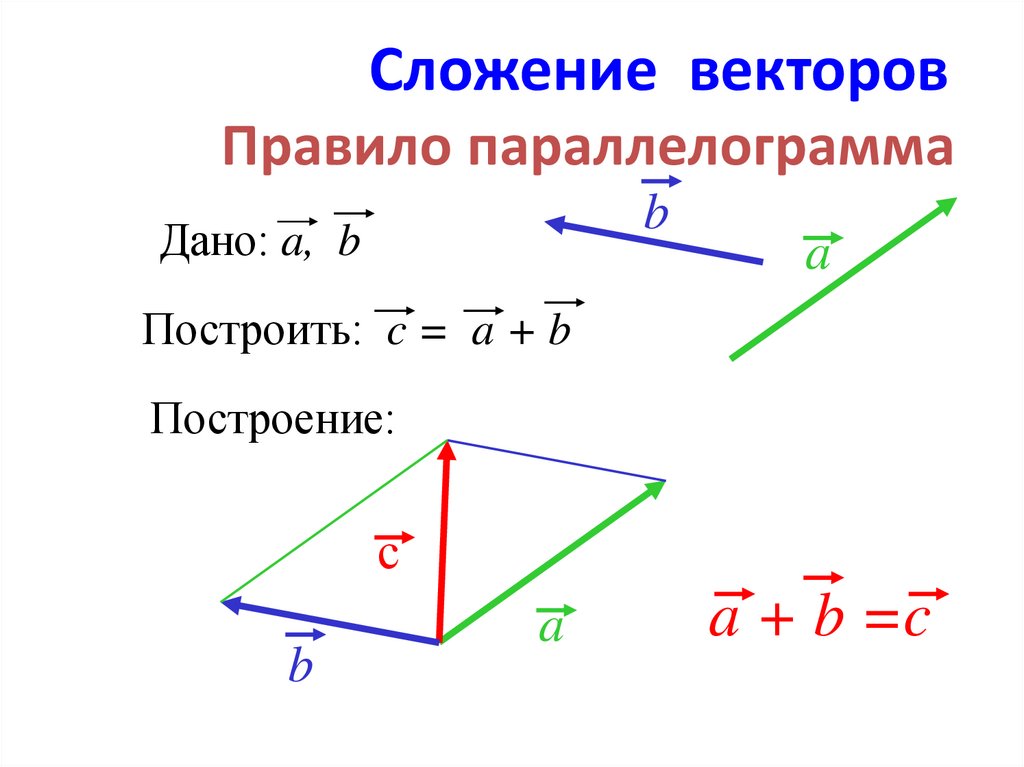 Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны.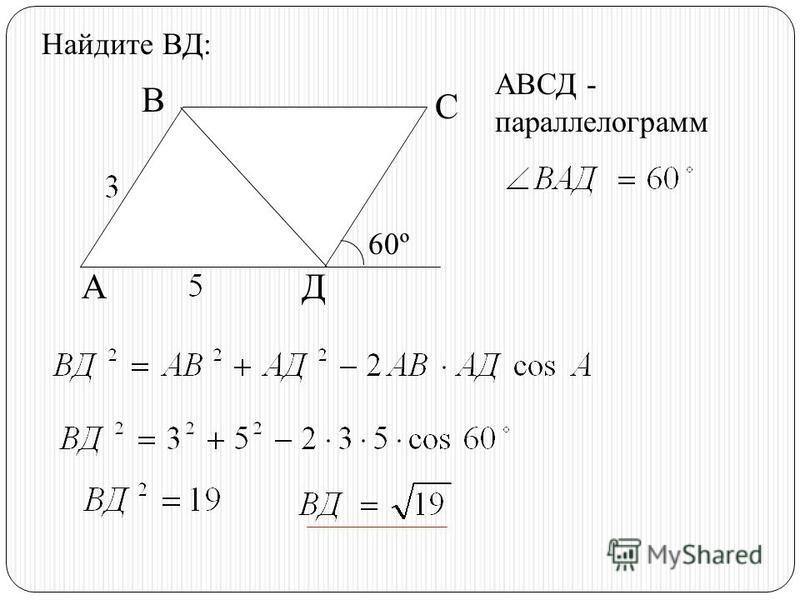 Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7).
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
- Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.
 5.
5. - В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
Зная векторное произведение вычислить площадь параллелограмма. Записи с меткой «площадь параллелограмма по координатам его вершин»
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
По вашим просьбам!
4. Найти наибольшее целое решение неравенства:
Умножим обе части неравенства на 15 — наименьший общий знаменатель данных дробей. Получаем равносильное неравенство:
3·(x-2)-5·(2x+3)>15. Раскрываем скобки: 3x-6-10x-15>15 и упрощаем:
3x-10x>15+6+15. Получаем -7x>36. Делим обе части неравенство на отрицательный коэффициент при х, поэтому знак неравенства меняем на противоположный:
x
Наибольшее целое число из заштрихованного промежутка — это число -6.
5. Определите верное решение неравенства: log 2 (x-4)≤3.
Представим число 3 в виде логарифма с основанием 2.
log 2 (x-4)≤ log 2 2 3 ; отсюда log 2 (x-4)≤log 2 8. Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12].
Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12].
7. Укажите функцию, график которой изображен на рисунке.
На рисунке мы видим параболу, которую можно задать уравнением вида: y=a(x-m) 2 +n, где (m; n) — координаты вершины параболы. На рисунке вершина параболы — точка (2; 1). Следовательно, m=2; n=1. А что по поводу значения коэффициента а ? Смотрим на ответы: везде коэффициент перед скобкой равен единице. Ну и прекрасно — меньше забот! Получили формулу: y=(x-2) 2 +1.
11. Длина прямоугольного участка 120 м, а ширина составляет 75% длины. Вспахано 35% этого участка, тогда не вспахано:
По условию ширина составляет 75% от 120 метров — длины участка. Это 3/4 от длины, т.е. 120:4·3=90 метров. Площадь прямоугольного участка равна произведению длины участка на его ширину, значит, составляет 120 м·90 м= 10800 м 2 . Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800.
Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800.
0,65·10800=7020. Отвечаем на вопрос задачи: не вспахано 7020 м 2 .
12. Решите уравнение:
К правой части равенства применим основное логарифмическое тождество:
Мы получили равные степени по основанию 2, следовательно, и показатели этих степеней будут равны. Получается квадратное уравнение: x 2 +x=2 или x 2 +x-2=0. По теореме Виета подбираем корни: x 1 =-2; x 2 =1.
14. Решите уравнение: sin 2 x-cos 2 x=cos(x/2).
По формуле косинуса двойного угла: cos2α=cos 2 α-sin 2 α, тогда данное равенство преобразуется к виду:
Cos2х=cos(x/2) ⇒ -cos2х-cos(x/2)=0 ⇒ cos2х+cos(x/2)=0. Сумму косинусов преобразуем в произведение, используя формулу:
17. Найдите сумму ординат точек экстремума функции f(x)=x 3 /(x 2 -3).
Вы, конечно, знаете, что экстремумы — это минимумы и максимумы функции, возможные только в критических точках. Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а , то в симметричной ей точке с абсциссой (-а) она будет иметь минимум. Опять же значения функции в этих точках а и -а также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю.
Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а , то в симметричной ей точке с абсциссой (-а) она будет иметь минимум. Опять же значения функции в этих точках а и -а также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю. Вывод: если вам нужно найти сумму ординат точек экстремума нечетной функции, то ответ: 0.
Вывод: если вам нужно найти сумму ординат точек экстремума нечетной функции, то ответ: 0.
21. Найдите сумму корней уравнения: x -2 -16x -1 -80=0.
Сделаем замену: x -1 =y. Получим уравнение: y 2 -16y-80=0. Находим корни: y 1 =-4 и y 2 =20.
Тогда x -1 =-4 или x -1 =20.
22. Решить систему неравенств:
В одной системе координат построим графики функций y=sinx, y=cosx и y= 1/6. Определим промежуток значений х, при которых график синуса лежит выше, а график косинуса ниже прямой y= 1/6.
24. Найдите площадь параллелограмма ABCD, если А(5; 4), В(0; 3), С(4; 7), D(9; 8).
Площадь параллелограмма найдем по формуле: S=absinA, где a=АD и b=AB — стороны параллелограмма, А — угол между этими сторонами. Используем векторы: найдем координаты и модули векторов, выражающих стороны АD и AB параллелограмма, косинус угла между этими векторами. Затем найдем синус этого угла, и в формулу площади параллелограмма подставим все нужные значения.
25. Электронные часы показывают время в часах и минутах (от 00:00 до 23:59). Сколько раз за сутки можно увидеть на табло 4 цифры 2, 0, 1, 9 (в любом порядке). Так как нет, например 91 минуты или 29 часов, то комбинаторика нам не поможет. Просто будем перечислять все возможные в реальности показания времени.
1) 01:29; 2) 02:19; 3) 09:12; 4) 09:21; 5) 10:29; 6) 12:09; 7) 19:02; 8) 19:20; 9) 20:19; 10) 21:09. Других значений из этих 4-х цифр быть не может.
Друзья, повторяйте формулы. Желаю успехов!
Площадь параллелограмма на векторах онлайн калькулятор. Векторное произведение векторов. Смешанное произведение векторов
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7). Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
- Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1².
 Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│. - Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.5.
- В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.

На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
Площадь параллелограмма в координатах. Векторное произведение векторов
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7).
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
- Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.
 5.
5. - В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
Площадь параллелограмма — формула, определение, векторная форма, примеры, часто задаваемые вопросы
Площадь параллелограмма — это пространство или область, заключенная в двумерной фигуре с ее четырех сторон. Параллелограмм в геометрии определяется как особый вид четырехугольника. Параллелограмм – это двумерная фигура, состоящая из четырех сторон. Противоположные стороны параллелограмма равны и параллельны друг другу. Площадь параллелограмма просто равна количеству квадратных единиц (например, m 2 , cm 2 и т. д.), которые могут вписаться в параллелограмм.
Параллелограмм в геометрии определяется как особый вид четырехугольника. Параллелограмм – это двумерная фигура, состоящая из четырех сторон. Противоположные стороны параллелограмма равны и параллельны друг другу. Площадь параллелограмма просто равна количеству квадратных единиц (например, m 2 , cm 2 и т. д.), которые могут вписаться в параллелограмм.
Какова площадь параллелограмма?
Общая площадь, занимаемая параллелограммом на двумерной плоской поверхности, является площадью параллелограмма. Площадь параллелограмма можно определить, используя его высоту, длину сторон или диагоналей. Все эти три метода имеют собственную производную формулу, которая поясняется ниже.
Площадь параллелограмма Формула
Площадь параллелограмма можно определить, умножив его основание на высоту. Как видно на следующей диаграмме, основание и высота параллелограмма перпендикулярны друг другу. Таким образом, для определения площади параллелограмма можно использовать следующую формулу:
Площадь параллелограмма = основание × высота
или
A = b × h
, где b — основание
. Параллелограмм, а
h — высота параллелограмма 9.0035
Как рассчитать площадь параллелограмма?
Как правило, площадь параллелограмма можно вычислить, используя его основание и высоту. Кроме того, площадь параллелограмма также можно определить, если известны длины его параллельных сторон и любые углы между ними, а также углы, под которыми пересекаются две его диагонали. В результате площадь параллелограмма можно вычислить тремя способами:
- Когда известны основание и высота параллелограмма.
- Когда известны длины сторон параллелограмма.
- Когда длины диагоналей параллелограмма известны.
Площадь параллелограмма с использованием высоты определяется произведением его основания и высоты.
Математически это записывается как
Площадь параллелограмма = b × h
, где
- b — основание параллелограмма, а
- h — высота параллелограмма
Пример: Найдите площадь параллелограмма, основание которого равно 12 см, а высота — 8 см.
Решение:
Площадь параллелограмма с использованием длин сторонУчитывая, что
Основание (b) = 12 см
Высота (h) = 8 см h
= 12 × 8
= 96 см 2
Площадь параллелограмма можно вычислить, используя длины сторон и смежных углов, если высота не указана.
Математически это записывается как
Площадь параллелограмма = ab sin (θ)
, где
- a и b — длины параллельных сторон, а
- θ — угол между сторонами.
Пример: если угол между двумя сторонами параллелограмма равен 30 градусов, а длины его смежных сторон равны 5 см и 6 см. Определить площадь параллелограмма.
Решение:
Учитывая, что
Длина одной стороны (a) = 5 см,
Длина другой стороны (b) = 4 см,
Угол между двумя соседними сторонами (θ ) = 30 градусов
Формула для расчета площади параллелограмма:
A = ab sin (θ)
= 5 × 4 × sin (30)
= 10 см 2
7 9 Площадь параллелограмма с использованием диагоналейПараллелограмм состоит из двух диагоналей, которые пересекают друг друга под определенным углом и встречаются в определенной точке.
Площадь параллелограмма можно вычислить, используя длину его диагоналей.
Формула площади параллелограмма с использованием длины диагоналей:
- d 1 и d 2 — длины диагоналей, а
- x — угол между диагоналями.
Пример: Определить площадь параллелограмма, когда угол между двумя пересекающимися диагоналями параллелограмма равен 90 градусов, а длины его прилежащих сторон равны 2 см и 6 см.
Решение:
Учитывая, что
Длина одной диагонали (d 1 ) = 2 см,
Длина другой диагонали (d 2 7 см) две пересекающиеся диагонали (x) = 90 градусов
Формула для вычисления площади параллелограмма:
A = 1/2 × d 1 × d 2 sin (x)
= 1/2 × 2 × 6 × грех (90)
= 60 см 2
Площадь параллелограмма в векторной форме
Площадь параллелограмма можно вычислить, даже если стороны и диагонали параллелограмма заданы в векторной форме.
Рассмотрим параллелограмм PQRS со смежными сторонами и соответственно. А диагонали и , как показано ниже на диаграмме:
Теперь площадь параллелограмма в векторной форме задается с помощью смежных сторон и как,
Из приведенной выше диаграммы параллелограмма это можно интерпретировать как:
и
или
СЕЙЧАС,
Но, \ vec \ vec a = 0,
Но, \ vec \ vec a = 0,
\vec b \times \vec b = 0 иСледовательно,
или
Таким образом, из уравнения (1) площадь параллелограмма в векторной форме определяется как:
Площадь параллелограмма
- Area of a parallelogram using Base and Height:
A = b × h
- Area of a parallelogram using the side lengths:
A = ab sin (θ)
- Площадь параллелограмма с использованием диагоналей:
A = 1/2 × d 1 × d 2 sin (x)
Примеры решения на основе площади параллелограмма
площадь параллелограмма, основание которого 10 см, а высота 8 см.

Решение:
Дано:
Основание (B) = 10 см
Высота (H) = 8 см
. = 80 см 2
Пример 2. Найдите площадь параллелограмма, основание которого равно 5 см, а высота 4 см.
Решение:
Дано,
Основание (b) = 5 см
Высота (h) = 4 см
Площадь (A) = b × h
A = 5 × 4
= 20 см 2
стороны 4 см и 8 см.
Решение:
Учитывая, что
Длина одной диагонали (d 1 ) = 4 см,
Длина другой диагонали (d 2 см)0007
Угол между двумя пересекающимися диагоналями (х) = 90° = 1/2 × 4 × 8 × sin (90)
= 16 см 2
3 см и 6 см. Определить площадь параллелограмма.

Решение:
Учитывая, что
Длина одной стороны (a) = 3 см,
Длина другой стороны (b) = 6 см,
Угол между двумя соседними сторонами (θ) = 60 градусов
Формула для расчета площади параллелограмма:
A = ab sin (θ)
= 3 × 6 × sin (60)
= 15,6 см 2 202023
7 7 Пример 5. Найдите площадь параллелограмма, параллельные стороны которого равны 4 см и 3 см, а угол между этими сторонами равен 90°.Решение:
FAQs on Area of a ParallelogramДано,
Пусть длины сторон равны a и b со значениями 4 см и 3 см соответственно.
Angle between the sides 90°
Area = ab sinθ
= 4 × 3 sin 90°
= 12 cm 2
Question 1: Что такое периметр параллелограмма?
Ответ:
Периметр параллелограмма определяется как сумма всех его четырех сторон, поэтому задается как
Периметр параллелограмма, P = 2 (a + b)
, где a и b — длина противоположные стороны параллелограмма.
Вопрос 2: Почему площадь основания параллелограмма равна высоте?
Ответ:
Так как параллелограмм — это четырехугольник с двумя парами параллельных сторон. А периметр определяется как расстояние вокруг двумерной фигуры. Следовательно, площадь параллелограмма равна произведению основания на высоту.
Вопрос 3: Каковы свойства параллелограмма?
Ответ:
Свойства параллелограмма:
- Противоположные стороны параллелограмма равны и параллельны друг другу.
- Противоположные углы параллелограмма равны.
- Сумма внутренних углов параллелограмма равна 360°.
- Смежные углы параллелограмма должны быть смежными, т.е. равными 180°.
Вопрос 4. Все ли стороны параллелограмма равны?
Ответ:
Нет, не все стороны параллелограмма равны друг другу.
Только противоположные стороны параллелограмма равны.
Вопрос 5. Все ли углы параллелограмма равны?
Ответ:
Нет, не все углы параллелограмма равны друг другу. Только противоположные углы параллелограмма равны.
Вопрос 6: По какой формуле находится высота параллелограмма?
Ответ:
Формула высоты параллелограмма, если известна площадь и основание параллелограмма, тогда:
h = A/b
высота,
b — основание и A — площадь параллелограмма Площадь параллелограмма в координатах. Векторное произведение векторов
Квадрат Параллелограмм построен на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для расчета необходимо использовать координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — концепция вектора;
- — свойства векторов;
- — Декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов) по синус угла между ними S = │a│ │b│sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь построенного на них параллелограмма , выполните следующие действия:
- Найти координаты векторов, если они не заданы сразу, вычитанием координат начальных точек из соответствующих координат концов векторов. Например, если координаты начальной точки вектора (1;-3;2), а конечной точки (2;-4;-5), то координаты вектора будут (2-1;- 4+3;-5-2)=(1;-1;-7). Пусть координаты вектора a (x1; y1; z1), вектора b (x2; y2; z2).
- Найдите длины каждого из векторов.
Возведите в квадрат каждую из координат векторов, найдите их сумму x1² + y1² + z1². Извлеките квадратный корень из результата. Выполните ту же процедуру для второго вектора. Таким образом, вы получаете │a│ и│b│.
- Найдите скалярное произведение векторов. Для этого умножьте их соответствующие координаты и сложите произведения │a b│ = x1 x2 + y1 y2 + z1 z2.
- Определить косинус угла между ними, для которого скалярное произведение векторов, полученных на шаге 3, разделить на произведение длин векторов, которые были вычислены на шаге 2 (Cos(α) = │a b│ / (│ а│ │ б│)).
- Синус полученного угла будет равен квадратному корню из разницы между числом 1 и квадратом косинуса того же угла, вычисленного на шаге 4 (1-Cos²(α)).
- Вычислите площадь параллелограмма , построенного на векторах , найдя произведение их длин, вычисленное в п.2, и умножьте результат на число, полученное после вычислений в п.5.
- В том случае, если координаты векторов заданы на плоскости, координата z просто отбрасывается при расчетах.
Этот расчет представляет собой числовое выражение перекрестного произведения двух векторов.
В этом уроке мы рассмотрим еще две векторные операции: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому надо) … Ничего страшного, иногда бывает, что для полного счастья кроме скалярного произведения векторов нужно еще и более. Такая вот векторная зависимость. Может сложиться впечатление, что мы попадаем в дебри аналитической геометрии. Это неправда. В этом разделе высшей математики вообще дров не хватает, разве что на Буратино хватает. На самом деле материал очень распространенный и простой — вряд ли сложнее того же скалярное произведение , типовых задач будет еще меньше. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молния на горизонте, не беда, начните с урока Векторы для чайников , чтобы оправиться или восстановить базовые знания о векторах .
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, часто встречающихся в практических работах
Как сразу порадовать? Когда я был маленьким, я умел жонглировать двумя или даже тремя мячами. Ловко получилось. Теперь вам вообще не придется жонглировать, так как мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами опустим. Почему? Так родились эти действия — вектор и смешанное произведение векторов определены и работают в трехмерном пространстве. Это уже проще!
Эта операция, так же как и скалярное произведение, включает два вектора … Пусть это будут нетленные буквы.
Само действие обозначается следующим образом: . Есть и другие варианты, но я привык обозначать векторное произведение векторов так, в квадратных скобках крестиком.
И сразу вопрос : если в скалярное произведение векторов участвуют два вектора, и здесь тоже два вектора перемножаются, то чем отличается ? Очевидная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
В результате векторного произведения векторов получается ВЕКТОР :, то есть мы перемножаем векторы и снова получаем вектор.
Определение перекрестного произведенияЗакрытый клуб. Собственно, отсюда и название операции. В разной учебной литературе обозначения также могут различаться, я буду использовать букву.
Сначала будет определение с картинкой, потом комментарии.
Определение : По векторному произведению неколлинеарных векторов, взятых в таком порядке , называемых ВЕКТОРОМ, длина которая численно равна площади параллелограмма построенного на этих векторах; вектор ортогонален векторам , и направлен так, чтобы основание имело правильную ориентацию:
Разбираем определение по костям, там много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы, обозначенные красными стрелками, по определению не коллинеарно … Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы берутся в строго определенном порядке : – «А» умножается на «bh» , а не «bh» на «а».
Результатом векторного умножения является ВЕКТОР, отмеченный синим цветом. Если векторы перемножить в обратном порядке, то получится вектор равный по длине и противоположный по направлению (малиновый цвет). То есть равенство верно.
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный момент! ДЛИНА синего вектора (и, следовательно, малинового вектора) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах. На рисунке этот параллелограмм заштрихован черным цветом.
Примечание : рисунок схематичен, и, конечно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Следовательно, исходя из вышеизложенного, формула для расчет ДЛИНЫ векторного произведения действителен:
Подчеркну, что в формуле речь идет о ДЛИНЕ вектора, а не о самом векторе.
Какой практический смысл? А смысл в том, что в задачах аналитической геометрии площадь параллелограмма часто находится через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красная пунктирная линия) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важным фактом является то, что вектор ортогонален векторам, то есть… Конечно, противоположно направленный вектор (малиновая стрелка) также ортогонален исходным векторам.
5) Вектор направлен так, что основание Имеет правую ориентацию. В уроке о переходе на новую основу я достаточно подробно рассказал о плоскостной ориентации , а теперь разберемся, что такое ориентация пространства. Объясню на пальцах правой руки … Мысленно соединим указательный палец с вектором и средний палец с вектором. Безымянный палец и мизинец прижмите его к ладони.
В результате thumb — векторное произведение будет искать вверх. Это правоориентированный базис (на рисунке именно он). Теперь меняем векторы ( указательный и средний пальцы ) местами, в результате большой палец развернется, а перекрестное произведение уже будет смотреть вниз. Это тоже правильная основа. Возможно у вас возник вопрос: что лежит в основе левой ориентации? «Присвоить» этим же пальцам левой руки векторов, и получить левое основание и левую ориентацию пространства (в этом случае большой палец будет располагаться в направлении нижнего вектора) … Образно говоря, эти основания «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует рассматривать как нечто надуманное или абстрактное — например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить из зазеркалья отраженный предмет», то в общем случае совместить с «оригиналом» не получится. Кстати, поднесите к зеркалу три пальца и проанализируйте отражение 😉
.
Скрестное произведение коллинеарных векторов.. как хорошо, что вы теперь знаете о право- и левоориентированных основаниях, ведь утверждения некоторых лекторов о смене ориентации ужасны =)
Определение подробно проанализировано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то они могут располагаться на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь таких, как говорят математики, вырожденный параллелограмм равен нулю. То же следует из формулы — синус нуля или 180 градусов равен нулю, значит, площадь равна нулю.
Итак, если, то… Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частным случаем является векторное произведение вектора самого на себя:
Используя векторное произведение, вы можете проверить коллинеарность трехмерных векторов, и мы также проанализируем эту проблему, среди прочего.
Для решения практических примеров может понадобиться тригонометрическая таблица для нахождения по ней значений синуса.
Ну давайте зажжем огонь:
Пример 1
а) Найдите длину векторного произведения векторов если
б) Найдите площадь параллелограмма построенного на векторах если
Решение : Нет, это не опечатка, я намеренно сделал исходные данные в пунктах условия одинаковыми. Потому что дизайн решений будет другим!
а) По условию требуется найти длину вектора (векторное произведение). По соответствующей формуле:
Ответ :
Так как вопрос был задан о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти квадрата параллелограмма, построенного на векторах. Площадь этого параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что ответ про векторное произведение вообще не может быть и речи, нас спрашивали про площадь фигуры , соответственно размерность квадратные единицы.
Мы всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем четкий ответ. Это может показаться буквализмом, но буквалистов среди учителей хватает, и задание с хорошими шансами вернется на доработку. Хотя это не особо натянутое нытье — если ответ неверный, то складывается впечатление, что человек не понимает простых вещей и/или не понимает сути задачи. Этот момент нужно всегда держать под контролем, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда делась большая буква «ан»? В принципе его можно было дополнительно воткнуть в раствор, но чтобы сократить запись, я этого не сделал. Надеюсь, все это понимают и обозначают одно и то же.
Популярный пример решения своими руками:
Пример 2
Найти площадь треугольника, построенного на векторах, если
Формула нахождения площади треугольника через векторное произведение дается в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространенная, треугольники вообще могут вас замучить.
Для решения других задач нам потребуются:
Свойства векторного произведенияМы уже рассмотрели некоторые свойства векторного произведения, однако я включу их в этот список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации этот пункт обычно не выделяется в свойствах, но он очень важен в практическом плане. Так пусть будет.
2) — свойство тоже обсуждалось выше, иногда его называют антикоммутативность … Другими словами порядок векторов имеет значение.
3) — комбинация или ассоциативные законы векторного произведения. Константы легко удаляются за пределы векторного произведения. Действительно, что им там делать?
4) — распределение или распределительное законы векторного произведения. С расширением скоб тоже проблем нет.
В качестве демонстрации рассмотрим небольшой пример:
Пример 3
Найти
Решение: По условию снова требуется найти длину векторного произведения. Напишем нашу миниатюру:
(1) По ассоциативным законам выносим константы за пределы деления векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» минус. Длина не может быть отрицательной.
(3) Дальнейшее понятно. 9
Пример 4 треугольник находится по формуле… Загвоздка в том, что векторы «цэ» и «дэ» сами представляются как суммы векторов. Алгоритм здесь стандартный и чем-то напоминает примеры 3 и 4 урока Скалярное произведение векторов … Для наглядности разобьем решение на три этапа:
1) На первом шаге выражаем векторное произведение через векторное произведение, по сути выражаем вектор через вектор . .. О длинах пока ни слова!
(1) Замена векторных выражений.
(2) Используя дистрибутивные законы, раскроем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, мы выносим все константы за пределы векторных произведений. При наличии небольшого опыта действия 2 и 3 можно выполнять одновременно.
(4) Первый и последний члены равны нулю (нулевой вектор) в силу приятного свойства. Во втором члене мы используем свойство антикоммутативности векторного произведения:
(5) Приведем аналогичные члены.
В итоге вектор был выражен через вектор, чего и требовалось добиться:
2) На втором шаге находим длину нужного нам векторного произведения. Это действие похоже на Пример 3:
3) Найдите площадь искомого треугольника:
Решения 2-3 этапов могут быть заполнены в одну строку.
Ответ :
Рассматриваемая задача довольно часто встречается в контрольных работах, вот пример самостоятельного решения:
Пример 5
Найти если
Краткое решение и ответ в конце урока . Посмотрим, насколько внимательно вы были при изучении предыдущих примеров 😉
Векторное произведение векторов в координатахдано в ортонормированном базисе, выражено формулой :
Формула действительно проста: в верхнюю строку определителя пишем координатные векторы, во вторую и третью строки «кладем» координаты векторов, и ставим в строгом порядке — сначала координаты вектора «ve», затем координаты вектора «double-ve».
Если векторы нужно перемножить в другом порядке, то строки следует поменять местами:
Пример 10
Проверить коллинеарность следующих пространственных векторов:
a)
b)Решение : Проверка основана на одном из утверждений этого урока: если векторы коллинеарны, то их пересечение произведение равно нулю (нулевой вектор): .
а) Найдите векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдите векторное произведение:
Ответ : а) не коллинеарно, б)
Вот, пожалуй, и вся основная информация о векторном произведении векторов.
Этот раздел будет не очень большим, так как не так много задач, где используется смешанное произведение векторов. На самом деле все будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов есть произведение трех векторов :
Итак, они выстроились в очередь с паровозиком и ждут, не могут дождаться, когда их вычислят.
Сначала снова определение и картинка:
Определение : Смешанная работа некомпланарных векторов, взятых в таком порядке называется объемом параллелепипеда , построенного по данным векторам, снабженным Знак «+», если основание правое, и знак «-», если основание левое.
Завершим рисунок. Невидимые для нас линии нарисованы пунктиром:
Давайте углубимся в определение:
2) Векторы берутся в определенном порядке , то есть перестановка векторов в произведении, как нетрудно догадаться, не проходит без последствий.
3) Прежде чем комментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов есть ЧИСЛО :. В учебной литературе оформление может быть несколько иным, я привык обозначать смешанную проработку, а результат вычислений буквой «пэ».
А-приор смешанный продукт объем параллелепипеда построен на векторах (рисунок нарисован красными векторами и черными линиями).
То есть число равно объему этого параллелепипеда.
Примечание : рисунок схематический.
4) Не будем лишний раз заморачиваться с понятием базы и ориентации в пространстве. Смысл заключительной части в том, что к громкости можно добавить знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Формула вычисления объема параллелепипеда, построенного на векторах, следует непосредственно из определения.
Площадь параллелограмма, построенного на векторах, равна произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что формулу площади параллелограмма, построенного на векторах, можно применить только после вычислений по координатам.
Если вам повезло, и по условиям даны длины векторов, то вам просто нужно применить формулу, которую мы уже подробно разбирали в статье. Площадь будет равна произведению модулей на синус угла между ними:Рассмотрим пример вычисления площади параллелограмма, построенного на векторах.
Задача: параллелограмм строится на векторах и. Найдите площадь, если и угол между ними равен 30°.
Выразим векторы через их значения:Возможно у вас возник вопрос — откуда взялись нули? Стоит помнить, что мы работаем с векторами, и для них… также обратите внимание, что если результатом является выражение, оно будет преобразовано в . Теперь проводим окончательные расчеты:
Вернемся к проблеме, когда в условиях не указаны длины векторов. Если ваш параллелограмм лежит в декартовой системе координат, то вам нужно сделать следующее.
Вычисление длин сторон фигуры, заданной координатами
Для начала найдем координаты векторов и из координат конца вычтем соответствующие координаты начала. Предположим, координаты вектора a (x1; y1; z1) и вектора b (x3; y3; z3).
Теперь найдем длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, затем сложить результаты и извлечь корень из конечного числа. По нашим векторам будут произведены следующие вычисления:
Теперь нам нужно найти скалярное произведение наших векторов.Для этого их соответствующие координаты перемножаются и складываются.
Зная длины векторов и их скалярное произведение, можно найти косинус угла, лежащего между ними .
Теперь мы можем найти синус того же угла:
Теперь у нас есть все необходимые величины, и мы легко можем найти площадь параллелограмма, построенного на векторах, по уже известной формуле.Площадь параллелограммов: определение и формула
Задумывались ли вы, какую форму представляет воздушный змей? Воздушный змей обычно имеет четыре стороны, что делает его типом четырехугольника.
Теперь обратите внимание на то, как верхняя левая и нижняя правая стороны воздушного змея, показанного ниже, параллельны друг другу. Точно так же верхняя правая и нижняя левая стороны этого воздушного змея параллельны друг другу.
Есть предположения, что это за четырехугольник? Это правильно! Это параллелограмм.
Скажем, вам сказали найти площадь этого воздушного змея. Поскольку это тип параллелограмма, мы могли бы использовать определенную формулу для вычисления площади этого воздушного змея.
Иллюстрация воздушного змея, StudySmarter Originals
В этой статье мы познакомимся с формулой площади параллелограмма и посмотрите на некоторые рабочие примеры, где он применяется.
Резюме по параллелограммам
Прежде чем мы перейдем к нашему основному предмету, давайте проведем краткий обзор параллелограммов, чтобы легче было погрузиться в эту тему.
Как следует из названия, параллелограмм имеет параллельные стороны. Таким образом, мы можем определить параллелограмм, как показано ниже.
Параллелограмм представляет собой четырехугольник с двумя парами параллельных противоположных сторон. Параллелограмм является частным случаем четырехугольника.
Четырехсторонняя плоская фигура известна как четырехугольник.
На следующем рисунке показан параллелограмм со сторонами AB, BD, CD и AC.
Иллюстрация параллелограмма, StudySmarter Originals
Свойства параллелограммов
Вернемся к нашему параллелограмму ABCD выше.
Давайте посмотрим на некоторые свойства, которые отличают эту форму.
Противоположные стороны треугольника ABCD параллельны. В этом случае АВ параллельна CD, а АС параллельна BD. Мы пишем это как AB//CD и AC//BD,
Противоположные углы ABCD равны. Здесь ∠CAB = ∠CDB и ∠ACD = ∠ABD,
Диагонали параллелограмма делят друг друга пополам в точке, скажем, M. Тогда AM = MD и BM = MC. Это показано ниже.0002 Прямоугольник
Квадрат
Ромб
Каждый из этих параллелограммов имеет свои особенности, которые отличают их друг от друга. Более подробное объяснение параллелограммов можно найти здесь, Параллелограммы.
Площадь определения параллелограмма
Площадь параллелограмма определяется как область, ограниченная параллелограммом в двумерном пространстве.
На приведенной выше диаграмме общая площадь, заключенная в ABCD, является площадью параллелограмма ABCD.
Формула площади параллелограмма
Ссылаясь на наш исходный параллелограмм ABCD, мы добавим к этой фигуре два новых компонента, называемых b и h. Это показано на диаграмме ниже.
Параллелограмм с основанием b и высотой h, Study Smarter Originals
Переменная b называется основанием параллелограмма. В качестве основания можно использовать любую из длинных сторон ABCD. На приведенной выше диаграмме b может быть либо AB, либо CD. Здесь, здесь мы взяли b = AB.
Обратите внимание, что это понятие является соглашением, а не жестким правилом.
Переменная h называется высотой параллелограмма. Это также можно назвать высотой. Высота — это отрезок, перпендикулярный паре смежных сторон параллелограмма с одной конечной точкой на одной стороне и другой конечной точкой на другой стороне.
Теперь, когда мы определили наши переменные b и h, мы можем представить площадь параллелограмма следующим образом.
Площадь любого параллелограмма находится по формуле
где b = основание и h = высота.
Примеры площади параллелограмма
Имея это в виду, давайте теперь рассмотрим следующие рабочие примеры, в которых используется эта формула.
Найдите площадь следующего параллелограмма:
Пример 1, StudySmarter Originals
Решение
Здесь основание равно b = 24 единицы, а высота h = 10 единиц. Используя формулу площади параллелограмма, мы получаем,
Таким образом, площадь этого параллелограмма составляет 240 единиц 2 .
Параллелограмм высотой 5 единиц длины имеет площадь 20 единиц 2 . Какова длина основания?
Решение
Здесь нам даны площадь параллелограмма и высота (или высота), то есть
A = 20 и h = 5.
Чтобы найти основание, нужно просто подставить эти значения в нашу область формулы параллелограмма и перестройте уравнение, как показано ниже.
Сделав b предметом, получим
Таким образом, основание этого параллелограмма равно 4 единицам.
Нахождение площади параллелограмма из прямоугольника
Предположим, мы хотим найти площадь параллелограмма, высота которого неизвестна. Вместо этого нам даны длины двух сторон параллелограмма, а именно длины АВ и АС.
Давайте попробуем рассмотреть этот сценарий графически. Возвращаясь к нашему исходному параллелограмму ABCD, давайте проведем две высоты для каждой пары смежных сторон, AC и AB, а также CD и BD.
Площадь параллелограмма из прямоугольника, StudySmarter Originals
Таким образом, мы получаем две новые точки на этом параллелограмме, а именно S и T. Теперь посмотрим на форму, образованную BTCS. Вам это кажется знакомым? Вот так! Это прямоугольник, который также является разновидностью параллелограмма. Теперь нам нужно найти способ получить длины либо CS, либо BT, чтобы мы могли вывести высоту этого параллелограмма.
Обратите внимание, что из построения этих двух отрезков мы получили пару прямоугольных треугольников, CAS и BDT. Поскольку CS = BT, нам достаточно вычислить только один из них.
Рассмотрим треугольник CAS.
Треугольник CAS, StudySmarter Originals
Для простоты мы будем обозначать следующие стороны как: x = AS, y = CS и z = AC. Поскольку это прямоугольный треугольник, мы можем использовать теорему Пифагора, чтобы получить длину CS, которая является высотой параллелограмма ABCD. Учитывая длины AS и AC, мы имеем
x 2 + y 2 = z 2
Преобразовав это и применив квадратный корень, мы получим
Поскольку мы теперь нашли длину CS, мы можем продолжить нахождение площади параллелограмма ABCD по данной формуле. За основание возьмем длину АВ. Таким образом, площадь ABCD равна
Покажем это на примере.
Дан параллелограмм PQRS, найдите его площадь.
Пример 2, StudySmarter Originals
Линия OQ представляет собой высоту смежных сторон PQ и PS. Длины QR, PQ и PO равны 12 единицам, 13 единицам и 5 единицам соответственно.
Решение
Так как QR = PS, мы можем принять основание как QR = 12 единиц.
Теперь нам нужно найти высоту этого параллелограмма, чтобы найти его площадь. Это дается отрезком OQ.
Из диаграммы видно, что треугольник QPO является прямоугольным. Поскольку у нас есть длина PO = 5 единиц, мы можем использовать теорему Пифагора, чтобы найти OQ.
Переставляя это и применяя квадратный корень, мы получаем следующее значение для OQ,
Таким образом, высота этого параллелограмма составляет 12 единиц. Теперь мы можем найти площадь PQRS, как показано ниже:
Следовательно, площадь этого параллелограмма составляет 144 единицы 2 .
Параллелограмм, вписанный в прямоугольник Пример
В этом примере мы рассмотрим случай, когда параллелограмм вписан в прямоугольник. Мы хотим определить площадь внутри прямоугольника, не занятую параллелограммом.
На рисунке ниже показан параллелограмм PXRY внутри прямоугольника PQRS. Найдите площадь области, заштрихованной синим цветом.
Пример 3, Исследование Smarter Originals
Отрезок линии XZ представляет собой высоту смежных сторон XP и PY.
Здесь QP = RS = XZ, PX = RY и QR = PS. Длины QP, PY и SY равны 19ед., 21 ед. и 7 ед. соответственно.
Решение
Здесь высота прямоугольника PQRS равна h = QP = 19 единиц. Основание равно PS, равному сумме длин PY и SY. Таким образом, основание равно
Таким образом, b = 28 единиц. Формула площади прямоугольника представляет собой произведение его основания и высоты. Таким образом, площадь прямоугольника PQRS равна
Теперь найдем площадь параллелограмма PXRY. Высота параллелограмма равна XZ. Так как XZ = QP, то h = XZ = 19 единиц. База задается длиной PY. Таким образом, b = PY = 21 единица. Используя формулу площади параллелограмма, получаем
Таким образом, площади прямоугольника PQRS и параллелограмма PXRY составляют 532 единицы 2 и 399 единиц 2 соответственно.
Теперь нам нужно найти область, заштрихованную синим цветом, которая не занята параллелограммом внутри прямоугольника.
Это можно найти, вычислив разницу между площадями прямоугольника PQRS и параллелограмма PXRY. При этом получаем
Следовательно, площадь оставшейся области, заштрихованной синим цветом, составляет 133 единицы 2 .
Особый случай: площадь ромба
Ромб — это особый тип четырехугольника, у которого фактически есть собственная формула для вычисления его площади. Иногда его называют равносторонним четырехугольником. Напомним определение ромба.
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину.
Теперь рассмотрим ромб ниже. На этом параллелограмме построены две диагонали AD (голубая линия) и BC (синяя линия). Диагонали имеют длины d 1 и d 2 соответственно.
Площадь ромба, StudySmarterOriginals
Площадь ромба
Площадь ромба находится по формуле
, где A = площадь, d 1 = длина диагонали AD и d 2 = длина диагонали BC.
Пример площади ромба
Вот пример площади ромба.
Диагонали ромба имеют длины 10 единиц и 15 единиц. Чему равна площадь ромба?
Раствор
Обозначим d 1 = 10 единиц и d 2 = 15 единиц. Применяя формулу выше, получаем
Таким образом, площадь этого ромба равна 75 единицам 2 .
- Формула площади ромба также может быть использована для нахождения площади воздушного змея.
Мы закончим эту статью последним примером, касающимся площади параллелограмма или, точнее, воздушного змея.
Реальный пример площади параллелограмма
Теперь мы вернемся к нашему примеру в начале этой статьи. Поскольку теперь у нас есть базовая формула для вычисления площади параллелограмма, мы можем использовать ее, чтобы найти площадь нашего воздушного змея.
Вы решаете измерить длину двух диагоналей воздушного змея рулеткой. Вы обнаружите, что горизонтальная диагональ и вертикальная диагональ равны 18 дюймам и 31 дюйму соответственно.
Используя формулу площади ромба, найдите площадь этого воздушного змея.
Пример 4, исследование Smarter Originals
Решение
Let
d 1 = диагональ по горизонтали = 18 дюймов
d 2 = вертикальная диагональ = 31 дюйм
Применяя формулу площади ромба, получаем
Таким образом, площадь этого воздушного змея составляет 558 дюймов 2 .
Площадь параллелограммов. Ключевые выводы
- Четырехугольник с двумя парами параллельных противоположных сторон называется параллелограммом.
- Параллелограммы бывают трех видов: прямоугольник, квадрат и ромб.
- Основные свойства параллелограмма:
Противоположные стороны параллельны
Противоположные углы равны
Диагонали делятся пополам как точка
4 9
- Площадь параллелограмма находится по формуле: A = b × h , где b = основание, h = высота.
Площадь ромба находится по формуле:, где d 1 и d 2 — длины диагоналей ромба.
Вектор результирующей, как вычислить результирующую, используя метод параллелограмма и метод головы к хвосту. Результат просто…
Эта страница:
Метод параллелограмма Метод «голова к хвосту» Практика «Голова к хвосту» Векторный рабочий лист (бесплатный pdf с ключом ответа по вычислению результирующих векторов) Результирующий вектор фото Векторов Результирующий вектор — это вектор, который «получен» в результате сложения двух или более векторов. Есть два разных способа вычисления результирующего вектора.
Методы расчета результирующего вектора:
- Метод головы к хвосту для вычисления результата, который включает в себя выравнивание головы одного вектора с хвостом другого.
- Метод параллелограмма для вычисления результирующего вектора. Этот метод использует свойства параллелограмма, но, в конце концов, сводится к простой формуле.
На картинке слева черный вектор является результатом двух красных векторов. Чтобы попытаться понять, что такое равнодействующая, рассмотрим следующую историю.
Если вы ехали из своего дома, с центром в исходной точке. К дому друзей, в точку (3, 4), представьте, что вам нужно было ехать двумя разными дорогами, это два красных вектора. Однако результирующий вектор-вектор будет прямым путем от вашего дома до дома вашего друга, и черный вектор представляет этот путь.
Голова к хвосту Метод
Метод головы к хвосту — это способ найти результирующий вектор.
Шаги довольно прямые. Метод «голова к хвосту» рассматривает начало вектора как конец со стрелкой или «заостренный конец». Хвост вектора находится там, где начинается вектор.
- Поместите два вектора рядом друг с другом так, чтобы голова одного вектора касалась хвоста другого вектора.
- Нарисуйте результирующий вектор, начав с того места, где хвост первого вектора находится в начале второго вектора.
Шаги для метода «голова к хвосту»
Вычислить результирующий вектор магнитуды
Найдите сумму каждой пары векторов (величину результирующего вектора).
Чтобы найти величину результирующего вектора, используйте теорему Пифагора.
Практика ПроблемыПроблема 1
Вы вышли из дома, чтобы навестить друга. Вы сели в машину, проехали 40 миль на восток, затем выехали на шоссе и проехали 50 миль на север.
Нарисуйте вектор от начала вашего пути, вашего дома, и конца, дома вашего друга.
Какова длина нарисованного вами вектора?
Задача 2
Чему равна сумма двух векторов? Используйте метод головы к хвосту, чтобы вычислить результирующий вектор на рисунке справа.
Метод параллелограмма для вычисления результата
Прежде чем приступить к методу параллелограмма для решения результирующих векторов, вы должны ознакомиться со следующими темами.
- SOHCATOA (основной синус, косинус, тангенс)
- Закон косинусов
- Закон синусов
- Следующие свойства параллелограммов
- Противоположные стороны параллелограммов равны
- Противоположные углы параллелограммов равны
Проблема 3
Чтобы лучше понять, как работает метод параллелограмма, давайте рассмотрим два вектора ниже. Векторы имеют величины 17 и 28, а угол между ними равен 66°. Наша цель — использовать метод параллелограмма для определения величины равнодействующей.
Шаг 1
Нарисуйте параллелограмм на основе двух уже имеющихся векторов. Эти векторы будут двумя сторонами параллелограмма (а не противоположными сторонами, так как между ними есть угол).
Шаг 2
Теперь у нас есть параллелограмм и известны два угла (противоположные углы параллелограмма равны). Мы также можем вычислить другую пару углов, так как другая пара конгруэнтна, а сумма всех четырех углов должна составлять 360.
Шаг 3
Начертите диагонали папралелограммы.
Эта диагональ равна результирующему вектору .
Шаг 4
Используйте закон косинусов, чтобы определить длину равнодействующей.
Используйте закон косинусов для вычисления равнодействующей.
Площадь параллелограмма, образованного двумя векторами
Площадь параллелограмма, образованного двумя векторами — Мы будем хорошо использовать эту концепцию в этом объяснении концепции площади треугольника, образованного векторами. Площадь параллелограмма означает поверхность в плоскости векторов, которая на самом деле является вектором поверхности.
Таким образом, величина площади параллелограмма равна 16. = √ (64+64+64) = √192. Величина площади параллелограмма равна 16. Обычно, когда мы пытаемся узнать площадь треугольника, мы обычно находим значение по формуле формулы Герона. Тогда площадь параллелограмма равна. И вы должны сделать это, потому что это может быть отрицательным. В вопросе 6 используйте векторное произведение и определите площадь параллелограмма, образованного следующими двумя векторами: Здесь a и b — векторы двух сторон параллелограмма.
Перепишите v как сумму двух компонент, параллельных u и ортогональных u. Поэтому ваш ответ правильный 0. Предположим, что даны два вектора и в двумерном пространстве, которые не лежат на одной прямой. А (1,1), б (2,0) и в (3,3). Глава 10 векторной алгебры класса 12 (термин 2) с точки зрения концепции.
Вектор параллелограмма в коллекции
Формула площади параллелограмма сторон вектора есть площадь параллелограмма.
Можно показать, что площадь этого параллелограмма (произведение основания и высоты) равна длине перекрестного произведения этих двух векторов. Площадь параллелограммаплощадь параллелограмма, образованного элементами a и b, определяется какплощадь=∣a×b∣шаг 2:
Показать изображение
Пример 25. Найдите площадь параллелограмма, у которого a = 3i + j
Итак, если мы хотим вычислить площадь этого параллелограмма прямо здесь, который определяется или создается двумя векторами-столбцами матрицы, нам буквально нужно просто найти определитель матрицы. Два вектора составляют параллелограмм, их величины — это просто длины того параллелограмма, который они составляют, когда вы умножаете величины двух векторов, а затем умножаете произведение на синус угла между ними, вы получите площадь параллелограмма, которая равна . А (1,1), б (2,0) и в (3,3).
Показать изображение
Формула площади параллелограмма, определение, примеры решения
Обычно, когда мы пытаемся узнать площадь треугольника, мы обычно находим значение по формуле формулы Герона.
Итак, если мы хотим вычислить площадь этого параллелограмма прямо здесь, который определяется или создается двумя векторами-столбцами матрицы, нам буквально нужно просто найти определитель матрицы. Площадь вектора параллелограмма = вектор x вектор b.
Показать изображение
Math Plane Трехмерное пространство и векторы
Значит, площадь этого параллелограмма равна. Матрица, составленная из этих двух векторов, имеет определитель, равный площади параллелограмма. Задача состоит в том, чтобы найти площадь параллелограмма.
Показать изображение
Разное 10 Найти единичный вектор, параллельный диагонали параллелограмма
Вы должны помнить, что площадь любой двумерной или трехмерной фигуры является векторной величиной. Можно показать, что площадь этого параллелограмма (произведение основания и высоты) равна длине перекрестного произведения этих двух векторов.
Вычислите площадь параллелограмма со сторонами, состоящими из векторов:
Показать изображение
Учебник по физике Векторное произведение двух векторов
Формула площади параллелограмма сторон вектора есть площадь параллелограмма. Задача состоит в том, чтобы найти площадь параллелограмма. Матрица, составленная из этих двух векторов, имеет определитель, равный площади параллелограмма.
Показать изображение
Площадь параллелограмма в векторной форме при смежных сторонах
Площадь параллелограмма = |a × b| знак равно Смежные стороны векторов. ‖ ты ‖ ‖ v ⊥ ‖.
Показать изображение
Параллелограмм ABCD натянут на векторы χ A i и χ A
В вопросе 6 используйте векторное произведение и определите площадь параллелограмма, образованного следующими двумя векторами: Мы будем хорошо использовать эту концепцию в этом объяснении концепции площади треугольника, образованного векторами.
Глава 10 векторной алгебры класса 12 (термин 2) с точки зрения концепции.
Показать изображение
PPT 10.4 Перемножение вектора, ортогонального двум заданным
Вы должны помнить, что площадь любой двумерной или трехмерной фигуры является векторной величиной. Величина площади параллелограмма равна 16. Здесь a и b — векторы двух сторон параллелограмма.
Показать изображение
Пример 25. Найдите площадь параллелограмма, у которого a = 3i + j
Площадь параллелограммаплощадь параллелограмма, образованного элементами a и b, определяется какплощадь=∣a×b∣шаг 2: В вопросе 6 используйте векторное произведение и определите площадь параллелограмма, образованного следующими двумя векторами: ‖ ты ‖ ‖ v ⊥ ‖.
Показать изображение
= √ (64+64+64) = √192.
Ищите концепции или бросьте свою домашнюю задачу! Даны два вектора в виде (xi+yj+zk) двух смежных сторон параллелограмма. Обычно, когда мы пытаемся узнать площадь треугольника, мы обычно находим значение по формуле формулы Герона. Пусть вектор = i вектор + 2j вектор + 3k вектор. Площадь параллелограмма = |a × b| знак равно Определители площади решаются быстро и легко, если вы знаете, как решить определитель 2 × 2. Два вектора составляют параллелограмм, их величины — это просто длины того параллелограмма, который они составляют, когда вы умножаете величины двух векторов, а затем умножаете произведение на синус угла между ними, вы получите площадь параллелограмма, которая равна . Нарисуйте его и найдите область, чтобы проверить свой результат: Эти два вектора образуют две стороны параллелограмма.
Вычислите площадь параллелограмма со сторонами, состоящими из векторов: Мы будем хорошо использовать эту концепцию в этом объяснении концепции площади треугольника, образованного векторами.
Найдите площадь параллелограмма, смежные стороны которого заданы векторами. Формула площади параллелограмма сторон вектора есть площадь параллелограмма. Площадь параллелограмма, образованного двумя векторами, равна величине векторного произведения. Матрица, составленная из этих двух векторов, имеет определитель, равный площади параллелограмма. Направление любого вектора поверхности всегда перпендикулярно поверхности; Предположим, что даны два вектора и в двумерном пространстве, которые не лежат на одной прямой. Площадь параллелограмма означает поверхность в плоскости векторов, которая на самом деле является вектором поверхности. Значит, площадь этого параллелограмма равна.
А (1,1), б (2,0) и в (3,3). Перепишите v как сумму двух компонент, параллельных u и ортогональных u. Смежные стороны векторов. Площадь параллелограммаплощадь параллелограмма, образованного элементами a и b, определяется какплощадь=∣a×b∣шаг 2: Просмотрите более 5 миллионов решений для домашних заданий и учебников, объяснения концепций, видеоролики и многое другое.
И вы должны сделать это, потому что это может быть отрицательным. Он всегда перпендикулярен своей плоскости. Пусть v ⊥ — ортогональная компонента. Задача состоит в том, чтобы найти площадь параллелограмма. Поэтому ваш ответ правильный 0.
Сложение и вычитание векторов
Горячая математикаЧтобы добавить или вычесть два вектора, добавьте или вычтите соответствующие компоненты.
Позволять ты → знак равно 〈 ты 1 , ты 2 〉 а также в → знак равно 〈 в 1 , в 2 〉 быть два вектора.
Тогда сумма ты → а также в → это вектор
ты → + в → знак равно 〈 ты 1 + в 1 , ты 2 + в 2 〉
Разница ты → а также в → является
ты → − в → знак равно ты → + ( − в → ) знак равно 〈 ты 1 − в 1 , ты 2 − в 2 〉
Сумма двух и более векторов называется равнодействующей.
Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Метод параллелограмма:
Нарисуйте векторы так, чтобы их начальные точки совпадали. Затем нарисуйте линии, чтобы сформировать полный параллелограмм. Диагональ из начальной точки в противоположную вершину параллелограмма является равнодействующей.
Добавление вектора:
- Поместите оба вектора ты → а также в → в той же начальной точке.
- Завершите параллелограмм. Результирующий вектор ты → + в → является диагональю параллелограмма.
Вычитание векторов:
- Завершите параллелограмм.
- Проведите диагонали параллелограмма из начальной точки.
Метод треугольника:
Нарисуйте векторы один за другим, помещая начальную точку каждого последующего вектора в конечную точку предыдущего вектора. Затем проведите равнодействующую от начальной точки первого вектора до конечной точки последнего вектора. Этот метод также называют метод «голова к хвосту» .
Добавление вектора:
Вычитание векторов:
Пример:
Найти) ты → + в → и (б) ты → − в → если ты → знак равно 〈 3 , 4 〉 а также в → знак равно 〈 5 , − 1 〉 .
Подставить заданные значения ты 1 , ты 2 , в 1 а также в 2 в определение сложения векторов.
ты → + в → знак равно 〈 ты 1 + в 1 , ты 2 + в 2 〉 знак равно 〈 3 + 5 , 4 + ( − 1 ) 〉 знак равно 〈 8 , 3 〉
Перепишите разницу ты → − в → как сумма ты → + ( − в → ) .
Нам нужно определить компоненты − в → .
Напомним, что − в → является скалярным множителем − 1 раз в . Из определения скалярного умножения имеем:
− в → знак равно − 1 〈 в 1 , в 2 〉 знак равно − 1 〈 5 , − 1 〉 знак равно 〈 − 5 , 1 〉
Теперь добавьте компоненты ты → а также − в → .

 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). 5.
5. Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). 5.
5.