Формула дискриминанта d1: Решите уравнение, используя формулу корней квадратного уравнения с четным коэффициентом при х : а)…

Квадратные уравнения — презентация онлайн

1. Квадратные уравнения

2. Квадратное уравнение

Квадратным уравнением называется
уравнение вида
ах2 + bx + c = 0,
где а, b, с – числа, а ≠ 0, х – неизвестное.
3х2 — 2x + 7 = 0;
-3,8х2 + 67 = 0;
18х2 = 0 .
Квадратное уравнение называют еще уравнением
второй степени с одним неизвестным.

3. Коэффициенты квадратного уравнения

Числа а, b и с называют коэффициентами
квадратного уравнения.
ах2 + bx + c = 0,
старший
свободный
коэффициент
второй
коэффициент
член
3х2 + 4x — 8 = 0,
старший
свободный
коэффициент
второй
коэффициент
член

4. Неполное квадратное уравнение

Квадратное уравнение, в котором хотя бы
один из коэффициентов b или с равен нулю,
называется неполным.
-11х2 = 0;
5х2 + 13х = 0;
-24х2 +1 = 0.

5. Виды неполных квадратных уравнений и их корни

ах2 + c = 0, где с ≠ 0.
c
2
Тогда x
a
c
Если c 0 ,
0
Если a
,то корни
a
1.
c
c
x , x
1
2
a
a .
а)
1
3x 0
3
2
б) -х2-4 = 0
1
3x
3
2
х2 = -4
то
1
x
9
2
корней нет .
1
1
x или x .
3
3
нет корней.

6. Виды неполных квадратных уравнений и их корни

2.
ах2 + bx = 0, где b ≠ 0.
b
Тогда x ∙ (ax +b) = 0. Корни: х1 =0 и х2 = .
a
а) 2х2 + 7x = 0
x ∙ (2x +7) = 0
7
х = 0 или 2х + 7 = 0, т.е. х = .
2
Ответ: 0 и -3,5.
б) -х2 + 5x = 0
Ответ: 0 и 5.
-x ∙ (x — 5) = 0
х = 0 или х = 5.

7. Виды неполных квадратных уравнений и их корни

3.
ах2 = 0
Имеем единственный корень х = 0 .
128х2 = 0
х2 = 0 х = 0.
-3,8х2 = 0
х2 = 0
х = 0.

8. Метод выделения полного квадрата

Решить уравнение х2 + 14x + 24 = 0.
Решение.
х2 + 14x + 24 = (х2 + 14x + 49) – 49 + 24 =
= (х + 7)2 – 25.
(х + 7)2 – 25 = 0,
(х + 7)2 = 25.
х + 7 = -5 или х + 7 = 5.
х1 = -12;
х2 = -2.
Ответ: -12; -2.

9. Формула корней квадратного уравнения

Корни квадратного уравнения ах2 + bx + c = 0
можно найти по формуле
b D
x
, где D = b2 – 4ac 2a
дискриминант квадратного уравнения.

10. Формула корней квадратного уравнения

Возможны 3 случая:
1.
D > 0.
Тогда уравнение имеет 2 различных корня:
b D,
x
1
2a
b D
x
2
2a
2х2 + 7x — 4 = 0.
a = 2, b = 7, c = -4.
D = 72 – 4 ∙ 2 ∙ (-4) = 81 > 0,
7 81
x
4 ,
1
2 2
.
7 81 1 .
x
2
2 2
2

11. Формула корней квадратного уравнения

2.
D = 0.
Тогда уравнение имеет единственный корень:
b
x
2a
х2 — 4x + 4 = 0.
4
2
D = (-4) – 4 ∙ 1 ∙ 4 = 0, x
2.
2 1

12. Формула корней квадратного уравнения

3.
D < 0.
Тогда уравнение не имеет корней,
т. к. не существует D .
3х2 — x + 7 = 0.
D = (-1)2 – 4 ∙ 3 ∙ 7 = -83 < 0,
значит корней нет.

13. Корни квадратного уравнения с четным вторым коэффициентом

Если b = 2k, то корни уравнения
ах2 + 2kx + c = 0 находятся по формуле
b
k D D1
1
,
x
2
a
2a
2
d
b
2
где D k ac ac .
1
4
2

14. Корни квадратного уравнения с четным вторым коэффициентом

1.
Решить уравнение
х2 + 18x + 32 = 0.
а = 1; b = 18
k = b : 2 = 9; c = 32.
D1 = D : 4 = (18 : 2) – 1 ∙ 32 = 49 > 0,
значит уравнение имеет 2 корня:
9 49
x
16, x 9 7 2.
1
2
1

15. Корни квадратного уравнения с четным вторым коэффициентом

2.
3.
Решить уравнения
3х2 + 2x + 1 = 0.
а = 3; b = 2
k = b : 2 = 1; c = 1.
D1 = D : 4 = 12 – 1 ∙ 3 = -2 < 0,
значит корней нет.
196х2 — 28x + 1 = 0.
а = 196; b = -28
k = b : 2 = -14; c = 1.
D1 = D : 4 = (-14)2 – 196 = 0,
14
1
значит уравнение имеет 1 корень x
.
196 14

16. Приведенное квадратное уравнение

Приведенное квадратное уравнение – это
уравнение вида х2 + px + q = 0.
х2 + 14x + 24 = 0.
Для каждого квадратного уравнения можно
записать равносильное ему приведенное
уравнение, разделив обе части квадратного на
старший коэффициент.
5х2 + 3x — 2 = 0
х2 + 0,6x – 0,4 = 0.

17. Формула корней приведенного квадратного уравнения

х2 + px + q = 0.
2
p
p
x q
2
2
х2 — x — 6 = 0.
p = -1, q = -6,
2
1
1
1
25 1 5
x ( 6)
,
2
2
4 2 2
2
1 5
1 5
x 2, x 3.
1
2
2 2
2 2

18. Теорема Виета

Теорема. Если х1 и х2 – корни приведенного
квадратного уравнения х2 + px + q = 0, то
х1 + х2 = -р
формулы Виета
х1 ∙ х 2 = q
х1 = -1; х2 = 3 – корни уравнения х2 — 2x — 3 = 0.
р = -2, q = -3.
х1 + х2 = -1 + 3 = 2 = -р,
х1 ∙ х2 = -1 ∙ 3 = q.

19. Теорема Виета для квадратного уравнения общего вида

Теорема. Если х1 и х2 – корни квадратного
уравнения а х2 + bx + c = 0, то
b
x x
1
2
a
c
x x
1
2
a
х1 = 1,5; х2 = 2 – корни уравнения 2 х2 — 7x + 6 = 0.
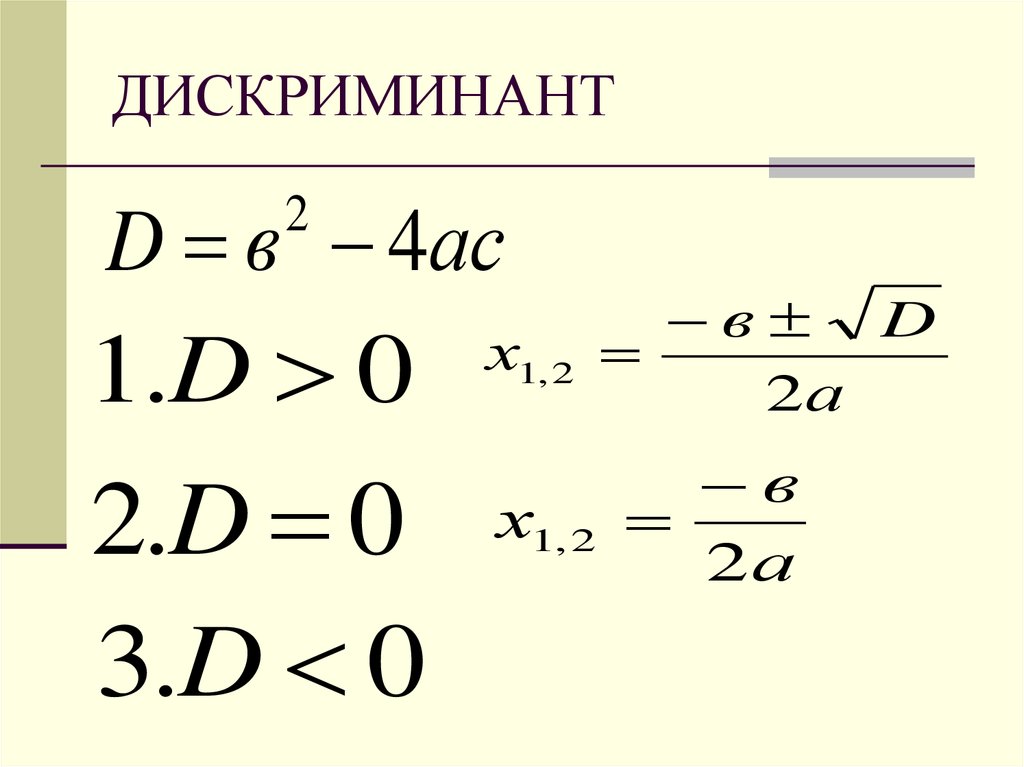
х1 + х2 = 3,5,
х1 ∙ х2 = 3.

20. Теорема, обратная теореме Виета

Теорема. Если числа х1, х2, р и q связаны условиями
х1 + х2 = -р
х1 ∙ х 2 = q
то х1 и х2 – корни приведенного
квадратного уравнения х2 + px + q = 0.
Составим квадратное уравнение по его корням
x 2 3
1
и
p x x 4
1
q x
1
2
x 2 3.
2
p 4;
x (2 3 ) (2 3 ) 4 3 1.
2
Искомое уравнение имеет вид х2 — 4x + 1 = 0.

21. Квадратный трехчлен

Квадратным трехчленом называется
многочлен вида а х2 + bx + c,
где а, b, с – числа, а ≠ 0, х – переменная.
3х2 — 2x + 7;
Корни квадратного трехчлена а х2 + bx + c –
это корни уравнения а х2 + bx + c = 0 .

22. Разложение квадратного трехчлена на линейные множители

Теорема. Если х1 и х2 – корни квадратного
трехчлена а х2 + bx + c, то
а х2 + bx + c = а(х — х1)(х — х2 ).
Разложить на множители 12 х2 — 5x — 2.
1
2 — корни уравнения 12 х2 — 5x – 2= 0.
x ;x
1
4 2 3
Значит 12 х2 — 5x – 2 =
1
2
4 x 3 x (4x 1)(3x 2).
4
3

23. Неприводимый многочлен

Если квадратный трехчлен ах2 + bx + c не имеет
корней, то соответствующий многочлен
b
c
2
x x (со старшим коэффициентом 1)
a
a
называется
неприводимым
многочленом
второй степени (так как его невозможно
разложить на множители меньшей степени).
Квадратный трехчлен 5х2 + 3x + 2 не имеет корней.
Его невозможно разложить на множители первой
степени. Можно вынести числовой коэффициент за
скобки 5х2 + 3x + 2 =5(х2 + 0,6x + 0,4).

24. Уравнения, содержащие неизвестное в знаменателе

1.
2.
3.
4.
Схема решения:
Найти общий знаменатель дробей, входящих
в уравнение.
Умножить обе части уравнения на общий
знаменатель.
Решить получившееся уравнение.
Исключить из его корней те числа, которые
обращают в нуль общий знаменатель.

25. Уравнения, содержащие неизвестное в знаменателе

t
t 2
1
t 1 t 2
Общий знаменатель: (t + 1)(t — 2).
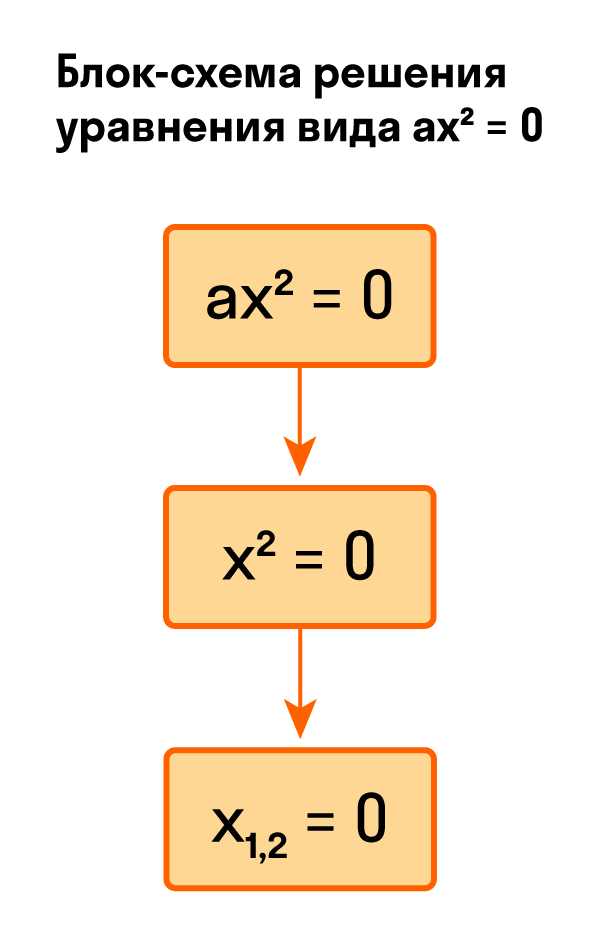
Умножим на него обе части уравнения:
t(t – 2) – (t +2)(t + 1) = 1∙(t + 1)(t – 2)
t2 – 2t – t2 – 3t – 2 = t2 – t – 2
t2 + 4t = 0
t(t + 4) = 0
t1 = 0, t2 = -4.
Ни одно из чисел не обращает в нуль
общий знаменатель.
Ответ: 0; -4.

26. Уравнения, содержащие неизвестное в знаменателе

2
1
6 x
2
2
x 9 x 3x x(x 3)
Общий знаменатель: х(х – 3)(х + 3) . Тогда:
2х – (х – 3) = (6 – х)(х – 3)
х2 – 8х + 15 = 0
х1 = 3 – посторонний корень, так как при х = 3
общий знаменатель х(х – 3)(х + 3) = 0.
х2 = 5 – корень.
Ответ: 5.

27. Биквадратные уравнения

Уравнение вида ах4 + bx2 + c = 0,
где а ≠ 0, b и с — заданные числа, называется
биквадратным.
9х4 + 17х2 — 2 = 0
Заменой х2 = t сводится к квадратному уравнению.
9t2 + 17t — 2 = 0
1
1
2
t
или t 2
x или x 2 2
9
9
Ответ:
1 1
,
.
3 3
1
1
x , x
1
2
3
3
Нет корней

28.

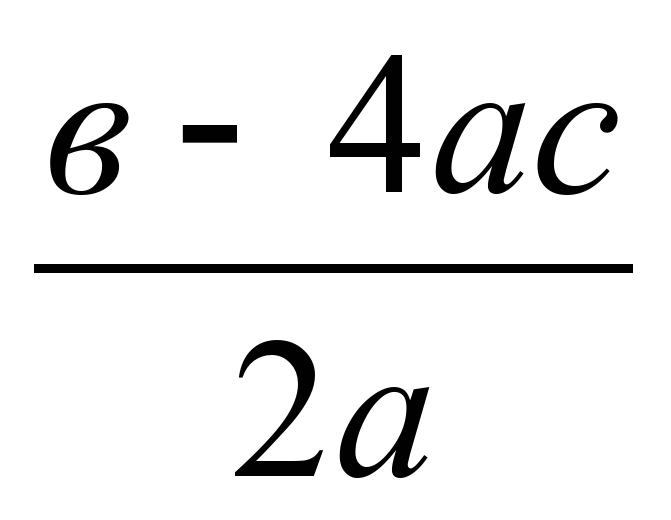Решение уравнений методом замены неизвестногоx 5 x 7 13 0.
x 7 5 x 7 6 0.
t x 7 , x 7 t2
t 2 5t 6 0.
t 1
x 7 1
Нет корней
Ответ: 43.
t 6.
x 7 6.
x 43.

29. Модуль

Модуль числа х – это расстояние от начала
отсчета до точки х на координатной прямой.
|x| = 6 означает, что расстояние от начала отсчета до
точки х равно 6.
6
-6
|а| =
6
О
6
х
а, если а > 0
-а, если а < 0
0, если а = 0

30. Уравнения, содержащие неизвестное под знаком модуля

| х2 — 2х — 39| = 24.
х2 — 2х — 39 = 24
х1 = 9; х2 = -7
Ответ: 1,6; 1; -1; 6/11.
х2 — 2х — 39 = -24
х3 = -3; х4 = 5.

31. Уравнения, содержащие неизвестное под знаком модуля

9х2
x > 0,
x
2
9х =0
x
x > 0,
9х2 – 1 = 0
1
x
3
1 .
Ответ:
3
x
= 0.
x
x < 0,
x
2
9х = 0.
-x
x < 0,
9х2 + 1 = 0.
нет решений

32.

Уравнения, содержащие неизвестное под знаком модуляМодули двух чисел равны тогда и только тогда,
когда эти числа равны или противоположны.
|8х2 — 4х + 1| = |3х2 + 9х — 7|.
8х2 — 4х + 1 = 3х2 + 9х – 7
х1 = 1,6; х2 = 1
Ответ: 1,6; 1; -1; 6/11.
8х2 — 4х + 1= –(3х2 + 9х – 7)
х3 = -1; х4 = 6/11.

Решение квадратных уравнений | План-конспект урока по алгебре (8 класс) по теме:

                               Конспект урока по алгебре в 8 классе

             на тему «Решение квадратных  уравнений по  формуле №2

                             с чётным  вторым  коэффициентом»

Цели урока:

                     1. Вывести формулу корней квадратного уравнения с четным вторым

                        коэффициентом.

                     2. Продолжить формирование навыка решений квадратных уравнений .

                     3.Расширение знаний и навыков решения квадратных уравнений.

                     4.Развитие интеллекта , сознательного отношения к учебе.

                                      СОДЕРЖАНИЕ   УРОКА:

I .ПРОВЕРКА   ДОМАШНЕГО   ЗАДАНИЯ

 1.В парах по заранее  приготовленным заданиям на доске проверяют правильность выполненных уравнений.

№542  а)5х2= 9х+2

              5х2 —  9х-2 =0

                Д=b2 – 4ac=81+40=121,Д >0 ,2 корня :

х1,2 =

Х1,2 = ;  х1=2; х2=-0,2

     

           б)-х2 =5х -14

              -х2 —5х +14 =0

               х2 +5х  — 14=0,          

         Д=b2 – 4ac=25+56= 81; Д >0 ,2 корня : х1,2  === — 7; 2

           в) 6х+9 =х2

               х2 – 6х – 9=0

         

Д=b2 – 4ac=35+36=72; Д >0 ,2 корня : х1,2  === 3 +3;3 —  3;

          г ) z -5 = z2 -25

           z2 –z -20 =0

   

   Д=b2 – 4ac=1+80=81; Д >0 ,2 корня : х1,2  === 5 ; — 4

           д ) у2 =52у -576

              у2   -52у +76 =0

Д=b2 – 4ac=2704 -2304=400; Д >0 ,2 корня : х1,2  === 36 ; -16

            е ) 15 у2 -30 =22у +7

                  15 у2 -22у  -37 =0

Д=b2 – 4ac=484 +2220=2704; Д >0 ,2 корня : х1,2  === -1; 2

       ж ) 25p2 -10p +1=0

   

Д=b2 – 4ac=100-100=0; Д =0 ,1 корень : х= = 0,2

       з ) 299х2 +100х =500- 101х2

           400х2 +100х-500 =0| : 100

           4х2 + х -5 =0

       Д=b2 – 4ac=1+80 =81; Д >0 ,2 корня : х1,2  === 1; -1

№543

        а) 25=26х-х2 

          х2 -26х +25 =0

     

      Д=b2 – 4ac=676-100 =576; Д >0 ,2 корня : х1,2  === 25 ;1

        б)3х2 =10 -29х

           3х2 +29х -10 =0

Д=b2 – 4ac=841+120= 961; Д >0 ,2 корня : х1,2  === -10 ;

       в )у2 = 4у +96

         у2 — 4у -96 =0

       

Д=b2 – 4ac=16+384= 400; Д >0 ,2 корня : х1,2  === -8 ;12

      г   )  3p2 +3=10р

           3p2 — 10р  +3 =0

     Д=b2 – 4ac=100-36= 64; Д >0 ,2 корня : х1,2  === 3 ;

    д )   х2 -20х=20х+100

          х2 -40х -100 =0

Д=b2 – 4ac=1600+400= 2000; Д >0 ,2 корня :

х1,2  ===20+10; 20 -10;

     е ) 25х2 -13 х =10х2 -7

          15х2 -13х +7 =0

Д=b2 – 4ac=169 -420= -259; Д

II. УСТНЫЕ   УПРАЖНЕНИЯ

1.Докажите ,что -1 является корнем уравнения : х3 +1=0, х2 -1=0,х2+х =0,х2+3х+2=0.

2.Укажите коэффициенты квадратного уравнения:

2х2 -5х+10 = 0 , 2+х+х2=0 ,   х2 +3х -0,5 =0    , 5х2 -4х =3   , 0,5х2 –х -3 =0 , 8х -7 =х2

1-3х-2х2 =0   ,    11-2х2 =4х.

3.Замените уравнение равносильным ему приведённым квадратным уравнением:

3х2-6х -12 =0;    х2 -3х +6=0;       -х2+2х -2 =0;   10х2 -20х +30 =0.

4.Имеет ли квадратное уравнение корни ; если имеет, то сколько; рациональными или иррациональными числами являются   корни:  4х2-12х +9 =0 , 2х2+3х -9 =0;

5х2-х+2=0 ;  4х2+7х -1 =0;   х2-3х +5 =0;   3х2+2х -2 =0;   3х2-11х +10=0; 25х2+10х+1=0

5.Подберите какие-нибудь значения с , при   которых  уравнение имеет   корни:

    х2-3х +с =0;                5х2- 2х +с =0.

III.АКТУАЛИЗАЦИЯ ОПОРНЫХ  ЗНАНИЙ :

(проводится в виде  диктанта с взаимопроверкой в парах, двое учащихся выполняют задания на отворотах доски)

1. Запишите общий вид  квадратного  уравнения  и  формулу  дискриминанта:

2.При каком условии полное квадратное уравнение :

Имеет  единственный корень                         |          не имеет  корней

3.Вычислите дискриминант  квадратного уравнения :

3х2 -8х — 3=0                                                    |              2х2 -3х -2=0

4.Решите квадратное уравнение :

х2-4х+9=0                                                      |               х2-6х+5=0

5. Подберите  какое-нибудь значение  с , при котором уравнение имеет  корни:

  х2 -3х +с=0;                                                  |             х2-2х+с=0.

IV.     ИЗУЧЕНИЕ   НОВОГО     МАТЕРИАЛА:

 Поручить уч-ся самостоятельно изучить в течение 5 минут  вывод формулы из п.21(стр.115).Затем сильный ученик выполняет вывод на доске ,  дети записывают в тетради. Для квадратных уравнений, у которых второй коэффициент является четным числом , формулу корней  удобно записывать в другом виде:

               ах2 +2kх +с =0

     D=b2 – 4ac=4k2-4ас =4(k2 –ас),D1 = k2 –ас; если D1>0,  то

 х1,2  ===, где D1  = k2 –ас ,

если D1

   Привести  вторую запись данной формулы при условии  , если  в приведенном квадратном  уравнении  второй коэффициент чётный :

х2 +2kх +с =0; , где b =2k , то есть : х1,2 =   (формулаII)

   Для быстрого запоминания формулы  привожу стихотворные строки:

 «  …б  со знаком взяв обратным  , мы на два его поделим  ,

И от корня аккуратно  знаком   „минус-плюс”  отделим ,

а под корнем очень кстати – половина  б в квадрате, минус це (с)  и вот решенье небольшого уравненья»

  V.    ЗАКРЕПЛЕНИЕ   ИЗУЧЕННОГО:

 Решить на доске : №539 (а,б,в,ж)

    а )3х2 -14х+16=0                                           б) 5х2 -16х+3=0                                          

Д1=72-3·16=1, х1,2 == 2 ;2                 Д1=82-15=49, х1,2 == ;3

в ) х2  +2х-80=0                                            ж)7z2 -20z+14=0                                      

х1,2 = -1=-19 =8; -10                Д1=102-7∙14=2, х1,2 =.

Обучающая самостоятельная работа :№539 (г, д , е, з)   с последующей проверкой. Ответы :

г	23;  -1
д	5,5; 3,5
е	-1; 2
з	5+ 5 ; 5 — 5

VI.  ИТОГ   УРОКА:

1.воспроизвести буквенную запись формулы на доске.

2.Словесная формулировка нового правила :

   А ) Что означаетД1 ?

   Б)Как быстро запомнить формулу корней?

VII  . Приёмы устного решения некоторых квадратных уравнений

Сообщение о случаях устного решения отдельных видов квадратных уравнений готовится с  помощью учителя заранее сильным учеником.

В сообщении ученика приводятся приёмы для квадратных  уравнений ах2+bх+с =0:

1.Если а+b+с=0 , то х1 =1 , х2 =;

2.Если а+ с =b  , то х1 = -1;  х2 =.

Решаем устно :

1)   х2 +17х-18=0,   2) х2 -19х+18=0;    3)13х2 -29х+16=0 ;     4) х2 +2009х-2010=0;

5) х2 -5х-6=0  ;         6)17 х2 -19х-36=0;         7) х2 +17х+16=0

1	2	3	4	5	6	7
1;  -18	1;18	1;	1,-2010	-1;6	-1;	-1;-16

VII  . ДОМАШНЕЕ ЗАДАНИЕ :

 запомнить выведенные формулы п21учебника,№540,№543.          

         

Квадратичная формула

Квадратичная формула

Квадратичная формула

Давайте заполним квадрат для

топор ² + бх + в

1. а(х ² + б/а х) + в
2.    -б
   
   2а       
   
   
3.     б ²
   
   4а ²     
   
4. б б ²           б ²           
   а( х ²   + х + — ) + в                 
   а 4а ²        4a ²     
   
5. б б ² б ²           
   а[ ( х ²   + х + ) — ]  + в                 
   а 4а ² 4а ²     
   
6. б б ²           
   а [ ( х + ) ²  — ]  + в                 
   2а 4a ²               
7. б б ²           
   а( х + ) ²   — + в                 
   2а 4а              
   

 

А что, если мы хотим решить уравнение

топор ² + Ьх + с = 0

Мы можем эквивалентно решить

б б ²           
а( х + ) ²   — + с = 0               
2а 4а              

корневым методом

б б ²           
а( х + ) ²   = — в                 
2а 4а              

б б

2 с
( х + ) ²   = —                    
2а 4а ² а     

b ²     —    4ac  
=                                   
4а ²     

Теперь извлеките квадратный корень из обеих частей, чтобы получить

.

Наконец вычтите b/2a из обеих частей, чтобы получить квадратичную формулу.

 

Квадратичная формула решение  ax 2 + bx + c = 0 равно

Запомните эту формулу!

Пример

Решать

3x ² — 2x + 5

Решение

     а = 3         б = -2          с = 5

У нас есть

---

Дискриминант

Мы определяем дискриминант как

Д = б ²  — 4ас

является удобной мерой определения того, сколько существует действительных корней (решений) являются. Обратите внимание, что D — это выражение внутри знака квадратного корня в квадратной формуле. Поскольку площадь корень отрицательного числа дает только комплексные числа, мы видим, что если D отрицательно, то действительных корней не будет. Если D положительный число, то квадратичная формула даст два корня (один для плюса и один минус). Если D равно 0, то плюс 0 и минус 0 — это одно и то же число, поэтому мы получаем только один корень. таблица ниже резюмирует.

Д	Количество действительных корней
Положительный	2
Отрицательный	0
Ноль	1

Пример:

Сколько корней имеет уравнение:

3x ² — 5x + 1 = 0

У нас есть

Д =  25–12  >  0

следовательно, есть два действительных корня.

---

Сумма и произведение корней

Так как два корня квадратного числа равны

и

то если мы сложим два корня, то получим:

и если мы умножим два корня, мы получим

Обратите внимание, что если a равно 1, то сумма корней равна -b и произведение c. Это относится к факторингу, когда мы находим два числа, которые складываются с b и умножить на с.

---

Пример

Чему равны сумма и произведение корней

4x ² -3x + 2

Решение

Сумма

б          3
— =           
а          4

а произведение корней равно

с 2           1
«=» =                                     
а 4           2

---

Определение квадратного уравнения из корней

Если мы знаем корни квадратного числа, то легко найти исходное число. квадратичным, используя формулу нулевого произведения в обратном порядке.

Пример

Найдите уравнение квадратного уравнения, которое имеет корни 2 и -4/3.

Решение

Мы можем написать:

(х — 2)(х — (-4/3)) = (х — 2)(х + 4/3)

4 8 2           8
=  х ² + х — 2х —         = х ² —       х —        
3 3 3           3

Упражнение:  

Найдите квадратное число со следующими корнями

1. 0 и -1/2

2. 3 — и     3 +

3. 4 + я     и     4 — я

 

---

Назад на страницу квадратичных функций и линейных неравенств

Назад на страницу «Основная алгебра, часть II»

Назад к математике Домашняя страница отдела

электронная почта Вопросы и предложения

Примечания о дискриминанте квадратного уравнения

Рецепт дискриминанта используется для отслеживания количества схем квадратного уравнения. В полиномиальной математике дискриминант — это имя, данное артикуляции, которая появляется под знаком квадратного корня (экстремистский) в квадратичном рецепте.

Рецепт для дискриминанта:

Дискриминант многочлена является компонентом его коэффициентов и обозначается заглавной буквой «D» или дельта-образом (Δ). Он показывает идею, лежащую в основе любого квадратичного условия, где a, b и c являются нормальными числами.

Подлинные корни или количество x-блоков эффективно отображаются с квадратичным условием. Этот рецепт используется, чтобы увидеть, являются ли основные основания квадратичного условия подлинными или несуществующими.

Формула дискриминанта в квадратичном условии ax² + bx + c = 0 равна

△ = b² − 4ac

По какой причине важна формула дискриминанта?

Используя дискриминант, число оснований квадратичного условия не является полностью фиксированным. Дискриминант может быть уверенным, отрицательным или нулевым. Зная значение детерминанта, идея корней не исчерпывается следующим образом:

• Если дискриминантная оценка положительна, квадратичное условие имеет два истинных и безошибочных расположения.
• Если дискриминантная оценка равна нулю, квадратичное условие имеет только одно расположение или два истинных и эквивалентных расположения.
• Если дискриминантная оценка отрицательна, квадратичное условие не имеет истинных механизмов.

Дискриминантная формула для решения квадратного уравнения:

Поскольку квадратичное условие имеет уровень 2, таким образом, оно будет иметь два порядка. Таким образом, переменная x, для которой выполняется условие, имеет две положительные стороны. Как указано в дискриминантном рецепте, квадратичное условие структуры ax2 + bx + c = 0 имеет два корня, определяемых формулой:

x = -(b ±√D)/2a

где D = b² − 4ac

Знаки ± демонстрируют два безошибочных ответа на ситуацию. В случае, если дискриминант оказывается отрицательным, данное условие не имеет настоящих корней, поскольку отрицательное число под квадратным корнем будет рассматриваться как несуществующее, а не подлинное число.

Дискриминантная формула для решения квадратного уравнения:

Поскольку квадратичное условие имеет уровень 2, таким образом, оно будет иметь две схемы. Таким образом, переменная x, для которой выполняется условие, имеет две положительные стороны. Как указано в дискриминантном рецепте, квадратичное условие структуры ax² + bx + c = 0 имеет два корня, определяемых формулой:

x = (- b ± √ (b² – 4ac))/2a

где D = b² − 4ac

Знаки ± демонстрируют два безошибочных ответа на ситуацию. В случае, если дискриминант оказывается отрицательным, данное условие не имеет настоящих корней, поскольку отрицательное число под квадратным корнем будет рассматриваться как несуществующее, а не подлинное число.

Квадратное уравнение имеет вид x = (- b ± √ (b² – 4ac))/2a. Таким образом, это можно составить как x = (- b ± √ D)/2a. Поскольку дискриминант D находится в квадратном корне, мы можем определить идею корней, полагаясь на то, является ли D положительным, отрицательным или нулем.

Природа корней Когда D > 0

Тогда приведенный выше рецепт принимает вид

x = (- b ± √ положительное число)/2a

и также дает нам два подлинных и различных корня. Соответственно, квадратичное условие имеет два настоящих и различных корня, когда b² – 4ac > 0.

Природа корней Когда D < 0

Тогда приведенный выше рецепт принимает вид

x = (- b ± √ отрицательное число)/ 2a

также дает нам два комплексных корня (которые уникальны), поскольку квадратное основание отрицательного числа является загадочным числом. Соответственно, квадратичное условие имеет два комплексных корня, когда b² – 4ac < 0,

Примечание: квадратичное условие никогда не может иметь один комплексный корень. Сложные корни обычно встречаются по два. т. е. в том случае, если a + bi является корнем, то a – bi является дополнительно корнем.

Природа корней Когда D = 0

Тогда, в этот момент, вышеприведенный рецепт принимает вид только один подлинный корень.