Формула для понижения степени синуса: Формулы понижения степени — урок. Алгебра, 10 класс.

Графики тригонометрических функций кратных углов. Основные формулы тригонометрии Формулы суммы и разности тригонометрических функций

Словари. Энциклопедии. История. Литература. Русский язык » Медицина » Графики тригонометрических функций кратных углов. Основные формулы тригонометрии Формулы суммы и разности тригонометрических функций

В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.

Итак, нам нужны косинус двойного угла и тригонометрическая единица:

Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:

и подставить его в косинус двойного угла, то получим:

Это — еще одна формула косинуса двойного угла:

Эта формула — ключ к получению формулы понижения степени:

Итак, формула понижения степени синуса:

Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:

Теперь из тригонометрической единицы выразим синус:

Подставим это выражение в формулу косинуса двойного угла:

Получили еще одну формулу косинуса двойного угла:

Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.

Таким образом, формула понижения степени косинуса:

Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:

Так как тангенс — отношение синуса к косинусу то формула для тангенса:

Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:

Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.

Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.

Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.

Основные тригонометрические тождества

Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.

Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .

Формулы приведения

Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.

Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .

Формулы сложения

Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.

Формулы двойного, тройного и т.д. угла

Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.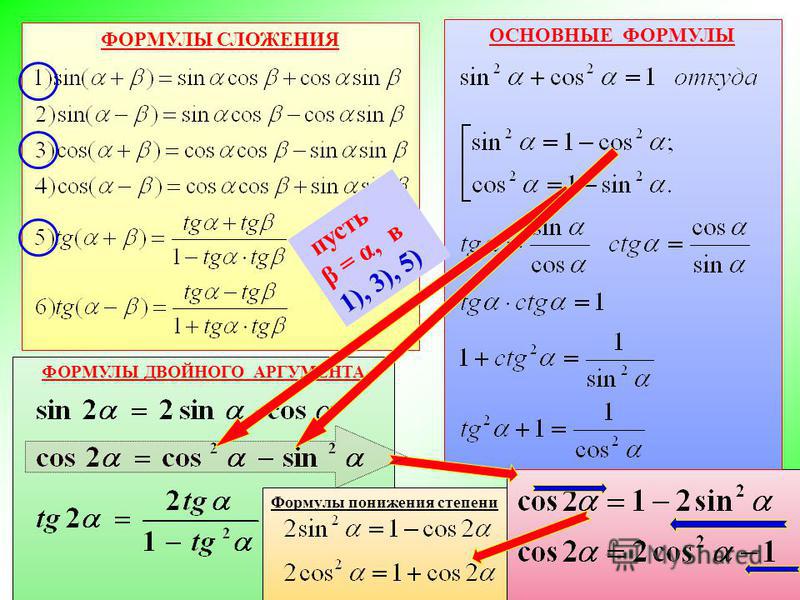 д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.

Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .

Формулы половинного угла

Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.

Их вывод и примеры применения можно посмотреть в статье .

Формулы понижения степени

Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.

Формулы суммы и разности тригонометрических функций

Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.

Формулы произведения синусов, косинусов и синуса на косинус

Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .

Универсальная тригонометрическая подстановка

Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.

Список литературы.

• Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М. : Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
• Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.

Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда

у 0 = sin x 0 .

Преобразуем это соотношение следующим образом:

Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение

у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.

Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.

График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.

Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции

у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π / x / 2 = 4π .

Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :

Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.

График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.

На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.

График функции

у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.

И, наконец, анимация, выполненная программой Maple:

Упражнения

1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.

а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3

б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3

в). y = tg 4x / 3 е). у = sin 2x / 3

2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).

3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.

4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом

π / 2 .

5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.

6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.

Тригонометричні функції.

Тригонометрические функции

Знаки тригонометрических функций

      Знаки чисел

sin α ,   cos α ,   tg α ,   ctg α

определяются тем, в каком квадранте (четверти) координатной плоскости   Oxy   лежит луч   OM   (рисунки 1, 2, 3, 4).

Рис.1. Знак sin α   Рис. 2. Знак cos α . Знак cos α cos α
Рис.3. Знак tg α                                            Рис.4. Знак сtg α     косинус – четная функция, а синус, тангенс и котангенс – нечетные функции период косинус, синус -2п, тангенс и котангенс—п

Графики тригонометрических функций

      На рисунках 1, 2, 3, 4 приведены графики тригонометрических функций

Рис.1. График функции   y = sin x

Рис.2. График функции   y = cos x

Рис.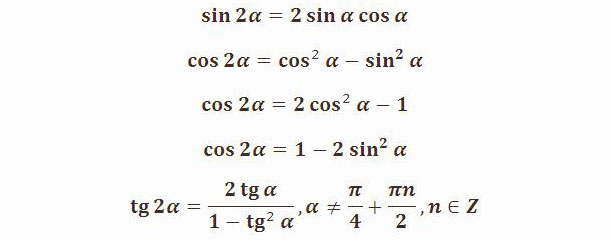 3. График функции   y = tg x

Рис.4. График функции   y = ctg x

Таблица формул приведения

Аргумент	Формула приведения
	синус	косинус	тангенс	котангенс
– α	– sin α	cos α
	cos α	sin α
	cos α	– sin α
π – α	sin α	– cos α
π + α	– sin α	– cos α
	– cos α	– sin α
	– cos α	sin α
2π – α	– sin α	cos α
2π + α	sin α	cos α

Связи между тригонометрическими функциями одного угла

sin2α + cos2α = 1

Тригонометрические функции суммы и разности двух углов

Формула	Название формулы
sin (α + β) = sin α cos β + cos α sin β	Синус суммы
sin (α – β) = sin α cos β – cos α sin β	Синус разности
cos (α + β) = cos α cos β – sin α sin β	Косинус суммы
cos (α – β) = cos α cos β + sin α sin β	Косинус разности
	Тангенс суммы
	Тангенс разности

Тригонометрические функции двойного угла

Формула	Название формулы
sin 2α = 2 sin α cos α	Синус двойного угла
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α	Косинус двойного угла
	Тангенс двойного угла

Формулы понижения степени для квадратов тригонометрических функций

Формула	Название формулы
	Выражение квадрата синуса через косинус двойного угла
	Выражение квадрата косинуса через косинус двойного угла
	Выражение квадрата тангенса через косинус двойного угла

 

Формулы понижения степени для кубов синуса и косинуса

Формула	Название формулы
	Выражение куба синуса через синус угла и синус тройного угла
	Выражение куба косинуса через косинус угла и косинус тройного угла

 

 

 

Выражение тангенса через синус и косинус двойного угла

 

Преобразование суммы тригонометрических функций в произведение

Формула	Название формулы
	Сумма синусов
	Разность синусов
	Сумма косинусов
	Разность косинусов
	Сумма тангенсов
	Разность тангенсов

 

 

Преобразование произведения тригонометрических функций в сумму

Формула	Название формулы
	Произведение синусов
	Произведение косинусов
	Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

Формула	Название формулы
	Выражение синуса угла через тангенс половинного угла
	Выражение косинуса угла через тангенс половинного угла
	Выражение тангенса угла через тангенс половинного угла

 

Тригонометрические функции тройного угла

Формула	Название формулы
sin 3α = 3sin α – 4sin3α	Синус тройного угла
cos 3α = 4cos3α –3cos α	Косинус тройного угла
	Тангенс тройного угла

 

      Предположим, что число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают   x = arcsin a, если выполнены два условия:

      Предположим, что число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают   x = arccos a, если выполнены два условия:

      Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают   x = arctg a, если выполнены два условия:

      Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают   x = arcctg a, если выполнены два условия:

      Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:

arcsin (– a) = – arcsin a ,

arccos (– a) = π – arccos a ,

arctg (– a) = – arctg a ,

arcctg (– a) = π – arcctg a .

        Простейшие тригонометрические уравнения

 Простейшими тригонометрическими уравнениями называют уравнения вида:

sin x = a ,     cos x = a ,     tg x = a ,     ctgx = a .

где a – произвольное число.

Решение уравнения   sin x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Решение уравнения   cos x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Решение уравнения   tg x = a

Обычная форма записи решения:
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

Решение уравнения   ctg x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

 

 

7.

3: Двойной угол, половинный угол и формулы приведения

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

19003

• OpenStax
• OpenStax

Развитие навыков

• Используйте формулы двойного угла, чтобы найти точные значения.
• Используйте формулы двойного угла для проверки тождества.
• Используйте формулы сокращения для упрощения выражения.
• Используйте формулы половинного угла, чтобы найти точные значения.

Велосипедные рампы, сделанные для соревнований (см. рисунок \(\PageIndex{1}\)) должны различаться по высоте в зависимости от уровня навыков участников. Для продвинутых участников угол, образованный рампой и землей, должен быть \(\theta\) таким, что \(\tan \theta=\dfrac{5}{3}\). Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.

Рисунок \(\PageIndex{1}\): Велосипедные рампы для опытных райдеров имеют более крутой наклон, чем для новичков.

Использование формул двойного угла для нахождения точных значений

В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы

\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta. \nonumber\]

Если мы позволим \(\alpha=\beta=\theta\), то получим

\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \ потому что \тета+\кос \тета \sin \тета\\ \sin(2\тета)&= 2\sin \тета \cos \тета.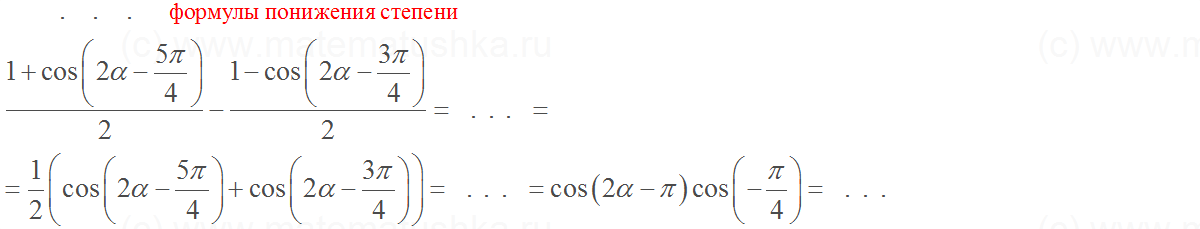 \end{align*}\]

Существует три варианта формулы двойного угла для косинуса. Во-первых, исходя из формулы суммы \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), и пусть \(\alpha=\beta=\ тета\), у нас есть 92\theta} \end{align*}\]

Как: Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение

1. Нарисуйте треугольник, чтобы отражать предоставленную информацию.
2. Определите правильную формулу двойного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример \(\PageIndex{1}\): Использование формулы двойного угла для нахождения точного значения, включающего тангенс

Учитывая, что \(\tan \theta=−\dfrac{3}{4}\) и \(\theta\) находится в квадранте II, найдите следующее:

1. \(\sin(2\theta) \)
2. \(\cos(2\тета)\)
3. \(\загар(2\тета)\)

Решение

Если мы нарисуем треугольник, отражающий предоставленную информацию, мы сможем найти значения, необходимые для решения задач на изображении. Нам даны \(\tan \theta=−\dfrac{3}{4}\), такие что \(\theta\) находится в квадранте II. Тангенс угла равен противолежащей стороне относительно прилежащей стороны, а поскольку  \(\theta\)  находится во втором квадранте, прилежащая сторона находится на 92\\ c&= 5 \end{align*}\]

Теперь мы можем нарисовать треугольник, подобный показанному на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\)

1. Начнем с написания формулы двойного угла для синуса.

   \(\sin(2\theta)=2 \sin \theta \cos \theta\)

   Мы видим, что нам нужно найти \(\sin \theta\) и \(\cos \theta\). На основании рисунка \(\PageIndex{2}\) мы видим, что гипотенуза равна \(5\), поэтому \(\sin θ=35\), \(\sin θ=35\) и \(\ cos θ=−45\). Подставьте эти значения в уравнение и упростите. 92}\\
   &= \dfrac{-\dfrac{3}{2}}{1-\dfrac{9}{16}}\\
   &= -\dfrac{3}{2}\left(\ dfrac{16}{7}\right)\\
   &= -\dfrac{24}{7}
   \end{align*}\]

Упражнение \(\PageIndex{1}\)

Учитывая \(\sin \alpha=\dfrac{5}{8}\),с \(\theta\) в квадранте I, найдите \(\cos(2 \альфа)\).

Ответить

\(\cos(2\alpha)=\dfrac{7}{32}\)

Пример \(\PageIndex{2}\): использование формулы двойного угла для косинуса без точных значений 92 3x \конец{выравнивание*}\]

Анализ

Этот пример показывает, что мы можем использовать формулу двойного угла без точных значений. Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.

Использование формул двойного угла для проверки тождественности

Установление тождества с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для получения формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной. 92 \theta}{\tan \theta}}\\ &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Используйте взаимное тождество для } \dfrac{1}{\tan \ тета} \end{выравнивание*}\]

Анализ

Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотели показать

92 \тета\)

Использование формул приведения для упрощения выражения

Формулы двойного угла можно использовать для получения формул приведения, которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла. 92 x\\[5pt]
&= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8}+\dfrac{1}{8} \cos(4x)\\[5pt]
&= \dfrac{3}{8}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8} \cos(4x)
\конец{выравнивание*}\]

Анализ

Решение находится путем двойного использования формулы приведения, как уже отмечалось, и формулы полного квадрата из алгебры. 3(2x)=\left[ \dfrac{ 1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[5pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[5pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[5pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]

Использование формул половинного угла для нахождения точных значений

Следующий набор тождеств — это набор из формул половинного угла , которые могут быть получены из формул приведения и могут использоваться, когда у нас есть угол, равный половине размера особого угла. Если мы заменим \(\theta\) на \(\dfrac{\alpha}{2}\), формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для \(\sin\left(\dfrac{ \alpha}{2}\right)\). Обратите внимание, что формулам половинного угла предшествует знак \(\pm\) . Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается \(\dfrac{\alpha}{2}\) . 92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \alpha}{1+\cos \alpha}} \end{align*}\]

ФОРМУЛЫ ПОЛУУГЛОВ

Формулы для полууглов следующие:

\[\begin{align} \ sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos\alpha}{2}} \label{halfsine} \\[5pt] \cos\ влево (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1+ \ cos \ alpha} {2}} \\ [5pt] \ tan \ left (\ dfrac {\ alpha {2}\right) &=\pm \sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}} =\dfrac{\sin\alpha}{1+\cos\alpha} =\dfrac{1-\cos\alpha}{\sin\alpha}\end{align}\] 9{\circ}}{2}}\\
&= \sqrt{\dfrac{1-\dfrac{\sqrt{3}}{2}}{2}}\\
&= \sqrt{\dfrac{ \dfrac{2-\sqrt{3}}{2}}{2}}\\
&= \sqrt{\dfrac{2-\sqrt{3}}{4}}\\
&= \dfrac{ \sqrt{2-\sqrt{3}}}{2}
\end{align*}\]

Помните, что мы можем проверить ответ с помощью графического калькулятора.

Анализ

Обратите внимание, что мы использовали только положительный корень, потому что \(\sin(15°)\) положительно.

Howto: Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.

1. Нарисуйте треугольник для представления данной информации.
2. Определите правильную формулу половинного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример \(\PageIndex{8}\): поиск точных значений с использованием тождеств половинного угла III, найдите точное значение следующего:

1. \(\sin\left(\dfrac{\alpha}{2}\right)\)
2. \(\cos\влево(\dfrac{\alpha}{2}\вправо)\)
3. \(\загар\влево(\dfrac{\alpha}{2}\вправо)\)

Решение

Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке \(\PageIndex{3}\). Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).

Рисунок \(\PageIndex{3}\)

1. Прежде чем мы начнем, мы должны помнить, что если \(α\) находится в квадранте III, то \(180°<\alpha<270°\),so \(\dfrac{180°}{2}<\dfrac {\альфа}{2}<\dfrac{270°}{2}\). Это означает, что конечная сторона  \(\dfrac{\alpha}{2}\) находится в квадранте II, так как \(90°<\dfrac{\alpha}{2}<135°\). Чтобы найти \(\sin \dfrac{\alpha}{2}\), начнем с записи формулы половинного угла для синуса. Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3}\), и упрощаем. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\ &= \pm \sqrt{\ dfrac{1-(-\dfrac{15}{17})}{2}}\\ &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\ &= \ pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\ &= \pm \sqrt{\dfrac{16}{17}}\\ &= \pm \dfrac{ 4}{\sqrt{17}}\\ &= \dfrac{4\sqrt{17}}{17} \end{align*}\] Мы выбираем положительное значение \(\sin \dfrac{\alpha} {2}\) поскольку угол оканчивается в квадранте II, а синус положителен в квадранте II.
2. Чтобы найти \(\cos \dfrac{\alpha}{2}\), мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3} \) и упростить. \[\ begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\ &= \pm \sqrt{\ dfrac {1+\left(-\dfrac{15}{17}\right)}{2}}\\ &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\ \ &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\ &= \pm \sqrt{\dfrac{1}{17}}\\ &= — \dfrac{\sqrt{17}}{17} \end{align*}\] Мы выбираем отрицательное значение \(\cos \dfrac{\alpha}{2}\) , потому что угол находится в квадранте II, потому что косинус отрицательно во II квадранте.
3. Чтобы найти \(\tan \dfrac{\alpha}{2}\), запишем формулу половинного угла для тангенса. Снова подставляем значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3}\), и упрощаем. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\ &= \ pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\ &= \ pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\ &= \pm \sqrt{\dfrac{32}{2}}\\ &= — \sqrt{16}\\ &= -4 \end{align*}\] Мы выбираем отрицательное значение \(\tan \dfrac{\alpha}{2}\) потому что \(\dfrac{\alpha}{ 2}\)  лежит в квадранте II, а тангенс отрицателен в квадранте II.

Упражнение \(\PageIndex{5}\)

Учитывая, что \(\sin \alpha=-\dfrac{4}{5}\) и \(\alpha\)  лежит в квадранте IV, найдите точное значение \(\cos \влево(\dfrac{\alpha}{2}\вправо)\).​​​​​

Ответить

\(-\dfrac{2}{\sqrt{5}}\)

Пример \(\PageIndex{9}\): нахождение измерения половинного угла

Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом \(θ\) , образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если \(tan θ=53\) для соревнований более высокого уровня, каково измерение угла для соревнований новичков? 92&=34\\ c&=\sqrt{34} \end{align*}\]

Рисунок \(\PageIndex{4}\)

Мы видим, что \(\cos \theta= \dfrac{3}{\sqrt{34}}=\dfrac{3\sqrt{34}}{34}\). Мы можем использовать формулу половинного угла для тангенса: Поскольку \(\tan \theta\) находится в первом квадранте, то и \(\tan \dfrac{\theta}{2}\).

\[\begin{align*}
\tan \dfrac{\theta}{2}&= \sqrt{\dfrac{1-\dfrac{3\sqrt{34}}{34}}{1+\ dfrac{3\sqrt{34}}{34}}}\\ 9{−1}(0,57)≈29,7°\). Таким образом, угол рампы для соревнований новичков равен \(≈29,7°\).

Носитель

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.

• Двухугольные удостоверения
• Полуугольные тождества

Ключевые уравнения

92 \тета=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\)

Формулы двойного угла
Формулы половинного угла	\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\)

Ключевые понятия

• Тождества двойных углов получаются из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса. См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).
• Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена. См. Пример \(\PageIndex{5}\) и Пример \(\PageIndex{6}\).
• Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. Пример \(\PageIndex{7}\), Пример \(\PageIndex{8}\) и Пример \(\PageIndex{9}\).

Авторы

---

Эта страница под названием 7.3: Формулы двойного угла, половинного угла и сокращения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. расчет: да
   2. формулы двойного угла
   3. формула половинного угла
   4. формулы половинного угла
   5. Теорема Пифагора
   6. формулы приведения
   7. источник@https://openstax. org/details/books/precalculus

Тригонометрические и геометрические преобразования, Sin(A + B), Sin(A

Список всех тригонометрических тождеств (формул)

Отношения для суммы углов

Как показали примеры, иногда нам нужны углы, отличные от 0, 30, 45, 60 и 90 градусов. В этой главе вам нужно усвоить две вещи:
1. Sin(A + B) не равен sin A + sin B . Это не работает, как удаление скобок в алгебре.
2. Формула, чему равен sin(A + B).

Во-первых, чтобы показать, что удаление скобок не «работает». Здесь: сделайте A 30 градусов и B 45 градусов.

Грех 30 равен 0,5. Грех 45 равен 0,7071. Добавление двух равно 1,2071.

Вы знаете, что никакой синус (или косинус) не может быть больше 1. Почему? отношение имеет гипотенузу в качестве знаменателя. Максимум, что может быть в числителе, равно знаменателю. Синус или косинус никогда не могут быть больше 1, поэтому значение 1,2071 должно быть неправильным.

Требуемый синус, косинус или тангенс целого угла (A + B)

Нахождение греха (А + В)

Самый простой способ найти sin(A + B) использует показанную здесь геометрическую конструкцию. Большой угол (А + В) состоит из двух меньших, А и В. Построение (1) показывает, что противолежащая сторона состоит из двух частей. Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).

Обратите внимание на маленький прямоугольный треугольник (5). Заштрихованный угол А, потому что линия на его верхней стороне параллельна базовой линии. Подобные прямоугольные треугольники с углом A показывают, что верхний угол, отмеченный A, также равен исходному A. Верхняя часть противоположного (6) на самом длинном из этого заштрихованного треугольника равна cos A. Противоположный угол на главной гипотенузе (7) есть sin B. Поскольку сторона, отмеченная как «противоположная» (7), находится как в числителе, так и в знаменателе, когда cos A и sin B умножаются вместе, cos A sin B является верхней частью исходной противоположности — для (A + B) — деленная на главную гипотенузу (8).

Теперь соберите все вместе (9). Sin(A + B) — это две противоположные части, разделенные гипотенузой (9). Поместив это в форму триггера:

sin(A + B) = sin A cos B + cos A sin B

Нахождение cos(A + B)

Очень похожая конструкция находит формулу косинуса угла, составленного из двух сложенных углов.

Используя ту же конструкцию (1), обратите внимание, что соседняя сторона представляет собой полную базовую линию (для cos A), часть которой вычитается справа. Каждая часть должна использовать один и тот же знаменатель, гипотенузу треугольника (A + B).

Полная базовая линия, разделенная разделительной линией между углами A и E, равна cos A (2).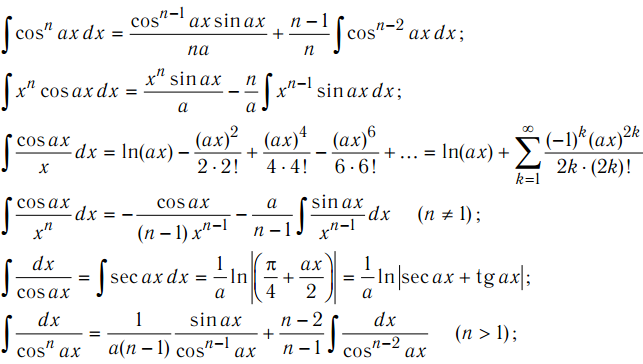 Эта разделительная линия, разделенная гипотенузой треугольника (A + B), равна cos B (3). Таким образом, полное основание, деленное на гипотенузу, равно произведению cos A и cos B (4).

Теперь о той части, которую нужно вычесть. Заштрихованная часть (5) представляет собой грех A, который, умноженный на заштрихованную часть (6), представляет собой грех E, который дает другой необходимый вам кусок (7). Вычитание дает cos(A + B) (8), так что нужная нам формула:

cos(A + B) = cos A cos B — sin A sin B

Обнаружение загара (A + B)

Полный геометрический вывод формулы для tan(A + B) сложен. Самый простой способ — вывести его из двух формул, которые вы уже сделали. Тангенс любого угла равен синусу, деленному на косинус. Используя этот факт, tan(A + B) = sin(A + B)/cos(A + B). Таким образом, что делает это, но вы можете расширить это до:
$\tan(A + B) = \frac{\sin\ A \cos\ B + \cos\ A\ \sin\ B}{\cos\ A \cos\ B — \sin\ A\ \sin\ Б}$
Разделить верх и низ на cos A и cos B, что превращает все члены в касательные, что дает:
$\tan(A + B) = \frac{\tan\ A + \tan\ B}{1 — \tan\ A\ \tan\ B}$

Передаточные числа для 75 градусов

Покажите отношения для синуса, косинуса и тангенса, подставив их в формулу суммы, а затем приведя результат к его простейшей форме, прежде чем оценивать сурды. После выполнения основных замен в каждом случае черновая работа заключается в штриховке — показать, как результат приводится к простейшему для оценки виду.

Если вы используете свой карманный калькулятор для вычислений, вероятно, не будет никакой разницы, упростите ли вы сначала выражения или просто проработаете их! Все зависит от калькулятора: что-то имеет значение, что-то нет!

Отношения углов больше 90 градусов

До сих пор рассматривались соотношения острых углов (от 0 до 90 градусов). Другие треугольники с тупыми углами (более 90 градусов) в более поздних задачах могут превысить 180 градусов. Для упрощения классификации углов по величине их делят на квадранты.

Квадрант — это четверть круга. Поскольку круг обычно делится на 360 градусов, квадранты называются сегментами по 90 градусов. 0-90 градусов — это 1-й квадрант, 90-180 — 2-й, 180-270 — 3-й и 270-360 — 4-й.

Рисование линий для представления границ квадрантов, с 0 или 360 по горизонтали вправо, 90 по вертикали вверх, 180 по горизонтали влево и 270 по вертикали вниз. Теперь используйте этот метод для построения графиков.

Постепенно увеличивающиеся углы определяются вращающимся вектором, начиная с нуля и вращаясь против часовой стрелки. Горизонтальные элементы равны x: положительный справа, отрицательный слева. Вертикальные элементы равны y. положительный вверх, отрицательный вниз. Вращающийся вектор равен r. Итак, синус угла равен y/r, косинус x/r и тангенс y/x. Вектор r всегда положителен. Итак, знак отношений может быть цифрой для различных квадрантов.

Здесь знаки трех отношений сведены в таблицу для четырех квадрантов. Также как эквивалентный угол в первом квадранте «переключается», когда вектор переходит из одного квадранта в другой. В первом квадранте стороны были определены в соотношениях для синуса, косинуса и тангенса. Когда вы двигаетесь к большим углам в оставшихся квадрантах, противоположная сторона всегда является вертикалью (y). То, что называлось соседним, всегда является горизонталью (х). Гипотенуза всегда является вращающимся вектором (r). Вы начнете видеть закономерность в том, как меняются эти тригонометрические отношения углов.

Соотношения в четырех квадрантах

Коэффициенты разности углов

Теперь у вас есть два способа получить формулы для разностных углов. Во-первых, используйте геометрическую конструкцию, такую ​​как та, которая использовалась для суммы углов, перевернув ее так, чтобы (A — B) был угол B, вычтенный из угла A.

В рассуждениях, аналогичных тем, которые использовались для суммы углов, здесь несколько сокращенно представлены формулы синуса и косинуса:

sin(A — B) = sin A cos B — cos A sin B

и

cos(A — B) = cos A cos B + sin A sin B

Геометрическая конструкция

Формулы суммы и разности

Второй способ нахождения формулы разности углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных квадрантов отрицательные углы из 1-го квадранта окажутся в 4-м квадранте.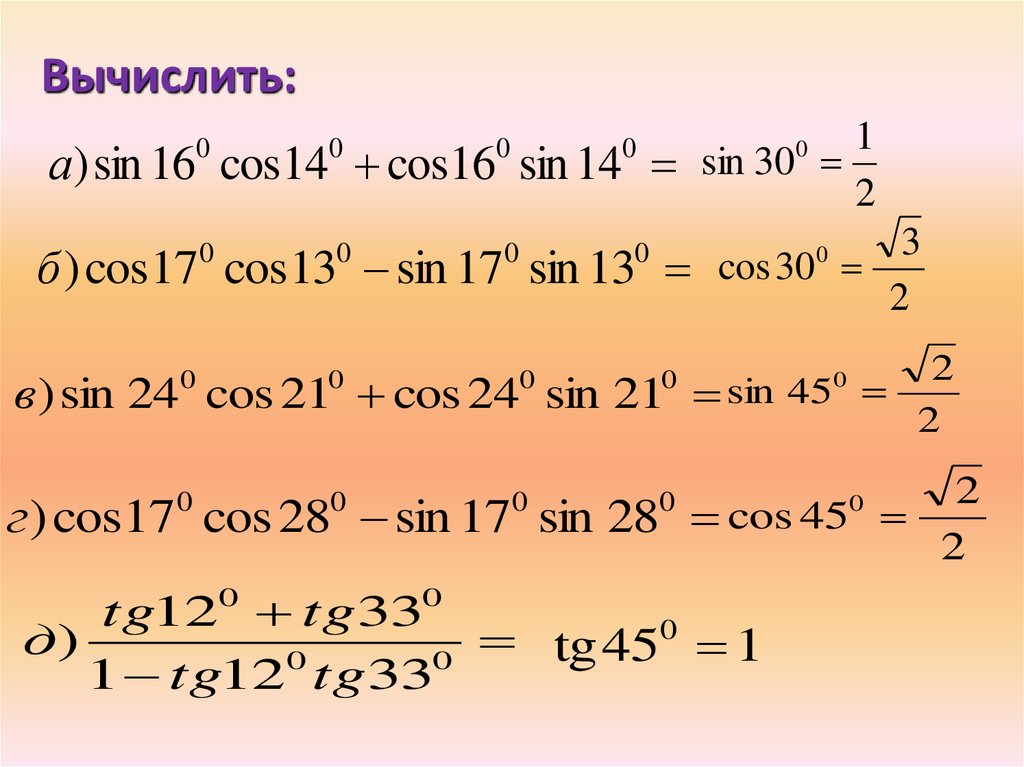 Выполнение этой замены приводит к тем же результатам, которые были получены геометрически в предыдущем разделе.

Нахождение формулы тангенса следует тому же методу, либо путем подстановки в формулы синуса и косинуса, либо, более непосредственно, путем преобразования tan(-B) = — tan B. В любом случае вы получите:
$\tan(A — B) = \frac{\tan\ A — \tan\ B}{1 + \tan\ A\ \tan\ B}$

Соотношения по четырем квадрантам

Вы можете вывести еще несколько отношений с помощью формул суммы и разности. Вы уже делали соотношения для 75 градусов. Теперь сделайте это для 15 градусов. Эти формулы дают соотношения для углов с интервалом в 15 градусов в четырех квадрантах. Разложив их на все 360 градусов, вы можете увидеть, как меняются эти три соотношения по мере того, как вектор проходит через четыре квадранта.

И синус, и косинус «колеблются» вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов одна относительно другой. Этот факт становится важным позже.

Тангенс начинается как синусоида, но быстро достигает бесконечности при 90 градусах. Зашкаливая в положительную сторону, она «заходит» с отрицательной стороны на другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы это видите). При 270 градусах он повторяет то, что делал при 9.0 градусов.

Пифагор в тригонометрии

Формулу часто можно упростить, как это было обнаружено, путем вывода формул тангенса из формул синуса и косинуса и замены слагаемых, использующих одно отношение, на слагаемые, использующие другое отношение. При этом очень удобна теорема Пифагора, выраженная в тригонометрических соотношениях.

Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1 единицу. Тогда одна из других сторон будет иметь длину sin A, а другая — cos A. Отсюда теорема Пифагора показывает, что: cos ² A + sin ² A = 1. Это утверждение верно всегда для любого значения A.

Немного о том, как это написано. Cos ² A означает (cos A) ² . Если бы вы написали это потому, что A ² , уравнение означало бы что-то другое. A — это число в некотором угловом представлении, представляющее угол. ² будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, поэтому этот термин не подходит для использования. Имеется в виду квадрат синуса или косинуса угла, а не сам угол.

Формулу Пифагора можно транспонировать. Например, две другие формы:
, потому что ² А = 1 — sin ² А, и sin ² = 1 — потому что ² А.

Несколько углов

Формулы суммы, наряду с теоремой Пифагора, используются для углов, которые являются 2, 3 или более точными кратными любому исходному углу. Здесь приведите формулы для 2А и 3А. Тот же метод используется далее в частях 3 и 4 этой книги.

Формула суммы работает независимо от того, одинаковы оба угла или различны: sin(A + B) или sin(A + A). Однако sin(A + A) на самом деле является sin 2A. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.

Сходным образом,

cos 2A = cos A cos A — sin A sin A,

что также можно записать:

cos 2A = cos ² A — sin ² A.

Используя теорему Пифагора, измените это на: 92 А}$

Теперь тройной угол (3А) используется только для того, чтобы показать, как получаются дополнительные кратные.

По сути, это так же просто, как написать 3A = 2A + A и повторно применить формулы суммы. Но затем, чтобы получить результирующую формулу в работоспособном виде, вам нужно заменить часть 2А, чтобы получить все в терминах отношений для простого угла А.

Проработайте три деривации, показанные здесь. Вы можете видеть, что для 4 А и более (в частях 3 и 4 этой книги) все будет сложнее.

НЕСКОЛЬКО УГЛОВ       Получено из формул суммы

НЕСКОЛЬКО УГЛОВ       Коэффициенты для 3A

Свойства равнобедренного треугольника

Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько иное применение. Но факт, на котором основаны эти употребления, заключается в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр из третьего угла (не из равных) на третью сторону (не из равных) делит эту третью сторону пополам. То есть делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.

При равнобедренных треугольниках любой треугольник, кроме прямоугольного, можно разделить на три смежных равнобедренных треугольника, разделив каждую сторону на две равные части и возведя перпендикуляры из точек бисекции. Там, где встречаются любые два из этих биссектриссирующих перпендикуляров, если провести линии к углам исходного треугольника, эти три линии должны быть равны, потому что две из них образуют стороны равнобедренного треугольника. Значит, перпендикуляр с третьей стороны исходного треугольника тоже должен пересечься в той же точке.

Это утверждение верно, как мы покажем здесь, независимо от того, является ли исходный треугольник остроугольным или тупоугольным. Отличие тупоугольного треугольника в том, что точка встречи находится вне исходного треугольника, а не внутри.

Что делает прямоугольный треугольник? Перпендикуляры из середины гипотенузы к двум другим сторонам разделят эти две стороны пополам — вы получите два из трех! Место встречи находится на гипотенузе.

Углы по окружности

Основное свойство круга состоит в том, что его центр находится на одинаковом расстоянии от каждой точки окружности. Это равное расстояние является радиусом окружности.

Если вы начертите любой треугольник внутри круга, перпендикуляры из середины его сторон встретятся в центре круга, а радиусы из углов треугольника разделят его на три равнобедренных треугольника.

Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике, A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A + B, один угол B + C и один угол A + C. Три угла в сумме составляют 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.

В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Из-за факта, выведенного в предыдущем абзаце, 180 — 2A должно быть таким же, как, например, 2B + 2C.

Рассмотрим углы, противоположные той части круга, против которой прилегает верхняя левая сторона треугольника. Угол в центре равен 2B + 2C, как только что выведено. Угол при окружности равен B + C. «Вы обнаружите, что для любого сегмента круга угол в центре всегда вдвое больше угла при окружности.

Приведенное выше доказательство приводит к интересному факту об углах в окружностях. Вместо того, чтобы отождествлять углы со стороной треугольника, используйте дугу (часть окружности) окружности. Важен угол, который соответствует дуге в центре. Часть окружности круга, определяемая углом в центре, называется хордой окружности.

Угол в центре в два раза больше угла на окружности

Любой угол, нарисованный относительно окружности с использованием этой хорды в качестве окончания линий, ограничивающих угол, должен составлять только половину угла в центре. Таким образом, все углы в окружности, опирающиеся на одну и ту же хорду, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.

Частным случаем является полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол при окружности полукруга равен ровно 90 градусов (прямой угол). Любой треугольник в полуокружности является прямоугольным треугольником.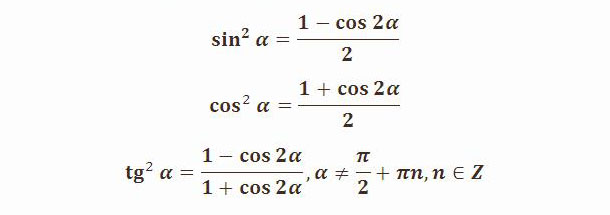

Определения

Выше мы часто использовали углы, которые в сумме составляют либо прямой угол (90 градусов), либо два прямых угла (180 градусов). Когда два угла в сумме составляют 180 градусов (два прямых угла), они называются дополнительными . Когда два угла в сумме составляют 90 градусов (один прямой угол), они называются дополнительными .

Вопросы и проблемы

1. Синус угла А равен 0,8, а синус угла В равен 0,6. Из различных соотношений, полученных к настоящему времени, найдите следующее: тангенс А, тангенс В, грех(А + В), соз (А + В), грех (А — В), соз (А — В), тангенс (А + B) и tan(A — B), без использования таблиц или триггерных кнопок калькулятора.

2. На экваторе радиус Земли составляет 4000 миль. Углы вокруг экватора измеряются в меридианах долготы с линией с севера на юг, проходящей через Гринвич, Англия, в качестве нулевой точки отсчета. Для наблюдения за Луной используются два места: одно — гора Кения на экваторе в 37,5° к востоку от Гринвича; другой — Суматра, на экваторе, в 100,5 восточной долготы. Как далеко друг от друга находятся эти два места, измеряемые воображаемой прямой линией, проходящей через Землю?

3. Если бы из точек наблюдения, рассматриваемых в вопросе 2, велись горизонтальные наблюдения (на восток от первой и строго на запад от второй), под каким углом пересеклись бы линии визирования?

4. В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении высота линии прямой видимости с центром на спутнике составляет 58 градусов над горизонталью в восточном направлении. На Суматре высота составляет 58 градусов над горизонтом, в западном направлении. Как далеко находится спутник? Используйте расстояние между точками, рассчитанное в вопросе 2.

5. Косинус определенного угла ровно в два раза больше синуса того же угла. Чему равен тангенс этого угла? Для этого вопроса вам не нужны ни таблицы, ни калькулятор.

6. Синус определенного угла ровно 0,28. Найдите косинус и тангенс без таблиц или функций триггера на вашем калькуляторе.

7. Синус некоторого угла равен 0,6. Найдите синус удвоенного и умноженного на этот угол втрое.

8. Найдите синус и косинус угла ровно в два раза больше, чем в вопросе 7.

9. Используя 15 градусов в качестве единицы угла и формулы для отношений 2А и ?>А, найдите значения синусов 30 и 45 градусов.

10. Используя 30 градусов в качестве единицы измерения угла, найдите значения синусов 60 и 90 градусов.

11. Используя 45 градусов в качестве единичного угла, найдите значения тангенсов 90 и 135 градусов.

12. Используя 60 градусов в качестве единицы угла, найдите значения косинусов 120 и 180 градусов.

13. Используя 90 градусов в качестве единицы угла, найдите значения косинусов 180 и 270 градусов.

14. Используя формулы тангенса для нескольких углов и таблицы, найдите тангенсы для трех углов, умноженных на 29, 31, 59 и 61 градус. Учитывайте изменения знака между тремя умножениями на 29 и 31 градус и между 59 и 61 градусом.