Формула для вычисления координат середины отрезка: Найдите координаты середины отрезка AB если A(6;5) B (3;6)

Координаты точки на плоскости, координаты середины отрезка, расстояние между двумя точками

Запомнить

Восстановить пароль

Регистрация

Конспект

Каждой точке координатной плоскости соответствуют две координаты. Координаты точки на плоскости – это пара чисел, в которой на первом месте стоит абсцисса, а на втором – ордината точки.

Например, точка \(A\) с координатами \((x; y)\) обозначается как \(A(x; y)\).

У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.

Середина отрезка – это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка. 2}\).

Порядок точек не играет роли.

Вопросы

1. Даны точки \(M(-4; 1), N(2; -2), P(1; 3)\). Определите координаты точки О, если\(\ \vec{MN} = \vec{OP}\).

2. Точка М – середина отрезка АВ. Найдите координаты точки А, если В(–8; –3), М(–12; 4).

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

выведите формулы выражающие координаты середины отрезка через

Вы искали выведите формулы выражающие координаты середины отрезка через? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выведите формулы выражающие координаты середины отрезка через координаты его концов, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «выведите формулы выражающие координаты середины отрезка через».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как выведите формулы выражающие координаты середины отрезка через,выведите формулы выражающие координаты середины отрезка через координаты его концов,как найти координату середины отрезка,как найти координаты середины отрезка,как найти координаты середины отрезка зная координаты его концов,как найти середину отрезка на координатной плоскости,координата середины отрезка,координата середины отрезка формула,координаты отрезка,координаты отрезка через координаты его концов,координаты середины отрезка,координаты середины отрезка формула,координаты середины отрезка через координаты его концов,найти координаты середины отрезка,найти координаты середины отрезка ав,найти середину отрезка по координатам,определение отрезка середины отрезка,определение середины отрезка,середина отрезка,середина отрезка по координатам,формула для вычисления координат середины отрезка,формула координат середины отрезка,формула координата середины отрезка,формула координаты середины отрезка,формула середины отрезка,формула середины отрезка по координатам,формулы выражающие координаты середины отрезка через координаты его концов.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и выведите формулы выражающие координаты середины отрезка через. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти координату середины отрезка).

Где можно решить любую задачу по математике, а так же выведите формулы выражающие координаты середины отрезка через Онлайн?

Решить задачу выведите формулы выражающие координаты середины отрезка через вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Формула средней точки – легко

В вашем браузере отключен JavaScript.

Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

• Математика
• Алгебра 1
• Радикальные выражения/уравнения
• Формула средней точки

Рейтинг

Ø 5,0 / 2 балла

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти в Google

Авторы

Сьюзен Сайфан

Основы по теме

Формула средней точки

Чтобы найти середину отрезка на плоскости, мы должны использовать формулу середины.

Координаты концов отрезка играют важную роль в формуле; формула средней точки утверждает, что середина отрезка представляет собой среднее значение x- и y-координат его конечных точек, соединяющихся вместе.

Например, найдем середину отрезка на плоскости, концами которого являются координаты (5, 1) и (7, 3). Мы знаем, что x-координаты точек равны 5 и 7, а y-координаты равны 1 и 3. Получив среднее значение x- и y-координат, мы получаем (5+7)/2 = 6 и (1 +3)/2 = 2. Сопоставив наши ответы, мы получим, что середина отрезка равна (6, 2).

Формула средней точки необходима во многих реальных жизненных ситуациях. Например, вы хотите разрезать палку пополам, но у вас нет измерительных приборов. В этой ситуации вы все равно можете разрезать палочку пополам, положив палочку на миллиметровую бумагу и определив координаты ее концов. Затем примените формулу средней точки, чтобы найти середину палки.

Представление комплексных чисел и операций над ними на комплексной плоскости.

CCSS. MATH.CONTENT.HSN.CN.B.6

Стенограмма

Формула средней точки

Познакомьтесь с Имке, заядлым скалолазом и орнитологом-любителем. Вы знаете, она любит птиц. Имке хочет увидеть очень редкую птицу, которая вьет гнездо в пещере на горе Массив в Колорадо. Поэтому она должна тщательно спланировать свое восхождение для трудного путешествия. Путь к гнезду разбит на три сегмента . Чтобы обеспечить безопасное восхождение, Имке нужно будет использовать кулачки, чтобы прикрепить свою веревку к горе в разных точках пути.

Формула средней точки

Имке может использовать формулу средней точки, чтобы помочь ей. Взгляните на эту карту маршрута. Обратите внимание на координатную сетку ? Нам даны упорядоченные пары для местоположения начальной точки и трех точек наблюдения. Хорошо, давайте займемся первым сегментом. Имке хочет определить три равноудаленных местоположения вдоль маршрута для размещения своих камер.
Или, если быть более абстрактным, координаты двух точек (x1, y1) и (x2, y2). Чтобы найти точную середину между этими двумя точками, вы можете использовать формулу средней точки , где вы добавляете два x-значения и делите на 2, чтобы получить x-координату ; а также , добавив к двум y-значениям , а затем снова , разделив на 2, чтобы получить y-координату .

Пример 1

Подставим наши известные упорядоченные пары (1, 2) и (11, 8) для x1, x2, y1 и y2. Теперь упростим , чтобы найти середину первого сегмента . Имке следует разместить кулачок в месте заказанной пары (6, 5). Теперь, чтобы определить, где Imke должен разместить другой кулачок, нам нужно найти среднюю точку между только что найденной средней точкой и начальной точкой. Мы уже знаем, что начальная точка расположена в упорядоченной паре (1,2), поэтому мы подключаем x- и y-значения начальной точки и средней точки соответственно: (1, 2) и (6, 5) и мы упрощаем . Имке нужно будет поставить кулачок на заказанную пару (3,5, 3,5).

Теперь давайте прикинем, где Имке должна разместить свою последнюю камеру на этом отрезке: Мы уже знаем координаты первой средней точки камеры и координаты первой наблюдательной точки. Таким образом, нам нужно использовать упорядоченные пары (6, 5) и (11, 8), чтобы определить конечную среднюю точку . Посчитайте, и третий кулачок должен быть размещен в указанной паре (8.5, 6.5).

Отлично. Мы вычислили расположение трех точек, равноудаленных на и друг от друга. Мы сделали это, сначала разделив на сегмент пополам, а затем разделив на результирующие сегменты еще раз пополам. Имке точно знает, где разместить свои кулачки, чтобы обеспечить безопасный подъем.

Пример 2

Имке планирует переночевать в месте прямо посредине первой и второй смотровых площадок. Первая смотровая площадка находится в (11, 8), а вторая — в (-3, 12). Выяснить, где Имке нужно разбить лагерь, легко; мы просто используем формула средней точки с координатами точек наблюдения для расчета средней точки. Будьте осторожны со знаками! Сладких снов в (4,10), Имке! После омолаживающего отдыха Имке готова приступить к третьему и последнему сегменту.

Пример 3

Птичье гнездо должно быть ровно посередине третьего сегмента между смотровой площадкой (-3,12) и смотровой площадкой (-3, 17). Имке снова может использовать формулу средней точки . Но на этот раз она видит сходство в координатах. Поскольку значения x обеих конечных точек одинаковы, она знает, что значение x средней точки тоже будет таким же, отрицательное 3. Теперь ей просто нужно вычислить среднюю точку 9.0085 y-значения путем нахождения среднего из суммы из 12 и 17, что равно 14,5.

Наконец-то Имке почти у цели. Просто немного дальше. Ой!! Посмотрите на птенцов!! Они просто такие очаровательные! О, нет! Это мама, и я вам скажу, она злая птица!!

Упражнение «Формула средней точки»

Хотели бы вы применить полученные знания? Вы можете просмотреть и попрактиковаться с заданиями к видео

The Midpoint Formula .

• Определить среднюю точку.

  Подсказки

  Просто посмотрите на пример рядом, если обе точки имеют одинаковую координату $x$.

  Координата $y$ является средней арифметической между $-2$ и $4$, а именно $1$.

  Для заданных точек слева средняя точка равна $(-3,14,5)$.

  Координата $y$ получается следующим образом:

  $14,5=\frac{12+17}{2}=\frac{29}2$.

  В общем случае формула средней точки для двух точек $(x_1,y_1)$ и $(x_2,y_2)$ задается как

  $\left(\frac{x_1+x_2}2,\frac{y_1+y_2}2\right)$

  Решение

  Первая точка обзора $(11,8)$, вторая $ (-3,12)$.

  Используйте формулу средней точки с координатами заданных точек:

  • Суммируем $x$-координаты и делим сумму на $2$. Получаем $\frac{11-3}2=\frac82=4$.
  • Таким же образом действуем с координатами $y$, чтобы получить $\frac{8+12}2=\frac{20}2=10$.

  Таким образом, мы получаем среднюю точку $(4,10)$.

• Подсчитайте три точки.

  Подсказки

  Формула средней точки для двух точек $P_1=(x_1,y_1)$ и $P_2=(x_2,y_2)$ задается как

  $\left(\frac{x_1+x_2}2,\frac{ у_1+у_2}2\справа)$.

  Вы должны использовать эту формулу средней точки три раза.

  • Один раз для средней точки $M$ между $P_1$ и $P_2$.
  • Далее для средней точки между $P_1$ и $M$.
  • Наконец, средняя точка между $M$ и $P_2$.

  Координаты $M$ — целые числа.

  Решение

  Имке хочет разделить путь, начинающийся с $P_1=(1,2)$ и заканчивающийся $P_2=(11,8)$, на три равноудаленные точки. Итак, сначала мы должны найти середину $M$ этих двух точек, а затем еще две середины: одну между начальной точкой $P_1$ и средней точкой $M$, а другую — между средней точкой $M$ и конечной точкой $P_2. $.

  Начнем со средней точки между $P_1$ и $P_2$.

  Мы используем формулу средней точки,

  $\left(\frac{x_1+x_2}2,\frac{y_1+y_2}2\right)$,

  и помещаем координаты в

  $M=\left( \frac{1+11}2,\frac{2+8}2\right)=\left(\frac{12}2,\frac{10}2\right)=\left(6,5\right) $.

  Затем мы снова используем формулу средней точки для начальной точки и $M=(6,5)$:

  $\left(\frac{1+6}2,\frac{2+5}2\right) =\left(\frac{7}2,\frac{7}2\right)=\left(3.5,3.5\right)$.

  И снова для $M=(6,5)$ и конечной точки:

  $\left(\frac{6+11}2,\frac{5+8}2\right)=\left(\frac{17}2,\frac{13}2\right)=\left(8. 5 ,6.5\справа)$.

• Найдите середины заданных точек.

  Подсказки

  В общем случае середина двух точек $P_1=(x_1,y_1)$ и $P_2=(x_2,y_2)$ определяется по формуле середины:

  $\left(\frac{x_1+x_2} 2,\frac{y_1+y_2}2\right)$.

  Обратите внимание на знак.

  Если две точки имеют общую координату, то эта координата остается одинаковой для средней точки.

  Порядок добавления координат не имеет значения.

  Решение

  Формула средней точки для двух точек $P_1=(x_1,y_1)$ и $P_2=(x_2,y_2)$ определяется как

  $\left(\frac{x_1+x_2}2,\frac {y_1+y_2}2\справа)$.

  Давайте используем эту формулу для нескольких примеров:

  Для $P_1=(-3,2)$ и $P_2=(2,-3)$ мы получаем среднюю точку

  $M=\left(\frac {-3+2}2,\frac{2+(-3)}2\right)=\left(\frac{-1}2,\frac{-1}2\right)=(-0.5,- 0,5)$.

  Точки $P_1=(2,2)$ и $P_2=(2,4)$, получаем середину

  $M=\left(\frac{2+2}2,\frac{2+4}2\right)=\left(\frac{4}2,\frac{6}2\right)=( 2,3)$.

  Середина $P_1=(2,-4)$ и $P_2=(6,8)$ задается как

  $M=\left(\frac{2+6}2,\frac{-4 +8}2\вправо)=\влево(\frac{8}2,\frac{4}2\вправо)=(4,2)$.

  Середина двух последних точек $P_1=(3,3)$ и $P_2=(-7,9)$ определяется как

  $M=\left(\frac{3+(-7)} 2,\frac{3+9}2\right)=\left(\frac{-4}2,\frac{12}2\right)=(-2,6)$.

• Рассчитайте место встречи Имке и ее подруги.

  Подсказки

  Вы должны сложить координаты и разделить на $2$.

  Координата $x$ — рациональное число, а координата $y$ — натуральное число.

  Здесь вы видите вычисление средней точки $(3,7)$ и $(7,8)$.

  Решение

  Здесь мы должны определить среднюю точку $(2,7)$ и $(9,15)$. Для этого воспользуемся формулой средней точки. Это означает, что для получения координаты середины мы добавляем соответствующие координаты этих точек и делим полученную сумму на $2$:

  $M=\left(\frac{2+9}2,\frac{7+15}2\right)=\left(\frac{11}2,\frac{22}2\right)=( 5. 5,11)$.

• Определите формулу средней точки.

  Подсказки

  Если обе точки имеют одну и ту же координату $x$ или $y$, среднюю точку можно получить следующим образом:

  • Общая координата средней точки остается неизменной.
  • Несовпадающая координата является арифметической серединой данных (двух) координат.

  Например, средняя точка $(4,4)$ и $(6,10)$ равна $(5,7)$.

  Решение

  Середина двух заданных точек $(x_1,y_1)$ и $(x_2,y_2)$ определяется по формуле середины:

  $\left(\frac{x_1+x_2}2, \frac{y_1+y_2}2\right)$.

  Чтобы получить $x$-координату средней точки, сложите $x$-координаты двух точек и разделите сумму на $2$. Чтобы получить $y$-координату, действуйте аналогичным образом с $y$-координатами двух точек.

• Найдите середины заданных точек.

  Подсказки

  Вы можете рассчитать среднюю точку следующим образом:

  • Для координаты $x$ сложите координаты точек $x$ и разделите сумму на $2$.
  • Аналогичным образом поступите с координатой $y$.

  Имейте в виду, что только три точки являются средними.

  Середина между $(-2,3)$ и $(4,3)$ равна $M=(1,3)$.

  Решение

  Используем формулу средней точки для каждой пары точек: складываем координаты и делим сумму на $2$:

  Начнем с $A$ и $B$:

  $M=\left(\frac{3+7}2,\frac{1+3}2\right)=\left(\frac{10} 2,\frac{4}2\right)=(5,2)$.

  Для $A$ и $C$ получаем среднюю точку

  $M=\left(\frac{3+1}2,\frac{1+5}2\right)=\left(\frac{4) }2,\frac{6}2\right)=(2,3)$.

  Наконец, мы определяем середины $B$ и $C$:

  $M=\left(\frac{1+7}2,\frac{5+3}2\right)=\left(\frac {8}2,\frac{8}2\right)=(4,4)$.

Еще видео по теме Подкоренные выражения / уравнения

Упрощение подкоренных выражений

Решение радикальных уравнений

Рационализировать знаменатель

Формула расстояния

Формула средней точки

Добавление и вычитание подкоренных выражений

Умножение подкоренных выражений

Деление подкоренных выражений

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический

• Условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Свяжитесь с нами!

help@sofatutor. com

• дивантутор.com
• диван-репетитор.ch
• диван-репетитор.ат
• дивантутор.com
• ru.sofatutor.co.uk

Есть вопросы? Свяжитесь с нами!

[email protected]

Калькулятор средней точки

Используйте этот бесплатный калькулятор средней точки, который помогает найти расстояние и среднюю точку отрезка линии и показывает пошаговые расчеты.

Средняя точка обычно используется в геометрии, и наш калькулятор координат средней точки использует простую геометрическую формулу средней точки, чтобы найти недостающие координаты средней точки между точками.

Итак, пришло время продолжить изучение статьи, чтобы узнать такие термины, как нахождение средней точки с помощью уравнения средней точки и калькулятора средней точки, а также многое другое, связанное с расчетами средней точки.

Что такое средняя точка?

Средняя точка существует для любых двух упорядоченных пар, лежащих точно посередине между каждой упорядоченной парой.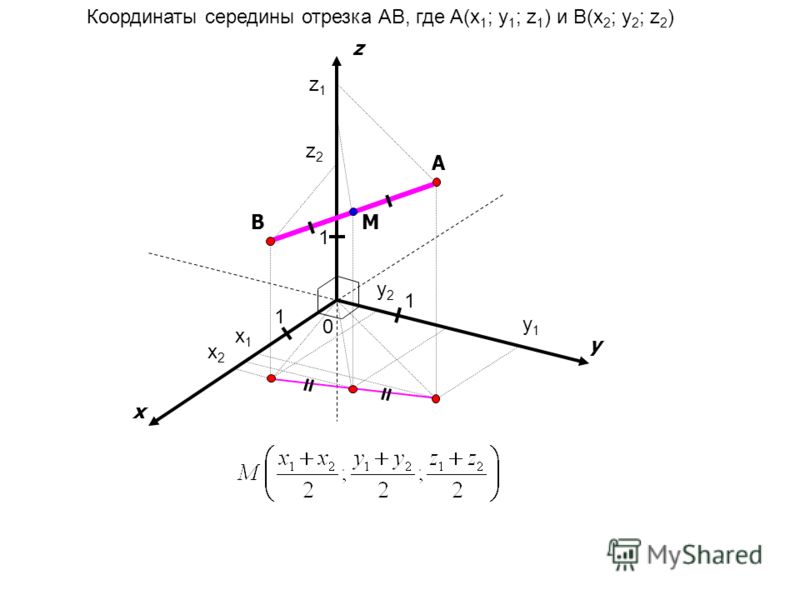 Помните, что это точно в двух измерениях (координаты x и y) и трех измерениях (координаты x, y и z). Но не волнуйтесь, так как наш калькулятор нахождения средней точки между двумя точками поможет вам найти среднюю точку от 1 до 6 измерений для соответствующих координат.

Когда речь идет о двух измерениях, у вас есть только две конечные точки, поэтому помните, что средняя точка (или среднее значение) также называется медианой и упрощает ваши расчеты. Середины и конечные точки являются коррелирующими терминами, поэтому попробуйте этот калькулятор отсутствующих конечных точек, чтобы найти конечную точку сегмента линии, используя координаты начальной и средней точек.

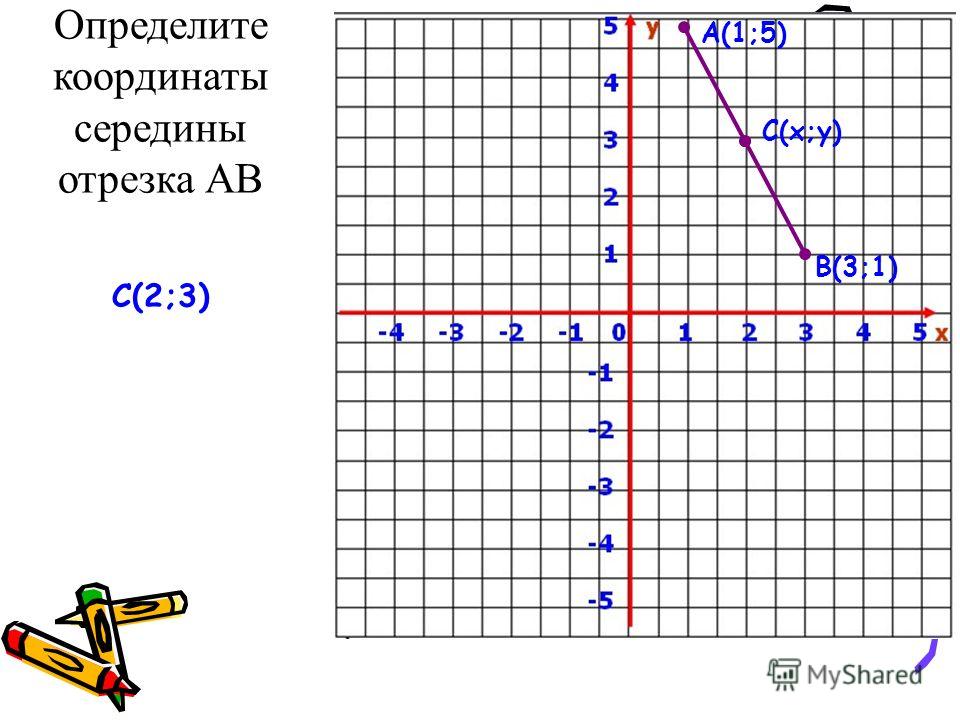
Что такое середина отрезка?

В математической геометрии середина называется точкой, которая находится посередине между конечными точками отрезка. Проще говоря, это средняя точка отрезка.

Средняя точка — это точка, которая делит сегмент на два равных сегмента. Если (x1, y1) и (x2, y2) являются двумя заданными конечными точками отрезка прямой, то используйте приведенную ниже формулу средней точки, чтобы найти значения средней точки для координат.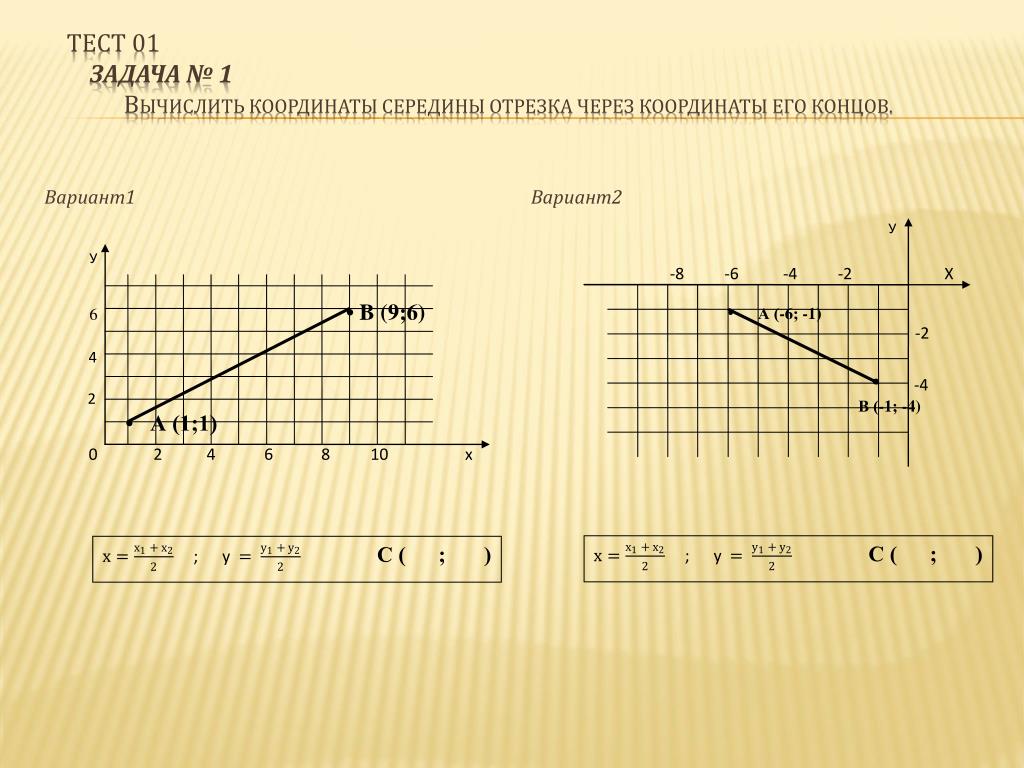

Что такое формула средней точки?

Формула для средней точки используется для определения точного центра отрезка. Используйте это уравнение средней точки, чтобы вычислить точку, которая делит отрезок пополам.

Средняя точка Формула: 9где;

• M указан как середина
• xm = координата x средней точки
• ym = координата y средней точки

Онлайн-калькулятор формулы средней точки также использует ту же формулу средней точки для нахождения средней точки для заданных координат. Таким образом, помимо ручных вычислений, введите значения в решатель формулы средней точки, чтобы найти средние точки линии.

Вы можете использовать этот онлайн-калькулятор формулы расстояния, чтобы найти расстояние между любыми двумя точками, параллельными или прямыми линиями, которые имеют координаты (x, y, z, k) в 1-4 измерениях.

Как найти среднюю точку и расстояние с помощью этого калькулятора средней точки:

Решатель средней точки абсолютно бесплатен и использует простую формулу средней точки, чтобы найти точную среднюю точку между точками. Выполните указанные шаги:

Ввод:

• Прежде всего, вы должны выбрать одно измерение (от 1D до 6D) из выпадающего списка этого калькулятора
• Далее необходимо ввести значения координат в соответствии с выбранным измерением
• Когда закончите, пора нажать кнопку расчета этого калькулятора

Вывод:

Калькулятор расстояний и средних точек покажет:

• Середина заданных точек
• Пошаговый расчет с использованием формулы для заданных входных данных
• Расстояние для заданных входов
• Пошаговый расчет с использованием формулы уравнения расстояния
• Кроме того, этот калькулятор графика средней точки показывает график для заданных координат

Неважно, хотите ли вы найти среднюю точку между двумя точками или любыми точками, просто выберите измерение из раскрывающегося списка, добавьте значения и рассчитайте точное значение средней точки с помощью этого инструмента.

Основные характеристики Калькулятор средней точки:

• Этот калькулятор средней точки помогает найти расстояние и среднюю точку между двумя или более точками
• Работа в качестве калькулятора средней точки между двумя числами, чтобы найти расстояние и среднюю точку отрезка прямой

Часто задаваемые вопросы:

Какова средняя точка 0 и 5?

Только 2,5! Чтобы найти середину, нужно всего лишь сложить два числа и разделить результат на 2. В данном случае 0 + 5/2, 5/2, 2,5.

Каково среднее между 30 и 60?

Чтобы вычислить среднюю точку любых двух чисел, вам нужно найти среднее этих двух чисел, просто сложив их вместе и разделив результат на 2. В данном случае 30 + 60 = 90. Кроме того, наш калькулятор уравнения средней точки использует простое геометрическое уравнение для нахождения средней точки между двумя заданными координатами.

Вы ​​округляете середину?

В соответствии с математическими терминами границы и средние точки не должны округляться.