Хорда окружности — определение, свойства, теорема
Термин «хорда» используется в различных науках. Например, в биологии это означает скелетный гибкий стержень, в математике — отрезок, вписанный в окружность. В геометрии хорда окружности — это отрезок, который соединяет две точки окружности. Она является частью секущей, проведенной через окружность.
Содержание
- Хорда в геометрии
- Свойства отрезка окружности
- Ключевая теорема
- Касательная и секущая
- Решение задач
Хорда в геометрии
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
 Он обязательно будет проходить через центр круга.
Он обязательно будет проходить через центр круга.Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Касательная и секущая
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Предыдущая
ГеометрияИкосаэдр — понятие, свойства и структура двадцатигранника
Следующая
ГеометрияДлина дуги окружности — формула, обозначение, примеры расчета
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
| Отрезки и прямые, связанные с окружностью |
| Свойства хорд и дуг окружности |
| Теоремы о длинах хорд, касательных и секущих |
| Доказательства теорем о длинах хорд, касательных и секущих |
| Теорема о бабочке |
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Радиус | Отрезок, соединяющий центр окружности с любой точкой окружности | |
| Хорда | Отрезок, соединяющий две любые точки окружности | |
| Диаметр | Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности | |
| Касательная | Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания | |
| Секущая | Прямая, пересекающая окружность в двух точках |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Радиус |
Отрезок, соединяющий центр окружности с любой точкой окружности |
| Хорда |
Отрезок, соединяющий две любые точки окружности |
| Диаметр |
Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности |
| Касательная |
Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания |
| Секущая |
Прямая, пересекающая окружность в двух точках |
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. | |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. | |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины | Большая из двух хорд расположена ближе к центру окружности. | |
| Равные дуги | У равных дуг равны и хорды. | |
| Параллельные хорды | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды |
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. |
| Равные хорды |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности |
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. |
| Две хорды разной длины |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |
У равных дуг равны и хорды. |
| Параллельные хорды |
Дуги, заключённые между параллельными хордами, равны. |
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды | Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | Справедливо равенство: Посмотреть доказательство |
| Пересекающиеся хорды | |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | |
Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | |
Справедливо равенство: Посмотреть доказательство | |
| Пересекающиеся хорды |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство |
| Касательные, проведённые к окружности из одной точки |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство |
| Касательная и секущая, проведённые к окружности из одной точки |
Справедливо равенство Посмотреть доказательство |
| Секущие, проведённые из одной точки вне круга |
Справедливо равенство: Посмотреть доказательство |
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Рис. 1
Тогда справедливо равенство
Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Рис. 2
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис. 3).
3).
Рис. 3
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).
Рис. 4
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке. Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Рис. 5
Доказательство. Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным.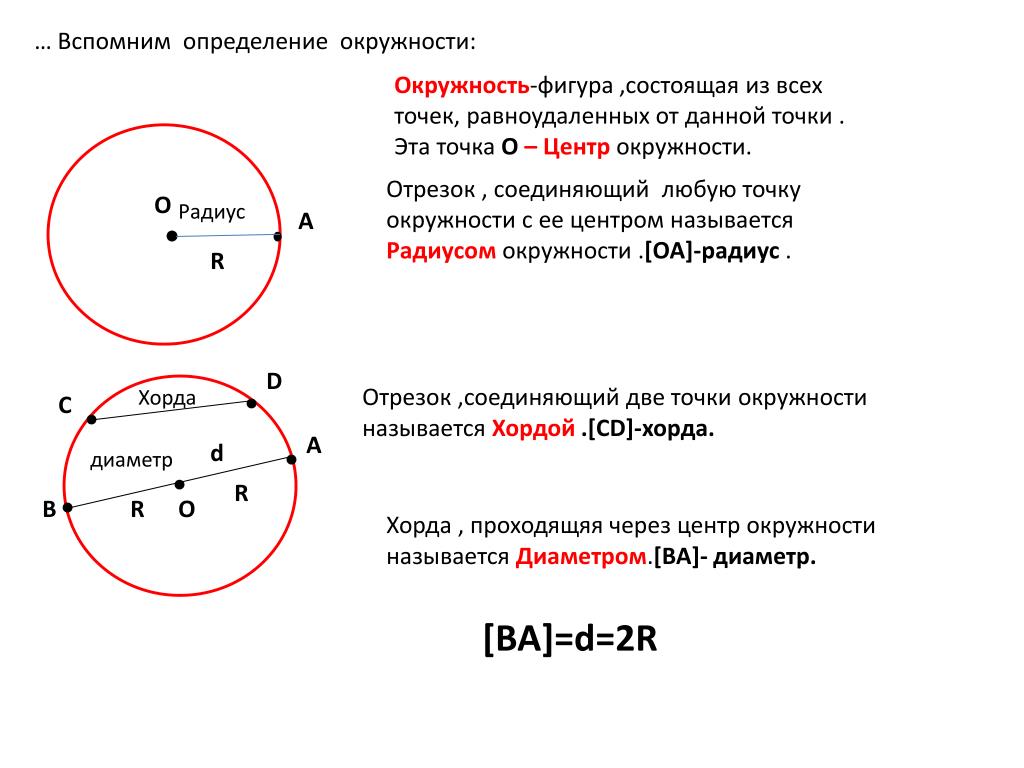 Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:
Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG, получим
| (1) |
Воспользовавшись теоремой синусов, применённой к треугольнику AKG, получим
| (2) |
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Поэтому
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL, получим равенство
откуда вытекает равенство
x = y ,
что и завершает доказательство теоремы о бабочке.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Хорда. Cвойство пересекающихся хорд. Свойства перпендикулярных хорд.
- Альфашкола
- Статьи
- Хорда. Свойства хорды
Что такое хорда?
Хорда — отрезок, соединяющий две точки данной кривой, (например окружность, эллипс, круг, параболы, гиперболы).
\(CB\) — хорда
Также хорда может описывать отрезки линий, нарисованные на эллипсах и конических сечениях.
Длина дуги — это меньшая длина окружности на которую опирается хорда, обозночается \(◡ AB\).
Свойства хорды:
- Если длины двух хорд равны, то они лежат на одном расстоянии от центра:
- Длину хорды \(AB\) можно вычислить по формуле:
\(AB = 2R sin α\)
- Если две хорды равны между собой, то равны и длины этих хорд.

Синус половинного угла будет равен длине хорды, деленный на \(2\) радиуса:
\(sin[\frac{α}{2}]=\frac{AB}{2r}\)
- \(AH*HB=QH*HM\)
- Если \( AB = CD\), то \(ON=OK\)
Диаметр-это хорда, проходящая через центр.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Александровна Волынкина
Репетитор по математике
Стаж (лет)
Образование:
ГОУ ВПО Самарский государственный педагогический университет, Куйбышевское педагогическое училище №1
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Я учитель начальных классов с 30-ти летним стажем. Могу помочь ребенку освоить предметы: математику, русский язык, литературное чтение, окружающий мир за курс начальной школы. А также закрепить знания, полученные в школе, наверстать пропущенный материал, подтянуть качество знаний по предметам с 1-4 класс и по математике, по русскому языку 5 класс. Подготовиться к ВПР по предметам за курс начальной школы и за 5 класс по русскому языку и математике..
Мой принцип работы: «Если хочешь, чтобы скорее расцвел цветок, не раскрывай насильно его лепестки, а создай условия, при которых он сам распустится.» Л.Н.Толстой.
Могу помочь ребенку освоить предметы: математику, русский язык, литературное чтение, окружающий мир за курс начальной школы. А также закрепить знания, полученные в школе, наверстать пропущенный материал, подтянуть качество знаний по предметам с 1-4 класс и по математике, по русскому языку 5 класс. Подготовиться к ВПР по предметам за курс начальной школы и за 5 класс по русскому языку и математике..
Мой принцип работы: «Если хочешь, чтобы скорее расцвел цветок, не раскрывай насильно его лепестки, а создай условия, при которых он сам распустится.» Л.Н.Толстой.
Елена Николаевна Чехлякова
Репетитор по математике
Стаж (лет)
Образование:
Самарский педагогический институт им.В.В.Куйбышева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов с 10-летним стажем работы. Успешно готовлю к ОГЭ, ЕГЭ (имеются высокие результаты-100 — 96 баллов), ВПР. Помогаю справиться с трудностями в обучении. На занятиях работаю на результат, создаю ситуацию успеха. Стараюсь всегда достигать поставленных целей и задач.
Успешно готовлю к ОГЭ, ЕГЭ (имеются высокие результаты-100 — 96 баллов), ВПР. Помогаю справиться с трудностями в обучении. На занятиях работаю на результат, создаю ситуацию успеха. Стараюсь всегда достигать поставленных целей и задач.
Надежда Викторовна Хасанова
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский Государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку и литературе. Обучаю учеников 5-11 классов. Готовлю к сдаче ОГЭ и ЕГЭ, а также к олимпиадам по русскому языку. При обучении русскому языку стараюсь найти индивидуальный подход. Перед собой ставлю задачу найти пробелы в знаниях учеников и устранить их. Уроки строю только на позитиве.
Обучаю учеников 5-11 классов. Готовлю к сдаче ОГЭ и ЕГЭ, а также к олимпиадам по русскому языку. При обучении русскому языку стараюсь найти индивидуальный подход. Перед собой ставлю задачу найти пробелы в знаниях учеников и устранить их. Уроки строю только на позитиве.
Похожие статьи
- Радикальные уравнения: примеры решения
- РУДН: Прикладная информатика (учебный план, проходной балл)
- EГЭ по математике, базовый уровень. Задачи на движение по прямой (вариант 2)
- Летние хобби: 5 нестандартных способов рисования
- Лайфхаки для уставших родителей: как не кричать
- 10 познавательных YouTube-каналов для детей
- 7 способов избавиться от насморка у детей
- Почему многие вкусные продукты вредные?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как рассчитать длину хорды?
Как рассчитать длину хорды?
Формула длины хорды окружности
- α = градус
- α = радиан
- α = x / радиан
Как определить длину хорды окружности?
Чтобы найти длину окружности, нужно либо диаметр окружности умножить на π♓5…, либо найти удвоенное произведение радиуса и числа π.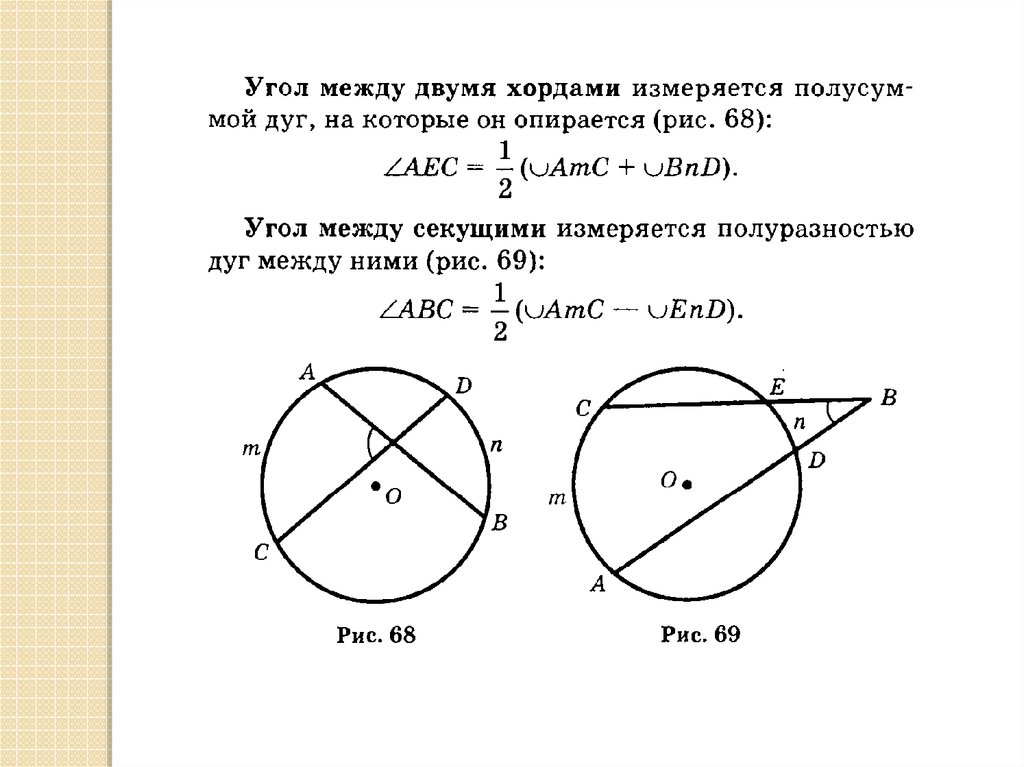 Здесь r — это радиус заданной окружности, а d — диаметр, π♓5…. Радиусом окружности — отрезок, который соединяет центр окружности с точкой окружности.
Здесь r — это радиус заданной окружности, а d — диаметр, π♓5…. Радиусом окружности — отрезок, который соединяет центр окружности с точкой окружности.
Где находится хорда у человека?
Тянется вдоль тела ниже центральной нервной системы и выше полости тела. Во время эмбрионального развития хорда есть у всех хордовых. У большинства взрослых оболочников она исчезает, а у большинства взрослых позвоночных замещается позвоночником.
Как хорда связана с радиусом?
Свойства хорд Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Как можно было найти хорду если известна диаметр окружности?
Пол хорды и расстояние от хорды до центра окружности — это два катета. По теореме Пифагора находите гипотенузу. Гипотенуза — это радиус.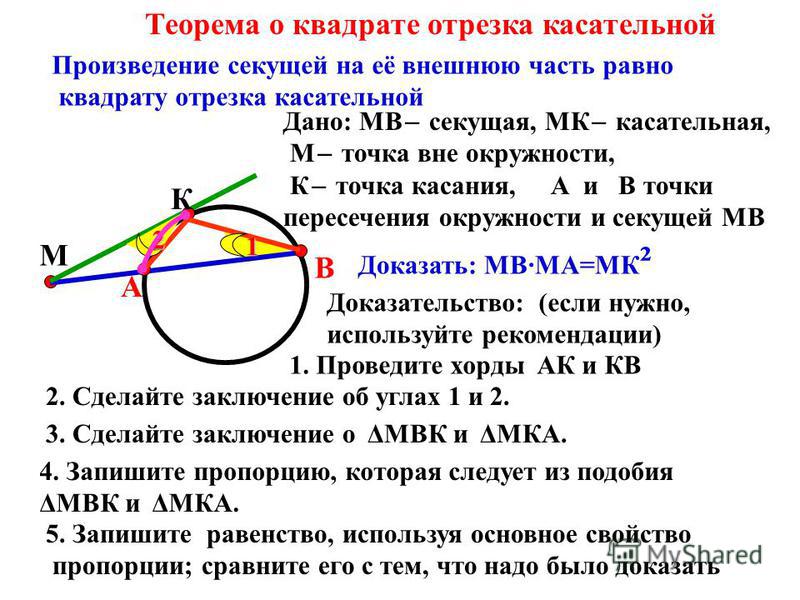 Соответственно, чтобы получить диаметр, умножьте его на два.
Соответственно, чтобы получить диаметр, умножьте его на два.
Что такое хорда пример?
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы). … Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой.
Какой буквой обозначается хорда в геометрии?
Радиус обозначается буквой R или r. Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности. Диаметр обозначается буквой D.
Что такое хорда в сердце?
По другому предположению, аномальные хорды — мышечные трабекулы, втягивающиеся в полость желудочка при его дилатации или образовании аневризмы. Название «хорда» отражает положение аномального тяжа как геометрического тела, пересекающего камеру сердца. Истинные хорды — фиброзные тяжи, состоящие из коллагеновых волокон.
Истинные хорды — фиброзные тяжи, состоящие из коллагеновых волокон.
Что такое диаметр и радиус окружности?
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно. Радиус: расстояние от центра окружности до его границы. Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
Как определить радиус и диаметр?
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина: Формула для расчета диаметра круга через его длину: D=P/π
- Если нам известна площадь: Формула для расчета диаметр круга через площадь: D=2√S/π
- Если нам известен диаметр: Формула для расчета диаметр круга через радиус: D=2R.
Как вычислить диаметр по длине окружности?
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором.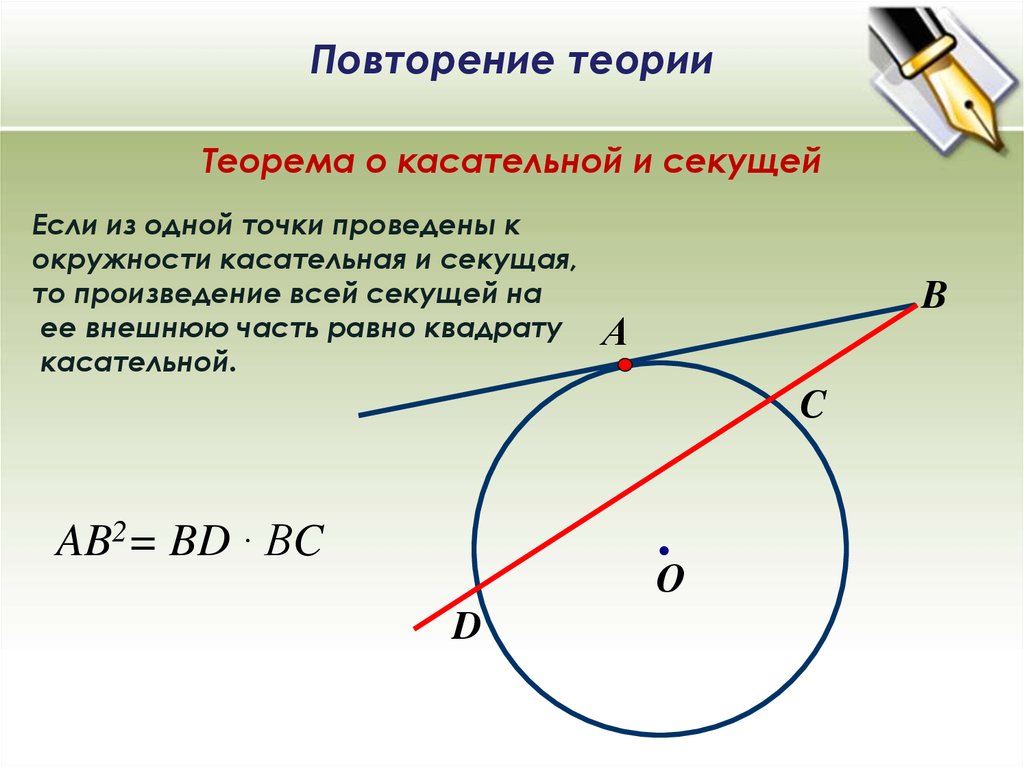 Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
Как определить радиус?
Радиус круга рассчитывается по следующим формулам:
- Если нам известна длина: Формула для расчета радиуса круга через его длину: R=P/(2π)
- Если нам известна площадь: Формула для расчета радиус круга через площадь: R=√S/π
- Если нам известен диаметр: Формула для расчета радиус круга через диаметр: R=D/2.
Как узнать длину окружности по диаметру?
Запишите формулу для вычисления длины окружности через диаметр. Формула имеет вид: C = πd, где C — длина окружности, d — диаметр окружности. То есть длина окружности равна произведению диаметра на число пи (π примерно равно 3,14). Подставьте данные вам значения в формулу и найдите длину окружности.
Как вычислить длину дуги окружности?
Если измерение дуги (или центрального угла) задано в радианах, то формула для длины дуги окружности является произведением радиуса и измерения дуги. где r-радиус окружности, а m-мера дуги (или центрального угла) в градусах.
где r-радиус окружности, а m-мера дуги (или центрального угла) в градусах.
Как рассчитать круг?
Формула для вычисления длины окружности. Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14) X Источник информации , r – радиус окружности, d – диаметр окружности.
Чему равна длина окружности?
Мы получили две важные формулы: С=πD и С=2πR, где С — длина окружности, R -радиус окружности, D — диаметр окружности.
Чему равна длина окружности если ее радиус равен 1 54 м 5 67?
С=2пиR, если R = 1,54m, а пи= 22:7, то С= 2*22*1,54:7=9,68 метров. Если R=5,67дм, то С=2*22*5,67:7=35,64.
Чем больше диаметр тем больше длина окружности?
Длина окружности тем больше, чем больше ее диаметр. Длина окружности прямо пропорциональна длине ее диаметра.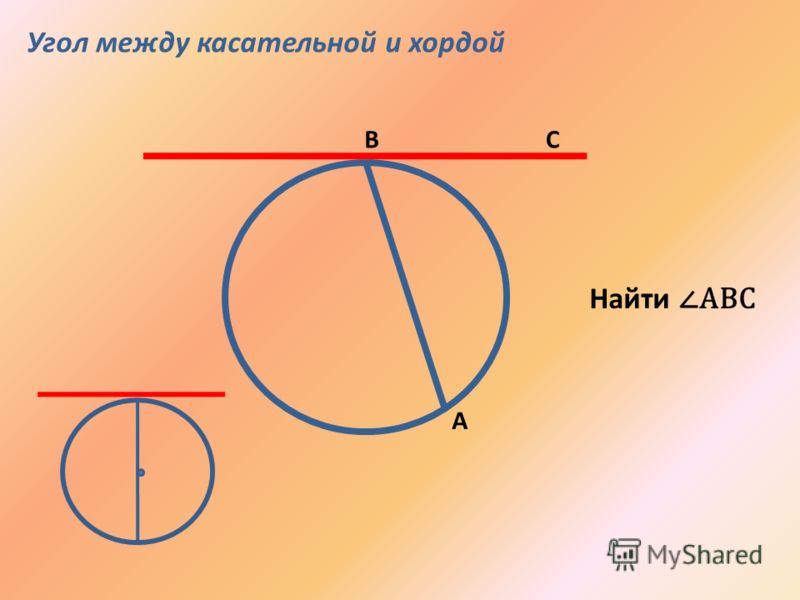 Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Это отношение обозначают греческой буквой (читают: «Пи»).
Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Это отношение обозначают греческой буквой (читают: «Пи»).
Как найти число Пи на окружности?
Разделите каждую окружность на ее диаметр. Чем точнее ваши измерения, тем ближе полученное значение будет к числу Пи (3.
Как вычислить число Пи?
Вычисление Пи с использованием предела Сначала выберите большое число. Чем больше это число, тем точнее будет результат. Затем подставьте это число (обозначим его х) в формулу для расчета Пи: x * sin(180 / x)’.
Как определить число на окружности?
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении. Чтобы отметить на окружности точку соответствующую числу 2 , нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы 3 – расстояние равное трем радиусам и т. д.
д.
Как можно вычислить число Пи?
(произносится «пи») — математическая постоянная, равная отношению длины окружности к её диаметру. Обозначается буквой греческого алфавита «π».
Как перевести число в пи?
Формула перевода проста — градусы * Пи/180. Если градусы указываются в форме «градусы минуты секунды», то сначала их надо перевести в десятичную форму, примерно так — «градусы + (минуты + секунды/60)/60».
Как найти число пи 6 класс?
Это число принято обозначать буквой π (читается как «пи»). Чаще всего используют приближённое значение числа π ≈ 3.
Сколько цифр после запятой в числе пи?
Установлен новый рекорд по вычислению знаков числа Пи — фундаментальная математическая константа была посчитана с точностью до 10 триллионов (1012) знаков после запятой, сообщается на официальном сайте проекта numberworld.org.
Что такое число Пи простым языком?
Число Пи – это отношение длины окружности к ее диаметру и оно является математической константой.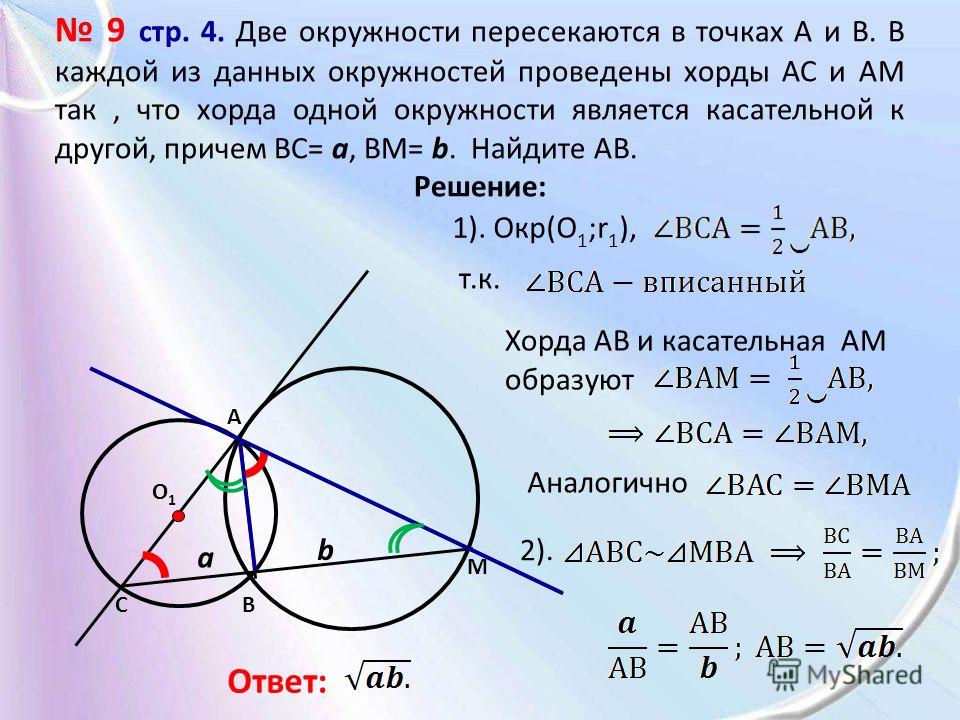 Если говорить о том, что такое число Пи простым языком, то можно сформулировать так: если диаметр окружности принять за единицу, то длина окружности и является числом Пи.
Если говорить о том, что такое число Пи простым языком, то можно сформулировать так: если диаметр окружности принять за единицу, то длина окружности и является числом Пи.
Чему равно полное число Пи?
Число Пи – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,.. Обозначается греческой буквой — π.
Почему число π бесконечно?
Образования никакого так и не получил. Число Пи не бесконечно. … Бесконечен остаток от деления длинны окружности на диаметр этой окружности.
Окружность | matematicus.ru
Окружность — это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости на заданное расстояние (рисунок 1).
Круг — часть плоскости, которая ограниченна окружностью (рисунок 1).
Другое понятие круга.
Круг — это часть плоскости, которая лежит внутри окружности, вместе с самой окружностью (рисунок 1).
Рисунок 1
Радиус r — это любой отрезок, соединяющий центр окружности и точку окружности. На рисунке 2 это отрезок OC.
Также радиус от лат. называли спицу в колесе.
Рисунок 2
Хорда — это отрезок AB, соединяющий две точки окружности (рисунок 2).
Диаметр — это хорда BE, проходящая через цент окружности (рисунок 2).
Если на окружности взять две точки, то они разобьют окружность на две части (рисунок 2). Каждая из этих кривых называется дугой окружности, а точки A и D — концы этих дуг.
Дуга обозначается как ∪ AD (рисунок 2).
Длина дуги окружности ∪AB (рисунок 3) находится по формуле:
Рисунок 3
Сектор круга — это часть плоскости, ограниченная двумя радиусами и его дугой (рисунок 3).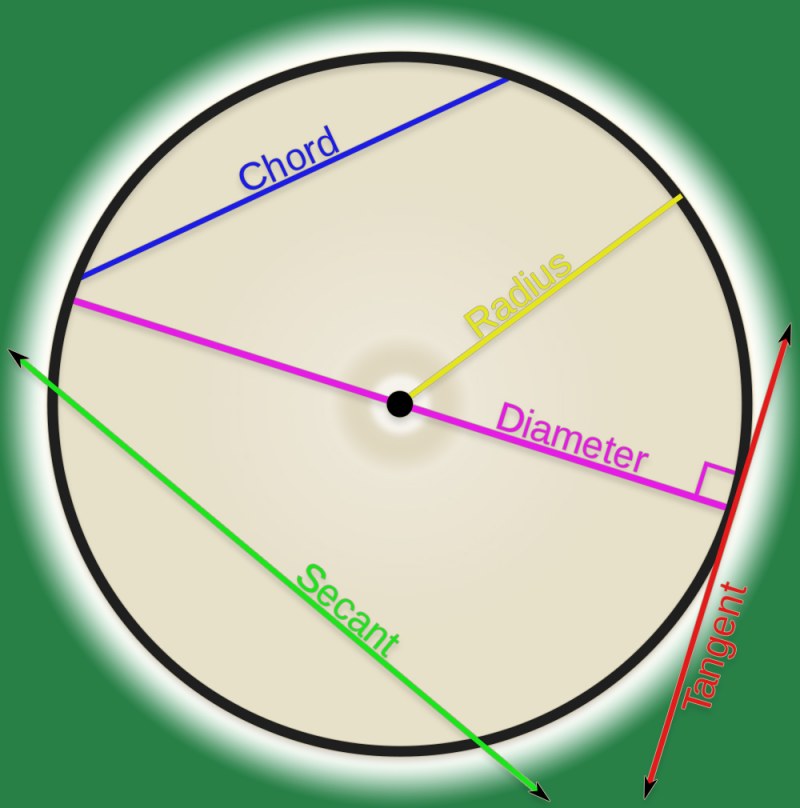
Площадь сектора, формула:
Сегмент круга — это часть плоскости, ограниченная хордой и дугой (рисунок 3).
Площадь сектора окружности, формула:
Касательной называется прямая a, имеющая с окружностью только одну общую точку A (рисунок 5).
Формула для расчета длины окружности через радиус:
L=2πr
Формула для расчета длины окружности через диаметр:
L=2πd
Формула для определения площади круга через радиус:
S=πR2
Формула для определения площади круга через диаметр:
Рисунок 4
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Формула для определения длины хорды ∪ AB через радиус и центральный угол ∠BOA:
AB=2rsin α/2
Формула для определения длины хорды через радиус и вписанный угол ∠CED:
CD=2rsinα
Свойства касательной к окружности
Одно из свойств касательной к окружности (рисунок 5) заключается в том, что касательная a к окружности перпендикулярна ее радиусу OA. Из этого вытекает аналогичное свойство, т.е. касательная , проходящая через точку касания с окружностью, перпендикулярна диаметру.
Из этого вытекает аналогичное свойство, т.е. касательная , проходящая через точку касания с окружностью, перпендикулярна диаметру.
OA⊥a
Рисунок 5
Рисунок 6
CA, CB – касательные
A, B – точки касания
CA = CB
В соответствии с рисунком 6, получаем свойство
∠1 = ∠2; ∠3 = ∠4
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойства секущей окружности
Секущая окружности — это прямая BE, имеющая с окружностью две общие точки (рисунок 7).
В соответствии с рисунком 7, получаем свойство
BA2=BF⋅BD
BA2=BE⋅BC
где AB — касательная
BE, BF — секущие
Из этого свойства вытекает следующее свойство, произведения отрезков секущих, проведенных из одной точки равны:
BF⋅BD=BE⋅BC
Рисунок 7
Свойства окружности
- Диаметр окружности равен сумме двух радиусов, то есть
d =r+r=2·r
- Через три точки, не лежащих на одной прямой, можно построить только единственную окружность.

- Если взять все замкнутые кривые с одинаковой длиной, то окружность имеет максимальную величину площади.
Кратчайшее расстояние от центра окружности к секущей или хорде всегда меньше величины радиуса.
- Если две окружности соприкасаются внешне или внутренне в одной точке, то точка касания и центры этих окружностей лежат на одной прямой.
Свойства углов окружности
На рисунке 8
∪ CB — дуга окружности
∠COB — центральный угол
∠CAB — вписанный угол
Получаем следующее тождество:
∠CAB = ∠COB/2
при этом длина дуги окружности ∪ CB должна быть меньше длины полуокружности.
Рисунок 8
Вписанные углы, опирающиеся на одну и ту же дугу, равны (рисунок 9).
Рисунок 9
Вписанный угол, опирающийся на полуокружность – прямой (рисунок 10).
Рисунок 10
Свойство хорд окружности
Рисунок 11
AB; CD – хорды
E — точка пересечения хорд
AE · EB = CE · ED
Если две хорды окружности пересекаются, то произведение отрезков одной хорды AB равно произведению отрезков другой хорды CD
Рисунок 12
Если хорда AB равна хорде DC, то их дуги тоже равны, т.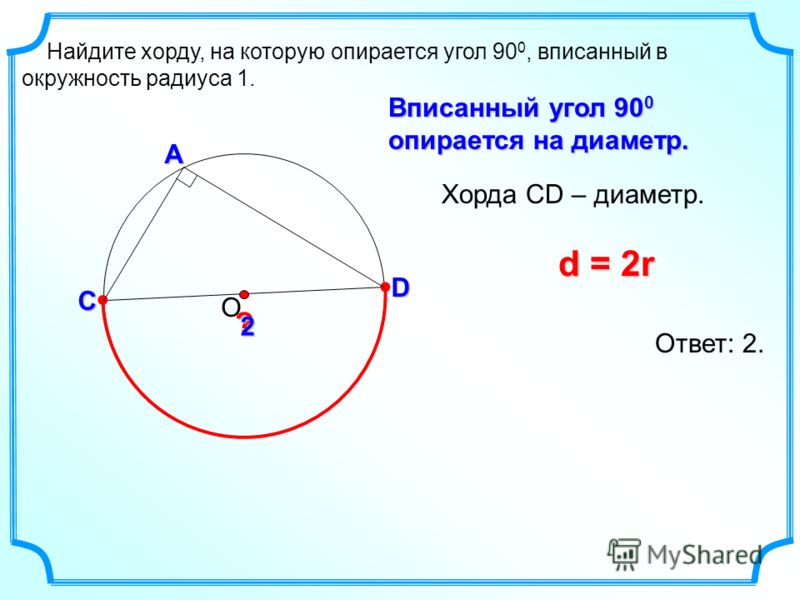 е.
е.
AB=DC ⇒ ∪AB=∪DC
Рисунок 13
Если хорда AB параллельна хорде DC, то их дуги равны, т.е.
AB//DC ⇒ ∪AB=∪DC
Рисунок 14
Если радиус окружности OD перпендикулярен хорде AB, то он делит хорду пополам в точке их пересечения С, т.е.
OD⊥AB ⇒ ∪AC=∪BC
Рисунок 15
Сумма двух вписанных углов, опирающих на одну хорду и находящихся по разные стороны от нее, равна 180°, т.е.
α + β = 180°
Рисунок 16
Формула хорда – Формула длины хорды окружности
Что такое хорда геометрия
Хорда — это отрезок, который Соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т. д.
Часть кривой, заключенной между двумя точками хорды, называется Дугой.
На рисунке дуга хорды AB обозначена зеленым цветом.
Плоская фигура, заключенная между дугой и ее хордой называется Сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.
Хорда, проходящая через центр окружности, называется Диаметром окружности. Диаметр окружности — самая длинная хорда окружности.
Свойства хорды к окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное Наибольшая возможная хорда является диаметром Серединный перпендикуляр к хорде проходит через центр окружности
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
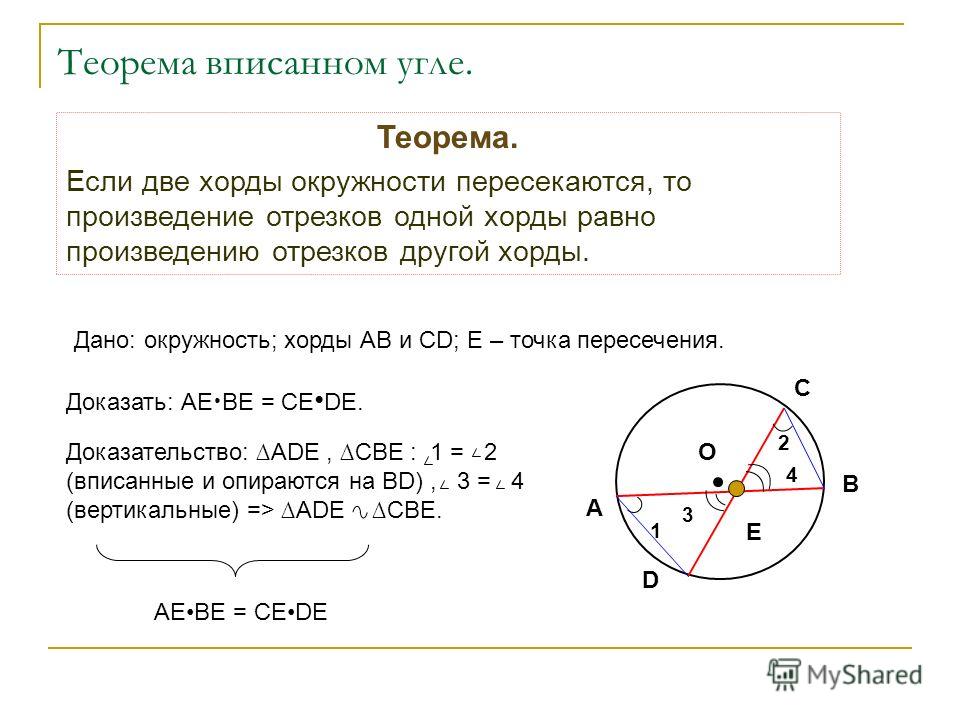 Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу
Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугуСвойства хорды и вписанного угла
- Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны. Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°. Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла. Если вписанный угол опирается на диаметр, то этот угол является прямым.
Свойства хорды и центрального угла
- Если хорды стягивают равные центральные углы, то эти хорды равны. Если хорды равны, то эти хорды стягивают равные центральные углы. Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол. Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Формулы нахождения хорды
Обозначения в формулах:
L — длина хорды
Α — величина центрального угла
R — радиус окружности
D — длина перпендикуляра, проведенного от центра окружности к хорде
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.
Решение задач
Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Задача.
| Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. |
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS x SB = CS x SD, тогда
2х * 3х = 5 * 12
6х 2 = 60
Х 2 = 10
X = √10
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
3,5х + 5,5х + 3х = 360
12х = 360
Х = 30
Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
Углы образовавшегося треугольника являются углами, вписанными в окружность.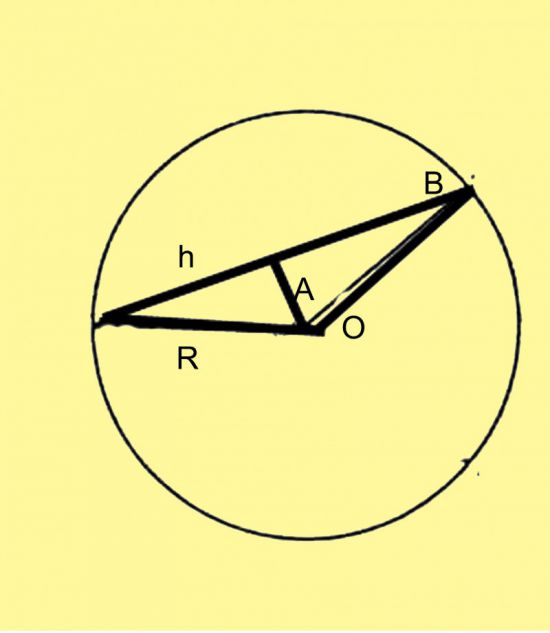 Вписанный угол равен половине градусной меры дуги, на которую опирается.
Вписанный угол равен половине градусной меры дуги, на которую опирается.
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Задачи про окружность | Описание курса | Треугольник (Трикутник)
Хорда (геометрия) — это… Что такое Хорда (геометрия)?
У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — Хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зеленым цветом), 4 — дуга
Хорда в планиметрии — отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегмент.
Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности.
Свойства хорд
- Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине.
 Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.Дуга AB равна дуге CD. Дуга BC равна дуге DA
Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED
Основные формулы
Связанные понятия и утверждения
Ссылки
Длина хорды: основные понятия
Бывают случаи в жизни, когда знания, полученные во время школьного обучения, очень полезны. Хотя во время учебы эти сведения казались скучными и ненужными. Например, как можно использовать информацию о том, как находится длина хорды? Можно предположить, что для специальностей, не связанных с точными науками, такие знания малопригодны. Однако можно привести много примеров (от конструирования новогоднего костюма до сложного устройства аэроплана), когда навыки решения задач по геометрии являются нелишними.
Понятие «хорда»
Данное слово означает «струна» в переводе с языка родины Гомера. Оно было введено математиками древнего периода.
Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.
Часть плоскости, ограниченная прямой, пересекающей окружность, и ее дугой называют сегментом. Можно отметить, что с приближением к центру длина хорды увеличивается. Часть окружности, находящуюся между двумя точками пересечения данной прямой, называют дугой. Ее мерой измерения является центральный угол. Вершина данной геометрической фигуры находится в середине круга, а стороны упираются в точки пересечения хорды с окружностью.
Свойства и формулы
Длина хорды окружности может быть вычислена по следующим условным выражениям:
L =D×Sinβ или L=D×Sin(1/2α), где β – угол при вершине вписанного треугольника;
D – диаметр окружности;
Α – центральный угол.
Можно выделить некоторые свойства данного отрезка, а также других фигур, связанных с ним. Эти моменты приведены в следующем списке:
- Любые хорды, находящиеся на одинаковом расстоянии от центра, имеют равные длины, при этом обратное утверждение также верно. Все углы, которые вписаны в окружность и опираются на общий отрезок, который объединяет две точки (при этом их вершины находятся в одной стороне от данного элемента), являются идентичными по величине. Самая большая хорда является диаметром. Сумма любых двух углов, если они опираются на данный отрезок, но при этом их вершины лежат в разных сторонах относительно него, составляет 180 о. Большая хорда — по сравнению с аналогичным, но меньшим элементом — лежит ближе к середине данной геометрической фигуры. Все углы, которые вписаны и опираются на диаметр, равны 90˚.
Другие вычисления
Чтобы найти длину дуги окружности, которая заключена между концами хорды, можно использовать формулу Гюйгенса. Для этого необходимо провести такие действия:
Обозначим искомую величину р, а хорда, ограничивающая данную часть окружности, будет иметь название АВ. Найдем середину отрезка АВ и к ней поставим перпендикуляр. Можно отметить, что диаметр окружности, проведенный через центр хорды, образует с ней прямой угол. Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М. Тогда отрезки АМ и ВМ можно назвать соответственно, как l и L. Длина дуги может быть вычислена по следующей формуле: р≈2l+1/3(2l-L). Можно отметить, что относительная погрешность данного выражения при возрастании угла увеличивается. Так, при 60˚ она составляет 0,5%, а для дуги, равной 45˚, эта величина уменьшается до 0,02%.
Найдем середину отрезка АВ и к ней поставим перпендикуляр. Можно отметить, что диаметр окружности, проведенный через центр хорды, образует с ней прямой угол. Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М. Тогда отрезки АМ и ВМ можно назвать соответственно, как l и L. Длина дуги может быть вычислена по следующей формуле: р≈2l+1/3(2l-L). Можно отметить, что относительная погрешность данного выражения при возрастании угла увеличивается. Так, при 60˚ она составляет 0,5%, а для дуги, равной 45˚, эта величина уменьшается до 0,02%.
Длина хорды может использоваться в различных сферах. Например, при расчетах и конструировании фланцевых соединений, которые широко распространены в технике. Также можно увидеть вычисление этой величины в баллистике для определения расстояния полета пули и так далее.
Хорда (геометрия) — Википедия. Что такое Хорда (геометрия)
Материал из Википедии — свободной энциклопедии 1 — секущая, 2 — Хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.
Свойства хорд окружности
Хорда и расстояние до центра окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Если хорды равны, то расстояния от центра окружности до этих хорд равны. Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше.
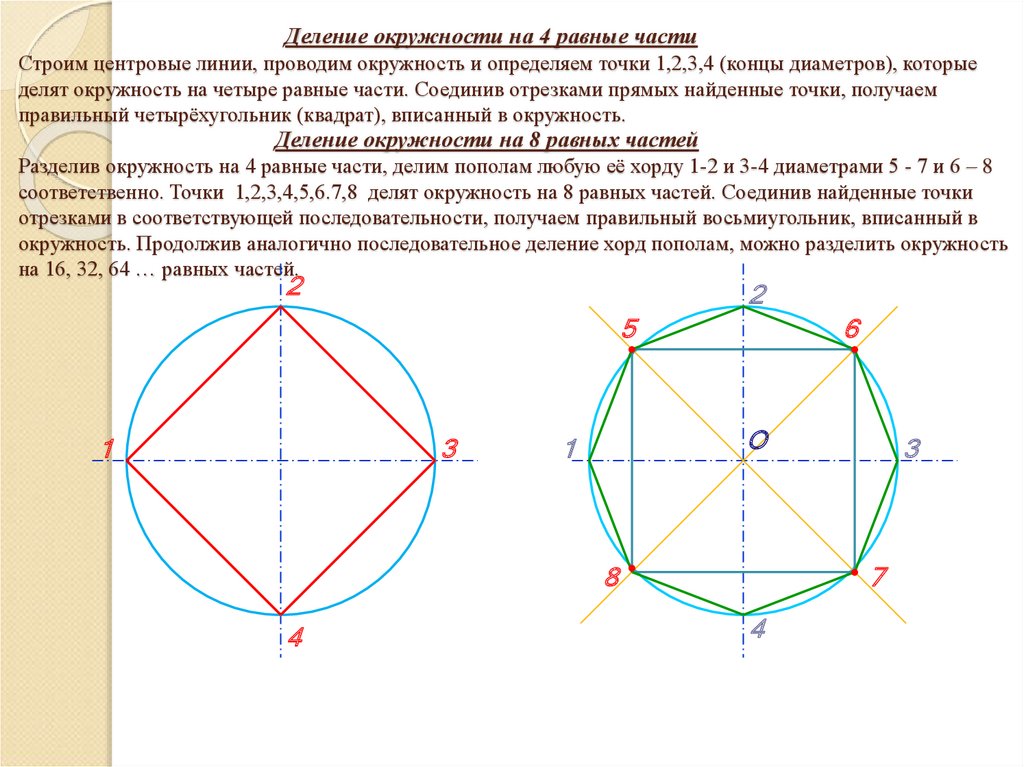 Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше. Наибольшая возможная хорда является диаметром. Наименьшая возможная хорда является точкой. Если хорда проходит через центр окружности, то эта хорда является диаметром. Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой. Серединный перпендикуляр к хорде проходит через центр окружности.
Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше. Наибольшая возможная хорда является диаметром. Наименьшая возможная хорда является точкой. Если хорда проходит через центр окружности, то эта хорда является диаметром. Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой. Серединный перпендикуляр к хорде проходит через центр окружности.Хорда и диаметр
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам. Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу. Если диаметр перпендикулярен хорде, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
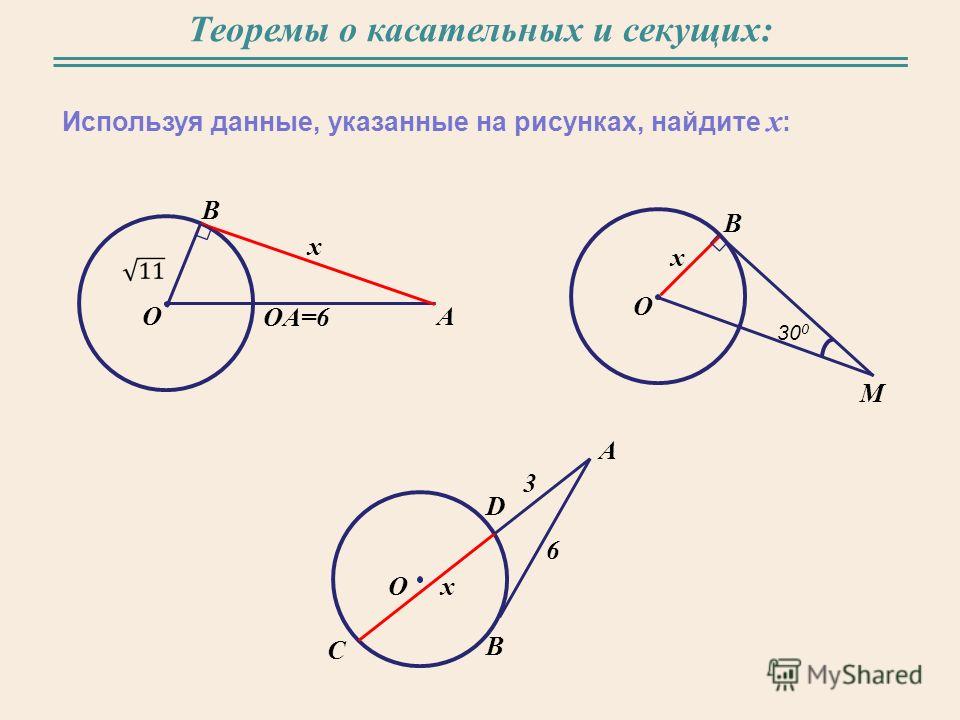 Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.
Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.Хорда и радиус
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам. Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу. Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.
Хорда и вписанный угол
- Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны. Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
 Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла. Если вписанный угол опирается на диаметр, то этот угол является прямым.
Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла. Если вписанный угол опирается на диаметр, то этот угол является прямым.Хорда и центральный угол
- Если хорды стягивают равные центральные углы, то эти хорды равны. Если хорды равны, то эти хорды стягивают равные центральные углы. Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол. Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.
Хорда и дуга
- Если хорды стягивают равные дуги, то эти хорды равны. Если хорды равны, то эти хорды стягивают равные дуги. Из дуг, меньших полуокружности, большая дуга стягивается большей хордой, меньшая дуга стягивается меньшей хордой. Из дуг, меньших полуокружности, большая хорда стягивает большую дугу, меньшая хорда стягивает меньшую дугу. Из дуг, больших полуокружности, меньшая дуга стягивается большей хордой, большая дуга стягивается меньшей хордой.
 Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу. Хорда, стягивающая полуокружность, является диаметром. Если хорды параллельны, то дуги, заключённые Между этими хордами (не путать с дугами, стягиваемыми хордами), равны.
Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу. Хорда, стягивающая полуокружность, является диаметром. Если хорды параллельны, то дуги, заключённые Между этими хордами (не путать с дугами, стягиваемыми хордами), равны.Другие свойства
- При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рис. 1): AE⋅EB=CE⋅ED. Если хорда делится пополам какой-либо точкой, то её длина самая маленькая по сравнению с длинами проведённых через эту точку хорд.
Свойства хорд эллипса
Основные формулы
Связанные понятия
Ссылки
Что такое хорда и как найти её длину
Учебник скурили штоль?
Отрезок прямой линии, соединяющий две точки данной кривой (например, окружности, эллипса, параболы). длина (l) = 2rsin (a/2)
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.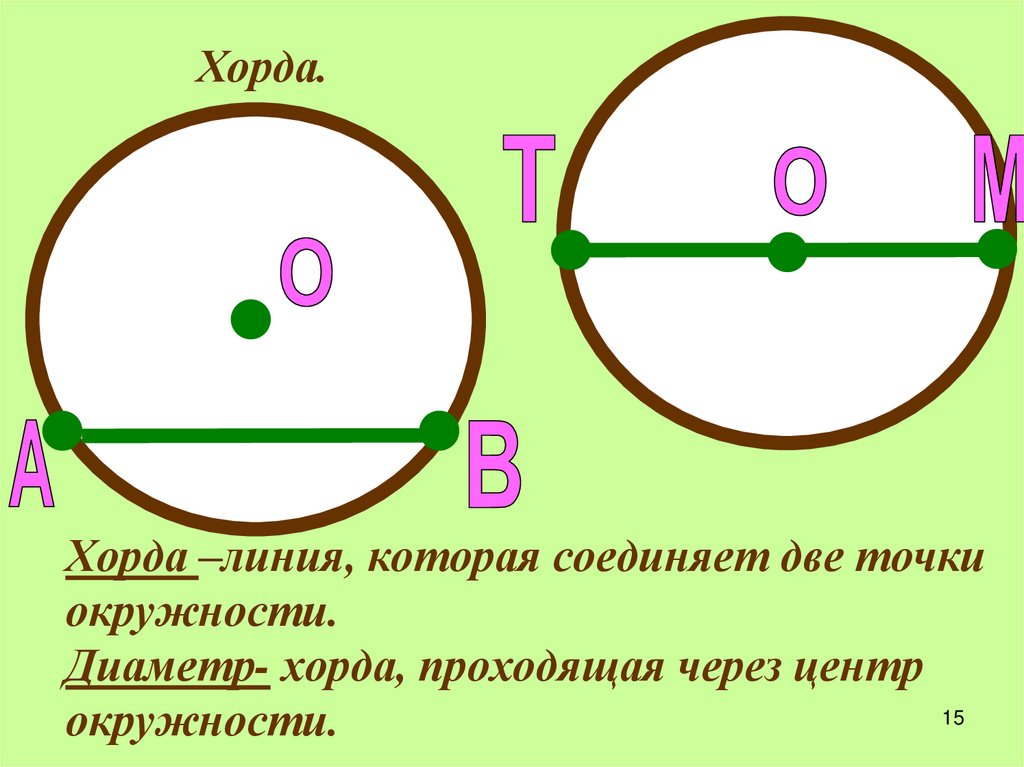 Длина хорды окружности может быть определена по формуле: Длина хорды формула L = 2r × sin ( α / 2 ) r – радиус окружности α – центральный угол
Длина хорды окружности может быть определена по формуле: Длина хорды формула L = 2r × sin ( α / 2 ) r – радиус окружности α – центральный угол
В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром. Длина хорды окружности может быть определена по формуле: Длина хорды формула L = 2r × sin ( α / 2 ) L – хорда r – радиус окружности O – центр окружности α – центральный угол
Хорда — отрезок соединяющий любые две Хорда — отрезок соединяющий любые две точки окружности. точки окружности.
Хорда? Что такое хорда в геометрии?
1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зеленым цветом), 4 — дуга Хорда в планиметрии — отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы). Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках.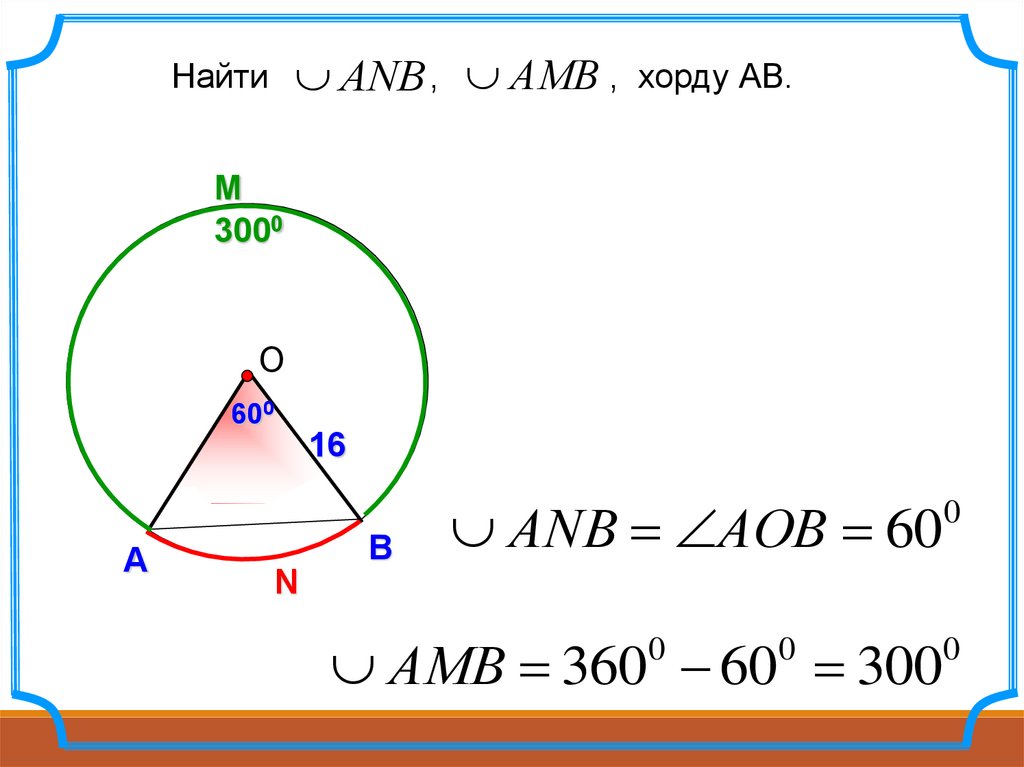 Плоская фигура, заключённая между кривой и её хордой называется сегмент. Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности. Содержание 1 Свойства хорд 2 Основные формулы 3 Связанные понятия и утверждения 4 Ссылки Свойства хорд Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине. Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды. Дуга AB равна дуге CD. Дуга BC равна дуге DA Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED Основные формулы Длина хорды: L = 2 R \sin(\frac) Связанные понятия и утверждения Касательная Диаметр Теорема Сальмона Ссылки Справочник.
Плоская фигура, заключённая между кривой и её хордой называется сегмент. Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности. Содержание 1 Свойства хорд 2 Основные формулы 3 Связанные понятия и утверждения 4 Ссылки Свойства хорд Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине. Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды. Дуга AB равна дуге CD. Дуга BC равна дуге DA Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED Основные формулы Длина хорды: L = 2 R \sin(\frac) Связанные понятия и утверждения Касательная Диаметр Теорема Сальмона Ссылки Справочник. Окружности. Архивировано из первоисточника 3 декабря 2012. Есть более полная статья Категория: Планиметрия Wikimedia Foundation. 2010. ХоргошХорев (Локачинский район) Смотреть что такое «Хорда (геометрия) » в других словарях: Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия Хорда окружности — Окружность и её центр Окружность геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром. В Викисловаре есть статья «окружность» Вписанная окружность Описанная окружность Окружность Аполлония Единичная… … Википедия Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.
Окружности. Архивировано из первоисточника 3 декабря 2012. Есть более полная статья Категория: Планиметрия Wikimedia Foundation. 2010. ХоргошХорев (Локачинский район) Смотреть что такое «Хорда (геометрия) » в других словарях: Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия Хорда окружности — Окружность и её центр Окружность геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром. В Викисловаре есть статья «окружность» Вписанная окружность Описанная окружность Окружность Аполлония Единичная… … Википедия Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов. Практически, начертательная геометрия ограничивается исследованием объектов … Википедия Начертательная геометрия* — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия История тригонометрии — Геодезические измерения (XVII век) … Википедия Диаметр — в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка.
Практически, начертательная геометрия ограничивается исследованием объектов … Википедия Начертательная геометрия* — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия История тригонометрии — Геодезические измерения (XVII век) … Википедия Диаметр — в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. Содержание 1 Диаметр ге
Диаметр равен двум радиусам. Содержание 1 Диаметр ге
Что такое хорда. А что такое учебник по геометрии ты знаешь? Лень школоло уже переходит все границы
Линия между двумя точками окружности или спирали, хорда проведенная через центр является диаметром
Хорда — прямая, соединяющая две точки кривой линии.
Хорда (геометрия) — Gpedia, Your Encyclopedia
У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — Хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды.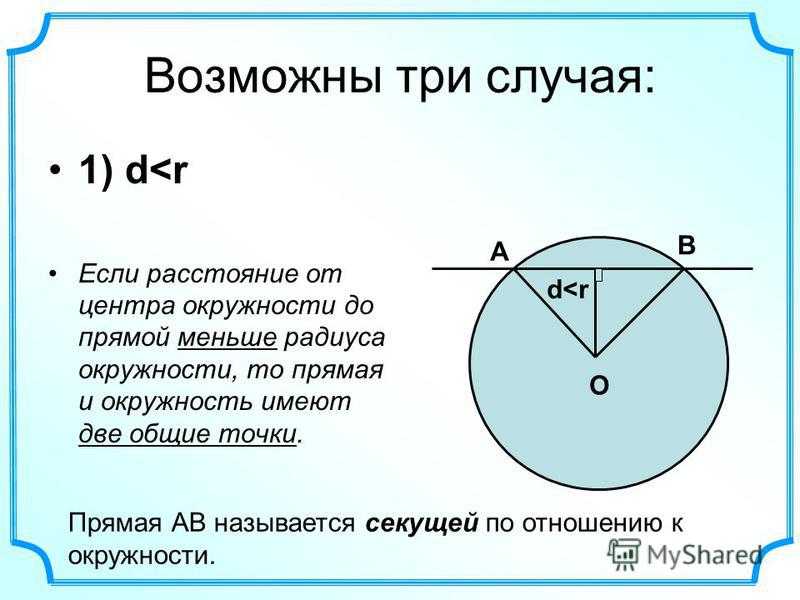 Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.
Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.
Что такое хорда и как найти её длину
Часть кривой, заключенной между двумя точками хорды, называется дугой.
Xn—-8sbanwvcjzh9e. xn--p1ai
04.02.2017 15:09:43
2017-02-04 15:09:43
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe/formula-xorda-formula-dliny-xordy-okruzhnosti. html
Хорда (геометрия) | это. Что такое Хорда (геометрия)? » /> » /> . keyword { color: red; }
keyword { color: red; }
Что такое хорда геометрия
Хорда в планиметрии — отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегмент.
Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности.
Содержание
Свойства хорд
- Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине. Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.

Дуга AB равна дуге CD. Дуга BC равна дуге DA
Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED
Основные формулы
)» width=»» height=»» />
Связанные понятия и утверждения
Ссылки
- Справочник. Окружности. Архивировано из первоисточника 3 декабря 2012.
- Планиметрия
Wikimedia Foundation. 2010 .
Полезное
Смотреть что такое «Хорда (геометрия)» в других словарях:
Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия
Хорда окружности — Окружность и её центр Окружность геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром. В Викисловаре есть статья «окружность» Вписанная окружность Описанная окружность Окружность Аполлония Единичная… … Википедия
Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.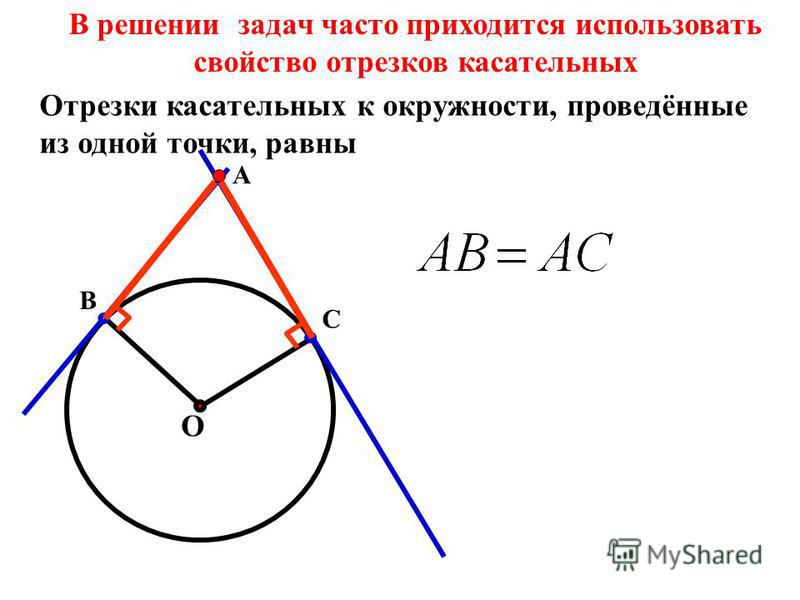 Практически, начертательная геометрия ограничивается исследованием объектов … Википедия
Практически, начертательная геометрия ограничивается исследованием объектов … Википедия
Начертательная геометрия* — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
История тригонометрии — Геодезические измерения (XVII век) … Википедия
Диаметр — в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. Содержание 1 Диаметр геометрических фигур … Википедия
Диаметр равен двум радиусам. Содержание 1 Диаметр геометрических фигур … Википедия
Кривая второго порядка — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида в котором по крайней мере один из коэффициентов отличен от нуля. Содержание 1 История 2 … Википедия
)» width=»» height=»» />
Содержание
- Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине. Перпендикуляр с середины хорды окружности проходит через центр этой окружности. Радиус, перпендикулярный к хорде, делит эту хорду пополам. Дуги, заключенные между равными хордами, равны. Дуги, заключенные между параллельными хордами, равны. При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
Дуга AB равна дуге CD. Дуга BC равна дуге DA
Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED
При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
Dic. academic. ru
17.04.2018 19:04:16
2018-04-17 19:04:16
Источники:
Https://dic. academic. ru/dic. nsf/ruwiki/1343257
Окружность: радиус, хорда, диаметр и дуга | Геометрия » /> » /> .keyword { color: red; }
Что такое хорда геометрия
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется Центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — Внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это Круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — Циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки.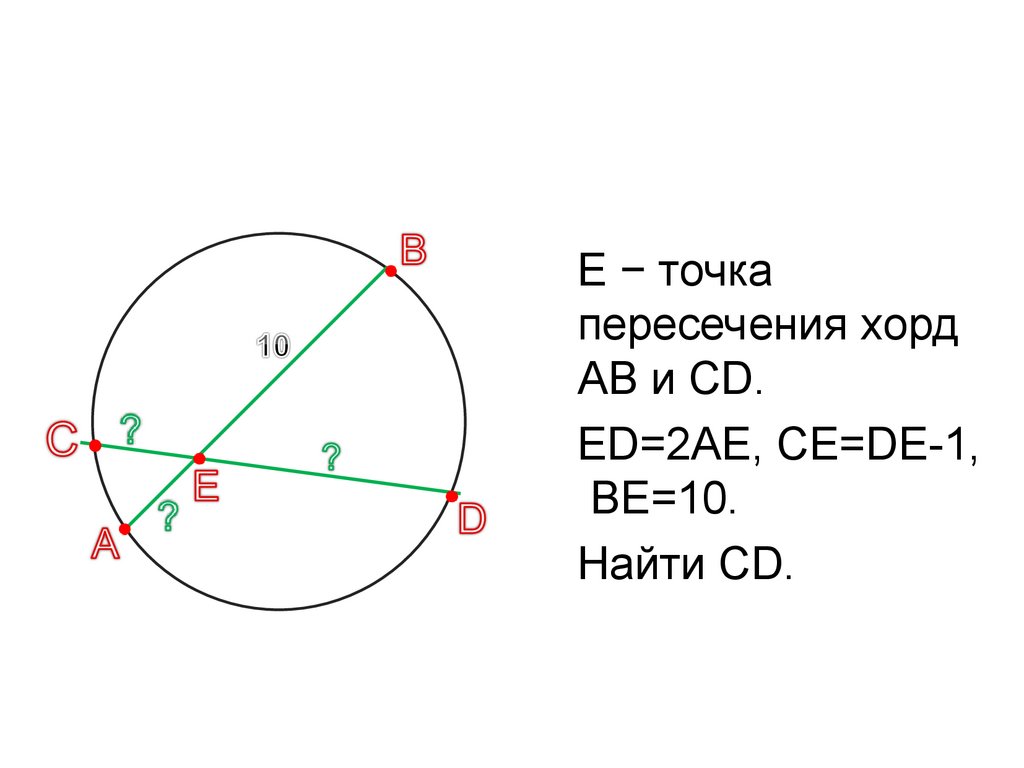 Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или R.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется Диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
D = 2R.
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ :
Для обозначения дуг используется символ :
Установим циркулю произвольный раствор расстояние между ножками циркуля и, поставив его ножку с остриём в какую-нибудь точку плоскости например, на листе бумаги, станем вращать циркуль вокруг этой точки.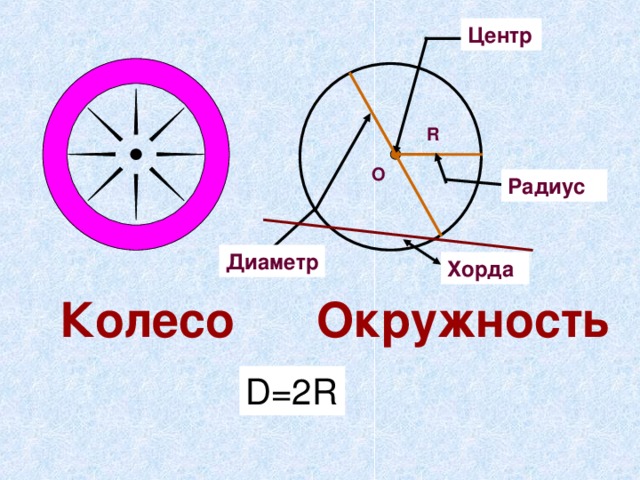
Izamorfix. ru
02.06.2018 7:27:13
2018-06-02 07:27:13
Источники:
Https://izamorfix. ru/matematika/planimetriya/okruzhnost. html
Формула длины хорды – объяснение, формулы, примеры решений и важные часто задаваемые вопросы
Хорда окружности может быть представлена как отрезок, соединяющий две точки на окружности окружности. Диаметр — это самая длинная хорда окружности, проходящая через центр окружности. Фигура, показанная ниже, представляет окружность и ее хорду.
В приведенном выше круге с центром O AB представляет диаметр круга (самая длинная хорда круга), OE представляет радиус круга, а CD представляет хорду круга.
Рассмотрим CD как хорду окружности и точки P и Q, лежащие где угодно на окружности. Если две конечные точки хорды CD пересекаются в точке P, то угол ∠CPD называется продолжением хорды CD в точке P. Угол ∠CQD называется углом, продолженным хордой CD в точке Q. Угол ∠CPD известен как угол, продолженный хордой CD в точке P.
В этой статье мы изучим, что такое хорда в окружности, формулы длины хорды, как найти длину хорды, длину общей формулы хорды двух окружностей, формулы радиуса хорды и т. д. 92} \]
Формула длины хорды с использованием тригонометрии
Длина хорды =\[ 2 \times r \times sin(\frac{c}{2}) \]
В приведенной выше формуле для длины хорды
R представляет радиус окружности
C представляет собой угол, продолженный в центре хордой.
D представляет собой перпендикулярное расстояние от шнура до центра круга.
Формула радиуса хорды
Формула радиуса хорды при заданных длине и высоте хорды равна 92}{8h} + \frac{h}{2} \]
В приведенной выше формуле радиуса хорды
R — радиус окружности
L — длина хорды
h — высота th chord
Длина общей хорды двух окружностей Формула
Длина общей хорды двух окружностей формул, когда радиус двух окружностей и расстояние между центрами двух окружностей приведены ниже.
Длина общей хорды формулы двух окружностей:
2 × радиус 1 × радиус 2 ÷ Расстояние между центрами двух окружностей
Другие части круга
Радиус круга: Радиус круга определяется как расстояние от центра до любой другой точки на границе данного круга.
Диаметр круга: Диаметр круга — это прямая линия, проходящая через центр круга и соединяющая две точки на границе. Диаметр данного круга всегда вдвое больше радиуса данного круга.
Окружность круга: Окружность круга описывается как периметр круга. Это расстояние вокруг границы данного круга. Он находится по формуле-
C = 2 × π × r (где r — радиус данного круга)
Площадь круга.
 Площадь, окруженная кругом, или область, которую он занимает в двумерной плоскости, равна называется площадью круга. Площадь данного круга) A = π × r2
Площадь, окруженная кругом, или область, которую он занимает в двумерной плоскости, равна называется площадью круга. Площадь данного круга) A = π × r2Дуга круга: Дуга представляет собой кривую часть или часть окружности круга. Математически это можно рассчитать как — s = 2 π r (θ /3600) (где s — длина дуги, r — радиус окружности, а θ — центральный угол окружности)
Секущая окружности. Секущей окружности называется линия, пересекающая две точки на окружности окружности. Слово «секанс» буквально означает «разрезать» на латыни. Существует правило касательной секущей, которое гласит, что, когда линия секущей и касательная данной окружности строятся из общей внешней точки, произведение секущей и ее внешнего сегмента всегда равно квадрату касательной.
Касательная: Касательная — это линия, пересекающая границу круга ровно в одной точке.
 Точка касания не входит внутрь окружности. Окружность может иметь бесконечные касательные, поскольку она состоит из бесконечных точек. Касательные всегда будут перпендикулярны радиусу данной окружности.
Точка касания не входит внутрь окружности. Окружность может иметь бесконечные касательные, поскольку она состоит из бесконечных точек. Касательные всегда будут перпендикулярны радиусу данной окружности.Сегмент круга: Сегмент круга — это площадь, ограниченная хордой и соответствующей дугой в данном круге. Сегменты делятся на 2 типа — малый сегмент и большой сегмент. Площадь сегмента = r2 (θ — sinθ) ÷ 2 (где r — радиус круга, а θ — в радианах)
Сектор круга: Сектор круга — это площадь, заключенная в 2 радиусы и соответствующие дуги. Сектора делятся на 2 типа секторов, второстепенный сектор и основной сектор. Если сектор пересекает угол θ (в радианах) в центре, площадь сектора данного круга = (θ x r2 ) ÷ 2 92}\]
Длина хорды = \[2 \sqrt{49 — 16}\]
Длина хорды = \[2 \sqrt{33}\]
Длина хорды = 2 \[\times\] 5,744
Или длина хорды = 11,488 см
В приведенном ниже круге найдите меру ∠POQ, если значение ∠PRQ равно 62°.

(Изображение будет загружено в ближайшее время)
Решение:
Согласно свойству хорды окружности, угол, проведенный в центре окружности, и дуга в два раза больше угла, продолженного ею в любой точке на окружность.
Следовательно, ∠POQ в два раза больше ∠PRQ. Следовательно, \[\угол POQ = 2 \times \sqrt{PRQ}\]
∠POQ = 2 x 62° = 124°.
Quiz Time
Find the length of the chord in the above- given circle
(Image will be Uploaded soon)
5
4
7
6
Самая длинная хорда окружности равна
RADIUS
Диаметр
Сегмент
ARC
IF -CREDS PQUERS PQUERS.

PQ = RS
PQ > RS
PQ < RS
Ничего из вышеперечисленного
Гитарные аккорды: Справочная таблица0001
Объяснение обозначений аккордов и тонов
Приступая к гармонии и аккордам в первый раз, гитаристы часто ошеломлены странный символы они нашли в схемы аккордов . Обозначения аккордов, особенно те, которые используются в джазе, поначалу нелегко понять. переварить.
Аккорды в основном набор интервалов, уложенных друг на друга . И что интервал? Интервал – это расстояние между две заметки.
В зависимости от качества этих интервалов мы можем иметь различные виды аккордов, а затем разные аккорды формулы.
 Представление интервалов, составляющих аккорд, в виде таблицы очень помогает понять аккорд
формулы и структура и создайте основу для более сложных тем, таких как
замена аккордов
.
Представление интервалов, составляющих аккорд, в виде таблицы очень помогает понять аккорд
формулы и структура и создайте основу для более сложных тем, таких как
замена аккордов
.На этой странице вы найдете полезную таблицу формул аккордов, которая поможет вы понимаете, что стоит за обозначением аккордов.
Чтобы узнать, как строятся аккорды на грифе, посмотрите также нашу гитара теория музыки руководство.
Аккордовые символы и формулы
На следующих диаграммах для каждого аккорд вы найдете его символ ( мажор, минор, 7, 9так далее ) а интервалы, составляющие аккорд ( 1,3,5,6 и т.д. ).
Цифры в скобках — это необязательные тона, которые вы можете использовать в аккорде.
 Затем вы видите диаграмму, состоящую из цветных прямоугольников.
Затем вы видите диаграмму, состоящую из цветных прямоугольников.Каждая ячейка соответствует одному из полутонов (полутона), составляя октаву, начиная с основного тона. В случае удлиненных хорд (с 9, 11 или 13) вы найдете другую блочную диаграмму, которая представляет верхнюю октаву.
Полный список символов и структуры аккордов
- 13 (# 9)
- майор
- 6
- добавить9
- май7
- 6/9
- 6(#11)
- май9
- май13
- м
- м (maj7)
- м6
- м7
- м (maj9)
- м6/9
- м9
- м11
- м13
- 5
- сус2
- сус4
- 7sus4
- август
- 7 (# 5)
- +(#11)
- май7 (# 5)
- 9(#5)
- 13 (# 5)
- тусклый
- тусклый7
- m7b5
- 7
- 7b5
- 7(б13)
- 7(б9)
- 7 (# 11)
- 7(#9)
- 9
- 9b5
- 11
- 9(#11)
- 13
- 13(б9)
- 13 (# 11)
Основные аккорды
майор Как строится мажорный аккорд:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы, составляющие аккорд Cmaj, — это Root, Major Third и Perfect Fifth.

Аккорд до мажор пишется следующим образом:
- до мажор
- до мажор
- СМ
- До мажорное трезвучие
- Cмай
Аккорд до мажор состоит из нот до, ми и соль.
Пример: до мажорЕще схемы аккордов
6 Формула мажорного шестого аккорда:1
B2
2
B3
3
4
B5
5
#5
2
2
2
22
22
22
2 22
2922
2
22
2 22
2922
2
2922
2
2922н.
С6
шестой аккорд
состоит из основного тона, мажорной терции, совершенной квинты и мажорной шестой
В некоторых книгах этот аккорд показан как:
- до мажор шестая
- С6
Ноты этого аккорда: C, E, G и A.
Пример: С 6 Еще схемы аккордов
добавить9
Формула аккорда: 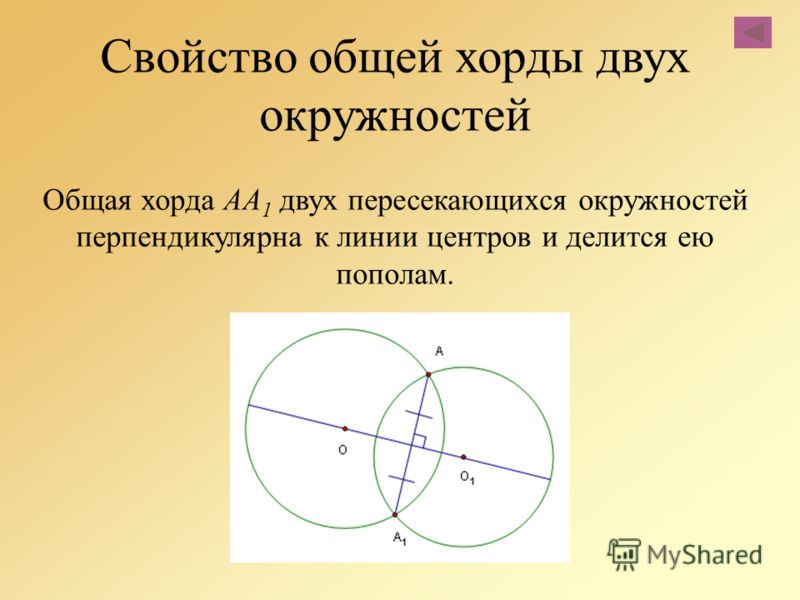
1
б2
2
б3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Этот аккорд состоит из основного тона, мажорной терции, чистой квинты и мажорной девятки.
Аккорд Cadd9 известен как:
- Добавлена девятая до мажор
- до май9
- До мажор Добавить 9
- Кэдд9
Ноты аккорда Cadd9: C, E, G и D.
Пример: C add9Еще схемы аккордов
май7 Аккордовая структура мажорного септаккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы этого аккорда: основной тон, мажорная терция, совершенная квинта и мажорная септаккорд.
Септаккорд до мажор пишется следующим образом:
- до мажор седьмая
- до мажор 7
- Cmaj7
Ноты аккорда Cmaj7: C, E, G и B.
Пример: До мажор7Еще схемы аккордов
6/9 Тоны мажорной шестой девятки Добавлен аккорд:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Этот аккорд состоит из основного тона, мажорной терции, чистой квинты, мажорной шестой и мажорной девятой.
Варианты названия этого аккорда:
- Добавлена до мажорная шестая девятка
- С 6 Добавить 9
- С6/9
Ноты в этом аккорде: C, E, G, A и D.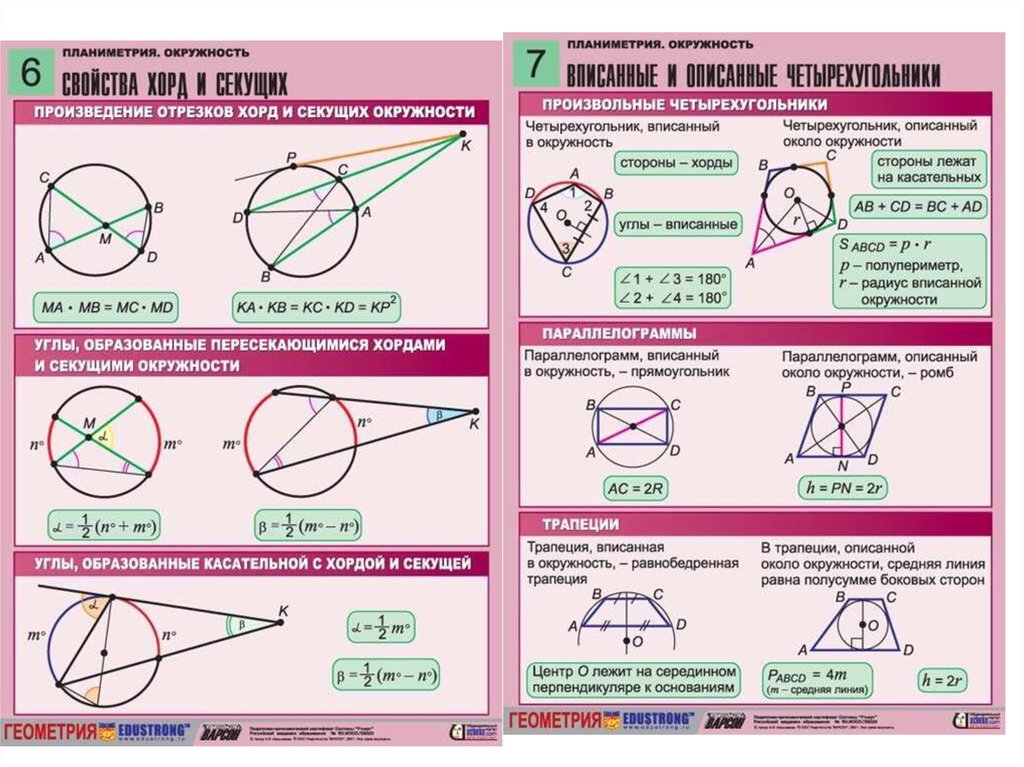
Еще схемы аккордов
6(#11) Структура аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, чистая квинта, мажорная шестая и диез. Одиннадцатый
Варианты названия аккорда C6(#11):
- Добавлена одиннадцатая до мажорная шестая диез
- С 6 # 11
- С 6+11
- C 6 авг. 11 г.
- С6(#11)
Ноты в этом аккорде: C, E, G, A и F#.
май9 Формула аккорда для мажорного девятого аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы, составляющие до мажорный девятый аккорд, — это основной тон, мажорная терция, идеальная квинта, мажор. Седьмая и большая девятая
Седьмая и большая девятая
В некоторых книгах этот аккорд показан как:
- до мажор девятая
- до май9
- до мажор 9
- Cmaj9
Этот аккорд состоит из нот C, E, G, B и D.
Пример: до мажор 9Еще схемы аккордов
май13 Тоны мажорного тринадцатого аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы, из которых состоит тринадцатый аккорд до мажор: основной тон, мажорная терция, совершенная квинта, мажор. Седьмой, майор девятый, майор одиннадцатый и майор тринадцатый
Аккорд Cmaj13 пишется следующим образом:
- до мажор тринадцать
- до май13
- до мажор 13
- Cmaj13
Ноты в аккорде Cmaj13: C, E, G, B, D, F и A.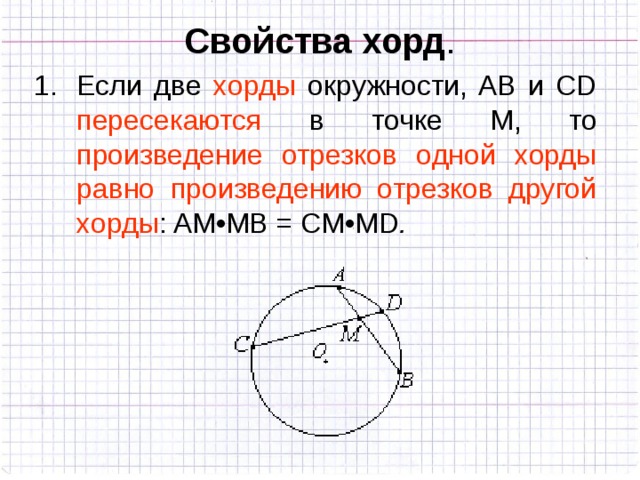
Еще схемы аккордов
Минорные аккорды
м Как строится минорный аккорд:1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Аккорд Cm состоит из основного тона, минорной терции и совершенной квинты.
Аккорд Cm известен как:
- до минор
- С Мин.
- до минор трезвучие
- См
Аккорд до минор состоит из нот до, ми-бемоль и соль.
Пример: С м Еще схемы аккордов
м (maj7)
Аккордовая структура минорного мажорного септаккорда:
1
б2
2
b3
3
4
b5
5
#5
6
0 7 20203 9
3 9
Интервалы в септаккорде до минор мажор: корень, минорная терция, совершенная квинта и мажор. Седьмой
Седьмой
Аккорд Cm(maj7) пишется следующим образом:
- до минор мажор седьмая
- до мин мажор 7
- См (maj7)
Этот аккорд состоит из нот C, Eb, G и B.
Пример: C m(maj7) Еще схемы аккордов
м6
Тоны минорного шестого аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Этот аккорд состоит из основного тона, минорной терции, совершенной квинты и мажорной шестой.
Этот аккорд также пишется следующим образом:
- до минор шестая
- до минор 6
- С мин 6
- см6
Аккорд Cm6 состоит из нот C, Eb, G и A.
Пример: C m6 Еще схемы аккордов
м7
Формула минорного септаккорда:
2
22
2 22
2922222
2922н.
Аккорд Cm состоит из основного тона, минорной терции и совершенной квинты.
Аккорд Cm известен как:
- до минор
- С Мин.
- до минор трезвучие
- См
Аккорд до минор состоит из нот до, ми-бемоль и соль.
Пример: С м Еще схемы аккордов
м (maj7)
Аккордовая структура минорного мажорного септаккорда:
1
б2
2
b3
3
4
b5
5
#5
6
0 7 20203 9
3 9
Интервалы в септаккорде до минор мажор: корень, минорная терция, совершенная квинта и мажор. Седьмой
Седьмой
Аккорд Cm(maj7) пишется следующим образом:
- до минор мажор седьмая
- до мин мажор 7
- См (maj7)
Этот аккорд состоит из нот C, Eb, G и B.
Пример: C m(maj7) Еще схемы аккордов
м6
Тоны минорного шестого аккорда:
2
2922222
2922н.
Аккорд Cm состоит из основного тона, минорной терции и совершенной квинты.
Аккорд Cm известен как:
- до минор
- С Мин.
- до минор трезвучие
- См
Аккорд до минор состоит из нот до, ми-бемоль и соль.
Пример: С м Еще схемы аккордов
м (maj7)
Аккордовая структура минорного мажорного септаккорда:
922н. Аккорд Cm состоит из основного тона, минорной терции и совершенной квинты.
Аккорд Cm известен как:
- до минор
- С Мин.
- до минор трезвучие
- См
Аккорд до минор состоит из нот до, ми-бемоль и соль.
Пример: С мЕще схемы аккордов
м (maj7)1
б2
2
b3
3
4
b5
5
#5
6
0 7 20203 9
3 9
Интервалы в септаккорде до минор мажор: корень, минорная терция, совершенная квинта и мажор.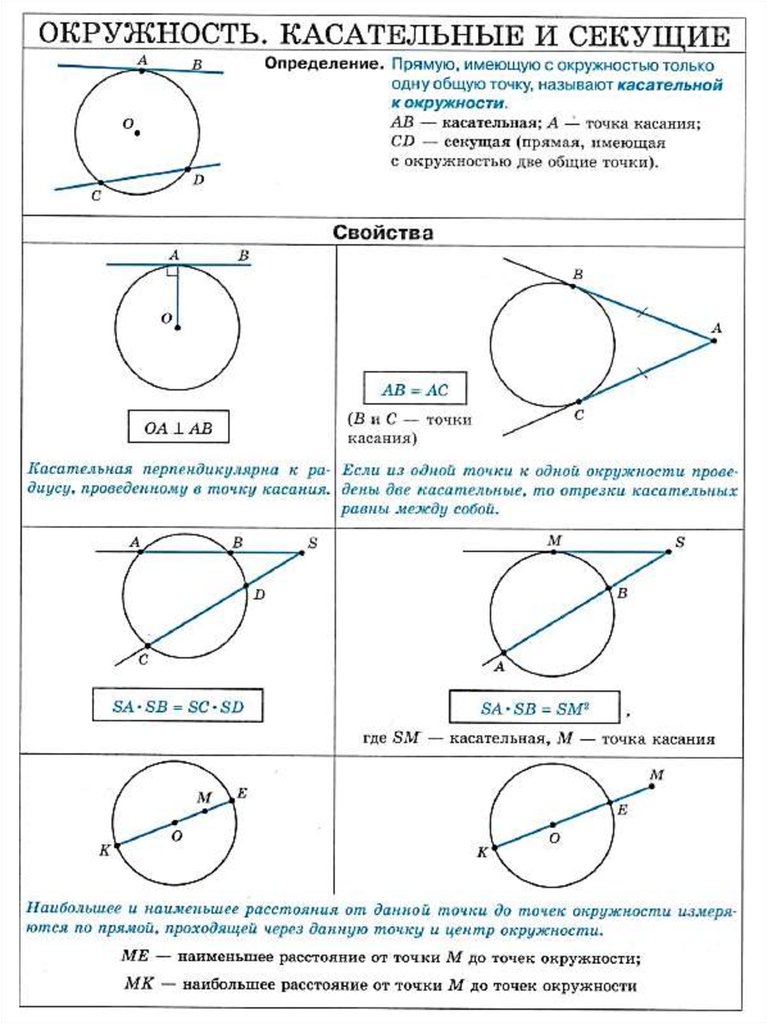 Седьмой
Седьмой
Аккорд Cm(maj7) пишется следующим образом:
- до минор мажор седьмая
- до мин мажор 7
- См (maj7)
Этот аккорд состоит из нот C, Eb, G и B.
Пример: C m(maj7)Еще схемы аккордов
м61
b2
2
b3
3
4
b5
5
#5
6
b7
7
Этот аккорд состоит из основного тона, минорной терции, совершенной квинты и мажорной шестой.
Этот аккорд также пишется следующим образом:
- до минор шестая
- до минор 6
- С мин 6
- см6
Аккорд Cm6 состоит из нот C, Eb, G и A.
Еще схемы аккордов
м71
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Интервалы этого аккорда: основной тон, минорная терция, совершенная квинта и минорная септаккорд.
Варианты названия для септаккорда до минор:
- до минор седьмая
- см7
Ноты в септаккорде до минор: C, Eb, G и Bb.
Пример: C m7 Еще схемы аккордов
м (maj9)
Формула аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд Cm(maj9) состоит из основного тона, минорной терции, совершенной квинты, мажорной септимы и мажора. Девятый
Девятый
Варианты названия девятого аккорда до минор мажор:
- до минор мажор девятая
- до мин мажор 9
- См (maj9)
Ноты девятого аккорда до минор мажор: C, Eb, G, B и D.
м6/9
Как создать минорный шестой девятый аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы этого аккорда: корень, минорная терция, совершенная квинта, мажорная шестая и мажорная квинта.
Девятый
Аккорд шестой девятки до минор пишется следующим образом:
- до минор шестая девятая
- До минор 6 Добавить 9
- До минор 6 Добавлено Ninemin 6 Добавлено 9
- см6/9
Этот аккорд состоит из нот C, Eb, G, A и D.
Пример: C m6/9 Еще схемы аккордов
м9
Формула аккорда для минорного девятого аккорда:
2
22
2 22
2922222
2922н.
Интервалы этого аккорда: основной тон, минорная терция, совершенная квинта и минорная септаккорд.
Варианты названия для септаккорда до минор:
- до минор седьмая
- см7
Ноты в септаккорде до минор: C, Eb, G и Bb.
Пример: C m7 Еще схемы аккордов
м (maj9)
Формула аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд Cm(maj9) состоит из основного тона, минорной терции, совершенной квинты, мажорной септимы и мажора. Девятый
Девятый
Варианты названия девятого аккорда до минор мажор:
- до минор мажор девятая
- до мин мажор 9
- См (maj9)
Ноты девятого аккорда до минор мажор: C, Eb, G, B и D.
м6/9
Как создать минорный шестой девятый аккорд:
2
2922222
2922н.
Интервалы этого аккорда: основной тон, минорная терция, совершенная квинта и минорная септаккорд.
Варианты названия для септаккорда до минор:
- до минор седьмая
- см7
Ноты в септаккорде до минор: C, Eb, G и Bb.
Пример: C m7 Еще схемы аккордов
м (maj9)
Формула аккорда:
922н. Интервалы этого аккорда: основной тон, минорная терция, совершенная квинта и минорная септаккорд.
Варианты названия для септаккорда до минор:
- до минор седьмая
- см7
Ноты в септаккорде до минор: C, Eb, G и Bb.
Пример: C m7Еще схемы аккордов
м (maj9)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд Cm(maj9) состоит из основного тона, минорной терции, совершенной квинты, мажорной септимы и мажора.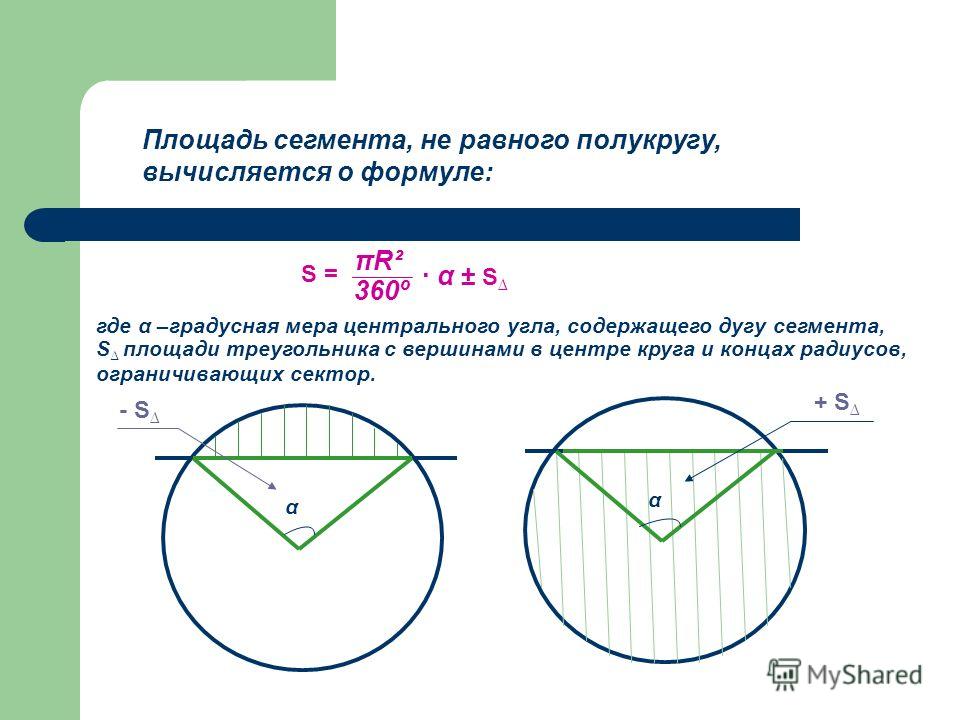 Девятый
Девятый
Варианты названия девятого аккорда до минор мажор:
- до минор мажор девятая
- до мин мажор 9
- См (maj9)
Ноты девятого аккорда до минор мажор: C, Eb, G, B и D.
м6/91
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы этого аккорда: корень, минорная терция, совершенная квинта, мажорная шестая и мажорная квинта. Девятый
Аккорд шестой девятки до минор пишется следующим образом:
- до минор шестая девятая
- До минор 6 Добавить 9
- До минор 6 Добавлено Ninemin 6 Добавлено 9
- см6/9
Этот аккорд состоит из нот C, Eb, G, A и D.
Еще схемы аккордов
м91
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд Cm9 состоит из основного тона, минорной терции, совершенной квинты, минорной септимы и мажора. Девятый
Варианты названия аккорда Cm9:
- до минор девятая
- С мин 9
- до минор 9
- см9
Аккорд Cm9 состоит из нот C, Eb, G, Bb и D.
Пример: C m9Еще схемы аккордов
м11 Как строится минорный одиннадцатый аккорд:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
До-минорный одиннадцатый аккорд состоит из основного тона, минорной терции, совершенной квинты, минорной септимы, Майор Девятый и Майор Одиннадцатый
Этот аккорд также пишется следующим образом:
- до минор одиннадцатая
- С мин 11
- до минор 11
- см11
Ноты в аккорде Cm11: C, Eb, G, Bb, D и F.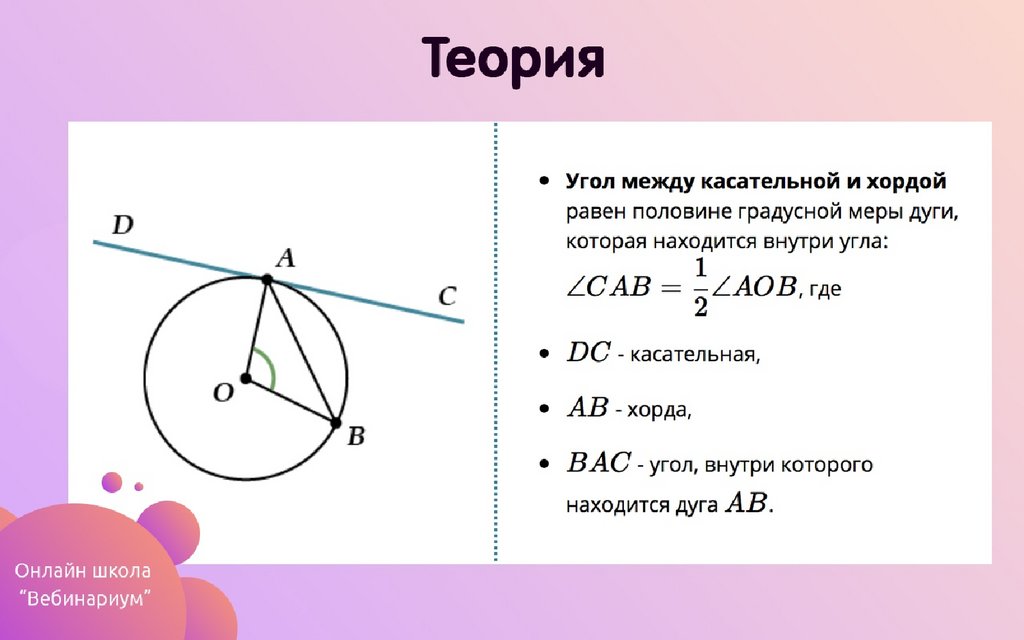
Еще схемы аккордов
м13 Структура аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд Cm13 состоит из основного тона, минорной терции, совершенной квинты, минорной септимы, мажорной девятки, Майор Одиннадцатый и Майор Тринадцатый
Различные обозначения аккорда Cm13:
- до минор тринадцать
- С мин 13
- до минор 13
- см13
Ноты тринадцатого аккорда до минор: C, Eb, G, Bb, D, F и A.
Пример: C m13Еще схемы аккордов
Шестые аккорды
Подвесные/мощные аккорды
5 Формула аккорда Powerchord:1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C5 состоит из основного тона и совершенной квинты.
C Powerchord известен как:
- C Powerchord
- С5
Ноты C Powerchord: C и G.
Пример: С 5Еще схемы аккордов
сус2 Тоны приостановленного второго аккорда:1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
подвесной 2 хорд
состоит из основного тона, большой секунды и совершенной квинты
Аккорд Csus2 известен как:
- C Подвешенный второй
- Csus2
Этот аккорд состоит из нот C, D и G.
Пример: Csus2 Еще схемы аккордов
сус4
Формула аккорда для приостановленного четвертого аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы, составляющие аккорд Csus4, — это Root, Perfect Fourth и Perfect Fifth.
Различные обозначения для подвешенного четвертого аккорда C:
- C Подвесной четвертый
- Csus4
Ноты этого аккорда: C, F и G.
Пример: Csus4 Еще схемы аккордов
7sus4
Тоны доминирующего септаккорда, приостановленного четвертого аккорда:
1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Интервалы этого аккорда: корень, совершенная четвертая, совершенная квинта и минорная септаккорд.
Различные обозначения аккорда C7sus4:
- C Доминирующая седьмая приостановленная четвертая
- C дом7сус4
- C 7 Подвесной 5
- C7sus4
Ноты в аккорде C7sus4: C, F, G и Bb.
Пример: C 7sus4 Еще схемы аккордов
Расширенные аккорды
август
Структура аккорда:
1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты,
и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.
Пример: C 7 (# 5) Еще схемы аккордов
+(#11)
Формула аккорда для Augmented Fifth Sharp Eleventh добавила аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, увеличенная квинта и диез одиннадцатая.
Различные обозначения для дополненного аккорда C Augmented Fifth Sharp Eleventh:
- C Дополненная пятая диез Одиннадцатая добавлена
- C авг № 11
- С # 5 # 11
- С+(#11)
Добавленный аккорд C Augmented Fifth Sharp Eleventh состоит из нот C, E, G# и F#.
май7 (# 5)
Как создать аккорд Major Seventh Sharp Fifth:
1
б2
2
B3
3
4
B5
5
#5
6
B7
7
222222222222 2
7
222222222222222 2
7
2222222222222222 2
2
2
Интервалы в аккорде до мажор септаккорд диез квинта: корень, мажорная терция, расширенная квинта,
и майор седьмой
Вы можете найти этот аккорд обозначенным как:
- До мажор Седьмая диез Квинта
- До мажор7+5
- До мажор 7 # 5
- Cmaj7 (# 5)
Ноты в этом аккорде: C, E, G# и B.
9(#5)
Как строится аккорд Dominant Ninth Sharp Fifth:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы, составляющие аккорд C9 (# 5): основной тон, мажорная терция, увеличенная квинта, минорная септима,
и майор девятый
Различные обозначения аккорда C9 (# 5):
- C Доминантная девятая Острая квинта
- С 9 # 5
- C 9 августа 5
- С 9+5
- С Дом9#5
- С9(#5)
Этот аккорд состоит из нот C, E, G#, Bb и D.
Пример: C 9 (# 5) Еще схемы аккордов
13 (# 5)
Тоны в аккорде Dominant Thirteen Sharp Fifth:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы этого аккорда следующие: корень, мажорная терция, увеличенная квинта, минорная септима, мажорная девятка,
Майор Одиннадцатый и Майор Тринадцатый
Варианты названия аккорда C13(#5):
- C Доминантная Тринадцатая Острая Пятая
- С 13+5
- C 13 авг 5
- С 13 # 5
- С13(#5)
Аккорд C Dominant Thirteen Sharp Fifth состоит из нот C, E, G#, Bb, D, F и A.
Уменьшенные аккорды
тусклый
Формула уменьшенной хорды:
2
22
2 22
2922222
2922н.
подвесной 2 хорд
состоит из основного тона, большой секунды и совершенной квинты
Аккорд Csus2 известен как:
- C Подвешенный второй
- Csus2
Этот аккорд состоит из нот C, D и G.
Пример: Csus2 Еще схемы аккордов
сус4
Формула аккорда для приостановленного четвертого аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы, составляющие аккорд Csus4, — это Root, Perfect Fourth и Perfect Fifth.
Различные обозначения для подвешенного четвертого аккорда C:
- C Подвесной четвертый
- Csus4
Ноты этого аккорда: C, F и G.
Пример: Csus4 Еще схемы аккордов
7sus4
Тоны доминирующего септаккорда, приостановленного четвертого аккорда:
2
2922222
2922н.
подвесной 2 хорд
состоит из основного тона, большой секунды и совершенной квинты
Аккорд Csus2 известен как:
- C Подвешенный второй
- Csus2
Этот аккорд состоит из нот C, D и G.
Пример: Csus2 Еще схемы аккордов
сус4
Формула аккорда для приостановленного четвертого аккорда:
922н. подвесной 2 хорд состоит из основного тона, большой секунды и совершенной квинты
Аккорд Csus2 известен как:
- C Подвешенный второй
- Csus2
Этот аккорд состоит из нот C, D и G.
Пример: Csus2Еще схемы аккордов
сус41
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы, составляющие аккорд Csus4, — это Root, Perfect Fourth и Perfect Fifth.
Различные обозначения для подвешенного четвертого аккорда C:
- C Подвесной четвертый
- Csus4
Ноты этого аккорда: C, F и G.
Пример: Csus4Еще схемы аккордов
7sus41
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Интервалы этого аккорда: корень, совершенная четвертая, совершенная квинта и минорная септаккорд.
Различные обозначения аккорда C7sus4:
- C Доминирующая седьмая приостановленная четвертая
- C дом7сус4
- C 7 Подвесной 5
- C7sus4
Ноты в аккорде C7sus4: C, F, G и Bb.
Пример: C 7sus4 Еще схемы аккордов
Расширенные аккорды
август
Структура аккорда:
1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты,
и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.
Пример: C 7 (# 5) Еще схемы аккордов
+(#11)
Формула аккорда для Augmented Fifth Sharp Eleventh добавила аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, увеличенная квинта и диез одиннадцатая.
Различные обозначения для дополненного аккорда C Augmented Fifth Sharp Eleventh:
- C Дополненная пятая диез Одиннадцатая добавлена
- C авг № 11
- С # 5 # 11
- С+(#11)
Добавленный аккорд C Augmented Fifth Sharp Eleventh состоит из нот C, E, G# и F#.
май7 (# 5)
Как создать аккорд Major Seventh Sharp Fifth:
1
б2
2
B3
3
4
B5
5
#5
6
B7
7
222222222222 2
7
222222222222222 2
7
2222222222222222 2
2
2
Интервалы в аккорде до мажор септаккорд диез квинта: корень, мажорная терция, расширенная квинта,
и майор седьмой
Вы можете найти этот аккорд обозначенным как:
- До мажор Седьмая диез Квинта
- До мажор7+5
- До мажор 7 # 5
- Cmaj7 (# 5)
Ноты в этом аккорде: C, E, G# и B.
9(#5)
Как строится аккорд Dominant Ninth Sharp Fifth:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы, составляющие аккорд C9 (# 5): основной тон, мажорная терция, увеличенная квинта, минорная септима,
и майор девятый
Различные обозначения аккорда C9 (# 5):
- C Доминантная девятая Острая квинта
- С 9 # 5
- C 9 августа 5
- С 9+5
- С Дом9#5
- С9(#5)
Этот аккорд состоит из нот C, E, G#, Bb и D.
Пример: C 9 (# 5) Еще схемы аккордов
13 (# 5)
Тоны в аккорде Dominant Thirteen Sharp Fifth:
2
22
2 22
2922222
2922н.
Интервалы этого аккорда: корень, совершенная четвертая, совершенная квинта и минорная септаккорд.
Различные обозначения аккорда C7sus4:
- C Доминирующая седьмая приостановленная четвертая
- C дом7сус4
- C 7 Подвесной 5
- C7sus4
Ноты в аккорде C7sus4: C, F, G и Bb.
Пример: C 7sus4 Еще схемы аккордов
Расширенные аккорды
август
Структура аккорда:
1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты,
и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.
Пример: C 7 (# 5) Еще схемы аккордов
+(#11)
Формула аккорда для Augmented Fifth Sharp Eleventh добавила аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, увеличенная квинта и диез одиннадцатая.
Различные обозначения для дополненного аккорда C Augmented Fifth Sharp Eleventh:
- C Дополненная пятая диез Одиннадцатая добавлена
- C авг № 11
- С # 5 # 11
- С+(#11)
Добавленный аккорд C Augmented Fifth Sharp Eleventh состоит из нот C, E, G# и F#.
май7 (# 5)
Как создать аккорд Major Seventh Sharp Fifth:
1
б2
2
B3
3
4
B5
5
#5
6
B7
7
222222222222 2
7
222222222222222 2
7
2222222222222222 2
2
2
Интервалы в аккорде до мажор септаккорд диез квинта: корень, мажорная терция, расширенная квинта,
и майор седьмой
Вы можете найти этот аккорд обозначенным как:
- До мажор Седьмая диез Квинта
- До мажор7+5
- До мажор 7 # 5
- Cmaj7 (# 5)
Ноты в этом аккорде: C, E, G# и B.
9(#5)
Как строится аккорд Dominant Ninth Sharp Fifth:
2
2922222
2922н.
Интервалы этого аккорда: корень, совершенная четвертая, совершенная квинта и минорная септаккорд.
Различные обозначения аккорда C7sus4:
- C Доминирующая седьмая приостановленная четвертая
- C дом7сус4
- C 7 Подвесной 5
- C7sus4
Ноты в аккорде C7sus4: C, F, G и Bb.
Пример: C 7sus4 Еще схемы аккордов
Расширенные аккорды
август
Структура аккорда:
922н. Интервалы этого аккорда: корень, совершенная четвертая, совершенная квинта и минорная септаккорд.
Различные обозначения аккорда C7sus4:
- C Доминирующая седьмая приостановленная четвертая
- C дом7сус4
- C 7 Подвесной 5
- C7sus4
Ноты в аккорде C7sus4: C, F, G и Bb.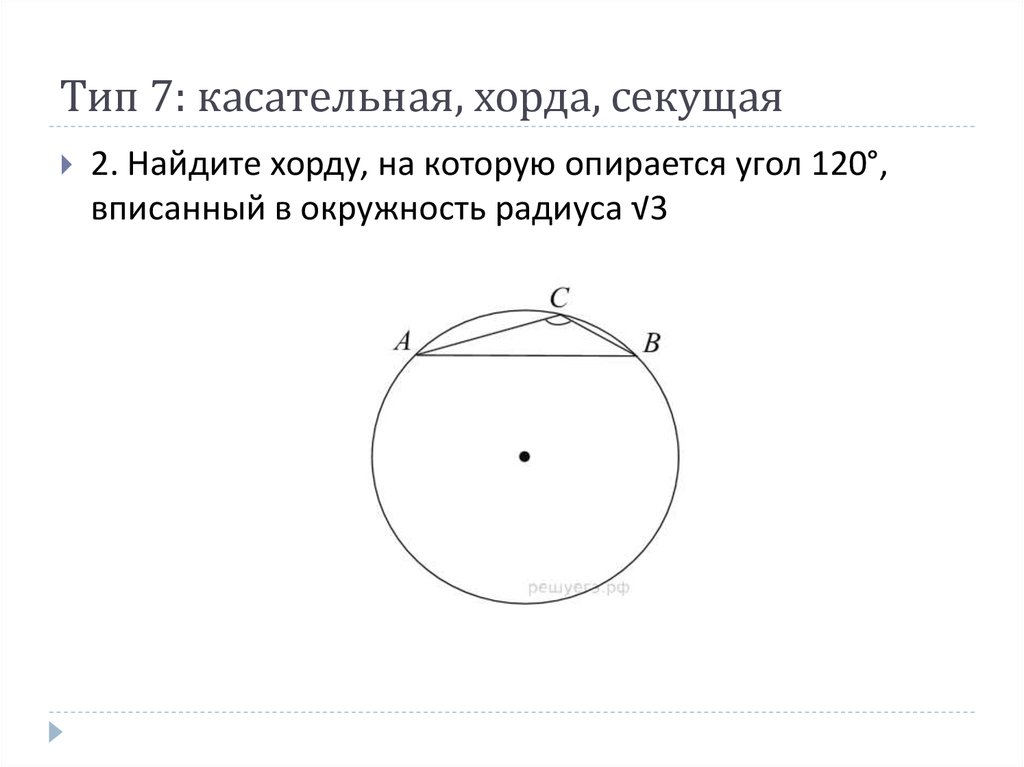
Еще схемы аккордов
Расширенные аккорды
август1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты,
и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.
Пример: C 7 (# 5) Еще схемы аккордов
+(#11)
Формула аккорда для Augmented Fifth Sharp Eleventh добавила аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, увеличенная квинта и диез одиннадцатая.
Различные обозначения для дополненного аккорда C Augmented Fifth Sharp Eleventh:
- C Дополненная пятая диез Одиннадцатая добавлена
- C авг № 11
- С # 5 # 11
- С+(#11)
Добавленный аккорд C Augmented Fifth Sharp Eleventh состоит из нот C, E, G# и F#.
май7 (# 5)
Как создать аккорд Major Seventh Sharp Fifth:
2
22
2 22
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты,
и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.
Пример: C 7 (# 5) Еще схемы аккордов
+(#11)
Формула аккорда для Augmented Fifth Sharp Eleventh добавила аккорд:
2
2922222
2922н.
Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августа Еще схемы аккордов
7 (# 5)
Формула аккорда Доминант Септаккорд Диез Квинта:
922н. Этот аккорд состоит из основного тона, мажорной терции и увеличенной квинты.
Аккорд C Augmented Fifth известен как:
- C Дополненный пятый
- C Расширенная триада
- С +5
- С # 5
- Кауг
Ноты в расширенном пятом аккорде C: C, E и G#.
Пример: C августаЕще схемы аккордов
7 (# 5)1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Аккорд C Dominant Seventh Sharp Fifth состоит из основного тона, мажорной терции, дополненной квинты, и второстепенная седьмая
Аккорд C7 (# 5) известен как:
- C Доминантная седьмая острая квинта
- С Дом+5
- С 7 # 5
- С 7+5
- C 7 августа 5
- С7(#5)
Аккорд C7(#5) состоит из нот C, E, G# и Bb.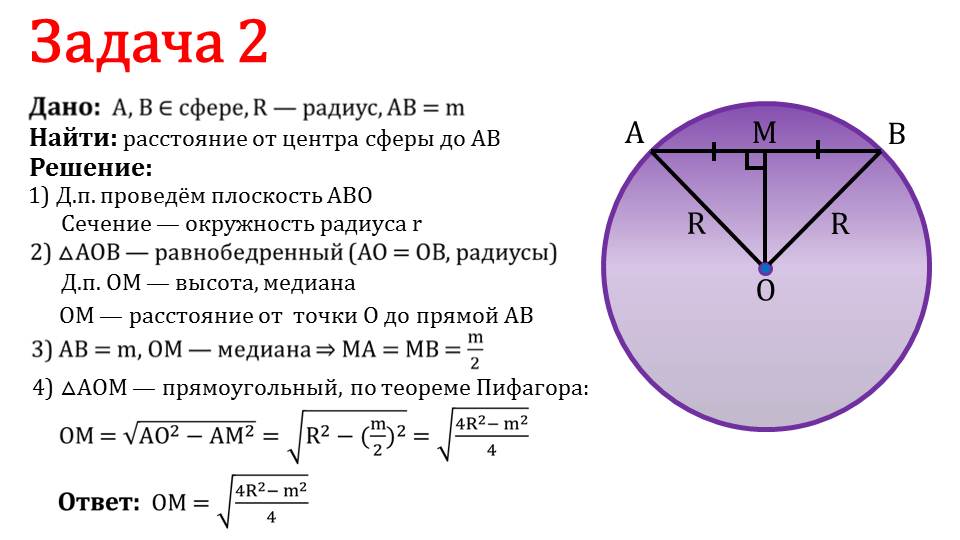
Еще схемы аккордов
+(#11)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, увеличенная квинта и диез одиннадцатая.
Различные обозначения для дополненного аккорда C Augmented Fifth Sharp Eleventh:
- C Дополненная пятая диез Одиннадцатая добавлена
- C авг № 11
- С # 5 # 11
- С+(#11)
Добавленный аккорд C Augmented Fifth Sharp Eleventh состоит из нот C, E, G# и F#.
1
б2
2
B3
3
4
B5
5
#5
6
B7
7
222222222222 2
7
222222222222222 2
7
2222222222222222 2
2
2 Интервалы в аккорде до мажор септаккорд диез квинта: корень, мажорная терция, расширенная квинта, и майор седьмой
Вы можете найти этот аккорд обозначенным как:
- До мажор Седьмая диез Квинта
- До мажор7+5
- До мажор 7 # 5
- Cmaj7 (# 5)
Ноты в этом аккорде: C, E, G# и B.
9(#5)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы, составляющие аккорд C9 (# 5): основной тон, мажорная терция, увеличенная квинта, минорная септима, и майор девятый
Различные обозначения аккорда C9 (# 5):
- C Доминантная девятая Острая квинта
- С 9 # 5
- C 9 августа 5
- С 9+5
- С Дом9#5
- С9(#5)
Этот аккорд состоит из нот C, E, G#, Bb и D.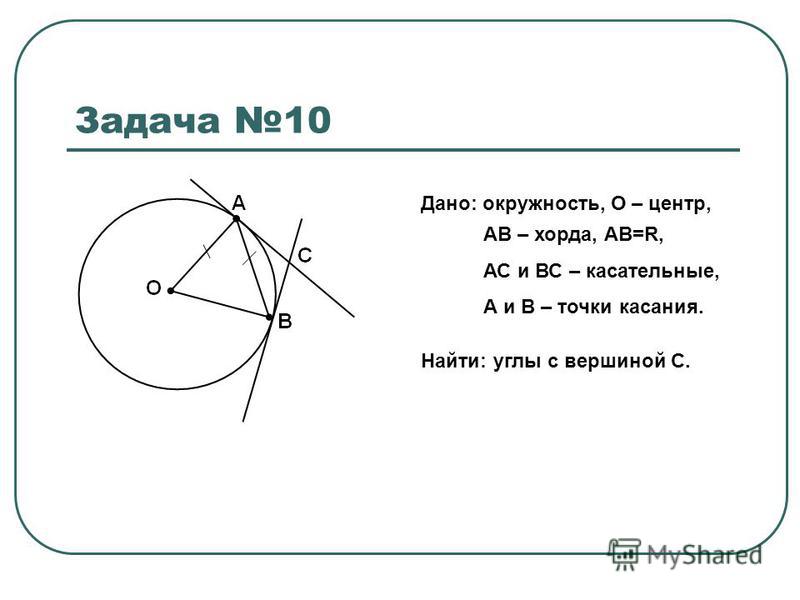
Еще схемы аккордов
13 (# 5)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы этого аккорда следующие: корень, мажорная терция, увеличенная квинта, минорная септима, мажорная девятка, Майор Одиннадцатый и Майор Тринадцатый
Варианты названия аккорда C13(#5):
- C Доминантная Тринадцатая Острая Пятая
- С 13+5
- C 13 авг 5
- С 13 # 5
- С13(#5)
Аккорд C Dominant Thirteen Sharp Fifth состоит из нот C, E, G#, Bb, D, F и A.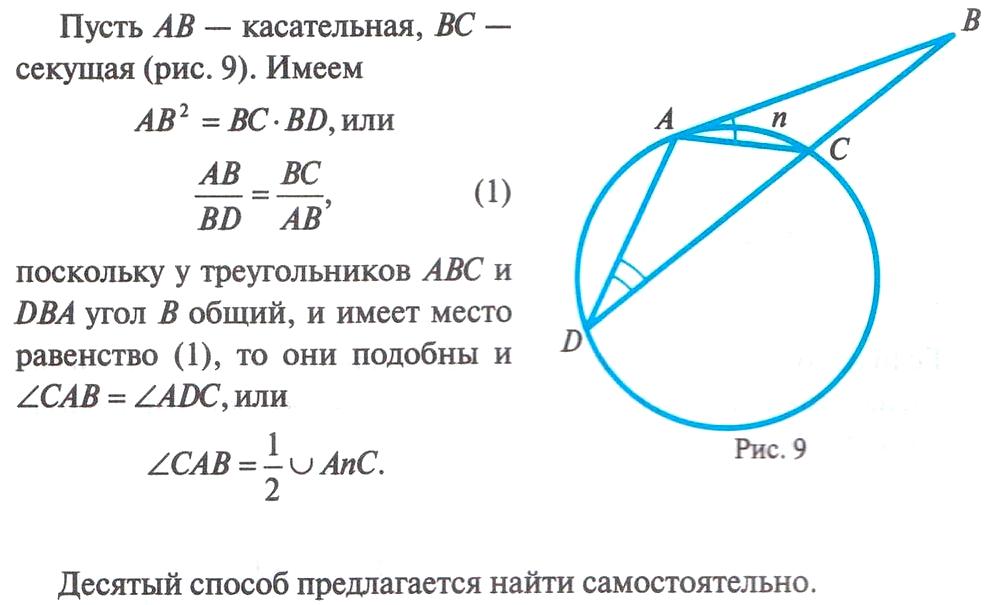
Уменьшенные аккорды
тусклый1
б2
2
b3
3
4
b5
5
#5
6
0 7 20203 9
3 9 Аккорд Cdim состоит из основного тона, минорной терции и уменьшенной квинты.
Варианты названия этого аккорда:
- C Уменьшенный
- С Дим
- C Уменьшенная триада
- С Ø
- Cdim
Ноты уменьшенного аккорда C: C, Eb и Gb.
Пример: C тусклыйЕще схемы аккордов
тусклый7 Тоны уменьшенного септаккорда:1
B2
2
B3
3
4
B5
5
#5
2222229
#5
22222229
#5
2222222
#5
22222222
#5
2222220003
7
Интервалы, составляющие C Уменьшенный септаккорд корень, минорная терция, уменьшенная Пятая и уменьшенная седьмая
Уменьшенный септаккорд C пишется следующим образом:
- C Уменьшенная седьмая
- С Дим
- C Уменьшенный 7
- С О7
- Cdim7
Ноты уменьшенного септаккорда C: C, Eb, Gb и Bbb.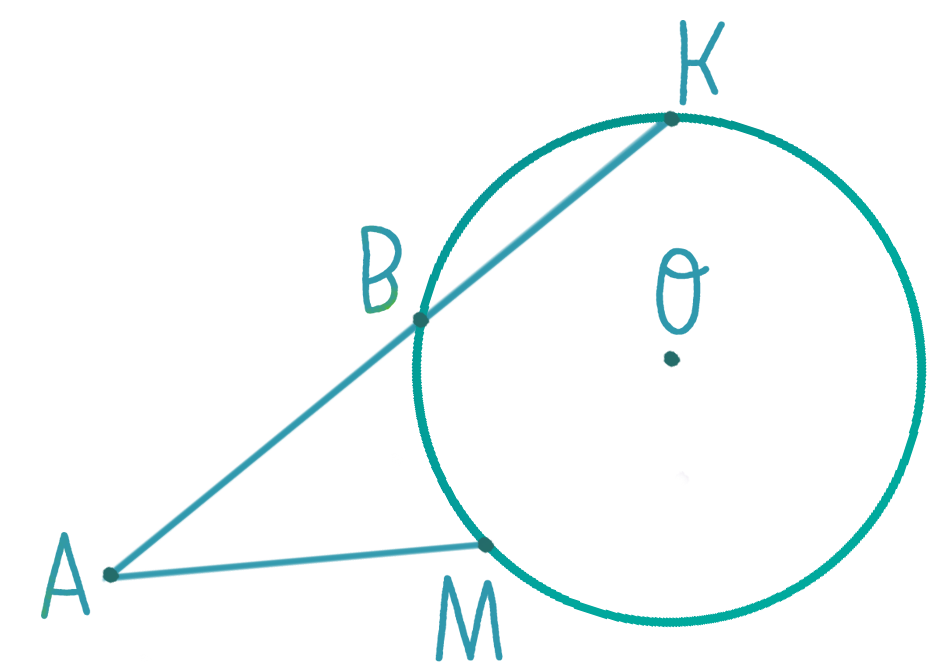
Еще схемы аккордов
m7b5 Аккордовая структура минорной септаккордной пятерки:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Интервалы в пятом аккорде до минор септаккорд-бемоль — это основной тон, минорная терция, уменьшенная квинта и Малая седьмая
Варианты названия для пятого аккорда до минор септаккорд-бемоль:
- До минор Седьмая бемольная пятерка
- C Полууменьшенная Седьмая
- C Полууменьшенный 7
- С Ø7
- С М7-5
- С Мин7-5
- см7b5
Ноты в этом аккорде: C, Eb, Gb и Bb.
Еще схемы аккордов
Доминирующие аккорды
7 Формула доминирующего септаккорда:1
B2
2
B3
3
4
B5
5
#5
2
222229222222222
2
2222н 222 2
2 2
5
2
2
2 2
2
2
2
2
2
2
2
2
2
2
2
Интервалы, составляющие C Доминантный седьмой аккорд: основной тон, мажорная терция, совершенная квинта и Малая седьмая
Доминантный септаккорд C известен как:
- C Доминантная седьмая
- С Дом
- С7
Этот аккорд состоит из нот C, E, G и Bb.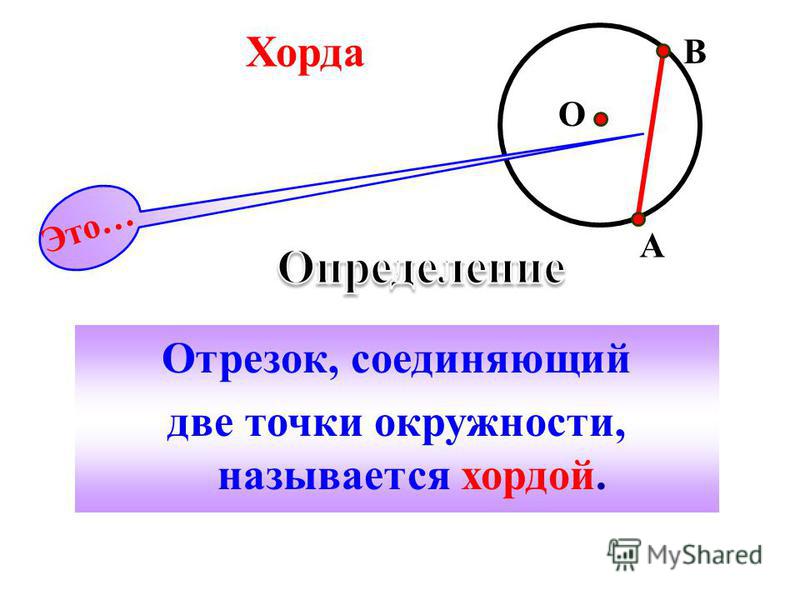
Еще схемы аккордов
7b5 Структура аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
Аккорд C7b5 состоит из основного тона, мажорной терции, уменьшенной квинты и минорной септимы.
Варианты названия этого аккорда:
- C Доминантная седьмая плоская пятерка
- С 7-5
- С 7(б5)
- С Дом7b5
- C7b5
Ноты в этом аккорде: C, E, Gb и Bb.
Пример: С 7b5Еще схемы аккордов
7(б13) Аккордовая структура Dominant Seventh Flat Thirteen Добавлен аккорд:1
B2
2
B3
3
4
B5
5
#5
2
22
22
22
22
2 22
2922222
2922н.
 Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать
Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать Различные обозначения для C Dominant Seventh Flat Thirteen Добавлен аккорд:
- C Доминантная седьмая плоская тринадцать добавлена
- С Дом7b13
- С 7b13
- С 7-13
- С7(б13)
Ноты аккорда C7(b13): C, E, G, Bb и Ab.
7(б9)
Структура аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Аккорд C Dominant Seventh Flat Nine Added состоит из основного тона, мажорной терции, совершенной квинты,
Малая седьмая и малая девятая
Аккорд C Dominant Seventh Flat Nine Added известен как:
- Добавлена доминантная седьмая плоская девятка C
- С 7b9
- С 7-9
- С Дом7b9
- С7(б9)
Аккорд C7(b9) состоит из нот C, E, G, Bb и Db.
Пример: С 7(b9) Еще схемы аккордов
7 (# 11)
Как создать доминантный септаккорд Sharp Eleventh Добавленный аккорд:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, совершенная квинта, минорная септима и диез.
Одиннадцатый
Аккорд C7 (# 11) пишется следующим образом:
- C Доминирующая Седьмая Диез Одиннадцатая Добавлена
- С Дом+11
- С 7 # 11
- С 7+11
- C 7 августа 11 г.
- С7(#11)
Ноты аккорда C7 (# 11): C, E, G, Bb и F#.
Пример: C 7 (# 11) Еще схемы аккордов
7(#9)
Структура аккорда:
2
22
2 22
2922222
2922н.
 Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать
Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать Различные обозначения для C Dominant Seventh Flat Thirteen Добавлен аккорд:
- C Доминантная седьмая плоская тринадцать добавлена
- С Дом7b13
- С 7b13
- С 7-13
- С7(б13)
Ноты аккорда C7(b13): C, E, G, Bb и Ab.
7(б9)
Структура аккорда:
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Аккорд C Dominant Seventh Flat Nine Added состоит из основного тона, мажорной терции, совершенной квинты,
Малая седьмая и малая девятая
Аккорд C Dominant Seventh Flat Nine Added известен как:
- Добавлена доминантная седьмая плоская девятка C
- С 7b9
- С 7-9
- С Дом7b9
- С7(б9)
Аккорд C7(b9) состоит из нот C, E, G, Bb и Db.
Пример: С 7(b9) Еще схемы аккордов
7 (# 11)
Как создать доминантный септаккорд Sharp Eleventh Добавленный аккорд:
2
2922222
2922н.
 Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать
Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать Различные обозначения для C Dominant Seventh Flat Thirteen Добавлен аккорд:
- C Доминантная седьмая плоская тринадцать добавлена
- С Дом7b13
- С 7b13
- С 7-13
- С7(б13)
Ноты аккорда C7(b13): C, E, G, Bb и Ab.
7(б9)
Структура аккорда:
922н.
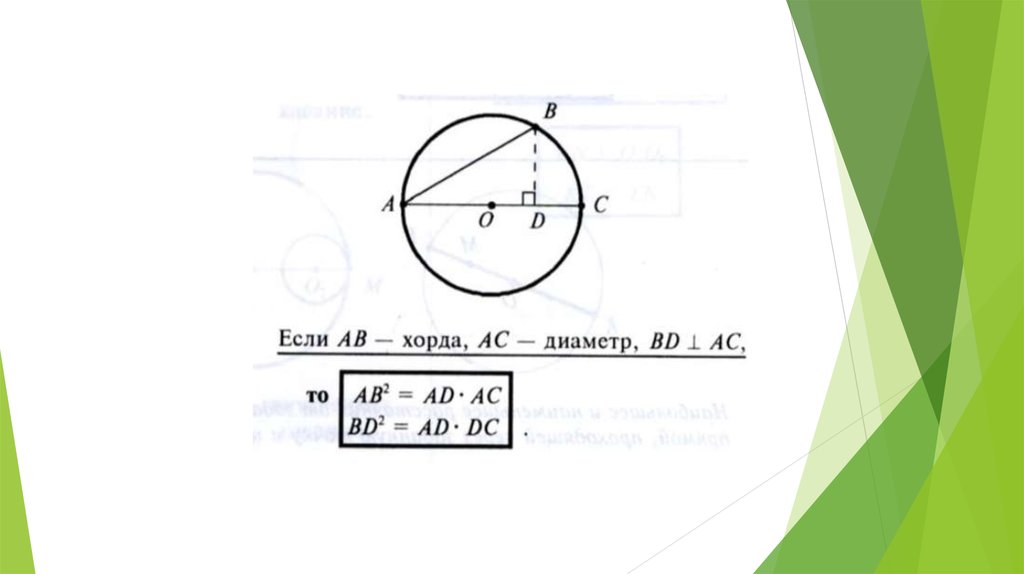 Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
Тринадцать
Этот аккорд состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и бемоля.
ТринадцатьРазличные обозначения для C Dominant Seventh Flat Thirteen Добавлен аккорд:
- C Доминантная седьмая плоская тринадцать добавлена
- С Дом7b13
- С 7b13
- С 7-13
- С7(б13)
Ноты аккорда C7(b13): C, E, G, Bb и Ab.
7(б9)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Аккорд C Dominant Seventh Flat Nine Added состоит из основного тона, мажорной терции, совершенной квинты, Малая седьмая и малая девятая
Аккорд C Dominant Seventh Flat Nine Added известен как:
- Добавлена доминантная седьмая плоская девятка C
- С 7b9
- С 7-9
- С Дом7b9
- С7(б9)
Аккорд C7(b9) состоит из нот C, E, G, Bb и Db.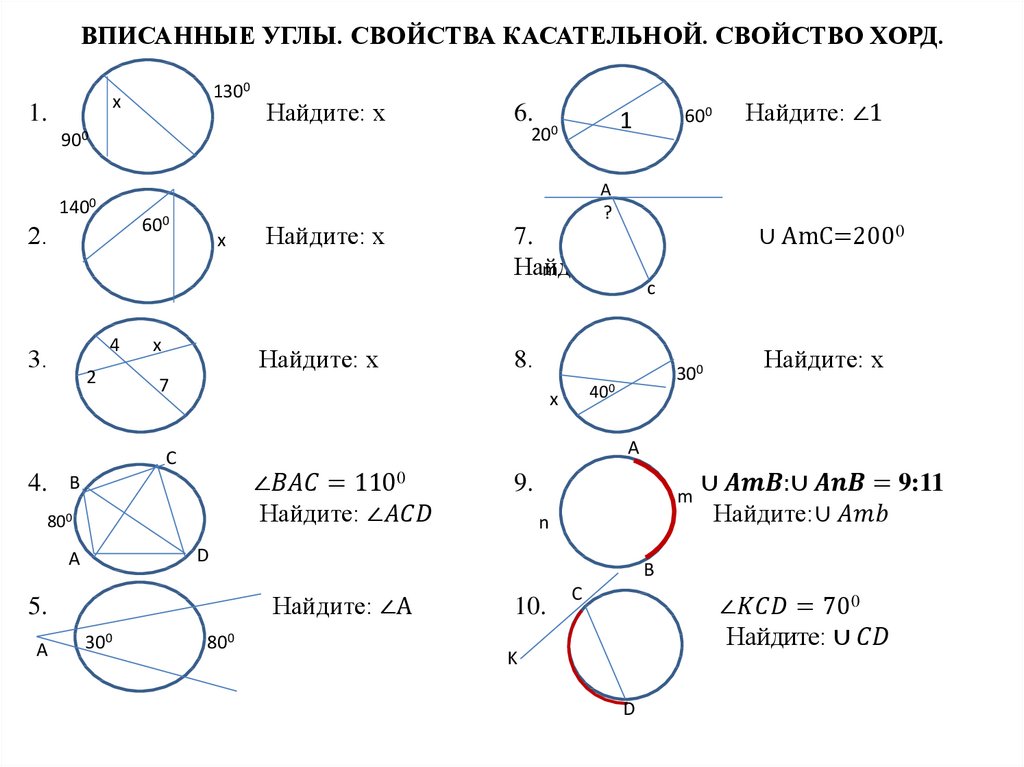
Еще схемы аккордов
7 (# 11)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда: корень, мажорная терция, совершенная квинта, минорная септима и диез. Одиннадцатый
Аккорд C7 (# 11) пишется следующим образом:
- C Доминирующая Седьмая Диез Одиннадцатая Добавлена
- С Дом+11
- С 7 # 11
- С 7+11
- C 7 августа 11 г.
- С7(#11)
Ноты аккорда C7 (# 11): C, E, G, Bb и F#.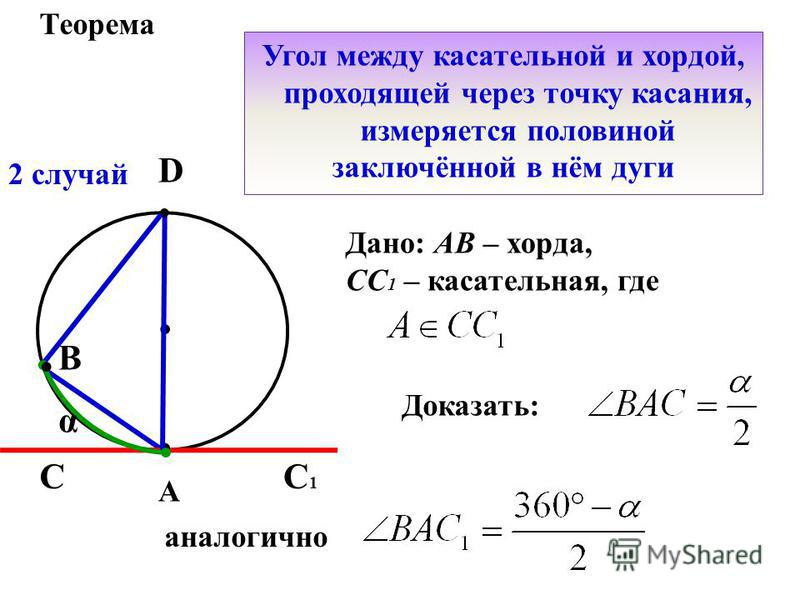
Еще схемы аккордов
7(#9)1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы, составляющие C7(#9) аккорд: основной тон, мажорная терция, совершенная квинта, минорная септима и Острая девятая
Этот аккорд также пишется следующим образом:
- C Добавлена доминантная седьмая диез девятая
- С Дом7#9
- С 7 # 9
- С 7+9
- C 7 августа 9
- С7(#9)
Аккорд C7(#9) состоит из нот C, E, G, Bb и D#.
Еще схемы аккордов
9 Тоны в доминантном девятом аккорде:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Доминантный девятый аккорд C состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы и Майор Девятый
Некоторые таблицы аккордов называют этот аккорд следующим образом:
- C Доминантная девятая
- С Дом9
- С9
Аккорд C9 состоит из нот C, E, G, Bb и D.
Пример: С 9Еще схемы аккордов
9b5 Тоны в пятом аккорде Dominant Ninth Flat:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы в этом аккорде: корень, мажорная терция, уменьшенная квинта, минорная септима и мажор. Девятый
Девятый
Пятый аккорд C Dominant Ninth Flat известен как:
- C Доминантная девятая плоская пятерка
- С 9-5
- С 9(b5)
- С Дом9b5
- C9b5
Аккорд C9b5 состоит из нот C, E, Gb, Bb и D.
Пример: С 9b5Еще схемы аккордов
11 Формула аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
# 9
11
#11
13
Интервалы этого аккорда следующие: основной тон, мажорная терция, чистая квинта, минорная септима, мажорная девятая и майор одиннадцатый
Вы можете найти этот аккорд обозначенным как:
- C Доминантная одиннадцатая
- С Дом 11
- С Доминанта 11
- С11
Аккорд C11 состоит из нот C, E, G, Bb, D и F.
Еще схемы аккордов
9(#11) Формула аккорда для Dominant Ninth Sharp Eleventh Добавлен аккорд:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Аккорд C9 (#11) состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы, мажора. Девятый и острый одиннадцатый
Некоторые таблицы аккордов называют этот аккорд следующим образом:
- C Добавлена доминантная девятая диез одиннадцатая
- С 9 # 11
- С 9+11
- C дом9авг11
- С Дом9+11
- С9(#11)
Аккорд C Dominant Ninth Sharp Eleventh Added состоит из нот C, E, G, Bb, D и фа#
13 Формула аккорда для аккорда Dominant Thirteen:1
b2
2
b3
3
4
b5
5
#5
6
B7
7
8
B9
9
#
11
#
213
11
#
13
21
#110003
13
2
Аккорд C Dominant Thirteen состоит из основного тона, мажорной терции, совершенной квинты, минорной септимы, Майор Девятый, Майор Одиннадцатый и Майор ТринадцатыйВарианты названия аккорда C Dominant Thirteen:
- C Доминантная Тринадцать
- С13
Ноты в аккорде C Dominant Thirteen: C, E, G, Bb, D, F и A.
Еще схемы аккордов
13(б9) Как строится аккорд Dominant Thirteen Flat Nine:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы в этом аккорде: корень, мажорная терция, совершенная квинта, минорная септима, минорная девятка, Майор Одиннадцатый и Майор Тринадцатый
Аккорд C Dominant Thirteen Flat Nine пишется следующим образом:
- C Доминантная тринадцать, плоская девятка
- С 13-9
- С 13b9
- С13(б9)
Ноты в этом аккорде: C, E, G, Bb, Db, F и A.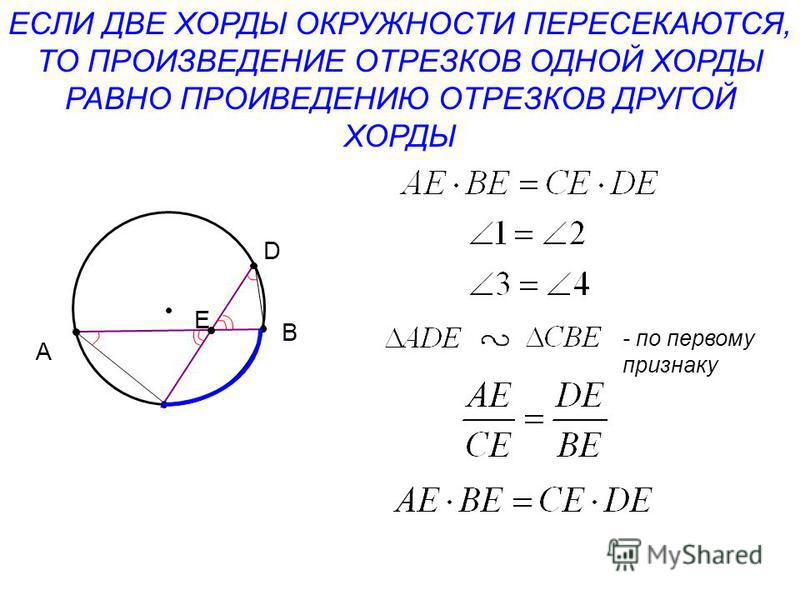
Еще схемы аккордов
13 (# 11) Формула аккорда Dominant Thirteen Sharp Eleventh:1
б2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
# 11
13
Аккорд C Dominant Thirteen Sharp Eleventh состоит из основного тона, мажорной терции, совершенной квинты, Малая седьмая, большая девятая, острая одиннадцатая и большая тринадцатая
Аккорд C Dominant Thirteen Sharp Eleventh известен как:
- C Доминантная Тринадцатая Диез Одиннадцатая
- С 13 # 11
- С 13+11
- C 13 авг. 11 г.

- С13(#11)
Ноты в аккорде C13 (# 11): C, E, G, Bb, D, F# и A.
13 (# 9) Тоны доминантного тринадцатого диезного девятого аккорда:1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13
Интервалы этого аккорда следующие: корень, мажорная терция, совершенная квинта, минорная септима, диез девятая, Майор Одиннадцатый и Майор Тринадцатый
Некоторые таблицы аккордов называют этот аккорд следующим образом:
- C Доминантная Тринадцатая Острая Девятая
- С 13+9
- C 13 авг 9
- С 13 # 9
- С13(#9)
Этот аккорд состоит из нот C, E, G, Bb, D#, F и A.
Формула длины хорды — GeeksforGeeks
Геометрия — это раздел математики, который имеет дело с линиями, углами, точками, сегментами и т. д. и помогает нам определять пространственные отношения между различными пространствами. Она считается одной из старейших областей математики. Фигуры — это фигуры, которые показывают поверхности, границы, линии и т. д. объекта. Все вокруг нас имеет разные формы и размеры. Некоторые из них прямоугольной формы, а некоторые треугольной формы. По размерности они делятся на два типа. Двумерные фигуры, которые имеют длину и ширину, но не имеют высоты, называются 2D-формами. Например: прямоугольник, квадрат, треугольник и т. д. Трехмерные формы, которые имеют длину, ширину и высоту, называются трехмерными фигурами. Например: сфера, куб, прямоугольный параллелепипед и т. д.
Представленная ниже статья посвящена изучению аккордов. Содержание включает определение хорды, объясняет ее свойства и содержит формулы для расчета длины хорды с использованием различных методов. В статье также есть несколько решенных примеров задач для лучшего понимания.
В статье также есть несколько решенных примеров задач для лучшего понимания.
Окружность
Окружность — это идеальная круглая форма, состоящая из всех точек на плоскости, расположенных на заданном расстоянии от данной точки. Они состоят из замкнутой изогнутой линии вокруг центральной точки. Точки, присутствующие на прямой, находятся на одинаковом расстоянии от центральной точки. Расстояние до центра окружности называется радиусом.
Хорда окружности
Отрезок, соединяющий любые две точки на окружности окружности, называется хордой окружности. Все мы должны знать, что диаметр считается самой длинной хордой окружности, проходящей через центр окружности. Среди всех других отрезков хордой считается тот, концы которого лежат на окружности окружности. Ниже приведена диаграмма, приведенная для справки.
Свойства хорды окружности
- Перпендикуляр к хорде, проведенный из центра окружности, делит хорду пополам.
- Хорды, равноудаленные от центра окружности, равны.

- Существует только одна окружность, проходящая через три точки, лежащие на одной прямой.
- Хорды равной длины образуют равные углы в центре окружности.
- Когда углы, образуемые хордой, равны, то равны и длины хорд.
Формулы для расчета хорд
Существует два основных метода или формулы для расчета длины хорды. длину хорды можно определить, используя перпендикулярное расстояние от центра окружности, а также тригонометрическим методом.
Длина хорды с использованием тригонометрии
длина хорды = 2 радиуса × Sin [угол/2]
Длина хорды с использованием длины перпендикуляра от центра р 2 – d 2
При условии, что две окружности имеют одну и ту же хорду, то длину этих хорд можно определить по формуле.
Длина общей хорды двух окружностей = 2R 1 × R 2 / Расстояние между двумя центрами окружности
где
R относится к радиусам.
Примеры задач
Задача 1. Окружность представляет собой угол в 70 градусов, радиус которого равен 5 см. Вычислите длину хорды окружности.
Решение:
Дано
Радиус = 5 см
Угол = 70 °
СЕЙЧАС,
Длина хорда = 2r × sin/2]
1 = 2 × 2 [2 SIN [ул/2]
2222222 гг. 2]
= 10 × sin35 °
= 10 × 0,5736
= 5,73 см
Задача 2: В круге , его хорды 6 см. Вычислите длину хорды.
Solution:
Given
Radius = 7cm
Distance = 6cm
Now,
Length of the chord = 2 √r 2 – d 2
= 2 √7 2 — 6 2
= 2 √ 49- 36
= 2 √13cm
Задача 3: Круг- угол 60 градусов, радиус которого составляет 12 см. Вычислите длину хорды окружности.
Вычислите длину хорды окружности.
Решение:
Дано
Радиус = 12 см
Угол = 60 °
Теперь,
Длина хорда = 2R × SIN [ул/2]
222222222 2 × 2 [6010 2
2222222 гг. /2]
=> 24 × sin30°
=> 24 × 0,5
=> 12 см
хорды 5 см. Вычислите длину хорды.
Solution:
Given
Radius = 16cm
Distance = 5cm
Now,
Length of the chord = 2 √r 2 – d 2
=> 2 √(16 ) 2 — (5) 2
=> 2 √ 256-25
=> 2 √231
=> 2 × 15,1
=> 30,2см
9 . общей хорды между окружностями радиусами 6см и 5см соответственно. И расстояние между двумя центрами было измерено как 8 см.
Решение:
Дано
Расстояние между двумя центрами равно 8см.
Радиусы двух окружностей R1 и R2 с длинами 6 см и 5 см соответственно.
Теперь,
длина общей хорды двух окружностей = 2R1 × R2 / расстояние между двумя центрами окружности
=> 2 × 5 × 6/8
=> 60/8
=> 7,5 см
Конструкция аккордов — Guitar Lesson World
Это полное руководство по построению аккордов с простыми правилами, которые вырвали меня из моей игровой колеи. Вы узнаете, как строить аккорды двумя способами, как давать имена аккордам, как аккорды связаны друг с другом, простые правила для запоминания аккордов и многое другое.
Купить PDF-версию этого урока
Это полное руководство по построению аккордов с простыми правилами, которые вырвали меня из моей игровой колеи. Вы узнаете, как строить аккорды двумя способами, как давать имена аккордам, как аккорды связаны друг с другом, простые правила для запоминания аккордов и многое другое.
Чем полезно построение аккордов
Когда я впервые импровизировал, я запомнил гаммы.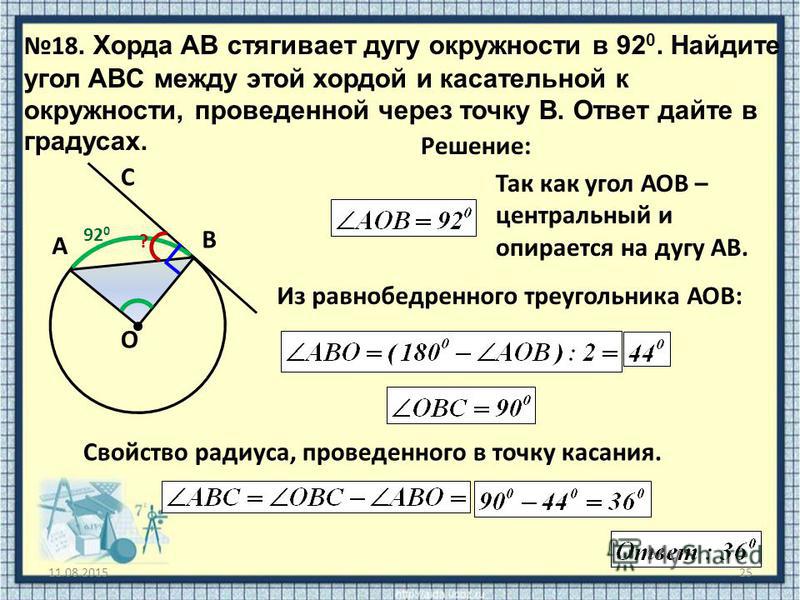 Это было очень весело, потому что я мог неожиданно играть соло во многих аккордах и песнях. Паттерн упростил задачу, но я начал играть одни и те же фразы снова и снова. Я не мог сломать эту колею, потому что не знал по-настоящему ни ноты аккордов, которые играл, ни ноты гаммы, которую использовал. В результате моя игра стала скучной.
Это было очень весело, потому что я мог неожиданно играть соло во многих аккордах и песнях. Паттерн упростил задачу, но я начал играть одни и те же фразы снова и снова. Я не мог сломать эту колею, потому что не знал по-настоящему ни ноты аккордов, которые играл, ни ноты гаммы, которую использовал. В результате моя игра стала скучной.
Когда я выучил ноты аккордов, я смог находить и воспроизводить ноты аккордов и мыслить музыкально. Я не просто выучил ноты, я начал владеть нотами и заставлять их работать на меня. Этот урок охватывает все, что вам нужно знать о построении аккордов, а также мои практические советы и интуицию, чтобы упростить изучение.
Этот урок требует некоторых знаний об интервалах. Если вы их еще не знаете, рекомендую прочитать мой урок по интервалам. Вы также должны знать мажорную гамму, так как она используется в одном из двух методов построения аккордов. Вы также можете найти эту информацию в Guitar Lesson World The Book.
Три типа аккордов
Для практических целей вам следует знать три разных типа аккордов.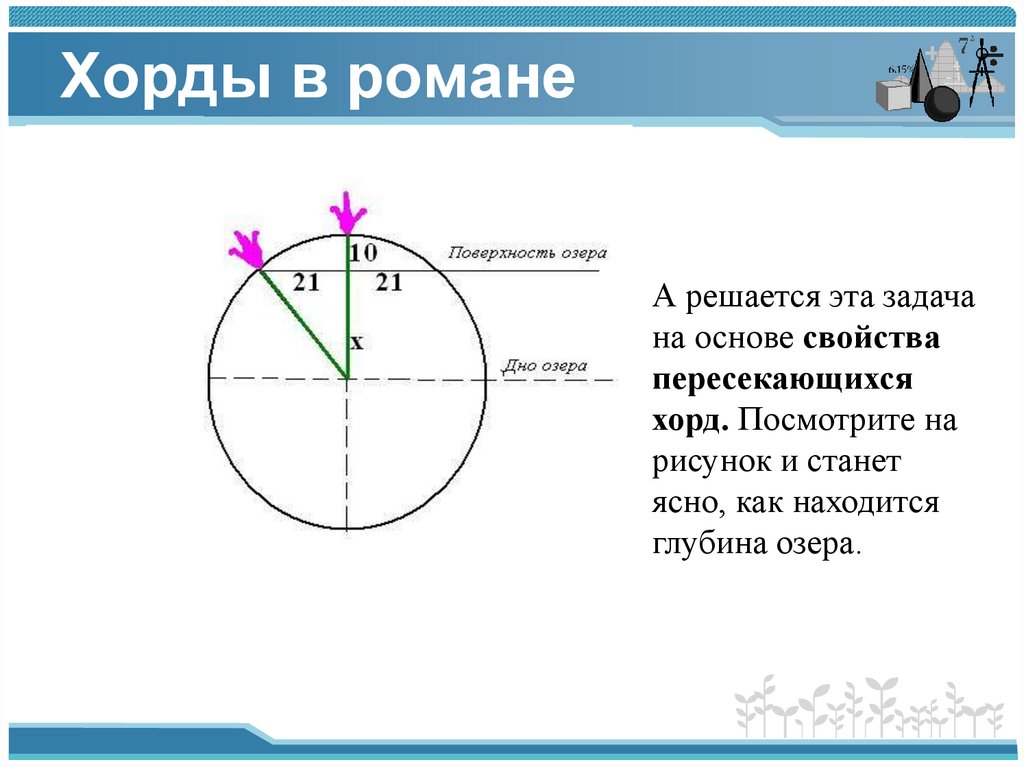 Я не говорю о качествах аккордов, я говорю о категориях аккордов. Это трезвучия, септаккорды и расширенные аккорды.
Я не говорю о качествах аккордов, я говорю о категориях аккордов. Это трезвучия, септаккорды и расширенные аккорды.
Трезвучия
Трезвучия — это аккорды из трех нот. Это могут быть мажорные, минорные, уменьшенные, увеличенные или приостановленные аккорды. Хотя трезвучия состоят ровно из 3 нот, вы можете играть мажорные, минорные, уменьшенные, дополненные и приостановленные аккорды с большим количеством нот, просто удвоив некоторые из нот. Все формы аккордов CAGED, которые изучают большинство начинающих, используют двойные ноты.
Септаккорды
Это 4-х нотные аккорды, которые имеют седьмую ступень, то есть ноту, обычно являющуюся мажорной или минорной септаккордой над тоникой. Наиболее распространенными септаккордами являются мажорный 7, минорный 7 и доминантный 7.
Расширенные аккорды
Расширенные аккорды — это просто аккорды, содержащие девятую, одиннадцатую или тринадцатую. Они считаются расширенными нотами. Обратите внимание, что их также можно рассматривать как 2-ю, 4-ю или 6-ю.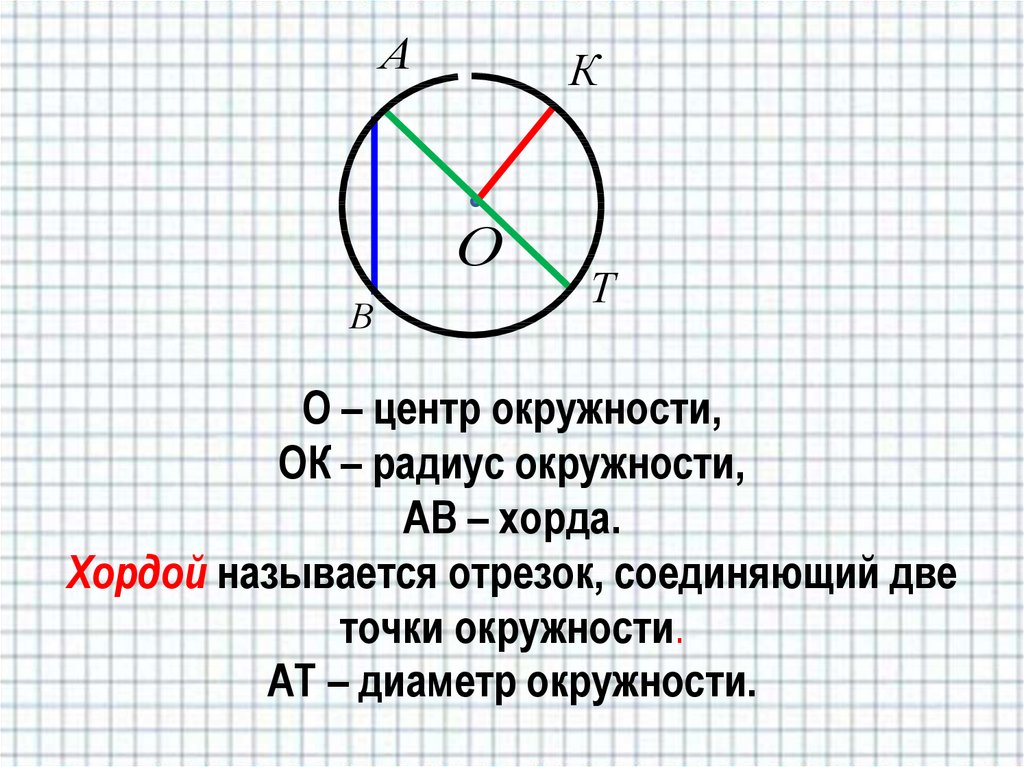 Например, в тональности C 2-я и 9-я — это D. 4-я и 11-я — это F. 6-я и 13-я — это A.
Например, в тональности C 2-я и 9-я — это D. 4-я и 11-я — это F. 6-я и 13-я — это A.
Вам может быть интересно, почему мы вообще используем названия 9, 11, 13, когда 2, 4 и 6 — это одни и те же ноты. Есть несколько причин. Самая простая причина в том, что 9, 11 и 13 используются, когда вы расширяете септаккорды. Высшая ступень септаккорда — септаккорд, они дополняются нотами с более высокими номерами.
2 способа обучения построению аккордов
Существует два распространенных способа обучения построению аккордов. У каждого есть свои плюсы и минусы. Мне нравится учить их обоих, потому что они оба полезны по-своему.
Метод 1: Формула + мажорная гамма
Если вы знаете мажорную гамму, это простой способ.
- Вы выбираете основную ноту, например C
- Вы получаете ноты мажорной гаммы: C-D-E-F-G-A-B.
- Вы применяете формулу аккорда из списка, который я предоставлю позже.
Например, формула мажорных аккордов: 1-3-5.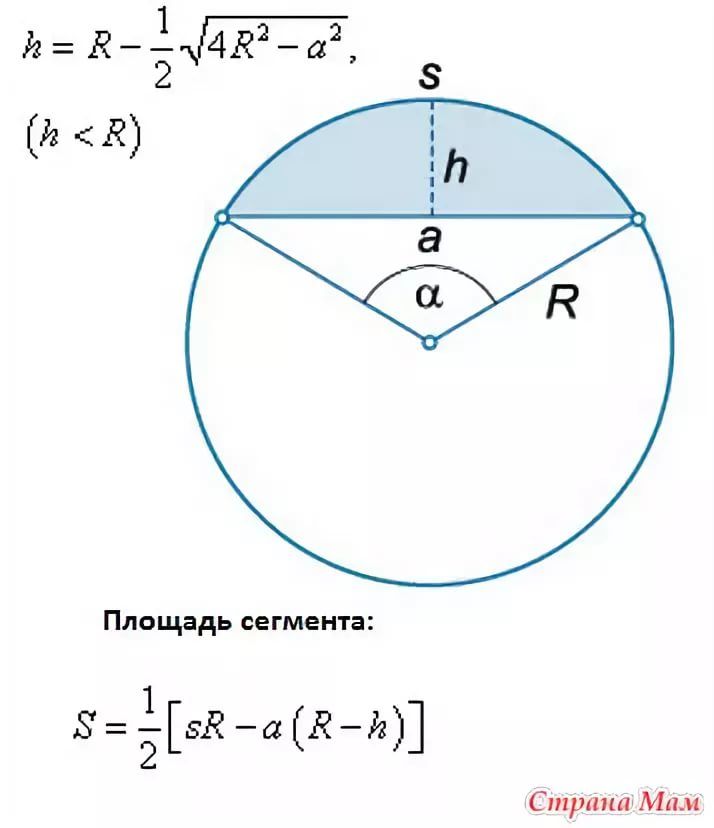 Мы берем первую, третью и пятую ноты мажорной гаммы, чтобы создать этот аккорд. Таким образом, аккорд до мажор имеет ноты C-E-G.
Мы берем первую, третью и пятую ноты мажорной гаммы, чтобы создать этот аккорд. Таким образом, аккорд до мажор имеет ноты C-E-G.
Некоторые формулы изменяют одну из степеней акциденцией. Например, формула минорного аккорда 1-♭3-5. Это означает, что аккорд до минор имеет ноты C-E♭-G.
Триада до минорВажно отметить, что аккорды могут удваивать ноты. Например, до мажор в открытой позиции удваивает до (2-я и 5-я струны) и ми (1-я и 4-я струны).
Открытая позиция до мажорПоскольку в мажорной гамме 7 нот, вам может быть интересно, как мы играем расширенные аккорды, включающие 9, 11 или 13. Вы просто повторяете названия нот. Например, ноты до-мажорной гаммы (повторяющиеся): C-D-E-F-G-A-B-C-D-E-F-G-A-B.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| С | Д | Е | Ф | Г | А | Б | С | Д | Е | Ф | Г | А | Б |
Список всех нот мажорной гаммы и формулы аккордов можно найти в разделе моих ресурсов.
Метод 2: интервалы
Аккорды могут быть сформированы с использованием интервалов формул , которые я приведу в следующем разделе. Они могут быть заданы как интервал от корня или относительно предыдущей ноты. Если вам нужно освежить свои знания об интервалах, рекомендую прочитать мой урок об интервалах.
Относительно основного тона
Если вы формируете аккорд до мажор 7 с интервалами основного тона, вы должны использовать следующую формулу: мажорная терция, чистая квинта, мажорная септаккорд.
Другими словами, это ноты: до (тоника), ми (большая терция вверх от до), соль (чистая квинта вверх от до) и си (большая септима вверх от до).
Относительно предыдущей ноты
Иногда интервалы указываются относительно предыдущей ноты, потому что аккорды (обычно) складываются терциями. Для до мажор 7 формула будет большой терцией, малой терцией, большой терцией. Ноты: C (тоника), E (мажорная терция выше C), G (младшая терция выше E) и B (мажорная терция выше G).
Соблюдайте алфавитное расстояние между нотами. C до E — большая терция. Это третий, потому что он охватывает 3 буквенных названий нот C-D-E. Это важно, потому что до и ми разделены на 2 полных шага в шаге . От ми до соль — второстепенная терция, потому что она охватывает 3 названия нот в алфавитном порядке, ми-фа-соль, но между ми и солью всего 1–1/2 шага. Знание этого поможет вам определить высоту аккорда.
Некоторые музыканты говорят, что аккорды складываются терциями, потому что они располагаются друг над другом на нотоносце, как показано выше.
Знание того, что большинство аккордов сложены или записаны в терциях, полезно и поможет вам идентифицировать ноты и играть более вдумчиво.
Формулы аккордов
В следующем списке приведены формулы. Это, вероятно, охватывает 90% аккордов, с которыми вы столкнетесь. Другие могут быть получены с практическими знаниями построения аккордов.
Формулы трезвучий
Большинство трезвучий содержат корень, терцию и квинту.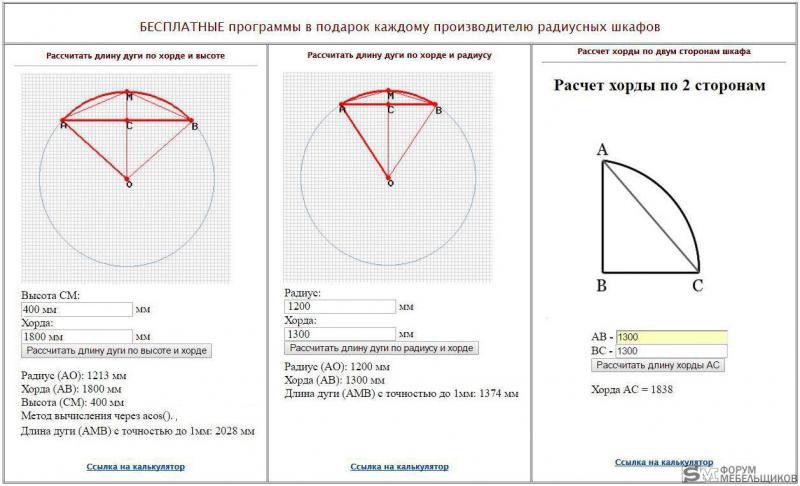 Подвешенные аккорды заменяют терцию либо на 2, либо на 4. Эти аккорды названы с использованием 2 и 4, потому что они заменяют терцию, а не продолжают аккорд. Я расскажу об этом более подробно, когда мы будем обсуждать расширенные формулы аккордов.
Подвешенные аккорды заменяют терцию либо на 2, либо на 4. Эти аккорды названы с использованием 2 и 4, потому что они заменяют терцию, а не продолжают аккорд. Я расскажу об этом более подробно, когда мы будем обсуждать расширенные формулы аккордов.
Формулы септаккорда
Здесь вы можете заметить закономерность. Седьмые аккорды строятся на трезвучиях. Ниже я перечислил наиболее распространенные формулы септаккорда. Потратьте минуту, чтобы понаблюдать за соотношением трезвучия и септаккорда. Например, Major 7 и Dominant 7 добавляют септимы к мажорному трезвучию. Позже в этом уроке я дам вам несколько простых правил, которые помогут вам выучить несколько моделей аккордов.
Меня часто спрашивают о дабл-бемоль на уменьшенном септаккорде. Септаккорд с двойной бемолью энгармоничен с 6. Другими словами, высота звука точно такая же, но название другое. Он назван так, чтобы сохранить образец добавления 7-го к трезвучию. Например, в тональности C 7-й является B, а ♭♭B на два полутона ниже, чем B.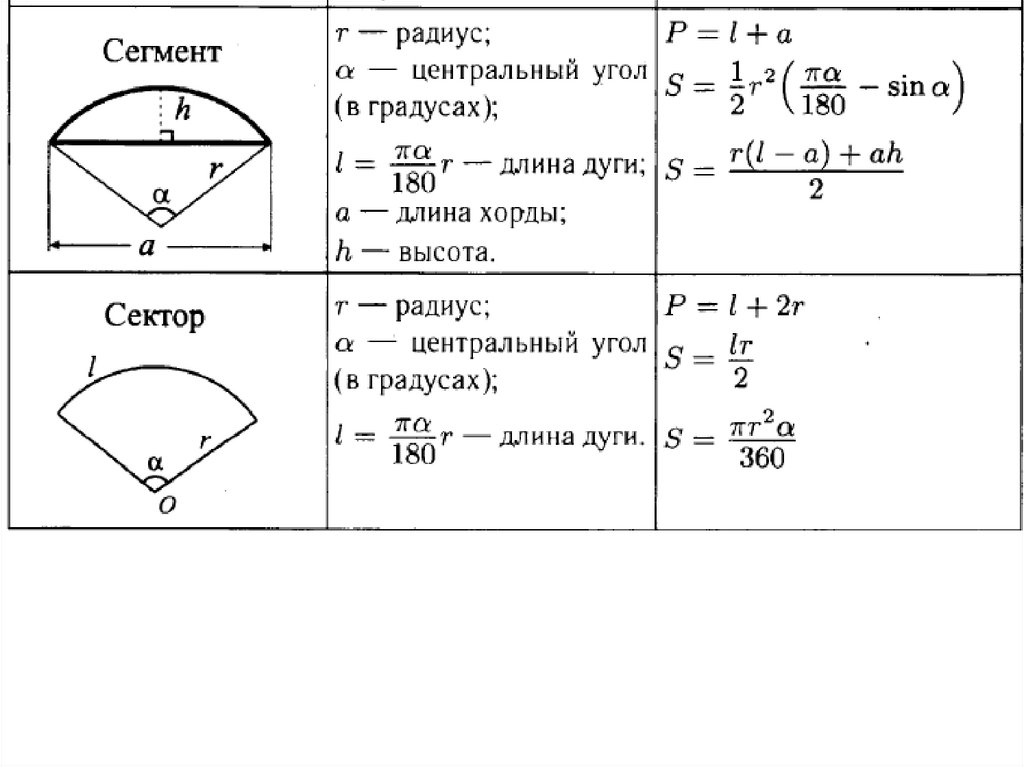 Он имеет ту же высоту звука, что и A, который является 6-й нотой гаммы C мажор (C-D-E-F-G-A-B).
Он имеет ту же высоту звука, что и A, который является 6-й нотой гаммы C мажор (C-D-E-F-G-A-B).
| Аккорд | Формула | Интервальная формула | Аудио |
| Майор 7 | 1-3-5-7 | Корень-M3-P5-M7 | Скоро |
| Доминант 7 | 1-3-5-♭7 | Корень-M3-P5-m7 | Скоро |
| Незначительный 7 | I–♭3–5–♭7 | Корень-m3-P5-m7 | Скоро |
| Малый 7 Плоский 5 | I–♭3–♭5–♭7 | Корень-m3-dim5-m7 | Скоро |
| Уменьшенный 7 | I–♭3 –♭5–♭♭7 (или 6) | Корень-m3-dim5-dim7 | Скоро |
Расширенные формулы аккордов
Ниже приведены некоторые распространенные расширенные аккорды. Их полезность зависит от стиля. Джазовые музыканты часто начинают с септаккордов и со временем добавляют расширенные аккорды. Блюзовые музыканты часто сразу учат доминирующий 9-й аккорд. Между тем, стили рок и поп используют их время от времени, но вы можете долго не изучать их.
Блюзовые музыканты часто сразу учат доминирующий 9-й аккорд. Между тем, стили рок и поп используют их время от времени, но вы можете долго не изучать их.
Вы заметите, что расширенные аккорды строятся на септаккордах так же, как септаккорды строятся на трезвучиях. Поскольку мы строим предыдущие аккорды, мы восходим по порядку. Поэтому мы начинаем использовать «расширенные» имена 9-й, 11-й и 13-й вместо 2-й, 4-й и 6-й.
Вы заметите, что доминирующий аккорд 13 состоит из 7 нот, тогда как на гитаре всего 6 струн. Некоторые ноты будут пропущены, когда вы сыграете этот аккорд самостоятельно, но другой участник группы может сыграть пропущенные вами ноты.
| Аккорд | Формула | Интервальная формула | Аудио |
| Майор 9 | 1-3-5-7-9 | Корень-M3-P5-M7-M9 | Скоро |
| Доминант 9 | 1-3-5-♭7-9 | Корень-M3-P5-m7-M9 | Скоро |
| Доминант 11 | 1-3-5-♭7-9-11 | Корень-M3-P5-m7-M9-P11 | Скоро |
| Доминант 13 | 1-3-5-♭7-9-11-13 | Корень-M3-P5-m7-M9-M13 | Скоро |
Краткий обзор
- Я обещал практический подход к построению аккордов… но это еще не все!
- Существует три основных типа аккордов: трезвучия, септаккорды и расширенные аккорды.

- Вы можете сформировать аккорд, используя формулу, основанную на мажорной гамме или интервалах.
- Аккорды строятся на терциях (мы вернемся к этому позже).
Простые способы запомнить формулы аккордов
Здесь начинается практический подход. Начнем с некоторых общих наблюдений.
Three Observations
- Все аккорды, кроме подвесных, содержат основной тон, терцию и квинту. Подвешенные аккорды заменяют терцию на 2-ю или 4-ю.
- Аккорды пропускают ноты. Другими словами, 1 (пропустить 2) 3 (пропустить 4) , 5, (пропустить 6), 7 и т. д. В примечаниях: C, (пропустить D), E, (пропустить F), G, (пропустить A), B. Итак, ноты C, E, G, B (для C Maj 7)
- Я пропустил пауэр-аккорды, потому что они содержат только две ноты: основной тон и чистую квинту. Пауэр-аккорд C обозначается как C5 и содержит ноты C и G.
7 правил для получения формул аккордов
Эти правила полезны, потому что они сообщают вам важные ноты для каждого качества аккорда! Вы также можете составить практически любой аккорд с помощью этих правил.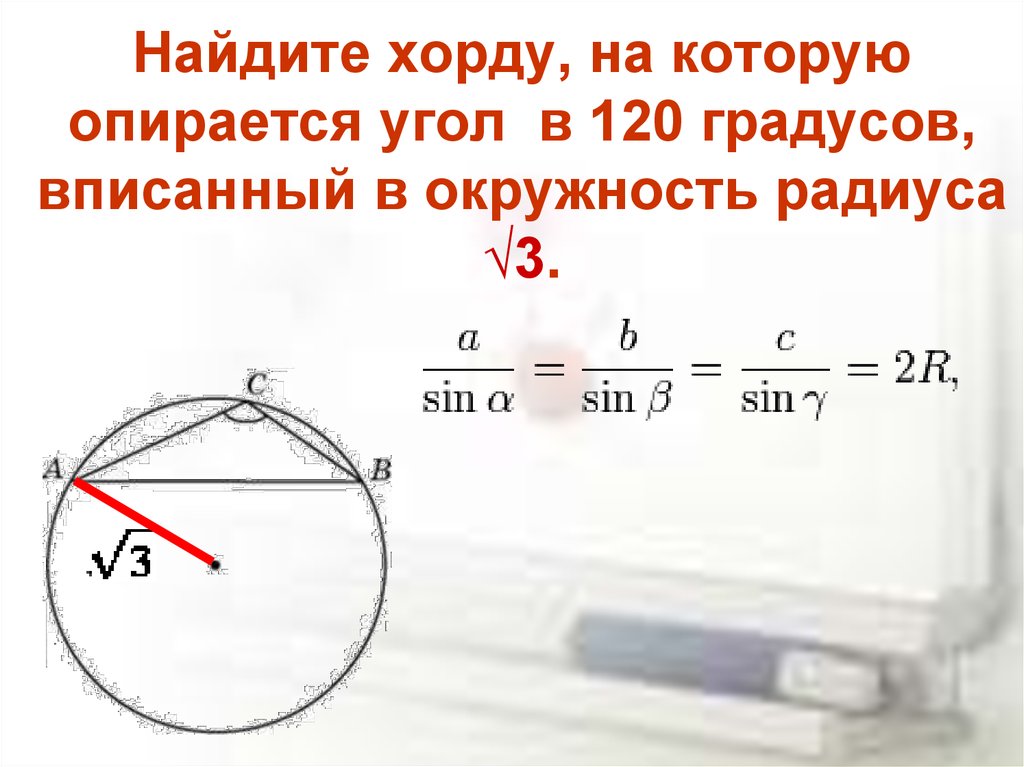
Как названия аккордов соотносятся с 3-ми, 5-ми и 7-ми аккордами
- Все мажорные и доминирующие аккорды имеют мажорную терцию (3)
- Все минорные и уменьшенные аккорды имеют минорную терцию (♭3)
- Мажорные 7 аккордов имеют мажорную септаккорд (7)
- Минорные 7 и доминантные аккорды имеют минорную септиму (♭7) [в дополнение к минорной терции (♭3)]
- Уменьшенные аккорды имеют уменьшенную квинту (♭5) [в дополнение к малой терции (♭3)]
- Расширенные аккорды имеют расширенную квинту (♯5)
- Подвешенные аккорды заменяют терцию большой секундой (2) или чистой четвертой (4)
7 Правила в формате таблицы
| Аккорд | 3 р-д | 5 -й | 7 -й |
| Мажор и доминанта | 3 | ||
| Несовершеннолетний | ♭3 | ||
| Майор 7 | 7 | ||
| Минорный 7 и доминантный 7 | ♭7 | ||
| Уменьшенный | ♭3 | ♭5 | |
| Расширенный | 3 | ♯5 | |
| Сус2 | 2 | ||
| Сус4 | 4 |
Совет.
Джазовые музыканты часто сосредотачиваются на 3-м и 7-м аккордах. Это важные аккордовые тона, которые вы можете выделить во время импровизации.
Модификаторы аккордов
Приведенные выше формулы охватывают многие аккорды, которые вам необходимо знать. Следующие правила модификаторов помогут вам изменить их, чтобы узнать почти все остальное.
- Добавить аккорды — это аккорды, которые просто добавляют ноту. Например, аккорд Cadd9 — это аккорд до мажор с добавленной девятой (ре). Поскольку в нем нет септаккорда, это не девятый аккорд. Для 9-го аккорда вам понадобится вся последовательность тоники, терции, пятой, седьмой, девятой.
- Пропустить аккорды – Эти аккорды просто пропускают ноту из аккорда. Аккорды часто играют с пропущенными нотами, но это редко указывается. Когда это так, композитор подчеркивает необходимость опустить эту ноту.
- Модифицированные ноты — Вы можете столкнуться с аккордами с измененными нотами.
 Некоторые примеры включают минор 7 ♭ 5, который произносится как минор семь плоских пять. Это просто минорный 7 аккорд с плоской квинтой. Другой пример — модифицированный аккорд, похожий на доминанту 7 ♯ 9.аккорд. Это просто доминирующий 7-й аккорд с добавленной и резкой 9-й. E7♯9 или E7(♯9) иногда называют аккордом Хендрикса.
Некоторые примеры включают минор 7 ♭ 5, который произносится как минор семь плоских пять. Это просто минорный 7 аккорд с плоской квинтой. Другой пример — модифицированный аккорд, похожий на доминанту 7 ♯ 9.аккорд. Это просто доминирующий 7-й аккорд с добавленной и резкой 9-й. E7♯9 или E7(♯9) иногда называют аккордом Хендрикса.
Краткий обзор 2
Перед ДЕЙСТВИТЕЛЬНО практической частью этого урока давайте повторим.
- Аккорды обычно состоят из третей, которые пропускают каждую вторую ноту.
- Есть несколько простых правил, которые помогают музыкантам построить гармонию аккорда и продумать ее.
- 3-й и 7-й являются важными тонами аккорда.
- Добавленные, опущенные или измененные ноты могут быть указаны в названии аккорда.
Практические секреты построения аккордов
На этом этапе некоторые учителя советуют вам запомнить несколько аккордов или остановиться на этом и дать вам выучить аккорды по мере необходимости для исполнения песни.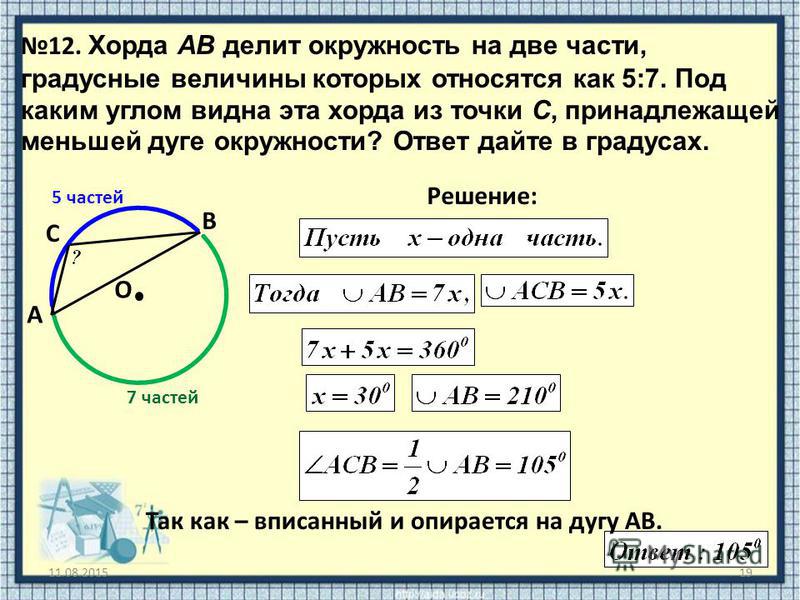 Ни один из подходов не является неправильным, но они не дают вам интуиции или упрощенных правил для улучшения вашей игры. В этом разделе я раскрою несколько простых правил, которые научат вас, как строятся большинства гитарных аккордов. Это поможет вам быстрее думать и играть вдумчиво, помня о конкретных нотах.
Ни один из подходов не является неправильным, но они не дают вам интуиции или упрощенных правил для улучшения вашей игры. В этом разделе я раскрою несколько простых правил, которые научат вас, как строятся большинства гитарных аккордов. Это поможет вам быстрее думать и играть вдумчиво, помня о конкретных нотах.
Большая проблема хватки
Аккорды на фортепиано часто играются упорядоченно. Другими словами, самая низкая нота — это основной тон, следующая высота тона — 3-я, за ней следует 5-я. Все чисто и аккуратно. Однако этот приказ не является обязательным. На самом деле гитаристы редко играют ноты в таком порядке, потому что их трудно уловить, если вы не измените порядок. Давайте посмотрим на C7 с корнем на шестой струне. Первая рукоятка удерживает ноты в таком порядке, как если бы их играл пианист. Вторая рукоятка меняет порядок нот, облегчая игру на гитаре.
При стандартном строе играть аккорды как пианист нецелесообразно, поэтому гитаристы обычно играют разные голоса .
С точки зрения гитары, голоса — это разные захваты одного и того же аккорда. Точнее говоря, голос определяет порядок нот, вместе с которыми ноты удваиваются.
Инверсии
Аккордовые аккорды, изменяющие порядок нот, часто называют инверсиями. Например, ваше базовое трезвучие R-3-5. Первая инверсия этого аккорда упорядочивает ноты как 3-5-R. Вторая инверсия упорядочивает ноты как 5-R-3. Этот урок не научит вас нескольким обращениям аккордов, но это полезно знать. Вы можете получить несколько аккордовых захватов, пытаясь найти все комбинации. Я изучу это в будущем уроке, но я дам вам несколько практических советов по формированию аккордов с более легким хватом в следующих нескольких разделах..
Решение проблемы отличного сцепления
Проблема отличного сцепления возникает из-за того, что мы используем стандартную настройку, а это означает, что наша гитара настроена в идеальных четвертях, за исключением интервала между 2-й и 3-й струной, где интервал составляет большую терцию. Ранее вы узнали, что аккорды строятся в терциях (или что в них пропускаются ноты). Когда вы хотите сыграть терцию на следующей струне, вам нужно почти каждый раз переходить на нижний лад. Когда вы добавляете терции, хват становится все сильнее и сильнее. Например, от R до 3 занимает 2 лада. Когда вы добавляете квинту, аккорд занимает 4 лада. Когда вы добавляете септаккорд, аккорд занимает 6 ладов. Трудно растянуть пальцы на 6 ладах.
Ранее вы узнали, что аккорды строятся в терциях (или что в них пропускаются ноты). Когда вы хотите сыграть терцию на следующей струне, вам нужно почти каждый раз переходить на нижний лад. Когда вы добавляете терции, хват становится все сильнее и сильнее. Например, от R до 3 занимает 2 лада. Когда вы добавляете квинту, аккорд занимает 4 лада. Когда вы добавляете септаккорд, аккорд занимает 6 ладов. Трудно растянуть пальцы на 6 ладах.
Аккорды состоят из терций, что заставляет вас переходить на нижние лады на каждой струне. Нам нужно найти способ двигаться вперед!
The 45 Divide
Ключ к построению великолепных аккордов заключается в чередовании нот, перемещающих вас вверх и вниз по грифу . До сих пор мы знали, что трети двигают нас назад, но что двигает нас вперед? Это просто более высокий интервал, а следующий аккордовый тон после терции — это квинта. На приведенной ниже диаграмме показаны основная нота и ноты следующей более высокой струны.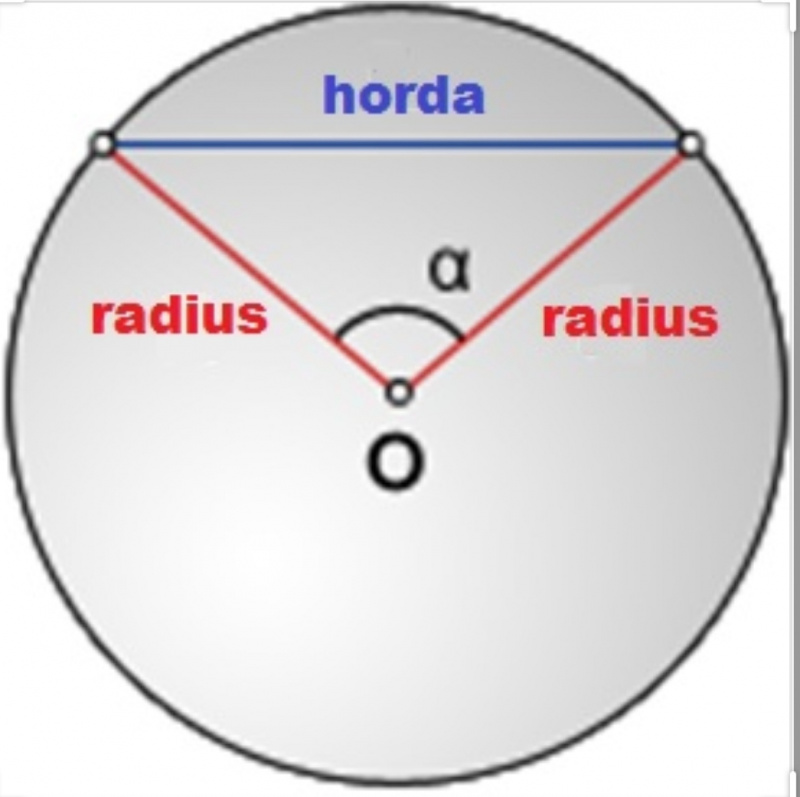 Обратите внимание, как третьи перемещают вас назад, а пятые — вперед.
Обратите внимание, как третьи перемещают вас назад, а пятые — вперед.
Разделительная линия между движением назад и вперед — это то, что я называю делением на 45. Я назвал его так, потому что он помогает вам находить ноты в формуле аккорда. Нота на том же ладу, что и основная нота, но на соседней более высокой струне, является идеальной квартой. Нота на том же ладу, что и основная нота, но на соседней нижней струне, является идеальной квинтой (для целей формулы аккорда). Поскольку это четвертое в одну сторону и пятое в другую, я называю это делением на 45.
Например, аккорды sus4 содержат основной тон, чистую кварту и чистую квинту. Csus4 содержит C (корень), F (4-й) и G (5-й). Если вы играете C на 3-м ладу 5-й струны. Вы найдете F на 3-м ладу 4-й струны и G на 3-м ладу 6-й струны.
Будьте осторожны при перемещении между 3-й и 2-й струнами, вместо этого они разделены делением на 36 (мажорная 3-я по возрастанию, минорная 6-я по убыванию). Если вы не уверены, почему, посмотрите, как настроена гитара, или свяжитесь со мной для уточнения.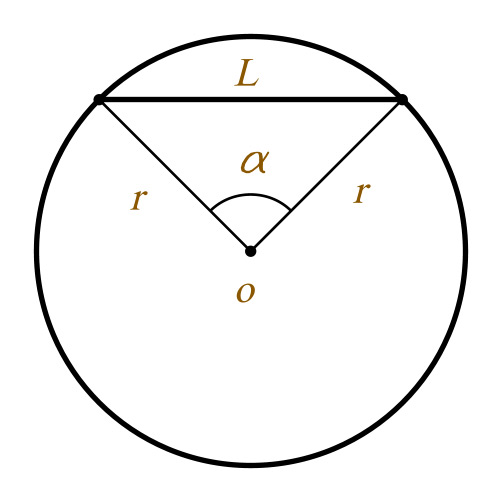
Полное деление на 45
Полное деление на 45 — это просто аккордовые ноты в пределах 3 ладов от основного лада. Давайте посмотрим, когда мы укоренились на 6-й струне. Я включил плоские терции и септимы, так как они очень распространены. Обратите внимание, как вы можете найти аккорды в форме ми и соль на следующей диаграмме. Есть и другие диаграммы, которые основаны на других строках и соответствуют другим формам CAGED.
Цель этой схемы — дать вам краткий обзор тонов аккордов.
2 Практические формулы для наиболее распространенных аккордов
Давайте посмотрим, как строятся популярные формы аккордов CAGED. Вы увидите похожие шаблоны.
E-Form, A-Form, D-Form: R-5-R-3-(5)-(R)
Обратите внимание, что все следующие аккорды начинаются с основного аккорда, затем 5-го, повторите основной тон , затем играйте в третью. Это очень распространенный паттерн в гитарных аккордах. Я обозначил эту форму R-5-R-3-(5)-(R).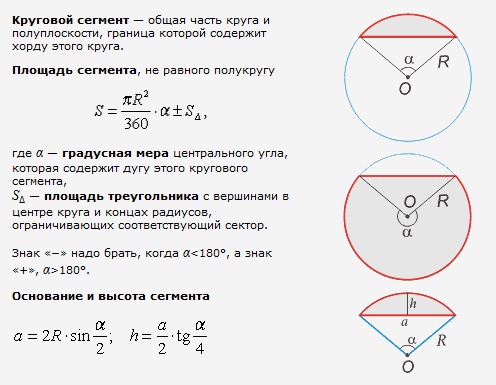 Необязательные примечания показаны в скобках.
Необязательные примечания показаны в скобках.
Аккорды формы ми, ля и ре используют один и тот же образец. Они просто начинаются с другой строки!
C-форма, G-форма: R-3-5-(R)-(3)-(R)
Формы C и G играют с корнем, 3-м, 5-м, затем повторяют корень. Они используют одну и ту же схему: R-3-5-(R)-(3)-(R). Еще раз, необязательные примечания заключены в круглые скобки.
C FormG Form
Подобно форме C и G используется один и тот же шаблон интервала. Они просто начинаются с другой строки.
Формирование септаккордов с модификациями
Мы можем легко изменить эти аккорды, чтобы сформировать септаккорды! Обычно это делается путем изменения двойных нот или квинты, которая иногда опускается.
Форма C мажор 7 — корень опускается до мажорной септимы на второй струне. Форма C Dominant 7 — повышается квинта до бемольской септимы (и опускается) Форма E мажор 7 — корень 4-й струны понижается до мажора 7 и 5-я струны не играются для облегчения аппликатуры. Это обычно используется, когда двойные ноты нежелательны. Этот доминирующий аккорд 7 формы E изменяет удвоенный корень на ♭ 7 на 4-й струне.
Это обычно используется, когда двойные ноты нежелательны. Этот доминирующий аккорд 7 формы E изменяет удвоенный корень на ♭ 7 на 4-й струне.
Формирование расширенных аккордов с модификациями
Расширенные аккорды обычно формируются путем изменения удвоенной ноты или той, которую мы сознательно опускаем. Ниже приведены примеры доминантного аккорда 9 и доминантного аккорда 13.
Аккорд формы C с квинтой, увеличенной до ♭7, удвоенным корнем, повышенным до 9, и необязательной квинтой, добавленной к 1-й струне. , и увеличивает вторую строку 5 до 13. Все 5, 9 и 11 опущены.
Практические правила построения аккордов
Теперь давайте повторим то, что мы только что узнали, а затем выучим несколько дополнительных правил.
Две распространенные формы
Наиболее распространенные аккорды основаны на следующих формах.
- R-5-R-3-(5)-(R) — используется в формах аккордов E, A и D
- R-3-5-(R)-(3)-(R) — Используется в аккордовых формах G и C.

Общие модификации построения септаккордов
- Заменить удвоенные корни на септаккорды.
- Пропустить или изменить квинты, обычно вместо них играть септимы.
Аккорды с пропуском струн обычно пропускают струну после самой нижней ноты.
Общие модификации построения расширенных аккордов
Мы знаем, что не всегда можем сыграть каждую ноту расширенного аккорда. Сначала мы пытаемся модифицировать двойные ноты, но часто приходится идти на компромисс. Обычно он использует следующие правила.
- Замените основной тон, чтобы создать 9-й аккорд.
- Замените квинту, чтобы создать 11-й или 13-й аккорд.
Движение струны к струне
Вы заметите, что следующие правила применимы почти ко всем гитарным аккордам при переключении с более низкой струны на более высокую струну.
- Корень либо опускается на 3-й, либо восходит на 5-й
- 3-й либо опускается до 5-го, либо поднимается до 7-го
- 5-й либо спускается к 7-му, либо восходит к корню
- 7-й либо спускается в корень, либо восходит к 3-му.

Его можно упростить до еще более простого и мощного правила:
Любой интервал спускается к следующему интервалу или восходит к интервалу после него.
Практика для изучения тонов аккордов
Все, что вы узнали в этом уроке, было предназначено для того, чтобы дать вам интуицию и упростить многие правила. Тем не менее, это все еще много информации. Вам все равно нужно практиковать это, чтобы не забыть. Вот несколько практических рекомендаций.
Практика
Ниже приведен список того, что нужно практиковать, в том порядке, который я рекомендую.
- Сначала выучите трезвучия: мажор, минор
- Выучите следующие септаккорды: мажорный 7, минорный 7 и доминантный 7
- Выучить уменьшенный и минорный 7♭5
- Выучите подвесные аккорды
- Выучите усиленные аккорды.

- Выучите расширенные аккорды.
Как практиковать
Я рекомендую использовать правило 3-3. В течение данной недели (или 7-дневного промежутка) выполняйте 3 упражнения не менее 3 дней. Продолжайте практиковаться, пока вы действительно не выучите аккорды.
- Играйте диатоническую последовательность в общих тональностях. Например, в тональности C сыграйте C, Dm, Em, F, G, Am Bdim. Затем сыграйте септаккорды: CMaj7, Dm7, Em7, FMaj7, G7, Am7, Bm7♭5.
- Сыграйте аккорды диатонической последовательности, но поднимитесь на квинту вверх, а затем на кварту вниз. Например, сыграйте C, G, Dm, Am, Em, Bdim, F, C. Вы можете сыграть эту последовательность с одной формой (например, с формой E) и перемещать ее или попытаться остаться в той же позиции.
- Сыграйте один аккорд вверх по грифу, используя формы CAGED. Например, сыграйте C-форму, затем A-форму, G-форму, E-форму и D-форму. Если играть сложно, ищите варианты на той же позиции. Обычно G-форму трудно играть, но у вас обычно есть вариант на струнах 1-4.

- Практикуйтесь в импровизации над последовательностью аккордов, играя аккордовые тона известных вам форм.
- Хотя я не объяснял это здесь, вы можете играть арпеджио и пытаться визуализировать формы аккордов, которые вы играете.
- Выучите наборы аккордов, такие как Drop 2, Drop 3 и Drop 2&4. Они обеспечат несколько комбинаций аккордов.
При изменении аккордов прислушивайтесь к различиям в звучании аккордов. Также обратите внимание на различия в захватах. Цель состоит в том, чтобы выучить ноты, которые вы играете.
Заключение
Как ни странно, изучение построения аккордов помогло мне лучше импровизировать. Я смог понять ноты, которые я играл. Это помогло мне эффективно связать мелодию с гармонией. Это действительно сломало колею для меня, и это может сделать то же самое для вас.
Я планирую несколько новых уроков, которые расширят этот урок. Мой урок по аккордам Drop-2 – хороший дополнительный урок, потому что он охватывает несколько комбинаций аккордов.
Это был большой урок. Если вы дочитали до этого места, вы должны стать будущим гитарным героем, но я хочу поблагодарить вас за это. Я искренне надеюсь, что это поможет вам стать лучше.
Если вам понравился этот урок, рассмотрите возможность покупки версии в формате PDF для поддержки подобного содержания. В качестве альтернативы, самая большая благодарность, которую я могу получить, это то, что вы лайкнули мою страницу в Facebook и оставили пост с тем, что вам понравилось в ней. Как всегда, не стесняйтесь обращаться ко мне с вашими вопросами, проблемами и т. д. Я здесь, чтобы помочь!
Купить PDF-версию этого урока
Как использовать формулы аккордов и их преимущества
Поделись со своими друзьями-гитаристами!
Последнее обновление: 10 сентября 2022 г., Клаус Кроу
Bigstock photo
Зачем нужны формулы аккордов? Почему вы хотите узнать о них в первую очередь и каковы их преимущества?
Знание основ теории аккордов может существенно изменить вашу игру.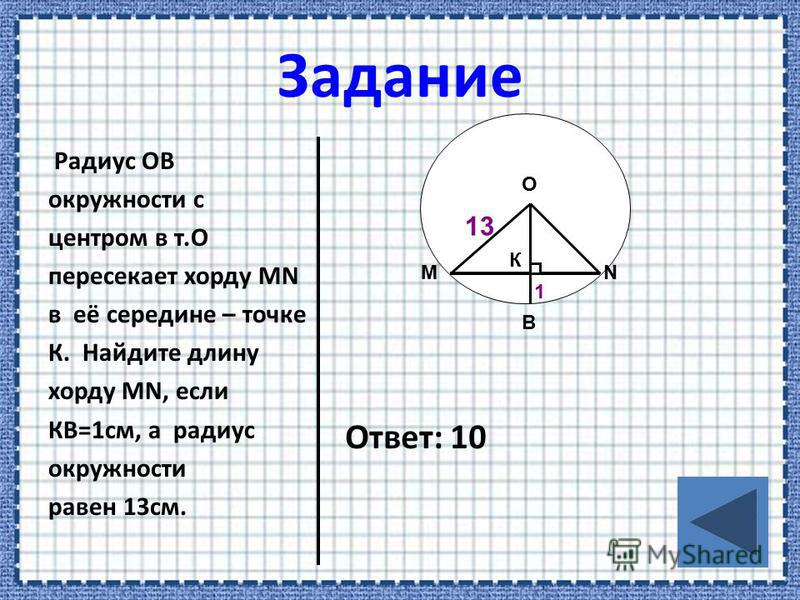 Это делает игру на гитаре более увлекательной, интересной, и многое из того, что вы играете, становится более осмысленным. Части головоломки встанут на свои места.
Это делает игру на гитаре более увлекательной, интересной, и многое из того, что вы играете, становится более осмысленным. Части головоломки встанут на свои места.
Знание того, как работают формулы аккордов, и знание нот на струнах — это идеальное сочетание.
Что можно делать с формулами аккордов?
– Научитесь создавать собственные аккорды.
– Понимание теории музыки.
— Выясните, как играть аккорд, когда у вас есть только название аккорда.
– Понимание разницы между такими аккордами, как Dom7, Maj7 и min7.
– Упростите игру аккорда, если ваш мизинец не может дотянуться до мажорной семерки или любой другой неприятной ноты.
— Быстро превратите аккорд соль мажор в Gsus4, G7, Gmaj7, G13 или любой другой вариант, который вы придумаете.
— Узнайте, как легко перейти от мажорного к минорному или любому другому аккорду.
– Примените полученные знания к игре ритма, написанию песен, соло и импровизации.
— Узнайте, как формулы аккордов связаны с каждым аспектом игры на гитаре, по мере того, как ваши знания расширяются с течением времени.
Формулы аккордов раскрывают структуру аккордов. Он показывает все ноты, сыгранные в аккорде, другими словами, какие конкретные ноты составляют конкретный аккорд.
Ноты в аккорде берутся из мажорной гаммы.
Ноты мажорной гаммы обозначаются цифрами 1 2 3 4 5 6 7 и 8 (=1)
Пример:
Приведенные ниже ноты взяты из гаммы до мажор, обозначенной цифрами от 1 до 8.
В Г Д Е Ж А Б В 1 2 3 4 5 6 7 8
Из 8 ноты повторяются только на октаву выше: 8, 9, 10, 11, 12 и 13.
8 = 1 (C)
9 = 2 (D)
10 = 3 (E)
11 = 4 (F)
12 = 5 (G)
13 = 6 (A)
Ниже вы можете выбрать тональность мажорной гаммы для аккордов, которые мы собираемся построить в следующем разделе.
Мажорные гаммы в каждой тональности: Гамма ля мажор = A B C# D E F# G# A
Гамма Bb мажор = Bb C D Eb F G A Bb
Гамма B мажор = B C# D# E F# G# A# B
Гамма C мажор = C D E F G A B C
Гамма Db мажор = Db Eb F Gb Ab Bb C Db
Гамма D мажор = D E F# G A B C# D
Гамма Eb мажор = Eb F G Ab Bb C D Eb
Гамма E мажор = E F# G# A B C# D# E
Гамма F мажор = F G A Bb C D E F
Гамма Gb мажор = Gb Ab Bb Cb (=B) Db Eb F Gb
Гамма G мажор = G A B C D E F# G
Гамма Ab мажор = Ab Bb C Db Eb F G Ab
Для построения аккорда нам нужна формула аккорда и мажорная гамма. Давайте построим аккорд до мажор.
Давайте построим аккорд до мажор.
Формула мажорного аккорда = 1 – 3 – 5
До-мажорная гамма = C D E F G A B C
Теперь возьмите 1-ю, 3-ю и 5-ю ноты мажорной гаммы. При одновременном воспроизведении этих нот получится мажорный аккорд. Это означает, что аккорд до мажор состоит из нот: C E G (1 – 3 – 5)
Вы можете задаться вопросом: «Как можно услышать только три ноты, когда на гитаре шесть струн?» Некоторые ноты в аккорде появляются дважды. Когда вы играете аккорд до мажор, вы слышите следующие ноты от нижней струны ми до высокой струны ми:
Низкая струна ми = без звука
Струна ля = нота до
Струна ре = нота ми
Струна соль = нота соль
Струна си = нота до
высокая струна ми = нота ми
Посмотрите другие примеры мажорных аккордов:
Гамма ля мажор = A B C# D E F# G# A
Аккорд ля мажор = A C# E (1 – 3 – 5)
Гамма G мажор = G A B C D E F# G
Аккорд G мажор = G B D (1 – 3 – 5)
на приведенных ниже диаграммах аккордов показано расположение нот на струнах:
Построение минорного аккорда В качестве примера возьмем аккорд ля минор.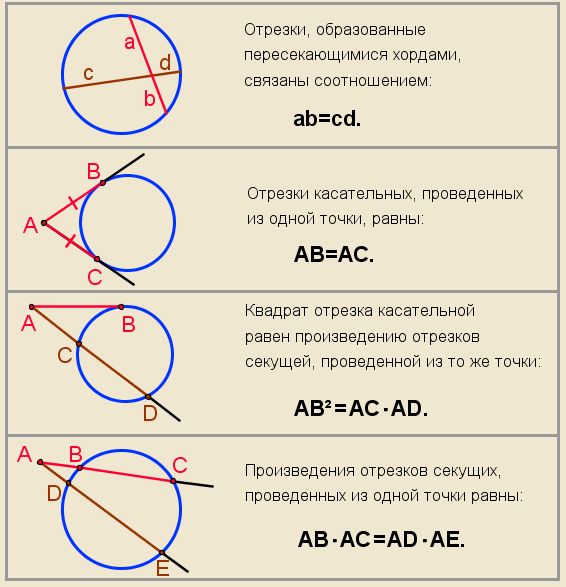
Формула аккорда для минорного аккорда = 1 – b3 – 5.
Мажорная гамма = A B C# D E F# G# A
b3 (три бемоль) означает, что вы берете третью ноту мажорной гаммы только на полтона ниже. Третья нота ля-мажорной гаммы — C#, поэтому, если вы опустите C# на полтона вниз, она станет C. Это означает, что ноты ля-минорного аккорда состоят из нот A C E (1 — b3 — 5)
Построение Maj7 Аккорд Последний пример: Gmaj7
G мажорная гамма = G A B C D E F# G
Формула аккорда Maj7 = 1 – 3 – 5 – 7
Gmaj7 = G B D F#
Ниже вы можете увидеть наиболее распространенные аккорды и их формулы аккордов. Я взял корень C в качестве примера для всех названий аккордов.
Название аккорда = формула аккорда | Основной тон C + название аккорда
Общие типы аккордов: Мажор = 1 – 3 – 5 | C или Cmaj
Минор = 1 – b3 – 5 | см, см мин, C-
Подвесная секунда = 1 – 2 – 5 | Csus2
Подвесной четвертый = 1 – 4 – 5 | Csus4
Добавлено девятое = 1 – 3 – 5 – 9 | Cadd9
Доминантная седьмая = 1 – 3 – 5 – b7 | C7, Cdom7
Большая септима = 1 – 3 – 5 – 7 | Cmaj7
Малая септима = 1 – b3 – 5 – b7 | Cm7, Cmin7, C-7
Мажор = 1 – 3 – 5 | C или Cmaj
Major Sixth = 1 – 3 – 5 – 6 | C6, Cmaj6
Шесть Девять = 1 – 3 – 5 – 6 – 9 | C6/9
Добавлено девятое = 1 – 3 – 5 – 9 | Cadd9
Большая септаккорд = 1 – 3 – 5 – 7 | Cmaj7
Большая септаккорд-бемоль пятерка = 1 – 3 – b5 – 7 | Cmaj7b5
Большая седьмая острая пятерка = 1 – 3 – #5 – 7 | Cmaj7#5
Большая девятая = 1 – 3 – 5 – 7 – 9 | Cmaj9
Major Одиннадцатый = 1 – 3 – 5 – 7 – (9) – 11 | Cmaj11
Тринадцатая майор = 1 – 3 – 5 – 7 – (9) – (11) – 13 | Cmaj13
Major Seven Sharp Eleventh = 1 – 3 – 5 – 7 – #11 | Cmaj7#11
Пятерка мажорных бемолей = 1 – 3 – b5 | Cb5
Минор = 1 – b3 – 5 | Cm, Cmin, C-
Малая шестая = 1 – b3 – 5 – 6 | Cm6, Cmin6, C-6
Малая септима = 1 – b3 – 5 – b7 | Cm7, Cmin7, C-7
Малая добавленная девятка = 1 – b3 – 5 – 9 | Cmadd9
Малая шестерка Добавить девятку = 1 – b3 – 5 – 6 – 9 | Cm6/9
Малая девятая = 1 – b3 – 5 – b7 – 9 | Cm9
Малая одиннадцатая = 1 – b3 – 5 – b7 – (9) – 11 | Cm11
Малая тринадцатая = 1 – b3 – 5 – b7 – (9) – (11) – 13 | Cm13
Малая мажорная септима = 1 – b3 – 5 – 7 | Cm(Maj7)
Минор Мажор Девятая = 1 – b3 – 5 – 7 – 9 | Cm(Maj9)
Минор Мажор Одиннадцатая = 1 – b3 – 5 – 7 – (9) – 11 | Cm(Maj11)
Малая Большая Тринадцатая = 1 – b3 – 5 – 7 – (9) – (11) – 13 | Cm(Maj13)
Малая семерка Пять пятерка = 1 – b3 – b5 – b7 | Cm7b5
Доминантный септаккорд = 1 – 3 – 5 – b7 | C7, Cdom7
Девятый = 1 – 3 – 5 – b7 – 9 | C9
Эльвенский = 1 – (3) – 5 – b7 – (9) – 11 | C11
Тринадцатый = 1 – 3 – 5 – b7 – (9) – (11) – 13 | C13
Семь острых пятерок = 1 – 3 – #5 – b7 | C7 # 5
Семерка Flat Five = 1 – 3 – b5 – b7 | C7b5
Семь плоских девяток = 1 – 3 – 5 – b7 – b9 | C7b9
Семерка острая девятая = 1 – 3 – 5 – b7 – #9 | C7#9
Девятка Острая пятерка = 1 – 3 – #5 – b7 – 9 | C9#5
Девятка Плоская Пятерка = 1 – 3 – b5 – b7 – 9 | C9b5
Семерка Острая Пятерка Острая Девятка = 1 – 3 – #5 – b7 – #9 | C7#5#9
Семерка Острая Пятерка Плоская Девятка = 1 – 3 – #5 – b7 – b9 | C7#5b9
Семерка-плоская пятерка Острая девятка = 1 – 3 – b5 – b7 – #9 | Cb5#9
Семерка Пять Плоская Девятка = 1 – 3 – b5 – b7 – b9 | C7b5b9
Seven Sharp Eleven = 1 – 3 – 5 – b7 – #11 | C7#11
Уменьшенный = 1 – b3 – b5 | Cdim
Уменьшенная седьмая = 1 – b3 – b5 – bb7 | Cdim7
Уменьшенное наполовину = 1 – b3 – b5 – b7 | Cm7b5
Подвесной седьмой = 1 – 4 – 5 – b7 | C7sus4, C7sus
Расширенный = 1 – 3 – #5 | Caug, C+
Расширенный седьмой = 1 – 3 – #5 – b7 | Caug7, C7#5, C7+
Пятая, Power Chord = 1 – 5 | C5
Плоская квинта = 1 – b5 | Cb5, C-, C-5
Подвешенная секунда = 1 – 2 – 5 | Csus2
Подвесной четвертый = 1 – 4 – 5 | Csus4
1 – Каковы ноты аккорда Am7?
(Используйте гамму ля-мажор и формулу минорной септимы)
2 – Нарисуйте схему аккордов Am7 и запишите ноты, которые берутся на каждой струне.
(проверьте наиболее распространенные типы септаккордов)
3 – Проверьте, совпадают ли ноты из формулы аккорда и ноты на диаграмме аккорда.
4 – Теперь соберите уменьшенный септаккорд G. (Выполните шаги с 1 по 3)
5 – Сыграйте случайный аккорд на гитаре. Используйте соответствующую формулу аккорда и проверьте
, соответствуют ли все ноты аккорда на вашей гитаре нотам формулы аккорда.
5 – Запишите разницу между формулой мажорного аккорда и минорного аккорда?
6 – Запишите формулы для аккорда Maj7, Dom7 и Min7.
Что у них общего и в чем отличия?
7 – Начните с запоминания формул общих типов аккордов.
Наслаждайтесь созданием аккордов!
📨 Привет, . Присоединяйтесь к Guitarhabits и получайте бесплатные качественные видеоуроки игры на гитаре, лучший контент, советы, рекомендации, ресурсы и (би)еженедельный электронный рюкзак Guitarhabits, полный полезных материалов. 🎸🎁
ЗАРЕГИСТРИРУЙТЕСЬ ЗДЕСЬ: https://www. guitarhabits.com/sign-up-guitarhabits/
guitarhabits.com/sign-up-guitarhabits/
Поддержка Guitarhabits здесь : https://www.guitarhabits.com/donate/
🎸☕ 🌿 Поддержите Guitarhabits 🎸☕ 🌿
Присоединяйтесь к Guitarhabits и получите
Бесплатные качественные уроки игры на гитаре
Да, подпишитесь на бесплатную рассылку новостей Guitarhabits по электронной почте.
Я прочитал и согласен с Политикой конфиденциальности
Как построить аккорд в любой тональности
ПОДЕЛИТЕСЬ ЭТИМ:
Ты умеешь играть аккорд до мажор?
Возможно.
Как насчет G# мажора?
Дб минор?
Возможно, у вас получится, но я покажу вам, как играть мажорный или минорный аккорд в основной позиции на ЛЮБОЙ ноте на фортепиано.
Да… даже G#.
Как?
Аккорд ФормулаЭто очень простая, легко запоминающаяся формула, которую вы можете выучить за считанные секунды и сразу начать играть. Сегодня мы сохраним все наши аккорды в основной позиции, чтобы упростить задачу и сохранить формулу одинаковой для любой ноты на фортепиано.
Первое, что вам нужно сделать, это выбрать заметку.
Любая нота…
Это основная нота. Мы собираемся построить мажорный и минорный аккорд поверх него.
Как построить аккордПрежде чем мы построим мажорное или минорное трезвучие (это причудливое название аккорда с тремя нотами, наложенными друг на друга), это помогает построить внешнюю «оболочку».
Здесь применяется первая часть формулы аккорда.
От основной ноты (той, которую вы выбрали, помните) отсчитайте 7 ПОЛУШАГОВ.
Полушаг — это кратчайшее расстояние между двумя нотами на фортепиано. Для большинства нот это будет расстояние от белой клавиши до черной или наоборот.
Вот как выглядят полутона на фортепиано:
Супер короткие, да?!
Итак — отсчитываем 7 полутонов от основной ноты. Например, если вы выбрали C, то, подсчитав 7 полушагов, вы получите G.
Если вы начали с G#, то, считая 7 полушагов, вы получите D#.
Работает на ЛЮБОЙ ноте на клавиатуре. Попытайся.
Итак, теперь у нас есть внешняя оболочка, пришло время ее заполнить.
🎹 Hack Into Chords 👊
Понимание того, как работают аккорды, даст вам БОЛЬШУЮ ногу в обучении игре на пианино. Знание всего нескольких аккордов откроет доступ к сотням, если не тысячам поп-песен. Чтобы начать сегодня, ознакомьтесь с нашим бесплатным 9Курс 3625 Chord Hacks или прочитайте Как играть на фортепианных аккордах.
Самое интересное! Это та часть, где мы решаем, будет ли аккорд мажорным или минорным.
Начнем с мажорного аккорда.
От основной ноты отсчитайте 4 полутона вверх.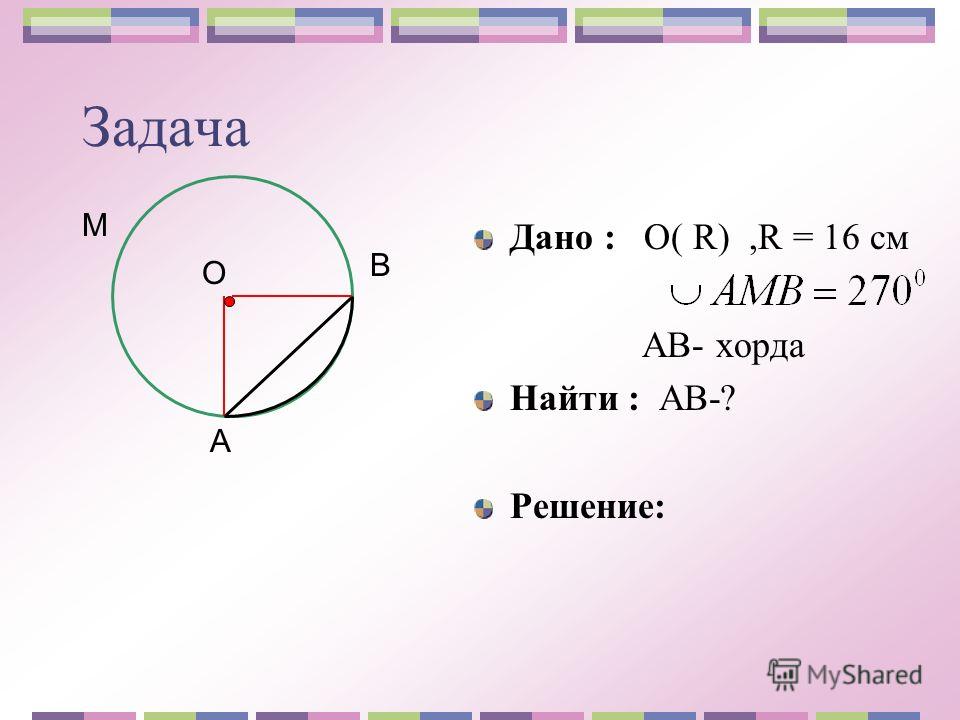 Эта нота называется третьей, и именно она делает аккорд мажорным.
Эта нота называется третьей, и именно она делает аккорд мажорным.
Вернемся к формуле. Мы начали с основной ноты (1), а затем считаем 4 полутона, чтобы получить среднюю ноту (4), и 7 полутонов, чтобы получить верхнюю ноту (7).
Это означает, что формула аккорда для мажорного трезвучия:
1 – 4 – 7
И это работает на КАЖДОМ. НЕ ЗАМУЖЕМ. ПРИМЕЧАНИЕ.
Теперь давайте посмотрим на минорный аккорд. Он очень похож на мажорный аккорд, но средняя нота на полшага НИЖЕ, чем мажорный аккорд.
Так что же это за формула?
Ну, если мажорная формула 1 – 4 – 7 , а минорный аккорд имеет среднюю ноту на полтона ниже, то будет:
(знаю, ты знаешь)
1 – 3 – 7
Обратите внимание, как по-другому звучит аккорд, просто изменив ОДНУ ноту? Теперь это называется минорная терция, а не мажорная терция.
Теперь пришло время попрактиковаться Кажется, я уже много раз говорил об этом, но вы можете попробовать это на ЛЮБОЙ ноте на фортепиано.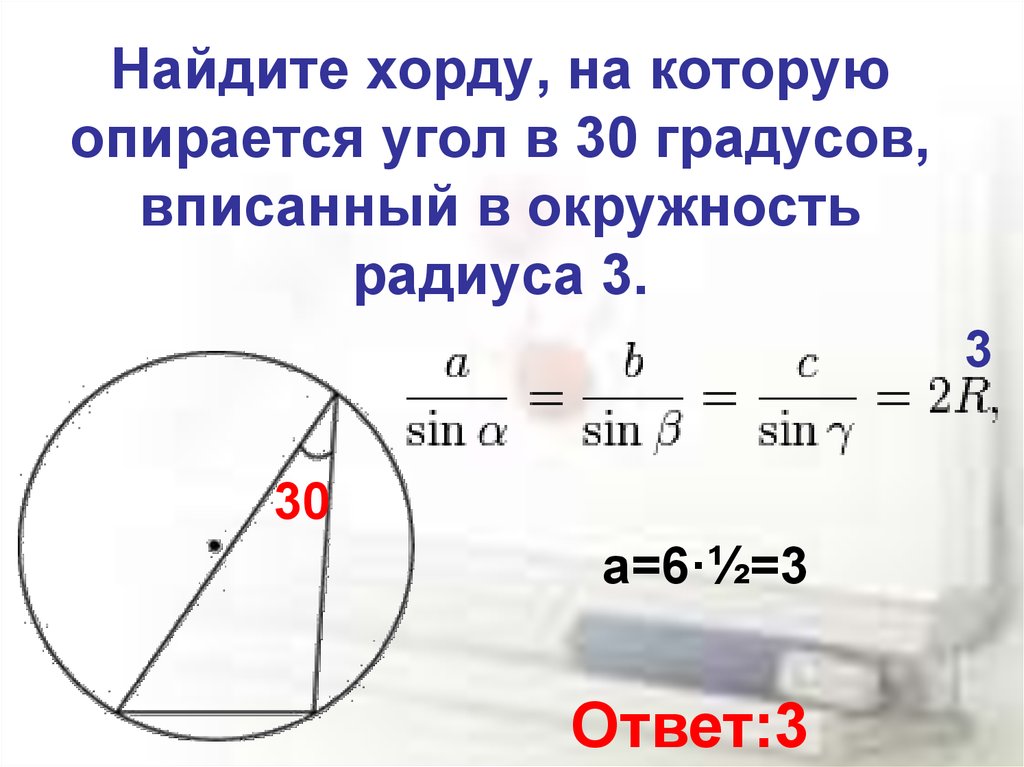
Попрактикуйтесь в построении мажорных и минорных аккордов по формуле. Чем больше вы это сделаете, тем быстрее вы получите. Вскоре вам даже не придется использовать формулу — но это отличный способ освоиться и начать играть аккорды.
И когда вы их играете, старайтесь действительно СЛУШАТЬ разницу между мажорными и минорными аккордами. Это поможет тренировать слух, чтобы вам было легче слышать и воспроизводить музыку.
Но я буду честен…
Играть только мажорные и минорные аккорды может довольно быстро надоесть.
Итак, пришло время изменить егоВместо того, чтобы просто играть аккорды, попробуйте разбить их и сыграть ноты отдельно. Таким образом, вы играли бы снизу — посередине — сверху — посередине и повторяли.
Сделайте это как для мажорных, так и для минорных аккордов и перемещайтесь по фортепиано, начиная с разных нот.
Это сделает репетицию более музыкальной, а также поможет вам научиться играть самые разные аккорды.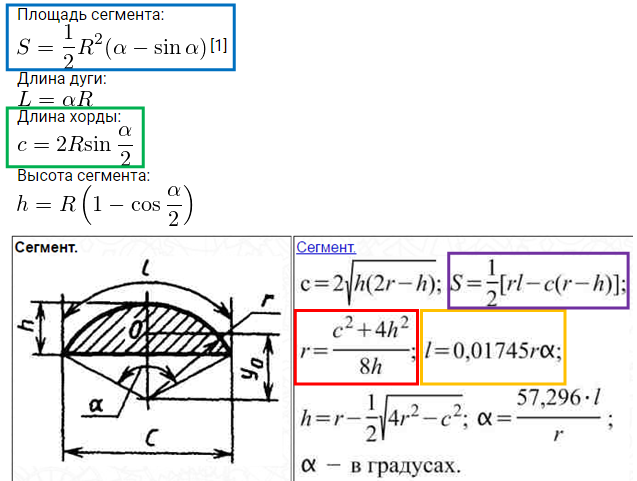

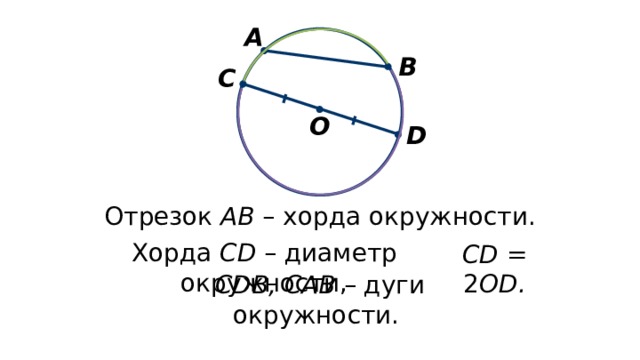
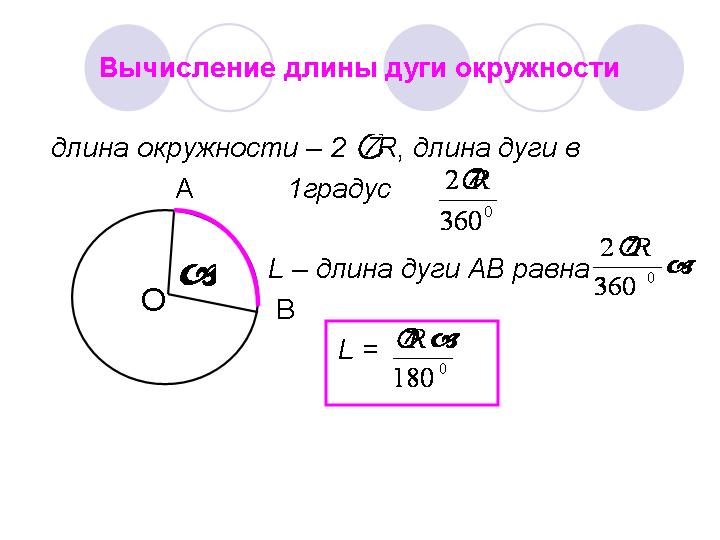
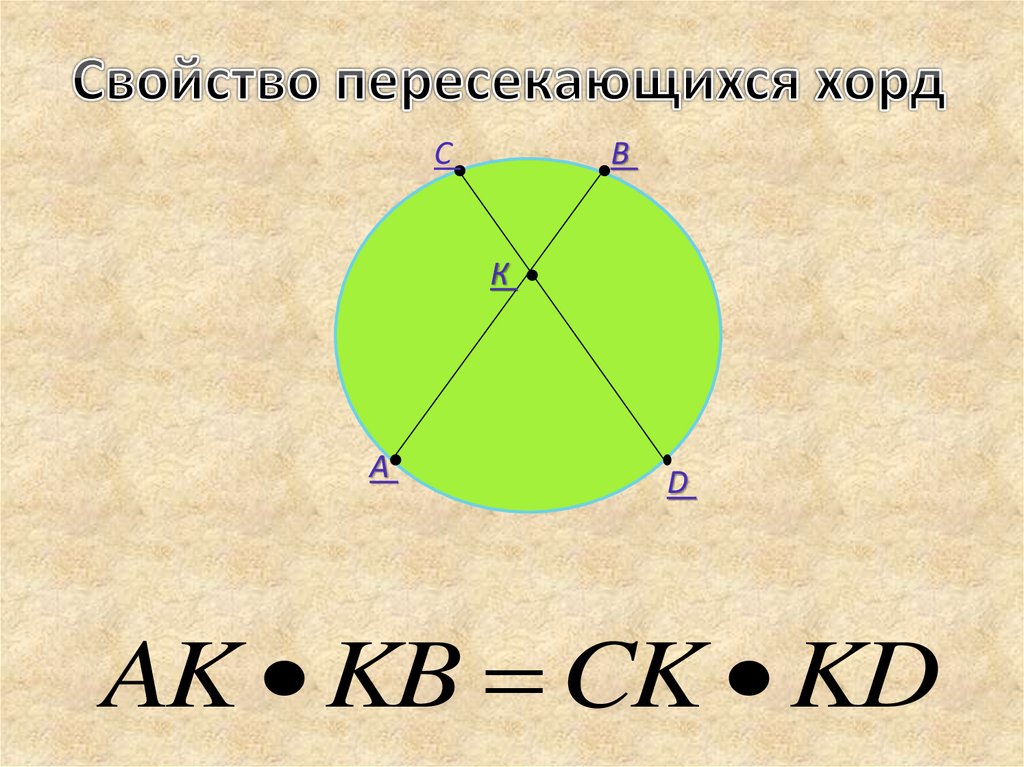
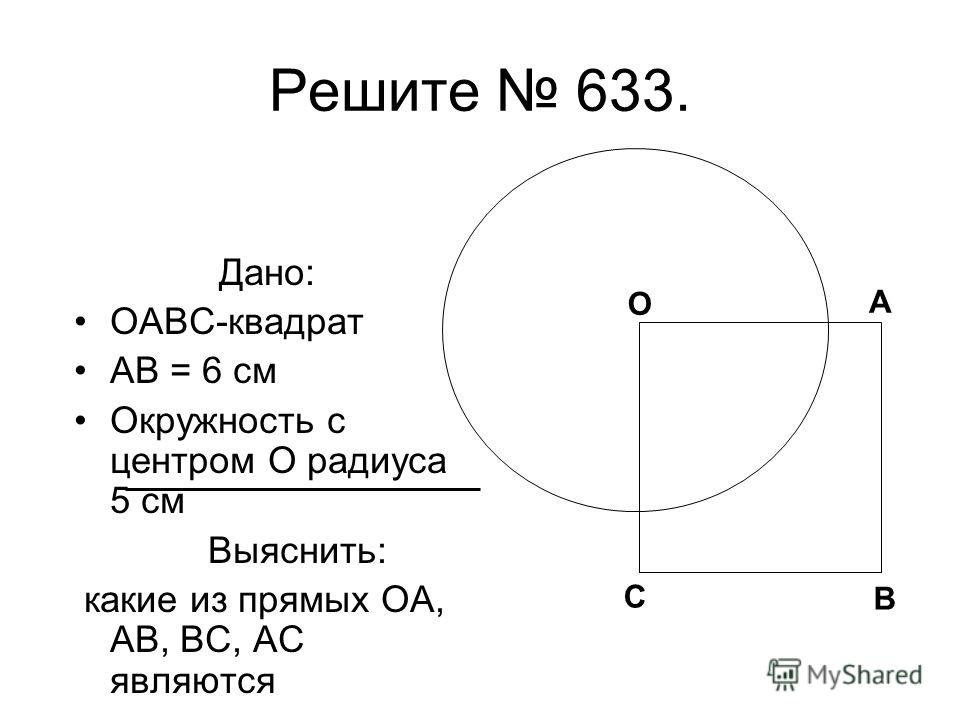

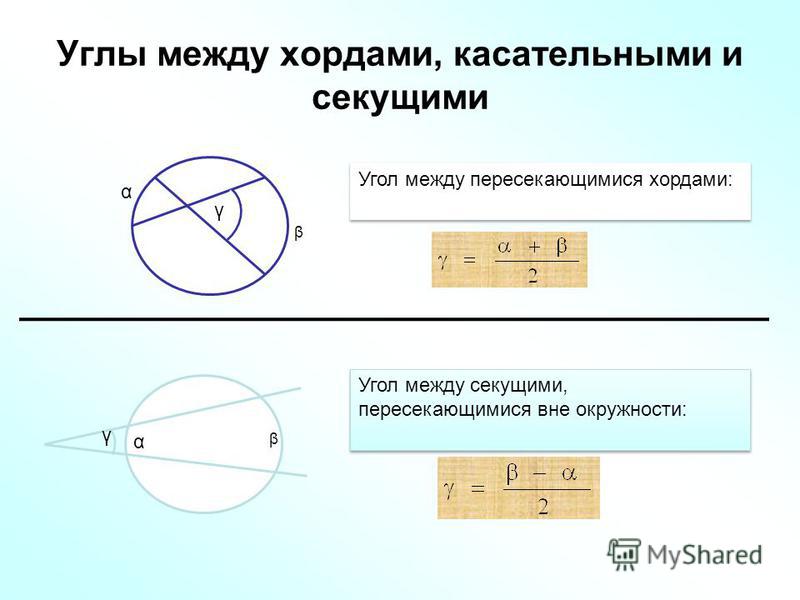
 Площадь, окруженная кругом, или область, которую он занимает в двумерной плоскости, равна называется площадью круга. Площадь данного круга) A = π × r2
Площадь, окруженная кругом, или область, которую он занимает в двумерной плоскости, равна называется площадью круга. Площадь данного круга) A = π × r2 Точка касания не входит внутрь окружности. Окружность может иметь бесконечные касательные, поскольку она состоит из бесконечных точек. Касательные всегда будут перпендикулярны радиусу данной окружности.
Точка касания не входит внутрь окружности. Окружность может иметь бесконечные касательные, поскольку она состоит из бесконечных точек. Касательные всегда будут перпендикулярны радиусу данной окружности.

 Представление интервалов, составляющих аккорд, в виде таблицы очень помогает понять аккорд
формулы и структура и создайте основу для более сложных тем, таких как
замена аккордов
.
Представление интервалов, составляющих аккорд, в виде таблицы очень помогает понять аккорд
формулы и структура и создайте основу для более сложных тем, таких как
замена аккордов
.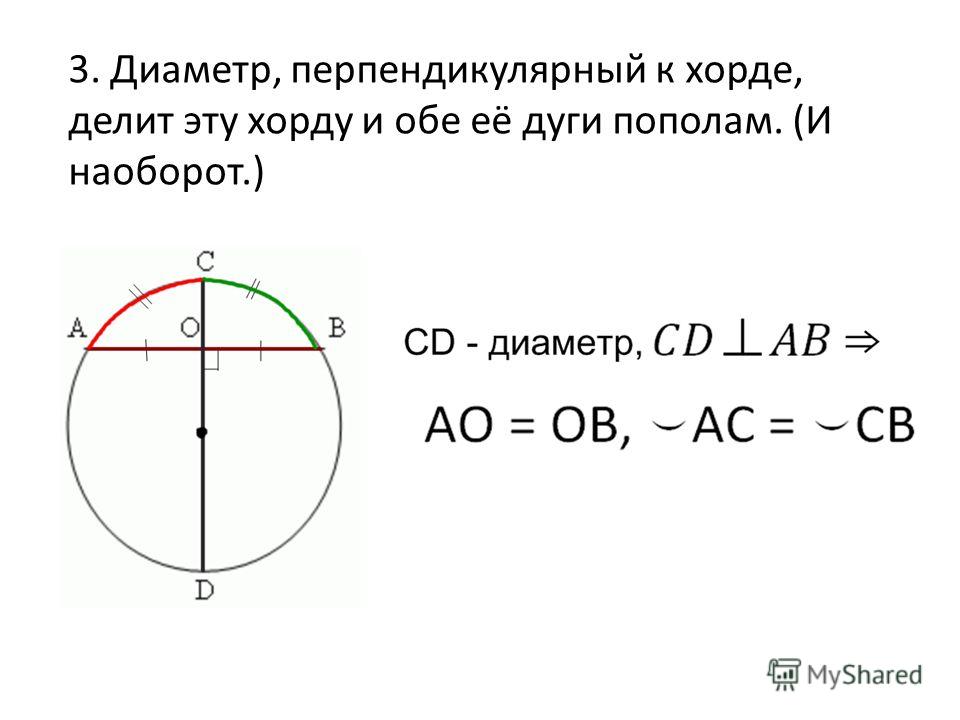 Затем вы видите диаграмму, состоящую из цветных прямоугольников.
Затем вы видите диаграмму, состоящую из цветных прямоугольников.
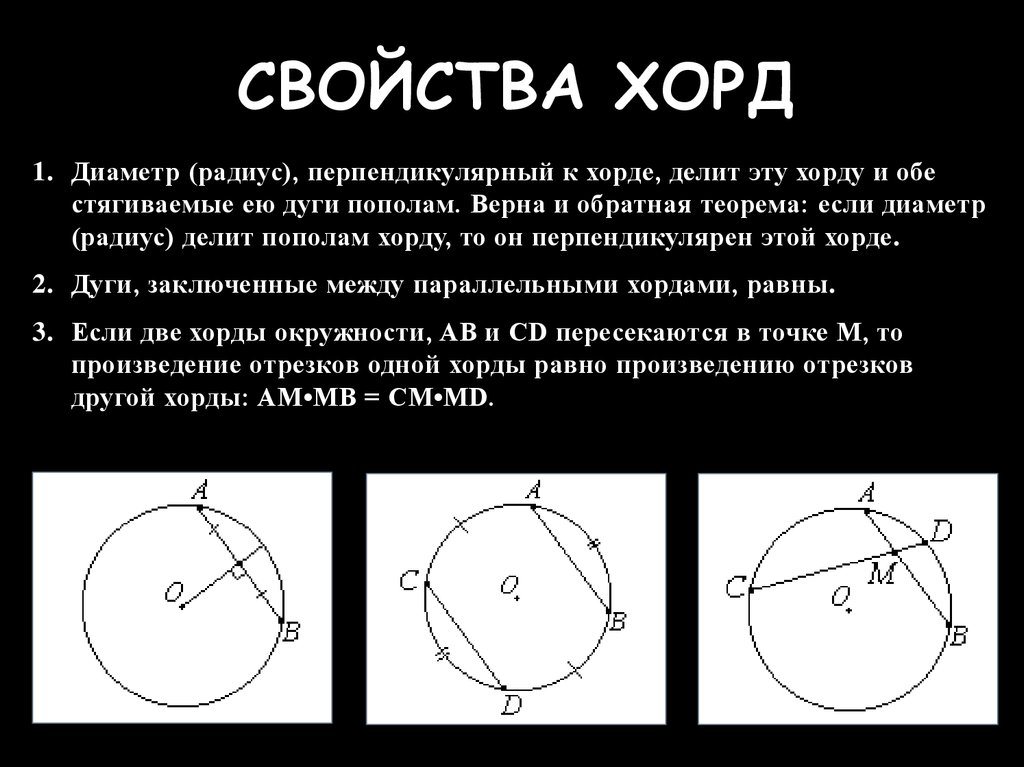
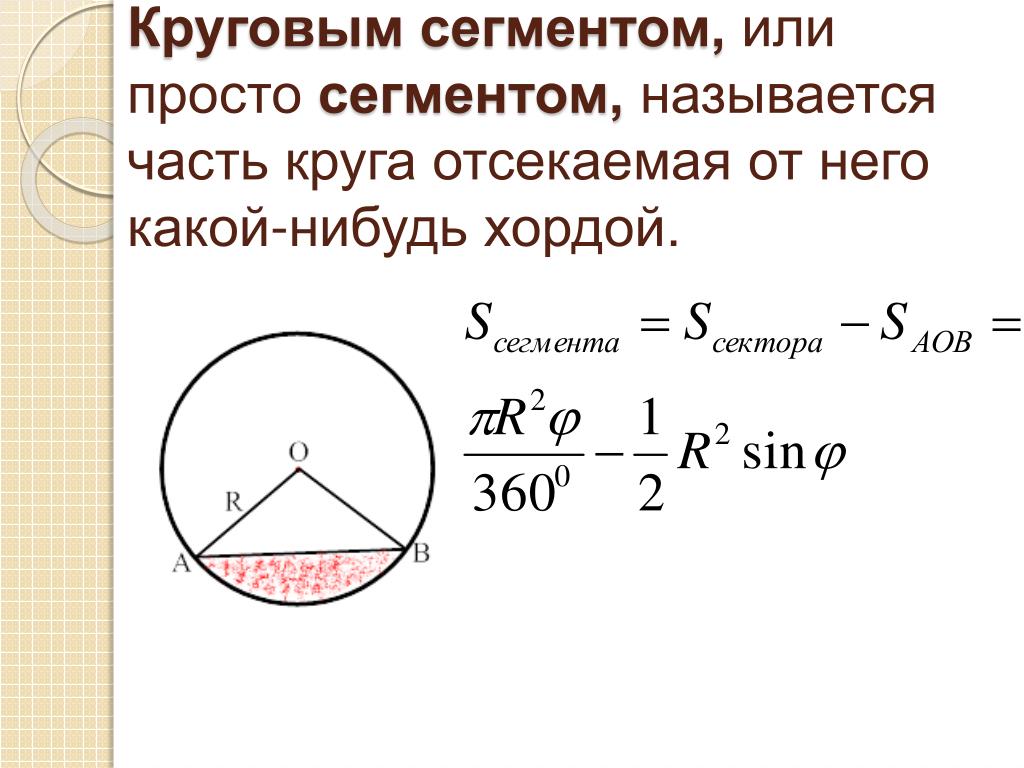


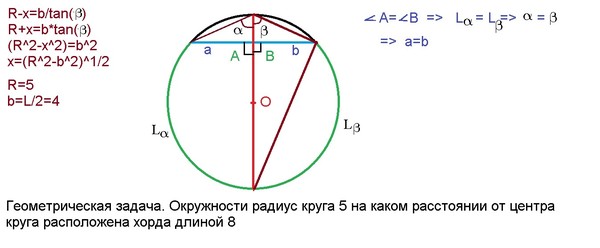
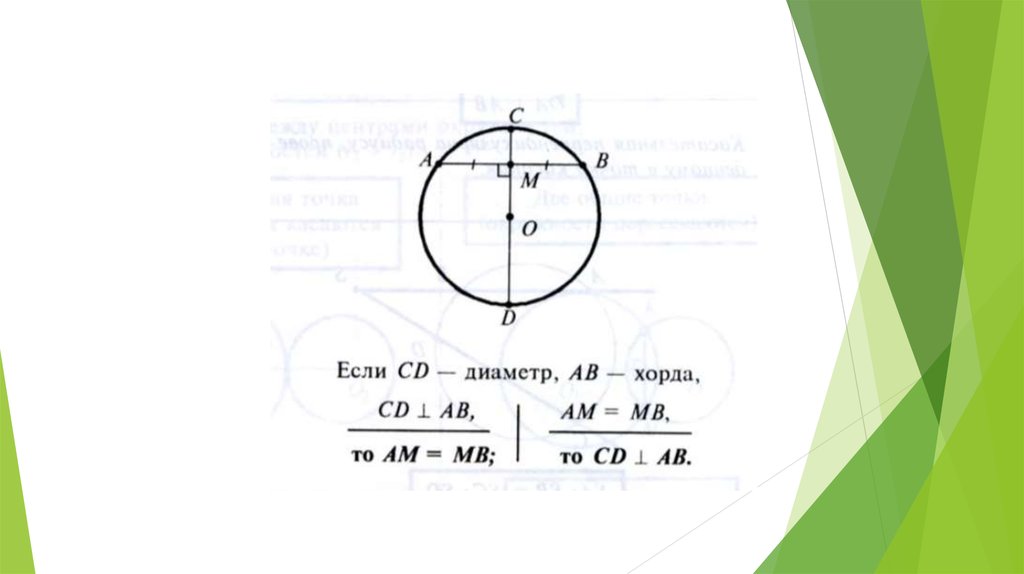
 Джазовые музыканты часто сосредотачиваются на 3-м и 7-м аккордах. Это важные аккордовые тона, которые вы можете выделить во время импровизации.
Джазовые музыканты часто сосредотачиваются на 3-м и 7-м аккордах. Это важные аккордовые тона, которые вы можете выделить во время импровизации.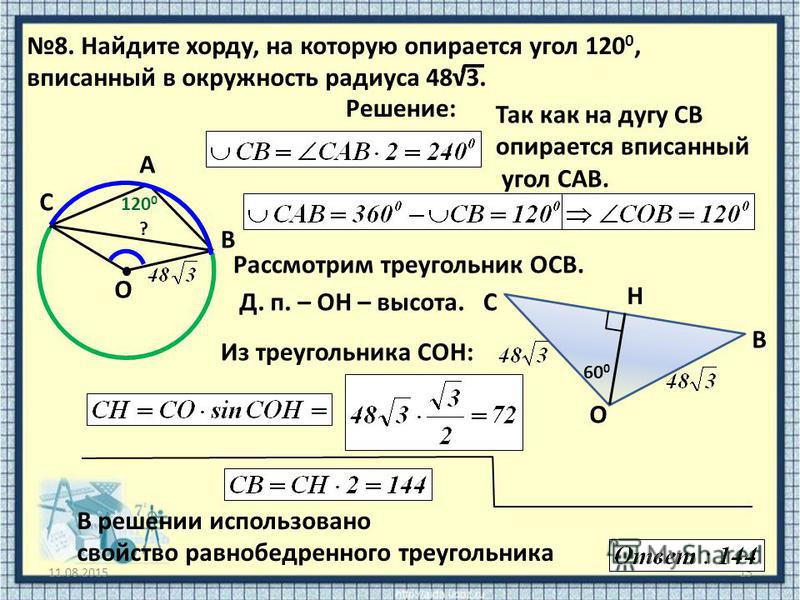 Некоторые примеры включают минор 7 ♭ 5, который произносится как минор семь плоских пять. Это просто минорный 7 аккорд с плоской квинтой. Другой пример — модифицированный аккорд, похожий на доминанту 7 ♯ 9.аккорд. Это просто доминирующий 7-й аккорд с добавленной и резкой 9-й. E7♯9 или E7(♯9) иногда называют аккордом Хендрикса.
Некоторые примеры включают минор 7 ♭ 5, который произносится как минор семь плоских пять. Это просто минорный 7 аккорд с плоской квинтой. Другой пример — модифицированный аккорд, похожий на доминанту 7 ♯ 9.аккорд. Это просто доминирующий 7-й аккорд с добавленной и резкой 9-й. E7♯9 или E7(♯9) иногда называют аккордом Хендрикса. С точки зрения гитары, голоса — это разные захваты одного и того же аккорда. Точнее говоря, голос определяет порядок нот, вместе с которыми ноты удваиваются.
С точки зрения гитары, голоса — это разные захваты одного и того же аккорда. Точнее говоря, голос определяет порядок нот, вместе с которыми ноты удваиваются.