|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 7 из 12Следующая ⇒ Пусть в пространстве имеется два базиса: и . Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса: (5.1) Новые базисные векторы получаются из старых с помощью матрицы При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица называется матрицей перехода от базиса к базису . Определитель матрицы не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы , были бы линейно зависимы. Обратно, если , то столбцы матрицы линейно независимы, и следовательно векторы , получающиеся из базисных векторов с помощью матрицы , линейно независимы и значит образуют некоторый базис. Рассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть в старом базисе и — в новом. Подставляя в последнее равенство вместо их выражение из (5.1), получим, что Таким образом, старые координаты вектора получатся из новых его координат с помощью той же матрицы , только коэффициенты соответствующих разложений образуют строки этой матрицы. 8. Определение ранга матрицы и необходимые дополнительные понятия. Прежде чем озвучить определение ранга матрицы, следует хорошо разобраться с понятием минора, а нахождение миноров матрицы подразумевает умение вычисления определителя. Так что рекомендуем при необходимости вспомнить теорию статьи методы нахождения определителя матрицы, свойства определителя. Возьмем матрицу А порядка . Пусть k – некоторое натуральное число, не превосходящее наименьшего из чисел m и n, то есть, . Определение. Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка , составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется. Другими словами, если в матрице А вычеркнуть (p–k) строк и (n–k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы есть минор порядка k матрицы А. Разберемся с определением минора матрицы на примере. Рассмотрим матрицу . Запишем несколько миноров первого порядка этой матрицы. К примеру, если мы выберем третью строку и второй столбец матрицы А, то нашему выбору соответствует минор первого порядка . Иными словами, для получения этого минора мы вычеркнули первую и вторую строки, а также первый, третий и четвертый столбцы из матрицы  Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор . Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор .Проиллюстрируем процедуру получения рассмотренных миноров первого порядка Таким образом, минорами первого порядка матрицы являются сами элементы матрицы. Покажем несколько миноров второго порядка. Выбираем две строки и два столбца. К примеру, возьмем первую и вторую строки и третий и четвертый столбец. При таком выборе имеем минор второго порядка . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов. Другим минором второго порядка матрицы А является . Проиллюстрируем построение этих миноров второго порядка Аналогично могут быть найдены миноры третьего порядка матрицы А. Так как в матрице А всего три строки, то выбираем их все. Если к этим строкам выбрать три первых столбца, то получим минор третьего порядка Он также может быть построен вычеркиванием последнего столбца матрицы А. Другим минором третьего порядка является Вот рисунок, показывающий построение этих миноров третьего порядка Для данной матрицы А миноров порядка выше третьего не существует, так как . Сколько же существует миноров k-ого порядка матрицы А порядка ? Число миноров порядка k может быть вычислено как , где и — число сочетаний из p по k и из n по k соответственно. Как же построить все миноры порядка k матрицы А порядка p на n? Нам потребуется множество номеров строк матрицы и множество номеров столбцов . Записываем все сочетания из p элементов по k (они будут соответствовать выбираемым строкам матрицы А при построении минора порядка k). К каждому сочетанию номеров строк последовательно добавляем все сочетания из nэлементов по k номеров столбцов. Эти наборы сочетаний номеров строк и номеров столбцов матрицы А помогут составить все миноры порядка k. Разберем на примере. Пример. Найдите все миноры второго порядка матрицы . Решение. Так как порядок исходной матрицы равен 3 на 3, то всего миноров второго порядка будет . Запишем все сочетания из 3 по 2 номеров строк матрицы А: 1, 2; 1, 3 и 2, 3. Все сочетания из 3 по 2 номеров столбцов есть 1, 2; 1, 3 и 2, 3. Возьмем первую и вторую строки матрицы А. Выбрав к этим строкам первый и второй столбцы, первый и третий столбцы, второй и третий столбцы, получим соответственно миноры Для первой и третьей строк при аналогичном выборе столбцов имеем Осталось ко второй и третьей строкам добавить первый и второй, первый и третий, второй и третий столбцы: Итак, все девять миноров второго порядка матрицы А найдены. Сейчас можно переходить к определению ранга матрицы. Определение. Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Ранг матрицы А обозначают как Rank(A). Можно также встретить обозначения Rg(A)или Из определений ранга матрицы и минора матрицы можно заключить, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы не меньше единицы. ⇐ Предыдущая234567891011Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Интересное: Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 13 из 28Следующая ⇒ Для аппроксимации информационных множеств прямоугольными параллелепипедами используются алгоритмы перехода от одного базиса к другому [Изв. Пусть в пространстве имеются два базиса: старый и новый . Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса [Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. М.: ЮНИТИ, 2001. – 471с.]: (1) Полученная система означает, что переход от старого базиса к новому задается матрицей перехода и т.д. , причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы. Матрица – неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса к старому базису осуществляется с помощью обратной матрицы . Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор имеет координаты относительно старого базиса и координаты относительно нового базиса, т.е. . (2) Подставив значения из системы (1) в левую часть равенства (2), получим после преобразований: т.е. в матричной форме или . (3) Пример. В базисе заданы вектора , и . Вектор , заданный в базисе , выразить в базисе . Решение. Выразим связь между базисами: Матрица перехода от базиса к базису имеет вид . Вычисляем . Рассмотрим получение обратной матрицы для матрицы : , где – определитель исходной матрицы , — определитель матрицы, полученной из матрицы , вычеркиванием – строки и – столбца. Теперь по (3) , т.е. новые координаты вектора в базисе есть 0,5; 2 и –0,5 и вектор может быть представлен в виде: .
Для некоторых функций остановка (или большое количество итераций) по методу Гаусса-Зайделя может произойти при наличии «оврагов». В овражном методе производится минимизация функции при различных начальных условиях. Оптимальные точки и определяют новое направление минимизации. Движение осуществляется к точке c наименьшим значением функции.
Формирование движения по прямой в многомерном пространстве: Рис. 2.
Точка 1: . Точка 2: .
Алгоритм преобразования фигуры в плоскостных координатах Пусть M — произвольная точка на плоскости с координатами и , вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел связанных с заданными числами и следующими соотношениями:
Рис. 6. Преобразование координат точки на плоскости в однородные координаты
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке на плоскости ставится в соответствие точка в пространстве (рис. Заметим, что производная точка на прямой, соединяющей начало координат, точку , с точкой , может быть задана тройкой чисел вида . Будем считать, что неравно 0. Вектор с координатами является направляющим вектором прямой, соединяющей точки и . Эта прямая пересекает плоскость в точке , которая однозначно определяет точку координатной плоскости . Тем самым между произвольной точкой с координатами и множеством троек чисел вида , при неравной 0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа новыми координатами этой точки. В проективной геометрии для однородных координат принято следующее обозначение: или, более обще, (напомним, что здесь непременно требуется, чтобы числа одновременно в нуль не обращались). Применение однородных координат оказывается удобным уже при решении простейших задач. Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения (например, ) точку с однородными координатами представить нельзя. Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами можно взять, например, . В результате получим . Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям. При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости. В самом деле, считая , сравним две записи: помеченную символом * и нижеследующую, матричную: . Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство . Тем самым сравниваемые записи можно считать равносильными. Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов. На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В и Г, обладающих хорошо выраженными геометрическими свойствами. Выпишем соответствующие матрицы третьего порядка. ⇐ Предыдущая891011121314151617Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Матрица преобразований
Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.
Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме [x y 1]. Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.
Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:
Координатные преобразования выражаются в виде матричных умножений:
Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:
Координаты трансформации высчитываются по следующим формулам:
Единичная матрица
Единичной матрицей называется, та у которой значения матрицы a и d равны 1, а остальные равны 0. Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.
Масштабирование
Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.
Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.
Высчитываем новые координаты объекта:
Отражение
Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1, по вертикали d = -1. Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.
Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.
Наклон
Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.
Например: Для наклона объекта по вертикали вверх установим значение b = 1
Высчитываем новые координаты объекта:
В итоге к наклону объекта приводит только координата y, которая увеличивается на значение x.
Поворот
Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.
Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.
Перемещение
Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.
Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке Геометрия.
Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF [a b c d e f]. Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:
- Перемещения указываются как [1 0 0 1 tx ty], где tx и ty — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
- Масштабирование указывается как [sx 0 0 sy 0 0].
 Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и sx и sy единиц в старой координатной системе соответственно.
Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и sx и sy единиц в старой координатной системе соответственно. - Повороты производятся матрицей [cosθ sinθ −sinθ cosθ 0 0], что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
- Наклон указывается как [1 tanα tanβ 1 0 0], что соответствует наклону оси x на угол α и оси y на угол β.
На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.
Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.
В таблице ниже приведены допустимые преобразования и значения матрицы.
| Исходный рисунок | Трансформированный рисунок | Матрица | Описание |
|---|---|---|---|
| 1 0 0 2 0 0 | Масштаб по вертикали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается. | ||
| 2 0 0 1 0 0 | Масштаб по горизонтали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается. | ||
| -1 0 0 1 0 0 | Отражение по горизонтали. | ||
| 1 0 0 -1 0 0 | Отражение по вертикали. | ||
| 1 1 0 1 0 0 | Наклон по вертикали вверх. | ||
| 1 -1 0 1 0 0 | Наклон по вертикали вниз. | ||
| 1 0 1 1 0 0 | Наклон по горизонтали вправо. | ||
| 1 0 -1 1 0 0 | Наклон по горизонтали влево. | ||
| 1 0 0 1 0 1 | Смещение по вертикали вверх в пикселях. | ||
| 1 0 0 1 0 -1 | Смещение по вертикали вниз в пикселях. | ||
| 1 0 0 1 1 0 | Смещение по горизонтали вправо в пикселях. | ||
| 1 0 0 1 -1 0 | Смещение по горизонтали влево в пикселях. |
Несмотря на все выше сказанное, матрица преобразований очень простой и эффективный инструмент для трансформации. Конечно, применять ее, например, для поворота нецелесообразно, так как во вкладке Геометрия имеется функция Поворот, но для отражения объекта она просто необходима.
Владимир Лермонтов — Живой свет новых миров. Матрица пятого измерения читать онлайн
12 3 4 5 6 7 …26
Владимир Лермонтов
Живой свет новых миров. Матрица пятого измерения
© Лермонтов В. Ю., 2012
© Издательство «Вектор», 2012
Все права защищены. Никакая часть электронной версии этой книги не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в сети Интернет и в корпоративных сетях, для частного и публичного использования без письменного разрешения владельца авторских прав.
©Электронная версия книги подготовлена компанией ЛитРес (www.litres.ru)
Совсем немного, и человечество будет готово к переходу к новой цивилизации. Но погибнет ли цивилизация Человека подобно цивилизациям Титанов, Атлантов и Гиперборейцев? Что будет с нами, когда наступит эпоха Великого Перехода? Путешествуя по священным горам Гималаев, названным Н. Рерихом Мировой Сокровищницей Духа, Владимир Лермонтов постиг тайну квантового перехода, который ожидает каждого из нас в 2012 году.
Конец старого света – начало новой эпохи живого света
Эпоха заката и рассвета
Подобно тому, как Земля вращается вокруг своей оси и каждый день, каждые сутки делятся на четыре цикла: закат, ночь, рассвет, день, или как Земля вращается вокруг Солнца и проходит свои четыре цикла: лето, осень, зима, весна, существование нашей Солнечной системы так же циклично, только вращается она вокруг центра Галактики. Там кроются источники двух видов энергии – света и тьмы. День или лето – это рассвет духовности цивилизации, осень – это закат духовности, когда божественный свет в людях уменьшается наполовину. Зима или ночь – этот цикл называется Кали Югой, когда свет духовности в людях почти отсутствует. Мы живем в эпоху завершения Кали Юги, перед рассветом, или началом весны.
В центре Галактики находятся два огромных пузыря. Это скопления космического вещества, мы будем их называть солнцами. Одно располагается над центром Галактики, второе – под ее центром. То, что выше, – солнце света, то, что под центром, – солнце тьмы.
Эпоха тьмы, или зимы, завершается, и Солнечная система входит в зону, когда появляются первые лучи духовного центра Галактики, солнца света.
Это и есть энергии Великого Перехода, энергии, которые изменят все на Земле, трансформируют и людей, и землю, произведут очищение. Энергии Великого Перехода – это и есть Живой Свет Всепроницающей Любви, который пересилит и уничтожит всю тьму на Земле.
Этот процесс начался в 1993 году и завершится в 2017-м. С каждым годом сила света духовного солнца Галактики нарастает. Максимальное его воздействие приходится на 2012, 2013 и 2014 годы. После этого трехлетнего периода свет стабилизируется на определенном уровне. До 2036 года интенсивность галактического солнца света будет оставаться неизменной. С 2037 до 2057 года сила света снова начнет увеличиваться. С 2057 по 2081 год сила света вновь будет находиться на одном уровне. А с 2082 по 2099 год сила света духовного солнца Галактики станет опять нарастать. И с 2100 рост силы остановится. Так завершится весна цивилизации, и с 2100 года начнется период лета духовности. За это время произойдет колоссальная световая трансформация человечества. Люди обретут биологическое бессмертие, биологическая жизнь трансформируется в биокристаллическую.
Так завершится весна цивилизации, и с 2100 года начнется период лета духовности. За это время произойдет колоссальная световая трансформация человечества. Люди обретут биологическое бессмертие, биологическая жизнь трансформируется в биокристаллическую.
На Земле за 40 тысяч лет существования человечества было немало закатов и рассветов, лет и зим, но при этом не происходило биологического скачка, то есть перехода к новому виду жизни. Цивилизации расцветали, потом впадали во мрак невежества и бездуховности, потом вновь расцветали – и все повторялось.
Особенность нынешнего Великого Перехода состоит в том, что произойдет квантовый скачок и человечество перейдет от старого вида к новому, а такого ранее еще не случалось. Апостол Павел сказал про этот переход так: «Не все мы умрем, но изменимся». Сорок тысяч лет человек, подобно евреям, бродил по пустыне в поисках «Земли обетованной». И вот наступило время обретения этой земли. Надо понять, что находится она не снаружи, а внутри человека, в клетках человеческого тела, а точнее – в программах, управляющих телом, в структуре ДНК. То, что происходит сейчас с нами, совершенно уникальный новый процесс, и опыта такой ДНК-трансформации нет ни у кого. Есть лишь инструмент – Живой Свет Всепроницающей Любви (Энергии Великого Перехода), идущий от духовного центра Галактики. С его помощью следует заменить негативные программы (коды) ДНК на коды Живого Света. По сути это замена программ страха, болезней, старости, смерти на программы любви, бессмертия и вечной молодости.
То, что происходит сейчас с нами, совершенно уникальный новый процесс, и опыта такой ДНК-трансформации нет ни у кого. Есть лишь инструмент – Живой Свет Всепроницающей Любви (Энергии Великого Перехода), идущий от духовного центра Галактики. С его помощью следует заменить негативные программы (коды) ДНК на коды Живого Света. По сути это замена программ страха, болезней, старости, смерти на программы любви, бессмертия и вечной молодости.
Законы кармы
Мы с вами живем в мире, которым управляет по сути один закон: закон причинно-следственной связи, или кармы. Закон кармы побуждает мир развиваться и эволюционировать. Закон кармы выражается для человека в изречении ученика Христа: «Что посеешь, то и пожнешь». Посеешь зло – пожнешь зло, посеешь добро – пожнешь добро. Однако есть в этом законе переменная величина: время исполнения последствий, которое может совершенно непредсказуемо изменяться. Раньше законы кармы работали следующим образом: если ты проживаешь эту жизнь добродетельно, то в следующем воплощении получишь благую жизнь. Соответственно, если человек провел свою жизнь во тьме, невежестве, творил негативные поступки, то в следующей жизни его ожидает жизнь, полная лишений и страданий.
Соответственно, если человек провел свою жизнь во тьме, невежестве, творил негативные поступки, то в следующей жизни его ожидает жизнь, полная лишений и страданий.
С приближением к Великому Переходу время реализации стало сокращаться, и результат своей деятельности человек получает уже в этой жизни. Так происходит потому, что время есть энергия, а чем больше энергии, тем больше скорость течения времени. Солнечная система, а вместе с ней и Земля, все более входят в поток энергий Великого Перехода.
В прошлом, каким бы человек добродетельным ни был, результат своей деятельности он мог получить только в следующей жизни. Сейчас, во время Великого Перехода, закон кармы работает очень быстро. Сегодня ты совершил поступок, завтра получил результат. Но это еще не предел, потому что скоро закон кармы будет работать так: совершил поступок и тут же, через мгновение, получаешь результат.
Вместе с тем закон кармы работает для разных людей по-разному: чем более духовно развит человек, чем ближе он к свету, тем быстрее для него работает закон. В жизни мы наблюдаем следующую картину: духовный человек за свои негативные мысли и поступки тут же «получает по шапке», а негативный человек «по шапке» получает через месяц или даже через год. Это происходит оттого, что духовный человек живет в четвертом измерении, а бездуховный – в третьем или еще более низком, втором и даже первом. Каждому измерению свойственно свое течение времени.
В жизни мы наблюдаем следующую картину: духовный человек за свои негативные мысли и поступки тут же «получает по шапке», а негативный человек «по шапке» получает через месяц или даже через год. Это происходит оттого, что духовный человек живет в четвертом измерении, а бездуховный – в третьем или еще более низком, втором и даже первом. Каждому измерению свойственно свое течение времени.
Читать дальше
12 3 4 5 6 7 …26
Маркировка обуви в рознице — порядок перехода на маркировку обуви
Соглашение о конфиденциальности
и обработке персональных данных
1.Общие положения
1.1.Настоящее соглашение о конфиденциальности и обработке персональных данных (далее – Соглашение) принято свободно и своей волей, действует в отношении всей информации, которую ООО «Инсейлс Рус» и/или его аффилированные лица, включая все лица, входящие в одну группу с ООО «Инсейлс Рус» (в том числе ООО «ЕКАМ сервис»), могут получить о Пользователе во время использования им любого из сайтов, сервисов, служб, программ для ЭВМ, продуктов или услуг ООО «Инсейлс Рус» (далее – Сервисы) и в ходе исполнения ООО «Инсейлс Рус» любых соглашений и договоров с Пользователем. Согласие Пользователя с Соглашением, выраженное им в рамках отношений с одним из перечисленных лиц, распространяется на все остальные перечисленные лица.
Согласие Пользователя с Соглашением, выраженное им в рамках отношений с одним из перечисленных лиц, распространяется на все остальные перечисленные лица.
1.2.Использование Сервисов означает согласие Пользователя с настоящим Соглашением и указанными в нем условиями; в случае несогласия с этими условиями Пользователь должен воздержаться от использования Сервисов.
1.3.Сторонами (далее – «Стороны) настоящего Соглашения являются:
«Инсейлс» – Общество с ограниченной ответственностью «Инсейлс Рус», ОГРН 1117746506514, ИНН 7714843760, КПП 771401001, зарегистрированное по адресу: 125319, г.Москва, ул.Академика Ильюшина, д.4, корп.1, офис 11 (далее — «Инсейлс»), с одной стороны, и
«Пользователь» –
либо физическое лицо, обладающее дееспособностью и признаваемое участником гражданских правоотношений в соответствии с законодательством Российской Федерации;
либо юридическое лицо, зарегистрированное в соответствии с законодательством государства, резидентом которого является такое лицо;
либо индивидуальный предприниматель, зарегистрированный в соответствии с законодательством государства, резидентом которого является такое лицо;
которое приняло условия настоящего Соглашения.
1.4.Для целей настоящего Соглашения Стороны определили, что конфиденциальная информация – это сведения любого характера (производственные, технические, экономические, организационные и другие), в том числе о результатах интеллектуальной деятельности, а также сведения о способах осуществления профессиональной деятельности (включая, но не ограничиваясь: информацию о продукции, работах и услугах; сведения о технологиях и научно-исследовательских работах; данные о технических системах и оборудовании, включая элементы программного обеспечения; деловые прогнозы и сведения о предполагаемых покупках; требования и спецификации конкретных партнеров и потенциальных партнеров; информацию, относящуюся к интеллектуальной собственности, а также планы и технологии, относящиеся ко всему перечисленному выше), сообщаемые одной стороной другой стороне в письменной и/или электронной форме, явно обозначенные Стороной как ее конфиденциальная информация.
1.5.Целью настоящего Соглашения является защита конфиденциальной информации, которой Стороны будут обмениваться в ходе переговоров, заключения договоров и исполнения обязательств, а равно любого иного взаимодействия (включая, но не ограничиваясь, консультирование, запрос и предоставление информации, и выполнение иных поручений).
2.Обязанности Сторон
2.1.Стороны соглашаются сохранять в тайне всю конфиденциальную информацию, полученную одной Стороной от другой Стороны при взаимодействии Сторон, не раскрывать, не разглашать, не обнародовать или иным способом не предоставлять такую информацию какой-либо третьей стороне без предварительного письменного разрешения другой Стороны, за исключением случаев, указанных в действующем законодательстве, когда предоставление такой информации является обязанностью Сторон.
2.2.Каждая из Сторон предпримет все необходимые меры для защиты конфиденциальной информации как минимум с применением тех же мер, которые Сторона применяет для защиты собственной конфиденциальной информации. Доступ к конфиденциальной информации предоставляется только тем сотрудникам каждой из Сторон, которым он обоснованно необходим для выполнения служебных обязанностей по исполнению настоящего Соглашения.
2.3.Обязательство по сохранению в тайне конфиденциальной информации действительно в пределах срока действия настоящего Соглашения, лицензионного договора на программы для ЭВМ от 01. 12.2016г., договора присоединения к лицензионному договору на программы для ЭВМ, агентских и иных договоров и в течение пяти лет после прекращения их действия, если Сторонами отдельно не будет оговорено иное.
12.2016г., договора присоединения к лицензионному договору на программы для ЭВМ, агентских и иных договоров и в течение пяти лет после прекращения их действия, если Сторонами отдельно не будет оговорено иное.
2.4.Не будут считаться нарушением настоящего Соглашения следующие случаи:
(а)если предоставленная информация стала общедоступной без нарушения обязательств одной из Сторон;
(б)если предоставленная информация стала известна Стороне в результате ее собственных исследований, систематических наблюдений или иной деятельности, осуществленной без использования конфиденциальной информации, полученной от другой Стороны;
(в)если предоставленная информация правомерно получена от третьей стороны без обязательства о сохранении ее в тайне до ее предоставления одной из Сторон;
(г)если информация предоставлена по письменному запросу органа государственной власти, иного государственного органа, или органа местного самоуправления в целях выполнения их функций и ее раскрытие этим органам обязательно для Стороны. При этом Сторона должна незамедлительно известить другую Сторону о поступившем запросе;
При этом Сторона должна незамедлительно известить другую Сторону о поступившем запросе;
(д)если информация предоставлена третьему лицу с согласия той Стороны, информация о которой передается.
2.5.Инсейлс не проверяет достоверность информации, предоставляемой Пользователем, и не имеет возможности оценивать его дееспособность.
2.6.Информация, которую Пользователь предоставляет Инсейлс при регистрации в Сервисах, не является персональными данными, как они определены в Федеральном законе РФ №152-ФЗ от 27.07.2006г. «О персональных данных».
2.7.Инсейлс имеет право вносить изменения в настоящее Соглашение. При внесении изменений в актуальной редакции указывается дата последнего обновления. Новая редакция Соглашения вступает в силу с момента ее размещения, если иное не предусмотрено новой редакцией Соглашения.
2.8.Принимая данное Соглашение Пользователь осознает и соглашается с тем, что Инсейлс может отправлять Пользователю персонализированные сообщения и информацию (включая, но не ограничиваясь) для повышения качества Сервисов, для разработки новых продуктов, для создания и отправки Пользователю персональных предложений, для информирования Пользователя об изменениях в Тарифных планах и обновлениях, для направления Пользователю маркетинговых материалов по тематике Сервисов, для защиты Сервисов и Пользователей и в других целях.
Пользователь имеет право отказаться от получения вышеуказанной информации, сообщив об этом письменно на адрес электронной почты Инсейлс — [email protected].
2.9.Принимая данное Соглашение, Пользователь осознает и соглашается с тем, что Сервисами Инсейлс для обеспечения работоспособности Сервисов в целом или их отдельных функций в частности могут использоваться файлы cookie, счетчики, иные технологии и Пользователь не имеет претензий к Инсейлс в связи с этим.
2.10.Пользователь осознает, что оборудование и программное обеспечение, используемые им для посещения сайтов в сети интернет могут обладать функцией запрещения операций с файлами cookie (для любых сайтов или для определенных сайтов), а также удаления ранее полученных файлов cookie.
Инсейлс вправе установить, что предоставление определенного Сервиса возможно лишь при условии, что прием и получение файлов cookie разрешены Пользователем.
2.11.Пользователь самостоятельно несет ответственность за безопасность выбранных им средств для доступа к учетной записи, а также самостоятельно обеспечивает их конфиденциальность. Пользователь самостоятельно несет ответственность за все действия (а также их последствия) в рамках или с использованием Сервисов под учетной записью Пользователя, включая случаи добровольной передачи Пользователем данных для доступа к учетной записи Пользователя третьим лицам на любых условиях (в том числе по договорам или соглашениям). При этом все действия в рамках или с использованием Сервисов под учетной записью Пользователя считаются произведенными самим Пользователем, за исключением случаев, когда Пользователь уведомил Инсейлс о несанкционированном доступе к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи.
Пользователь самостоятельно несет ответственность за все действия (а также их последствия) в рамках или с использованием Сервисов под учетной записью Пользователя, включая случаи добровольной передачи Пользователем данных для доступа к учетной записи Пользователя третьим лицам на любых условиях (в том числе по договорам или соглашениям). При этом все действия в рамках или с использованием Сервисов под учетной записью Пользователя считаются произведенными самим Пользователем, за исключением случаев, когда Пользователь уведомил Инсейлс о несанкционированном доступе к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи.
2.12.Пользователь обязан немедленно уведомить Инсейлс о любом случае несанкционированного (не разрешенного Пользователем) доступа к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи. В целях безопасности, Пользователь обязан самостоятельно осуществлять безопасное завершение работы под своей учетной записью по окончании каждой сессии работы с Сервисами. Инсейлс не отвечает за возможную потерю или порчу данных, а также другие последствия любого характера, которые могут произойти из-за нарушения Пользователем положений этой части Соглашения.
В целях безопасности, Пользователь обязан самостоятельно осуществлять безопасное завершение работы под своей учетной записью по окончании каждой сессии работы с Сервисами. Инсейлс не отвечает за возможную потерю или порчу данных, а также другие последствия любого характера, которые могут произойти из-за нарушения Пользователем положений этой части Соглашения.
3.Ответственность Сторон
3.1.Сторона, нарушившая предусмотренные Соглашением обязательства в отношении охраны конфиденциальной информации, переданной по Соглашению, обязана возместить по требованию пострадавшей Стороны реальный ущерб, причиненный таким нарушением условий Соглашения в соответствии с действующим законодательством Российской Федерации.
3.2.Возмещение ущерба не прекращают обязанности нарушившей Стороны по надлежащему исполнению обязательств по Соглашению.
4.Иные положения
4.1.Все уведомления, запросы, требования и иная корреспонденция в рамках настоящего Соглашения, в том числе включающие конфиденциальную информацию, должны оформляться в письменной форме и вручаться лично или через курьера, или направляться по электронной почте адресам, указанным в лицензионном договоре на программы для ЭВМ от 01. 12.2016г., договоре присоединения к лицензионному договору на программы для ЭВМ и в настоящем Соглашении или другим адресам, которые могут быть в дальнейшем письменно указаны Стороной.
12.2016г., договоре присоединения к лицензионному договору на программы для ЭВМ и в настоящем Соглашении или другим адресам, которые могут быть в дальнейшем письменно указаны Стороной.
4.2.Если одно или несколько положений (условий) настоящего Соглашения являются либо становятся недействительными, то это не может служить причиной для прекращения действия других положений (условий).
4.3.К настоящему Соглашению и отношениям между Пользователем и Инсейлс, возникающим в связи с применением Соглашения, подлежит применению право Российской Федерации.
4.3.Все предложения или вопросы по поводу настоящего Соглашения Пользователь вправе направлять в Службу поддержки пользователей Инсейлс www.ekam.ru либо по почтовому адресу: 107078, г. Москва, ул. Новорязанская, 18, стр.11-12 БЦ «Stendhal» ООО «Инсейлс Рус».
Дата публикации: 01.12.2016г.
Полное наименование на русском языке:
Общество с ограниченной ответственностью «Инсейлс Рус»
Сокращенное наименование на русском языке:
ООО «Инсейлс Рус»
Наименование на английском языке:
InSales Rus Limited Liability Company (InSales Rus LLC)
Юридический адрес:
125319, г. Москва, ул. Академика Ильюшина, д. 4, корп.1, офис 11
Москва, ул. Академика Ильюшина, д. 4, корп.1, офис 11
Почтовый адрес:
107078, г. Москва, ул. Новорязанская, 18, стр.11-12, БЦ «Stendhal»
ИНН: 7714843760 КПП: 771401001
Банковские реквизиты:
Р/с 40702810600001004854
В ИНГ БАНК (ЕВРАЗИЯ) АО, г.Москва,
к/с 30101810500000000222, БИК 044525222
Электронная почта: [email protected]
Контактный телефон: +7(495)133-20-43
Жильцов переводят на «умные» счетчики
Санникова Виктория
Юрист юридической фирмы «ЮСТ»
06 Июля 2020
Советы
С 1 июля началась бесплатная установка интеллектуальных приборов учета электроэнергии. За отказ от такого «подарка» повысят плату за услуги ЖКХ
1 июля начали действовать правила перехода на интеллектуальные системы учета электрической энергии1. Старые приборы учета электроэнергии будут заменяться на новые, интеллектуальные, после выхода из строя отслуживших счетчиков или по истечении межповерочного интервала (временного отрезка, в течение которого изготовитель счетчика гарантирует его точную работу).
Чем новые счетчики отличаются от старых?
- Главное отличие новых счетчиков состоит в том, что после их установки не потребуется снимать и передавать показания. Интеллектуальный счетчик хранит и сам передает данные в энергетическую компанию, после чего потребителю выставляют счет на оплату. Способ передачи информации определяет поставщик – с помощью сотовой связи или через интернет-соединение.
- Потребители смогут отслеживать показания онлайн и проверять их на приборе учета.
- «Умные» счетчики фиксируют уровень напряжения и частоту, позволяя следить за качеством электроэнергии.
- Появится возможность смены тарифа на электроэнергию онлайн (сейчас существуют три группы тарифов в зависимости от времени потребления в течение суток).
- Если потребитель задерживает оплату счетов, интеллектуальная система учета предоставляет возможность поставщику электроэнергии дистанционно ограничить или приостановить ее подачу.

- Интеллектуальные системы учета должны соответствовать установленным требованиям по защите информации и реагировать на факты несанкционированного доступа к системе. Предполагается, что это поможет предотвратить случаи хищения электроэнергии.
- Большинство ошибок в начислениях платы за электричество связаны с неправильной передачей показаний абонентами. Поскольку с введением «умных» счетчиков достоверные данные о потребленной электроэнергии будут вовремя передаваться в дистанционном режиме, должно уменьшиться количество споров между поставщиками электроэнергии и потребителями.
- Установка «умных» счетчиков должна способствовать сокращению длительности перерывов электроснабжения – согласно требованиям к интеллектуальной системе она передает информацию об отключении электроэнергии и восстанавливает питание.
В какие сроки всех должны перевести на интеллектуальные системы учета электроэнергии?
Замена приборов учета будет проходить поэтапно. С 1 июля 2020 г. сетевые организации могут устанавливать на свое усмотрение как привычные приборы учета, так и интеллектуальные. Многоквартирные дома, вводимые в эксплуатацию после 1 января 2021 г., должны быть оснащены интеллектуальными приборами учета. С 1 января 2022 г. устанавливать будут только «умные» счетчики.
С 1 июля 2020 г. сетевые организации могут устанавливать на свое усмотрение как привычные приборы учета, так и интеллектуальные. Многоквартирные дома, вводимые в эксплуатацию после 1 января 2021 г., должны быть оснащены интеллектуальными приборами учета. С 1 января 2022 г. устанавливать будут только «умные» счетчики.
Полный переход на новые счетчики должен быть завершен к 1 января 2023 г. С этой даты начнут штрафовать компании, которые не обеспечили потребителям возможность использовать интеллектуальные приборы учета.
Можно ли отказаться от установки новых счетчиков?
Права у потребителя отказаться от установки «умного» счетчика не будет. В случае двукратного недопуска представителей гарантирующего поставщика или сетевой организации для установки прибора учета плата за электроснабжение рассчитывается исходя из нормативов потребления коммунальных услуг с применением к стоимости повышающего коэффициента, равного 1,5. То есть платить за услуги ЖКХ придется больше.
Кто заплатит за новые счетчики?
Закон предусматривает перенос обязанности платить за установку, эксплуатацию, поверку и замену приборов учета электроэнергии с потребителей на поставщиков ресурсов: с жильцов многоквартирных домов – на гарантирующих поставщиков, с остальных потребителей – на сетевые организации. Потребитель должен лишь обеспечивать целостность прибора учета в случае, если счетчик находится внутри принадлежащего ему помещения или в границах его земельного участка.
Обязанность по приобретению и монтажу устройства возложена на сетевую организацию. В дальнейшем, согласно закону, такие расходы подлежат включению в состав тарифа на услуги по передаче электрической энергии.
Как понять, что новый счетчик предлагает установить мошенник?
Во время перехода на интеллектуальные системы учета электроэнергии возможно распространение случаев мошенничества. Злоумышленники могут предлагать жильцам установить новые счетчики «по льготной цене». Поэтому важно помнить: представитель электросетевой или энергосбытовой организации обязан показать удостоверение с печатью организации. За установку новых счетчиков денежные средства напрямую с потребителей не взимаются – расходы ресурсоснабжающих организаций будут включены в тарифы на электроэнергию. О тарифах и правилах перехода на новые счетчики можно узнать в управляющей компании или у поставщика услуг.
Поэтому важно помнить: представитель электросетевой или энергосбытовой организации обязан показать удостоверение с печатью организации. За установку новых счетчиков денежные средства напрямую с потребителей не взимаются – расходы ресурсоснабжающих организаций будут включены в тарифы на электроэнергию. О тарифах и правилах перехода на новые счетчики можно узнать в управляющей компании или у поставщика услуг.
1 Федеральный закон от 27 декабря 2018 г. № 522-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации в связи с развитием систем учета электрической энергии (мощности) в Российской Федерации».
Калькулятор цепей Маркова — вектор вероятности перехода, вектор установившегося состояния
Цепь Маркова
Калькулятор цепи Маркова и калькулятор стационарного вектора. Вычисляет вектор вероятности n-го шага, вектор устойчивого состояния, поглощающие состояния и этапы вычисления.
Что такое цепь Маркова?
Цепь Маркова — это математическая система, используемая для моделирования случайных процессов, в которой следующее состояние системы зависит только от ее текущего состояния, а не от ее истории.
В этой стохастической модели используются дискретные временные шаги. Цепь Маркова — это стохастическая модель, которая описывает, как система перемещается между различными состояниями на дискретных временных шагах.
Есть несколько состояний, и вы знаете вероятность перехода из любого состояния в любое состояние. Если вы не можете перейти из одного состояния в другое, то вероятность равна нулю.
Что такое шаги дискретного времени?
Изменение системы происходит только поэтапно, между шагами система остается в том же состоянии.
При срабатывании шага система может перейти в другое состояние или остаться в том же состоянии.
Время между шагами не обязательно постоянно, например, в настольной игре каждый раз, когда игрок делает ход, является шагом.
Каковы предположения цепи Маркова?
- Марковское свойство — история не имеет значения, вероятность перехода в каждое состояние зависит только от последнего состояния.

- Свойство стационарности во времени — распределение вероятностей не зависит от шага (n).
Что такое состояние поглощения?
Поглощающее состояние — это состояние, однажды войдя в которое невозможно выйти из состояния. В матрице перехода строка, начинающаяся с этого шага
Формула цепи Маркова
Следующая формула представлена в матричной форме , S 0 — вектор, а P — матрица.
S n = S 0 × P n
S 0 — вектор начального состояния.
P — матрица переходов, содержит вероятности перехода из состояния i в состояние j за один шаг (p i,j ) для каждой комбинации i, j.
n — номер шага.
S n — вектор вероятности n-го шага.
Пример:
S 0 = [P 1 , стр. 2 , стр. 3 ]
[с 1,1 , стр. ,3 ] ,3 ] | |
| P= | [стр. 2,1 , с 2,2 , с 2,3 ] |
| [с 3,1 , с 3,2 , с 3,1 , стр 3,2 , с 3,3 , стр. ] |
p 2,1 — вероятность перехода из состояния-2 в состояние-1 за один шаг.
Введите данные в калькулятор цепи Маркова
- Введите количество шагов (n) — результатом будет вектор вероятности после n шагов.
- Нажмите «Вставить состояние» или «Удалить состояние», чтобы увеличить или уменьшить количество состояний.
- Войдите в начальное состояние — с какого состояния вы начинаете? это может быть также вероятностная комбинация состояний. Если вы знаете состояние, вы должны ввести один (1) для начала состояния и ноль (0) для всех остальных состояний.
- Введите матрицу перехода — (P) — содержит вероятность перехода из состояния-i в состояние-j для любой комбинации i и j.
Для комбинации состояний введите вектор вероятности, разделенный между несколькими состояниями, например [0.
 2,0.8,0,0]
2,0.8,0,0] В этом примере вы можете начать только с состояния-1 или состояния-2, а вероятность начать с состояния-1 — 0,2, а вероятность начать с состояния-2 — 0,8.
Вектор начального состояния расположен под матрицей перехода.
Что такое вектор вероятности?
Вектор вероятности показывает вероятность пребывания в каждом состоянии. Сумма всех элементов вектора вероятности равна единице. Вектор вероятности n-го шага (S n ) представляет собой вектор вероятности после n шагов при запуске в начальном состоянии. (С 0 )
Что такое стационарный вектор?
Обычно вектор вероятности после одного шага не совпадает с вектором вероятности после двух шагов.
Но много раз после нескольких шагов вектор вероятности после n шагов равен вектору вероятности после n-1 шагов.
S n = S n-1
Чтобы получить вектор, вам нужно решить следующее уравнение в матричной форме.
Вам нужно найти собственный вектор, собственное значение которого равно 1, а затем разделить каждый элемент на сумму, так как сумма вероятностей должна быть равна 1.
S × P = S
Другой метод состоит в том, чтобы найти матрицу P n , которая удовлетворяет следующему уравнению: вектором будет любая строка в матрице P n .
P n = P n-1
Когда все строки в матрице P n идентичны , начальное состояние не влияет на результат. Неважно, с какого состояния вы начали, и есть только один вектор.
Когда все строки в P n матрица не идентична , начальное состояние влияет на результат. В этом случае имеется более одного вектора, и вектор зависит от состояния, с которого вы начали.
Когда имеется более одного вектора и начальное состояние непостоянно, вектор представляет собой комбинацию векторов соответствующих состояний:
S 0 × P n
Пример стационарного вектора
Матрица перехода| P= | [0. 7, 0.3] 7, 0.3] |
| [0.2, 0.8] |
[1, 0]
Steps
| Step | State-1 | State- 2 |
|---|---|---|
| S 0 | 1 | 0 |
| S 1 | 0.7 | 0.3 |
| S 2 | 0.55 | 0.45 |
| … | … | … |
| S 13 | 0.4001 | 0.5999 |
| S 14 | 0.4 | 0.6 |
| S 15 | 0.4 | 0,6 |
Как видите, начиная с шага 14 вектор вероятности не меняется: [0,4, 0,6].
С 15 = С 14 .
Точнее, если округлить до 10 знаков после запятой, то можно увидеть, что два вектора не равны:
S 14 = [0,4000366211, 0,5999633789].
S 15 = [0,4000183105, 0,5999816895].
Но когда n -> ∞, S n -> [0,4, 0,6].
Цепи Маркова — Практические задачи по переходным матрицам онлайн
Предположим, процесс начинается в одном состоянии и переходит в другое состояние после 3 ходов. Какая пара (((начало, конец))) наиболее вероятна?
(А, А) (А, Б) (Б, А) (Б, Б) (С, Б)Показать объяснение
View wiki
Цепь Маркова имеет переходную матрицу
(0. 50.30.20.40.40.20.60.40).\begin{pmatrix}
0,5 и 0,3 и 0,2\
0,4 и 0,4 и 0,2\
0,6 и 0,4 и 0
\end{pmatrix}.⎝⎛0.50.40.60.30.40.40.20.20⎠⎞.
50.30.20.40.40.20.60.40).\begin{pmatrix}
0,5 и 0,3 и 0,2\
0,4 и 0,4 и 0,2\
0,6 и 0,4 и 0
\end{pmatrix}.⎝⎛0.50.40.60.30.40.40.20.20⎠⎞.
Какова его 222-шаговая матрица перехода?
(А) : (0.490.350.160.480.360.160.460.340.2)\begin{pmatrix} 0,49 и 0,35 и 0,16\ 0,48 и 0,36 и 0,16\ 0,46 и 0,34 и 0,2 \end{pmatrix}⎝⎛0,490.480.460.350.360.340.160.160.2⎠⎞
(B) : (0.250.350.40.390.250.360.360.390.25)\begin{pmatrix} 0,25 и 0,35 и 0,4\ 0,39 и 0,25 и 0,36\ 0,36 и 0,39 и 0,25 \end{pmatrix}⎝⎛0.250.390.360.350.250.390.40.360.25⎠⎞
(C) : (0.490.350.160.480.360.160.480.320.2)\begintrix} 0,49 и 0,35 и 0,16\ 0,48 и 0,36 и 0,16\ 0,48 и 0,32 и 0,2 \end{pmatrix}⎝⎛0.490.480.480.350.360.320.160.160.2⎠⎞
(D) : (0.490.350.160.40.440.160.480.320.2)\begin{pmatrix} 0,49 и 0,35 и 0,16\ 0,4 и 0,44 и 0,16\ 0,48 и 0,32 и 0,2 \end{pmatrix}⎝⎛0.490.40.480.350.440.320.160.160.2⎠⎞
(А) (Б) (С) (Д)Показать объяснение
View wiki
Финеас несколько раз подбрасывает честную монету и записывает результаты. Тем не менее, он питает слабость к орлам, поэтому в половине случаев, когда он метит орлы, он метит орлы снова. (Это означает, что он, возможно, мог бы выбрасывать решку много раз подряд, фактически не подбрасывая монету снова.) Результирующая последовательность состояний может быть смоделирована цепью Маркова, где первое возможное состояние (и строка матрицы) — это решка и второе возможное состояние — решка. Какова его матрица перехода?
Тем не менее, он питает слабость к орлам, поэтому в половине случаев, когда он метит орлы, он метит орлы снова. (Это означает, что он, возможно, мог бы выбрасывать решку много раз подряд, фактически не подбрасывая монету снова.) Результирующая последовательность состояний может быть смоделирована цепью Маркова, где первое возможное состояние (и строка матрицы) — это решка и второе возможное состояние — решка. Какова его матрица перехода?
(А) : (12121212)\begin{pmatrix} \tfrac{1}{2} и \tfrac{1}{2} \\ \tfrac{1}{2} и \tfrac{1}{2} \end{pmatrix}(21212121)
(B) : (12121434)\begin{pmatrix} \tfrac{1}{2} и \tfrac{1}{2} \\ \tfrac{1}{4} и \tfrac{3}{4} \end{pmatrix}(21412143)
(C) : (34121412)\begin{pmatrix} \tfrac{3}{4} и \tfrac{1}{2} \\ \tfrac{1}{4} и \tfrac{1}{2} \end{pmatrix}(43412121)
(D) : (34141212)\begin{pmatrix} \tfrac{3}{4} и \tfrac{1}{4} \\ \tfrac{1}{2} и \tfrac{1}{2} \end{pmatrix}(43214121)
(А) (Б) (С) (Д)Показать объяснение
View wiki
Цепь Маркова может быть построена для погоды на основе следующей таблицы.
| Государства | Дождь завтра | Облачно завтра | Солнечный завтра |
| Дождь сегодня | 12 \ TFRAC {1}}}}} 3194977777 37 3777 | 16\tfrac{1}{6}61 | |
| Сегодня облачно | 13\tfrac{1}{3}31 | 13\tfrac{1}{3}31 | 13\ tfrac{1}{3}31 |
| Солнечный день | 000 | 19\tfrac{1}{9}91 | 89\tfrac{8}{9}98 |
Если сегодня идет дождь, какова вероятность того, что через три дня будет дождь?
56243\фрак{56}{243}24356 125486\фрак{125}{486}486125 181648\фракция{181}{648}648181 221972\фракция{221}{972}972221 3111458\фракция{311}{1458}1458311Показать объяснение
View wiki
Если цепь Маркова {X0, X1, … }\{X_0, \, X_1, \, \dots\}{X0,X1,…} имеет переходную матрицу PPP и состояния iii и jjj, тогда каково значение Pi,jP_{i,j}Pi,j?
P(X1=j∣X0=i)\mathbb{P}(X_{1} = j \mid X_0 = i)P(X1=j∣X0=i) P(X1=i∣X0=j)\mathbb{P}(X_{1} = i \mid X_0 = j)P(X1=i∣X0=j) P(X0=j∣X1=i)\mathbb{P}(X_{0} = j \mid X_1 = i)P(X0=j∣X1=i) P(Xi=0∣Xj=1)\mathbb{P}(X_{i} = 0 \mid X_j = 1)P(Xi=0∣Xj=1) 9m\) для фиксированных значений n и m и уникален для преобразования. В этом уроке мы сосредоточимся на том, как именно найти ту матрицу A, называемую стандартной матрицей для преобразования.
В этом уроке мы сосредоточимся на том, как именно найти ту матрицу A, называемую стандартной матрицей для преобразования. реклама
Как найти матрицу линейного преобразования
Чтобы найти эту матрицу, мы должны сначала определить специальный набор векторов из области, называемой стандартным базисом. Большая концепция базиса будет обсуждаться, когда мы будем рассматривать общие векторные пространства. Пока нам просто нужно понять, из каких векторов состоит этот набор. 9m\) имеет столбцы \(T(\vec{e_1})\), \(T(\vec{e_2})\), … , \(T(\vec{e_n})\), где \(\ vec{e_1}\),…,\(\vec{e_n}\) представляет собой стандартный базис. То есть:
\(T(\vec{x}) = A \vec{x} \iff A = \left[T(\vec{e_1})\;\; T(\vec{e_2})\;\; \ cdots \;\; T(\vec{e_n})\right]\)
Следовательно, чтобы найти стандартную матрицу, мы найдем образ каждого стандартного базисного вектора. Это показано в следующем примере.
Пример
Найдите стандартную матрицу преобразования T, где: 93\). Чтобы найти столбцы стандартной матрицы преобразования, нам потребуется найти:
Чтобы найти столбцы стандартной матрицы преобразования, нам потребуется найти:
\(T(\vec{e_1})\), \(T(\vec{e_2})\) и \(T(\vec{e_3})\)
Использование данного правила для T:
\(\begin{align}T(\vec{e_1}) &= T\left(\begin{bmatrix} 1 \\ 0\\ 0\\ \end{bmatrix}\right)\\ &= \begin{ bmatrix} 1 – 0 \\ 2(0)\\ \end{bmatrix}\\ &= \begin{bmatrix} 1 \\ 0\\ \end{bmatrix}\end{align}\)
\(\begin{align}T(\vec{e_2}) &= T\left(\begin{bmatrix} 0 \\ 1\\ 0\\ \end{bmatrix}\right)\\ &= \begin{ bmatrix} 0 – 1 \\ 2(0)\\ \end{bmatrix}\\ &= \begin{bmatrix} -1 \\ 0\\ \end{bmatrix}\end{align}\)
\(\begin{align}T(\vec{e_3}) &= T\left(\begin{bmatrix} 0 \\ 0\\ 1\\ \end{bmatrix}\right)\\ &= \begin{ bmatrix} 0 – 0 \\ 2(1)\\ \end{bmatrix}\\ &= \begin{bmatrix} 0 \\ 2\\ \end{bmatrix}\end{align}\)
Используя их в качестве наших столбцов, стандартная матрица для T:
\(A = \begin{bmatrix} 1 & -1 & 0\\ 0 & 0 & 2\\ \end{bmatrix}\)
Проверка нашего ответа
Мы можем легко проверить, что у нас есть матрица, которая реализует то же отображение, что и T. Если мы правы, то:
Если мы правы, то:
\(T(\vec{x}) = A\vec{x}\)
Итак, проверим! Нам просто нужно убедиться, что когда мы подставляем общий вектор \(\vec{x}\), мы получаем тот же результат, что и при применении правила для T.
\(\begin{align} A\vec{x} &= \begin{bmatrix} 1 & -1 & 0\\ 0 & 0 & 2\\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \ \ x_3 \\ \end{bmatrix}\\ &= x_1\begin{bmatrix}1\\0\\ \end{bmatrix} + x_2\begin{bmatrix}-1\\0\\ \end{bmatrix} + x_3\begin{bmatrix}0\\2\\ \end{bmatrix}\\ &= \begin{bmatrix}x_1 – x_2\\ 2x_3\\ \end{bmatrix}\end{align}\) 9m\), для некоторых \(m\) и \(n\) можно найти матрицу, реализующую отображение. Это означает, что умножение вектора в области определения T на A даст тот же результат, что и применение правила для T непосредственно к элементам вектора. Для любого заданного преобразования существует только одна стандартная матрица, и она находится путем применения матрицы к каждому вектору в стандартном базисе области.
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), чтобы узнавать о новинках!
The Matrix Online и еще 9 громких MMO, о которых вы совершенно забыли
Было время, когда MMO были самой большой дойной коровой в индустрии видеоигр. В течение многих лет World of Warcraft печатала деньги для Blizzard и стала одной из самых успешных когда-либо созданных игр. Вот почему так много компаний бросились пытаться сделать что-то свое, что привело к появлению множества клонов 9.0452 Warcraft и другие забываемые игры.
СВЯЗАННЫЙ: Super Mario Bros. и еще 9 игр, которые ошибочно считаются началом жанра
Некоторые из этих игр были довольно громкими, прежде чем они потеряли актуальность (если не исчезли), Matrix Online является ярким примером. Некоторые из этих игр до сих пор цепляются за жизнь, но многие из них либо выброшены на пастбище, либо почти заброшены компаниями, которые их создали.
10 Матрица никогда не собиралась переходить в игру Ну и Матрица Онлайн является доказательством этого
Слишком сложно воспроизвести бой, который произошел в фильмах «Матрица », и «Матрица онлайн » стала идеальной демонстрацией этого. Ничто не казалось жидким вообще. Бои были излишне сложными, а занятия казались полностью приукрашенными и бессмысленными.
Вся игра представляла собой большой беспорядок, который избавился от своих страданий намного быстрее, чем большинство MMO с такой же шумихой, как Matrix Online был. Он едва продержался четыре года, закрывся менее чем с 500 активными игроками. Даже самые обычные MMO обычно не имеют такой плохой участи.
9 Star Trek Online решили сосредоточиться на боях, а не на том, что сделало франшизу популярной
Так много решений, принятых с Star Trek Online , не имели никакого смысла. Когда человек думает о Star Trek , первое, что приходит на ум, это космические корабли. Вы могли бы подумать, что MMO сосредоточится на этом, имея множество космических сражений и исследований.
Вы могли бы подумать, что MMO сосредоточится на этом, имея множество космических сражений и исследований.
Хотя этого может быть недостаточно для создания суперпопулярной игры, она займет свою нишу, как это сделала EVE Online . Вместо этого они сделали его боевым, и даже не в космосе. Нет, этот бой шел по унылым коридорам. Это настолько глупое решение, что удивительно, как игра все еще работает спустя 11 лет.
8 Wildstar обещал стать мечтой хардкорных рейдеров, но не смог воплотить
Wildstar едва продержался четыре года, как и Matrix Online сделал. Однако, в отличие от Matrix Online, , Wildstar ни в коем случае не была плохой игрой. Жилье в игре было фантастическим и было одним из лучших в любой MMO, не названной Final Fantasy . Эстетически игра была красивой, с чем многие ранние MMO боролись.
СВЯЗАННЫЙ: Zelda и еще 9 игр, в которых люди не могут договориться об их жанре
Проблема заключалась в том, что он был продан хардкорным рейдерам и не дал того, чего они хотели. Рейдам потребовалось слишком много времени, чтобы даже войти в игру, а бои, хотя и были забавными, были катастрофой, чтобы следить за ними.
Рейдам потребовалось слишком много времени, чтобы даже войти в игру, а бои, хотя и были забавными, были катастрофой, чтобы следить за ними.
7 У Теры был инновационный бой с пустой сюжетной линией
Боевая система Tera была значительным шагом вперед по сравнению с наведением на вкладки и статическим геймплеем World of Warcraft и других подобных игр. Игрокам нужно было уделять гораздо больше внимания, активно пытаясь уклоняться от атак, прежде чем они попадут в них. Это сделало игровой процесс более захватывающим и увлекательным. Многие из боев с боссами также казались забавными из-за того, насколько они были большими.
Что мешало ему стать более популярным, так это то, насколько он был гриндовым и что на самом деле не было никакой истории, о которой можно было бы рассказать. Вещи убивали только ради добычи и ничего более.
6 Star Wars Galaxies была идеальной песочницей для фанатов Звездных войн… Сначала
Поклонники Star Wars постарше наверняка с любовью помнят Star Wars Galaxies , но он исчез так давно, что большинство моложе двадцати никогда не слышали об игре. Обидно, ведь это была ММО, не похожая ни на одну другую.
Обидно, ведь это была ММО, не похожая ни на одну другую.
У игрока не было линейного пути, что создавало полное ощущение песочницы. Игроки могли быть кем угодно, даже если это были просто танцоры. Это заставило мир чувствовать себя живым так, как немногие игры могут воспроизвести. К сожалению, к концу срока службы он был испорчен ненужными изменениями.
5 Rift на короткое время почувствовал себя соперником World Of Warcraft, но не смог угнаться за темпами
Когда он впервые вышел, Rift был встречен с большим успехом, и это справедливо. С игрой была связана интересная история, и она предлагала новый метод получения опыта с помощью разломов. Из разломов будут выходить существа, и игроки должны будут активно их закрывать.
СВЯЗАННЫЕ: 10 видеоигр, на которые сильно повлияли фильмы об инопланетянах
Это было свежо по сравнению с обычными квестами, которые засоряют ММО. Это также позволяло плавно переключаться между талантами или душами, позволяя кому-то быть DPS, танком или целителем на одном и том же персонаже одним нажатием кнопки. К сожалению, после горячего старта игра не смогла сохранить свою динамику.
К сожалению, после горячего старта игра не смогла сохранить свою динамику.
4 Age Of Conan был раскручен до забвения, но быстро затонул
Многие люди были невероятно увлечены Age of Conan , игрой, которая предположительно поможет продвинуть жанр MMO вперед. Он не делал ничего из этого, а только давал красивую графику, лишенную какой-либо сути.
Предполагались массовые осады замков и сложные боевые действия. Ничего этого там не было. Бой был небольшим шагом вперед по сравнению с таргетингом на вкладки, но далеко не огромным изменением. С осадами не было связано никакого эпического чувства. Увы, вся игра провалилась из-за того, как много было обещано и недоделано.
3 Город героев был создан не в то десятилетие
City Of Heroes была успешной, когда она вышла в 2004 году, но была бы намного больше, если бы она была выпущена десятью годами позже. Учитывая, насколько сейчас популярны супергерои, возможно, франшиза получит цифры, которые соперничают с 9. 0452 Final Fantasy тянет сегодня.
0452 Final Fantasy тянет сегодня.
Использование сверхспособностей по сравнению с типичным мечом и заклинаниями было глотком свежего воздуха тогда и будет тем более сейчас. Игра также была очень отточена, показывая, что NCSOFT находится на пике своего развития как компания. Если какая-то несуществующая MMO заслуживает второго шанса и может действительно иметь шанс во второй раз, то это определенно City of Heroes .
2 DC Universe Online так и не удалось должным образом извлечь выгоду из бума супергероев
Нет никаких причин, по которым DC Universe не могла быть игрой высшего уровня. Супергерои никогда не были популярны, и все же DC не может извлечь из этого выгоду. В игре нет плавности, она кажется жесткой каждый раз, когда в нее играют.
Когда основной геймплей настолько некачественный, как здесь, не имеет значения, сколько в нем знаменитых героев и злодеев компании. Работа с Бэтменом не имеет такого же очарования, когда игра чувствует себя запертой в капсуле времени, из которой она не планирует выходить. Игра все еще подключается и даже получила порт Nintendo Switch в 2019 году., но он просто никогда не достигает той критической массы, которую имеет что-то вроде FFXIV .
Игра все еще подключается и даже получила порт Nintendo Switch в 2019 году., но он просто никогда не достигает той критической массы, которую имеет что-то вроде FFXIV .
1 Everquest — часть старой гвардии, которая никогда не успевала за временем
Everquest — одна из оригинальных MMO, которая исчезла вдали после того, как World of Warcraft застолбила трон. Многие элементы современных MMO появились благодаря Everquest , например поиск группового инструмента или использование подклассов.
В свое время он тоже был просто великолепен. К сожалению, срок годности этой игры уже давно истек, несмотря на то, что они продолжают выпускать расширения для Everquest 2 . С отменой Everquest Next эту серию нужно отправить на пастбище и осознать свое место в качестве первопроходца, но не текущего игрока.
СЛЕДУЮЩИЙ: Покемоны: каждое поколение в рейтинге их главного соперника
Уравнения Чепмена-Колмогорова | Темы в Вероятность
Стохастические процессы и цепи Маркова представлены в этом предыдущем посте. Вероятности перехода являются неотъемлемой частью теории цепей Маркова. Пост, предшествующий этому, представляет собой начальный взгляд на вероятности перехода. В этом посте показано, как рассчитать вероятность перехода -step. Также обсуждаются и выводятся уравнения Чепмена-Колмогорова.
Вероятности перехода являются неотъемлемой частью теории цепей Маркова. Пост, предшествующий этому, представляет собой начальный взгляд на вероятности перехода. В этом посте показано, как рассчитать вероятность перехода -step. Также обсуждаются и выводятся уравнения Чепмена-Колмогорова.
Вводный пример
Предположим, цепь Маркова с матрицей переходной вероятности . Элементы матрицы представляют собой вероятности одношагового перехода. Число — это вероятность того , что цепь Маркова перейдет в состояние в момент времени при условии , что она находится в состоянии в момент времени , независимо от того , где цепь находилась до момента времени . Таким образом, можно выразить в виде следующей условной вероятности.
Таким образом, будущее состояние зависит только от периода, непосредственно предшествующего ему. Это называется марковским свойством. Также обратите внимание, что это не зависит от периода времени. Любая цепь Маркова с этим свойством называется однородной во времени цепью Маркова или стационарной цепью Маркова.
В этой статье показано, как рассчитать вероятность того, что цепь Маркова перейдет в состояние в момент времени, если она находится в состоянии в момент времени. Эта вероятность обозначается . Другими словами, это вероятность того, что цепь будет в состоянии после того, как цепь Маркова пройдет через большее количество периодов, при условии, что она находится в состоянии в текущем периоде. Вероятность , как условную вероятность, можно записать следующим образом:
В (2) вероятности перехода в -шаге удовлетворяют . Обратите внимание, что когда , для и для . Включение случая для улучшит работу уравнений Чепмена-Колмогорова.
Прежде чем обсуждать общий метод, мы используем примеры, чтобы проиллюстрировать, как вычислить 2-шаговые и 3-шаговые вероятности перехода. Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей.
Вычислить вероятности двухшагового перехода , и . Затем вычислите вероятность трехэтапного перехода, используя вероятности двухэтапного перехода.
Сначала займемся . Мы можем обусловить первые шаги. Чтобы перейти из состояния 0 в состояние 2 за два шага, цепочка должна сначала перейти в промежуточное состояние, а затем из этого состояния перейти в состояние 2.
Обратите внимание, что приведенный выше расчет перечисляет три возможных пути перехода из состояния 0 в состояние 2 в два этапа — из состояния 0 в состояние 0 и затем из состояния 0 в состояние 2, из состояния 0 в состояние 1 и затем из состояния 1 в состояние 2 и из состояния 0 в состояние 2, а затем из состояния 2 в состояние 2. При более внимательном рассмотрении вычисления приведенное выше вычисление в основном представляет собой первую строку (строку, соответствующую состоянию 0), умноженную на третий столбец ( столбец, соответствующий состоянию 2).
Следуя той же идее, ниже приведены вероятности двух других двухшаговых переходов.
Как обсуждалось, приведенные выше два вычисления можно рассматривать как сумму всех возможных путей перехода из начального состояния в конечное (с учетом промежуточного состояния в середине) или как строку в вероятности перехода, умножающую столбец в . Ниже показаны все три расчета с точки зрения матричного расчета.
Ниже показаны все три расчета с точки зрения матричного расчета.
Представление о вычислении матриц будет иметь решающее значение для понимания уравнений Чпана-Колмогорова, обсуждаемых ниже. В заключение примера рассмотрим вероятность трехступенчатого перехода. Мы также можем обусловить первый шаг. Цепочка переходит от состояния 0 к следующему шагу (3 возможности), а затем переходит от этого состояния к состоянию 2 за два шага.
Пример показывает, что вычисление вероятности 3-этапного перехода основано на 2-этапных вероятностях. Таким образом, вероятности перехода большей длины могут быть построены из вероятностей перехода меньшей длины. Тем не менее, стоит сосредоточиться на более общей структуре, прежде чем выполнять дополнительные расчеты. Продемонстрированный выше вид вычисления матрицы поможет понять общую структуру.
Уравнения Чепмена-Колмогорова
Примеры показывают, что нахождение вероятностей перехода -шаг включает матричный расчет. Позвольте быть матрицей вероятности перехода шага. Теперь цель состоит в том, чтобы иметь систематический способ вычисления элементов в матрице. Расчет основан на уравнениях Чепмена-Колмогорова. Вот эти уравнения:
Позвольте быть матрицей вероятности перехода шага. Теперь цель состоит в том, чтобы иметь систематический способ вычисления элементов в матрице. Расчет основан на уравнениях Чепмена-Колмогорова. Вот эти уравнения:
для и для всех . Для цепи Маркова с конечным числом состояний суммирование в (3) не стремится к бесконечности и имело бы верхний предел. Число — это вероятность того, что цепочка будет находиться в состоянии после выполнения шагов, если она находится в состоянии в настоящее время. Ниже приводится вывод (3).
Вот идея вывода. Путь от состояния к состоянию по шагам можно разбить на два пути: один от состояния к промежуточному состоянию при первых переходах, а другой от состояния к состоянию при остальных переходах. Суммирование всех промежуточных состояний дает вероятность того, что процесс будет переходить из состояния в состояние при переходах.
Записи в матрице могут быть вычислены с помощью (3). Есть интересная полезная интерпретация (3). Ниже приводится другой способ формулировки уравнений Чепмена-Колмогорова:
Ниже приводится другой способ формулировки уравнений Чепмена-Колмогорова:
- .
Типичным элементом матрицы является и типичным элементом матрицы является . Обратите внимание, что при изменении — это строка в (строка, соответствующая состоянию), а при изменении — столбец в (столбец, соответствующий состоянию).
Произведение вышеуказанной строки и столбца есть вероятность перехода.
Степени матрицы вероятности одношагового перехода
Пусть — матрица вероятности одношагового перехода цепи Маркова. Пусть — матрица вероятности перехода -шаг, которую можно вычислить с помощью уравнений Чепмена-Колмогорова. Теперь выведем еще один важный факт.
Матрица вероятности одношагового перехода получается путем умножения матрицы вероятности одношагового перехода на саму себя раз, т.е. является й степенью .
Этот факт важен с точки зрения расчета переходных вероятностей. Вычислите , степень (в терминах матричных вычислений). Затем это просто запись в (в строке, соответствующей состоянию, и в столбце, соответствующем состоянию). Если размер матрицы велик и/или велик, умножение матриц можно выполнить с помощью программного обеспечения или с помощью онлайн-калькулятора матриц (вот один калькулятор матриц).
Затем это просто запись в (в строке, соответствующей состоянию, и в столбце, соответствующем состоянию). Если размер матрицы велик и/или велик, умножение матриц можно выполнить с помощью программного обеспечения или с помощью онлайн-калькулятора матриц (вот один калькулятор матриц).
Конечно, указанный выше факт важен и для теории цепей Маркова в целом. Почти все математические свойства цепей Маркова основаны на этом основном факте.
Мы можем установить этот основной факт, используя аргумент индукции. Четко . Предположим, что этот факт верен для . На основании (4), . Продолжаем вывод: .
Вектор-строка и вектор-столбец
Как было продемонстрировано в предыдущем разделе, , степень , является матрицей вероятностей ступенчатого перехода. Рассмотрим матрицу более внимательно. Предположим, что цепь Маркова имеет пространство состояний . Ниже показана матрица с особым вниманием к общей строке и общему столбцу.
Теперь посмотрите на строку, соответствующую состоянию, и вызовите ее. Также посмотрите на столбец, соответствующий состоянию, и назовите его. Они отделены от матрицы ниже.
Также посмотрите на столбец, соответствующий состоянию, и назовите его. Они отделены от матрицы ниже.
Вектор-строка является условным распределением. Он дает вероятности перехода процесса (после переходов) в одно из состояний при условии, что процесс начинается в состоянии . Если достоверно, что процесс начинается в состоянии , то дает функцию вероятности для случайной величины, поскольку .
С другой стороны, если начальное состояние не определено, то вектор-столбец дает вероятности перехода процесса (после переходов) в состояние из любого из возможных начальных состояний. Таким образом, столбец матрицы дает вероятность нахождения процесса в данном состоянии в й период из всех возможных начальных состояний. Ниже приводится распределение вероятностей для (состояние цепи Маркова в момент времени).
Расчет в (5) можно рассматривать как матричный расчет. Если мы поместим вероятности в вектор-строку, то произведение этого вектора-строки на вектор-столбец будет равно . Следующее (5) в матричном умножении.
Следующее (5) в матричном умножении.
Дополнительные комментарии к Чепмену-Колмогорову
Несмотря на то, что расчет матрицы для должен выполняться с помощью программного обеспечения, полезно понимать ориентацию матрицы. В предыдущем разделе мы узнали, что ряд — это условное распределение (состояние процесса в момент времени при заданном начальном состоянии). В предыдущем разделе мы также узнали, что столбец в матрице дает вероятности того, что процесс попадет в фиксированное состояние из любого из начальных состояний.
Уравнения Чепмена-Колмогорова в (3) говорят нам, что запись в матрице — это просто произведение строки и столбца в . Это наблюдение позволяет сосредоточиться только на вероятности перехода, которая задается в данной задаче, а не на вычислении всей матрицы. Например, чтобы вычислить элемент матрицы , умножьте строку (строку, соответствующую состоянию) и столбец (строку, соответствующую состоянию). Нет необходимости вычислять всю матрицу, если целью является только одна запись .
Нет необходимости вычислять всю матрицу, если целью является только одна запись .
Чтобы вычислить запись , существует значительное количество вариаций в подходах к умножению. Например, несколько строк и столбцов или несколько строк и столбцов . Или несколько строк и столбцов .
Если строка вероятностей перехода умножается на матрицу перехода, результатом является строка в матрице вероятности перехода с более высоким значением. Например, если строка в умножает матрицу , результатом будет строка в . Более конкретно, первая строка при умножении матрицы дает первую строку . Первая строка умножения матрицы дает первую строку в и т. д.
С другой стороны, когда матрица вероятности перехода умножает столбец вероятностей перехода, результатом является столбец в матрице вероятности перехода с более высоким значением. Например, матрица умножает столбец в , результатом является столбец в . Более конкретно, когда матрица умножает первый столбец матрицы , результатом является первый столбец матрицы . Когда матрица умножает столбец в матрице, результатом является первый столбец в и т. д.
Когда матрица умножает столбец в матрице, результатом является первый столбец в и т. д.
Примеры
Теперь мы приведем несколько примеров того, как рассчитать вероятность перехода.
Пример 1
Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей.
Определить и .
Конечно, проще всего вычислить . Тогда будет (0,1)-я запись и будет (0,1)-я запись . На самом деле, для этой задачи рекомендуется использовать онлайн-калькулятор матриц. При этом получаются следующие браки.
Из матрицы мы видим, что и . Обратите внимание, что вычисляется во вводном примере ранее.
Пример 2
Для матрицы перехода в Примере 1 используйте идеи, обсуждавшиеся в разделе Дополнительные комментарии к Чепмену-Колмогорову , чтобы вычислить первую строку и первый столбец в матрице перехода.
Как обсуждалось ранее, первая строка получается путем умножения первой строки на матрицу .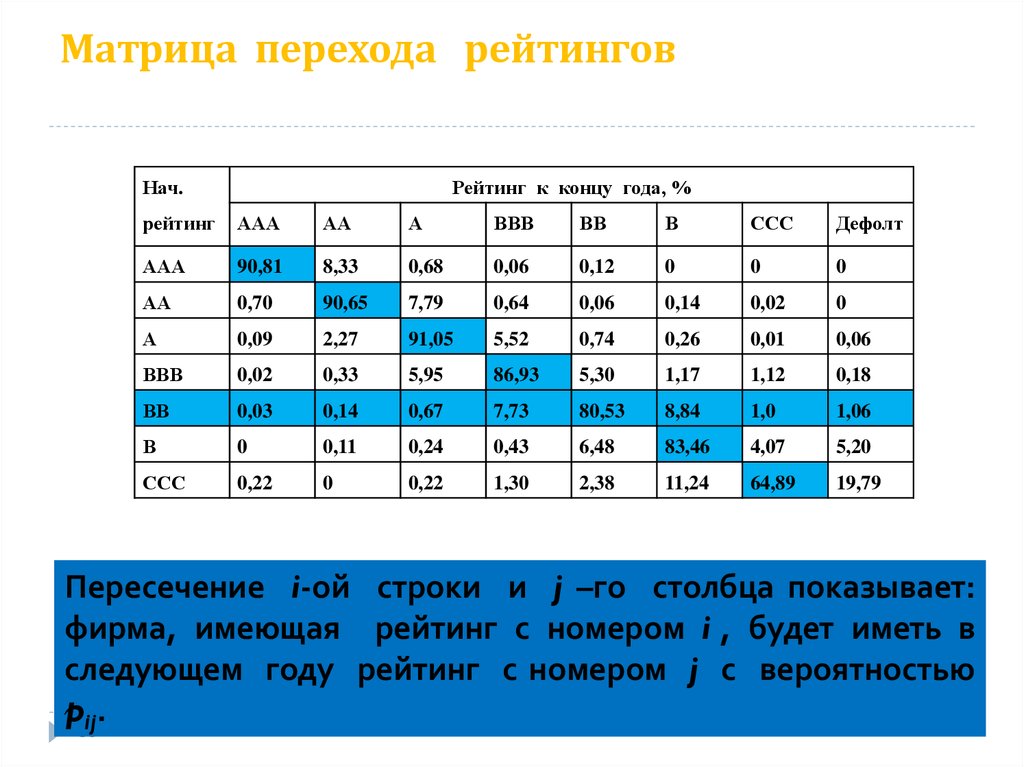 Первый столбец получается умножением матрицы на первый столбец матрицы .
Первый столбец получается умножением матрицы на первый столбец матрицы .
Пример 3
Частица перемещается между состояниями 0, 1 и 2 в соответствии с марковским процессом со следующей матрицей вероятности перехода.
Пусть — положение частицы после го хода. Предположим, что вначале частица находится в состоянии 1. Определить вероятность при .
Поскольку начальное состояние процесса определено, . Таким образом, проблема состоит в том, чтобы найти вторую строку .
Пример 4
Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей.
Предположим, что изначально процесс с одинаковой вероятностью может находиться в состоянии 0 или в состоянии 1. Определить и .
Чтобы найти , нам нужен первый столбец . Чтобы найти , нам нужен второй столбец . С помощью онлайн-калькулятора получается .
Следующие расчеты дают ответы.
Пример 5
Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей.
В момент времени 0 марковский процесс находится в состоянии 0. Пусть . Обратите внимание, что состояние 2 называется поглощающим состоянием. Процесс Маркова в конце концов достигнет состояния 2 и будет поглощен им (он остается в нем навсегда всякий раз, когда процесс достигает состояния 2). Таков первый период времени, за который процесс достигает состояния 2. Предположим, что наблюдается марковский процесс и поглощение не произошло. Тогда нас будет интересовать эта условная вероятность: вероятность того, что процесс находится в состоянии 0 или в состоянии 1 при условии, что процесс не был поглощен. Определять .
Ключевая идея здесь в том, что событие должно произойти, или . Таким образом,
- .
Обратите внимание, что, поскольку начальным состоянием обязательно будет состояние 0, и . Использование онлайн-калькулятора дает следующую матрицу.
Следующее дает желаемый результат.
Таким образом, если поглощение не произошло в 4-м периоде, процесс находится в состоянии 0 около 71% времени.
Пример 6
Продолжить с цепью Маркова из примера 5. Определить .
Обратите внимание, что . Вероятность уже определяется с помощью . Для определения нам нужна верхняя строка .
Итак. Таким образом . Таким образом, примерно в 12% случаев абсорбция происходит в 4-м периоде примерно в 12% случаев.
Упражнения
Мы даем несколько практических задач, чтобы закрепить концепции и вычисления, обсуждаемые здесь. Дальнейшие практические задачи — в сопутствующем блоге (здесь и здесь).
Упражнение 1
Рассмотрим цепь Маркова со следующей матрицей переходных вероятностей.
Определите эти условные вероятности.
Упражнение 2
Частица перемещается между состояниями 1, 2 и 3 в соответствии с марковским процессом со следующей матрицей переходных вероятностей.

 Все правила по сольфеджио
Все правила по сольфеджио
 Таким образом, матрицей перехода может служить любая квадратная матрица порядка
Таким образом, матрицей перехода может служить любая квадратная матрица порядка 
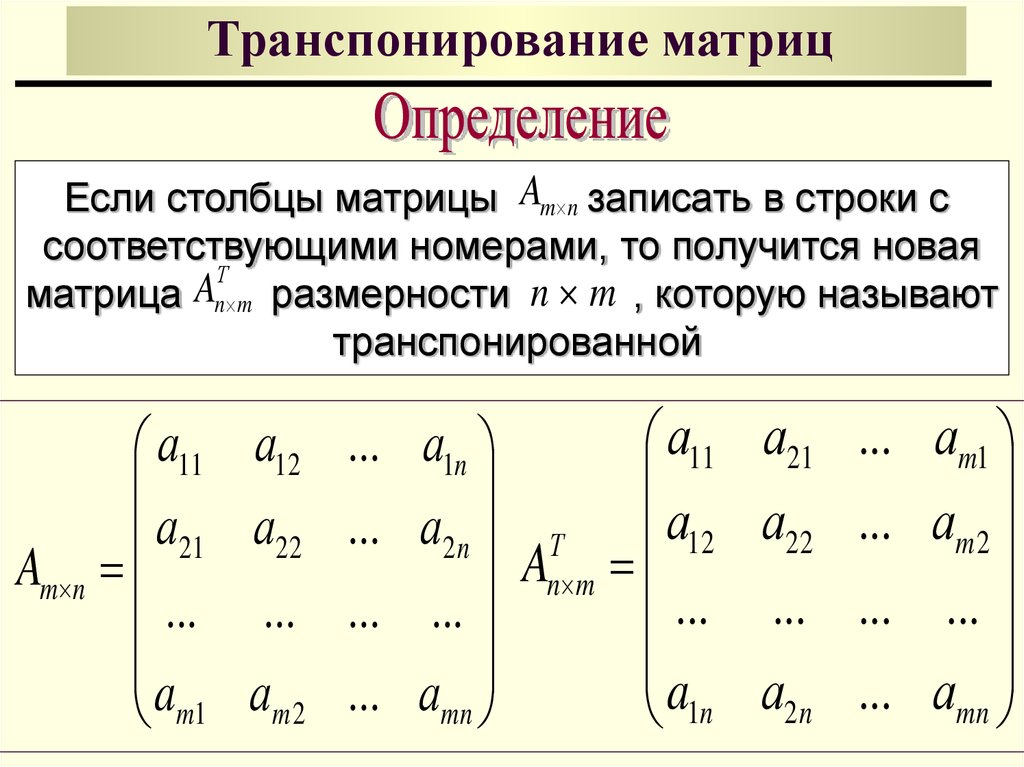



 АН СССР. Техн. кибернет., 1983, №2, с. 94-102]. Поскольку аппроксимация прямоугольными параллелепипедами является основой алгоритма последовательного визуального решения задач математического программирования рассмотрим этот вопрос подробнее.
АН СССР. Техн. кибернет., 1983, №2, с. 94-102]. Поскольку аппроксимация прямоугольными параллелепипедами является основой алгоритма последовательного визуального решения задач математического программирования рассмотрим этот вопрос подробнее.
 Тогда применяютовражный метод минимизации с помощью метода Гаусса-Зайделя (метод минимизации при наличии оврагов)
Тогда применяютовражный метод минимизации с помощью метода Гаусса-Зайделя (метод минимизации при наличии оврагов) 6).
6). Однако при разумном выборе можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при для рассматриваемого примера имеем .
Однако при разумном выборе можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при для рассматриваемого примера имеем .
 ..
.. Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и sx и sy единиц в старой координатной системе соответственно.
Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и sx и sy единиц в старой координатной системе соответственно.