Длина хорды: основные понятия
Бывают случаи в жизни, когда знания, полученные во время школьного обучения, очень полезны. Хотя во время учебы эти сведения казались скучными и ненужными. Например, как можно использовать информацию о том, как находится длина хорды? Можно предположить, что для специальностей, не связанных с точными науками, такие знания малопригодны. Однако можно привести много примеров (от конструирования новогоднего костюма до сложного устройства аэроплана), когда навыки решения задач по геометрии являются нелишними.
Понятие «хорда»
Данное слово означает «струна» в переводе с языка родины Гомера. Оно было введено математиками древнего периода.
Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.
В случае окружности длина хорды заключена между двумя точками этой фигуры.
Часть плоскости, ограниченная прямой, пересекающей окружность, и ее дугой называют сегментом. Можно отметить, что с приближением к центру длина хорды увеличивается. Часть окружности, находящуюся между двумя точками пересечения данной прямой, называют дугой. Ее мерой измерения является центральный угол. Вершина данной геометрической фигуры находится в середине круга, а стороны упираются в точки пересечения хорды с окружностью.
Свойства и формулы
Длина хорды окружности может быть вычислена по следующим условным выражениям:
L =D×Sinβ или L=D×Sin(1/2α), где β – угол при вершине вписанного треугольника;
D – диаметр окружности;
α – центральный угол.
Можно выделить некоторые свойства данного отрезка, а также других фигур, связанных с ним. Эти моменты приведены в следующем списке:
- Любые хорды, находящиеся на одинаковом расстоянии от центра, имеют равные длины, при этом обратное утверждение также верно.

- Все углы, которые вписаны в окружность и опираются на общий отрезок, который объединяет две точки (при этом их вершины находятся в одной стороне от данного элемента), являются идентичными по величине.
- Самая большая хорда является диаметром.
- Сумма любых двух углов, если они опираются на данный отрезок, но при этом их вершины лежат в разных сторонах относительно него, составляет 180о.
- Большая хорда — по сравнению с аналогичным, но меньшим элементом — лежит ближе к середине данной геометрической фигуры.
- Все углы, которые вписаны и опираются на диаметр, равны 90˚.
Другие вычисления
Чтобы найти длину дуги окружности, которая заключена между концами хорды, можно использовать формулу Гюйгенса. Для этого необходимо провести такие действия:
- Обозначим искомую величину р, а хорда, ограничивающая данную часть окружности, будет иметь название АВ.
- Найдем середину отрезка АВ и к ней поставим перпендикуляр. Можно отметить, что диаметр окружности, проведенный через центр хорды, образует с ней прямой угол.
 Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М.
Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М. - Тогда отрезки АМ и ВМ можно назвать соответственно, как l и L.
- Длина дуги может быть вычислена по следующей формуле: р≈2l+1/3(2l-L). Можно отметить, что относительная погрешность данного выражения при возрастании угла увеличивается. Так, при 60˚ она составляет 0,5%, а для дуги, равной 45˚, эта величина уменьшается до 0,02%.
Длина хорды может использоваться в различных сферах. Например, при расчетах и конструировании фланцевых соединений, которые широко распространены в технике. Также можно увидеть вычисление этой величины в баллистике для определения расстояния полета пули и так далее.
Длина окружности основания. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса.
 Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой . {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника
. {\circ}
{\circ}Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415
.
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \) – диаметр.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
В декартовой системе координат \(xOy \)
мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой \(X \)
, которая будет иметь координаты \((x_0,y_0) \)
. Пусть радиус этой окружности равняется \(τ \)
. Возьмем произвольную точку \(Y \)
, координаты которой обозначим через \((x,y) \)
(рис.
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52
дм.
(π
≈ 3,14
).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Хорда окружности
- Хорда (c), также называемая длинной хордой (LC), находится между любыми двумя точками на окружности.
- Угол (\(\Delta\)) – два луча, имеющие общую точку.
- Обратная касательная (BT) — линия касательной перед началом кривой.
- Center (rp) — Все точки на окружности линии находятся на равном расстоянии от центральной точки.
- Окружность — все точки находятся на фиксированном одинаковом расстоянии от точки радиуса (rp).
- Окружность (C) — внешняя часть круга или полная дуга окружности.
- Угол отклонения (D\(\Delta\)) — Угол отклонения от полной круговой кривой, измеренный от касательной в PC или PT.
 Углы между касательной и концами хорд из ПК.
Углы между касательной и концами хорд из ПК. - Внешнее расстояние (E) — радиальное расстояние от точки отсчета до средней точки на простой круговой кривой.
- Касательная вперед (FT) — линия касательной после окончания кривой.
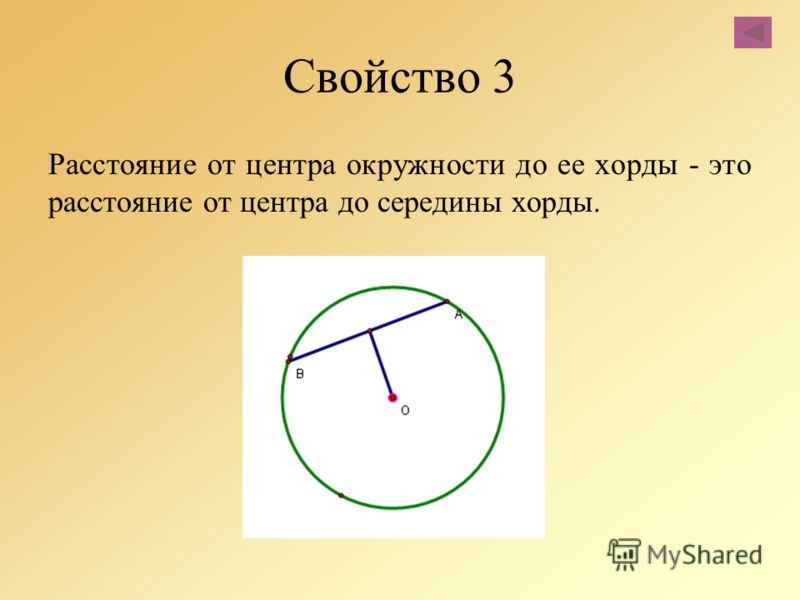
- Высота (h) — длина радиуса от центра радиуса до середины хорды.
- Высота (h’) – Длина радиуса от середины хорды до точки на окружности.
- Длина (L) — общая длина любой круговой кривой, измеренная вдоль дуги.
- Середина (M) — центр или середина сегмента линии.
- Средняя ордината (м) — расстояние от середины кривой до середины длинной хорды.
- Точка кривизны (ПК) — точка, в которой прямая линия начинает изгибаться, точка касания кривой
- Точка пересечения (ТП) — пересечение двух точек касания или пересечение двух непараллельных прямых.
- Точка касания (PT) — точка, в которой заканчивается кривая и начинается точка касания кривой.
- Радиус (r) — половина диаметра окружности.

- Радиусная точка (rp) — центральная точка радиуса круглой кривой.
- Касательная (T) — линия, которая касается кривой только в одной точке, так что она перпендикулярна линии радиуса кривой.
Длина дуги (l) – это общая длина любой круговой кривой, измеренная вдоль дуги, начиная с кривой PC (точка на кривой) до конца дуги PT (точка на касательной).
Длина дуги хорды Формулы | ||
\(\large{L = \Delta\; r}\) \(\large{ L = \frac{ r \; \Delta \; \pi }{ 180 } }\) \(\large{ L = \frac {\Delta} { 180 } \; 2 \; \pi \; r }\) | ||
| Символ | Английский | Метрическая система |
| \(\large{L}\) = длина | \(\большой{в}\) | \(\большой{мм }\) |
| \(\large{\Delta}\) = угол | \(\большой{градус}\) | \(\большой{рад}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3,141 592 653 . ..}\) ..}\) | |
| \(\большой{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
Длина хорды (c), также называемая длинной хордой (LC), представляет собой прямую линию от начала кривой PC (точка на кривой) до конца дуги PT (точка на касательной).
Длина хорды Формулы | ||
\(\large{ c = 2 \; r \; \sin \; \frac {\Delta}{2} }\) 92} }\) | ||
| Символ | Английский | Метрическая система |
| \(\большой{с}\) = хорда | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{h}\) = расстояние от центра хордовой окружности до середины | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{\Delta}\) = угол 92 }{ 4 } } }\) | ||
| Символ | Английский | Метрическая система |
| \(\large{h}\) = расстояние от центра хордовой окружности до середины | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{r}\) = радиус окружности | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{L}\) = длина | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{h’}\) = высота сегмента | \(\большой{в}\) | \(\большой{мм}\) |
Длина радиуса от середины хорды до точки на круговой кривой в сегменте.
от середины хорды до середины дуги Формула | ||
\(\большой{ ч’ = г — ч }\) \(\large{ h’ = r \; \left( 1 — cos \; \frac{ \Delta}{ 2 } \right) }\) | ||
| Символ | Английский | Метрическая система |
| \(\large{h’}\) = высота сегмента | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{\Delta}\) = угол | \(\большой{градус}\) | \(\большой{рад}\) |
| \(\large{h}\) = расстояние от центра хордовой окружности до середины | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{r}\) = радиус окружности | \(\большой{в}\) | \(\большой{мм}\) |
Радиальное расстояние (E) от точки пересечения (PI) до середины на круговой кривой.
Внешнее расстояние до дуги Формулы | ||
| \(\large{ E = T \; tan \frac{ \Delta }{ 4 } }\) | ||
| Символ | Английский | Метрическая система |
| \(\large{E}\) = внешнее расстояние | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{\Delta}\) = угол | \(\большой{градус}\) | \(\большой{рад}\) |
| \(\large{T}\) = длина касательной | \(\большой{в}\) | \(\большой{мм}\) |
ОТНОШЕНИЕ ДУГИ К ХОРДЕ
ОТНОШЕНИЕ ДУГИ К ХОРДАМ Отношение дуги к хорде
_____________________________
Вы, наверное, хорошо знакомы с формулой для определения длины окружности: Если бы мы хотели определить длину части окружности (известной как дуга ), то формула была бы следующей: Если мы проведем прямую линию из точки А в точку В (то, что известно как хорда ), тогда формула для длины хорды: Теперь предположим, что радиус окружности равен 100, тогда мы можем вычислить длины дуги и хорды как: Разделив длину дуги на длину хорды, мы получим отношение дуги к хорде , что в данном случае равно 1,1107207345.  Всякий раз, когда у нас есть окружность, центральный угол которой равен 90 °, она всегда будет опираться на дугу и хорду, соотношение которых всегда будет равным 1,1107207345. Для всех остальных центральных углов мы рассчитали это отношение от 1 до 180 градусов. Если вам просто нужно приблизительное представление о том, каково отношение дуги к хорде для определенного центрального угла, то эти таблицы подойдут. Однако, если вам нужен точный , затем воспользуйтесь калькулятором, расположенным здесь, и выберите пункт меню «Chord AB & Arc AB». |
ARC ÷ Угол соотношения хорды
| Дуга ÷ Хорда Соотношение Угол
| Arc ÷ Chord Ratio Angle
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

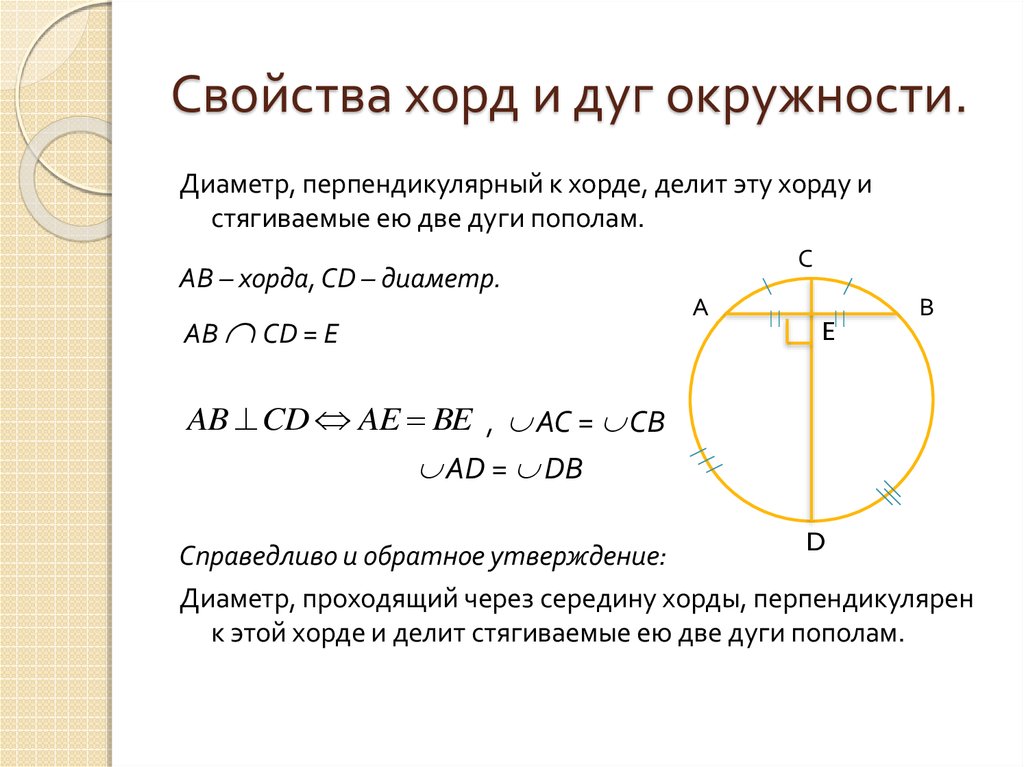
 Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М.
Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4. Углы между касательной и концами хорд из ПК.
Углы между касательной и концами хорд из ПК.
 0000507714
0000507714  0021482395
0021482395  0073484055
0073484055  01571
01571 0273707383
0273707383  0424598231
0424598231  0575052762
0575052762  0794152016
0794152016  1055000609
1055000609 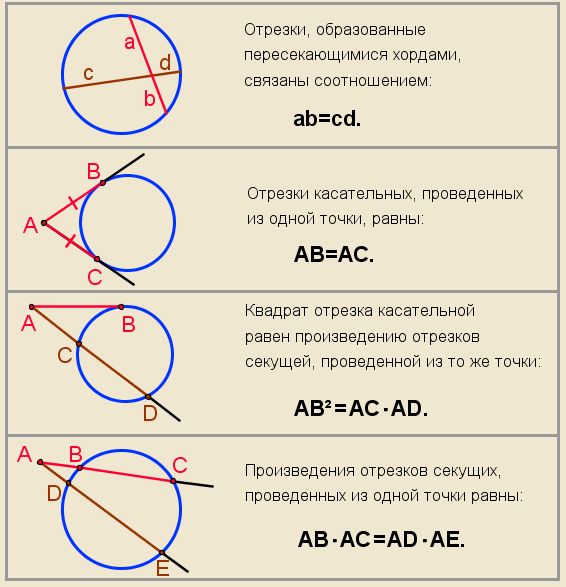 1361536059
1361536059 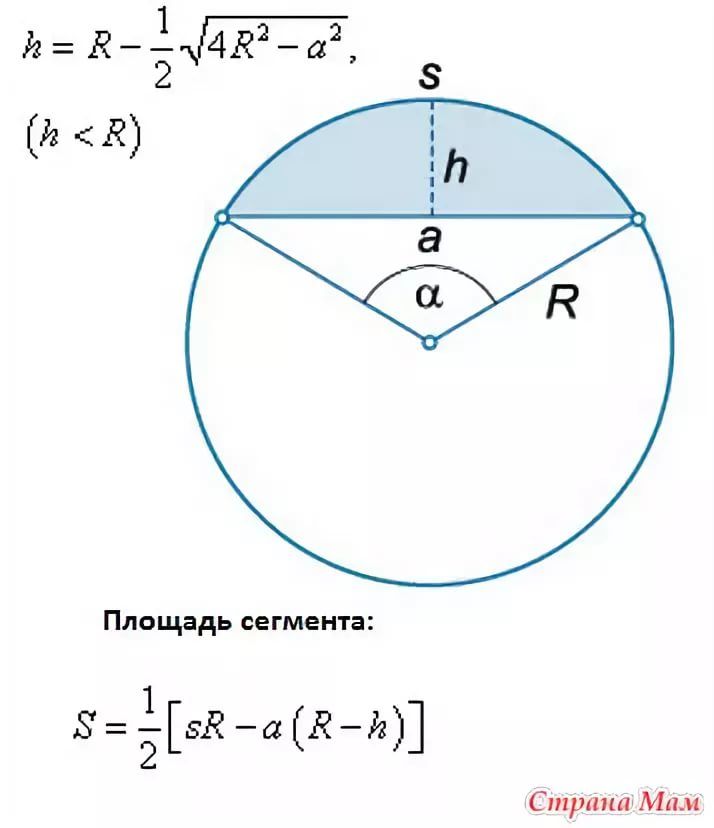 1718594799
1718594799  2132099582
2132099582  2609304733
2609304733  315
315 3792537072
3792537072  4523214442
4523214442 