Формула исправленная дисперсия: Дисперсия: генеральная, выборочная, исправленная

Исправленная выборочная дисперсия : Вероятность, статистика

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

ivanmixmix	Исправленная выборочная дисперсия 06. 03.2014, 13:51
06/03/14 5	Добрый день, Пожалуйста, помогите разобраться: 1. Чем отличается исправленная статистическая выборочная дисперсия от классической дисперсии (какова ее суть)? 2. Почему она именно , нафига нужен этот коэффициент? — я понимаю, что он для того, чтобы оценка была несмещенной, но не понимаю почему: 2.1 Почему она смещенная без него? Ведь по определению, несмещенность характеризуется 2.2 Как этот коэффициент решает проблему смещенности? Заранее спасибо

Евгений Машеров	Re: Исправленная выборочная дисперсия 06. 03.2014, 14:22
Заслуженный участник 11/03/08 8654 Москва	1. Ничем. Просто это оценка параметра дисперсии. Выборочная оценка. Одна из многих (и даже многих оптимальных, поскольку много критериев оптимальности) выборочных оценок. 2. Дисперсия есть матожидание квадрата отклонения от матожидания. Матожидание нам неизвестно, мы можем располагать лишь его оценками. Если нам кто-то принесёт истинное значение матожидания (скажем, есть физические основания считать, что оно ноль) — нам поправки не понадобится. То есть возводим отклонения в квадрат, усредняем — вуаля, дисперсия! Однако это редкое везение, обычно мы используем оценку матожидания, которую и подставляем в формулу для дисперсии. В качестве таковой оценки как традиция, так и множество критериев оптимальности нам предлагают среднее арифметическое. Чем обычно и пользуются. Однако выборочное среднее отклоняется от истинного матожидания, что приводит к снижению суммы квадратов. Это можно увидеть, просто выписав выражение для суммы квадратов отклонений. Принимая без потери общности, что истинное матожидание равно нулю, и обозначая выборочное среднее, получим Вот занижение, вызванное последним слагаемым, и компенсирует этот коэффициент. Численный пример: Выборка с истинным нулевым матожиданием (-2; -1; 1; 6), для которой сумма квадратов отклонений от матожидания должна составить 4+1+1+36=42, при вычислении отклонений от среднего по выборке, равного 1, составит 9+4+0+25=38

Александрович	Re: Исправленная выборочная дисперсия 06. 03.2014, 14:36
21/01/09 3904 Дивногорск	ivanmixmix в сообщении #833365 писал(а): 2.1 Почему она смещенная без него? Ведь по определению, несмещенность характеризуется Выборочная оценка генеральной дисперсии смещена влево из-за того что для её нахождении используется выборочное среднее, а не матожидание. Поэтому . Поправка Бесселя устраняет это смещение, поэтому матожидание исправленной оценки равняется генеральной дисперсии.

ivanmixmix	Re: Исправленная выборочная дисперсия 06.03.2014, 15:23
06/03/14 5	Евгений Машеров, Александрович, большое спасибо за ответы! Удивительно, почему про поправку Бесселя так мало написано в рунете. В американской вики все есть: http://en.wikipedia.org/wiki/Bessel’s_correction

Александрович	Re: Исправленная выборочная дисперсия 06.03.2014, 15:39
21/01/09 3904 Дивногорск	Евгений Машеров в сообщении #833379 писал(а): Численный пример: Выборка с истинным нулевым матожиданием (-2; -1; 1; 6), для которой сумма квадратов отклонений от матожидания должна составить 4+1+1+36=42, при вычислении отклонений от среднего по выборке, равного 1, составит 9+4+0+25=38 Стоит отметить что не каждая выборка обязательно даст заниженную дисперсию, встречаются что и завышенную.

ewert	Re: Исправленная выборочная дисперсия 06.03.2014, 15:48
Заслуженный участник 11/05/08 32154	ivanmixmix в сообщении #833399 писал(а): Удивительно, почему про поправку Бесселя так мало написано в рунете. О ней написано везде . Вот первая же ссылка из Яндекса по запросу «выборочная дисперсия»: http://ru.wikipedia.org/wiki/%C2%FB%E1%EE%F0%EE%F7%ED%E0%FF_%E4%E8%F1%EF%E5%F0%F1%E8%FF Цитата: Выборочная дисперсия — это случайная величина где символ обозначает выборочное среднее. Несмещённая (исправленная) дисперсия — это случайная величина

ivanmixmix	Re: Исправленная выборочная дисперсия 06.03.2014, 15:58
06/03/14 5	ewert, я имел в виду обоснование. Определение, слава Богу, найти можно.

Otta	Re: Исправленная выборочная дисперсия 06.03.2014, 15:58
Заслуженный участник 09/05/13 18/06/23 8903	ivanmixmix в сообщении #833365 писал(а): Почему она смещенная без него? Ведь по определению, несмещенность характеризуется Именно по определению она и смещенная. Матожидание выборочной дисперсии . Понятно, на что нужно домножить смещенную оценку дисперсии, чтобы получилась несмещенная. Отсюда и коэффициент.

ewert	Re: Исправленная выборочная дисперсия 06.03.2014, 15:59
Заслуженный участник 11/05/08 32154	ivanmixmix в сообщении #833412 писал(а): ewert, я имел в виду обоснование. А оно написано в любом учебнике.

ivanmixmix	Re: Исправленная выборочная дисперсия 06.03.2014, 16:06
06/03/14 5	ewert , значит не в любом, если у меня возник такой вопрос. При всем уважении, Вы не внесли в тему ничего полезного. К чему Ваши реплики? Otta, спасибо!

ewert	Re: Исправленная выборочная дисперсия 06.03.2014, 16:31
Заслуженный участник 11/05/08 32154	ivanmixmix в сообщении #833422 писал(а): Вы не внесли в тему ничего полезного. К чему Ваши реплики? К тому, чтобы Вы оставили мысль учиться по Викам и вообще по интернету. Не хочется открывать книжку (хотя бы в электронном варианте) — ищите в интернете какой-нибудь сайт с курсом по ТВ (они есть). Но именно с курсом, а не какие-то обрывочные сведения; просто потому, что и представление о предмете у Вас сложится в лучшем случае обрывочное и бессвязное — ведь разные авторы используют разную терминологию и разные подходы. Случай с термином «поправка Бесселя» — прекрасный тому пример: большинство его не употребляют попросту за ненадобностью. И даже в этой ветке: сильно сомневаюсь, что Вы поняли то объяснение, которое пытался донести до Вас Евгений Машеров . Поскольку до конца он сильно не договорил, а намёков Вам (судя по постановке вопросов) явно недостаточно.

ivanmixmix	Re: Исправленная выборочная дисперсия 06. 03.2014, 16:47
06/03/14 5	ewert Передо мной сейчас лежат два учебника, бумажные. Не могу ручаться за их качество — какие есть. Поверьте, я не ткнул пальцем в тему «Исправленная выборочная дисперсия» и, не поняв вне контекста формулу, вбил сюда вопрос. То, что говорил Евгений Машеров есть по той ссылке в Вики, которую я написал выше, где все расписано. Я без сарказма рад, что Вы заботитесь о вопросе образования. Однако предлагаю закрыть этот вопрос.

—mS—	Re: Исправленная выборочная дисперсия 06. 03.2014, 19:31
Заслуженный участник 23/11/06 4171	ivanmixmix в сообщении #833438 писал(а): ewert Передо мной сейчас лежат два учебника, бумажные. Не могу ручаться за их качество — какие есть. И что это за учебники? Объяснение искомого факта есть даже в учебнике Гмурмана.

Евгений Машеров	Re: Исправленная выборочная дисперсия 07. 03.2014, 07:40
Заслуженный участник 11/03/08 8654 Москва	Кстати, да. В каком учебнике этого нет? Единственное, что мне приходит в голову — это не учебник по матстатистике. А какой-нибудь специальный, в котором расчёт дисперсии приводится «рецептурно».

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 14 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

29.

Генеральная и выборочная дисперсия. Исправленная дисперсия. Стандарт.

Генеральная дисперсия.Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

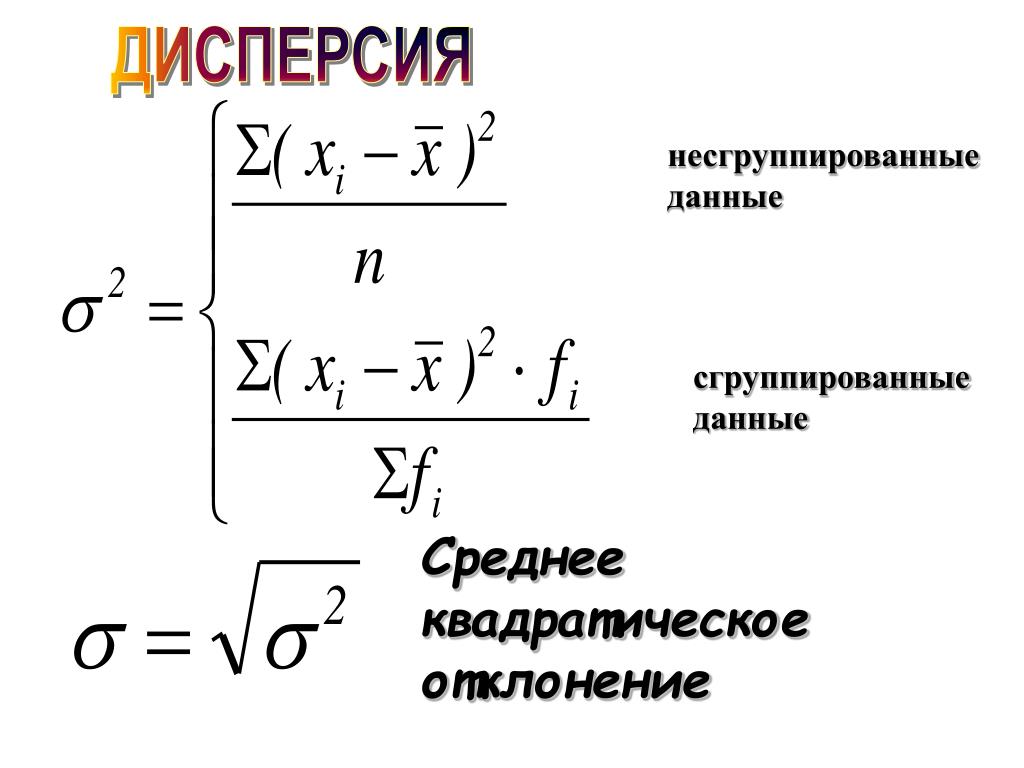
Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения. Если все значения признака генеральной совокупности объема N различны, то

Dг= ()/N.

Если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

Dг= ()/N.

Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: Ϭг = √Dг. 2.

Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.

Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее.

Таким образом, положительное число d характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки называют вероятность g, с которой осуществляется неравенство |Q—Q* | <d .

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| <d равна g: P(|Q- Q*| <d)= g.

Заменив неравенство равносильным ему двойным неравенством получим: Р [Q* —d< Q < Q* +d] = g

Это соотношение следует понимать так: вероятность того, что интервал Q* — d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.

Интервал (Q* — d Q* +d) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью g.

Скорректированная выборочная дисперсия

Марко Табога, доктор философии

Скорректированная дисперсия выборки — это мера дисперсии выборки вокруг Это подло.

Его получают:

1. суммирование квадратов отклонений от среднего;

2. деление полученного таким образом результата на число наблюдений минус один.

Ниже мы даем точное определение, иллюстрируем его вычисление пример, и мы введем некоторые его свойства.

СОДЕРЖАНИЕ

1. Синонимы

2. Определение

3. Пример

4. Корректированная против Ненаправленного

5. DEGREES

50. 9000 9000 9000 9000
51. 0012

52. Компромисс смещения и дисперсии

53. Подробнее

54. Продолжайте читать глоссарий

Синонимы

Его также часто называют несмещенной выборочной дисперсией , потому что при определенных условиях это несмещенная оценка дисперсия населения.

Определение

Он определяется следующим образом.

Определение Учитывая образец из наблюдений, их скорректированная выборочная дисперсия это здесь их образец среднее:

Прилагательное «скорректированный» указывает на то, что сумма квадратов отклонений делится на а не по .

Пример

Предположим, что мы наблюдали следующую выборку из шести наблюдения:

Образец означает это

Скорректированная выборочная дисперсия

Скорректированный и нескорректированный

Другим распространенным способом вычисления выборочной дисперсии является который называется нескорректированная или смещенная выборка дисперсия.

Основное отличие состоит в том, что сумма квадратов отклонений:

Регулировка степеней свободы

Мы можем записать скорректированную дисперсию через нескорректированную один:

Соотношение является называется регулировкой степеней свободы . Это также иногда называется поправкой Бесселя .

Несмещенный оценщик

Предположим, что наблюдения все взяты из вероятностных распределений, имеющих одно и то же среднее и такая же дисперсия .

Можно доказать (см. Дисперсия оценка), что, если являются независимый, тогда скорректированная выборочная дисперсия является несмещенной оценкой .

Компромисс смещения и дисперсии

Регулировка степеней свободы не является бесплатным обедом: она устраняет смещение, но это обычно увеличивает дисперсию выборочной дисперсии.

Это можно доказать строго, когда взяты из нормальный распространение (см. Дисперсия оценка).

Подробнее

Лекция под названием Дисперсия оценка представляет более подробную информацию о скорректированной выборочной дисперсии и его свойства (например, его последовательность и отсутствие предвзятости).

Для получения более подробной информации о предвзятой версии вы можете просмотреть глоссарий запись по нескорректированной выборке дисперсия.

Продолжайте читать глоссарий

Предыдущая запись: Абсолютно непрерывный случайный вектор

Следующая запись: Почти уверен

Как цитировать

Пожалуйста, цитируйте как:

Taboga, Marco (2021). «Скорректированная выборочная дисперсия», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/glossary/adjusted-sample-variance.

Обоснование поправки Бесселя: n-1 | Брайтон Холл

Стандартное отклонение кажется достаточно простой концепцией. Это мера дисперсии данных и корень суммированных различий между средним значением и его точками данных, деленный на количество точек данных… минус один для поправки на погрешность .

Я считаю, что это самая упрощенная и сводящая с ума концепция для любого учащегося, и цель этого поста — дать ясное и интуитивно понятное объяснение поправки Бесселя, или n-1.

Гелиометр для измерения звездного параллакса, впервые достигнутый Фридрихом Вильгельмом Бесселем, общественное достояние

Для начала вспомните формулу среднего значения генеральной совокупности:

Формула среднего значения генеральной совокупности

А как насчет среднего значения выборки?

Sample Mean Formula

Ну, они выглядят одинаково, за исключением строчной буквы N. В каждом случае вы просто добавляете каждый xᵢ и делите на количество x. Если мы имеем дело со всей совокупностью, мы будем использовать N вместо n, чтобы указать общее количество точек в совокупности.

Что такое стандартное отклонение σ (называемое сигмой)?

Если совокупность содержит N точек, то стандартное отклонение равно квадратному корню из дисперсия , которая является суммой и усреднением квадратов разностей каждой точки данных и среднего значения генеральной совокупности, или μ :

Формула стандартного отклонения совокупности

Но как насчет выборочного стандартного отклонения, s, с n данными точки и выборочное среднее x-bar:

Формула выборочного стандартного отклонения

Увы, появляется страшное n-1. Почему? Разве это не должна быть та же самая формула? Это была практически одна и та же формула для среднего значения генеральной совокупности и среднего значения выборки!

Краткий ответ: это очень сложно , до такой степени, что большинство преподавателей объясняют n-1, говоря, что стандартное отклонение выборки будет «предвзятой оценкой», если вы этого не сделаете.

Объяснение Википедии можно найти здесь.

Это бесполезно.

Чтобы по-настоящему понять n-1, как и любая другая короткая попытка объяснить поправку Бесселя, нужно одновременно держать в голове много . Я и не говорю о доказательствах. Я говорю о действительном понимании различий между выборкой и генеральной совокупностью .

Что такое образец?

Выборка всегда представляет собой подмножество совокупности , предназначенной для представления (подмножество может быть того же размера, что и исходное множество, в необычном случае выборки всей совокупности без замены). Это огромный скачок в одиночку. После того, как выборка взята, в эту выборку-представление встроены предполагаемых гипотетических параметров и распределений.

Само слово статистика относится к некоторой части информации о выборка (например, среднее значение или медиана), которая соответствует некоторой части аналогичной информации о совокупности (опять же, например, среднее значение или медиана), называемой параметром . Область «Статистика» названа так, а не «Параметрика», чтобы передать это отношение вывода от меньшего к большему, и этот скачок, опять же, имеет много встроенных допущений. Например, если предварительные предположения о генеральной совокупности выборки фактически определены количественно, это приводит к байесовской статистике. Если нет, то это приводит к частотности, выходящей за рамки этой статьи, но, тем не менее, важным аспектам, которые следует учитывать в контексте коррекции Бесселя. (фактически, в байесовском выводе поправка Бесселя не используется, поскольку априорные вероятности параметров совокупности предназначены для обработки систематической ошибки другим способом, заранее. Дисперсия и стандартное отклонение рассчитываются с помощью старого доброго и ).

Но не будем терять фокус. Теперь, когда мы указали важное фундаментальное различие между выборкой и совокупностью, давайте рассмотрим значение выборки. Я буду использовать нормальное распределение для следующих примеров для простоты, а также этот блокнот Jupyter, который содержит один миллион смоделированных точек данных с нормальным распределением для визуализации интуитивных представлений об образцах. Я настоятельно рекомендую поиграть с ним самостоятельно или просто использовать из sklearn.datasets import make_gaussian_quantiles 9.0206, чтобы получить практическое представление о том, что на самом деле происходит с сэмплированием.

Вот изображение одного миллиона случайно сгенерированных нормально распределенных точек. Мы назовем это нашей совокупностью:

Всего один миллион точек

Для дальнейшего упрощения мы будем рассматривать только среднее значение, дисперсию, стандартное отклонение и т. д. на основе значений x. (То есть я мог бы использовать для этих визуализаций простую числовую линию, но наличие оси Y более эффективно отображает распределение по оси X).

Это популяция, поэтому N = 1 000 000. Он нормально распределен, поэтому среднее значение равно 0,0, а стандартное отклонение равно 1,0.

Я взял две случайные выборки, первая только 10 точек, а вторая 100 точек:

100-точечная выборка черного цвета, 10-точечная выборка оранжевого цвета, красные линии - это одно стандартное значение от среднего

Теперь давайте посмотрим на эти две выборки, без поправки Бесселя и с поправкой Бесселя, а также их стандартные отклонения (со смещением и без смещения, соответственно). Первая выборка всего 10 баллов, а вторая выборка 100 баллов.

Похоже, коррекция помогает!

Внимательно посмотрите на изображение выше. Поправка Бесселя действительно помогает. Это имеет смысл: очень часто стандартное отклонение выборки будет ниже стандартного отклонения генеральной совокупности, особенно если выборка мала, потому что нерепрезентативные точки («предвзятые» точки, т.е. влияние на расчет дисперсии. Поскольку 90 137 разность 90 138 между каждой точкой данных и средним значением выборки возводится в квадрат, диапазон возможных различий будет меньше, чем реальный диапазон, если использовалось среднее значение генеральной совокупности. Кроме того, извлечение квадратного корня является вогнутой функцией и, следовательно, вносит в оценки «смещение вниз».

Другой способ думать об этом таков: чем больше ваша выборка, тем у вас больше возможностей столкнуться с большим числом точек, репрезентативных для населения, т. е. с точками, близкими к среднему значению. Следовательно, у вас меньше шансов получить выборочное среднее, что приводит к слишком малым различиям, что приводит к слишком малой дисперсии, и у вас остается недооцененное стандартное отклонение.

В среднем выборки нормально распределенной совокупности дают дисперсию, равную смещено вниз на коэффициент n-1 в среднем . (Между прочим, я полагаю, что само распределение смещений выборки описывается t-распределением Стьюдента, определяемым как n ). Поэтому, разделив дисперсию с квадратным корнем на n-1, мы уменьшаем знаменатель, тем самым увеличивая результат и приводя к так называемой «непредвзятой» оценке.

Здесь важно подчеркнуть, что поправка Бесселя или деление на n-1 на самом деле не всегда помогает! Поскольку потенциальные выборочные дисперсии сами по себе являются t-распределенными, вы будете невольно столкнутся со случаями, когда n-1 превысит стандартное отклонение реальной популяции. Так уж получилось, что n-1 — лучший инструмент, который мы можем исправить на смещение большую часть времени .

Чтобы доказать это, проверьте тот же блокнот Jupyter, где я просто изменил случайное начальное число , пока не нашел несколько выборок, стандартное отклонение которых уже было близко к стандартному отклонению генеральной совокупности, и где n-1 добавило больше смещения :

В данном случае Поправка Бесселя действительно навредила нам!

Таким образом, поправка Бесселя не всегда является поправкой.

No related posts.