формула по длине стороны, диагонали
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади квадрата: формула и примеры
Квадрат – это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).
- Формула вычисления площади
- Примеры задач
Формула вычисления площади
1. По длине стороны:
Площадь квадрата (S) равняется квадрату длины его стороны:
S = a2
Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:
S = a*b
А т.к. все стороны квадрата равны, то вместо стороны b мы снова подставляем в формулу сторону a, т.
е. S = a*a = a2.
2. По по длине диагонали
Площадь квадрата равняется половине квадрата длины его диагонали:
S = d2/2
Соотношение стороны и диагонали квадрата: d=a√2.
Примеры задач
Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.
Решение:
Используем формулу по длине стороны, т.е. S = 72 = 49 см2.
Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.
Решение 1:
Воспользуемся второй формулой (по длине диагонали): S = 42/2 = 8 см2.
Мы можем выразить длину стороны через диагональ: a = 4/√2. И тогда, используя первую формулу, S = (4/√2)2 = 8 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как найти площадь прямоугольника и квадрата 4 класс
Площадь прямоугольника равна произведению его длины и ширины: ・.
Площадь квадрата равна произведению двух его соседних сторон: ・.
- Как находить площадь прямоугольника 4 класс
- Как найти площадь квадрата и прямоугольника
- Что такое площадь квадрата 4 класс
- Как найти площадь и периметр прямоугольника 4 класс
- Как находить площадь прямоугольника
- Как вычисляется площадь прямоугольника
- Какая площадь у квадрата
- Как найти площадь и периметр прямоугольника и квадрата
- Как можно вычислить площадь прямоугольника двумя способами
- Как объяснить ребёнку площадь квадрата
- Как найти площадь квадрата 7 см 4 класс
- Что такое площадь квадрата и как её найти
- Как найти периметр прямоугольника 4 класса
- Как найти периметр квадрата 4 класс
- Как вычислить площадь и периметр квадрата
- Как найти периметр прямоугольника 4 класс
- Как найти площадь и периметр треугольника 4 класс
- Как можно найти пример и площадь прямоугольника
Как находить площадь прямоугольника 4 класс
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга.
S = a × b, где S — площадь; a, b — длина и ширина.
Как найти площадь квадрата и прямоугольника
1) Для того, чтобы найти площадь прямоугольника нужно умножить длину на ширину. S = a * b. 2) Для того, чтобы найти площадь квадрата нужно умножить сторону саму на себя. S = a2.
Что такое площадь квадрата 4 класс
Площадью квадрата называется часть плоскости, которая ограничивается сторонами этого квадрата. Квадрат является частным случаем прямоугольника, то его площадь можно найти как произведение одной его стороны на другую, а так как все стороны квадрата равны, то его площадь будет равна квадрату длины его стороны: S = a².
Как найти площадь и периметр прямоугольника 4 класс
Ответы1. Периметр прямоугольника — это сумма всех его сторон. Формула нахождения площади прямоугольника: S = a × b, где а — ширина, b — длина прямоугольника.
Как находить площадь прямоугольника
2) Для вычисления площади прямоугольника нужно умножить его длину на ширину.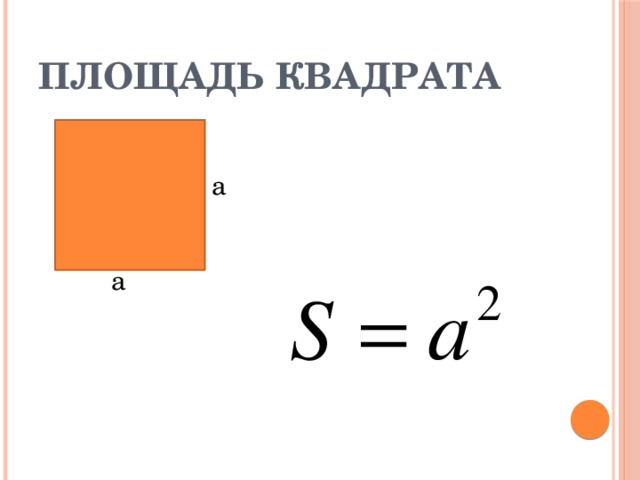
Формула для вычисления площади прямоугольника имеет следующий вид: S = a*b.
Как вычисляется площадь прямоугольника
Площадь прямоугольника находится как произведение ширины на его длину. S = a * b.
Какая площадь у квадрата
Мы получим площадь квадрата, если возведём диагональ в квадрат, то есть умножим длину диагонали на саму себя, а потом разделим получившуюся величину на два. Где d — это диагональ.
Как найти площадь и периметр прямоугольника и квадрата
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = (+ b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
Как можно вычислить площадь прямоугольника двумя способами
S = b * a. Оба полученных выражения равны (по тому же переместительному свойству умножения), т. e: S = a * b = b * a.
Как объяснить ребёнку площадь квадрата
Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее).
2=9$ (см2)
Как найти периметр прямоугольника 4 класса
Формула нахождения периметра прямоугольника
P = a + b + c + d, где a, b, c, d — стороны. P = 2 × (a + b), где a и b — соседние стороны.
Как найти периметр квадрата 4 класс
P = a + a + a + a, где a — сторона.
Как вычислить площадь и периметр квадрата
Периметр квадрата — это сумма длин его сторон. Вычисляется по формуле P = 4 * a, так как у квадрата все стороны равны. Площадь квадрата — это число единичных квадратов в этой фигуре. Вычисляется по формуле S = a2, так как у квадрата все стороны равны.
Как найти периметр прямоугольника 4 класс
Формула нахождения периметра прямоугольника
P = a + b + c + d, где a, b, c, d — стороны. P = 2 × (a + b), где a и b — соседние стороны.
Как найти площадь и периметр треугольника 4 класс
Формула площади треугольника:
- Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
- Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p.
Как можно найти пример и площадь прямоугольника
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = (+ b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
Площадь квадрата — формула, как найти площадь квадрата?
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой фигуры. Другими словами, площадь квадрата — это область, занимаемая в его границах. Когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата также можно вычислить с помощью других измерений, таких как диагональ и периметр квадрата.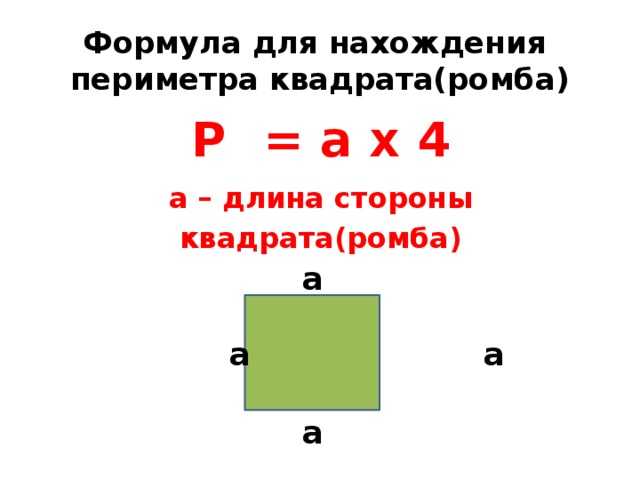
Давайте узнаем больше о площади квадрата и формуле площади квадрата на этой странице.
| 1. | Какова площадь квадрата? |
| 2. | Площадь квадрата Формула |
| 3. | Как найти площадь квадрата? |
| 4. | Часто задаваемые вопросы о площади квадрата |
Какова площадь квадрата?
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общее пространство, занимаемое фигурой, — это площадь квадрата. Это четырехугольник, который обладает следующими свойствами.
- Противоположные стороны квадрата параллельны.
- Все четыре стороны квадрата равны.
- Все углы квадрата равны 90º.
Квадраты можно найти повсюду вокруг нас.
Вот некоторые часто встречающиеся объекты, имеющие форму квадрата. Шахматная доска, часы и школьная доска — все это примеры квадрата.
Площадь квадрата Определение
Площадь квадрата – это мера занимаемой им площади или поверхности. Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.
Обратите внимание на квадрат, указанный ниже. Он занял 25 кв. Следовательно, площадь квадрата равна 25 квадратных единиц. Из рисунка видно, что длина каждой стороны равна 5 единицам. Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.
Квадрат Определение
Квадрат – это четырехугольник, у которого все четыре стороны равны и параллельны друг другу. Все углы в квадрате равны 90 градусов.
Формула площади квадрата
Формула площади квадрата, если известна сторона:
Площадь квадрата = сторона × сторона = S 2
Алгебраически площадь квадрата можно найти, возведя число в квадрат представляет собой меру стороны квадрата.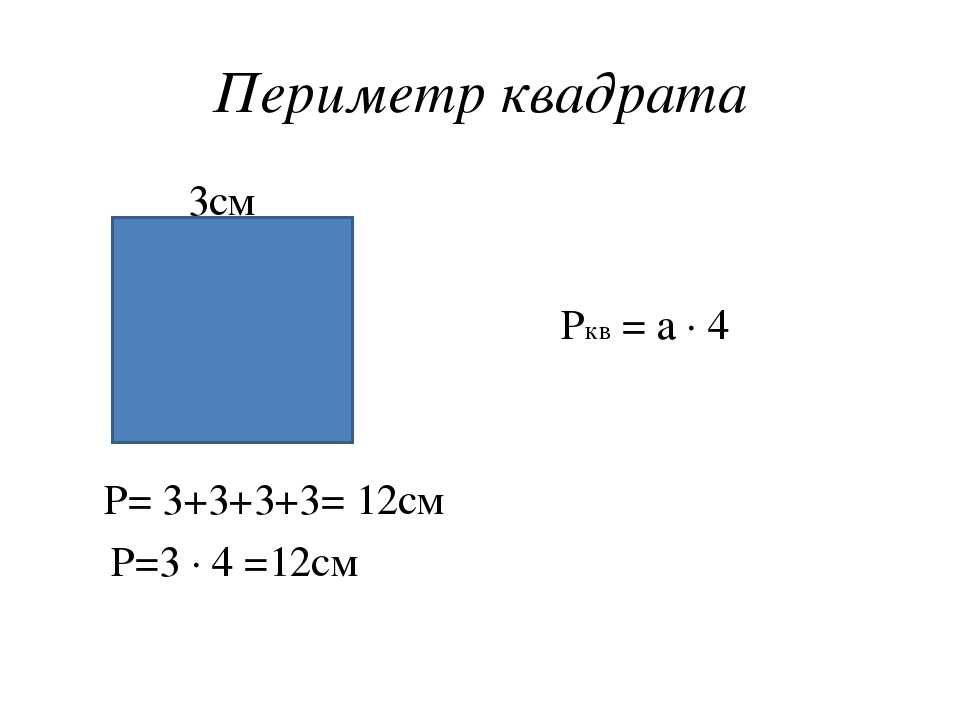
Теперь воспользуемся этой формулой, чтобы найти площадь квадрата со стороной 7 см. Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны как 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см 2 .
Площадь квадрата также можно найти с помощью диагонали квадрата. Формула, используемая для нахождения площади квадрата по диагонали:
Площадь квадрата по диагоналям = Диагональ 2 /2.
Давайте разберемся в выводе этой формулы с помощью следующего рисунка, где «d» — диагональ, а «s» — стороны квадрата.
Здесь сторона квадрата «s», а диагональ квадрата «d». Применяя теорему Пифагора, мы имеем d 2 = s 2 + s 2 ; д 2 = 2s 2 ; д = √2с; с = d/√2. Теперь эта формула поможет нам найти площадь квадрата, используя диагональ. Площадь = s 2 = (d/√2) 2 = d 2 /2. Следовательно, площадь квадрата равна d 2 /2.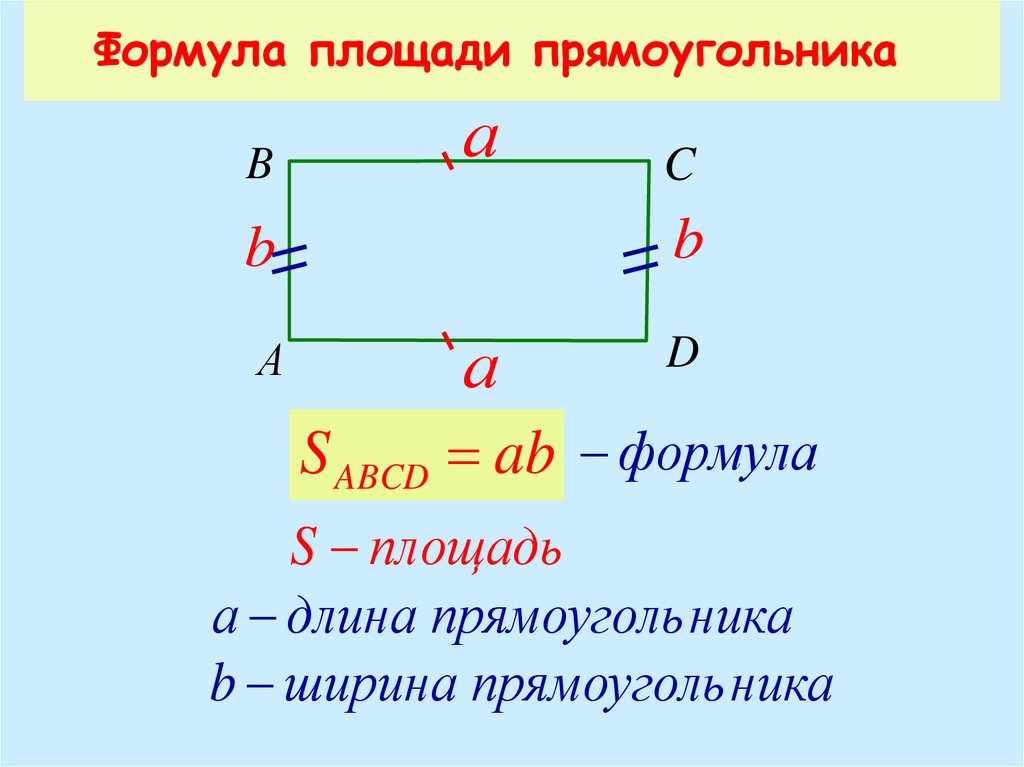
Как найти площадь квадрата?
Мы можем найти площадь квадрата, используя различные методы в зависимости от значений, которые нам даны. Давайте посмотрим, какими способами мы можем найти площадь квадрата, если известны его периметр, стороны или диагонали.
Площадь квадрата, если известен периметр квадрата
Пример: Найдите площадь квадратного парка, периметр которого равен 360 футов.
Решение:
Дано: периметр квадратного парка = 360 футов
Мы это знаем,
Периметр квадрата = 4 × сторона
⇒ 4 × сторона = 360
⇒ сторона = 360/4
⇒ сторона = 90 футов
Площадь квадрата = сторона 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка с периметром 360 футов составляет 8100 футов.
Решение:
Дано: Сторона квадрата = 6 см
Мы знаем, что
Площадь квадрата = сторона 2
Следовательно, площадь квадрата = 6 7 2 90 6 = 36 см 2
Площадь квадрата Если известна диагональ квадрата
Пример: Найдите площадь квадрата, диагональ которого равна 12 см.
Решение:
Дано: Диагональ квадрата = 12 см
Мы знаем, что
Формула площади квадрата при заданной диагонали = d 2 /2
Следовательно, площадь квадрата = (12 × 12)/2 = 72 см 2
Советы по нахождению площади квадрата
Обратите внимание на следующие моменты, которые следует помнить при вычислении площади квадрата.
☛ Статьи по теме
- Диагональ квадрата
- Площадь квадратов и прямоугольников Рабочие листы
- Периметр площади
- Площадь поверхности квадратной призмы
- Калькулятор площади квадрата
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.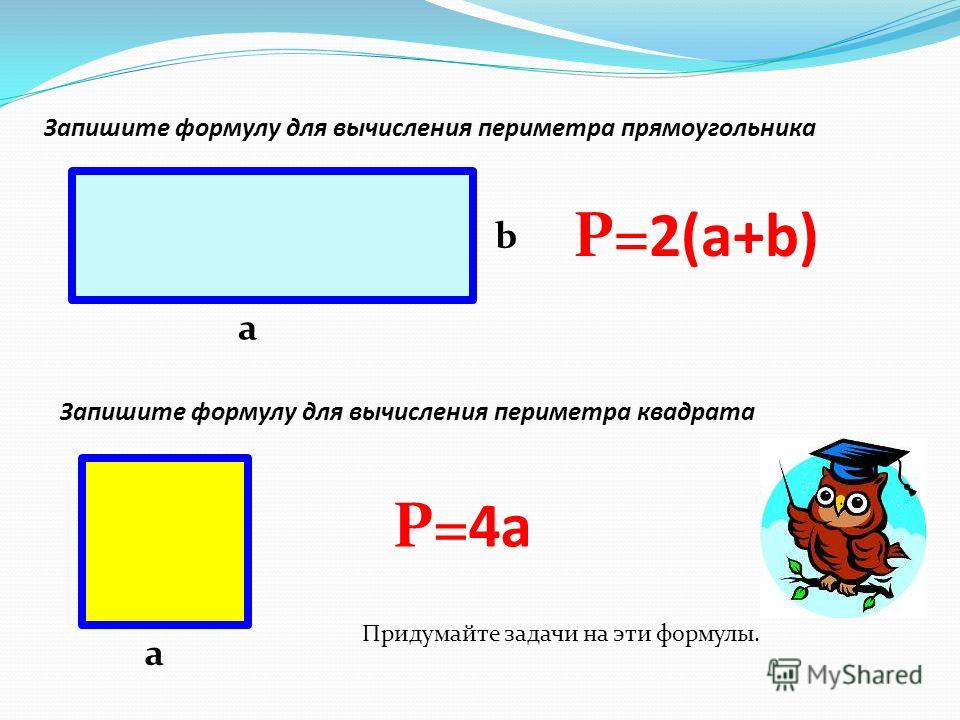
Площадь квадрата Формула Примеры
Пример 1: Какова площадь квадратного бассейна, одна сторона которого равна 8 м?
Решение:
Мы знаем, что одна сторона бассейна равна 8 м, поэтому воспользуемся формулой: Площадь квадрата = сторона × сторона = 8 × 8 = 64 м 2 . Следовательно, площадь бассейна составляет 64 квадратных метра.
Пример 2: Площадь квадратной доски составляет 3600 см 2 . Какова длина его стороны?
Решение:
Площадь квадратной доски = 3600 см 2 . Мы знаем, что Площадь = сторона × сторона = сторона 2 . Значит, сторона = √Площадь = √3600 = 60 см. Следовательно, сторона доски для каррома равна 60 см.
Пример 3: Найдите площадь квадрата с диагональю 4 фута.
Решение:
Площадь квадрата, если дана его диагональ, равна площади квадрата = диагонали 2 /2.
Дано, диагональ (d) = 4 фута. Площадь квадрата = (4 × 4)/2 = 16/2 = 8 квадратных футов. Следовательно, площадь квадрата равна 8 кв.
Дано, диагональ (d) = 4 фута. Площадь квадрата = (4 × 4)/2 = 16/2 = 8 квадратных футов. Следовательно, площадь квадрата равна 8 кв.перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Запись на бесплатный пробный урок
Практические вопросы на площади Square
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади квадрата
Что такое площадь квадрата в геометрии?
Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата: площадь = сторона × сторона, и ответ дается в квадратных единицах.
Какова площадь квадратной формулы?
Когда дана сторона квадрата, мы вычисляем площадь квадрата по формуле Площадь квадрата со стороной s: Площадь = s × s = s 2 .
Если дана диагональ ‘d’ квадрата, то формула, используемая для нахождения площади квадрата, выглядит так: Площадь = d 2 /2.
Как вычислить площадь квадрата?
Площадь квадрата рассчитывается по формуле: Площадь = s × s, где s — одна сторона квадрата. Поскольку площадь квадрата является двумерной величиной, она всегда выражается в квадратных единицах. Например, если мы хотим вычислить площадь квадрата со стороной 4 единицы, это будет: A = 4 × 4 = 16 единиц 2 . Проверьте площадь квадратного калькулятора для быстрых расчетов.
Что такое площадь и периметр квадратных формул?
Периметр квадрата представляет собой сумму четырех сторон квадрата, то есть Периметр = 4 × Сторона. Она выражается в м, см, футах и дюймах.
Площадь квадрата = Площадь = s × s, где s — одна сторона квадрата. Дается в единицах м 2 , см 2 , фут 2 , а в 2 .
Проверка:
- Формулы периметра
- Объемные формулы
- Формулы площади поверхности
- Формулы измерения
Как найти площадь квадрата по диагонали квадрата?
Площадь квадрата также можно найти, если известна его диагональ.
В этом случае используется следующая формула: Площадь квадрата по диагоналям = Диагональ²/2. Например, диагональ квадрата равна 6 единицам, Площадь = 6²/2 = 36/2 = 18 квадратных единиц.
Как найти площадь квадрата по периметру квадрата?
Площадь квадрата можно вычислить, если известен его периметр. Поскольку периметр квадрата: P = 4 × сторона, мы можем найти сторону квадрата ‘s’ = периметр/4. После получения стороны площадь квадрата можно вычислить по формуле: A = s × s. Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона. 32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
Каковы единицы площади квадрата?
Площадь квадрата является двумерной величиной, поэтому всегда выражается в квадратных единицах. Общие единицы площади квадрата: м 2 , дюймы 2 , см 2 и футы 2 .
Какова площадь квадрата, вписанного в окружность?
Если квадрат вписан в круг, то диагональ квадрата равна диаметру круга. Итак, если диаметр круга дан, это значение можно использовать как диагональ квадрата, а площадь квадрата можно рассчитать по формуле: Площадь квадрата с использованием диагоналей = Диагональ²/2.
Найдите сторону квадрата, площадь которого равна 36 квадратных единиц.
Если площадь квадрата составляет 36 квадратных единиц, сторону квадрата можно рассчитать по той же формуле, подставив заданное значение. Мы знаем, что площадь квадрата = сторона 2 . Подставив значение площади в 36, мы получим 36 = сторона 2 . Итак, сторона = √36 = 6 единиц.
Чему равна формула стороны квадрата, если дана площадь?
Когда дана площадь квадрата, тогда формула стороны квадрата: Сторона квадрата = √(Площадь квадрата). Например, найдем сторону квадрата, площадь которого равна 2304 квадратных единиц. После подстановки этого значения в формулу получаем Сторона квадрата = √2304 = 48 единиц.
Следовательно, сторона квадрата равна 48 единицам.
Что такое периметр и площадь квадрата?
Периметр квадрата — это длина всей границы квадрата. Если мы знаем одну сторону квадрата, мы можем найти его периметр, используя формулу: Периметр квадрата = 4 × сторона. Площадь квадрата – это вся площадь, занимаемая его границей. Зная одну сторону квадрата, мы можем найти его площадь по формуле Площадь квадрата = сторона × сторона.
Какова площадь квадрата? Определение, формула, примеры
Какова площадь квадрата?
Количество квадратных единиц, необходимых для заполнения квадрата, равно его площади . Проще говоря, площадь — это внутренняя часть плоской поверхности (двухмерный рисунок).
В данном квадрате место, заштрихованное фиолетовым цветом, является площадью квадрата.
Например, пространство, занимаемое бассейном ниже, можно найти, найдя площадь бассейна.
Родственные игры
Формула площади квадрата
Площадь квадрата равна (стороне) × (стороне) квадратных единиц.
Площадь квадрата, если дана диагональ d, равна d 2 ÷2 квадратных единиц.
Например,
Площадь квадрата со стороной 8 футов равна 8 × 8 или 64 квадратных фута (фут 2 ).
Связанные рабочие листы
Решенные примеры на площади квадрата
Пример 1: Учитывая, что каждая сторона равна 5 см, найдите площадь квадрата.
Решение:
Площадь квадрата = сторона × сторона
Площадь = 5 × 5
Площадь = 25 см 2
. Какова стоимость покраски в размере 5000 руб. 2 на кв.м?Решение:
Сторона стены = 50 м
Площадь стены = сторона × сторона = 50 м × 50 м = 2500 кв.м
Стоимость покраски 1 кв.м = рупий. 2
Таким образом, стоимость покраски стены площадью 2500 кв. м = рупий. 2 × 2500 = 5000 рупий
Пример 3: Найдите площадь квадрата, диагональ которого равна 4 см.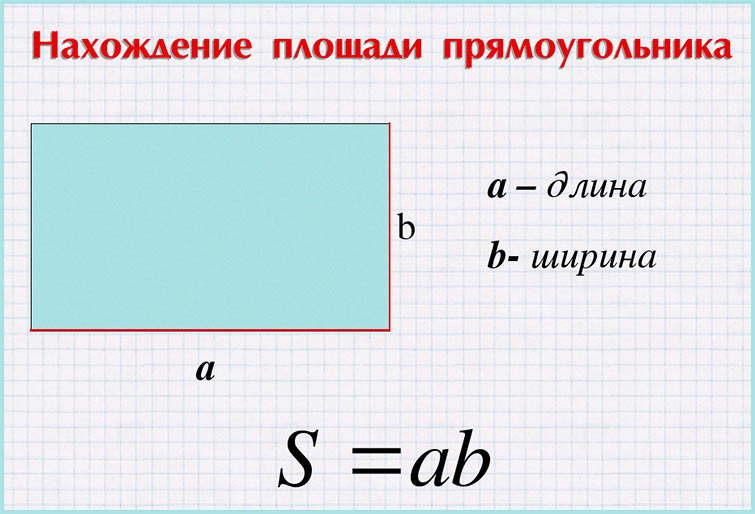
Решение:
Дано:
Сторона d = 4 см
Мы знаем, что формула для нахождения площади квадрата по диагонали d равна d 2 ÷2 квадратных единиц.
Подставляя диагональное значение, получаем:
= 4 2 ÷2 = 16 ÷ 2 = 8
9{2}$/2= 36/2
= 18
Таким образом, площадь квадратного стола составляет 18 квадратных футов.
2
Вычислите площадь квадратной комнаты, обставленной 250 квадратными плитками со стороной 30 дюймов.
180000 квадратных дюймов
180000 квадратных метров
220000 квадратных дюймов
240000 квадратных дюймов
Правильный ответ: 180000 квадратных дюймов
Общее количество плиток = 250
Сторона одной плитки = 30 дюймов.
Площадь 1 плитки = 30 x 30 дюймов 90 127 = 900 квадратных дюймов 9{2}$
Часто задаваемые вопросы о площади квадрата
В чем разница между периметром и площадью квадрата?
Периметр квадрата равен сумме его четырех сторон или длине его границы.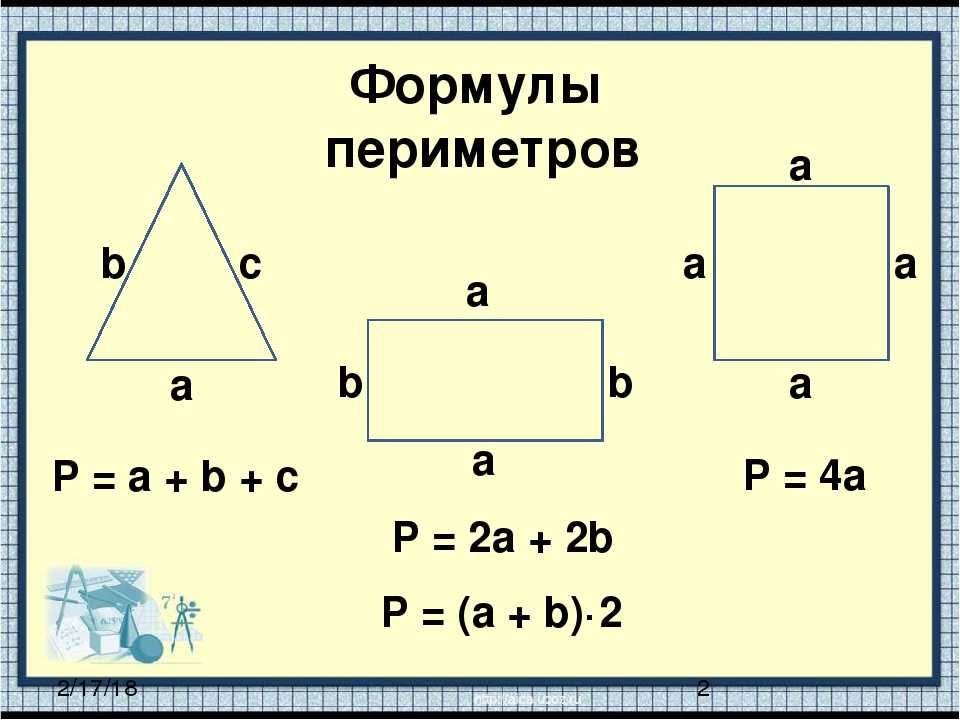
Это одномерное измерение, выраженное в линейных единицах. Площадь квадрата – это пространство, заполненное квадратом в двумерном пространстве. Выражается в квадратных единицах.
Как вычислить площадь квадрата, если известен его периметр?
Периметр квадрата равен сумме всех четырех сторон квадрата. Если задан периметр, то формула для вычисления площади квадрата A = Периметр 2 /16
В каких единицах измеряется площадь квадрата?
Площадь квадрата двумерная. Таким образом, площадь квадрата всегда представлена квадратными единицами, для которых общими единицами являются см 2 , м 2 , ин 2 или футы 2 .
Имеют ли два квадрата одинаковой площади равные периметры?
Да. Два квадрата равной площади, данные стороной x, будут иметь одинаковую длину сторон. Они конгруэнтны. Следовательно, периметры двух квадратов, равные 4-кратной длине стороны, также будут равны.
Заключение
Чтобы узнать об аналогичных концепциях, перейдите на SplashLearn.