Формула как найти площадь треугольника 9 класс – Все формулы площади треугольника — найти онлайн

План-конспект урока математики по теме «Формулы площадей треугольников». 9-й класс

Разделы: Математика

---

Цели урока: повторение и систематизация знаний и умений учащихся, необходимых для применения в практической деятельности по данной теме; формирование практических навыков вычисления площадей различных треугольников

Задачи:

1. Обучающая – расширить знания о формулах площади треугольников; учить применять формулы Герона и Пика при решение задач на площадь треугольника с опорой на готовые чертежи, изображенные на клетчатой бумаге с размером клетки 1см x 1см или треугольника, заданного на координатной плоскости.
2. Развивающая – развивать логическое мышление, развивать навыки и умения работать в парах и группах; развивать навыков самоорганизации и участия в работе группы и творческие способности учащихся.
3. Воспитательная

– повышать интерес к изучению математики, сознательное отношение к учебе, уважительное отношение друг к другу, умение слушать ответы товарищей, воспитывать стремление к непрерывному совершенствованию своих знаний.

Оборудование: компьютер, проектор, презентация, билеты для лото, задания для практической работы, карточки с рисунками к задачам, карточки с формулами площади треугольника и карточки с треугольниками и наглядности.

Тип урока: урок открытия новых знаний и совершенствования знаний, умений и навыков.

Формы работы учащихся: индивидуальная, групповая.

Необходимое техническое оборудование: компьютер, проектор, презентация, билеты для лото, задания для практической работы, карточки с рисунками к задачам, карточки с формулами площади треугольника и карточки с треугольниками и наглядности.

Структура и ход урока

I. Мотивирование к учебной деятельности (1 мин).

Цель: создание положительного эмоционального настроя на работу, включение обучающихся в деятельность на личностно-значимом уровне.

Деятельность учителя	Деятельность ученика	УУД
Организационная минутка. Проверка готовности к уроку. Учащиеся разделены на три группы. В каждой группе по 8 человек разного уровня знаний. На каждом столе лежит пакет с материалами к уроку, три отрезка разной длины. Доска развешана разноцветными многоугольниками и разного вида треугольниками. Приветствие гостей и учащихся. Ребята, поздоровайтесь друг с другом за руки. Давайте возьмемся за руки и пожелаем друг другу взаимоуважения, поддержки и хороших знаний. Впереди нас ждут экзамены. Наша задача успешно сдать ГИА. Каждый из вас должен уметь решать задачи базового уровня. Чтобы решить задачи надо учиться их решать различными способами. Определим, на какую тему будем решать задачи. Давайте, ребята, послушаем математическую сказку, которую сочинила ученица 8 класса.	Учащиеся стоя здороваются друг с другом за руки. Учащиеся внимательно слушают сказку.	Личностные – формирование положительного отношения к учебе и развитие мотивации к дальнейшему изучению математики.

II. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии (2 мин).

Цель: активизация изученного материала необходимого для “открытия нового знания”, и выявление затруднений в индивидуальной деятельности каждого ученика.

Устный рассказ сказки. В математическом царстве, планиметрическом государстве,…(Приложение 1.)

Личностные – развитие мотивации к дальнейшему изучению математики.

III. Постановка учебной задачи (4 мин)

Цель: обсуждение затруднения и развитие у учащихся умения самостоятельно сформулировать тему и цели урока.

Вот такая сказка. А вы догадались, о каком “простаке” сегодня на уроке пойдет речь? А что вы знаете о треугольниках Знания о треугольниках проверим, выполнив практическую работу (проверка д/з). У вас на столах лежат три отрезка. Составьте из них треугольник. У третьей группы треугольник не существует. Значит, есть условия, когда три отрезка дают треугольник. Учитель показывает произвольный треугольник, изображенный на рисунке (Приложение 2, 2а). Ребята, помогите мне. Я хочу покрасить этот треугольник. Но не знаю сколько нужно краски. Что для этого нужно знать? А как мы можем вычислить площадь треугольников? Ребята, как бы назвали тему нашего урока? Слайд 1. (Приложение 14) Да, сегодня у нас урок повторения и получения знаний на тему “Формулы площади треугольника”. Зная формулы для вычисления площади треугольника, можно посчитать площадь любого многоугольника, предварительно разбив его на треугольники. Эта тема является одной из важнейших тем геометрии. Какие же формулы для вычисления площади треугольника вы знаете? На магнитной доске даны формулы площади треугольника и треугольники. Установить соответствие. По рисунку найти формулу (Приложение 3 , 4, 5, 6, 7). Один треугольник остается без формулы. А где же формула для площади моего треугольника? Какую цель мы поставим перед собой?

Ответы детей о треугольнике. Мы знаем много о треугольниках. Дети составили треугольники. Ученики дают правильные ответы (длина любой стороны должна быть меньше суммы длин двух других сторон). Дети дают совет вычислить площадь этого треугольника. По различным формулам. Каждый ряд дает свою формулировку темы урока (Решение задач на вычисления площади треугольника по формулам). Учащиеся записывают в тетрадях число и тему урока. Из каждой группы по одному ученику выбирают билет с номером рисунка, и находят формулу для вычисления площади по данным элементам треугольника. Вторые ученики читают формулу (что означает каждая буква формулы). Найти формулу, для вычисления площади произвольного треугольника по трем сторонам.

Регулятивные – уметь ставить цели, планировать свои действия в соответствии с поставленной задачей.

IV. Открытие нового знания (5 мин).

Цель: построение проекта выхода из затруднения и формирование первичных практических навыков.

Значит, приведенные формулы для площади треугольника не исчерпывают все формулы, с помощью которых можно эту площадь находить. Слайд 2. Да, ребята. Если разумно провести необходимые преобразования при вычислении длины высоты, то мы получим эту формулу. Эту задачу решил еще в I в.н.э. выдающийся древнегреческий математик – Герон Александрийский. Он не знал заранее, что открыл(!) формулу, выражающую площадь треугольника через его три стороны. Несмотря на то, что эта формула достаточно длинная, она является одной из самых красивых и древних формул геометрии. На доске открываем таблицу с формулой Герона. (Приложение 8). Слайд 3. Доказательство этой формулы очень громоздкое и мы не будем на нём подробно останавливаться. Если оно вас заинтересует, то можно разобрать его после урока или изучить самостоятельно по материалам факультатива электронном портале интернета. Слайд 4. Формула площади треугольника по трём сторонам была открыта Архимедом в III в до нашей эры. Однако соответствующая работа до наших дней не дошла. Эта формула содержится в “Метрике” Герона Александрийского (I в н. э.) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых также являются целыми. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник .

Ученица. Во всех известных формулах есть высота треугольника. Поэтому проведем одну из трех высот. Вычислим длину высоты из двух прямоугольных треугольников по теореме Пифагора. Эту формулу я изучила по материалам виртуального факультатива “ГИА и ЕГЭ в математике” из интернета (автор учитель математики Горшкова Г.М.). И эта формула называется формулой Герона. Прочитали формулу – что означает каждая буква формулы. По этой формуле мы и сможем вычислить площадь вашего треугольника.

Познавательные. Коммуникативные.

V. Первичное закрепление (7 мин).

Цель: проговаривание нового знания и применение формулы Герона для вычисления площади треугольника.

1) Давайте решим одну замечательную задачу на применение формулы площади треугольника. На доске изображен треугольник на клетчатой бумаге с размером клетки 1 см x 1 см. Вычислить площадь треугольника. Рис. 1 У каждого ученика на столе есть карточка с условием задачи. (Приложение 9, 9а).	Ученики в тетрадях записывают число, классная работа и тему урока. Записывают формулу Герона. Ученики предлагают вычислить площадь этого треугольника различными способами. 1. Способом вычитания (дополнить до прямоугольника, из площади прямоугольника вычесть площади лишних прямоугольных треугольников). 2. Способ сложения (треугольник разбить на два прямоугольных треугольника и сложить площади этих треугольников). 3. По формуле 4. По формуле Герона. Один ученик работает у доски, а все остальные решают на местах. Цветными карандашами выполняют дополнительные построения. Каждая группа получает задание. Вычислить площадь данного треугольника различными способами. Записывают вычисления в тетради. Сравнивают ответы. Ответ один и тот же. У доски работает ученик по желанию. Вычислить длины сторон треугольника. Каждая группа объясняет, как можно вычислить длины сторон треугольника.	Регулятивные. Коммуникативные. Познавательные. Личностные.
2. Вычислим площадь треугольника по формуле Герона. З. Слайд 5. Задачи из ГИА. А как посчитать площадь треугольника, изображенного в системе координат?	а) Задача 1. Длины катетов равны: 9 – 1 = 8; 9 – 6 = 3; Длина гипотенузы равна квадратный корень из 73. б) Задача 2. Длину каждой стороны вычисляем как длину гипотенузы из прямоугольных треугольников или по правилу вычисления расстояния между двумя точками. Учащиеся записывают правила в тетради. Каждая группа вычисляет длину определенной стороны данного треугольника. Стороны этого треугольника выражены не целочисленными числами, поэтому вычисления получаются громоздкими и без калькулятора не обойтись.
А нет ли еще какой-нибудь формулы для вычисления площади треугольника? Т. е. как посчитать площадь треугольника, если хотя бы одна сторона выражена квадратным корнем? Да, есть такая формула. Эта II формула Герона. Слайд 6.	Ученики записывают эту формулу в тетради.
На доске появляется еще одна формула площади треугольника (Приложение 10). Рассмотрим решение задачи на применение этой формулы Правильность выполнения вычислений проверяем по Слайдам 7и 8. Слайд 9. Итак, теперь мы знаем 7 формул для нахождения площади треугольника. Но оказывается это не все формулы. Существуют ещё формулы и следствия из предыдущих формул. Слайд 10. Вычисление площади треугольника по стороне и прилежащим к ней углам. Итак, мы теперь знаем 9 формул. Но это ещё не предел. С таким же успехом можно получить ещё новые формулы, например, через тригонометрические формулы половинного угла, двойного угла. Такие исследования могут стать стартовой площадкой для написания научно-исследовательской работы.	Ученики замечают, что в этой формуле нет полупериметра. Текст задачи есть у каждого ученика. Один ученик выполняет задание у доски. Учащиеся получают оценки за работу у доски и ученики, принимавшие активное участие в разборе решения задач по различным способам. Учащиеся записывают эти формулы в тетради. Отмечают, что это темы проектных работ. Ученики приводят свои рабочие места в порядок.

Динамическая пауза (1 мин).

Физкультминутка.

Ученики встают, хлопают в ладошки, пожимают друг другу руки и благодарят друг друга за дружную работу, взаимопомощь. Группы меняются местами, перемещаясь по кругу.

Регулятивные. Познавательные. Личностные.

VI. Самостоятельная работа с самопроверкой по образцу (5 мин).

Цель: создание ситуации успеха, мотивирующей его к включению в дальнейшую познавательную деятельность

Игра-лотерея, посвященная ко дню Космонавтики (Приложение 11, 11а ). Ребята, обратите внимание на номера ваших билетов. Постарайтесь найти, по каким правилам эти номера составлены. На доске вывешивается таблица с правильными ответами.

Каждый ученик получает билет-лотерею на удачу, карточки вопросы с четырьмя ответами и рисунки чертежи. Ученики, отвечая на вопросы, вычеркивают номера правильных ответов. Выписывают номера не вычеркнутых ответов, считают их количество и заполняют линейку успешности. Если остались номеров: 8 – “5”; 9 – 11 – “4”; 12 – 13 – “3”. Ученики билеты подписывают и записывают результаты успешности на обратной стороне билета. Ученики довольно быстро нашли секреты номеров. Эти числа выражают: арифметическую или геометрическую прогрессии, число, месяц и год дня Космонавтики, продолжительность полета космического корабля “Восток-1” вокруг Земли. Каждый ученик получает оценку за ответы на вопросы и плюс за секреты номера билета. Ученики обмениваются билетами с соседними группами и выполняют взаимопроверку. Сравниваются ответы.

Регулятивные. Личностные. Познавательные.

VII. Включение нового знания в систему знаний и повторение (10 мин).

Цель: выявление границ применимости нового знания.

Ребята, а так ли уж важно изучать формулы треугольника и знать их для применения? В каких житейских ситуациях можно встретиться с треугольниками? Слайды 11и 12. Ребята, я хочу вам дать еще одну полезную информацию для успешной сдачи ГИА, а потом и ЕГЭ. На помощь приходит еще один практически полезный, красивый и точный прием, основанный на использовании формулы Пика. Формула Пика позволяет найти площадь любого многоугольника, вершинами которого являются узлы клеток. Часть узлов он содержит на своих сторонах (мы обозначим их количество буквой Г), а часть внутри себя (это количество обозначим буквой В). Тогда площадь такого многоугольника можно вычислить по формуле S= Г + В/2 – 1. Ее и называют формулой Пика.	Учащиеся считают, что важно знать формулы площади треугольников, так как треугольники встречаются очень часто в швейном деле, в столярном деле, в строительном деле и т. д. Ребята перечисляют еще, где нужны знания о треугольниках. А самое главное задачи на вычисления площади включены в задания ГИА и ЕГЭ. Ученики записывают эту формулу в тетради.	Коммуникативные Познавательные Личностные Усиление мотивации обучения и практической значимости знаний, воспитание устойчивого интереса к геометрии.
Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить… Формулу Пика открываю и на доске (Приложение 12). Презентация. Формула Пика. (Приложение 15) Посмотрим, как применить формулу для вычисления площади. Устная практическая работа по группам. Вычислить площадь по формуле Пика.	Ученики внимательно наблюдают за тем, как правильно считать узловые точки. От каждой группы по два ученика работают у доски. Один считает узловые точки на границе, а другой внутренние точки. Остальные ученики подсчитывают площадь. Так и загорелись, глаза учеников, увидев практическую пользу формулы Пика.

VIII. Информация о домашнем задании и инструкция по его выполнению (2 мин).

А дома я предлагаю вам выполнить творческий эксперимент. Проверить формулу Пика на задачах по чертежу.

Ученики записывают домашнее задание в дневник. Карточка – задачи на формулу Пика (Приложение 9, 9а). Задачи для подготовки к ГИА (варианты 1-7)

Регулятивные

IX. Рефлексия учебной деятельности на уроке. (2 мин)

Цель: осознание обучающимися своей учебной деятельности, самооценка результатов своей деятельности и всего класса

Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу. Один из самых простых и доступных способов вычисления площадей был открыт Евклидом. При вычислении площадей он использовал простой прием, называемый методом разбиения. Надеюсь, что вся эта информация поможет вам хорошо разобраться в этой теме, а значит правильно решить задачи на площади. Ребята, какой прием на ваш взгляд самый простой, практичный и полезный?

Ученики заполняют таблицу -рефлексия. Оценивают уровень своих знаний по данной теме. Какие цели были поставлены в начале урока? Что узнали нового? Что было интересного? Что не поняли? (Приложение 13)

Коммуникативные. Регулятивные. Личностные. Познавательные.

Итоги урока (1 мин).

Спасибо за работу на уроке. Составьте памятки по новым формулам. Посещайте факультативы, пользуйтесь дополнительной информацией и применяйте знания на практике.

Сдают билеты, отзыв об уроке. Выставляют оценки за урок.

Личностные

Литература

1. Геометрия, 7–9: Учеб. Для общеобразоват. Учредений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 14-е изд. – М.: Просвещение, 2011.:384 с.

Интернет-ресурсы:

1. http://ru.wikipedia.org
2. http://dcs.isa.ru
3. http://www.webmath.ru
4. http://hijos.ru
5. http://festival.1september.ru
6. http://morina71.my1.ru

16.07.2014

Поделиться страницей:

urok.1sept.ru

Площадь треугольника

Вопросы занятия:

·  вывести пять основных формул, которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров.

Материал урока

Начнём мы с формулы площади треугольника по стороне и высоте.

Итак, площадь треугольника равна половине произведения длины стороны треугольника на длину высоту, проведённую к ней.

Докажем это утверждение. Пусть  – некоторый треугольник. Проведём к стороне  высоту  и докажем, что площадь треугольника равна .

Достроим треугольник  до параллелограмма . И рассмотрим треугольники  и . У них стороны ,  равны, как противолежащие стороны параллелограмма . А сторона  – общая. Следовательно, треугольники  равны по трём сторонам, то есть по третьему признаку. А значит, .

Так как параллелограмм  состоит из рассмотренных треугольников  и , то его площадь равна . А так как треугольники имеют равные площади, то можем записать, что площадь параллелограмма равна . Отсюда площадь треугольника .

Мы уже знаем, что площадь параллелограмма равна произведению длины стороны на высоту, проведённую к ней. А тогда площадь нашего параллелограмма .

Подставим получившееся выражение в предыдущее равенство и получим, что площадь треугольника .

Что и требовалось доказать.

Из доказанного следует, что площадь прямоугольного треугольника равна половине произведения длин его катетов.

Возьмём некоторый прямоугольный треугольник .

Катет  – это и есть высота, проведённая к стороне , которая также является катетом. А тогда, так как площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней, получаем, что площадь треугольника  равна половине произведения длин катетов рассматриваемого треугольника.

Задача.

Найдите площадь треугольника , если длина стороны  см, а высота , проведённая к этой стороне, в  раза её меньше.

Так как по условию задачи длина высоты  в 2 раза меньше стороны , то запишем:

Мы доказали, что площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней. А тогда площадь рассматриваемого треугольника найдём как . Подставим известные нам значения  и . Выполним вычисления и получим,

Задача.

Найти длины катетов прямоугольного треугольника, если они относятся как , а его площадь равна  см².

Пусть  – прямоугольный треугольник, у которого катет . По свойству пропорции имеем . Откуда .

Выше мы выяснили, что площадь прямоугольного треугольника равна половине произведения длин его катетов. А тогда площадь рассматриваемого прямоугольного треугольника равна .

Подставим в эту формулу вместо . И выполнив преобразования, получим,

Так как из условия задачи известна площадь треугольника, то можем приравнять . Разделим обе части равенства на  и получим, что . Отсюда  (см). При этом обратите внимание, что мы взяли только положительное значение , так как длина стороны не может быть отрицательной.

Чтобы найти длину второго катета  подставим найденное значение  в равенство: . Выполним вычисления и получим,

Следующей вспомним формулу площади треугольника по трём сторонам.

Эта формула имеет своё название: формула Герона.

Площадь треугольника со сторонами ,  и  выражается следующей формулой: , где .

Докажем это утверждение.  Итак, рассмотрим треугольник , в котором ,  и .

Понятно, что в любом треугольнике по крайней мере два угла острые. Допустим, углы  и  – острые. Из вершины  треугольника опустим высоту  на сторону .

Тогда имеем два прямоугольных треугольника  и . Введём обозначения: ,  и . Понятно, что длина стороны .

По теореме Пифагора выразим общую сторону  треугольников  и .

; 

Затем приравняем правые части, получившихся равенств и преобразуем равенство. Теперь давайте разложим выражение в левой части нашего равенства на множители по формуле разности квадратов. Учтём, что длина стороны , разделим обе части равенства на .

И затем сложим последнее равенство с равенством .  И разделим обе части получившегося равенства на 2. Получим,

Теперь найдём высоту  треугольника . Применим формулу разности квадратов. Затем заменим . Упростим выражения в скобках. Потом в первой скобке воспользуемся формулой квадрата разности, а во второй – формулой квадрата суммы. А теперь разложим числители обеих дробей разложим на множители, применяя формулу разности квадратов:

Поскольку полупериметр равен . То имеем,

Подставим эти выражения в найденное выражение для . Получим,

Тогда  равно

Напомним, что площадь треугольника можно вычислить по формуле . Заменим высоту нашим выражением. Тогда получаем, что площадь треугольника можно вычислить по формуле:

А это и есть формула Герона.

Задача.

Найти площадь треугольника со сторонами  см,  см и  см.

Нам известны длины трёх сторон треугольника, значит, можем воспользоваться формулой Герона . Для этого вычислим полупериметр. Он равен  (см).

Теперь можем поставить все известные нам данные в формулу. Выполним вычисления и получим, что площадь данного треугольника равна

Следующей повторим формулу площади треугольника по двум сторонам и углу между ними.

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Докажем это утверждение. Пусть есть произвольный треугольник . Из вершины  опустим высоту .  

Рассмотрим треугольник . Он прямоугольный по построению, так как . По определению синуса острого угла в прямоугольном треугольнике имеем . Отсюда получаем, что высота .

Мы помним, что площадь треугольника равна . Подставим вместо . А тогда получаем, что площадь треугольника можно вычислить как:

Задача.

Найти площадь , если  см,  см, .

Запишем формулу для вычисления площади треугольника.

Подставим в эту формулу данные из условия задачи. Посчитаем и получим, что площадь треугольника равна

Теперь перейдём к формуле площади треугольника по трём сторонам и радиусу описанной окружности.

Докажем, что площадь данного треугольника можно вычислить по формуле:

Итак, пусть есть треугольник  со сторонами ,  и . И дана окружность с центром в точке О, которая описана вокруг треугольника.

Обозначим угол . Напомним, что площадь треугольника можно вычислить по двум сторонам и углу между ними. Подставим наши данные в ормулу.

По следствию из теоремы синусов имеем, что радиус описанной окружности равен

Выразим из этой формулы . И подставим полученное выражение в первую формулу.

Упростим. Получим, что площадь треугольника можно вычислить по следующей формуле.

Что и требовалось доказать.

Задача.

В окружность с радиусом  см вписан . Причем сторона  треугольника является диаметром этой окружности, а сторона  равна  см. Найти площадь треугольника.

Так как сторона  по условию задачи, то . Известно, что вписанный угол, опирающийся на диаметр, — прямой. Поэтому угол . А значит, треугольник  прямоугольный. По теореме Пифагора найдём его катет . Получаем, что  равно

Подставим все данные в формулу площади треугольника по трём сторонам и радиусу описанной окружности. Посчитаем и получим, что площадь данного треугольника равна

И рассмотри последнюю формулу площади треугольника по трём сторонам и радиусу вписанной окружности.

Площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности.

Докажем это утверждение. Итак, пусть есть треугольник , у которого ,  и . И дана окружность с центром в точке О, которая вписана в треугольник.

Докажем, что площадь данного треугольника можно вычислить по формуле: .

Рассмотрим треугольник . Отрезок , как радиус, проведенный в точку касания. Значит,  – высота .

Мы помним, что площадь треугольника можно вычислить, как половину произведения стороны на высоту, проведённую к ней. Тогда площадь треугольника равна .

Аналогично можем найти площади треугольников  и .

А так как площадь всего треугольника равна сумме площадей этих трёх треугольников, то получаем, что площадь треугольника  равна

Заметим, что первый множитель является полупериметров нашего треугольника. А тогда имеем площадь треугольника равна

Задача.

Дан равнобедренный треугольник со сторонами  см,  см и  см. Найдите радиус вписанной окружности.

Воспользуемся формулой площади треугольника по трём сторонам и радиусу вписанной окружности. Найдём площадь треугольника. Для этого опустим высоту . Так как в равнобедренном треугольнике высота является и медианой, то .

В прямоугольном треугольнике  по теореме Пифагора найдём . Получаем,

Напомним, что площадь треугольника можно вычислить как половину произведения стороны на высоту, проведённую к ней. Тогда площадь треугольника равна

Вычислим полупериметр. Он равен . А теперь из нашей первой формулы выразим радиус вписанной окружности. Подставим известные значения. Посчитаем и получим, что радиус окружности равен .

Итоги урока

На этом уроке мы говорили о «площади треугольника». А точнее вывели пять основных формул, которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров.

videouroki.net

Материал по геометрии (9 класс) по теме: Урок по геометрии в 9 классе по теме «Площадь треугольников»

«Теорема о площади треугольника». 9 класс

Цели урока:

— Доказать теорему о площади треугольника.

— Научить учащихся решать задачи на применение теоремы о площади треугольника.

— Развивать математическое и логическое мышление, самостоятельность. Учить  работать с книгой, чертежами и дополнительным материалом.

— Воспитывать уважительное отношение к своему и чужому труду, умение выступать и слушать.  

Оборудование:

— листы с заданиями с копировальной бумагой;

— распечатанные задания для устного счета и домашнего задания.

— готовые чертежи для демонстрации.

Ход урока.

1.Организационный момент.

2.Актуализация знаний. Повторение теории.

       Вчера вечером я пошла в магазин и все думала, сколько купить краски. Вы мне не поможете? На 1 квадратный дециметр расходуется 2 грамма. (Добиться от детей зависимость покраски от площади.)

       Как определить площадь прямоугольника? (Дети дают определение.)

     Одна торговая компания решила сделать рекламный щит вот такой неправильной формы. (Показать.) Как определить площадь этой поверхности? (Дети должны предложить разделить ее на треугольники, определить площадь каждой и найти сумму площадей.)

       Начиная с 5 класса, мы изучаем площадь треугольника. Изучили несколько способов и сегодня у нас новая тема « Теорема о площади треугольника». Давайте вспомним основные понятия, которые нам будут необходимы сегодня на уроке.

А) Пусть задана система координат и дана произвольная точка А(х;у) с неотрицательной ординатой (у). Скажите пожалуйста,

какие формулы используются для вычисления координат точки А?

( Ответ: x = OA * cosα  ; y = ОА *sin α ) (  Готовый чертеж на доске).  

Б) Как записывается основное тригонометрическое тождество?

(  cos² α + sin² α = 1 )

В) Давайте вспомним формулы приведения. ( sin ( 90° + α) = cos α ;  

  sin ( 180º – α) = sin α;   cos (180° – α) = — cos α ; cos ( 90º + α) = -sin α )                                                            

Посчитаем устно.

 ( Готовые чертежи на доске, а у детей распечатки на столе. При устном счете рассмотреть различные способы вычисления площади фигуры, деление на прямоугольники и по различным формулам, правилам.)

1)Вот обычный лист бумаги, его площадь 630 квадратных сантиметров, определите площадь заштрихованной части. (Заштрихован треугольник, образованный диагональю и смежными сторонами.)

2) На столе у вас есть рисунок к заданию В6 для подготовки к ЕГЭ № 5143. Определите площадь треугольника. ( Дети по клеточкам определяют площадь.)

На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

3) Следующее задание для устного счета В6 № 24271. Найдите площадь закрашенной фигуры на координатной плоскости.

Найдите площадь закрашенной фигуры на координатной плоскости.

4) Как определить площадь трапеции? Посмотрите рисунок В6

№ 5195.

На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

Хорошо познакомились с заданиями из ЕГЭ, которые можно просто решить по клеточкам или используя определение площади. А теперь вспомним другие способы определения площади треугольника. На доске  3 задачи (готовые чертежи) решаем группами. 1 группа 1 задачу, 2 группа 2 задачу, 3 группа 3 задачу.

№ 1 Дан прямоугольный треугольник гипотенуза 5 единиц, а основание 3 единицы ( высота = 4, площадь = 6 )

В

С        А

№ 2   Дан произвольный треугольник со сторонами 5, 6, и 7 единиц. Определить  площадь треугольника (По формуле Герона  полупериметр = 9, а площадь 6√6)

                  В

            5

         6

  А

        7                С

№ 3 Дан равнобедренный треугольник  основание которого 8 единиц, угол при основании равен 60°. Найти площадь треугольника. ( Высота 4√3 , площадь 16√3)

        

                   В

        

А              D              С

Решили, а теперь рассмотрим решения этих задач. (Дети объясняют у доски решения ).

№ 4  Дан произвольный треугольник  стороны, которого 6 и 5 единиц, угол между ними = 38º.  Каков план решения 4 задачи?

( Дети определяют, что пока не могут решить ее.)

                 

                                                       А

                                 6

          α

                    О

             5        В

 

3. Изучение нового материала.

Давайте решим эту задачу если стороны не конкретные числа, а некоторые переменные.

Пусть дан произвольный треугольник АВС, СВ = а, СА = в, ﮮС =ﮮα   .

Найти : площадь треугольника.

Введем систему координат с началом в точке С так, чтобы  точка А лежала на положительной полуоси Сх,  а точка В имела положительную  ординату.

По какой формуле определяется площадь треугольника?              

S   = 1/2* АС * ВН .    

Что является высотой, основанием?

Как определить координаты точки В? ( х = а * cos α     у = a * sin α )              

Высота треугольника чему равна?  ( Ординате точки В у = а * sinα)

Итак: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Вот вам еще одна формула для нахождения площади треугольника.

Прочитаем теорему в учебнике пункт 96.

В формуле площади треугольника, где по отношению к сторонам а и в треугольника расположен угол.

А теперь вернемся к решению нашей 4 задаче.

Так какую теорему мы доказали? Как она читается?

В формуле площади треугольника, где по отношению к сторонам а и в треугольника расположен угол?

4. Закрепление изученного материала. Тренировочные упражнения.

Решите задачи ( задания делаем через копировку). Решили, сдали. Рассмотрим решения на доске. (Дети показывают решения.)

№ 1 Дан остроугольный треугольник со сторонами 4 и 5√2 и углом между ними 45° . Определите площадь.(Площадь 10.)

                  В

            4

         

  А

        5√2                С

№ 2. Дан тупоугольный треугольник со сторонами 8 и 2√3 и углом между ними 120º  . Определите площадь треугольника.(Площадь 12.)

                 

         В

           

         

               2√3

                                                                               С

                120º              

          А        8

№ 3.Дан равнобедренный треугольник с боковой стороной равной 5. Угол у основания 15 . Найти площадь.( Площадь 6,25).

                  В

15º                                 

                                                                                       15°                                

                     5

    15º                                 

  С

                         А        5

5. Занимательный момент.

 Нужно разделить большой треугольный лоскут на пять небольших треугольников так, чтобы их площади относились как 1 : 2 : 2 : 3 : 4

6.Итог урока.

Какую теорему мы изучили?

В формуле площади треугольника, где по отношению к сторонам а и в треугольника расположен угол?

7.Домашнее задание. П 96; № 1020(а,б). № 4849,  и дать адрес сайта.

nsportal.ru

«Формулы для нахождения площади треугольника».

Просмотр содержимого документа
«Тема урока: «Формулы для нахождения площади треугольника».»

Добро пожаловать! МБОУ СОШ №1 с. НОГИР

Тема урока: «Формулы для нахождения площади треугольника» .

Учитель математики

МОУ-СОШ №1

С.Ногир

Качмазова Ира Даниловна

Тип урока

• Урок обобщения и систематизации знаний

Формируемые результаты

• Предметные: формировать навыки применения формул для нахождения площади треугольника
• Личностные: развивать навыки самостоятельной работы, анализа своей работы
• Метапредметные: формировать умение осуществлять контроль своей деятельности в процессе достижения результата

Планируемые результаты

• Учащийся научится применять формулы для нахождения площади треугольника

Основные понятия

1. Организационный этап

• Итак, урок я начинаю
• Всем успехов пожелаю
• Думать, мыслить не зевать,
• Быстро все в уме считать!

2. Мотивация урока

«Недостаточно овладеть премудростью,

Нужно также уметь пользоваться ею »

Цицерон

3. Актуализация опорных знаний. Проверка д/з

• Как можно найти площадь треугольника, зная его основание и высоту?
• Как можно найти площадь треугольника, если известны две его стороны и угол между ними?
• Запишите формулу Герона для вычисления площади треугольника.
• Как можно найти площадь треугольника, если известны три его стороны и радиус описанной окружности?
• Как можно найти площадь треугольника, если известны его полупериметр и радиус вписанной окружности?

4. Обобщение и систематизация знаний

Решаем № 134 из учебника

Два ученика решают у доски №138 (1,2)

Ответы: №134 — 20см²

№ 138 (1)- 84 см²

№ 138 (2)- 3√15 см²

4

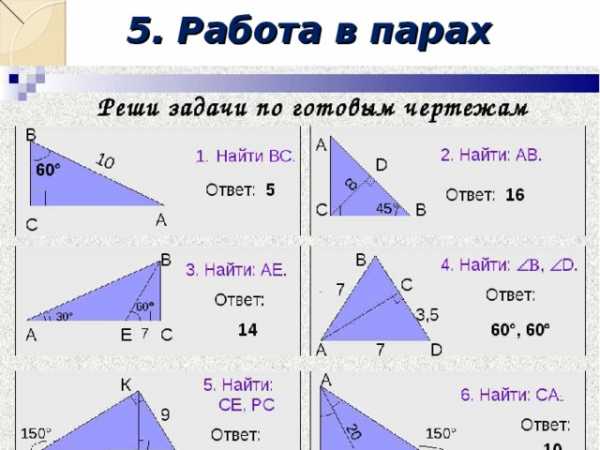
5. Работа в парах

• Решите уравнение:

6. Упражнения для глаз

• Закрыв глаза, мысленно представить по очереди как можно отчетливее все цвета радуги. «Нарисовать» глазами спираль в одном направлении, затем в другом направлении.

7. Самостоятельная работа . (Новые подходы в преподавании и обучении).

• Решение тестовых заданий.
• 1. Если стороны треугольника 4 см, 6 см, 6 см, то его площадь равна:
• А) 80 √2 см 2 , В) 18 см 2 , С) 24 см 2 , Д) 8 √2 см 2 .
• 2. В треугольнике АВС угол ВАС=30º . Если АВ=3 см, АС=8 см, то площадь треугольника АВС равна:
• А) 6 √3 см 2 , В) 6 см 2 , С) 12 см 2 , Д) 12 √3 см 2 .
• 3. Катеты прямоугольного треугольника равны. Найдите их длину, если площадь треугольника равна 20 см 2 .
• А) 5 см , В) √10 см , С) 4√10 см , Д) 2 √10 см .
• 4. Если стороны треугольника равны 5 см, 6 см, 9 см, то его площадь равна:
• А) 10 √2 см 2 , В) 10 см 2 ,
• С) 20 см 2 , Д) 6 √2 см 2 .

8. Рефлексия

На уроке мне было все понятно

Немного затруднялся в решении задач

Я узнал, запомнил формулы для нахождения площади треугольника

Я все понял, но ошибался в решении задач

Мне все понятно и было интересно решать задачи

9. Домашнее задание

• пар. 5 № 141,143,145,165

multiurok.ru

Презентация к уроку по геометрии (9 класс) по теме: Теорема о площади треугольника

Слайд 1

Теорема о площади треугольника

Слайд 2

Проверка домашней работы

Слайд 3

Устная работа Найдите площадь тре у гольника: h =7 4 5 4 5 8 3

Слайд 4

Формулы площади треугольника S=1/2ab, где а, в — катеты прямоугольного треугольника S= 1/2ah , где а — основание треугольника, h — высота S= р-полупериметр , а,в,с-стороны треугольника

Слайд 5

Теорема о площади треугольника Дано: ABC, BC=a, CA=b, S- площадь треугольника. Доказать : S=1/2absinC Док-во : S=1/2ah, h= bsinC . Сл. S=1/2absinC

Слайд 6

Формула нахождения площади треугольника S=1/2absinC

Слайд 7

Решение задач № 1020(а), 1024(а) Дополнительная задача: Найдите площадь равнобедренного треугольника с углом при основании 15 и боковой стороной, равной 5см. В треугольнике АВС АВ=4, ВС=6, В D -биссектриса, угол АВС=45 . Найдите площадь треугольников АВ D и СВ D

Слайд 8

План решения задачи Найти площадь треугольника АВ D . Найти отношение площадей треугольников АВ D и СВ D . Найти площадь треугольника АВС Выразить площади треугольников

Слайд 9

Подготовка к ГИА Задачи: 1. В параллелограмме ABCD AB=6, AD=4, sinA =0,8. Найдите большую высоту параллелограмма. 2. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону трапеции.

Слайд 10

Решение задач Решение: Решение: A B C D 6 4 A B C D 6 12

Слайд 11

Самостоятельная работа . Найдите SINA , если COSA=-1 /3 ( COSA=-1 /4) 2. Найдите COSA , если SINA= 2 /5 ( COSA=-2 /3) 3 . Проверьте, лежат ли на единичной окружности точки: В(7;3),С(0,5;0,5) (С(2;3), В(-0,5;0,5)) 4. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен А. Найдите координаты точки М, если ОМ=8,(ОМ=10) А=30 (А=60 )

Слайд 12

Домашнее задание П. 96 (доказательство теоремы) № 1020 (б, в ) , 1021, 1022

nsportal.ru

Найдите площадь треугольника изображённого

Здравствуйте! В этой статье мы разберём задачи на нахождение площади треугольника построенного на листке в клетку (масштаб клетки 1×1). Фигуры на листе в клетку с вычислением их площади — это целая группа типов задач входящая в экзамен по математике. Кроме треугольника рассматриваются следующие фигуры — трапеция, параллелограмм, ромб, квадрат.

Решение заданий с треугольником труда не представляет, относятся они к простейшим. Для решения необходимо знать формулу площади треугольника и знать один приём, о котором я вам расскажу ниже.

Вообще, способов нахождения площади любой фигуры, построенной на листе в клетку существует более пяти. Все здесь рассматривать не будем, в интернете вы без труда найдёте их описание. Уверен, что тех рекомендаций, которые представлены будет вполне достаточно для решения. 

Итак! Вам необходимо знать и понимать одну из основных формул площади треугольника, она наиболее часто используется при решении:

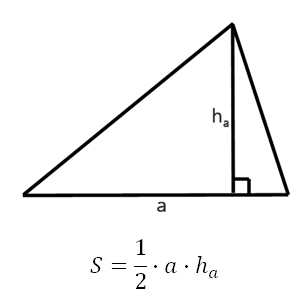
Длину основания и высоту считаем по клеткам. В задаче 27545 это наглядно показано. То есть, если перед вами задача, где треугольник построен именно таким образом, то считаем оговоренным способом. Например, рассмотрим треугольники:

 

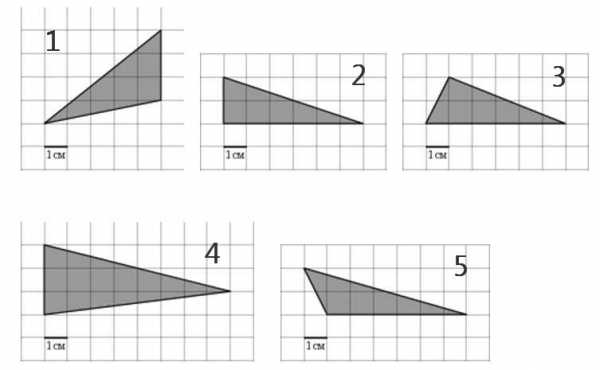
У всех этих треугольников можно по клеткам установить длину основания и высоту. У первого основание равно 3, высота 5; у второго основание 6, высота 2; у третьего основание 6, высота 2; у четвертого основание равно 3, высота 8; у пятого основание равно 6, высота 2. Подставив их в формулу, остаётся только вычислить площадь (без ошибки).

Есть задачи, в которых треугольники расположены так, что по клеткам длину основания и высоту посчитать неудобно (но можно), вот примеры:

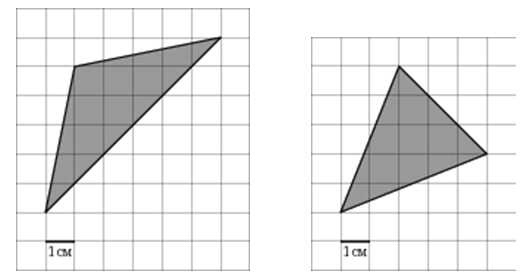
В задачах, где будут даны подобные треугольники, используйте способ, который по моему мнению универсален, его достоинство объясню в одной из следующих статей: «заключите» такой треугольник в прямоугольник, вычислите площадь прямоугольника, затем из его площади вычтите площади треугольников. Пример:

Найти площадь треугольника, изображённого на рисунке:

Заключим данный треугольник в прямоугольник:

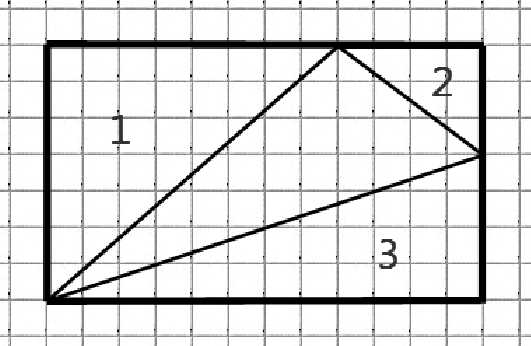
   Теперь вычислим площадь прямоугольника. Уверен, всем известно, что она равна произведению его соседних сторон:

Далее из его площади вычитаем площади трёх треугольников:

Ответ: 26

Есть ещё подобные задачи, но в них иначе представлено условие. Также нужно найти площадь треугольника, он построен на координатной плоскости, например:

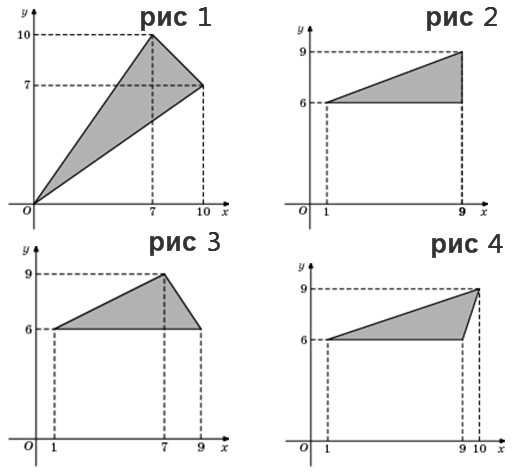
Решения аналогичны: если можем установить длину основания и высоту треугольника  по  координатам, то далее площадь вычисляем просто по формуле: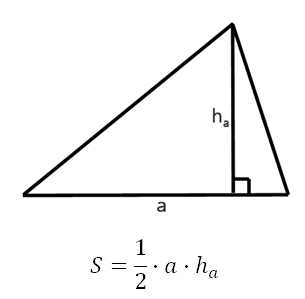

В треугольнике на рисунке 1  этого сделать  нельзя, поэтому советую построить данный треугольник по координатам на листе в клетку, и использовать уже рассмотренный нами метод, а именно описать около треугольника прямоугольник.

В будущем мы рассмотрим нахождения площадей параллелограммов, трапеций, четырёхугольников, элементов круга, а так же «сложных» фигур, не пропустите!

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru