\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
\[Re\ \tilde{x}=Re\left(A\cdot exp\ \left(i\left({\omega }_0t+\varphi \right)\right)\right)\left(3\right).\]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
\[T=2\pi \sqrt{\frac{m}{k}}\left(4\right).\]
Так как частота колебаний ($\nu $) — величина обратная к периоду, то:
\[\nu =\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\left(5\right). 2_0}}\left(6\right),\]
2_0}}\left(6\right),\]
начальная фаза при этом:
\[tg\ \varphi =-\frac{v_0}{x_0{\omega }_0}\left(7\right),\]
где $v_0$ — скорость груза при $t=0\ c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
\[E_p=-\frac{dF}{dx}(8)\]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
\[E_p=\frac{kx^2}{2}=\frac{m{{\omega }_0}^2x^2}{2}\left(9\right). 2}{2}$ — кинетическая энергия маятника.
2}{2}$ — кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600\ \frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1\ \frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
\[E_{pmax}=E_{kmax\ }\left(1.1\right),\]
где $E_{pmax}$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax\ }$ — кинетическая энергия шарика, в момент прохождения положения равновесия. 2 \left(\omega t\right)\ }}{2}\left(2.2\right).\]
2 \left(\omega t\right)\ }}{2}\left(2.2\right).\]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
\[\frac{E_{p0}}{F_0}=-\frac{A}{2}{\cos \left(\omega t\right)\ }\to t=\frac{1}{\omega }\ arc{\cos \left(-\frac{2E_{p0}}{AF_0}\right)\ }.\]
Ответ. $t=\frac{1}{\omega }\ arc{\cos \left(-\frac{2E_{p0}}{AF_0}\right)\ }$
Читать дальше: формулы равноускоренного прямолинейного движения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Свободные колебания. Пружинный маятник
Определение 1Свободные колебания могут совершаться под действием внутренних сил только после выведения из положения равновесия всей системы.
Чтобы колебания совершались согласно гармоническому закону, нужно, чтобы сила, возвращающая тело в положение равновесия, была пропорциональна смещению тела из равновесного положения и направлена в сторону, противоположную смещению.
F(t)=ma(t)=-mω2x(t).
Соотношение говорит о том, что ω является частотой гармонического колебания. Данное свойство характерно для упругой силы в пределах применимости закона Гука:
Fупр=-kx.
Определение 2Силы любой природы, которые удовлетворяют условию, называют квазиупругими.
То есть груз с массой m, прикрепляющийся к пружине жесткости k с неподвижным концом, изображенным на рисунке 2.2.1, составляют систему, способную совершать гармонические свободные колебания при отсутствии силы трения.
Груз, располагаемый на пружине, называют линейным гармоническим осциллятором.
Рисунок 2.2.1. Колебания груза на пружине. Трения нет.
Круговая частота
Нахождение круговой частоты ω0 производится с помощью применения формулы второго закона Ньютона:
ma=-kx=mω02x.
Значит, получаем:
ω0=km.
Определение 4Частоту ω0 называют собственной частотой колебательной системы.
Определение периода гармонических колебаний груза на пружине Т находится из формулы:
T=2πω0=2πmk.
Горизонтальное расположение системы пружина-груз, сила тяжести компенсируется силой реакции опоры. При подвешивании груза на пружину направление силы тяжести идет по линии движения груза. Положение равновесия растянутой пружины равняется:
x0=mgk, тогда как колебания выполняются около нового равновесного состояния. Формулы собственной частоты ω0 и периода колебаний Т в вышеуказанных выражениях являются справедливыми.
Определение 5При имеющейся математической связи между ускорением тела а и координатой х поведение колебательной системы характеризуется строгим описанием: ускорение является второй производной координаты тела х по времени t:
a(t)=x(t).
Описание второго закона Ньютона с грузом на пружине запишется как:
ma-mx=-kx, или x¨+ω02x=0, где свободная частота ω02=km.
Если физические системы зависят от формулы x¨+ω02x=0, тогда они в состоянии совершать свободные колебательные гармонические движения с различной амплитудой.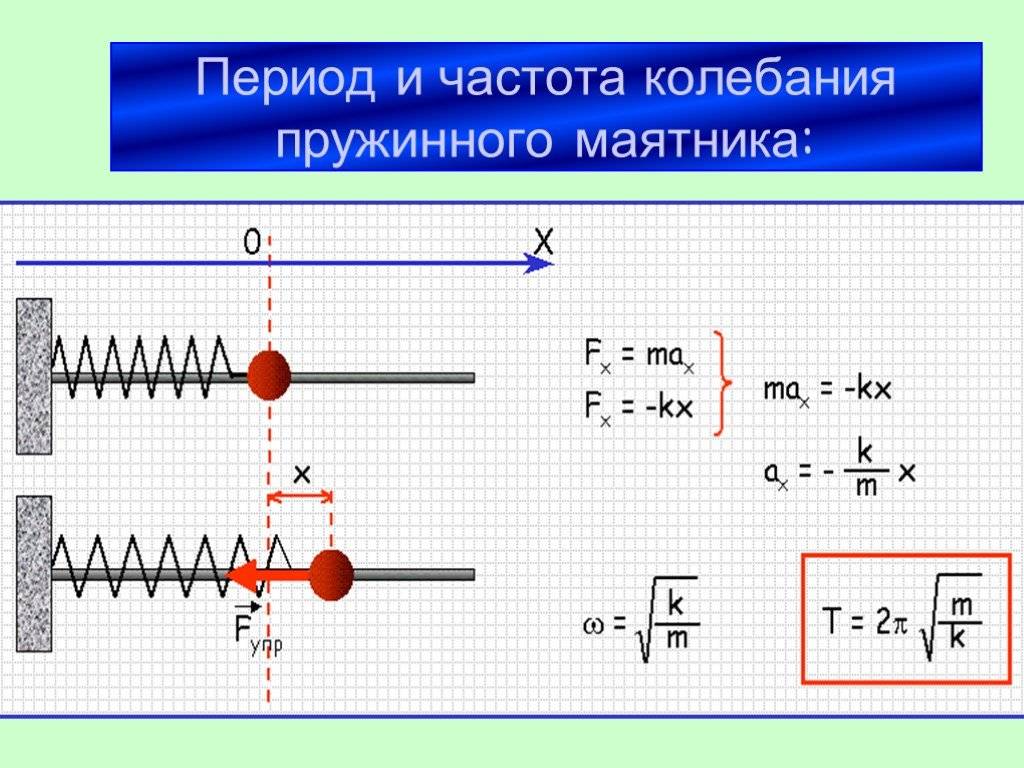 Это возможно, так как применяется x=xmcos (ωt+φ0).
Это возможно, так как применяется x=xmcos (ωt+φ0).
Свободные колебания
Определение 6Уравнение вида x¨+ω02x=0 получило название уравнения свободных колебаний
Амплитуда xm и начальная фаза φ0 находят при помощи способа, который вывел их из состояния равновесия начального момента времени.
Пример 1При наличии смещенного груза из положения равновесия на расстояние ∆l и моменте времени, равном t=0, производится его опускание без начальной скорости. Тогда xm=∆l, φ0=0. Если груз находился в положении равновесия, то при толчке передается начальная скорость ±υ0, отсюда xm=mkυ0, φ0=±π2.
Амплитуда xm с начальной фазой φ0 определяются наличием начальных условий.
Рисунок 2.2.2. Модель свободных колебаний груза на пружине.
Механические колебательные системы отличаются наличием сил упругих деформаций в каждой из них. Рисунок 2.2.2 показывает угловой аналог гармонического осциллятора, совершающий крутильные колебания.
Mупр=-xθ.
Данное выражение не соответствует закону Гука для деформации кручения. Величина x аналогична k жесткости пружины. Запись второго закона Ньютона для вращательного движения диска принимает вид
Iε=Mупр=-xθ или Iθ¨=-xθ, где моментом инерции обозначается I=IC, а ε – угловое ускорение.
Аналогично с формулой пружинного маятника:
ω0=xI, T=2πIx.
Применение крутильного маятника замечено в механических часах. Он получил название балансира, в котором создание момента упругих сил производится при помощи спиралевидной пружины.
Рисунок 2.2.3. Крутильный маятник.
Автор: Роман Адамчук
Преподаватель физики
ньютоновской механики.
 Почему простой маятник или система пружинных масс демонстрируют простое гармоническое движение только для малых амплитуд?
Почему простой маятник или система пружинных масс демонстрируют простое гармоническое движение только для малых амплитуд?Простой маятник не показывает строго гармоническое движение, если вы не допускаете некоторых приближений и неопределенностей. Он примерно ведет себя как гармонический осциллятор для малых амплитуд.
Говорят, что объект совершает простое гармоническое движение (без затухания, без вынужденных колебаний) тогда и только тогда, когда он удовлетворяет следующему условию: 92 \phi \tag{1}$$
где $\phi$ — переменная величина, такая как смещение, угловое смещение и т.д.
Совершает ли маятник простое гармоническое движение?
Уравнение движения маятника можно записать так:
$$\vec{F} = {m\vec{g}} — \vec{T}$$
Мы знаем, что маятник Боб будет двигаться по кругу (предположим, что струна не натянута), следовательно, движения в направлении струны нет. Это будет означать, что результирующая сила, действующая на груз, будет использоваться для обеспечения постоянной центростремительной силы.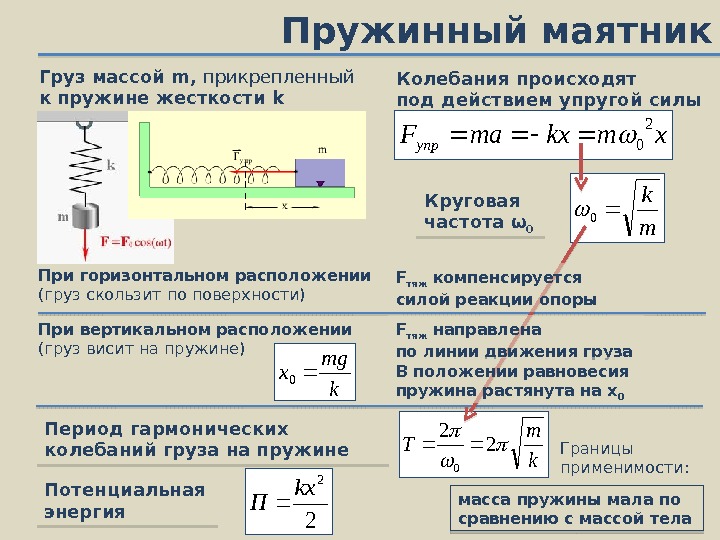 92} = -g \sin \theta \tag{4}$$
92} = -g \sin \theta \tag{4}$$
Если вы сравните уравнение $(4)$ с уравнением $(1)$, вы заметите, что они не совпадают.
Это означает, что маятник не совершает простого гармонического движения.
Однако если амплитуда мала, то и максимальное значение $\theta$ мало. Приближение малого угла можно сформулировать следующим образом:
$$\sin \theta \ приблизительно \theta$$
Источник изображения: Википедия
Используя приближение, вы можете переписать уравнение $(4)$ как 92} = -g\theta \tag{5}$$
Приведенное выше уравнение очень похоже на уравнение $(1)$. Оно идеально совпадает. Поэтому при малых амплитудах маятник совершает простое гармоническое движение с разумной неопределенностью.
Совершает ли система масса-пружина простое гармоническое движение?
Если пружина подчиняется закону Гука, то она всегда совершает простое гармоническое движение.
Закон Гука утверждает, что:
$$F_{восстановление} = ma = — kx \tag{6}$$
Из приведенного выше уравнения ясно видно, что ускорение прямо пропорционально смещению и действует в направлении, противоположном смещению.
Почему мы ограничиваем амплитуду пружинно-массовой системы?
При сильном растяжении пружина не подчиняется закону Гука. Это вроде как очевидно: если слишком сильно растянуть пружину, она деформируется навсегда. Следовательно, уравнение $(6)$ больше не выполняется. Если это уравнение не выполняется, то масса не будет совершать простое гармоническое движение.
Колебание простого маятника
Эта работа Дэна Рассела находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
На основе работы на http://www.acs.psu.edu/drussell/demos.html.
Уравнение движения
Простой маятник состоит из шара (масса точки) м , подвешенного на (безмассовой) нити длиной L и закрепленной в точке вращения P. При смещении на начальный угол и отпускании маятник качается назад и вперед с периодическим движением. Применяя второй закон Ньютона для вращательных систем, можно получить уравнение движения маятника. 2} + \frac{g}{L}\theta = 0 $$
Простое гармоническое решение
$$\theta(t) = \theta_o \cos(\omega t) \ , $$
где \(\theta_o\) — начальное угловое смещение, а \(\omega = \sqrt{g/L}\) собственная частота движения. Период этой системы (время одного колебания) равен
$$ T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{L}{g}} . $$
2} + \frac{g}{L}\theta = 0 $$
Простое гармоническое решение
$$\theta(t) = \theta_o \cos(\omega t) \ , $$
где \(\theta_o\) — начальное угловое смещение, а \(\omega = \sqrt{g/L}\) собственная частота движения. Период этой системы (время одного колебания) равен
$$ T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{L}{g}} . $$
Малые угловые смещения производят простое гармоническое движение
Период маятника зависит не от массы шара, а только от длины нити. Два маятника с разными массами, но одинаковой длины будут иметь одинаковый период. Два маятника разной длины будут иметь разные периоды; маятник с более длинной нитью будет иметь больший период.Сколько полных колебаний совершают синий и коричневый маятники за время одного полного колебания более длинного (черного) маятника?
Исходя из этой информации и определения периода простого маятника, каково отношение длин трех маятников?
В предположении малых углов частота и период маятника не зависят от начальной амплитуды углового смещения. Маятник будет иметь один и тот же период независимо от его начального угла. Это простое приближение показано на анимации слева. Все три маятника совершают одно полное колебание за одинаковое время, независимо от начального угла. 92} + \frac{g}{L}\sin\theta = 0 $$
Это дифференциальное уравнение не имеет решения в закрытой форме, а вместо этого должно решаться численно с помощью компьютера.
Маятник будет иметь один и тот же период независимо от его начального угла. Это простое приближение показано на анимации слева. Все три маятника совершают одно полное колебание за одинаковое время, независимо от начального угла. 92} + \frac{g}{L}\sin\theta = 0 $$
Это дифференциальное уравнение не имеет решения в закрытой форме, а вместо этого должно решаться численно с помощью компьютера.
Приближение малого угла справедливо для начальных угловых смещений около 20° или меньше. Если начальный угол меньше этой величины, то достаточно простого гармонического приближения. Но если угол больше, то различия между малоугловым приближением и точным решением быстро становятся очевидными.
На анимации внизу слева начальный угол мал. Темно-синий маятник — приближение малого угла, а светло-голубой маятник (изначально спрятанный сзади) — точное решение. Для малого начального угла требуется довольно большое количество колебаний, прежде чем разница между малоугловым приближением (темно-синий) и точным решением (светло-синий) начнет заметно расходиться.
