Формула комплексного числа модуля: Как найти модуль и аргумент комплексного числа: онлайн, примеры

Вся элементарная математика — Средняя математическая интернет-школа

Комплексные числа

Мнимые и комплексные числа. Абсцисса и ордината

комплексного числа. Сопряжённые комплексные числа.

Операции с комплексными числами. Геометрическое

представление комплексных чисел. Комплексная плоскость.

форма комплексного числа. Операции с комплексными

числами в тригонометрической форме. Формула Муавра.

Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая

D D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики

и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.

Комплексные числа записываются в виде: a + bi . Здесь a и b – действительные числа , а i – мнимая единица, т. e . i ² =

–1. Число a называется абсциссой , a b – ординатой комплексного числа a + bi . Два комплексных числа a + bi и a – bi называются сопряжёнными комплексными числами.

Основные договорённости:

1.  Действительное число а может быть также записано в форме комплексного числа: a + 0 i

или a – 0 i . Например, записи  5 + 0 i и  5 – 0 i означают одно и то же число 5 .

2.  Комплексное число 0 + bi называется чисто мнимым числом . Запись bi означает то же самое, что и  0 + bi .

3.  Два комплексных числа a + bi и c + di считаются равными, если

a = c и b = d . В противном случае комплексные числа не равны.

Сложение. Суммой комплексных чисел a + bi и c + di называется комплексное число ( a + c ) + ( b + d ) i . Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.

Это определение соответствует правилам действий с обычными многочленами.

Вычитание. Разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое) называется комплексное число ( a – c ) + ( b – d ) i .

Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.

Умножение. Произведением комплексных чисел a + bi и c + di называется комплексное число:

( ac – bd ) + ( ad + bc ) i . Это определение вытекает из двух требований:

1)  числа a + bi и c + di должны перемножаться, как алгебраические двучлены,

2)  число i обладает основным свойством: i ² = – 1.

П р и м е р .  ( a+ bi )( a – bi ) = a

² + b ² . Следовательно, произведение

двух сопряжённых комплексных чисел равно действительному

положительному числу.

Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) — значит найти третье число e + f i (частное), которое будучи умноженным на делитель c + di

,  даёт в результате делимое a + bi .

Если делитель не равен нулю, деление всегда возможно.

П р и м е р .  Найти  ( 8 + i ) : ( 2 – 3 i ) .

Р е ш е н и е . Перепишем это отношение в виде дроби:

Умножив её числитель и знаменатель на  2 + 3 i

и выполнив все преобразования, получим:

Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:

Здесь точка

A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р  с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью .

Модулем комплексного числа называется длина вектора OP , изображающего комплексное число на координатной ( комплексной ) плоскости.

Модуль комплексного числа a + bi обозначается  | a + bi | или буквой r и равен:

Сопряжённые комплексные числа имеют одинаковый модуль. __

Аргумент комплексного числа — это угол между осью OX и вектором OP , изображающим это комплексное число. Отсюда, tan = b / a .

Тригонометрическая форма комплексного числа.

Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент :

Операции с комплексными числами, представленными в тригонометрической форме.

Это знаменитая формула Муавра.

Здесь k — целое . Чтобы получить n различных значений корня n -ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .

Назад

определение, как найти, геометрический смысл

Что такое комплексное число

Комплексное число — это выражение типа \(z\;=\;a\;+\;ib\). Здесь a и b будут являться любыми действительными числами, а i — специальным числом, называемым мнимой единицей. Действительная часть комплексного числа обозначается как \(a\;=\;RE\;z \), а мнимая часть — \(b\;=\;Im\;z\).

Во множестве комплексных чисел содержится множество вещественных чисел. Если множество комплексных чисел — это всевозможные пары (x, y), то содержащееся в нем множество вещественных чисел — это пары (x, 0). Те же комплексные числа, которые задают пары (0, y) являются мнимыми.

Что такое модуль комплексного числа

Модуль комплексного числа — это длина вектора, который изображает комплексное число.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Любое комплексное число кроме 0 может быть выражено в тригонометрической форме.

\(z\;=\;\left|z\right|\;\cdot\;(\cos\left(\varphi\right)\;+\;i\sin\left(\varphi\right))\)

В этом виде \(\left|z\right|\) — модуль комплексного числа z. Может обозначаться как p и r. 

Если \(\left|z\right|\;=\;r,\) то r будет обозначать длину радиус-вектора точки M (x, y).

Вычисление модуля комплексного числа, если в алгебраической форме оно выглядит как z = x + iy, возможно по следующей формуле:

\(\left|z\right|\;=\;\sqrt{x^2\;+\;y^2}\)

То есть модуль комплексного числа можно вычислить как квадратный корень из суммы квадратов действительной и мнимой его частей. 2}\;=\;\sqrt5.\)

Так как \(Re z = 2 > 0\), \(Im z = -1 < 0\), точка расположена в 4 четверти. Тогда из равенства \(\tan\left(\varphi\right)\;=\;-\frac12\) следует:

\(\varphi\;=\;arc\tan\left(-\frac12\right)\)

Ответ: \(\varphi\;=\;arc\tan\left(-\frac12\right)\)

Модуль комплексного числа — формула, график, примеры

LearnPracticeDownload

Модуль комплексного числа — это расстояние комплексного числа от начала координат в аргандовой плоскости. Если z = x + iy — комплексное число, где x и y действительны, а i = √-1, то неотрицательное значение √(x ² + y ² ) называется модулем комплексного числа . (z = x + iy). Модуль комплексного числа также называют абсолютным значением комплексного числа.

В этой статье мы разберем понятие модуля комплексных чисел как алгебраически, так и графически вместе с его формулой и некоторыми решенными примерами для лучшего понимания.

1.	Что такое модуль комплексного числа?
2.	Модуль комплексного числа Формула
3.	Модуль комплексного числа с использованием графика
4.	Свойства модуля комплексного числа
5.	Часто задаваемые вопросы о модуле комплексного числа

Что такое модуль комплексного числа?

Модуль комплексного числа представляет собой квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа. Если z — комплексное число, то модуль комплексного числа z определяется выражением √{[Re(z)] ² + [Im(z)] ² } и обозначается |z|. Модуль комплексного числа z = a + ib — это расстояние между началом координат (0, 0) и точкой (a, b) на комплексной плоскости. Поскольку модуль комплексного числа — это расстояние, его значение всегда неотрицательно.

Модуль формулы комплексного числа

Модуль комплексного числа z = x + iy, обозначаемого |z|, определяется формулой |z| = √(х ² + у ² ) 92\) ⇒ \(|z| = \sqrt{z. \bar{z}}\).

Модуль комплексного числа с использованием графика

Когда комплексное число z отображается на графике, расстояние между координатами комплексного числа и началом координат на комплексной плоскости называется модулем комплексного числа. Расстояние комплексного числа, представленного в виде точки на аргановой плоскости (а, b), называется модулем комплексного числа. Это расстояние представляет собой линейное расстояние от начала координат (0, 0) до точки (a, b) и измеряется как r = √(a ² + б ² ).

Далее, это можно понимать так, как модуль комплексного числа можно вывести из теоремы Пифагора, где модуль представлен гипотенузой, действительная часть – основанием, а мнимая часть – высотой прямоугольного треугольник. Модуль комплексного числа a + bi — это то же самое, что и величина (или длина) вектора, представляющего a + bi.

Свойства модуля комплексного числа

Ниже приведены некоторые свойства комплексного числа. Если z и w два комплексных числа, то имеем:

• Модули комплексных чисел z и -z равны, то есть |z| = |-z|
• Модуль комплексного числа равен 0 тогда и только тогда, когда комплексное число равно нулю, то есть |z| = 0 тогда и только тогда, когда z = 0
• Модуль произведения комплексных чисел равен произведению модуля комплексных чисел, то есть |z.w| = |z|.|w|
• Модуль отношения двух комплексных чисел равен отношению модуля комплексных чисел, то есть |z/w| = |z|/|w|
• Модуль комплексного числа равен модулю сопряженного комплексного числа, то есть \(|z| = |\bar{z}|\)
• Модуль n-й степени комплексного числа равен n-й степени модуля комплексного числа, то есть |z ⁿ | = | г | ^п

Важные замечания по модулю комплексного числа

• Расстояние комплексного числа, представленного в виде точки на плоскости аргана (a, b) от начала координат (0, 0), называется модулем комплексного числа.
• Модуль комплексного числа равен 0 тогда и только тогда, когда комплексное число равно нулю.
• Модуль комплексного числа a + bi — это то же самое, что и модуль (или длина) вектора, представляющего a + bi.
• Модуль комплексного числа — это квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.

Связанные темы по модулю комплексного числа

• Комплексные числа
• Полярная форма комплексного числа
• Умножение комплексных чисел
• Деление комплексных чисел

 

Модуль комплексного числа Примеры

1. Пример 1: Определить модуль комплексного числа z = -6 + 3i.

   Решение: Модуль комплексного числа z = -6 + 3i определяется как,

   |з| = √((-6) ² + (3) ² )

   = √(36 + 9)

   = √45

   = 3√5

   91 Ответ: |z

   0 | = 3√5

2. Пример 2: Вычислите модуль комплексного числа v = (1 + 2i)(-2 + 3i), используя свойство модуля комплексного числа.

   Решение: Имеем v = (1 + 2i)(-2 + 3i). Пусть z = (1 + 2i), w = (-2 + 3i).

   Мы знаем, что |zw| = |z||w|, поэтому будем определять модуль комплексных чисел z и w отдельно.

   |з| = √((1) ² + (2) ² ) = √(1 + 4) = √5

   |w| = √((-2) ² + (3) ² ) = √(4 + 9) = √13

   Модуль комплексного числа v, |v| = |zw| = |г||ш| = √5.√13 = √65

   Ответ: Модуль комплексного числа (1 + 2i)(-2 + 3i) равен √65.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические задачи на модуль комплексных чисел

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о модуле комплексного числа

Что такое модуль комплексного числа?

Модуль комплексного числа представляет собой квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.

Что происходит с модулем комплексного числа при увеличении степени комплексного числа?

Когда степень комплексного числа увеличивается, модуль комплексного числа также увеличивается в той же степени. В этом можно убедиться, используя свойство модуля комплексного числа: модуль n-й степени комплексного числа равен n-й степени модуля комплексного числа, то есть |z ⁿ | = | г | ⁿ

Чему равен модуль комплексного числа z = x + iy?

Модуль комплексного числа z = x + iy, обозначаемого |z|, определяется формулой |z| = √(х ² + y ² ), где x — действительная часть, а y — мнимая часть комплексного числа z.

Как найти модуль комплексного числа?

Модуль комплексного числа представляет собой квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа. Его можно рассчитать по формуле |z| = √(х ² + у ² ).

Чему равен модуль комплексного числа z = 1?

Модуль комплексного числа z = 1 равен |z| = 1, поскольку z = 1 = 1 + 0i. Отсюда следует, что модуль комплексного числа z = 1 равен √(1 ² + 0 ² ) = 1

Когда модуль комплексного числа равен 0?

Модуль комплексного числа равен 0 тогда и только тогда, когда комплексное число равно нулю, то есть |z| = 0 тогда и только тогда, когда z = 0.

Рабочие листы по математике и
наглядная программа

Объяснение урока: модуль комплексного числа

В этом пояснении мы узнаем, как использовать общую формулу для вычисления модуля комплексного числа.

Помните, что комплексное число 𝑧=𝑎+𝑏𝑖 представляет собой комплекс двух вещей: вещественной части ((𝑧)=𝑎)Re и мнимой части ((𝑧)=𝑏)Im. Чисто мнимое число 𝑖 определяется как 𝑖=−1 или 𝑖=√−1. Комплексное число 𝑧=𝑎+𝑏𝑖 представлено точкой (𝑎,𝑏) на диаграмме Аргана.

Теперь определим модуль комплексного числа.

Определение: модуль комплексного числа

Модуль комплексного числа 𝑧=𝑎+𝑏𝑖 определяется как |𝑧|=√𝑎+𝑏.

Эквивалентно это можно записать как |𝑧|=((𝑧))+((𝑧)).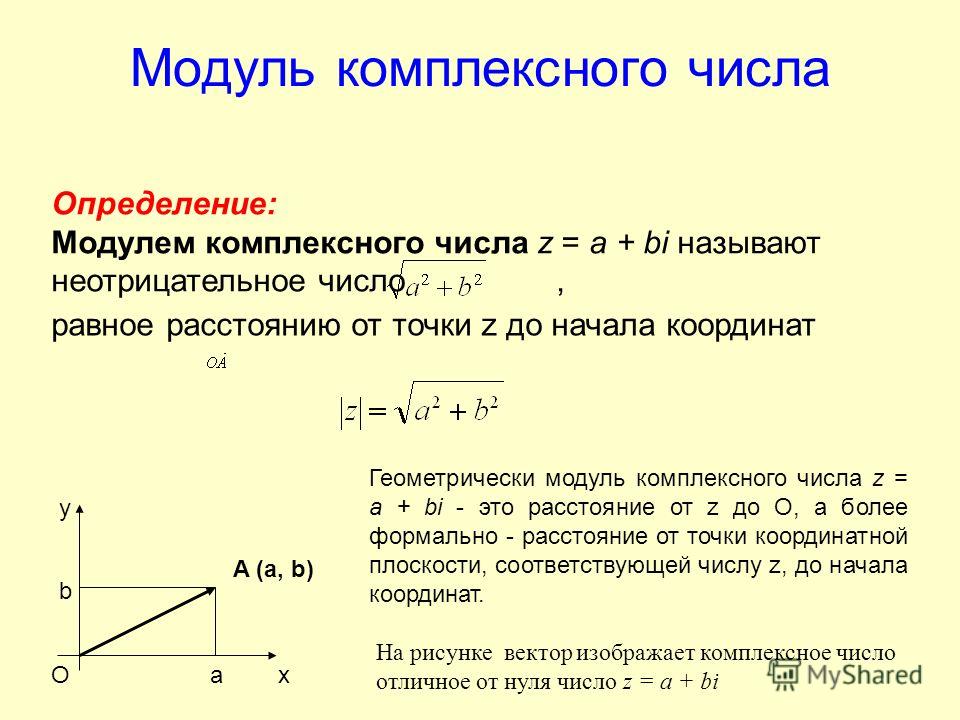 ReIm

Если 𝑧 — действительное число, его модуль как раз соответствует абсолютному значению. По этой причине модуль иногда называют абсолютным значением комплексного числа. Точно так же, если мы рассмотрим 𝑧=𝑎+𝑏𝑖 для представления вектора ⃑𝐴=(𝑎,𝑏) на диаграмме Аргана мы видим, что |𝑧| представляет величину вектора: ‖‖⃑𝐴‖‖.

Следовательно, модуль иногда называют также величиной комплексного числа. Это также подчеркивает геометрическую интерпретацию модуля как величины комплексного числа или его расстояния от начала координат.

Давайте посмотрим на наш первый пример, где нам нужно найти модуль данного комплексного числа.

Пример 1: модуль комплексного числа

Учитывая, что 𝑍=8+4𝑖, найдите |𝑍|.

Ответ

Модуль комплексного числа 𝑤=𝑎+𝑏𝑖 определяется следующим образом: |𝑤|=√𝑎+𝑏. Следовательно, |𝑍|=√8+4=√64+16=√80.

Учитывая, что 80=2×5, мы можем переписать это как |𝑍|=√2×√5=4√5.

Теперь в нашем втором примере мы рассмотрим связь между комплексно-сопряженным числом и модулем комплексного числа.

Пример 2: связь между комплексным сопряжением и модулем

Рассмотрим комплексное число 𝑧=−4+𝑖√5.

1. Рассчитать |𝑧|.
2. Вычислить ||𝑧||.
3. Определить 𝑧𝑧.

Ответ

Часть 1

Напомним, что для комплексного числа 𝑤=𝑎+𝑏𝑖 модуль определяется как |𝑤|=√𝑎+𝑏. Следовательно, |𝑧|=(−4)+√5=√16+5=√21.

Часть 2

Чтобы найти модуль комплексного числа, меняем знак мнимой части числа. Следовательно, 𝑧=−4−𝑖√5. Поэтому, |𝑧|=(−4)+−√5=√16+5=√21.

Часть 3

Используя значение 𝑧 из части 2, имеем 𝑧𝑧=−4+𝑖√5−4−𝑖√5.

Используя FOIL или другой метод, мы можем расширить скобки следующим образом: 𝑧𝑧=(−4)+4×𝑖√5−4×𝑖√5−𝑖√5=16−5𝑖.

Используя тот факт, что 𝑖=−1, имеем 𝑧𝑧=21.

Мы могли бы также вычислить это, используя тождество, которое для сложного число 𝑤=𝑎+𝑏𝑖, 𝑤𝑤=𝑎+𝑏.

В предыдущем примере были выделены некоторые свойства модуля, в частности связанные с сопряжением. В приведенном ниже поле приведены эти свойства.

Свойство: свойства модуля комплексного числа

Для комплексного числа 𝑧:

1. |𝑧|=|𝑧|,
2. |𝑧|=𝑧𝑧.

Теперь мы рассмотрим свойства модуля по отношению к другим операциям с комплексными числами, включая сложение, умножение и деление. Мы начнем с рассмотрения дополнения.

Пример 3: связь между сложением и модулем комплексного числа

Рассмотрим два комплексных числа 𝑤=−1+7𝑖 и 𝑧=5−3𝑖.

1. Рассчитать |𝑤|+|𝑧| до двух знаков после запятой.
2. Рассчитать |𝑧+𝑤| до двух знаков после запятой.
3. Каким из следующих отношений удовлетворяют 𝑤 и 𝑧?
   1. |𝑤|+|𝑧|=|𝑧+𝑤|
   2. |𝑤|+|𝑧|≥|𝑧+𝑤|
   3. |𝑤|+|𝑧|≤|𝑧+𝑤|
   4. |𝑤|+|𝑧|=2|𝑧+𝑤|
   5. √|𝑤|+|𝑧|=|𝑧+𝑤|

Ответ

Часть 1

Используя определение модуля комплексного числа, имеем |𝑤|=(−1)+7=√1+49=5√2. 

Аналогично, |𝑧|=5+(−3)=√25+9=√34.

Сложив эти два вместе, мы имеем |𝑤|+|𝑧|=5√2+√34.

Используя калькулятор, мы можем оценить это и округлить до двух знаков после запятой (2 d.p.) следующим образом: =12,9020…=12,90(2.).d.p

Часть 2

Начнем с вычисления 𝑧+𝑤 следующим образом: 𝑧+𝑤=5−3𝑖+(−1+7𝑖)=4+4𝑖. Теперь вычисляем его модуль: |𝑧+𝑤|=√4+4=4√2.

Подсчитав это на калькуляторе, получим |𝑧+𝑤|=5.6568…=5.66(2.).d.p

Часть 3

Очевидно, |𝑤|+|𝑧|≠|𝑧+𝑤|. Следовательно ответ не может быть (А). Вместо этого мы обнаруживаем, что |𝑤|+|𝑧|≥|𝑧+𝑤|, что одновременно подтверждает, что (B) является правильным ответом и что (C) это неверно. Кроме того, оценивая 2|𝑧+𝑤|=11,31(2.) д.п. мы видим, что вариант (D) также неверен. Наконец, мы проверяем вариант (E) оценивая √|𝑤|+|𝑧|=3,59(2.) д.п. Это подтверждает, что вариант (Е) также неверен. Следовательно, единственно правильный вариант (Б).

В предыдущем примере мы показали, что комплексы 𝑧 и 𝑤 удовлетворяют соотношению |𝑤|+|𝑧|≥|𝑧+𝑤|. Это соотношение верно не только для конкретных чисел 𝑧 и 𝑤. в примере, но на самом деле верно и для любых двух комплексных чисел. Это соотношение часто называют неравенством треугольника.

Неравенство: неравенство треугольника для комплексных чисел

Для двух комплексных чисел 𝑧 и 𝑧 выполняется следующее неравенство: |𝑧+𝑧|≤|𝑧|+|𝑧|.

Равенство имеет место, когда 𝑧=𝑐𝑧 для некоторого действительного 𝑐≥0.

Представим неравенство треугольника на диаграмме Аргана.

Мы видим, что мы можем составить треугольник со сторонами с длинами |𝑧|, |𝑧| и |𝑧+𝑧|. Неравенство треугольника, как следует из его названия, утверждает, что сумма длин двух сторон всегда больше, чем длина одной стороны. Если бы это было не так, то треугольник не мог бы образоваться, потому что две стороны не соединились бы.

Мы имеем равенство |𝑧+𝑧|=|𝑧|+|𝑧|, когда 𝑧=𝑐𝑧 для некоторого действительного 𝑐≥0, потому что в этом случае 𝑧 и 𝑧 выровнены с начала и находятся по одну сторону от начала координат. Тогда комплексное число 𝑧+𝑧 находится на том же луче из начала координат: у нас не треугольник, а три отрезка на одном луче.

Алгебраически мы видим, что |𝑧+𝑧|=|𝑧+𝑐𝑧|=|(𝑐+1)𝑧|.

Поскольку 𝑐≥0, имеем |𝑧+𝑧|=(𝑐+1)|𝑧||𝑧+𝑧|=𝑐|𝑧|+|𝑧|=|𝑧|+|𝑧|.

Мы Теперь изучите свойства модуля по отношению к умножению и делению.

Пример 4: Модуль произведений и частных

Рассмотрим комплексные числа 𝑧=3−4𝑖 и 𝑤=−15+8𝑖.

1. Найти |𝑧| и |𝑤|.
2. Рассчитать |𝑧𝑤|. Как это соотносится с |𝑧||𝑤|?
3. Вычислить ||𝑧𝑤||. Как это соотносится с |𝑧||𝑤|?

Ответ

Часть 1

Используя определение модуля, вычисляем |𝑧|=3+(−4)=√9+16=√25=5.

Аналогично находим |𝑤|=(−15)+8=√225+64=√289=17. 

Часть 2

Теперь вычислим произведение 𝑧𝑤 следующим образом: 𝑧𝑤=(3−4𝑖)(−15+8𝑖).

Раскрывая скобки ФОЛЬГОЙ или другим способом, получаем 𝑧𝑤=−45+24𝑖+60𝑖−32𝑖.

Поскольку 𝑖=−1, имеем 𝑧𝑤=−13+84𝑖.

Теперь рассчитаем модуль: |𝑧𝑤|=(−13)+84=√169+7056=√7225=85.

Используя ответы из части 1, мы имеем |𝑧||𝑤|=5×17=85. Отсюда получаем, что |𝑧||𝑤|=|𝑧𝑤|.

Часть 3

Начнем с расчета 𝑧𝑤 следующим образом: 𝑧𝑤=3−4𝑖−15+8𝑖.

Умножая и числитель, и знаменатель на комплексно-сопряженную часть знаменателя, мы имеем 𝑧𝑤=(3−4𝑖)(−15−8𝑖)(−15+8𝑖)(−15−8𝑖).

Раскрывая скобки в числителе и знаменателе, получаем 𝑧𝑤=−45−24𝑖+60𝑖+32𝑖225−120𝑖+120𝑖−64𝑖.

Используя 𝑖=−1, мы имеем 𝑧𝑤=−77+36𝑖289=−77289+36289𝑖.

Теперь мы можем вычислить его модуль следующим образом: ||𝑧𝑤||=−77289+36289.

Мы можем переписать это, взяв общий знаменатель вне квадратного корня следующим образом: ||𝑧𝑤||=√77+36289=√5929+1296289=√7225289=85289=517. 

Наконец, мы сравним это с |𝑧||𝑤|. Используя ответ из части 1, мы видим, что это равно 517. Следовательно, |𝑧||𝑤|=||𝑧𝑤||.

Используя методы, использованные в последнем примере, достаточно просто доказать, что для любых двух комплексных чисел 𝑧=𝑎+𝑏𝑖 и 𝑧=𝑐+𝑑𝑖 мы можем обобщить то, что мы показали в последнем примере, и запишите следующие тождества умножения и деления.

Идентичность: тождества умножения и деления

Для любых двух комплексных чисел 𝑧=𝑎+𝑏𝑖 и 𝑧=𝑐+𝑑𝑖 имеем |𝑧𝑧|=|𝑧||𝑧|,|||𝑧𝑧|||=|𝑧||𝑧|.

Следующий пример продемонстрирует, как мы можем решать задачи, применяя свойства модуля.

Пример 5: Решение уравнений, использующих модуль

Если 𝑍=1𝑍, где 𝑍 — комплексное число, что такое |𝑍|?

Ответ

Исходя из уравнения 𝑍=1𝑍, мы можем взять модуль обеих частей уравнения, чтобы получить |𝑍|=|||1𝑍|||.

Так как для любых двух комплексных чисел |||𝑍𝑍|||=|𝑍||𝑍|, мы можем переписать уравнение как |𝑍|=|1|||𝑍||.

Кроме того, мы знаем, что ||𝑍||=|𝑍| и |1|=1. Следовательно, |𝑍|=1|𝑍|.

Умножение обеих частей уравнения на |𝑍| дает |𝑍|=1.

Наконец, мы можем извлечь квадратный корень из обеих частей этого уравнения. Так как модуль всегда положительный число, нам нужно только рассмотреть положительный квадратный корень. Следовательно, |𝑍|=1.

В нашем последнем примере мы рассмотрим связь между модулем и степенями.

Пример 6: Степени комплексных чисел и модуль

Учитывая комплексное число 𝑧=𝑎+𝑏𝑖, каков модуль 𝑧?

Ответ

Мы знаем, что для любых двух комплексных чисел модуль их произведения равен произведению их модулей: |𝑧𝑧|=|𝑧||𝑧|.

Следовательно, в частном случае, когда 𝑧=𝑧=𝑧, имеем ||𝑧||=|𝑧||𝑧|=|𝑧|.

Используя определение модуля |𝑧|, имеем ||𝑧||=√𝑎+𝑏=𝑎+𝑏.

Используя аналогичную логику, примененную в предыдущем примере, мы можем видеть, что для комплексного числа 𝑧 модуль его 𝑛-й степени будет равен |𝑧|=|𝑧|.