Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств.  6. Сложение множеств. 7. Разбиение множеств. 8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений.  § 2. Уравнения с одним неизвестным 2. Метод разложения на множители. 3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 3. Сокращение показателей и приведение корней к общему показателю. 4. Извлечение корня из произведения и степени.  5. Вынесение алгебраических выражений из-под корня и внесение их под корень. 6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений.  6. Метод подстановки. 7. Метод алгебраического сложения уравнений. 8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел.  3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения. § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа.  7. Функции комплексного переменного и преобразования комплексной плоскости. § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения.  Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2. Комбинаторные задачи. Продолжение § 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
Как разложить на множители многочлены степени 3
••• формулы изображение Антона Гвоздикова с сайта Fotolia.com
Скай Смит
Разложение многочленов на множители помогает математикам определить нули или решения функции. Эти нули указывают на критические изменения возрастающих и убывающих скоростей и в целом упрощают процесс анализа. Для многочленов степени три или выше, что означает, что наивысший показатель степени переменной равен трем или выше, факторинг может стать более утомительным. В некоторых случаях методы группировки сокращают арифметику, но в других случаях вам может потребоваться больше узнать о функции или полиноме, прежде чем вы сможете продолжить анализ.
Для многочленов степени три или выше, что означает, что наивысший показатель степени переменной равен трем или выше, факторинг может стать более утомительным. В некоторых случаях методы группировки сокращают арифметику, но в других случаях вам может потребоваться больше узнать о функции или полиноме, прежде чем вы сможете продолжить анализ.
Проанализируйте полином, чтобы учесть факторинг по группировке. Если полином имеет форму, в которой удаление наибольшего общего делителя (НОД) из первых двух членов и двух последних членов показывает еще один общий делитель, вы можете использовать метод группировки. Например, пусть F(x) = x³ – x² – 4x + 4. Когда вы удалите GCF из первого и последнего двух членов, вы получите следующее: x²(x – 1) – 4 (x – 1). Теперь вы можете вытащить (x – 1) из каждой части, чтобы получить (x² – 4) (x – 1). Используя метод «разности квадратов», можно пойти дальше: (х – 2) (х + 2) (х – 1). Как только каждый фактор находится в своей первичной или нефакторизуемой форме, все готово.
Найдите разность или сумму кубов. Если многочлен имеет только два члена, каждый из которых имеет идеальный куб, вы можете разложить его на множители на основе известных кубических формул. Для сумм (x³ + y³) = (x + y) (x² – xy + y²). Для разностей (x³ – y³) = (x – y) (x² + xy + y²). Например, пусть G(x) = 8x³ – 125. Тогда разложение этого полинома третьей степени на множители зависит от разности кубов следующим образом: (2x – 5) (4x² + 10x + 25), где 2x – кубический корень из 8x³ а 5 — это кубический корень из 125. Поскольку 4x² + 10x + 25 — простое число, вы закончили разложение на множители.
Посмотреть, есть ли GCF, содержащий переменную, которая может уменьшить степень многочлена. Например, если H(x) = x³ – 4x, выделив GCF «x», вы получите x (x² – 4). Затем, используя метод разности квадратов, вы можете дополнительно разбить полином на x (x – 2) (x + 2).
Используйте известные решения для уменьшения степени многочлена. Например, пусть P(x) = x³ – 4x² – 7x + 10. Поскольку НОД или разности/суммы кубов нет, вы должны использовать другую информацию для факторизации многочлена. Как только вы обнаружите, что P (c) = 0, вы знаете, что (x — c) является фактором P (x), основанным на «Теореме о факторах» алгебры. Поэтому найдите такое «ц». В этом случае P(5) = 0, поэтому (x – 5) должен быть фактором. Используя синтетическое или длинное деление, вы получаете частное (x² + x – 2), которое делится на (x – 1) (x + 2). Следовательно, P(x) = (x – 5) (x – 1) (x + 2).
Поскольку НОД или разности/суммы кубов нет, вы должны использовать другую информацию для факторизации многочлена. Как только вы обнаружите, что P (c) = 0, вы знаете, что (x — c) является фактором P (x), основанным на «Теореме о факторах» алгебры. Поэтому найдите такое «ц». В этом случае P(5) = 0, поэтому (x – 5) должен быть фактором. Используя синтетическое или длинное деление, вы получаете частное (x² + x – 2), которое делится на (x – 1) (x + 2). Следовательно, P(x) = (x – 5) (x – 1) (x + 2).
Статьи по теме
Ссылки
- Университет Ламара: полиномы факторинга
Об авторе
Скай Смит пишет о психологии, электронике, здоровье и фитнесе с 2002 года для различных интернет-изданий. Он с отличием окончил Университет Флориды в 2005 году, получив степень бакалавра наук в области психологии и статистики со второстепенной степенью в области математики.
Фото Кредиты
формулы изображение Антона Гвоздикова с сайта Fotolia.com
3.
 Как разложить многочлены на множители
Как разложить многочлены на множителиНа этой странице
Как факторизовать многочлены с 3 членами?
Как факторизовать многочлены с 4 членами?
Как факторизовать многочлены с 5 членами?
Использование системы компьютерной алгебры
На этой странице мы научимся разлагать на множители многочлены с 3 членами (степень 2), 4 членами (степень 3) и 5 членами (степень 4).
Мы будем использовать теоремы об остатках и множителях для разложения многочленов на их множители.
Что мы ищем?
Пример 1
Пример полинома (со степенью
p ( x ) = 4 x 3 — 3 x 2 — 25 x — 6
множителей этого полинома:
( x — 3), (4 x + 1) и ( x + 2)
Обратите внимание, что существует 3 множителей для полинома степени 3 . Когда мы умножим эти 3 члена в скобках, мы получим полином p ( x ).
Когда мы умножим эти 3 члена в скобках, мы получим полином p ( x ).
Мы увидим, как найти эти множители ниже, в разделе Как разложить на множители многочлены с 4 членами?
Краткое описание процесса
В общем будем:
- Найдите один множитель , используя теорему об остатках
- Разделите многочлен на коэффициент мы нашли, что дает нам более простой полином для работы с
- Найдите один множитель более простого многочлена и разделите еще раз
- Продолжайте, пока не дойдете до трехчлена , который мы обычно легко можем разложить на множители.
Как факторизовать многочлены с 3 членами?
Пример 2
Вот пример многочлена с 3 членами:
q ( х ) = х 2 − х + 6
Мы понимаем, что это квадратичный многочлен (также называемый трехчленным из-за 3 членов), и мы видели, как факторизовать те, что были ранее в разделе Факторинг трехчленов и Решение квадратных уравнений методом факторинга.
Нам нужно найти числа a и b такие, что
q ( х ) = х
2 — 5 х + 6 = ( x − a )( x − b )
Обычно это включает в себя угадывание и проверку, чтобы получить правильную комбинацию чисел. Число 6 (константа многочлена) имеет делители 1, 2, 3 и 6 (и отрицательные значения каждого из них также возможны), поэтому очень вероятно, что наши a и b будут выбраны из этих числа.
После некоторых проб получаем:
х 2 — 5 х + 6 = ( х — 2)( х — 3)
Мы говорим, что делителей из x 2 — 5 x + 6 равны ( x — 2) и ( x — 3).
Обратите внимание, что наш трехчленный многочлен имеет степень 2 , и число множителей также равно 2.
Как разложить на множители многочлены с 4 членами?
Пример 3
Выше мы обсуждали кубический полином p ( x ) = 4 x 3 — 3 x 2 — 25 x — 6, что имеет степень 3 .
Найдем множители p ( x ).
Обратите внимание, что коэффициент x 3 равен 4, и нам нужно учесть это в нашем решении.
Ищем решение по следующей схеме (в скобках 3 выражения, потому что наибольшая степень нашего многочлена равна 3):
4 x 3 − 3 x 2 − 25 x − 6 = ( ax − b )( cx − d )( fx − г )
Множители 4 равны 1, 2 и 4 (и, возможно, их отрицательные значения), поэтому a , c и f будут выбраны из этих чисел. Это должно быть так, чтобы в нашем многочлене получилось 4 x 3 .
Мы наблюдаем -6 как постоянный член нашего многочлена, поэтому числа b , d и g будут, скорее всего, выбраны из множителей -6, которые равны ±1, ±2, ± 3 или ±6.
Однако нам потребовалось бы слишком много времени, чтобы опробовать все рассмотренные комбинации. Нам нужно перемножить их все, чтобы увидеть, какая комбинация на самом деле дает p ( x ).
Итак, мы пойдем другим путем.
Нахождение одного множителя: Пробуем некоторые из возможных более простых множителей и смотрим, «работают ли». Если мы разделим многочлен на выражение и получим без остатка , то мы нашли множитель .
Более простой способ — использовать Теорему об остатках , с которой мы познакомились в предыдущем разделе, Теоремы о факторах и остатках. Там написано:
Если многочлен f ( x ) разделить на ( x − r ) и получается остаток R , тогда f ( r ) = R .
Мы ищем выражение (называемое линейным членом) которое даст нам остаток 0, если мы разделим на него многочлен.
Испытание 1: Пробуем ( x − 1) и находим остаток, подставляя 1 (заметьте, что 1 положительная) в p ( x ).
р (1) = 4(1) 3 — 3(1) 2 — 25(1) — 6 = 4 — 3 — 25 — 6 = -30 ≠ 0
Испытание 2: Мы пробуем ( x + 1) и находим остаток, подставляя −1 (обратите внимание, что это отрицательное число 1) в p ( x ).
p (-1) = 4(-1) 3 — 3(-1) 2 — 25(-1) — 6 = -4 — 3 + 25 — 6 = 12 ≠ 0
Испытание 3: Мы пробуем ( x − 2) и находим остаток, подставляя 2 (заметьте, что он положительный) в р ( х ).
p (2) = 4(2) 3 − 3(2) 2 − 25(2) − 6 = 32 − 12 − 50 − 6 = −36 ≠ 0
Испытание 4: Мы пробуем ( x + 2) и находим остаток, подставляя −2 (обратите внимание, отрицательное значение) в p ( x ).
p (-2) = 4(-2) 3 — 3(-2) 2 — 25(-2) — 6 = -32 — 12 + 50 — 6 = 0
Поскольку остаток равен 0, мы можем заключить ( 92-22x`.
Теперь мы можем записать p ( х ) = ( х + 2)(4 х 2 — 11 х — 3).
Теперь эта вторая скобка представляет собой просто трехчлен (3-членный квадратичный многочлен), и мы можем довольно легко разложить его на множители, используя процесс факторизации трехчленов.
(4 х 2 — 11 х — 3) = (4 х +1)( х — 3)
Итак, сложив все вместе, полином p ( x ) можно записать:
P ( x ) = 4 x 3 — 3 x 2 — 25 x — 6 = ( x – 3) (4 5454.
4. x — 3) (4 4. x — 3) (4 4.10064. ( х + 2)
То есть факторов из p ( x ) составляют:
( x — 3), (4 x + 1) и ( x + 2)
Как факторизовать многочлены с 5 членами?
Пример 4
Factor the polynomial r ( x ) = 3 x 4 + 2 x 3 − 13 x 2 − 8 x + 4.
Решение
Поскольку степень этого многочлена равна 4, мы ожидаем, что наше решение будет иметь вид
3 x 4 + 2 x 3 — 13 x 2 — 8 x + 4 = (3 x — A 1 ) ( x — A 2 9005) ( — x .
3 )( x − a 4 )
Первая скобка имеет 3 (поскольку множители 3 равны 1 и 3, и она должна появиться в одной из скобок). Остальные неизвестные должны быть выбраны из множителей 4, которые равны 1, 2 или 4
Еще раз, мы будем использовать Остаток Теорема , чтобы найти один множитель. Мы разделим r ( x ) на на этот коэффициент, и это даст нам кубический многочлен (степень 3). Мы найдем коэффициент этого куба, а затем разделим куба на этот коэффициент. Тогда у нас остается трехчлен, который обычно относительно просто разложить на множители.
Испытание 1: Мы пытаемся подставить x = 1 и обнаруживаем, что это не удалось (ноль не получен).
r (1) = 3(1) 4 + 2(1) 3 − 13(1) 2 − 8(1) + 4 = −12
Испытание 2: Мы пытаемся заменить x = −1, и на этот раз мы нашли множитель.
r (1) = 3(−1) 4 + 2(−1) 3 − 13(−1) 2 − 8(−1) + 4 = 0
Мы заключаем, что ( x + 1) является коэффициентом из r ( х ). Таким образом, наши коэффициенты будут выглядеть примерно так:
.3 x 4 + 2 x 3 − 13 x 2 − 8 x + 4 = (3 x − a 1 )( x + 1)( x − a 3 )( x − a 4 )
Теперь нам нужно разделить ( х + 1) на r ( х 92-12x` Итак, сложив все вместе, мы имеем: R ( x ) = 3 x 4 + 2 x 3 — 13 x 2 — 8 x 9005 + 4 = 4 = 4 = 4 = 4 x . )( х + 1)( х — 2)( х + 2) Что, если бы нам нужно было разложить такие многочлены на множители? Пример 5: x 2 − 5,2 x + 6,751 У этого трехчлена нет «хороших» чисел, и потребуется некоторая возня, чтобы разложить его на множители путем проверки. Мы могли бы использовать квадратную формулу, чтобы найти факторы. Пример 6: 2,9 x 3 − π x 2 − 4,97 x + 43883 Приведенный выше кубический полином также имеет довольно неприятные числа. Пример 7: 3175 x 4 + 256 x 3 — 139 x 2 — 8 7x + 480703030 У этого многочлена четвертой степени (степень 4) есть «хорошие» числа, но комбинация чисел, которую нам придется испытать, огромна. Делители 480 равны {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32, 40, 48, 60, 80, 96, 120, 160, 240, 480} Мы также должны рассмотреть отрицательные стороны каждого из них. Когда полином имеет довольно высокую степень, даже с «хорошими» числами, работа по нахождению множителей будет довольно большой. Например: Пример 8: x 5 — 4 x 4 — 7 x 3 + 14 x 2 1 – 444971 + 140064 x 2 11,4 + x 2 1. Множители 120 следующие, и нам нужно продолжать, пока один из них не «сработает». {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120} На самом деле в этом случае первый множитель (после попыток `+-1` и `-2`) на самом деле равен `(x-2)`. В таких случаях лучше понимать следующее: Давайте рассмотрим лучшее решение. В примерах 5 и 6 на самом деле нет хороших факторов, даже когда мы получаем компьютер, чтобы найти их для нас. Пример 7 содержит коэффициенты (данные Wolfram|Alpha) `3175, `(x — 0,637867),` `(x + 0,645296),` ` (x + (0,0366003 — 0,604938 i)),` ` (x + (0,0366003 + 0,604938 i))` Я не спешу делать это на бумаге! Рассмотрим пример 8, который был: x 5 − 4 x 4 − 7 x 3 + 14 x 2 − 44 x + 120 Используя Wolfram|Alpha, мы получаем ( х — 2)( х — 5)( х + 3)( х 2 + 4) = 0 Обратите внимание, что в этом примере в скобках не указано 5 элементов. Следующий выглядит пугающе: Пример 9: x 4 + 0,4 x 3 — 6,49 x 2 + 7,244 x — 2,112 = 0 0003 Позволив Wolfram|Alpha сделать за нас работу, мы получим: `0,002 (2 x — 1) (5 x — 6) (5 x + 16) (10 x — 11) ` Так что, хотя интересно узнать, как найти эти факторы, лучше использовать доступные инструменты. `4x+4` `-8x-(-12x) ` `= 4x`. Сбить `4` `4x+4` `4(х+1)=4х+4` `0` `4-4=0` Это остаток.  2-12x+4` 92+5x-2 = (3x-1)(x+2)`
2-12x+4` 92+5x-2 = (3x-1)(x+2)` Использование системы компьютерной алгебры для факторизации многочленов
 Найти первый множитель, а затем разделить на него многочлен было бы довольно сложно.
Найти первый множитель, а затем разделить на него многочлен было бы довольно сложно.
Решение с использованием систем компьютерной алгебры



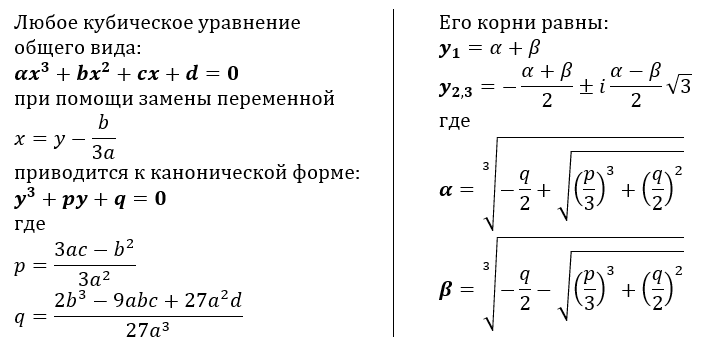
 4. x — 3) (4 4. x — 3) (4 4.10064. ( х + 2)
4. x — 3) (4 4. x — 3) (4 4.10064. ( х + 2) 3 )( x − a 4 )
3 )( x − a 4 )