Формула комплексных чисел: Комплексные числа, примеры с решением

2 = kx + b геометрически на координатной плоскости представляется, как пересечение параболы и прямой, при этом возникает 3 варианта:

парабола не пересекает прямую
парабола касается прямой
парабола пересекает прямую в 2-х местах

Поэтому с точки зрения математики здесь все было честно и у математиков не было мотивации искать мнимые корни из отрицательных чисел.

Все поменялось при решении кубических уравнений, в которых прямая всегда пересекает кубическую параболу. Но при этом в при аналитическом решении уравнения возникают ситуации, когда приходится извлекать корни из отрицательного числа, даже если уравнение имеет вещественные корни.

Понятие комплексного числа

Прежде чем перейти к определению комплексного числа необходимо сделать дисклеймер: не пытайтесь представить комплексное число в жизни — это тоже самое, что попытаться представить 4-ое измерение пространство в нашем бренном трехмерном мире.

Комплексные числа необходимы в математике, для того, чтобы определить ту область чисел, которую нельзя отобразить через вещественные числа.

Пока звучит непонятно, так что давайте разбираться.

Комплексное число имеет вид и стоит заметить, что это единое число, а не сложение. Но при этом все комплексные числа имеют геометрическую интерпретацию и представляется на комплексной плоскости:

Комплексная плоскость состоит из двух осей:
– Re — действительная ось
– Im — мнимая ось

Здесь все также как в геометрии 6-8 класса. Для примера построим 3 точки:

Корни n-й степени из единицы

Самый частая ситуация при которой используются комплексные числа — это простое извлечение корней из отрицательных чисел, поэтому рассмотрм примеры того, как это делается.

Начнем с простого примера:

Нельзя извлечь корень? В действительных числах здесь действительно не будет решений. В комплексных числах извлечь корень можно. А точнее даже два!

Проведем проверку:

Это был простой пример, а теперь давайте рассмотрим пример посложнее:

Сначала может показаться, что ответ достаточно просто найти, ведь , но что же в таком случае происходит с , ведь ? Что-то тут не сходится.

Поскольку для всех значений корня величина модуля одинакова, а меняется лишь его аргумент, все n значений корня располагаются на комплексной плоскости на окружности радиуса

c центром в начале координат. Корни делят эту окружность на n равных частей.

Таким образом будет иметь модуль 2, а все его корни будут располагаться на окружности в комплексной плоскости с одинаковым равноудаленным интервалом. Стоит отметить тот факт, что длина всех отрезков на окружности — это все еще длина радиуса и она также имеет размер 2, разница лишь в том, где в комплексной плоскости расположено число. На комплексной плоскости это будет выглядеть так:

Для того, чтобы аналитически рассчитать значение корня необходимо воспользоваться формулой Муавра:

Формула Муавра для комплексных чисел:

Для

∀ .

Таким образом, для корни будут находится на , что мы и видели уже на графике.

Положительные числа

А что же будет с положительными числами корня n-ной степени? Их тоже будет n штук! В общем-то принцип тут не меняется, их также можно найти по формуле Муавра, давайте сразу приведем ответ для уравнения

Т.е. решением уравнения х = будут корни:

Давайте это проверим:

Работает!

Бонусная картинка для тех, кто дочитал до конца:

Содержание

что это такое, виды, примеры задач с решением

Понятие комплексного числа

Определение 1

Комплексными числами в теории называют числа, которые записаны в виде: a + bi, где a, b являются вещественными числами, i играет роль мнимой единицы при условии, что i2=-1.

В качестве обозначения множества, которое составляют комплексные числа, в алгебре используют букву «С».

Любое комплексное число z=a+bi включает в состав пару компонентов, которые называются и обозначаются так:

a является вещественной составляющей числа z;
b является мнимым компонентом числа z.

В том случае, когда b бывает равно нулю, z считают вещественным числом. Заменой выражения a+0i является просто а. К примеру, чтобы обозначить комплексный ноль 0+0i, записывают кратко 0.

Комплексное число z=a+bi является противоположным числу -z=-a-bi. Это правило выполняется, к примеру, если дано число 1-2i, то противоположным ему станет число -1+2i.

Комплексные числа отличаются от вещественных еще и тем, что их нельзя сравнить между собой на «больше» или «меньше». С другой стороны, допустимо сравнение комплексных чисел на равенство или неравенство.

Если мнимая и вещественная части, из которых состоит одно комплексное число, равны соответствующим частям другого комплексного числа, то такие комплексные числа равны. Например, a+bi=c+di. Таким образом, a=c и b=d.

Формула 1

Комплексные числа можно записать в алгебраической форме, чтобы умножать и выполнять другие действия:

z = x + iy

Формула 2

Запись комплексного числа можно представить в тригонометрической форме:

z=r(cosφ+isinφ)

Формула 3

Формула для вычисления модуля комплексного числа имеет следующий вид:

|z|=x2+y2

Формула 4

Определить аргумент комплексного числа можно по формуле:

φ=arctgyx

Формула 5

Формула Эйлера имеет вид:

eiφ=cosφ+isinφ

Формула 6

В основе решения многих задач на комплексные числа лежит Формула Муавра, которая означает, что:

zn=(r(cosφ+isinφ))n=rn(cosnφ+isinnφ)

Действия над комплексными числами: сложение, вычитание, умножение, деление

Правило 1

Комплексные числа можно вычитать и складывать согласно следующим правилам:

a+bi+c+di=a+c+b+di

a+bi-c+di=a-c+b-di.

При сложении любых комплексных чисел u, v, w допускается использование следующих свойств:

переместительный закон: u + v = v + u;
сочетательный закон: u + (v + w) = (u + v) + w;
свойство нуля: u + 0 = u;
сложение чисел с противоположными знаками: u + (-u) = 0;
замена вычитания сложением: u – v = u +(- v).

Правило 2

Правило умножения комплексного числа a+bi и комплексного числа c+di:

(a+bi)·(c+di)=ac+bci+adi+bdi2=(ac+bdi2)+(bc+ad)i=(ac-bd)+(bc+ad)i.

В процессе умножения каких-либо комплексных чисел u, v, w пригодятся следующие свойства:

переместительный закон: u·v=v·u;
сочетательный закон: u·(v·w)=(u·v)·w;
свойство единицы: u·1=1;
свойство нуля: u·0=0;
распределительный закон по сложению: u·(v+w)=(u·v)+u·w.

Правило 3

Степени мнимой единицы комплексного числа определяются по следующему правилу:

i2=-1

i3=-i

i4=1

i5=i.

Комплексные числа часто встречаются при решении задач в средних классах школы, на курсах для математиков: школьников и студентов. Ознакомившись с правилами, предусмотренными для операций с комплексными числами, запись комплексного числа a+bi можно представить в качестве выражения, которое составлено на основании правил сложения и умножения комплексных чисел. Используя полученные знания, раскроем все переменные:

(a+0i)+(b+0i)·(0+1i)=(a+0i)+(0+bi)=a+bi

Любое комплексное число a+bi, отличное от нуля, имеет обратное комплексное число: такое, как 1a+bi. Получить обратное комплексное число легко. Это значит, что достаточно умножить числитель и знаменатель дроби на число a-bi, которое является комплексно сопряженным знаменателю. В качестве практического доказательства и объяснения запишем:

1a+bi=a-bi(a+bi)(a-bi)=a-bia2+b2=aa2+b2-ba2+b2i.

Правило 4

Разделить какое-либо комплексное число a+bi на комплексное число c+di, отличное от нуля, можно по схеме:

a+bic+di=a+bic-dic+dic-di=ac+bdc2+d2+bc-adc2+d2i.

Заметим, что по аналогии с вещественными числами, операцию деления комплексных чисел допускается заменить умножением делимого на число, которое является обратным к делителю. С помощью этого метода можно легко находить корни уравнений.

Примеры решения задач

Задача 1

Дано комплексное число, которое нужно записать в тригонометрической и показательной формах:

z = -1 + i

Решение

Определим, чему равен модуль комплексного числа:

|z|=(-1)2+(1)2=2

Вычислим аргумент:

argz=arctg-11+π=-π4+π=3π4

В тригонометрической форме комплексное число будет представлено таким образом:

-1+i=2cos3π4+isin3π4

Запишем показательную форму комплексного числа:

-1+i=2ei3π4

Ответ: 2cos3π4+isin3π4, 2ei3π4

Задача 2

Требуется представить комплексное число в тригонометрической и показательной формах:

z = -1

Решение

Модуль заданного числа составит:

|z|=(-1)2+(0)2=1

Далее определим аргумент:

argz=arctg0-1=π

Запишем число в тригонометрической форме:

-1=cosπ+isinπ

Переведем запись комплексного числа в показательную форму:

-1=eiπ

Ответ: cosπ+isinπ, eiπ

Задача 3

Сложить комплексные числа:

z1=5+4i

z2=2+3i

Решение

Воспользуемся правилом сложения комплексных чисел:

z1+z2=(5+4i)+(2+3i)=7+7i

Ответ: 7 + 7i

Задача 4

Посчитать разность пары комплексных чисел:

z1=5+2iиz2=4+8i

Решение

Здесь поможет применение правила вычитания комплексных чисел:

z1+z2=(5+2i)-(4+8i)=5+2i-4-8i=1-6i

Ответ: z1+z2=1-6i

Задача 5

Умножить комплексные числа:

z1=5(cosπ+isin3π)

z2=3(cos2π+isin3π)

Решение

Воспользуемся правилом умножения комплексных чисел и распишем подробное решение:

z1·z2=5·3(cos(π+2π)+isin(3π+3π))=15(cos3π+isin6π)

Ответ: z1·z2=15(cos3π+isin6π)

Задача 6

Требуется вычислить:

(1+3i)9

Решение

Представим комплексное число в тригонометрической форме:

r=1+(3)2=2

argz=arctg31=π3

z=2cosπ3+isinπ3

Используя в системе вычислений формулу Муавра, определим ответ:

(1+3i)9=29cos9π3+isin9π3=29cos3π+isin3π=29(-1)=-512

Ответ: -512

Задача 7

Вычислить частное от деления двух комплексных чисел:

z1=1+3i и z2=2+i

Решение

Воспользуемся правилом деления комплексных чисел и запишем ответ:

1+3i2+i=(1+3i)(2-i)(2+i)(2-i)=2-i+6i+34+1=5+i5=1+i

Ответ: 1 + i

Задача 8

Вычислить частное от деления двух комплексных чисел:

z1=3+2i и z2=2+3i

Решение

Воспользуемся правилом деления двух комплексных чисел и запишем ответ:

3+2i2+3i=(3+2i)2-3i)(2+3i)(2-3i)=6+4i-9i+64+9=12-5i13=1213-513i

Ответ: 1213-513i

Задача 9

Вычислить:

Решение

Запишем i в тригонометрической форме:

i=cosπ2+isinπ2

Решим пример:

i3=cosπ2+isinπ23=13cosπ2+2πk3+isinπ2+2πk3, k=0,1,2.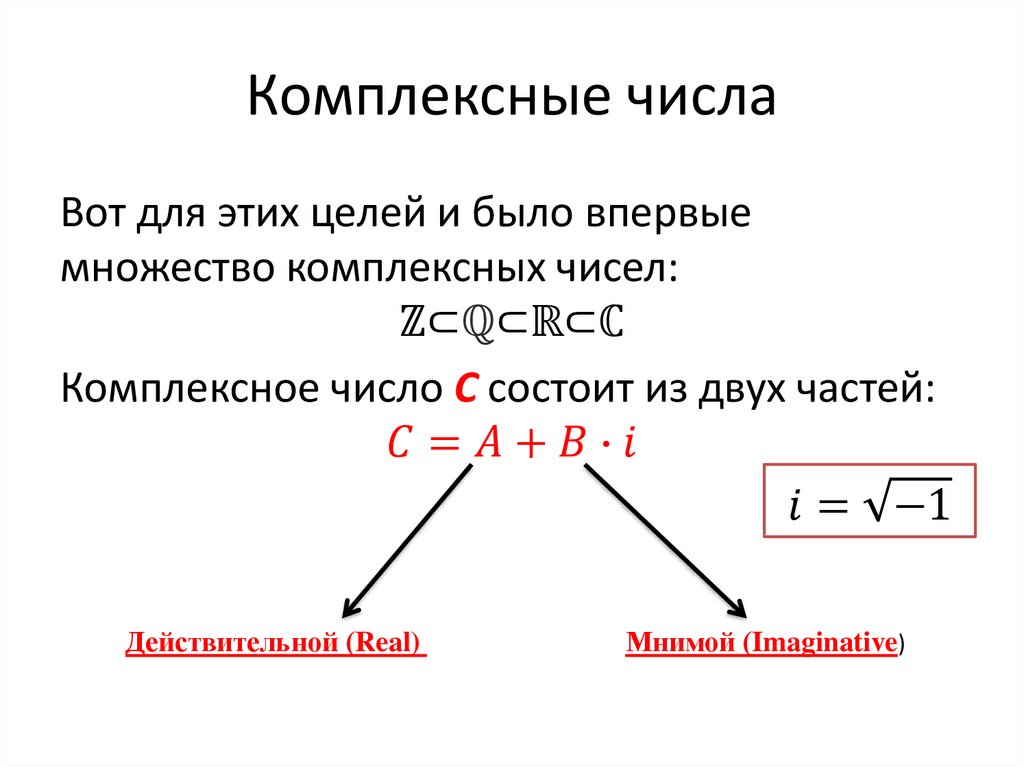

Если k = 0, получим:

cosπ6+isinπ6=32+i12

Если k = 1, получим:

cosπ2+2π3+isinπ2+2π3=cos5π6+isin5π6=-32+i12

Если k = 2, получим:

cos9π23+isin9π23=cos3π2+isin3π2=-i

Ответ: 32+i12 при k=0,-32+i12 при k = 1, -i при k = 2

Задания для самостоятельной работы

Задача 10

Дано два комплексных числа в показательной форме. Требуется определить их сумму и разность в алгебраической форме:

z1=2e-πi,z2=4eπi.

Задача 11

Умножить и найти частное от деления двух комплексных чисел:

z1=4+3i,z2=1-3i.

Задача 12

Вычислить все значения, которыми обладают корни из данного комплексного числа:

-94.

Задача 13

Определить значение выражения и записать результат в алгебраической и показательной формах:

1-i1+i40.

Задача 14

Найти модуль и аргумент комплексного числа z. Записать ответ в тригонометрической и показательной формах:

z=-3-i.

Задача 15

Записать тригонометрическую форму числа z при условии, что:

z=(3-3i3)(53+5i).

Задача 16

Дано число a:

a=13-i

Требуется представить число a в алгебраической и тригонометрической формах, а также решить уравнение:

z3+a=0.

Задача 17

Найти корни уравнения и записать результат в алгебраической форме:

sh z — ch z =2i.

Задача 18

Найти решения уравнения:

y-ixx+iy=4+i4i-1.

Задача 19

Дано уравнение, каждый комплексный корень которого требуется определить:

z6-7z3-8=0.

Формула, определения, свойства и операции

Комплексные числа представляются как z = a + ib, где a объявляется действительной частью и обозначается Rez, а ib описывается как мнимая часть и обозначается Imz числа z а комплекс нет. обозначается z. Например, если z = 4 + i5, то Re z = 4 и Im z = i5. Комплекс №. в математике также может пониматься как сумма действительного числа и мнимого числа.

В этой статье вы узнаете об определении комплексных чисел, символах, представлении, а также о том, как их изображать в виде графиков, различных свойствах и операциях с решенными примерами и многом другом.

Что такое комплексные числа?

Если x и y — любые два действительных числа, то любое число вида x + iy называется комплексным числом. Здесь x и y — действительные числа, а i в математике обозначает мнимое число, которое также читается как «йота». Кроме того, значение \(i = \sqrt{-1}\) и комплексный номер. обозначается z.

Прочтите эту статью о системе счисления.

Что такое действительные числа?

Согласно значению комплексного числа, это сложение двух чисел, одного действительного и одного мнимого. Давайте разберемся с этими двумя типами чисел. Всевозможные положительные, нулевые, отрицательные, целые, дробные, рациональные, иррациональные и т. д. подсчитываются под действительными числами. Например: 23, -35, 0, 1/8, 7,6, √5 и т. д. указаны под действительными числами.

Что такое мнимые числа?

В предыдущей рубрике мы читали о действительных числах, давайте теперь разберемся с мнимыми числами. Число, имеющее форму ix, обозначает мнимое число. Здесь значение \(i = \sqrt{-1}\) и выражается как Im().

Проще говоря, вы можете понять, что числа, которые не являются реальными, являются мнимыми. Возведение мнимого числа в квадрат дает отрицательный результат. Например, \(\sqrt{-3},\sqrt{-7},\sqrt{-13},\text{ и }i=\sqrt{-6}\) считаются под мнимыми числами.

Примеры комплексных чисел:

\(3+5i\), \(\sqrt{6}-10i\), \(\frac{4}{5}+i\), \(16i\), \(113\).

Вполне возможно, что \(x\) или \(y\) могут быть равны нулю, и поэтому в \(16i\) действительная часть равна нулю. Когда действительная часть равна нулю, мы называем комплексное число чисто мнимым числом. В последнем примере \(113\) мнимая часть равна нулю, а на самом деле мы имеем действительное число.

Представление комплексного номера

На данный момент можно сказать, что в конкретном комплексе нет. одна часть чисто реальная, а другая часть чисто воображаемая. Для комплекса нет. представлено z = x + iy, 9{4n+3}=i\), где n — целое число.

Также читайте о сумме n натуральных чисел здесь.

Графики комплексных чисел

Согласно определению, комплексное число можно рассматривать как упорядоченную пару (Re(z)+ Im(z)) чисел. Это также можно понять, нанеся координаты точек на график.

Для z = x + iy действительная часть, т. е. «x», отмечена на оси x, а мнимая часть, т. е. «iy», отмечена на оси y.

Модуль комплексного числа 92\)

Аргумент комплексного числа

Угол, образованный геометрическим представлением комплексного числа с началом координат, сохраняя положительную ось x в качестве ссылки в направлении против часовой стрелки, обозначает аргумент комплексного числа.

Математически аргумент комплекса нет. получается путем обратного деления тангенса мнимой части на действительную часть. Он обозначается обозначением arg(z).

Следовательно, если z = x + iy 9{-1}\влево(\фракция{у}{х}\вправо)\).

Свойства комплексного числа

Хорошо знаком с представлением, графическим подходом, модулем, аргументом и полярным представлением комплексного числа. давайте теперь изучим важные свойства комплексных чисел.

Сопряжение комплексного числа

Любые два комплексных числа, например \(z_1\text{ и }z_2\), называются сопряженными, если сумма и произведение \(z_1\text{ и }z_2\) оба настоящие.

т. е. Если z = a + ib, то его сопряжение определяется выражением;

\(\overline{z}=a-ib\)

Теоретически можно сказать, что конъюгат данного комплекса нет. создается путем сохранения действительной части такой же, как исходная, и изменения мнимой части комплексного числа на его аддитивную обратную.

Обратная величина комплексного числа

Обратная величина заданного комплексного числа, скажем, z = x + iy получается следующим образом:

Если z число, то его обратная величина равна \(\frac{1}{z} \)

Здесь z = x + iy

92}\).

Равенство комплексных чисел

Рассмотрим \(z_1=x_1+iy_1\text{and}\ z_2=x_2+iy_2\) любые два комплексных числа, где \(x_1,x_2,y_1,y_2\) принадлежат R и \(i=\sqrt{-1}\).

Тогда мы можем сказать \(z_1=z_2\), если \(x_1=x_2\) и \(y_1=y_2\).

Отсюда следует, что если \(z_1=z_2\), то \(Re z_1= Re z_2\) и \(Im z_1= Im z_2\).

Теоретически можно сказать, что два сложных нет. равны, если действительная часть обоих чисел равна плюс мнимые части обоих чисел также равны. 9{i\theta}=\cos(\theta)+i\sin(\theta)\),

и представляет собой комплексное число в координатной плоскости, где

\(\cos(\theta)\) — действительная часть, представленная относительно оси \(x\),
\(\sin(\theta)\) — мнимая часть, представленная относительно оси \(y\),
\(\theta\) — это угол, образованный по отношению к оси \(x\) и воображаемой прямой, соединяющей начало координат и комплексное число.

9{х}\sin(y)\).

Это разлагает экспоненциальную функцию на ее действительную и мнимую части.

Проверьте еще несколько объективных ответов на вопросы о свойствах комплексных чисел.

Операции над комплексными числами

В предыдущем заголовке мы читали о различных свойствах комплексных чисел, теперь давайте изучим различные задействованные операции.

Сложение комплексных чисел

Сложение комплексных чисел чем-то похоже на сложение натуральных чисел. Здесь реальная часть добавляется к реальной части, а мнимая часть добавляется к мнимой части.

Рассмотрим \(z_1=x_1+iy_1\text{ и }z_2=x_2+iy_2\) любые два комплексных числа, где \(x_1,x_2,y_1,y_2\in R\text{ и}\ i=\sqrt {-1}\)

затем \(z_1+z_2=\left(x_1+x_2\right)+i\left(y_1+y_2\right)\).

Комплексные числа следуют всем следующим свойствам сложения.

Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел \(z_{1}\) и \(z_{2}\) сумма \(z_{1}+z_{2}\) также является комплексным числом.
Коммутативный закон: Для двух комплексных чисел \(z_{1}\) и \(z_{2}\) имеем \(z_{1}+z_{2}=z_{2}+z_{ 1}\).
Ассоциативный закон: Для заданных трех комплексных чисел \(z_{1}\), \(z_{2}\) и \(z_{3}\) имеем \(z_{1}+ (z_{2}+z_{3})=(z_{1}+z_{2})+z_{3}\).
Аддитивная идентичность: Для комплексного числа \(z = x + iy\) существует \(0 = 0 + i0\), такое что \(z + 0 = 0 + z = 0\).

5. Аддитивное обращение: Для комплексного числа \(z = x + iy\) существует комплексное число \(-z = -x – iy\), такое что \(z + (-z) = (-z) + z = 0\). Здесь \(-z\) — аддитивный обратный.

Вычитание комплексных чисел

При вычитании этих чисел действительная часть вычитается отдельно и то же самое для мнимой части.

Если \(z_1=x_1+iy_1\text{ и }z_2=x_2+iy_2\) любые два комплексных числа, где \(x_1,x_2,y_1,y_2\in R\text{ и}\ i=\sqrt {-1}\)

затем \(z_1-z_2=\left(x_1-x_2\right)+i \left(y_1-y_2\right)\).

Умножение комплексных чисел

В умножении комплексных чисел no каждый элемент данных двух чисел умножается на любой другой элемент.

Если \(z_1=x_1+iy_1\text{ и }z_2=x_2+iy_2\) любые два комплексных числа, где \(x_1,x_2,y_1,y_2\in R\text{ и}\ i=\sqrt {-1}\)

тогда;

\(z_1.z_2=\влево(x_1+iy_1\вправо).\влево(x_2+iy_2\вправо)\)

\(=\влево(x_1.x_2-y_1.y_2\вправо)+i\ left(x_1.y_2+x_2.\ y_1\right)\)

Также узнайте о целых числах здесь.

Деление комплексных чисел

Деление комплексных типов чисел показано ниже:

Рассмотрим \(\ z_1=x_1+iy_1\ и\ \ z_2=x_2+iy_{2\ }\) любые два комплексных числа 9{2}+2z_{a}z_{b}+2z_{b}z_{c}+2z_{c}z_{a}\).

Точно так же вы можете понять и другие связанные свойства.

Прочтите эту статью о рациональных числах.

Важные сведения о комплексных числах

Все действительные числа являются комплексными числами, но не обязательно, чтобы все комплексные числа были действительными числами.
Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами.
Сопряженным комплексным числом \(z=x+iy\) является \(\overline{z}=x-iy\). 9{2}}\).

Решенный пример комплексных чисел

Теперь, когда вы знаете, что сложного нет с представлением, как их изобразить на графике с последующим полярным представлением, различными свойствами, операциями, а также тождествами, давайте попрактикуемся в некоторых решенных примерах, чтобы понять эти понятия более четко.

Решено Пример 1: Получить сумму и разность для заданного набора комплексных чисел.
\(z_1=−3+2i,\ z_2=5−3i\).

Решение: Дано;

\(z_1=−3+2i,\ z_2=5−3i\)

Суммирование или сложение \(z_1\text{и}z_2\) выглядит следующим образом;

\(z_1+z_2=\влево(−3+2i\вправо)+\влево(5−3i\вправо)\)

\(=\влево(−3+5\вправо)+\влево(2i −3i\right)\)

\(=2-i\)

Следовательно, \(z_1+z_2=2-i\)

Вычитание \(z_1\text{и}z_2\) выглядит следующим образом ;

\(z_1-z_2=\влево(−3+2i\вправо)-\влево(5−3i\вправо)\)

Используя формулу;

\(z_1-z_2=\влево(x_1-x_2\вправо)+i \влево(y_1-y_2\вправо)\)

\(z_1-z_2=\влево(−3-5\вправо)+i\влево(2+3\вправо)\)

\(z_1-z_2=-8+i5\)

Пример решения 2: Получите сопряжение 5+i4.

Решение: Дано;

В соответствии с определением Если z = a + ib, то его сопряжение определяется выражением; \(\overline{z}=a-ib\)

Здесь z = a + ib= 5+i4, поэтому сопряжение z равно \(\overline{z}=5-i4\).

Попрактикуйтесь еще с комплексными числами MCQ.

Решено Пример 3: Умножить 3 и (2 + 4i).

Решение: Дано;

Согласно алгебре комплексных чисел, мы можем записать 3 как (3 + 0i)

Нет по правилу умножения:

\((3+0i)\times(2+4i)=3\times( 2+4i)\)

\(=6+12i\)

Решено Пример 4: Найдите результат \(\frac{3}{2+i}\).

Решение: Для заданных данных мы должны найти результат деления \(\frac{3}{2+i}\)

Согласно правилу деления;

\(\frac{3}{2+i}\times\frac{2-i}{2-i}\)

\(=\frac{6-3i}{5}\)

\( =\frac{6}{5}-\frac{3i}{5}\)

Следите за новостями в приложении Testbook или посетите веб-сайт Testbook, чтобы быть в курсе последних новостей по похожим темам из математики, естественных наук и многих других предметов, а также можете даже проверить серию тестов, доступных для проверки ваших знаний о различных экзаменах.

Часто задаваемые вопросы о комплексных числах

В.1 Что такое комплексное число?

Ответ 1 Любое число, которое может быть представлено в виде x + iy, называется комплексным числом, где x обозначает действительную часть, а y представляет мнимую часть.

Q.2 Каково значение i(iota)?

Ответ 2 В представлении комплексных чисел i = √-1.

В.3 Как вы определяете йоту в математике?

Анс.3 В комплексе нет. x + iy, i обозначает мнимое число, которое также читается как «йота».

В.4 Что такое символ комплексного числа?

Анс.4 Комплекс №. обозначается символом «z» и записывается как z = a + ib.

В.5. При каком условии два комплексных числа равны?

Ответ 5 Два комплексных числа называются равными, если действительная часть первого числа равна действительной части второго числа, а мнимая часть первого числа равна мнимой части второго числа.

второй. 92}\).

Q.8 Найдите сопряженное число z = x + iy?

Ответ 8 Сопряжение z = x + iy задается \(\overline{z}=x-iy\).

Q.9 Является ли 2i комплексным числом?

Ответ 9 Комплексные числа в математике — это числа, у которых есть действительная часть + мнимая часть. Здесь мы можем сказать, что 2i является комплексным, поскольку 2i можно записать как 0+2i. То есть реальная часть здесь равна нулю.

Скачать публикацию в формате PDF Формула комплексного числа

0001

Сумма действительного числа и мнимого числа определяется как комплексное число, а числа, которые не являются действительными числами, называются мнимыми числами. Число можно записать в виде b+ic, где b и c — действительные числа, ic — мнимое число, а «i» — мнимая часть, которая называется йотой. следовательно, здесь значение i равно (√-1) . i ² =-1

Давайте подумаем над уравнением x ² +16=0

Вы можете переписать его как x²=-16. Однако, поскольку квадрат каждого действительного числа положителен или равен нулю, не существует действительного числа с квадратом -16. Это пример квадратного уравнения, которое до сих пор вы бы классифицировали как «не имеющее действительных корней».

Существование таких уравнений признавалось на протяжении сотен лет, точно так же, как греческие математики признали, что x ² + 16 = 0 не имеет решения, концепция отрицательного числа еще не была разработана. Система счисления расширялась по мере того, как математики увеличивали круг математических задач, которые они хотели решать.

Вы можете решить уравнение x ² +16=0, расширив систему счисления, включив в нее новое число i (иногда записывается как j). Обладает тем свойством, что i ² = -1 и это следует обычным законам алгебры, i называется мнимым числом .

Квадратный корень из любого отрицательного числа можно выразить через i. Например, решение уравнения x ² = -16 равно x = ±√-16. Это можно записать как

±√16 * √-1, что упрощается до ±4i.

Пример: Используйте квадратную формулу для решения квадратного уравнения z ² – 6z + 58 = 0, максимально упростив свой ответ.

Решение:

z ² – 6z + 58 = 0 6) ² – 4*1*58)) / (2*1)
z = (6 ±√(-196)) / 2 (так как √-196 = √196 * √-1 = 14i) ( также √196 = 14)
z = (6 ± 14i) / 2
z = 3 ± 7i 0031 3 + 7i и 3 – 7i квадратного уравнения z ² – 6z + 58 = 0 имеют как действительную часть , так и мнимую часть.
Если мы рассмотрим комплексное число z = 3 + 7i, то 3 называется действительной частью z, т.е. Re(z), а 7 называется мнимой частью z, т. е. Im(z).
Обозначение
Любое число z вида x + yi, где x и y действительны, называется комплексным числом . Буква z обычно используется для комплексных чисел, а 9Также используется 0562 w . В этой главе
комплексное число z часто обозначается как x + yi, но иногда используются и другие буквы, например a + bi.
x называется действительной частью комплексного числа, обозначается Re(z ), а y называется мнимой частью, обозначается Im(z) .
Работа с комплексными числами
Общие методы сложения, вычитания и умножения комплексных чисел просты.
Дополнение
Добавить действительную часть к действительной части и добавить мнимую часть к мнимой части.
. часть и вычесть мнимую часть с мнимой частью.
Например, (6 – 9i) – (1 + 6i) = 5 – 15i
Умножение
Умножьте комплексные числа, используя распределительное свойство умножения.
Например,
(7 + 2i) (3 -4i) = 21 -28i + 6i -8i ²
= 21 -22i -8 (-1) (как I ² = -1)
= 29 – 22i
Комплексно-сопряженные числа
Комплексно-сопряженное число – это другое комплексное число, действительная часть которого совпадает с исходным комплексным числом, а мнимая часть имеет ту же величину с противоположными знаками. Комплексные числа имеют вид a + ib. Где a и b — действительные числа, a называется действительной частью a+ib, а ib называется мнимой частью a+ib.
Комплексное сопряжение числа a + ib с действительной частью « a » и мнимой частью « ib » задается как a – ib с действительной частью « a » и мнимой частью «-ib ». a – ib является отражением a + ib с центром на действительной оси (оси X) плоскости Аргана. Комплексно-сопряженные комплексные числа используются для рационализации комплексных чисел.
Произведение комплексного числа и его комплексно-сопряженного числа равно квадрату модуля комплексного числа, что дает действительное число, т.е.
z.z*= |z| ² = √(x ² +y ² )

Пример: Найдите комплексно-сопряженное число комплексного числа 3z + iw, если z = 1 – i и w = 2 – i.
Решение:
Прежде всего упростим 3z + iw = 3(1 – i) + i( 2 – i) = 3 – 3i + 2i + 1 = 4 – i
Чтобы определить комплексное сопряжение 3z + iw = 4 – i, мы изменим знак i.
Следовательно, комплексно-сопряженное число 4 – i равно 4 + i.
Равенство комплексных чисел
Два комплексных числа z = x + yi и w = u + vi равны, если оба x = u и y = v.
Если x ≠ u или y ≠ v, или оба, то z и w не равны. Вам может показаться, что это очевидно, но интересно сравнить эту ситуацию с равенством рациональных чисел.
Чтобы два комплексных числа были равны, действительные части должны быть равны, а мнимые части должны быть равны. Использование этого результата описывается как , эквивалентное реальным 9.0032 и воображаемые части , как показано в следующем примере.
Пример: Комплексные номера Z ₁ и Z ₂ приведены по
Z ₁ = (3 — A) + (2B — 4) I
Z ₂ = Z
Z ₂ = Z
= Z = Z = Z = I
. (7б – 4) + (3а – 2)и.
Учитывая, что z ₁ и z ₂ равны, найдите значения a и b.
Решение:
Здесь, если приравнять действительную часть z ₁ и z ₂, затем
3 — A = 7b — 4 ⇒ 7b + a = 7 (1)
и если мы приравниваем мнимую часть z ₁ и z ₂ Then
2b – 4 = 3a – 2 ⇒ 3a – 2b = -2 (2)
решив (1) и (2) методом исключения , получим
a =0 и b = 1
Пример: Дано что = 3 + 5i, найдите
(i) z + (Здесь = a – ib, что называется сопряжением z)
(ii) z ×
Решение:
z = 3 + 5i,
Затем \ bar {z} = 3-5i
(i) z + = (3 + 5i) + (3 – 5i) = 6
(ii) z× = (3 + 5i) * (3 – 5i) = 9 + 15i – 15i – 25 i ² (i ^{2 —} 1)
= 9 + 25
= 34
Из приведенного выше примера видно, что z + и z оба действительны. Это пример важного общего
Важный результат:
Что сумма двух комплексно-сопряженных чисел действительна и что их произведение также действительно.
Деление комплексных чисел
Вы, наверное, уже знаете, что выражение типа 2 / (3 – √2) можно записать в виде дроби с рациональным знаменателем, умножив числитель и знаменатель на 3 + √2.
2 / (3 – √2) = ( 2 / (3 – √2)) * (3 + √2)/(3 + √2)
= (6 + 2√2) / (9– 2)
= (6 + 2√2) / 7
Поскольку zi всегда действительно, вы можете использовать аналогичный метод, чтобы записать выражение, подобное 2 / (3 – 5i), в виде дроби с действительным знаменателем, путем умножения числитель
и знаменатель на 3+ 5i. (поскольку 3 + 5i является комплексно-сопряженным числом 3 – 5i)
Это основание для деления одного комплексного числа на другое.
Пример: Найдите действительную и мнимую части числа 1/(3 + i).
Решение
Умножить числитель и знаменатель на 3 – i
(Поскольку 3 – i сопряжено со знаменателем 3 + i)
1/( 3 + i) = ( 3 – i) / [( 3 + i)( 3 – i]
= ( 3 – i) / (9 + 1)
= ( 3 – i) / 10
Действительная часть равна 3/10, а мнимая часть равна -1/ 10.
Модуль и аргумент комплексных чисел
На приведенном ниже рисунке показана точка, представляющая z = x + iy на диаграмме Аргана

Расстояние от этой точки до начала координат равно √x² + y².
Это расстояние называется модулем z и обозначается |z|.
Итак, для комплексного числа z = x + yi
|z| = √x² + y² .
Обратите внимание, что z\bar{z} = (x + iy)(x – iy) = x² + y², тогда |z| = z×\bar{z}
Аргумент, т.е. угол θ, измеряется против часовой стрелки от положительной действительной оси. По соглашению аргумент измеряется в радианах.
Arg z (θ) = tan¯ ¹ (б/а).
Форма модуля-аргумента / Полярная форма комплексного числа
На приведенном ниже рисунке вы можете увидеть взаимосвязь между компонентами комплексного числа и его модулем и аргументом.

Используя тригонометрию, вы можете видеть, что sinθ = y/r и поэтому y = rsinθ .
Аналогично, cosθ = x/r, поэтому x = rcosθ.
Следовательно, комплексное число z = x + yi можно записать как
z = r cosθ + r sinθ i
или
z = r (cosθ + i sinθ)
(г, θ).
Примеры задач
Вопрос 1: Решите уравнение (2 + 3i)z = 9 – 4i.
Решение:
Имеем (2 + 3i)z = 9 – 4i
⇒ z = (9 – 4i) / (2 + 3i)
4i) / (9 – 4i) + 3i)] * [(2 – 3i)(2 – 3i)]
= (18 — 27i — 8i + 12i ²) / (4 — 6i + 6i — 9i ²)
= (6 — 35i) / 13
= (6 /13) — (35 / 13)i

Вопрос 2: Найдите действительную и мнимую части числа 1/(5 + 2i).
Решение:
Умножить числитель и знаменатель на 5 – 2i
(Поскольку 5 – 2i сопряжено со знаменателем 5 + 2i)
1/(5 ) / [(5 + 2i)(5 – 2i)]
= (5 – 2i) / (25 + 4)
= (5 – 2i) / 29
Действительная часть равна 5/29, а мнимая часть равна -2/29.
Вопрос 3: Напишите следующие комплексные номера в форме модуля-аргумента
(i) z ₁ = √3 + 3i
(ii) z ₂ = a 3i
Решение:
(i) 0683 1 | = √(√3) ² + (3) ² = 2√3
θ = tan¯ ¹
(3 / √3 ) = π / 3
⇒ π 8 z 1₃
Итак, z ₁ = 2√3(cos(π / 3) + i sin(π / 3))
(ii) Для z ₂ = √3 – 3i имеем
модуль |z ₂ | = √(√3) ² + (3) ² = 2√3
θ = tan¯ ¹ (-3 / √3 ) = -π / 3
⇒ 4 = arg z 2 -π/3
Итак, z ₂ = 2√3(cos(-π/3) + i sin(-π/3))
Вопрос 4. Для данного комплексного числа найдите аргумент комплексного числа, давая ответы в радианах в точной форме или в 3 значащих
цифрах, в зависимости от обстоятельств.
(i) z ₁ = −5+ I
Решение:
θ ₁ = TAN¯ ¹ (1/5) = 0.1973… = _…. я
1 = π – 0,1973… = 2,94 (3 с.ф.)
Вопрос 5: Представить данное комплексное число (-4) в полярной форме.
Решение:
Комплексное число равно -4, т.е. z = -4 +0 i
Пусть r cos θ = -4 …(1)
и r sin θ = 0 …(2)
Now, squaring and adding (1) and (2), we get
r ² cos ² θ + r ² sin ² θ = (-4) ²
r ² (кос ² θ + sin ² θ) = 16
Мы знаем, что, cos ² θ + sin ² θ = 1, тогда приведенное выше уравнение,
R ² = 16
R.
No related posts.