Формулы половинного угла
- Синус половинного угла: \(sin \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 — cos \alpha }}{2}\normalsize}\). Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол \(\frac{\alpha}2\) в левой части. Данное правило справедливо также для других формул, приведенных ниже.
- Косинус половинного угла: \(cos \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 + cos \alpha }}{2}\normalsize}\).
- Тангенс половинного угла: \(tg \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 — cos \alpha }\normalsize}{{1 + cos \alpha }}} = \large\frac{{sin \alpha }}{{1 + cos \alpha }}\normalsize = \large\frac{{1 — cos \alpha }}{{sin \alpha }}\normalsize \).
- Котангенс половинного угла: \(ctg \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 + cos \alpha }\normalsize}{{1 — cos \alpha }}} = \large\frac{{sin \alpha }}{{1 — cos \alpha }}\normalsize = \large\frac{{1 + cos \alpha }}{{sin \alpha }}\normalsize\).

Упростите.
\( 1 – 8sin2x · cos2x\)
Упростите выражение.
\(\frac{1-cos2x+sin2x}{1+cos2x+sin2x}\)
Упростите выражение.
\(\frac{sin4x}{1+cos4x}\cdot \frac{cos2x}{1+cos2x}\)
Упростите выражение.
\(\frac{cos2\alpha}{1-sin2\alpha}-\frac{1+tg\alpha}{1-tg\alpha}\)
-
Найдите \(sin(\frac{7\pi}2-\alpha), если \ sin\alpha=0,8 \ и \ \alpha \in(\frac{\pi}2; \pi)\).
 2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]
2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin\hline \text\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin3\right)>\\\\ \hline \text\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin, \ \ \cos\phi=\dfrac a>, \ \sin\phi=\dfrac b>\\\\ \hline \end\]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно.
 2\alpha=\dfrac2\)
2\alpha=\dfrac2\)Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
 2=\dfrac=1\)
2=\dfrac=1\)Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:
\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1\sin x\pm\dfrac1\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac2\cos x\right)=2\,\sin\left(x\pm\dfrac3\right)\)
Источник
Материалы
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

sin суммы углов
cos суммы углов
tg суммы углов
ctg суммы углов
Тригонометрические формулы преобразования разности аргументов
sin разности углов
cos разности углов
tg разности углов
ctg разности углов
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
sin тройного угла
cos тройного угла
tg тройного углаctg тройного угла
sin половинного угла
cos половинного угла
tg половинного угла
ctg половинного угла
sin сумма функций
cos сумма функций
1+ sin двойного угла
tg сумма функций
Уравнения преобразования через синус и косинус
sin — разность функций
cos — разность функций
tg — разность функций
1- sin двойного угла
Уравнения разложения тригонометрических функций:
квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

sin в квадрате
cos в квадрате
tg в квадрате
ctg в квадрате
Тригонометрические уравнения преобразования кубических функций через синус и косинус
sin в кубе
cos в кубе
ctg в кубе
Значения функций для некоторых углов, α
Источник
Тригонометрические формулы — список всех формул: sin, cos, tg, ctg
О чем статья
Основные тригонометрические формулы
Тригонометрические формулы – это самые незаменимые математические выражения, необходимые для тригонометрических функций. Они выполняются для всех значений аргумента.
Для начала напомним, что синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg) – неразрывно связаны с понятием угла.
Синусом угла называется отношение противолежащего катета к гипотенузе.
 Следуя из этого правило, легко запомнить, что косинус угла – отношение близкого катета (прилежащего) к гипотенузе.
Следуя из этого правило, легко запомнить, что косинус угла – отношение близкого катета (прилежащего) к гипотенузе.А вот тангенс отличается от первых двух понятиях. Это отношение дальнего к близкому катету. Котангенс с точностью да наоборот от тангенса. Котангенс – отношение близкого к дальнему катету.
Теперь перейдём непосредственно к самим формулам. Эти формулы связывают синус, косинус, тангенс, котангенс одного угла. Каждая из них является следствием каких-то определений.
;
;
;
;
;
.
У вышеперечисленных тождеств соотношение между синусом, косинусом, тангенсом и котангенсом одного и того же угла. Благодаря им можно выразить одну тригонометрическую функцию через любую другую.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Формулы приведения
Формулы приведения – это формулы, при помощи которых значения тригонометрических функций аргументов выражаются через значения синуса, косинуса, тангенса и котангенса.

, .
, .
, .
, .
, .
, .
, .
Любая из семи формул приведения может быть записана и для градусной меры угла. Чтобы использовать эти формулы, не заучивая их, нужно помнить всего лишь два правила формул приведения:
- Правило знака: с правой части формулы ставится тот знак, который имеет значение выражения в левой части при условии, что угол принадлежит I четверти.
- Правило названий: это тогда, когда в левой части формулы угол равен или . В этом случае синус меняется на косинус, а тангенс на котангенс. Так же и наоборот. Когда же угол равен или , тогда названия выражения сохраняется.
Формулы сложения для синуса, косинуса, тангенса и котангенса
Формулы сложения нужны для того, чтобы выражать функции разности или же суммы двух углов при помощи тригонометрических функций этих углов.
Синус суммы – .
Синус разности двух углов – .
Косинус суммы – .
Косинус разности – .
Тангенс суммы – .

Тангенс разности – .
Котангенс суммы – .
Котангенс разности –
Благодаря тригонометрическим формулам сложения мы можем понять, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов.
Формулы двойного угла
Формулы двойного угла – это такие формулы, которые связывают тригонометрические функции угла (синус, косинус, тангенс, котангенс) с тригонометрическими функциями угла .
Из формулы сложения для синуса при получим и после приведения подобных слагаемых получается первое тождество . Второе тождество получается аналогичным путём. Что касается двух последних тождеств (3 и 4), они получаются при , соответственно из формул:
Формулы половинного угла
Формулы половинного угла даны для квадратов тригонометрических функций.
Первые две формулы (синус и косинус) справедливы любому углу . Третья формула (тангенс) предназначается для любых углов , при которых определён .
 И четвёртая, формула котангенса половинного угла справедлива для всех углов альфа, но при которых определён котангенс половинного угла (
И четвёртая, формула котангенса половинного угла справедлива для всех углов альфа, но при которых определён котангенс половинного угла (Формулы понижения степени
Формулы понижения степени – это такие тригонометрические формулы, которые позволяют перейти от степеней тригонометрических функций к функциям первой степени. Однако от кратного аргумента.
Формулы суммы и разности тригонометрических функций
Благодаря формулам суммы и разности можно легко упрощать тригонометрические выражения. Кроме того, они часто используются при решении тригонометрических уравнений. Рассмотрим формулы суммы и разности.
Формулы произведения косинусов, синусов и синуса на косинуса
При помощи этих формул можно перейти от произведения тригонометрических функций к разности или сумме.
Все формулы, которые переходят от произведения к сумме или разности осуществляется при помощи вышеописанных формул произведения косинусов, синусов и синус на косинус.
Универсальная тригонометрическая подстановка
Основные тригонометрические формулы завершаются такими формулами, которые выражают функции тригонометрии через тангенс половинного угла.
 Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.
Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.Эти формулы выражаются через тангенс половинного угла.
Итак, мы написали самые простые и самые основные формулы, которые необходимо знать каждому учащемуся. Ведь именно при их помощи изучается тригонометрия. Кроме того, многие формулы необходимо знать для более эффективной подготовки к ЕГЭ.
Основные формулы | Олимпиадный Центр МатРИЦА
Математика: Все главные формулы
Оглавление:
Таблица умножения
Таблица квадратов двухзначных чисел
Формулы сокращенного умножения
Квадратное уравнение и формула разложения квадратного трехчлена на множители
Свойства степеней и корней
Арифметическая прогрессия
Геометрическая прогрессия
Геометрия на плоскости (планиметрия)
Формулы с логарифмами
Тригонометрия
Тригонометрические уравнения
Геометрия в пространстве (стереометрия)
Координаты
Скачать расширенную версию «Все главные формулы по школьной математике»
Весь курс алгебры для ОГЭ в схемах и таблицах >>>
Весь курс геометрии для ОГЭ в схемах и таблицах >>>
Весь курс по реальной математике для ОГЭ >>>
Все графики функций >>>
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
#Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней.

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
#Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю.
 Для корня нечетной степени выполняется также следующее равенство:
Для корня нечетной степени выполняется также следующее равенство:Для корня четной степени имеется следующее свойство:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
bn = b1 · q n-1
bn+1 =bn · q, где bn ≠ 0, q ≠ 0
q – знаменатель прогрессии
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.
 е. в том числе для любых треугольников):
е. в том числе для любых треугольников): Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений.
 Для синуса существует две равнозначные формы записи решения:
Для синуса существует две равнозначные формы записи решения:Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (трёхмерная Теорема Пифагора):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.
 е. высота боковой грани):
е. высота боковой грани):Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Как успешно подготовиться к экзамену по математике?
Для того чтобы успешно подготовиться к ОГЭ или ЕГЭ по математике, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к экзамену по математике, изучению теории и решению задач хотя бы по часу, но каждый день.
 Дело в том, что ОГЭ или ЕГЭ — это экзамены, где мало просто знать математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно, но только, решив тысячи задач.
Дело в том, что ОГЭ или ЕГЭ — это экзамены, где мало просто знать математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно, но только, решив тысячи задач. - Выучить все формулы и методы в математике! На самом деле, выполнить это тоже очень просто, необходимых формул по математике меньше 200. В алгебре и геометрии есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить. И, таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ОГЭ или ЕГЭ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования (РТ) по математике в нашем Центре (ЦР). Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на РТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на реальном экзамене может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на реальном экзамене может показаться неподготовленному человеку очень непривычным.
Успешное и ответственное выполнение этих трех пунктов позволит Вам показать на экзамене отличный результат, максимальный из того на что Вы способны!
Нашли ошибку?Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно через контактную форму на данном сайте. В письме укажите предмет (математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
<<< Структура сайта подготовки к ОГЭ по математике
План подготовки к ОГЭ по математике >>>
Рекуррентная формула понижения степени для интегрирования некоторых дробей
Учимся интегрировать рациональные дроби.
 Вывод полезной рекуррентной формулы для интегрирования некоторых дробей.
Вывод полезной рекуррентной формулы для интегрирования некоторых дробей.Ну что, друзья, продолжаем наши игры с рациональными дробями! В прошлом уроке у нас было начальное знакомство с их интегрированием и тренировка на самых простейших примерах. В этом же уроке будет
хирургия без наркозаээээ… нет… всего лишь формула.) Одна единственная. Но зато какая! Рекуррентная! Прошу не пугаться этого страшного названия.) Для начала прочитаем ещё разок само это красивое слово, чтобы не косячить в простой орфографии. А то будем как безграмотные шеф-повара элитных ресторанов, путающих гаспаЧо (холодный испанский томатный суп) и карпаЧЧо (блюдо из тонко-тонко нарезанного мяса, рыбы или овощей).Ну как, аппетит прорезался? Тогда начинаем знакомиться и аккуратно выводить нашу рекуррентную формулу. 🙂
Для начала немного об устройстве рекуррентных формул вообще.

Как это ни странно, рекуррентные формулы знакомы вам ещё со школы. Прогрессии помните? Например, арифметическую? Вспомнили? Гуд.)
Как мы обычно задаём арифметическую прогрессию? Чаще всего формулой n-го члена:
an = a1 + d(n-1)
Это для вас привычно. Также прогрессию можно задать просто рядом чисел. Например, так:
1, 2, 3, 4, 5, …
А ещё можно задать общий член арифметической прогрессии через предыдущий член! Например, вот так:
an = an-1 + 2 (n = 2, 3, 4, …)
a1 = 3
Такой не очень привычный способ задания арифметической прогрессии называется рекуррентным способом. Здесь an — n-й член прогрессии. Тот, который нас интересует. А вот an-1 — это и есть предыдущий (n-1)-й член нашей прогрессии.
 Под номером n-1. На единичку меньше, чем n. Скажем, если интересующий нас член an = a10, то предыдущий член будет an-1 = a9. Элементарно, Ватсон!
Под номером n-1. На единичку меньше, чем n. Скажем, если интересующий нас член an = a10, то предыдущий член будет an-1 = a9. Элементарно, Ватсон!Ещё нам отдельно дан первый член a1 = 3. Зачем? А затем, что у первого члена нет предыдущего! Именно поэтому перечисление значений n я начал с двойки, а не с единицы.
Теперь, зная первый член, можно запросто посчитать второй:
a2 = a1 + 2 = 3+2 = 5
Третий член можно посчитать через второй:
a3 = a2 + 2 = 5+2 = 7
Четвёртый член можно посчитать через третий, пятый — через четвёртый, и так далее… Продолжая эту славную цепочку, можно добраться до любого интересующего нас члена. А как можно посчитать сразу, скажем, 30-й член? А никак! 🙂 Пока 29-й член не узнаем, 30-й найти не сможем! В этом принципиальное отличие рекуррентной формулы от формулы n-го члена.

Страшное слово «рекуррентный» переводится на простой русский язык как «возвратный». Или, более понятно, через предыдущий (соседний). И всё.)
Возможно, кто-то скажет: «И зачем городить огород с какой-то рекуррентной формулой, когда можно сразу посчитать любой член по обычной формуле n-го члена? Чего в рекуррентной формуле хорошего? Возиться, считать последовательно все члены подряд…»
Согласен, хорошего мало. Однако, если количество рассчитываемых членов n не очень большое (скажем, три или пять), рекуррентные формулы вовсе не так уж и плохи. И именно этим фактом мы и воспользуемся в сегодняшнем уроке.
Ну вот, про рекуррентные формулы немножко поговорили. На простейшем примере принцип их работы прочувствовали. Однако основная тема нашего урока — интегрирование рациональных дробей, не так ли? Так что начнём ближе к делу. 🙂 Итак!
Давайте, немножко вернёмся к прошлому уроку и вспомним, какие же дроби мы учились интегрировать в прошлый раз.

— дробно-линейные функции (числитель и знаменатель дроби — линейные конструкции)
— дроби, знаменатель которых — линейная функция (сама по себе, либо в степени), а числитель — любой многочлен
— дроби, в знаменателе которых стоит одиночный квадратный трёхчлен
И пока всё. Три вида дробей. Негусто, но уже кое что.) В первых двух типах интегралов мы тождественными преобразованиями выделяли из числителя знаменатель, раскладывали дробь в сумму более простых и последовательно интегрировали каждую из них. С квадратным трёхчленом мы расправлялись выделением полного квадрата. Вспомнили? Хорошо.)
В этом же уроке мы научимся интегрировать ещё один тип рациональных дробей с квадратным трёхчленом в знаменателе. Но у трёхчлена этого будет две важные особенности:
1. Квадратный трёхчлен дополнительно возводится в степень n;
2.
 Квадратный трёхчлен имеет отрицательный дискриминант. Или, что то же самое, неразложим на линейные множители.
Квадратный трёхчлен имеет отрицательный дискриминант. Или, что то же самое, неразложим на линейные множители.Таким образом, постановка задачи этого урока — научиться брать интегралы вот такого типа:
В числителе dx, а в знаменателе — неразложимый квадратный трёхчлен в степени.
Что для этого сегодня нам потребуется.
1. Формула интегрирования по частям:
Кто до сих пор не в курсе, что это за закорючки такие, читайте урок: «Неопределённый интеграл. Метод интегрирования по частям». Пока не поздно. Там всё популярно изложено, нарисовано, подписано… Старался как мог.)
2. Табличный интеграл №8 из нашей сводной таблицы:
Вот, собственно, и весь инструментарий. Теперь ближе к делу.
Для большей простоты изложения материала я сейчас проведу некоторые упрощения в нашем квадратном трёхчлене x2 + bx + c.
 А именно:
А именно:— обнулю коэффициент b (b = 0),
— свободный член c переобозначу как a2.
Все эти превращения я проделал чисто с целью подчеркнуть неразложимость нашего квадратного трёхчлена и упростить дальнейшие выкладки.
А сейчас я начну брать вот такой интересный интеграл:
Для начала я обозначу искомый интеграл латинской буквой I, но c индексом n (n-й степени). Вот так:
А теперь начинаем наше интегрирование. Первым делом я выделю в подынтегральной функции 1/(x2+a2)n знаменатель из числителя. Вы спросите: «Как же из единички можно выделить выражение (x2+a2)n ?» А вот так (расписываю по шагам):
1. Умножаем и тут же делим всю нашу дробь на а2:
2.
 В числителе прибавляем и тут же вычитаем слагаемое x2, а затем почленно делим числитель на знаменатель, раскладывая дробь на две. Это дело уже знакомо:
В числителе прибавляем и тут же вычитаем слагаемое x2, а затем почленно делим числитель на знаменатель, раскладывая дробь на две. Это дело уже знакомо:А теперь подставляем всё это добро в наш интеграл вместо исходной дроби. Константу 1/а2 сразу везде выносим за знак интеграла. Получаем:
Первый интеграл (тот, что обведён красным) получен из исходного интеграла понижением показателя степени n на единичку: (n-1). Его, для краткости, можно переобозначить как In-1. Итого пока что имеем следующее:
И теперь наша задача — взять оставшийся второй интеграл:
А его мы будем брать по частям!)
Те, кто в танке, прочитали соответствующий материал про части? Ну, ладно, я предупредил! Поехали! 🙂
Для начала разбиваем наше подынтегральное выражение на произведение функции u и дифференциала dv. В качестве функции u я предлагаю взять просто множитель х.
 Ну, а в качестве dv берём оставшуюся часть подынтегрального выражения. Также до кучи ищем v и du.
Ну, а в качестве dv берём оставшуюся часть подынтегрального выражения. Также до кучи ищем v и du. Вот так:
Кто не понял, как именно получена функция v, тот, к сожалению, плохо освоил интегрирование подведением под знак дифференциала. Перечитайте соответствующий урок, пока не поздно!
Отлично. Великолепная четвёрка u—dv—v—du получена, заполняем теперь нашу стандартную анкету:
Несуразные выражения, конечно. А что делать… Теперь интегрируем по частям. Имеем в виду, что весь процесс интегрирования у нас проходит по переменной икс. Стало быть, буковка n — это такая же константа, как и слагаемое a2. И поэтому множитель 2(n-1), сидящий в знаменателе функции v, можно целиком отправить за знак интеграла.

Вот как выглядит весь процесс интегрирования:
Отлично. Чем же хорош данный результат? А тем, что наш второй интеграл также оказался выраженным через интеграл степенью ниже In-1 ! Подставляем теперь этот результат в наше исходное равенство вместо второго интеграла, раскрываем все скобки и упрощаем:
Вот он, наш окончательный результат. Та самая рекуррентная формула понижения степени!
Почему данная формула носит название рекуррентной, да ещё и понижения степени? Разбираемся.
Для начала разберёмся с понижением степени. Ибо проще это. В чём суть: слева в формуле стоит интеграл степени n (In). А вот справа стоит тот же самый интеграл, но уже степени на единичку ниже (In-1).
 Под степенью здесь, конечно же, подразумевается не степень интеграла как такового, а всего лишь степень знаменателя подынтегральной дроби. Это и так понятно, я думаю.) Зачем же нам понижать степень интеграла (знаменателя)? Да потому, что с маленькой степенью работать всяко проще, чем с большой! И не только в интегралах. В тригонометрии, например. Там тоже есть свои формулы понижения степени. Например, для выражений типа sinnx, cosnx и тому подобных. Полистайте соответствующую литературу (или Гугл)).
Под степенью здесь, конечно же, подразумевается не степень интеграла как такового, а всего лишь степень знаменателя подынтегральной дроби. Это и так понятно, я думаю.) Зачем же нам понижать степень интеграла (знаменателя)? Да потому, что с маленькой степенью работать всяко проще, чем с большой! И не только в интегралах. В тригонометрии, например. Там тоже есть свои формулы понижения степени. Например, для выражений типа sinnx, cosnx и тому подобных. Полистайте соответствующую литературу (или Гугл)).Чем примечательна эта, казалось бы, громоздкая и малопонятная формула? А тем, что она позволяет свести исходный интеграл In к интегралу степенью ниже In-1. Именно поэтому она и называется формулой понижения степени.
Например, если n=3, то интеграл I3 можно сначала свести к интегралу I2, а I2, в свою очередь, уже свести к I1.
 Одним словом, устроена эта формула по принципу матрёшки. Или домино. Вот и вся суть понижения степени.)
Одним словом, устроена эта формула по принципу матрёшки. Или домино. Вот и вся суть понижения степени.)Однако, реально работать с этой формулой надо немного по-другому. И теперь мы плавненько переходим ко второй части названия данной формулы — почему же она именуется ещё и рекуррентной. А вот почему. Дело всё в том, что для получения исходного интеграла In нам надо знать предыдущий интеграл In-1.
Для поиска In-1 надо знать In-2.
Для In-2 надо знать In-3…
И так далее по снижающейся траектории приходим к выводу, что для поиска интеграла I2 надо знать интеграл I1.
Вопрос на засыпку: а что собой представляет интеграл 1-й степени I1? Ну, берём, подставляем единичку вместо n в наш исходный интеграл и смотрим… Да! Табличный интеграл №8, с арктангенсом:
И именно от него мы и начинаем плясать.
 А дальше — одеваем нашу матрёшку: по интегралу I1 считаем I2, по найденному I2 считаем I3 — и так далее, пока не доберёмся до исходного интеграла In. Того, который дан в примере. Именно так и нужно работать с данной формулой.) И именно по этой причине формула и называется рекуррентной.
А дальше — одеваем нашу матрёшку: по интегралу I1 считаем I2, по найденному I2 считаем I3 — и так далее, пока не доберёмся до исходного интеграла In. Того, который дан в примере. Именно так и нужно работать с данной формулой.) И именно по этой причине формула и называется рекуррентной.Вот мы и разобрались полностью с названием и сутью данной формулы.
Да, я не спорю, формула достаточно страшная и громоздкая. Ничего не поделать: мы тоже с вами всё-таки уже далеко не школьники, а вовсю изучаем высшую математику, правда ведь?
Ну что, посмотрим на рекуррентную формулу в действии?
Пример 1
Найти неопределённый интеграл:
Анализируем подынтегральную функцию:
n = 3,
a2 = 9, т.
 е. а=3.
е. а=3.Исходная степень квадратного трёхчлена в знаменателе — тройка. Значит, наше интегрирование будет происходить в три шага.
Шаг 1
Для интегрирования этой нехорошей дроби плясать начинаем от интеграла 1-й степени (I1, n=1). Он табличный:
Шаг 2
Вычисляем теперь интеграл 2-й степени (I2, n=2), используя рекуррентную формулу и результат предыдущего шага I1.
Выпишем нашу формулу, дабы иметь её перед глазами:
И теперь просто берём и аккуратно подставляем в формулу вместо n двойку, вместо a2 — девятку, а вместо In-1 — наш интеграл 1-й степени I1.
И считаем:
Есть.)
Шаг 3
Вот мы и добрались до последнего третьего шага.
 Считаем теперь интеграл 3-й степени I3. Для этого подставляем в рекуррентную формулу теперь уже n=3 и результат второго шага I2. И прибавляем (теперь уже) константу С. Вот так:
Считаем теперь интеграл 3-й степени I3. Для этого подставляем в рекуррентную формулу теперь уже n=3 и результат второго шага I2. И прибавляем (теперь уже) константу С. Вот так:Всё. Интегрирование завершено. Вот наш окончательный ответ:
Продифференцируйте, проверьте! 😉
Данная рекуррентная формула позволяет успешно интегрировать и более крутые дроби с квадратными трёхчленами в степенях. Например, такую:
Пример 2
В подобных примерах перед тем как что-то интегрировать, первым делом проверяем разложимость квадратного трёхчлена на множители. Считаем дискриминант:
D = 22 — 4∙1∙10 = 4–40 = -36 <0
Дискриминант отрицательный. Стало быть, наш трёхчлен действительных корней не имеет и неразложим на более простые множители. Ладно.)
Что делать, если трёхчлен (вдруг) окажется разложим на множители? Такие примеры будут разбираться дальше.
 В следующих уроках.)
В следующих уроках.)Что делать дальше? А дальше — запоминаем:
Если под интегралом дана дробь, содержащая квадратный трёхчлен, то первым делом выделяем из трёхчлена полный квадрат! А дальше — видно будет…
Вот и выделяем. Здесь это совсем просто:
Теперь, кстати, отчётливо видно, почему дискриминант получился отрицательным: если к неотрицательному выражению (х+1)2прибавить ещё девятку, то получится всяко положительное число. Но не ноль!
А дальше дело за малым. Подводим скобку (х+1) под дифференциал и заменяем эту самую скобку новой буквой t:
Интеграл свёлся к виду In. Берущемуся по рекуррентной формуле (n=3, a2=9).
А дальше я предлагаю немного схитрить и нагло скоммуниздить уже готовый результат предыдущего примера:
Найдите, как говорится, 7 отличий:
Ну да, вместо икса везде буква t появилась.
 Ну и что? Мы же знаем, что любому интегралу (даже самому навороченному) по барабану, что там за буква стоит — икс или тэ. Лишь бы везде одна и та же стояла — в функции и под дифференциалом.)
Ну и что? Мы же знаем, что любому интегралу (даже самому навороченному) по барабану, что там за буква стоит — икс или тэ. Лишь бы везде одна и та же стояла — в функции и под дифференциалом.)Вспоминаем, что наше t — это скобка (х+1) и смело записываем окончательный ответ:
Вот такие дела.)
Разумеется, заучивать наизусть данную рекуррентную формулу не нужно, а вот знать, как её вывести (в случае чего) и, главное, уметь применять – очень полезно.
Что делать, если в числителе — не dx, а многочлен?
Пример 3
Ну, если попался такой монстр, то тут, как говорится, ваше дело — труба… Ибо интегралы от таких дробей (в знаменателе неразложимый трёхчлен в степени n + ещё и многочлен в числителе) — самые скверные, да. Либо вы — студент мехмата, ВМК или физтеха, либо же попали под горячую руку преподавателя.
 Так что разберу и такой пример. На всякий пожарный. Чтобы быть во всеоружии.)
Так что разберу и такой пример. На всякий пожарный. Чтобы быть во всеоружии.)Как ни странно, и тут тоже можно обойтись БЕЗ метода неопределённых коэффициентов! Но придётся порядком попотеть с этой самой рекуррентной формулой из-за куба в знаменателе. Так что ближе к делу.
Первым делом разберёмся с квадратным трёхчленом в знаменателе:
Трёхчлен неразложим на множители, да сам ещё и в кубе. Дело попахивает рекуррентной формулой… Неохота с ней возюкаться, но ничего не поделать, да.
Выделяем полный квадрат в знаменателе:
Так, в скобках образовалось х+1. Теперь надо эту же скобку выделить в числителе. Зачем? А затем, чтобы можно было подвести эту скобку под дифференциал, ввести новую переменную t и немного упростить пример.
Процедура уже знакома:
Есть. Числитель дроби разложен по степеням (х+1). Теперь подводим скобку (х+1) под дифференциал и вводим замену х+1 = t:
Дальше полученный интеграл я почленным делением разобью на два.
 И для краткости обозначу его буквой I. Вот так:
И для краткости обозначу его буквой I. Вот так:Или, в краткой записи: I = (1) — (2)
Почему именно такое разбиение я выбрал, станет ясно дальше. Разбираемся теперь поочерёдно с каждым из интегралов (1) и (2). Для начала с первым. Вот тут уже начинается хардкор, да… Для успешной расправы с ним первым делом выделим в числителе знаменатель t2+1 и опять разобьём интеграл на два:
Хардкор данного этапа решения заключается в том, что оба полученных интеграла… берутся по рекуррентной формуле, да!) Дело в том, что наша конструкция, если как следует присмотреться, имеет вид I2 + 3I3. В обозначениях рекуррентной формулы. В первом интеграле в знаменателе сидит квадрат, во втором — куб. Всё логично. Запускаем в дело нашу формулу. Шагов нам потребуется всего три. Поскольку максимальная степень знаменателя — третья.
 Вперёд! Уже без лишних комментариев:
Вперёд! Уже без лишних комментариев:Шаг 1
Шаг 2
Шаг 3
Готово! Самая сложная часть примера осталась позади.) Теперь составляем нужное нам выражение I2 + 3I3 и получаем результат интеграла под цифрой (1).
Естественно, раскрываем скобки, приводим подобные и упрощаем, где надо (складываем арктангенсы и дроби с одинаковыми знаменателями). А, чтобы народ не заблудился в громоздких выкладках, я подпишу всё то, что мы подставляем и получаем:
Ну вот. Первый (и самый трудоёмкий) интеграл благополучно взят. А взять оставшийся второй интеграл (2) — пара пустяков. Ибо он берётся безо всяких ухищрений обычным подведением знаменателя под дифференциал, сводясь к степенной функции.)
Что ж, оба промежуточных интеграла успешно взяты.
 Вот и финишная прямая! Вычитаем теперь интеграл (2) из интеграла (1), приводим подобные, обратно заменяем переменную t на x+1, прибавляем константу С и получаем окончательный ответ нашего жуткого примера:
Вот и финишная прямая! Вычитаем теперь интеграл (2) из интеграла (1), приводим подобные, обратно заменяем переменную t на x+1, прибавляем константу С и получаем окончательный ответ нашего жуткого примера:Окончательно:
Вот так вот распутываются сложные примеры. Самое главное — аккуратность и предельное внимание, чтобы не запутаться в знаках, скобках и многочисленных коэффициентах и постоянно держать в уме, что именно вы вычисляете или подставляете.
Кстати, вы не поверите, но я взял черновик, продифференцировал этот длинный ответ, привёл ВСЁ к общему знаменателю, упростил и… Аллилуйя! Получилась исходная подынтегральная функция!)
Разумеется, разбор конкретного сложного примера — бестолковое дело, прямо скажем. Ибо не попадётся он. А вот разъяснить на конкретном примере, куда надо стремиться во всех подобных ситуациях — совсем другое дело, согласитесь! Кстати, открою приятный бонус: разобранные типы интегралов от дробей в этом уроке и в предыдущем — это вся необходимая база для нахождения интегралов от любых рациональных дробей.
 Да-да, любых! Дело в том, что интеграл от любой, даже очень навороченной, рациональной дроби будет сводиться к комбинации интегралов от уже рассмотренных типов дробей — с линейным многочленом или неразложимым квадратным трёхчленом в знаменателе. Все подробности — в следующих уроках по интегрированию рациональных дробей!
Да-да, любых! Дело в том, что интеграл от любой, даже очень навороченной, рациональной дроби будет сводиться к комбинации интегралов от уже рассмотренных типов дробей — с линейным многочленом или неразложимым квадратным трёхчленом в знаменателе. Все подробности — в следующих уроках по интегрированию рациональных дробей!Ну что ж, ладно, отмучились на сегодня! 🙂
А теперь пара несложных примеров для самостоятельного решения.
Пользуясь рекуррентной формулой понижения степени, найти неопределённые интегралы от рациональных дробей:
Ответы:
Разумеется, надо не просто тупо сдуть готовые ответы, а получить эти ответы! Иначе весь этот урок впустую. Уважьте мой труд.) До скорых встреч!
3x. Мы также поймем вывод этих формул, график sin3x и применение с помощью решенных примеров для лучшего понимания концепции.Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
ГОСТы, СНиПы
Карта сайта TehTab.
ru
Поиск по сайту TehTab.ru
Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Раздел: Таблицы численных значений + Таблицы Брадиса: - Таблица умножения — традиционная 10×10, 12х12 и 20х20
- Таблица деления — традиционная 10×10 и 12х12
- Таблицы квадратов.
 Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99. - Таблица квадратов натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ).
- Таблицы кубов. Натуральных чисел от 1 до 20 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
- Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней.
- Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.
- Таблица 4-ой и 5-ой степени чисел от 1 до 100.
- Точная и приблизительная таблицы факториалов (1-255)
- Таблицы логарифмов и основные формулы
- Таблица. Длина окружности диаметра D.
- Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.
- Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты.

- Таблица и формулы соотношений между стороной, радиусами вписанной и описанной окружности и площадью для правильных многоугольников
- Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
- Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
- Таблица синусов, она-же косинусов (см.примечание внутри). Углы в угловых градусах. Таблица значений синусов.
- Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица тангенсов, она же котангенсов (см.примечание внутри). Углы в угловых градусах.
- Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° — 360°.
 Углы с шагом в 1°. Таблица значений котангенса, ctg
Углы с шагом в 1°. Таблица значений котангенса, ctg - Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
- Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее
- Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)2, π2, π3, π4 и др.
- Численные значения числа e, 1/e, e2, log10 e и др.
- Постоянная Эйлера γ, золотое сечение (золотая пропорция) φ, ln γ, eγ, 1/φ и др.
- Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000
- Таблица случайных чисел.
- Таблицы : 100 случайных двузначных чисел и генератор случайных последовательностей.
Дополнительная информация от TehTab.
 ru:
ru:Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru
Реклама, сотрудничество: [email protected]
Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. 1. Что такое Sin3x в тригонометрии? 2. 
Sin3x Формула 3. График Sin3x 4. Доказательство формулы Sin3x 93x Формула7. Часто задаваемые вопросы по Sin3x Что такое тригонометрия Sin3x?
Sin3x — важное тождество в тригонометрии. Его можно выразить через sin x. Sin3x используется для определения значения функции синуса для угла, который в три раза больше угла x. График функции sin3x аналогичен графику функции sin x. Мы знаем, что период sin x равен 2π, поэтому период sin3x равен 2π/3. Это означает, что цикл sin3x повторяется через каждые 2π/3 радиана. Теперь давайте посмотрим на формулу для sin3x. 93x, что можно записать как sin3x = 3 sin x — 4 sin 3 x. Теперь нарисуем график тригонометрической формулы sin3x и проверим ее поведение. Кроме того, мы выведем формулу, используя тождество сложения углов.
График Sin3x
Поведение графика sin3x аналогично поведению тригонометрической функции sin x.
 Угол, рассматриваемый в sin3x, в три раза больше угла в функции sin x. Мы знаем, что для функции sin bx период равен 2π/|b| что подразумевает, что период sin3x равен 2π/3. Следовательно, график sin3x уже, чем график sin x, поскольку период sin3x составляет одну треть периода sin x (период sin x равен 2π)
Угол, рассматриваемый в sin3x, в три раза больше угла в функции sin x. Мы знаем, что для функции sin bx период равен 2π/|b| что подразумевает, что период sin3x равен 2π/3. Следовательно, график sin3x уже, чем график sin x, поскольку период sin3x составляет одну треть периода sin x (период sin x равен 2π)Теперь построим график функции sin3x, взяв несколько точек на графике и соединив их. Рассмотрим несколько точек для y = sin3x и y = sin x и нанесем их на график.
- Когда x = 0, 3x = 0 ⇒ sin x = 0, sin3x = 0
- Когда x = -π/6, 3x = -π/2 ⇒ sin x = -1/2, sin3x = -1
- Когда x = π/6, 3x = π/2 ⇒ sin x = 1/2, sin3x = 1
- Когда x = π/2, 3x = 3π/2 ⇒ sin x = 1, sin3x = -1
- Когда x = -π/2, 3x = -3π/2 ⇒ sin x = -1, sin3x = 1
Ниже приведен график sin3x и sin x:
Доказательство формулы Sin3x
Мы будем использовать формулу сложения углов функции синуса, чтобы вывести формулу sin3x. Мы будем использовать запись угла 3x как 3x = 2x + x, чтобы доказать тождество.
 Мы будем использовать следующие тригонометрические тождества, чтобы доказать тождество sin3x:
Мы будем использовать следующие тригонометрические тождества, чтобы доказать тождество sin3x:- sin (a + b) = sin a cos b + cos a sin b
- sin 2x = 2 sin x cos x
- cos 2x = 1 — 2sin 2 x
- sin 2 х + cos 2 х = 1
Мы будем использовать приведенные выше тождества и формулы для доказательства формулы sin3x. Используя формулу сложения углов для функции синуса, мы имеем
sin3x = sin (2x + x)
= sin2x cosx + cos2x sinx [Потому что sin (a + b) = sin a cos b + cos a sin b]
= (2 sin x cos x) cos x + (1 — 2sin 2 x) sin x
= 2cos 2 x sin x — 2sin 93x ⇒ sin 3 x = 1/cosec 3 x
- Формула для sin3x issin3x = 3 sin x — 4 sin 3 x
- График sin3x уже графика sin x, так как период sin 3 равен 2π/3.
- d(sin 3x)/dx = 3 cos 3x
- ∫sin 3x dx = (-1/3) cos 3x + C
- cos 2x 93x формула.
- Когда x = 0, 3x = 0 ⇒ sin x = 0, sin 3x = 0
- Когда x = -π/6, 3x = -π/2 ⇒ sin x = -1/2, sin 3x = -1
- Когда x = π/6, 3x = π/2 ⇒ sin x = 1/2, sin 3x = 1
- Когда x = π/2, 3x = 3π/2 ⇒ sin x = 1, sin 3x = -1
- Когда x = -π/2, 3x = -3π/2 ⇒ sin x = -1, sin 3x = 1
- Полярная форма комплексного числа
- Степени и корни комплексного числа
- Квадратный корень из i
- Основной корень любого числа
- Несколько корней
- Логарифм отрицательного числа
- Практические задачи
- Что нового
- 30 октября 2016 г. : Добавлена практика проблемы.
- 27 октября 2016 г. :
- В этом документе постепенно накапливалась масса несвязанных темы. Я вынес этот материал о комплексных числах с триггером в отдельную главу и добавил Резюме.
- Обновлены математические обозначения, в частности использование курсива и пробелов, для соответствия стандарту. Я использовал комплекс Jukka Korpelas Написание математических выражений (2014, Suomen E-painos Oy), ISBN 978-952-6613-25-3.
- (промежуточные изменения подавлены)
- 19 февраля 1997 г.
 : Новый документ.
: Новый документ. - . При переносе членов имеем
- 4 sin 3 x = 3sinx – sin 3x
- Разделим обе части уравнения 4 sin 3 x = 3sinx – sin 3x на 4,
- Получим sin 3 x = (3sinx – sin 3x)/4
Важные замечания по Sin 3x
☛ Статьи по теме:

Что такое формула Sin3x?
Sin3x используется для определения значения функции синуса для угла, который в три раза больше угла x. Формула тригонометрической функции sin3x имеет вид: sin3x = 3 sin x — 4 sin 3 x.
Что такое производная Sin3x?
Производная sin3x равна 3 cos 3x ⇒ d(sin3x)/dx = 3 cos 3x.
Какой период у = sin3x?
Мы знаем, что для функции sin bx период равен 2π/|b| что подразумевает, что период sin3x равен 2π/3.
Как построить график Sin3x?
Поведение графика sin3x похоже на поведение тригонометрической функции sin x. График sin3x уже, чем график sin x, поскольку период sin3x составляет одну треть периода sin x. Мы можем нанести несколько точек на график и соединить их, чтобы получить график sin3x.
Как интегрировать Sin3x?
Чтобы определить интеграл от sin3x, воспользуемся формулой ∫sin(ax + b) dx = (-1/a) cos(ax + b) + C. ⇒ ∫sin 3x dx = (-1/3) cos 3x + C.
⇒ ∫sin 3x dx = (-1/3) cos 3x + C.
Что такое Sin Cube x?
Куб синуса x — это тригонометрическая функция, которая дает значение всего куба синуса. Мы можем вывести его формулу, используя формулу sin3x в тригонометрии. 93x ⇒ sin 3 x = 1/cosec 3 x
Является ли Sin3x таким же, как 3sinx?
Нет, sin3x — это не то же самое, что 3sin x, поскольку sin3x — это значение функции синуса, когда угол в три раза больше x, а 3 sin x — это значение, в три раза превышающее значение sin x.
Видео-вопрос: Нахождение выражения, эквивалентного кубу функции синуса.
В этом вопросе нам нужно найти выражение для куба греха 𝜃 через синусы, кратные нашему углу 𝜃. У нас может возникнуть соблазн попробовать использовать такие вещи, как наша формула двойного угла для синуса, чтобы попытаться переписать синус в кубе в терминах этого. И это может сработать; однако это сложно и потребует много экспериментов. А на самом деле есть более простой способ.
А для этого нам сначала нужно вспомнить теорему де Муавра. Это говорит нам о том, что для любого целочисленного значения 𝑛 и действительного значения 𝜃, потому что 𝜃 плюс 𝑖 грех 𝜃, все возведенные в 𝑛-ю степень, равны косинусу 𝑛𝜃 плюс 𝑖 греху 𝑛𝜃. И это только одна версия теоремы. Существует несколько различных эквивалентных утверждений. И есть несколько очень полезных прямых результатов этой теоремы, которые помогут нам ответить на этот вопрос. И это стоит запомнить.
Если мы назовем наше комплексное число cos 𝜃 плюс 𝑖 sin 𝜃 равным 𝑍, то по теореме де Муавра 𝑍 в 𝑛-й степени будет cos 𝑛𝜃 плюс 𝑖 умноженный на грех 𝑛𝜃. И мы можем доказать следующие два полезных результата для любого целочисленного значения 𝑛. 𝑍 в 𝑛 степени плюс один сверх 𝑍 в 𝑛 степени будет равен удвоенному cos 𝑛𝜃 и 𝑍 в 𝑛 степени минус один сверх 𝑍 в 𝑛 степени будет два 𝑖 греха 𝑛𝜃.
Чтобы доказать эти два результата, мы просто помним, что один больше 𝑍 в 𝑛-й степени равен 𝑍 в отрицательной степени 𝑛. И мы можем применить теорему де Муавра для любого целочисленного значения 𝑛. Результат, который нас здесь интересует, является нижним результатом. И причина этого в том, что это поможет нам найти выражение для греха в кубе 𝜃. Давайте начнем с установки нашего значения 𝑛 равным единице. Установив наше значение 𝑛 равным единице в нашем нижнем результате, мы получаем, что два 𝑖 грех 𝜃 будет равен 𝑍 минус один сверх 𝑍.
И мы можем применить теорему де Муавра для любого целочисленного значения 𝑛. Результат, который нас здесь интересует, является нижним результатом. И причина этого в том, что это поможет нам найти выражение для греха в кубе 𝜃. Давайте начнем с установки нашего значения 𝑛 равным единице. Установив наше значение 𝑛 равным единице в нашем нижнем результате, мы получаем, что два 𝑖 грех 𝜃 будет равен 𝑍 минус один сверх 𝑍.
Конечно, в вопросе мы ищем выражение для греха в кубе 𝜃. Итак, нам нужно возвести в куб обе части этого выражения. Затем мы можем изменить порядок, чтобы найти выражение для греха в кубе 𝜃. Начнем с упрощения левой части этого выражения. Мы собираемся кубировать каждый из наших факторов отдельно. Это дает нам восьмикратное 𝑖 в кубе, умноженное на синус в 𝜃 в кубе. И в правой части нашего выражения мы видим в скобках два числа, и мы возводим их в степень. Это биномиальное выражение.
Итак, мы могли бы записать это полностью и умножить, используя метод FOIL, или мы могли бы использовать биномиальную теорему. Помните, это говорит нам, что 𝑎 плюс 𝑏 все, возведенное в 𝑛-ю степень, будет равно сумме от 𝑘 равно нулю до 𝑚 из 𝑚 выберите 𝑘, умноженное на 𝑎 в 𝑘-й степени, умноженное на 𝑏 в степени 𝑚 минус 𝑘, где 𝑚 равно положительное целое число. Мы сделаем это, используя биномиальную теорему. В развернутом виде это дает нам три выбора ноль умножить на 𝑍 в кубе плюс три выбора на единицу умножить на 𝑍 в квадрате умножить на минус один на 𝑍 плюс три выбрать два раза 𝑍 умножить на минус на один на 𝑍 все в квадрате плюс три выбрать три умножить на минус один на 𝑍 все в кубе.
Помните, это говорит нам, что 𝑎 плюс 𝑏 все, возведенное в 𝑛-ю степень, будет равно сумме от 𝑘 равно нулю до 𝑚 из 𝑚 выберите 𝑘, умноженное на 𝑎 в 𝑘-й степени, умноженное на 𝑏 в степени 𝑚 минус 𝑘, где 𝑚 равно положительное целое число. Мы сделаем это, используя биномиальную теорему. В развернутом виде это дает нам три выбора ноль умножить на 𝑍 в кубе плюс три выбора на единицу умножить на 𝑍 в квадрате умножить на минус один на 𝑍 плюс три выбрать два раза 𝑍 умножить на минус на один на 𝑍 все в квадрате плюс три выбрать три умножить на минус один на 𝑍 все в кубе.
А теперь мы можем начать упрощать. Во-первых, помните, что 𝑖 — это квадратный корень из отрицательной единицы. Итак, 𝑖 в квадрате равен отрицательной единице. Это означает, что 𝑖 в кубе равно отрицательному 𝑖. Таким образом, мы можем упростить левую часть нашего уравнения, чтобы получить отрицательное число, умноженное на восемь 𝑖, умноженное на синус, умноженный на 𝜃. И мы можем упростить каждое слагаемое в правой части нашего уравнения по отдельности. Во-первых, три выбирают ноль просто равным единице, поэтому наш первый член равен 𝑍 в кубе.
Во-первых, три выбирают ноль просто равным единице, поэтому наш первый член равен 𝑍 в кубе.
Чтобы упростить наш следующий термин, вспомним, что отрицательная единица над 𝑍 может быть записана как отрицательная 𝑍 в степени отрицательной единицы. И помните, чтобы умножить два члена с одним и тем же основанием, мы просто складываем их показатели степени. А в нашем показателе два минус один равно единице. Итак, мы получаем 𝑍 в первой степени, то есть просто 𝑍. И коэффициент будет равен трем выбрать единицу, умноженную на отрицательную единицу, что равно отрицательной тройке.
Мы можем сделать то же самое, чтобы оценить наш следующий член. Однако на этот раз у нас есть отрицательная единица над 𝑍 в квадрате. Это просто упростит, чтобы дать нам 𝑍 в степени отрицательных двух. Таким образом, 𝑍, умноженное на 𝑍 в степени отрицательной двойки, равно 𝑍 в степени отрицательной единицы. И наш коэффициент как раз три на выбор два, который, как мы знаем, равен трем. Итак, наш третий член равен трем 𝑍 в отрицательной степени.
Наконец, в нашем последнем члене мы можем распределить куб по скобкам. Мы получаем отрицательную единицу над 𝑍 в кубе. А три выбирают три как раз равно одному. Итак, наш последний член отрицателен над 𝑍 в кубе. Итак, наше уравнение теперь гласит: минус восемь 𝑖 в кубе греха 𝜃 равно 𝑍 в кубе минус три 𝑍 плюс три 𝑍 в степени минус один минус один в 𝑍 в кубе. И мы могли бы заметить кое-что интересное. У нас есть 𝑍 в кубе минус единица на 𝑍 в кубе. И это точно одно из наших утверждений для теоремы де Муавра с нашим значением 𝑛 равным трем. И на самом деле, это не единственный раз, когда это появляется. Помните, мы можем переписать 𝑍 в степени отрицательной единицы как единицу над 𝑍.
Итак, мы можем переписать наш третий член как три, разделенные на 𝑍. И мы хотим записать это в виде 𝑍 в 𝑛-й степени минус единица над 𝑍 в 𝑛-й степени. Мы хотим, чтобы наше значение 𝑛 было равно единице. И мы можем либо вычесть множитель в три, либо множитель в минус три. Мы уберем множитель отрицательной тройки. Убрав наш множитель минус три и перестроив наше уравнение, мы получим минус восемь 𝑖 в кубе греха 𝜃 равно 𝑍 в кубе минус один больше 𝑍 в кубе минус три раза 𝑍 минус один больше 𝑍.
Убрав наш множитель минус три и перестроив наше уравнение, мы получим минус восемь 𝑖 в кубе греха 𝜃 равно 𝑍 в кубе минус один больше 𝑍 в кубе минус три раза 𝑍 минус один больше 𝑍.
Теперь мы готовы начать писать это выражение через синусы, кратные 𝜃. И для этого нам снова понадобится теорема Муавра. Установив наше значение 𝑛 равным трем, мы знаем, что 𝑍 в кубе минус один на 𝑍 в кубе в два 𝑖 раза больше, чем три 𝜃. И установив наше значение 𝑛 равным единице, мы знаем, что 𝑍 минус один сверх 𝑍 равно двум 𝑖 греху 𝜃.
Подставив эти выражения и вспомнив, что нам нужно умножить два 𝑖 sin 𝜃 на минус три, мы получим следующее уравнение. Получаем, что отрицательные восемь 𝑖 грехов в кубе 𝜃 равны двум 𝑖 грехам трех 𝜃 минус шесть 𝑖 грехов 𝜃. Теперь все, что нам нужно сделать, это изменить это уравнение для куба греха 𝜃. Для этого нам нужно разделить обе части нашего уравнения на минус восемь 𝑖. Чтобы сделать это проще, для упрощения, мы разделим каждое слагаемое в правой части нашего уравнения отдельно на минус восемь 𝑖. Мы получаем, что грех в кубе 𝜃 равен двум 𝑖 греху трем 𝜃 по всему минусу восемь 𝑖 плюс минус шесть 𝑖 грех 𝜃 все делится на минус восемь 𝑖.
Мы получаем, что грех в кубе 𝜃 равен двум 𝑖 греху трем 𝜃 по всему минусу восемь 𝑖 плюс минус шесть 𝑖 грех 𝜃 все делится на минус восемь 𝑖.
А теперь мы можем начать упрощать. В обоих случаях у нас есть общий множитель 𝑖 в числителе и знаменателе. Точно так же и первый, и второй члены делят множитель два как в числителе, так и в нашем знаменателе. Итак, мы можем отменить это. Наконец, во втором члене мы можем отменить общий отрицательный множитель в числителе и знаменателе. Это оставляет нас с грехом три 𝜃 во всех отрицательных четырех плюс три греха 𝜃 во всех четырех. Мы могли бы оставить наш ответ так. Однако мы переставим эти два члена и удалим общий множитель одной четверти, что даст нам окончательный ответ одной четверти, умноженной на три греха 𝜃 минус грех трех 𝜃.
Следовательно, в этом вопросе мы смогли использовать теорему де Муавра, чтобы выразить синус в кубе 𝜃 через синусы кратных 𝜃. Мы показали, что куб греха 𝜃 равен одной четверти, умноженной на три греха 𝜃 минус грех трех 𝜃.
Тригонометрические тождества. Темы по тригонометрии.
Темы | Дом
20
Взаимные тождества
Тангенсные и котангенсные тождества
Пифагорейские тождества
Формулы суммы и разности
Формулы двойного угла
Формулы половинного угла
Продукты в сумме
Суммы как продукты
ИДЕНТИЧНОСТЬ — ЭТО РАВЕНСТВО, истинное для любого значения переменной. (Уравнение — это равенство, верное только для определенных значений переменной.)
Например, в алгебре у нас есть такое тождество:
( х + 5)( х — 5) = х 2 — 25.
Значение тождества состоит в том, что в расчетах мы можем заменить один член другим. Мы используем тождество, чтобы придать выражению более удобную форму. В исчислении и всех его приложениях тригонометрические тождества имеют центральное значение.
На этой странице мы представим основные тождества. У студента не будет лучшего способа попрактиковаться в алгебре, чем доказать их. Ссылки на доказательства ниже.
У студента не будет лучшего способа попрактиковаться в алгебре, чем доказать их. Ссылки на доказательства ниже.
Взаимные тождества
| sin θ | = | 1 csc θ | csc θ | = | 1 sin θ | |
| cos θ | = | 1 с θ | сек θ | = | 1 cos θ | |
| тан θ | = | 1 кроватка θ | кроватка θ | = | 1 желтовато-коричневый θ | |
Доказательство
Опять же, в расчетах мы можем заменить любой элемент идентичности другим. Итак, если мы видим «sin θ», то можем, если захотим, заменить его на «»; и, симметрично, если мы видим «», то мы можем заменить его на «sin θ».
Задача 1. Что значит сказать, что csc θ является обратное значение sin θ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Обновить»).
Это означает, что их произведение равно 1.
sin θ csc θ = 1.
Урок 5 Алгебры.
Задача 2. Оценить
загар 30° csc 30° cot 30°.
| загар 30° csc 30° cot 30° | = | коричневый 30° cot 30° csc 30° |
| = | 1 · csc 30 ° | |
| = | 2. | |
Тема 4.
Тождества тангенса и котангенса
| тангенс θ = | sin θ cos θ | детская кроватка θ = | cos θ sin θ |
Доказательство здесь.
Пример 1. Покажите: tan θ cos θ = sin θ.
Решение: Задача означает, что мы должны написать левую часть, а затем показать с помощью подстановок и алгебры, что мы можем преобразовать ее так, чтобы она выглядела как правая часть.
Начнем:
| = | при применении касательной идентичности, | ||
| = | при отмене cos θ s. | ||
Мы подошли к правой стороне.
Пифагорейские тождества
| а) | sin 2 θ + cos 2 θ | = | 1. |
| б) | 1 + желто-коричневый 2 θ | = | сек 2 θ |
| в) | 1 + детская кроватка 2 θ | = | csc 2 θ |
| a ‘ ) | sin 2 θ | = | 1 − cos 2 θ. |
| cos 2 θ | = | 1 − sin 2 θ. | |
Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они представляют собой тригонометрическую версию теоремы Пифагора.
Два тождества, обозначенные как ‘ ) — «а-простое» — это просто разные версии а). Первый показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.
Примечание: sin 2 θ — «синус в квадрате тета» — означает (sin θ) 2 .
Задача 3. Треугольник 3-4-5 прямоугольный.
а) Почему?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Обновить»).
Он удовлетворяет теореме Пифагора.
б) Оцените следующее:
| sin 2 θ | = | 16 25 | cos 2 θ | = | 9 25 | sin 2 θ + cos 2 θ | = | 1. |
Пример 2. Показать:
| Решение. Снова нужно преобразовать левую часть в правую. Начинаем: | ||
| Взаимные тождества | ||
| при сложении дробей | ||
| Пифагорейские тождества | ||
| Взаимные тождества | ||
Именно это мы и хотели показать.
Формулы суммы и разности
| грех (α + β) | = | sin α cos β + cos α sin β |
| sin (α − β) | = | sin α cos β − cos α sin β |
| потому что (α + β) | = | cos α cos β − sin α sin β |
| потому что (α − β) | = | cos α cos β + sin α sin β |
Примечание: В формулах синуса + или — слева также + или — справа. Но в формулах косинуса + слева становится — справа; наоборот.
Но в формулах косинуса + слева становится — справа; наоборот.
Поскольку эти тождества доказываются непосредственно из геометрии, от учащегося обычно не требуется овладевать доказательством. Однако все последующие тождества основаны на этих формулах суммы и разности. Студент обязательно должен их знать.
Вот доказательство формул суммы.
Пример 3. Вычислите sin 15°.
| Раствор. | sin 15° | |||
| Формулы | ||||
| Темы 4 и 5 | ||||
Пример 4. Докажите:
Докажите:
| Решение. | Тангенциальная идентичность | |||
| Формулы | ||||
| Теперь мы построим tan α, разделив первый член в числителе на cos α cos β. Но тогда мы должны разделить каждый член по cos α cos β: | ||||
Именно это мы и хотели доказать.
Формулы двойного угла
Доказательство
Существует три версии cos 2α. Первый с точки зрения обоих cos α и sin α. Второй только с точки зрения cos α. Третий — только с точки зрения sin α
| Пример 5. Показать: sin 2α |
| Раствор. | грех 2α | = 2 sin α cos α | Формулы | |
| Теперь мы построим tan α путем деления на cos α. Но чтобы сохранить равенство, мы должны также умножить на cos α. | ||||
| Урок 5 Алгебры | ||||
| Взаимные тождества | ||||
| Пифагорейские тождества | ||||
Именно это мы и хотели доказать.
| Пример 6. Показать: |
| Решение. | грех х |
— согласно предыдущему тождеству с α = .
Формулы половинного угла
Следующие формулы половинного угла являются инверсией формул двойного угла, потому что α составляет половину 2α.
Знак плюс или минус зависит от квадранта. Под радикалом косинус имеет знак +; синус, знак -.
Доказательство
| Пример 7. Вычисление cos | № 8 | . |
| Решение . С 90 012 | № 8 | это половина | № 4 | , то по |
| формула половины угла: | ||||
| Тема 4 | |||
| Урок 23 алгебры | |||
| Урок 27 алгебры | |||
Пример 8. Получение идентификатора для загара Получение идентификатора для загара | α 2 | . |
| Решение . | желтовато-коричневый | α 2 | = | Тангенциальная идентичность | ||
| = | Формулы половинного угла | |||||
| = | ||||||
| = | Урок 19 алгебры | |||||
| = | Пифагорейское тождество а ‘ | |||||
| = | ||||||
| = | ||||||
при делении числителя и знаменателя на cos α.
Продукты в сумме
| а) | sin α cos β | = | ½[sin (α + β) + sin (α − β)] | |
| б) | cos α sin β | = | ½[sin (α + β) − sin (α − β)] | |
| в) | cos α cos β | = | ½[cos (α + β) + cos (α − β)] | |
| г) | грех α грех β | = | −½[cos (α + β) − cos (α − β)] | |
Доказательство
Суммы как продукты
| д) | грех А + грех В | = | 2 sin ½ ( A + B ) cos ½ ( A − B ) |
| е) | грех А − грех В | = | 2 грех ½ ( А − В ) cos ½ ( А + В ) |
| ж) | cos A + cos B | = | 2 cos ½ ( A + B ) cos ½ ( A − B ) |
| з) | соз А − соз В | = | −2 sin ½ ( A + B ) sin ½ ( A − B ) |
В доказательствах учащийся увидит, что тождества с е) по з) являются инверсиями а) по d) соответственно, которые доказываются первыми. Тождество f) используется для доказательства одной из основных теорем исчисления, а именно производной sin x .
Тождество f) используется для доказательства одной из основных теорем исчисления, а именно производной sin x .
Учащийся не должен пытаться запомнить эти личности. Достаточно попрактиковаться в их доказательствах и увидеть, что они исходят из формул суммы и разности.
Темы | Дом
Copyright © 2022 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Забавы с комплексными числами (Запуск без слез, часть 10)
Забавы с комплексными числами (Запуск без слез, часть 10)Триггер без слез, часть 10:
Copyright 19972022 Stan Brown, BrownMath.com
Сводка: Триг может ответить на некоторые вопроса, на которые ваш учитель алгебры не ответил бы , например что такое √я? а также что такое журнал отрицательного числа?
Содержание:
Полярная форма комплексного числа
Как вы помните, комплексные числа, такие как 3+4i и
2−7i часто наносятся на комплексную плоскость. Это делает
легче визуализировать сложение и вычитание. Иллюстрация на
справа видно, что
Это делает
легче визуализировать сложение и вычитание. Иллюстрация на
справа видно, что
(3+4i) + (2−7i) = 5−3i
Оказывается, для умножения, деления и нахождения Силы и корни, с комплексными числами легче работать полярная форма . Это означает, что вместо того, чтобы думать о реальном и мнимые компоненты (−3 и 5 в −3+5i), вы думаете о длине и направлении линия.
Длина проста, просто старая добрая теорема Пифагора в факт:
r = √3 + 5 = √34 ≈ 5,83
(Длина r называется абсолютным значением или модуль комплексного числа.)
А как же направление? Вы можете видеть на картинке
что θ составляет около 120 или около 2 радиан (измерено
против часовой стрелки от положительной действительной оси, указывающей на восток), но
что именно? Ну, ты знаешь, что
загар θ = -5/3. Если вы возьмете
Arctan(-5/3) на вашем калькуляторе, вы получите -1,03, и
добавление π, чтобы попасть в правильный квадрант, дает θ = 2,11 радиана. (в градусах арктан(−5/3) = −59,04 и
добавление 180 дает θ = 120,96.) Вы можете написать
вот так:
(в градусах арктан(−5/3) = −59,04 и
добавление 180 дает θ = 120,96.) Вы можете написать
вот так:
−3+5i ≈ 5,83 е 2,11i или 5,83[cos 2,11 + i sin 2,11] или 5,83 цис 2,11 или 5,83∠120,96
Есть хороший трюк, который находит угол в правильном квадранте автоматически:
θ = 2 Арктан( y /( x + r ))
Встраивается в корректировку правильного квадранта, так что вы никогда не должны беспокоиться о том, добавить или вычесть 180 или π. Если вы проверите 2 Арктана(5/(−3 + √34)) на своем калькулятор, вы получите 2,11 радиана или 120,96, как раньше.
Эта формула особенно удобна, когда вы пишете программа или формула электронной таблицы, чтобы найти θ . Он течет прямо из формул тангенса половины угол, где функции выражаются с точки зрения x , y и r . Статья Роба Джонсона в июле 2003 г. заархивировано здесь, вдохновил меня добавить этот раздел.
Степени и корни комплексного числа
Одно из приложений формулы Эйлера (уравнение 47)
находит любую степень или корень любого комплексного числа. (Сойер не делает
это или, по крайней мере, не в той же книге.) Нетрудно разработать
формула, используя только формулу Эйлера и законы показателей.
(Сойер не делает
это или, по крайней мере, не в той же книге.) Нетрудно разработать
формула, используя только формулу Эйлера и законы показателей.
Начните с записи формулы Эйлера, умноженной влево и вправо с масштабным коэффициентом р :
r (cos x + i sin x ) = r e i x
Далее возводим обе стороны в n -ю степень:
[ r (поскольку x + i sin x )] n = [ r e i x ] n
Давайте на время оставим левую сторону в покое и упростим правая сторона. Во-первых, по законам показателей
[ r e i x ] n = r n e i n x
Примените формулу Эйлера к правой части, и вы получите
[ r e i x ] n = r n (cos n x + i sin n x )
Соедините эту правую сторону с исходной левой стороной и у вас есть Теорема Де Муавра :
(82) [ r (cos x + i sin x )] n = r n (cos n x + i sin n х )
Это говорит вам, что если вы введете число в
полярная форма, вы можете
найти любую силу или корень его. (Помните, что n -й корень
номер такой же, как мощность 1/ n .)
(Помните, что n -й корень
номер такой же, как мощность 1/ n .)
Квадратный корень из i
Поскольку этот учебник помогает вам,
, пожалуйста, нажмите, чтобы сделать пожертвование!Поскольку этот учебник помогает вам,
, пожалуйста, сделайте пожертвование на
BrownMath.com/donate.
Например, вы знаете, что квадратные корни из −1 равны i и −i, но каков квадратный корень из i? Вы можете использовать Теорема Де Муавра, чтобы найти его.
Сначала поместите i в e i x форма ( полярная форма ), используя вышеуказанное техника. я = 0+1i. cos x = 0 и sin x = 1 когда х = 90 или π/2. Поэтому
я = cos(π/2) + i sin(π/2)
√я = я = [cos(π/2) + i sin(π/2)]
И по уравнению 82
√i = cos(π/2) + i sin(π/2)
√i = cos(π/4) + i sin(π/4)
√i = 1/√2 + i1/√2
√i = (1+i)/√2
Другой квадратный корень минус это, как обычно.
Основной корень любого числа
Аналогичным образом можно найти любой корень любого комплексного числа, но обычно с одним предварительным шагом.
Например, предположим, что вы хотите кубические корни из 3+4i. Первый шаг — поставить это число в полярную форму. Абсолютное значение √3+4 = 5, и вы используете техника Arctan, данная выше, чтобы найти угол θ = 2 Arctan(4/(3+5)) = 2 Арктан() ≈ 53,13 или 0,9273 радиана. Полярная форма
3+4i ≈ 5(cos 53,13 + i sin 53,13)
Чтобы извлечь из этого кубический корень, используйте уравнение 82. с n = 1/3:
кубический корень из (3+4i) = 5 1/3 [ cos (53.13/3) + i sin (53.13/3)]
Кубический корень из 5 равен примерно 1,71. Разделив угол θ на 3, 53,13/3 ≈ 17,71; косинус и синус этого около 0,95 и 0,30. Поэтому
кубический корень из (3+4i) ≈ 1,71 (cos 17,71 + i sin 17,71)
кубический корень из (3+4i) ≈ 1,63+0,52i
Несколько корней
Вы, наверное, заметили, что я говорил о кубе . root s [множественное число] из 3+4i, и то, что мы нашли, было кубический корень из . Даже с квадратным корнем i,
Я махнул рукой и сказал, что другой квадратный корень минус
первый, как обычно.
root s [множественное число] из 3+4i, и то, что мы нашли, было кубический корень из . Даже с квадратным корнем i,
Я махнул рукой и сказал, что другой квадратный корень минус
первый, как обычно.
Вы уже знаете, что у каждого положительного вещественного числа есть два квадратных корня. В на самом деле каждое комплексное число имеет n n -й корней .
Как их найти? Это зависит от периодический характер функций косинуса и синуса. Для начала вернемся к формуле Эйлера,
.е я х = потому что x + i sin x
Что произойдет, если вы прибавите 2π или 360 к x ? У вас есть
e i( x +2π) = cos( x + 2π) + i sin( x + 2π)
Но если взять синус или косинус 2π плюс угол, это точно
то же самое, что взять синус или косинус исходного угла. Итак
правая часть равна
cos x + i sin x , что равно
е я х . Поэтому
Поэтому
e i( x +2π) = е я х
Фактически, вы можете продолжать добавлять 2π или 360 к x до тех пор, пока вам нравится, и никогда не меняйте значение результата. Символически
e i( x +2π k ) = е я х для всех целых к
Когда вы берете корень n th, вы просто используете этот личность.
Возвращаясь к кубическим корням из 3+4i, вспомним, что это число такое же, как 5e i θ , где θ составляет около 53,13 или 0,9273 радиана. три кубических корня из e i θ равны
e i( θ +2π k )/3 для к = 0,1,2
Расширив это, вы получите
е и θ /3 , e i( θ +2π)/3 , и e i( θ +4π)/3
или
е и θ /3 , е я( θ /3+2π/3) и e i( θ /3+4π/3)
Вычислите их как cos x + i sin x обычным способом, а затем
умножьте на (главный) кубический корень из 5. Я получаю эти три
корни:
Я получаю эти три
корни:
кубических корня из 3+4i ≈ 1,63+0,52i, -1,26+1,15i, -0,36-1,67i
В более общем смысле мы можем расширить теорему Де Муавра (уравнение 82), чтобы показать n n -й корень любого сложного номер:
(83) [ r (cos x + I SIN x )] (1 / N ) = R (1 / N ) [COS ( x /) [COS ( x /) [COSS x /) [COSS x /) n ) + i sin( x / n +2π k / n )] для k = 0,1,2,…, n −1 9000
Логарифм отрицательного числа
Другое приложение вытекает из известного частного случая формулы Эйлера. Подставьте x = π или 180 в уравнение 47. Поскольку sin 180 = 0, мнимый член выпадает. И cos 180 = −1, поэтому у вас есть знаменитая формула 9.0005
(84) −1 = e iπ
Интересно взять натуральное бревно с обеих сторон:
ln(−1) = ln e iπ
ln(−1) = iπ
Достаточно просто найти логарифм
любого другого отрицательного числа. С
С
пер аб = пер а + пер б
, тогда для всех реальных и у вас есть
ln(− a ) = ln( a -1) = ln a + ln(−1) = вл а + iπ
(85) ln(− a ) = ln a + iπ
Честно говоря, я не знаю, имеет ли все это какое-то практическое значение. заявление. Но если вы когда-нибудь задумывались о логарифме отрицательное число, теперь вы знаете.
Практические задачи
Чтобы получить максимальную пользу от этих проблем, работайте над ними без предварительного просмотра решений. Вернитесь к главе текст, если вам нужно освежить память.
Рекомендация : Работайте на бумаге труднее обмануть себя в том, действительно ли ты понять проблему полностью.
Вы найдете полный решения для всех проблем. Только не проверяй свой ответы, но проверьте и свой метод.
1
Выразите в a + b i форму:
(а) 62∠240
(б) 100e 1. 17i
17i
2 Выразите в полярной форме, как в градусах, так и в радианах: (а) −42+17i (б) 100i (в) −14,7
3 Найдите три кубических корня из −i в а + б я форма. Вы сможете дать точный ответ, а не округленные десятичные дроби.
4 Найти (1,04−0,10i) 16 .
Что нового
Поскольку этот учебник помогает вам,
, пожалуйста, нажмите, чтобы сделать пожертвование!Поскольку этот учебник помогает вам,
, пожалуйста, сделайте пожертвование на
BrownMath.com/donate.
Обновления и новая информация: https://BrownMath.com/twt/
Карта сайта | Поиски | Главная страница | Контакт
Тождества, уменьшающие степень – формулы, доказательство и применение
Тождества, уменьшающие степень, помогают нам переписывать различные тригонометрические функции, возведенные в степень. Они пригодятся, особенно когда мы хотим вычислить сложные тригонометрические функции и уравнения. Они обязательно пригодятся вам на уроках математического анализа.
Тождества, уменьшающие степень, — это тригонометрические тождества, которые позволяют нам переписывать тригонометрические выражения, возведенные в степень, в терминах более простых тригонометрических выражений.
В этой статье мы узнаем, как получать эти тождества, применять их для доказательства других тригонометрических тождеств и расширять наши знания, решая другие задачи, связанные с тригонометрическими выражениями.
Чтобы извлечь максимальную пользу из этой статьи, обязательно обновите свои знания по тригонометрическим тождествам , формулам двойного угла , формулам половинного угла и тригонометрическим уравнениям . А пока давайте разберемся с тремя основными способностями, уменьшающими идентичность, которые нам нужны больше всего. 92 \theta = \dfrac{1 – \cos \theta}{1 + \cos \theta}$.
Мы только что показали, как можно вывести три тождества, уменьшающих степень, используя формулу двойного угла. Мы также можем фактически проверить это тождество, используя тождество половинного угла. Давайте продолжим и освоим три личности, решив задачи, показанные ниже.
Пример 1
Проверьте формулы уменьшения мощности, используя тождества половинного угла.
Решение
Как мы уже упоминали, мы можем также доказать три тождества, уменьшающих мощность, используя тождества половинного угла. Начнем с того, что вспомним, что такое три тождества половинного угла:
\begin{aligned}\cos \dfrac{\alpha}{2} &= \pm \sqrt{\dfrac{1}{2}(1 + \ cos \ alpha)} \\\ sin \ dfrac {\ alpha} {2} &= \ pm \ sqrt {\ dfrac {1} {2} (1 — \ cos \ alpha)} \\\ tan \ dfrac {\ alpha}{2}&=\pm \sqrt{\dfrac{1 – \cos\alpha}{1 + \cos \alpha}}\end{aligned}
Мы можем просто возвести в квадрат обе части уравнения для всех трех тождеств. {\circ} = \dfrac{1}{2} – \dfrac{\sqrt{3}}{4}$ 92 \theta – \cos 2\theta &= \dfrac{5}{4}\\\dfrac{1}{2}(1 – \cos 2\theta) – \cos 2\theta &= \dfrac{5 }{4}\end{aligned}
{\circ} = \dfrac{1}{2} – \dfrac{\sqrt{3}}{4}$ 92 \theta – \cos 2\theta &= \dfrac{5}{4}\\\dfrac{1}{2}(1 – \cos 2\theta) – \cos 2\theta &= \dfrac{5 }{4}\end{aligned}
Умножьте обе части уравнения на $2$ и еще больше упростите левую часть.
\begin{выровнено}(1 – \cos 2\theta) – 2\cos 2\theta &= \dfrac{5}{2}\\1- 3\cos 2\theta&=\dfrac{5}{ 2} \\-3\cos 2\theta &=\dfrac{3}{2}\\\cos 2\theta &= -\dfrac{1}{2} \end{aligned}
Теперь найдем $\theta$ и убедитесь, что оно находится в заданном интервале $[0, 2\pi]$. 9{-1}\left(-\dfrac{1}{2}\right)\\2\theta &= \dfrac{2\pi}{3},\dfrac{4\pi}{3},\dfrac {8\pi}{3},\dfrac{10\pi}{3}\\\theta &= \dfrac{\pi}{3},\dfrac{2\pi}{3},\dfrac{4 \pi}{3},\dfrac{5\pi}{3} \end{aligned}
Следовательно, значения $\theta$, удовлетворяющие данному уравнению, равны $\left\{\dfrac{\pi} {3},\dfrac{2\pi}{3},\dfrac{4\pi}{3},\dfrac{5\pi}{3}\right\}$.
Пример 5
Проверьте следующие тригонометрические тождества, используя следующие тождества: 92 2\тета$.
\begin{выровнено}\cos 4\theta &= -3 + 4 \left[\dfrac{1}{2}(1 + \cos 2\cdot 2\theta) \right ]\\\cos 4\ theta &= -3 + 4\cdot\dfrac{1}{2} \left[(1 + \cos 2\cdot 2\theta) \right ]\\\cos 4\theta &= -3 + 2 + 2 \cos 4\theta \\\cos 4\theta &= 2\cos 4\theta – 1\end{aligned}
Тета-формула куба греха — Examtrix.com
Присоединяйтесь к нам на канале Telegram Кубик греха x формулаКакова формула тригонометрической функции sin cube theta : Значение Sin 3 x можно получить, используя тригонометрическое тождество sin 3x = 3sin x – 4sin 3 x. Мы докажем тета-формулу куба грехов шаг за шагом – давайте начнем – sin 3 x = (3sinx – sin 3x)/4
Тета-формула куба синуса -> sin 3 x = (3sinx – sin 3x)/4 Пожалуйста, перейдите по этой ссылке Объяснение математической формулы – Нажмите
Как упростить Sin Cube X?
sin 3 x = (3sinx – sin 3x)/4
Что такое sin в кубе X?
sin 3 x = (3sinx – sin 3x)/4
Что такое производная sin Cube X?
d(sin3x)/dx = 3 cos3x
Какова формула sin 3?
грех 3 ( θ ) знак равно 3 грех ( θ ) — грех ( 3 θ ) 4 , потому что 3 ( θ ) знак равно потому что ( 3 θ ) + 3 потому что ( θ ) 4 .
Что такое интегрирование sin 3 x?
∫sin 3x dx = (-1/3) cos 3x + C , C — константа интегрирования
Как решить sin 3x?
sin 3x = 3sin x – 4sin 3 x.
Присоединяйтесь к нам на канале Telegram Поиск:Архивы
Архивы Выберите Месяц Сентябрь 2022 (21) Июль 2022 (3) Июнь 2022 (4) Март 2022 (6) Февраль 2022 (34) Январь 2022 (49) Декабрь 2021 (11) Октябрь 2021 (2) Сентябрь 2021 (13) ) июль 2021 (16) май 2021 (13) апрель 2021 (15) март 2021 (14) январь 2021 (3) октябрь 2020 (5) сентябрь 2020 (53) август 2020 (3) июль 2020 (20) июнь 2020 (4) ) Май 2020 (48) Апрель 2020 (49) Март 2020 (36) Январь 2020 (19) Декабрь 2019 (1) Ноябрь 2019 (1) Октябрь 2019 (18) Сентябрь 2019(36) август 2019 г. (36) июль 2019 г. (62) июнь 2019 г. (16) май 2019 г. (7) апрель 2019 г. (15) март 2019 г. (29) февраль 2019 г. (49) январь 2019 г. (14) декабрь 2018 г. (40) ноябрь 2018 г. (27) Октябрь 2018 г. (36) Сентябрь 2018 г. (74)
(40) ноябрь 2018 г. (27) Октябрь 2018 г. (36) Сентябрь 2018 г. (74)Категории
КатегорииВыбрать категориюПримеры активного и пассивного залога с ответами (1)Вступительный экзамен B ed Вопросник и книга в формате PDF (3)Планы уроков B.Ed Шикшан Йоджана (1)BA MA Вопросы и книги в формате PDF (1)Заметки о банковских заказах (208)Онлайн-экзамен BARC (1)BHEL Executive Trainee Syllabus и примечания в формате PDF (1)Бихар-Дарога: опросный лист младшего инспектора полиции Дароги (1)Блоги (34) Читать блоги ( 32) Мотивационные истории (8)Результаты экзамена BNMU, часть 1 2 3, и дата онлайн-зачисления (1)Книга экзамена BSNL JE JTO TTA в формате PDF и отметки (4)Книги по химической инженерии в формате PDF (1)Книги по гражданскому строительству в формате PDF Скачать (3) Книги и PDF-файлы CSE по компьютерным наукам (3) Текущие события (91) Загрузить журнал Yojana Magazine в формате PDF (2) Журнал Kurukshetra в формате PDF (1) Ваджирам и Рави Текущие события в формате PDF (1) Vision IAS Текущие события в формате PDF (3) DMRC Question Paper and Book PDF (2) Download Free Pdf Notes (830) Anthropology ( 1) Искусство и культура (15) Банковская осведомленность (1) Бихар Г. К. PDF-заметки (2) Биология (55) Курс CCC по компьютерным концепциям (4) Химия (47) Чхаттисгарх Г.К. 150) Текущие события (90) Экономика (40) Английский (39)) Окружающая среда и экология (26) Написание эссе महत्वपूर्ण निबंध (2) Этика (11) Общие знания (131) Общая наука (81) География (90) Харьяна GK PDF Примечания (3) Грамматика хинди (29) История (100) Важные вопросы (140) Индийская политика (Конституция) (53) Внутренняя безопасность UPSC (5) Международные отношения (12) Madhya Pradesh GK (5) Математика (87) NIELIT DOEACC O Level Course (1) Физика (51) Политология (4) Психология Примечания (21) Государственное управление (3) Раджастхан, GK (7) Раджастан Патвари (7) Полиция Раджастана (5) Обоснование (25) REET (119) Санскрит (9) Наука и технологии (20) Социология (9) Примечания к экзаменам для учителей (173) TET (148) UP GK PDF Book (1) Книги Upkar Publication Books (1) Vajiram and Ravi Notes (1)DRDO Дата экзамена Программа Предыдущий Год Вопросник (2)DSSSB KVS PGT TGT PRT Вопросник и книга PDF (1)Электротехника Книги PDF (9)Электроника и техника связи MCQ PDF (7)Инженерная химия PDF-книга (1)Инженерная механика PDF-книги (5)Инженерия PDF-книга по физике (1)Инженерная термодинамика pk nag pdf-книга (2) ESIC UDC набор документов и книг pdf (1)Flipkart и Amazon Daily Quiz Answers Today (2)Гидромеханика pdf-книги (1)Бесплатные учебные материалы в формате PDF (807)Gate Книги по AR по архитектуре и планированию и вопросник в формате PDF (1)GATE Вопросник за предыдущий год в формате PDF (5)Общие принципы проектирования, чертежи и важность примечаний по технике безопасности в формате PDF скачать бесплатно (1)Книга по общим исследованиям и инженерным навыкам в формате PDF (1)Правительство Схемы PDF Заметки (1)Рукопись n Примечания PDF (173)Высшая инженерная математика в формате PDF (3)Книги в формате ISRO Exam в формате PDF (1)Предупреждения о вакансиях (11) Новости (3) Уведомление (2) Результаты (3) Стратегия/советы (4)Made Easy Book PDF (1) )Maharashtra 10th Board SSC Result www sscresult mkcl org mahahsscboard.
К. PDF-заметки (2) Биология (55) Курс CCC по компьютерным концепциям (4) Химия (47) Чхаттисгарх Г.К. 150) Текущие события (90) Экономика (40) Английский (39)) Окружающая среда и экология (26) Написание эссе महत्वपूर्ण निबंध (2) Этика (11) Общие знания (131) Общая наука (81) География (90) Харьяна GK PDF Примечания (3) Грамматика хинди (29) История (100) Важные вопросы (140) Индийская политика (Конституция) (53) Внутренняя безопасность UPSC (5) Международные отношения (12) Madhya Pradesh GK (5) Математика (87) NIELIT DOEACC O Level Course (1) Физика (51) Политология (4) Психология Примечания (21) Государственное управление (3) Раджастхан, GK (7) Раджастан Патвари (7) Полиция Раджастана (5) Обоснование (25) REET (119) Санскрит (9) Наука и технологии (20) Социология (9) Примечания к экзаменам для учителей (173) TET (148) UP GK PDF Book (1) Книги Upkar Publication Books (1) Vajiram and Ravi Notes (1)DRDO Дата экзамена Программа Предыдущий Год Вопросник (2)DSSSB KVS PGT TGT PRT Вопросник и книга PDF (1)Электротехника Книги PDF (9)Электроника и техника связи MCQ PDF (7)Инженерная химия PDF-книга (1)Инженерная механика PDF-книги (5)Инженерия PDF-книга по физике (1)Инженерная термодинамика pk nag pdf-книга (2) ESIC UDC набор документов и книг pdf (1)Flipkart и Amazon Daily Quiz Answers Today (2)Гидромеханика pdf-книги (1)Бесплатные учебные материалы в формате PDF (807)Gate Книги по AR по архитектуре и планированию и вопросник в формате PDF (1)GATE Вопросник за предыдущий год в формате PDF (5)Общие принципы проектирования, чертежи и важность примечаний по технике безопасности в формате PDF скачать бесплатно (1)Книга по общим исследованиям и инженерным навыкам в формате PDF (1)Правительство Схемы PDF Заметки (1)Рукопись n Примечания PDF (173)Высшая инженерная математика в формате PDF (3)Книги в формате ISRO Exam в формате PDF (1)Предупреждения о вакансиях (11) Новости (3) Уведомление (2) Результаты (3) Стратегия/советы (4)Made Easy Book PDF (1) )Maharashtra 10th Board SSC Result www sscresult mkcl org mahahsscboard.

 2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]
2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\] 2\alpha=\dfrac2\)
2\alpha=\dfrac2\) 2=\dfrac=1\)
2=\dfrac=1\)

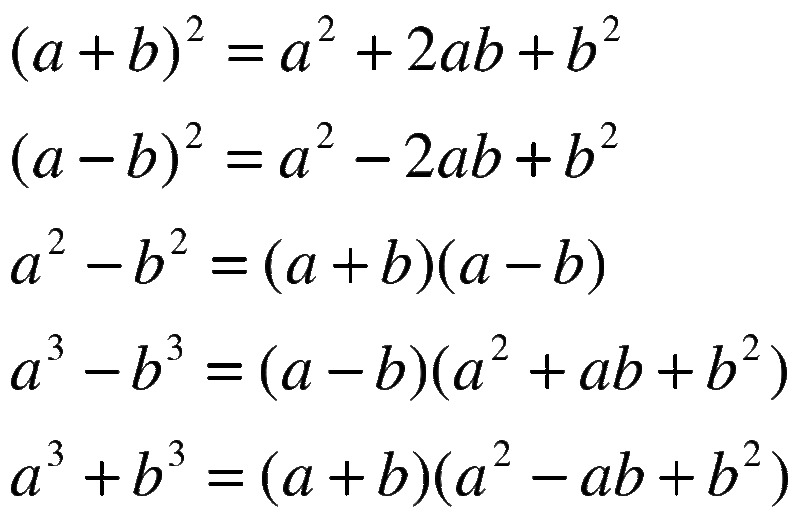 Следуя из этого правило, легко запомнить, что косинус угла – отношение близкого катета (прилежащего) к гипотенузе.
Следуя из этого правило, легко запомнить, что косинус угла – отношение близкого катета (прилежащего) к гипотенузе.

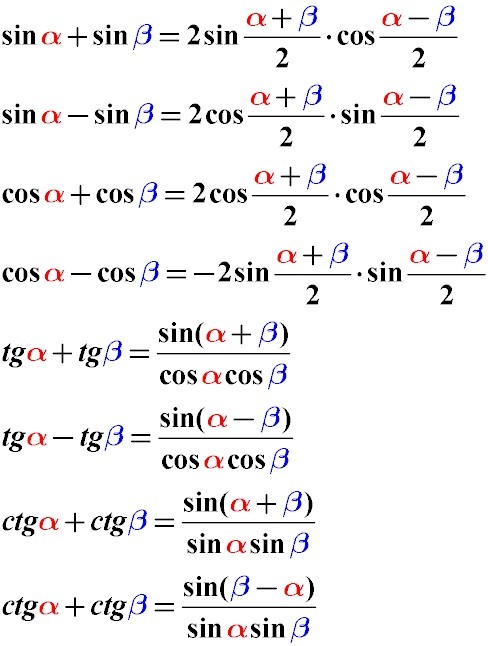 И четвёртая, формула котангенса половинного угла справедлива для всех углов альфа, но при которых определён котангенс половинного угла (
И четвёртая, формула котангенса половинного угла справедлива для всех углов альфа, но при которых определён котангенс половинного угла ( Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.
Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.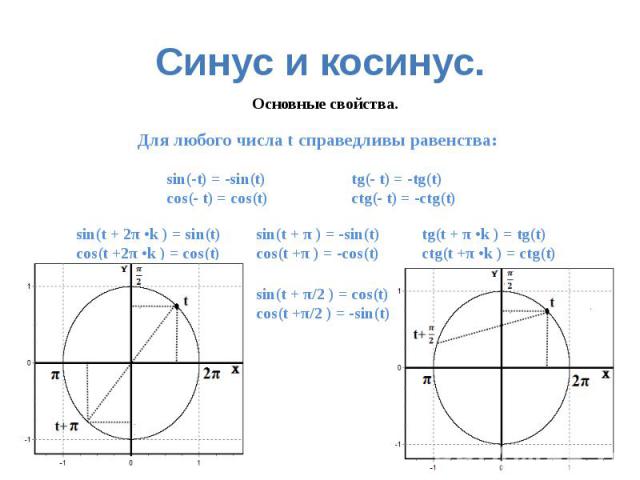
 Для корня нечетной степени выполняется также следующее равенство:
Для корня нечетной степени выполняется также следующее равенство: е. в том числе для любых треугольников):
е. в том числе для любых треугольников):