Сколько будет 3 в квадрате плюс 4 в квадрате С в квадрате?
Сколько будет 3 в квадрате плюс 4 в квадрате С в квадрате? Вот как вы делаете уравнение, например, 3 в квадрате плюс 4 в квадрате = 5 в квадрате, другими словами, 9 + 16 = 25, поэтому, поскольку все это целые числа, треугольник должен быть пифагорейской тройкой.
Что такое С в квадрате плюс а в квадрате? Теорема Пифагора
Теорема гласит, что если у прямоугольного треугольника две стороны равны a и b, а гипотенуза равна c, то квадрат плюс b в квадрате равен c в квадрате. Гипотенуза прямоугольного треугольника – это сторона, противолежащая прямому углу.
Работает ли Пифагор над всеми треугольниками? Теорема Пифагора работает только для прямоугольных треугольников, поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет.
Что такое 4 в квадрате 3 в квадрате? 4 в квадрате — это 4 × 4, что равно 36, а 3 в квадрате — это 3 × 3, что равно 9. Таким образом, ответ на задачу — 45.
Таким образом, ответ на задачу — 45.
Что такое квадрат С в теореме Пифагора?
Гипотенуза находится на противоположной стороне прямоугольного треугольника. Вот формула теоремы Пифагора. a в квадрате + b в квадрате = c в квадрате В этой формуле с представляет длину гипотенузы, а и b — длины двух других сторон.
Как найти C в треугольнике?
Формула гипотенузы просто берет теорему Пифагора и решает для гипотенузы, c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом мы получаем c = √(a² + b²) .
Закон синусов работает для всех треугольников?
Правило синусов можно использовать в любом треугольнике (не только прямоугольном), где известны сторона и противоположный ей угол. Вам понадобятся только две части формулы правила синусов, а не все три. Как и раньше, вам понадобятся только две части правила синусов, и вам по-прежнему нужны как минимум сторона и противоположный ей угол.
Какая самая длинная сторона треугольника?
В прямоугольном треугольнике гипотенуза — это самая длинная сторона, «противоположная» сторона — это та, которая находится напротив данного угла, а «прилежащая» сторона — это сторона, следующая за данным углом.
Работает ли теорема Пифагора для непрямоугольных треугольников?
Так что теорема Пифагора работает для любого треугольника. Когда мы начинаем с непрямоугольного треугольника, теорема работает, не давая равенства. Конечно, закон косинусов дает квадрат стороны любого треугольника, учитывая противолежащий угол и две другие стороны.
Чему равно 4 в степени 3?
Ответ: число 4 в 3-й степени, то есть 43 равно 64.
Является ли 3 квадратным корнем?
Квадратный корень из 3 — это положительное действительное число, которое при умножении само на себя дает число 3. Точнее его называют главным квадратным корнем из 3, чтобы отличить его от отрицательного числа с тем же свойством. Квадратный корень из 3 — иррациональное число.
Чему равны два квадратных корня из 100?
Ответ: Второй корень из 100, или 100 радикал 2, или квадратный корень из 100 записывается как 2√100=√100=±10.
Как вычислить квадратный корень?
Формула квадратного корня используется для нахождения квадратного корня из числа. Мы знаем формулу экспоненты: n√x x n = x1/n. Когда n=2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например разложение на простые множители, длинное деление и так далее.
Мы знаем формулу экспоненты: n√x x n = x1/n. Когда n=2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например разложение на простые множители, длинное деление и так далее.
ЧТО ЕСЛИ А в квадрате плюс В в квадрате меньше С в квадрате?
Теорема Пифагора утверждает, что в любом прямоугольном треугольнике квадрат плюс квадрат равен квадрату, где самая длинная сторона треугольника, известная как гипотенуза. Это означает, что когда угол острый, квадрат меньше, чем квадрат плюс квадрат.
Что такое математика 7 в квадрате?
72 = 7 • 7 = 49. Вы можете прочитать 72 как «семь в квадрате». Это потому, что умножение числа само на себя называется «возведением числа в квадрат». Точно так же возведение числа в степень 3 называется «возведение числа в куб». Вы можете прочитать 73 как «семь в кубе».
Какова формула любого треугольника?
Закон косинусов обобщает формулу Пифагора на все треугольники. В нем говорится, что c2, квадрат одной стороны треугольника, равен a2 + b2, сумме квадратов двух других сторон, минус 2ab cos C, удвоенное их произведение, умноженное на косинус противоположного угла.
В нем говорится, что c2, квадрат одной стороны треугольника, равен a2 + b2, сумме квадратов двух других сторон, минус 2ab cos C, удвоенное их произведение, умноженное на косинус противоположного угла.
По какому правилу определяются длины сторон треугольника?
Правило сторон треугольника утверждает, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. См. Длины сторон остроугольного треугольника ниже. Сумма длин двух самых коротких сторон, 6 и 7, равна 13.
Чему равно расстояние между двумя точками?
Что понимается под расстоянием между двумя точками? Расстояние между двумя точками определяется как длина прямой линии, соединяющей эти точки в координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками.
Какое множество сторон образует прямоугольный треугольник?
Все, что вам нужно, это длина основания и высота. В прямоугольном треугольнике основание и высота – две стороны, образующие прямой угол.
В прямоугольном треугольнике основание и высота – две стороны, образующие прямой угол.
Каковы длины сторон 30 60 90?
Треугольники 30°-60°-90°
Меры сторон равны x, x√3 и 2x. В треугольнике 30°-60°-90° длина гипотенузы в два раза больше длины более короткого катета, а длина более длинного катета в √3 раза больше длины более короткого катета.
Получится ли прямоугольный треугольник?
Если у вас есть длина каждой стороны, примените теорему Пифагора к треугольнику. Если вы получаете истинное утверждение при упрощении, то у вас действительно есть прямоугольный треугольник! Если вы получите ложное утверждение, то можете быть уверены, что ваш треугольник не является прямоугольным.
Что означает буква C в формуле a 2a 2 B 2b 2 c 2c 2?
Теорема Пифагора — это формула, которая дает отношение между сторонами прямоугольного треугольника. Теорема Пифагора применима только к ПРАВИЛЬНЫМ треугольникам. Сторона «с» называется гипотенузой. Стороны, примыкающие к прямому углу, называются «а» и «б».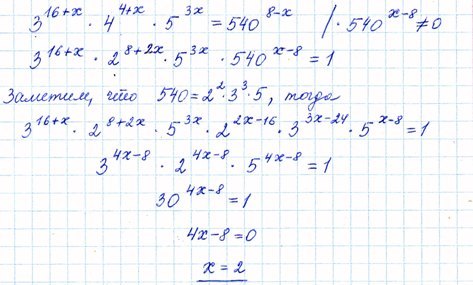
Какова формула a2 b2?
а2 – Ь2 = (а + Ь)(а – Ь). 8. а3 – Ь3 = (а – Ь) (а2 + аб + Ь2).
Работает ли закон синусов для тупоугольных треугольников?
Правило синусов справедливо и для тупоугольных треугольников. = для треугольника, в котором угол А тупой. Мы можем использовать расширенное определение тригонометрических функций, чтобы найти синус и косинус углов 0°, 90°, 180°. Следовательно, тангенс тупого угла равен отрицательной величине тангенса его дополнения.
Как называются 3 стороны треугольника?
Каждый треугольник имеет три стороны и три угла, некоторые из которых могут быть одинаковыми. В случае прямоугольного треугольника сторонам треугольника даются специальные названия, при этом сторона, противоположная прямому углу, называется гипотенузой, а две другие стороны известны как катеты.
Формулы сокращенного умножения. Разложение на множители. ⋆ СПАДИЛО
теория по математике 🎲 алгебраические выражения
Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.
Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
(a+b)2=a2+2ab+b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
(a–b)2=a2–2ab+b2
Если сравнить два этих правила и формулы, то видно, что при возведении в квадрат есть отличие в знаках только перед удвоенным произведением. Рассмотрим применение данных формул на примерах.
Пример №1. Преобразуем выражение в многочлен: (с+8)2. По правилу выполняем последовательно: квадрат первого выражения это с2; удвоенное произведение первого и второго выражения – это 2с8; квадрат второго выражения – это 82. Выполним запись: (с+8)2=с2+2с8+82. Теперь выполним умножение и возведение в степень чисел: (с+8)2=с2+2с8+82=с2+16с+64. Получим многочлен. Промежуточные действия, выделенные жирным шрифтом, можно не записывать, а выполнять их устно.
Выполним запись: (с+8)2=с2+2с8+82. Теперь выполним умножение и возведение в степень чисел: (с+8)2=с2+2с8+82=с2+16с+64. Получим многочлен. Промежуточные действия, выделенные жирным шрифтом, можно не записывать, а выполнять их устно.
Пример №2. Представим в виде многочлена выражение (2х–11)2. Выполним возведение в квадрат по правилу квадрата разности двух выражений: (2х–11) 2=(2х)2–2•2х•11+112=4х2–44х+121.
Пример №3. Представим в виде многочлена квадрат двучлена (–9х+4у)2. В данном выражении на первом месте стоит отрицательное число, на втором положительное, что не привычно для нас по работе с формулой. Но мы знаем, что можно просто поменять слагаемые местами, тогда получится разность двух выражений, которую возводим в квадрат по соответствующей формуле: (–9х+4у)2=(4у–9х)2=16у2–72ху+81х2.
Пример №4. Представим в виде многочлена выражение (–6с–10)2. Данное выражение содержит два слагаемых с минусом. Надо просто запомнить, что оно будет равносильно выражению (6с+10)2, потому что квадраты противоположных чисел равны (а2=(–а)2) . Возведем данное выражение в квадрат по формуле квадрата суммы двух выражений: (–6с–10)
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения:
(a+b)3=a3+3a2b+3ab2+b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения:
(a–b)3=a3–3a2b+3ab2–b3
Используя данные формулы, можно возводить в куб сумму и разность двух выражений. В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.
В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.
Пример №5. Возведем в куб сумму с+5а. Всё выполним и распишем строго по формуле:
(с+5а)3=с3+3с2 •5а+3с(5а)2+(5а)3=с3+15ас2+75а2с+125а3.
Пример №6. Возведем в куб разность:
(х–10)3=х3–3х210+3х102–103=х3–30х2+300х–1000.
Разность квадратовПроизведение разности двух выражений и их суммы равно разности квадратов этих выражений:
a2–b2=(a–b)(a+b)
Пример №7. Выполним умножение: (4–с)(4+с)=42–с2=16–с2 в данном выражении выполнили всё в соответствии с формулой: возвели в квадрат 4 и число с. Промежуточные записи (выделены жирным шрифтом) можно не делать, а выполнять их устно.
Пример №8. Упростим выражение: (5с+а)(5с–а)=25с2–а2 в данном выражении мы видим, что первый множитель сумма, а второй – разность. Для выполнения задания по данной формуле это не имеет значения, так как мы знаем, что от перестановки множителей произведение не изменяется.
Рассмотрим тождество, которое называют разностью квадратов двух выражений:
a2–b2=(a–b)(a+b)
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.
Пример №9. Разложить на множители многочлен 100–с2. Из условия видно, что число 100 – это квадрат числа 10, следовательно, 100–с2=102
–с2, значит можно разложить на множители по формуле: 100–с2=102–с2=(10–с)(10+с). Выделенное жирным шрифтом выражение можно не записывать, а выполнять устно.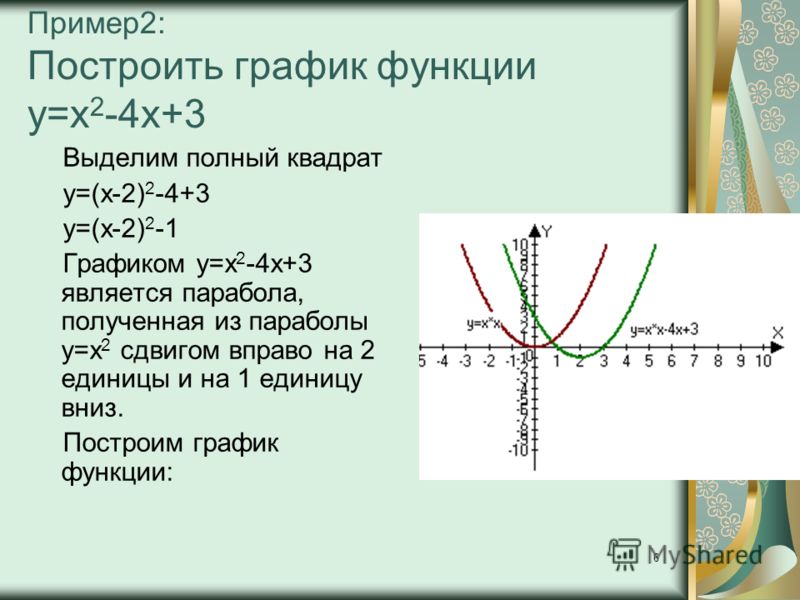
Пример №10. Разложить на множители: х2у2–81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.
Пример №11. Представим в виде произведения: х4–36=(х2–6)(х2+6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.
Пример №12. Представим в виде произведения х10с6–25=(х5с3–5)(х5с3+5). Здесь показаны разные четные степени переменных.
Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
a3+b3=(a+b)(a2–ab+b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
a3–b3=(a–b)(a2+ab+b2)
Пример №13. Разложим на множители многочлен 8+с3. В данном случае мы видим число 8, которое нужно представить в виде куба числа, это будет 23. Значит, 8+с3=23+с3. Далее распишем по формуле суммы кубов: 8+с3=23+с3=(2+с)(4–2с+с2).
Разложим на множители многочлен 8+с3. В данном случае мы видим число 8, которое нужно представить в виде куба числа, это будет 23. Значит, 8+с3=23+с3. Далее распишем по формуле суммы кубов: 8+с3=23+с3=(2+с)(4–2с+с2).
Пример №14.
Запишем в виде произведения разность х3–а12. В этом выражении есть степень, отличная от третьей, поэтому представим а12 в виде куба числа (а4)3. Получим: х3–а12=х3–(а4)3. Разложим на множители по формуле разности кубов: х3–а12=х3–(а4)3=(х–а4)(х2+ха4+а8).Разложение многочлена формулой квадрата суммы и разности
Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:
a2+2ab+b2=(a+b)2
a2–2ab+b2=(a–b)2
Пример №15. Преобразовать трехчлен 4х2+12х+9 в квадрат двучлена. Для этого определим, где здесь числа, которые можно представить в виде квадрата, это будут 4х
Преобразовать трехчлен 4х2+12х+9 в квадрат двучлена. Для этого определим, где здесь числа, которые можно представить в виде квадрата, это будут 4х
Пример №16. Разложить на множители многочлен –16с+с2+ Определяем, где здесь квадраты чисел – это с2 и 64=82. Слагаемое –16с не может быть квадратом числа, так как оно отрицательное и степень числа с первая, поэтому –16с это удвоенное произведение чисел с и 8. Выполняем разложение на множители: –16с+с2+64=(с–8)2. Обратим внимание на тот момент, что числа с и 8 можно записывать наоборот в ответе, так как квадраты противоположных чисел равны, то есть –16с+с 2+64=(8–с)2
P. S. Все формулы на одной картинке:
S. Все формулы на одной картинке:
Найдите значение выражения: (x + 5)2 — x (x- 10) при x = — 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5)2 – x (x – 10) = x2 + 2 • 5 • x + 25 – x2 + 10x
Затем приведем подобные слагаемые:
x2 + 2 • 5 • x + 25 – x2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24
Ответ: 24pазбирался: Даниил Романович | обсудить разбор | оценить
Даниил Романович | Просмотров: 6.1k | Оценить:
Уравнения
Уравнение – равенство двух выражений, содержащих неизвестное число (переменную).
 {x}=8\)
{x}=8\)
— показательное
Есть переменная в показателе степени
…и так далее.
Корень уравнения
При решении любого уравнения мы стремимся найти такое значение для переменной (обычно икса), при котором левая часть уравнения станет равна правой. Это значение и будет называться корнем уравнения (не путать с квадратным корнем — это разные понятия!)
Таким образом,
Корень уравнения есть такое число, при подстановке которого в уравнение вместо \(x\), получаются одинаковые значения выражений справа и слева от знака равно. А найти все такие числа (или показать, что их нет) и значит решить уравнение.
Решая, например, уравнение \(2x+1=x+4\), мы находим ответ: \(x=3\). И если мы подставим это число вместо икса, получим одинаковые значения слева и справа:
И если мы подставим это число вместо икса, получим одинаковые значения слева и справа:
\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)
И никакое другое число, кроме тройки такого равенства нам не даст. Значит, число \(3\) – единственный корень уравнения.
Еще раз: корень – это НЕ ИКС! Икс – это переменная, а корень – это число, которое превращает уравнение в верное равенство (в примере выше – тройка). И при решении уравнений мы это неизвестное число (или числа) ищем.
Как решать уравнения?
Для того, чтобы найти корни уравнения, используют равносильные преобразования. Смысл при этом в том, чтобы после преобразований получить более простое уравнение, имеющее такие же корни (то есть, равносильное исходному).
Пример: Решить уравнение \(2(1-x)=23-5x\)
Решение: Сразу найти такой икс, чтоб левая и правая части уравнялись – проблематично: перебирать долго. Давайте равносильно преобразуем (почему преобразования именно такие – читайте здесь).
Давайте равносильно преобразуем (почему преобразования именно такие – читайте здесь).
\(2-2x=23-5x\)
\(-2x+5x=23-2\)
\(3x=21\)
\(x=7\)
Ответ: \(7\)
Обратите внимание, что с каждым шагом уравнение становится проще: если в исходном уравнении понять, что корнем будет число \(7\) сложно, то в \(3x=21\) (а уж тем более в \(x=7\)) это очевидно. Но при этом семерка является корнем для любого из уравнений, полученных в процессе преобразований, и других корней в них нет.
Кстати, заметьте, что \(x=7\) — это тоже уравнение. Просто в нем очевиден корень, поэтому большинство учеников даже не воспринимают эту запись за уравнение, считая, что это, мол, ответ так записывается. Не-не-не, \(x=7\) — это тоже вполне себе полноценное уравнение, только очень простое. А ответ (то есть корень) – просто число \(7\).
ОДЗ — опасная ловушка
В некоторых типах уравнений (дробно-рациональных, логарифмических, иррациональных, а также тригонометрических с тангенсом или котангенсом) помимо решения самого уравнения необходимо также учитывать ограничения на ОДЗ (область допустимых значений). 2-4x-5=0\)
2-4x-5=0\)
Решаем квадратное уравнение и находим корни
\(x_{1}=5\) \(x_{2}=-1\)
Готово
Всё? Можно писать ответ?
Не так быстро. Дело в том, что один из корней тут лишний. Давайте подумаем. У нас в левой части есть квадратный корень. А он, как известно, во-первых, не извлекается из отрицательных значений, а во-вторых, сам не может быть равен отрицательному числу. Таким образом, у нас икс НЕ МОЖЕТ иметь значение, которое приведет нас к одной из этих ситуаций. Иными словами, икс должен быть таким, чтоб:
— подкоренное выражение было больше или равно нулю,
— правая часть была больше или равна нулю.
То есть в качестве ограничений на значения икса (так называемую область определения или область допустимых значений) мы имеем систему неравенств: \(\begin{cases}4x+5\geq0\\x \geq 0\end{cases}\)
Решая систему, получаем: \(\begin{cases}x\geq-1,25\\x \geq 0\end{cases}\) \(\Rightarrow\) \(x\in [0;+\infty)\)
Таким образом, получается, что нам подойдут только те иксы, которые больше нуля или равны нулю. А значит \(x_{2}=-1\) не подойдет по ОДЗ.
И действительно, если мы поставим \(-1\) в уравнение, получим:
\(\sqrt{4x+5}=x\)
\(\sqrt{4\cdot(-1)+5}=-1\)
\(\sqrt{1}=-1\)
Пришли к противоречию, ведь \(\sqrt{1}\neq-1\)
Окончательный ответ: \(5\)
3-8Пошаговое решение :
Шаг 1 :
Попытка факторизовать путем разделения среднего члена первый член равен x
2 , его коэффициент равен 1 .
Средний член равен -4x, его коэффициент равен -4.
Последний член, «константа», равен -5
Шаг-1: умножьте коэффициент первого члена на константу 1 • -5 = -5 равен коэффициенту среднего члена, который равен -4 .
| -5 | + | 1 | = | -4 | Это это |
Шаг -3: rewrite. Шаг 2 выше, -5 и 1
x 2 -5x+1x-5
Шаг-4: Складывайте первые 2 термина, вытягивая, как факторы:
x • (x-5)
. 2 термина, вытягивание общих множителей :
1 • (x-5)
Шаг-5: Сложите четыре члена шага 4:
(x+1) • (x-5)
, что является желаемой факторизация
Уравнение в конце шага 1:
(х + 1) • (х - 5) = 0
Шаг 2 :
Теория – корни произведения:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Решение единого переменного уравнения:
2,2 Решение: x+1 = 0
Вычитание 1 с обеих сторон уравнения:
x = -1
Решение единого переменного уравнения:
2.3. 5 = 0
Добавить 5 к обеим сторонам уравнения:
x = 5
Дополнение: Решение квадратичного уравнения напрямую
Решение x 2 -4x -5 = 0 непосредственноРанее мы фактически факту с этим полиномальным . давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
парабола, найдя вершину:
3.1 найдите вершину y = x 2 -4x-5
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум).
Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна 2,0000
Подставляя в формулу параболы 2,0000 вместо x, мы можем вычислить координату y:
y = 1,0 * 2,00 * 2,00 - 4,0 * 2,00 - 5,0
или y = -9,000Корневой график для: y = x 2 -4x-5
Ось симметрии (штриховая) {x}={ 2,00}
Вершина в {x,y} = {2,00,-9,00}
x -Перехваты (корни ) :
Корень 1 при {x,y} = {-1,00, 0,00}
Корень 2 при {x,y} = {5,00, 0,00}Решите квадратное уравнение, заполнив квадрат
3.
2 Решение x 2 -4x-5 = 0 путем заполнения квадрата.
Прибавьте 5 к обеим частям уравнения:
x 2 -4x = 5Теперь немного хитрости: возьмите коэффициент при x , равный 4, разделите на два, получите 2, и, наконец, возведите его в квадрат, получите 4
Прибавьте 4 к обеим частям уравнения:
В правой части имеем:
5 + 4 или (5/1)+(4/1)
/1)+(4/1) дает 9/1
Таким образом, прибавив к обеим сторонам, мы окончательно получим:
x 2 -4x+4 = 9Добавление 4 дополнит левую часть до полного квадрата:
x 2 -4x+4 = 9 0925 ( x-2) • (x-2) =
(x-2) 2
Вещи, равные одной и той же вещи, равны и друг другу. Поскольку
x 2 -4x+4 = 9 и
x 2 -4x+4 = (x-2) 2
, то по закону транзитивности
(x-2) 2 = 9Мы будем называть это уравнение уравнением #3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-2) 2 равен
(x-2) 2/2 =
(x-2) 1 =
Принцип квадратного корня в уравнении #3.2.1 получаем:
x-2 = √ 9Добавьте 2 к обеим частям, чтобы получить:
x = 2 + √ 9Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное,
x 2 - 4x - 5 = 0
имеет два решения:
x = 2 + √ 9
или
x = 2 9090 6 9090 9 Решение квадратного уравнения с помощью квадратной формулы3.3 Решение x 2 -4x-5 = 0 с помощью квадратной формулы .
Согласно квадратичной формуле, x , решение для Ax 2 +Bx+C = 0 , где A, B и C – числа, часто называемые коэффициентами, определяется следующим образом:
-B ± √ B 2 -4AC
x = ————————
2AВ нашем случае A = 1
B = -4
C = -5Ancroyly, Ancrovingy, Ancroyly, Acnovery, Ancroyly, Acnoverly, Acnoverly, Acnovery, Ancroyly, Ancroyly, Ancomly, Ancroyly, Ancomly, Acnovery, Acnoverly, Ancomly, Ancomly, Acnoverly, A -4
C = -5.
B 2 -4AC =
16-(-20) =
36Применение квадратичной формулы:
4 ± √ 36
x = ——— 9025 2 Можно ли упростить √ 36?
Да! Первичная факторизация числа 36 равна
2•2•3•3
Чтобы иметь возможность удалить что-то из-под корня, должно быть 2 этих экземпляра (потому что мы берем квадрат, т.е. второй корень).√ 36 = √ 2 • 2 • 3 • 3 = 2 • 3 • √ 1 =
± 6 • √ 1 =
± 6Итак, теперь мы смотрим на:
x = (4 ± 6)/2Два действительных решения:
x =(4+√36)/2=2+3= 5,000
или:
x =(4-√36)/2=2-3= -1,000
Было найдено два решения:
- x = 5
- x = -1
X в квадрате - Cuemath
В этом мини-уроке мы рассмотрим, что такое х в квадрате, разность квадратов и решение квадратного уравнения путем заполнения квадратов.
В алгебре мы обычно сталкиваемся с выражением x в квадрате. Знаете ли вы, что такое х в квадрате?
В этом мини-уроке мы узнаем, в частности, о \(x^2\).
План урока
1. Что такое x в квадрате? 2. Важные примечания по x Squared 3. Решенные примеры на х в квадрате 4. Загадочные вопросы по х в квадрате 5. Интерактивные вопросы по х в квадрате 92 = х \умножить на х\)\(2x = 2 \×x\) 3 \(3 х 3=9\)
2(3) = 6 -1 \(-1 \умножить на -1 = 1\)
2(-1) = -2 -2 \(-2 \умножить на -2 =4\)
2(-2) = -4 92-4 х-6 у+8=0\] 9:
Подсказка: сгруппируйте термины \(x\) отдельно и термины \(y\) отдельно, а затем заполните квадраты. Интерактивные вопросыВот несколько упражнений для практики.

Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Давайте подведем итогиМини-урок был посвящен увлекательной концепции x в квадрате. Мы исследовали х в квадрате, х в квадрате равно, квадратный корень, х в кубе, что такое х в квадрате х, х 2, х в квадрате умножить на х, х в квадрате плюс х в квадрате, символ х в квадрате, х в квадрате минус х, х в квадрате разделить на х, и х в квадрате плюс у в квадрате.
Математическое путешествие вокруг х в квадрате начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
О CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.
Часто задаваемые вопросы (FAQ) 92} = 3\]Завершение квадрата
" Завершение квадрата " вот где мы...
... возьмем квадратное уравнение
следующим образом:и превратите его
в это:топор 2 + Ьх + с = 0 а(х+ d ) 2 + е = 0 Для тех из вас, кто торопится, могу сказать, что: d = b 2a
и: e = c − b 2 4a
Но если у вас есть время, позвольте мне показать вам, как " Заполнить квадрат " самостоятельно.Завершение квадрата
Допустим, у нас есть простое выражение вида x 2 + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?
Ну, немного вдохновившись геометрией, мы можем преобразовать его, например, так:
Как видите x 2 + bx можно переставить почти в квадрат...
... и мы можем дополнить квадрат с помощью (b/2) 2
В алгебре это выглядит так:
x 2 + шт + (б/2) 2 = (х+b/2) 2 "Завершить квадрат
"Итак, сложив (b/2) 2 , мы можем завершить квадрат.
Результат (x+b/2) 2 имеет x только один раз , что проще в использовании.
Сохранение равновесия
Теперь... мы не можем просто прибавить (b/2) 2 без вычитания ! В противном случае меняется все значение.
Итак, давайте посмотрим, как это сделать правильно на примере:
Начните с: ("b" в данном случае равно 6) Заполните квадрат:
Также вычесть новый термин
Упростите это, и все готово.
Результат:
x 2 + 6x + 7 = (x+3) 2 − 2
И теперь x появляется только один раз, и наша работа сделана!
Быстрый подход
Вот быстрый способ получить ответ.
Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x+d) 2 + e
После разложения (x+d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы превратить наш пример в эту форму, чтобы обнаружить d и e
Пример: попробуйте вписать x
2 + 6x + 7 в x 2 + 2dx + d 2 + eТеперь мы можем «форсировать» ответ:
9116x3 Мы знаем, что
9116x3 Мы должны закончить вверх как 2dx, поэтому d должно быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть −2
И мы получаем тот же результат (x+3) 2 − 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений...
Решение общих квадратных уравнений путем заполнения квадрата
Мы можем дополнить квадрат до , решить квадратное уравнение (найти, где оно равно нулю).
Но общее квадратное уравнение может иметь коэффициент а перед х 2 :
топор 2 + Ьх + с = 0
Но с этим легко справиться... просто разделите сначала все уравнение на "а", а затем продолжайте:
х 2 + (б/а)х + с/а = 0
шагов
Теперь мы можем решить квадратное уравнение за 5 шагов:
- Шаг 1 Разделите все члены на a (коэффициент x 2 ).
- Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.
Теперь у нас есть что-то похожее на (x + p) 2 = q, которое можно довольно легко решить:
- Шаг 4 Извлеките квадратный корень из обеих частей уравнения.
- Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .
Примеры
Хорошо, несколько примеров помогут!
Пример 1: решить x
2 + 4x + 1 = 0Шаг 1 можно пропустить в этом примере, поскольку коэффициент при x 2 равен 1
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правую часть уравнения.
(б/2) 2 = (4/2) 2 = 2 2 = 4
x 2 + 4x + 4 = -1 + 4
(x + 2) 2 = 3
Шаг 4 Извлечь квадратный корень из обеих частей уравнения
9 x + 2 = ±√3 = ±1,73 (до 2 знаков после запятой) Шаг 5 Вычтите 2 с обеих сторон:
x = ±1,73 – 2 = -3,73 или -0,27
А вот еще интересная и полезная штука.
В конце шага 3 у нас было уравнение:
(х + 2) 2 = 3
Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3)
Шаг 108 Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 – 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правой части уравнения:
(b/2) 2 = (0,8/2) 2 = 0,4 2 = 0,16
x 2 – 0,8x + 0,16 0,16
(х – 0,4) 2 = 0,56
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)
Шаг 5 Вычтите (-0,4) из обеих частей (другими словами, добавьте 0,4 ):
x = ±0,748 + 0,4 = -0,348 или 1,148
Почему «Завершить квадрат»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу для решения квадратного уравнения?
Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.
Бывают также случаи, когда форма ax 2 + bx + c может быть частью более крупного вопроса , и перестановка ее как a(x+ d ) 2 + e 91 дает 11189 решение проще, потому что x появляется только один раз.
Например, "x" может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.
Также завершение квадрата является первым шагом в выводе квадратичной формулы
Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.
364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206
Сноска: значения "d" и "e"
Как я получил значения d и e из верхней части страницы?
92-8
Начните с Разделить уравнение на a Положите c/a на другую сторону Добавить (b/2a) 2 на обе стороны «Заполните квадрат» Теперь верни все назад. ..
... на левую сторону ... к исходному множителю a x 2 Факторы
Ниш Л.
спросил 25.02.13Мне нужны коэффициенты для этой математической задачи. Большое спасибо за поддержку
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Марк С. ответил 26.02.13
Репетитор
4.
9 (871)
Polymath репетиторство по математике, естественным наукам и письму
Об этом репетиторе ›
Об этом репетиторе ›
Привет, Ниш, и добро пожаловать в удивительный мир факторинговых многочленов степени 3 и выше. Этот дикий зверь является квартиком, потому что он имеет степень 4, и вот как я попытаюсь приручить его, разложив на множители на милые одомашненные полиномы степени 1 и 2. Это линейные и квадратичные полиномы, с которыми вы работали в прошлом. .
Первый шаг — проверить, есть ли у всех четырех членов общий множитель. Они этого не делают, потому что это было бы слишком просто. В алгебре 1 все четыре термина имели бы что-то общее.
Второй шаг — посмотреть, будет ли работать разложение по группам, поэтому взгляните на (x 4 −x 3 )+(4x 2 −8). Какие факторы являются общими для первых двух терминов? x 3 срок. И что общего у вторых двух терминов? Совсем немного 4.
Разложите эти выражения по одному, и у вас останется:
x 3 (x−1)+4(x 2 −2).
Ой-ой. В алгебре 1 эти выражения в скобках были бы идентичными, а теперь нет. Факторизация по группировке тоже не работает.
Третий шаг — посмотреть, сработает ли удобная замена. Вас, вероятно, просили разложить на множители квартику типа x 4 + x 2 −6 в прошлом. Установив y=x 2 , это выражение станет y 2 +y−6, и теперь ваша задача стала намного проще. Но для квартики в вашей задаче этот метод алгебры 2 тоже не работает. Вы, должно быть, принимаете предварительный расчет!
В предварительном исчислении вы должны знать некоторые факты о полиномах. Каждый курс предварительного исчисления требует, чтобы вы знали Фундаментальную теорему алгебры. Если вы включите кратность, то этот многочлен четвертой степени будет иметь четыре корня. Если бы вы хотели найти x, приравняв этот многочлен к нулю, эта теорема дала бы вам знать, что можно ожидать не более четырех решений.
Вы должны знать, как корни многочлена, равные нулю, связаны с факторами многочлена, и это отношение приводит к другой полиномиальной теореме.
Согласно теореме о линейных множителях, вы должны быть в состоянии разложить эту вещь на множители до вида (x−c 1 )(x−c 2 )(x−c 3 )(x− c 4 ), где четыре константы являются комплексными числами. Эти четыре константы могут быть или не быть реальными, и они могут повторяться или не повторяться более одного раза. Эта теорема дает вам некоторые рекомендации по решению этой проблемы. Если мы полностью разложим эту квартику, у нас будет максимум четыре линейных члена.
Правило знаков Декарта, теорема о сопряженных корнях для комплексных корней, теорема о сопряженных корнях для иррациональных корней и теоремы о верхних и нижних пределах для корней также могут помочь вам, и ваш курс может ожидать, что вы будете знать большую часть или все эти. К вашему выражению можно с пользой применить правило знаков Декарта, но мы воспользуемся теоремой о рациональных корнях.Согласно теореме о рациональных корнях, для многочленов с целыми коэффициентами каждый рациональный корень многочлена p/q должен иметь p как множитель постоянного члена многочлена и q как множитель старшего коэффициента многочлен. Это означает, что вы должны иметь возможность факторизовать термин (x−p/q) из многочлена. Вы можете понять, почему работает теорема о рациональных корнях, применив ее к квадратичным уравнениям. Мы начнем со знания факторизованной формы квадратного уравнения с двумя рациональными корнями:
(x−p 1 /q 1 )(x−p 2 /q 2 )=0
Multiplying both sides by q 1 q 2 gives us:
q 1 (x−p 1 /q 1 )q 2 (x−p 2 /q 2 )=0 или
(q 1) 2 x−p 2 )=0. После расширения с помощью FOIL мы получаем:
q 1 q 2 x 2 −(p 1 q 1 +p 2 q 2 )x+ p 1 p 2 =0.
Обратите внимание, что у коэффициента x 2 есть множители, которые являются знаменателями рациональных корней, а у коэффициента единиц есть множители, которые являются числителями.
Конечно, теорема о рациональных корнях работает только для многочленов с рациональными корнями. Но если в курсе предварительного исчисления вам дали квартику, которую нельзя разложить на множители другим методом, можете поспорить, что у нее будут рациональные корни. Если бы это было не так, вы не смогли бы ответить на вопрос, не используя калькулятор или компьютер.
Для вашей задачи мы ищем корни в форме p/q, где p — множитель −8, а q — множитель 1. Возможные варианты: ±1, ±2, ±4 и ±8. Проверяйте эти возможности по очереди, начиная с самых простых чисел, 1 и −1. Вы можете просто подставить эти числа в выражение и посмотреть, равняется ли оно нулю. Однако у использования синтетического деления при проверке рациональных корней могут быть преимущества, поскольку вы можете применять теоремы о верхних и нижних пределах корней, чтобы получить информацию о том, была ли неправильная попытка слишком большой или слишком маленькой.
Правило знаков Декарта может помочь вам сузить круг возможных вариантов, но давайте исходить из того, что −1 сработает!
После того, как вы найдете этот первый корень, вам нужно будет использовать синтетическое деление, чтобы определить частное, когда исходный многочлен делится на коэффициент, соответствующий этому корню.
(х 4 -3х 3 +4х 2 -8)/(х+1) = х 3 -4х 2 +8х-8.
Поздравляем! Теперь вместо факторизации квартики вам нужно факторизовать только кубическую. Попробуйте снова использовать те же теоремы и тесты. Вот каким должен быть ваш окончательный ответ:
92-8Голосовать за 1 Понизить
Подробнее
Отчет
Люк Б. ответил 26.02.13
Репетитор
4.
9 (90)
веселье + обучение = неизбежный прогресс
Смотрите таких репетиторов
Смотрите таких репетиторов 92( x ( x - 3 ) + 4) = 8
и определить, что -1 это один корень, а 2 это другой
Голосовать за 1 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос. 909:25 Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Обновления безопасности Apple — Служба поддержки Apple
Имя и ссылка на информацию
Доступно для
Дата выпуска
iOS 16.0.1
В этом обновлении нет опубликованных записей CVE.iPhone 14 (все модели) 15 сентября 2022 г. Сафари 16 macOS Big Sur и macOS Monterey 12 сент. 2022 г. tvOS 16 (подробности скоро появятся) Apple TV 4K, Apple TV 4K (2-го поколения) и Apple TV HD 12 сент. 2022 г. watchOS 9 (подробности скоро будут доступны) Apple Watch Series 4 и новее 12 сент. 2022 г. iOS 16 iPhone 8 и новее 12 сент. 2022 г. macOS Монтерей 12.6 macOS Монтерей 12 сент. 2022 г. macOS Big Sur 11. 7
macOS Биг Сюр 12 сент. 2022 г. iOS 15.7 и iPadOS 15.7 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 12 сент. 2022 г. iOS 12.5.6 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 31 августа 2022 Сафари 15.6.1 macOS Big Sur и macOS Catalina 18 августа 2022 watchOS 8.7.1
В этом обновлении нет опубликованных записей CVE.Apple Watch серии 3 17 авг 2022 macOS Монтерей 12.5.1 macOS Монтерей 17 авг 2022 iOS 15.6.1 и iPadOS 15.6.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 17 авг 2022 Сафари 15. 6
macOS Big Sur и macOS Catalina 20 июля 2022 watchOS 8.7 Apple Watch Series 3 и новее 20 июля 2022 Обновление безопасности 2022-005 Каталина macOS Каталина 20 июля 2022 macOS Big Sur 11.6.8 macOS Биг Сюр 20 июля 2022 macOS Монтерей 12,5 macOS Монтерей 20 июля 2022 ТВОС 15.6 Apple TV 4K, Apple TV 4K (2-го поколения) и Apple TV HD 20 июля 2022 iOS 15.6 и iPadOS 15.6 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 20 июля 2022 macOS Big Sur 11.6.7
В этом обновлении нет опубликованных записей CVE.macOS Биг Сюр 09 июня 2022 г. tvOS 15. 5.1
В этом обновлении нет опубликованных записей CVE.Apple TV 4K, Apple TV 4K (2-го поколения) и Apple TV HD 25 мая 2022 г. iTunes 12.12.4 для Windows Windows 10 и более поздние версии 18 мая 2022 г. Сафари 15,5 macOS Big Sur и macOS Catalina 16 мая 2022 г. ТВОС 15.5 Apple TV 4K, Apple TV 4K (2-го поколения) и Apple TV HD 16 мая 2022 г. Xcode 13.4 macOS Monterey 12 и более поздние версии 16 мая 2022 г. Обновление безопасности 2022-004 Каталина macOS Каталина 16 мая 2022 г. macOS Big Sur 11.6.6 macOS Биг Сюр 16 мая 2022 г. macOS Монтерей 12.4 macOS Монтерей 16 мая 2022 г. iOS 15.5 и iPadOS 15.5 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 16 мая 2022 г. watchOS 8.6 Apple Watch Series 3 и новее 16 мая 2022 г. watchOS 8.5.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 3 и новее 31 марта 2022 г. macOS Монтерей 12.3.1 macOS Монтерей 31 марта 2022 г. iOS 15.4.1 и iPadOS 15.4.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 31 марта 2022 г. tvOS 15.4.1
В этом обновлении нет опубликованных записей CVE.Apple TV 4K и Apple TV HD 31 марта 2022 г. Сафари 15.4 macOS Big Sur и macOS Catalina 15 марта 2022 г. Программное обеспечение Apple TV 7.9
В этом обновлении нет опубликованных записей CVE.Apple TV (3-го поколения) 14 марта 2022 г. GarageBand 10.4.6 macOS Big Sur 11.5 и более поздние версии 14 марта 2022 г. Логик Про 10.7.3 macOS Big Sur 11.5 и более поздние версии 14 марта 2022 г. Xcode 13.3 macOS Monterey 12 и более поздние версии 14 марта 2022 г. Обновление безопасности 2022-003 Каталина macOS Каталина 14 марта 2022 г. macOS Big Sur 11.6.5 macOS Биг Сюр 14 марта 2022 macOS Монтерей 12.3 macOS Монтерей 14 марта 2022 г. ТВОС 15.4 Apple TV 4K и Apple TV HD 14 марта 2022 г. watchOS 8.5 Apple Watch Series 3 и новее 14 марта 2022 г. iOS 15.4 и iPadOS 15.4 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 14 марта 2022 г. iTunes 12.12.3 для Windows Windows 10 и более поздние версии 08 мар 2022 macOS Big Sur 11.6.4
В этом обновлении нет опубликованных записей CVE.macOS Биг Сюр 14 фев 2022 Обновление безопасности 2022-002 Catalina
Это обновление не содержит опубликованных записей CVE.macOS Каталина 14 фев 2022 Safari 15.3 (версия 16612.4.9.1.8 и 15612.4.9.1.8) macOS Big Sur и macOS Catalina 10 фев 2022 macOS Монтерей 12.2.1 macOS Монтерей 10 фев 2022 watchOS 8.4.2
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 3 и новее 10 фев 2022 iOS 15.3.1 и iPadOS 15.3.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 10 фев 2022 watchOS 8. 4.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 4 и новее 01 фев 2022 Сафари 15.3 macOS Big Sur и macOS Catalina 26 января 2022 г. Обновление безопасности 2022-001 Каталина macOS Каталина 26 января 2022 г. macOS Big Sur 11.6.3 macOS Биг Сюр 26 января 2022 г. macOS Монтерей 12.2 macOS Монтерей 26 января 2022 г. ТВОС 15.3 Apple TV 4K и Apple TV HD 26 января 2022 г. iOS 15.3 и iPadOS 15.3 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 января 2022 г. watchOS 8.4 Apple Watch Series 3 и новее 26 января 2022 г. iOS 15. 2.1 и iPadOS 15.2.1
iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 12 января 2022 г. Сафари 15.2 macOS Big Sur и macOS Catalina 14 декабря 2021 г. iOS 15.2 и iPadOS 15.2 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 13 декабря 2021 г. macOS Монтерей 12.1 macOS Монтерей 13 декабря 2021 г. macOS Big Sur 11.6.2 macOS Биг Сюр 13 декабря 2021 г. Обновление безопасности 2021-008 Каталина macOS Каталина 13 декабря 2021 г. ТВОС 15.2 Apple TV 4K и Apple TV HD 13 декабря 2021 г. watchOS 8. 3
Apple Watch Series 3 и новее 13 декабря 2021 г. watchOS 8.1.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 7 (GPS + сотовая связь) 18 ноя 2021 iOS 15.1.1
В этом обновлении нет опубликованных записей CVE.iPhone 12 и новее 17 ноя 2021 iCloud для Windows 13 Windows 10 и более поздние версии через Microsoft Store 10 ноя 2021 tvOS 15.1.1
В этом обновлении нет опубликованных записей CVE.Apple TV 4K и Apple TV HD 01 ноя 2021 Сафари 15.1 macOS Big Sur и macOS Catalina 27 окт 2021 iOS 14.8.1 и iPadOS 14.8.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 окт 2021 macOS Monterey 12. 0.1 (Рекомендации включают содержимое безопасности macOS Monterey 12.0 и macOS Monterey 12.0.1)
Mac Pro (2013 г. и новее), MacBook Air (начало 2015 г. и новее), MacBook Pro (начало 2015 г. и новее), Mac mini (конец 2014 г. и новее), iMac (конец 2015 г. и новее), MacBook (начало 2016 г. и новее) ), iMac Pro (2017 г. и новее) 25 окт. 2021 macOS Монтерей 12.0 Предустановлен только на некоторых моделях Mac; обновите до macOS Monterey 12.0.1 Предустановлено macOS Big Sur 11.6.1 macOS Биг Сюр 25 окт. 2021 Обновление безопасности 2021-007 Каталина macOS Каталина 25 окт. 2021 watchOS 8.1 Apple Watch Series 3 и новее 25 окт. 2021 iOS 15.1 и iPadOS 15.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 25 окт. 2021
ТВОС 15.1 Apple TV 4K и Apple TV HD 25 окт. 2021 watchOS 8.0.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 3 и новее 11 окт. 2021 г. iOS 15.0.2 и iPadOS 15.0.2 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 11 окт. 2021 г. iOS 15.0.1 и iPadOS 15.0.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 01 окт. 2021 Обновление безопасности 2021-006 Каталина macOS Каталина 23 сентября 2021 г. iOS 12.5.5 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 23 сентября 2021 г. iTunes 12.12 для Windows Windows 10 и более поздние версии 20 сен 2021 Сафари 15 macOS Big Sur и macOS Catalina 20 сен 2021 Xcode 13 macOS Big Sur 11.3 и более поздние версии 20 сен 2021 ТВОС 15 Apple TV 4K и Apple TV HD 20 сен 2021 watchOS 8 Apple Watch Series 3 и новее 20 сен 2021 iOS 15 и iPadOS 15 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 20 сен 2021 iTunes U 3.8.3 iOS 12.4 и новее или iPadOS 12.4 и новее 15 сент. 2021 г. Сафари 14.1.2 macOS Catalina и macOS Мохаве 13 сент. 2021 г. Обновление безопасности 2021-005 Каталина macOS Каталина 13 сент. 2021 г.
macOS Big Sur 11.6 macOS Биг Сюр 13 сент. 2021 г. watchOS 7.6.2 Apple Watch Series 3 и новее 13 сент. 2021 г. iOS 14.8 и iPadOS 14.8 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 13 сент. 2021 г. iCloud для Windows 12.5 Windows 10 и более поздние версии через Microsoft Store 16 авг 2021 macOS Big Sur 11.5.2
В этом обновлении нет опубликованных записей CVE.macOS Биг Сюр 11 авг 2021 iTunes 12.11.4 для Windows Windows 10 и более поздние версии 09 авг 2021 watchOS 7.6.1 Apple Watch Series 3 и новее 29 июля 2021 iOS 14.7.1 и iPadOS 14.7. 1
iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 июля 2021 macOS Big Sur 11.5.1 macOS Биг Сюр 26 июля 2021 macOS Big Sur 11.5 macOS Биг Сюр 21 июля 2021 Обновление безопасности 2021-004 Каталина macOS Каталина 21 июля 2021 Обновление безопасности 2021-005 Мохаве macOS Мохаве 21 июля 2021 iPadOS 14.7 iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее 21 июля 2021 Сафари 14.1.2 macOS Каталина и macOS Мохаве 19 июля 2021 iOS 14.7 iPhone 6s и новее и iPod touch (7-го поколения) 19 июля 2021 watchOS 7. 6
Apple Watch Series 3 и новее 19 июля 2021 ТВОС 14.7 Apple TV 4K и Apple TV HD 19 июля 2021 iMovie 10.2.4 macOS Catalina 10.15.6 и более поздние версии 17 июня 2021 г. iOS 12.5.4 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 14 июня 2021 г. Сафари 14.1.1 macOS Каталина и macOS Мохаве 24 мая 2021 г. Обновление безопасности 2021-003 Каталина macOS Каталина 24 мая 2021 г. Обновление безопасности 2021-004 Мохаве macOS Мохаве 24 мая 2021 г. macOS Big Sur 11.4 macOS Биг Сюр 24 мая 2021 г. iOS 14.6 и iPadOS 14.6 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 24 мая 2021 г. ТВОС 14.6 Apple TV 4K и Apple TV HD 24 мая 2021 г. watchOS 7.5 Apple Watch Series 3 и новее 24 мая 2021 г. Учебный лагерь 6.1.14 Mac Pro (конец 2013 г. и новее), MacBook Pro (конец 2013 г. и новее), MacBook Air (середина 2013 г. и новее), Mac mini (середина 2014 г. и новее), iMac (середина 2014 г. и новее), MacBook (начало 2015 г. и новее) позже), iMac Pro (конец 2017 г.) 17 мая 2021 г. Сафари 14.1 macOS Каталина и macOS Мохаве 04 мая 2021 macOS Big Sur 11.3.1 macOS Биг Сюр 03 мая 2021 г. iOS 14.5.1 и iPadOS 14.5.1 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 03 мая 2021 г. iOS 12.5.3 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 03 мая 2021 г. watchOS 7.4.1 Apple Watch Series 3 и новее 03 мая 2021 г. iCloud для Windows 12.3 Windows 10 и более поздние версии через Microsoft Store 26 апр 2021 Xcode 12.5 macOS Big Sur 11 и более поздние версии 26 апр 2021 Сафари 14.1 macOS Каталина и macOS Мохаве 26 апр 2021 macOS Big Sur 11.3 macOS Биг Сюр 26 апр 2021 Обновление безопасности 2021-002 Каталина macOS Каталина 26 апр 2021 Обновление безопасности 2021-003 Мохаве macOS Мохаве 26 апр 2021 iOS 14.5 и iPadOS 14.5 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 апр 2021 watchOS 7. 4
Apple Watch Series 3 и новее 26 апр 2021 ТВОС 14.5 Apple TV 4K и Apple TV HD 26 апр 2021 iTunes 12.11.3 для Windows Windows 10 и более поздние версии 22 апр 2021 GarageBand 10.4.3 macOS Биг Сюр 06 апр 2021 iOS 14.4.2 и iPadOS 14.4.2 iPhone 6s и новее, iPad Pro (все модели), iPad Air 2 и новее, iPad 5-го поколения и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 мар 2021 iOS 12.5.2 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 26 мар 2021 watchOS 7.3.3 Apple Watch Series 3 и новее 26 мар 2021 Safari 14.0.3 (версия 14610.4.3.1.7 и 15610.4.3.1.7) macOS Каталина и macOS Мохаве 08 мар 2021 macOS Big Sur 11. 2.3
macOS Биг Сюр 08 мар 2021 watchOS 7.3.2 Apple Watch Series 3 и новее 08 мар 2021 iOS 14.4.1 и iPadOS 14.4.1 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 08 мар 2021 macOS Big Sur 11.2.2
В этом обновлении нет опубликованных записей CVE.macOS Big Sur 11.2.1 25 фев 2021 watchOS 7.3.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 5 и Apple Watch SE 15 фев 2021 macOS Big Sur 11.2.1, дополнительное обновление macOS Catalina 10.15.7, обновление безопасности macOS Mojave 10.14.6 2021-002 macOS Big Sur 11.2, macOS Catalina 10.15.7 и macOS Mojave 10.14.6 09 фев 2021 Сафари 14.0.3 macOS Catalina и macOS Мохаве 01 фев 2021 macOS Big Sur 11. 2, обновление для системы безопасности 2021-001 Catalina, обновление для системы безопасности 2021-001 Mojave
macOS Big Sur 11.0.1, macOS Catalina 10.15.7 и macOS Mojave 10.14.6 01 фев 2021 Xcode 12.4 macOS Catalina 10.15.4 и более поздние версии 26 января 2021 г. iCloud для Windows 12.0 Windows 10 и более поздние версии через Microsoft Store 26 января 2021 iOS 14.4 и iPadOS 14.4 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 26 января 2021 г. ТВОС 14.4 Apple TV 4K и Apple TV HD 26 января 2021 г. watchOS 7.3 Apple Watch Series 3 и новее 26 января 2021 г. iOS 12.5.1
В этом обновлении нет опубликованных записей CVE.iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 11 января 2021 г. iOS 14.3 и iPadOS 14.3 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 14 декабря 2020 г. macOS Big Sur 11.1, обновление для системы безопасности 2020-001 Catalina, обновление для системы безопасности 2020-007 Mojave macOS Big Sur 11.0.1, macOS Catalina 10.15.7 и macOS Mojave 10.14.6 14 декабря 2020 г. сервер macOS 5.11 macOS Биг Сюр 14 декабря 2020 г. ТВОС 14.3 Apple TV 4K и Apple TV HD 14 декабря 2020 г. watchOS 7.2 Apple Watch Series 3 и новее 14 декабря 2020 г. Сафари 14.0.2 macOS Каталина и macOS Мохаве 14 декабря 2020 г. iOS 12.5 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch (6-го поколения) 14 декабря 2020 г. watchOS 6.3 Apple Watch Series 1 и Apple Watch Series 2 14 декабря 2020 г. iCloud для Windows 11.5 Windows 10 и более поздние версии через Microsoft Store 02 дек. 2020 iOS 14.2.1
В этом обновлении нет опубликованных записей CVE.iPhone 12 Pro, iPhone 12 Pro Max, iPhone 12 и iPhone 12 mini 19 ноя 2020 macOS Big Sur 11.0.1 Mac mini (M1, 2020 г.), MacBook Air (M1, 2020 г.), MacBook Air (13 дюймов, 2020 г.) 17 ноя 2020 iTunes 12.11 для Windows Windows 10 и более поздние версии 17 ноя 2020 Сафари 14.0.1 macOS Каталина и macOS Мохаве 12 ноя 2020 Обновление безопасности 2020-006 High Sierra, Обновление безопасности 2020-006 Мохаве macOS High Sierra 10.13.6, macOS Мохаве 10.14. 6
12 ноя 2020 macOS Big Sur 11.0.1 (Рекомендации включают информацию о безопасности macOS Big Sur 11.0 и macOS Big Sur 11.0.1) Mac Pro (2013 г. и новее), MacBook Air (2013 г. и новее), MacBook Pro (конец 2013 г. и новее), Mac mini (2014 г. и новее), iMac (2014 г. и новее), MacBook (2015 и новее), iMac Pro (все модели) 12 ноя 2020 macOS Big Sur 11.0 Предустановлен только на некоторых моделях Mac; обновите до macOS Big Sur 11.0.1 Предустановлено Приложение Apple TV для Fire OS Apple TV версии 5.1 и выше 09 ноя 2020 watchOS 7.1 Apple Watch Series 3 и новее 05 ноя 2020 watchOS 6.2.9 Apple Watch Series 1 и Apple Watch Series 2 05 ноя 2020 watchOS 5.3.9 Apple Watch Series 1 и новее 05 ноя 2020 Дополнительное обновление macOS Catalina 10. 15.7, обновление macOS Catalina 10.15.7
macOS Каталина 10.15.7 05 ноя 2020 ТВОС 14.2 Apple TV 4K и Apple TV HD 05 ноя 2020 iOS 14.2 и iPadOS 14.2 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 05 ноя 2020 iOS 12.4.9 iPhone 5s, iPhone 6 и 6 Plus, iPad Air, iPad mini 2 и 3, iPod touch (6-го поколения) 05 ноя 2020 Apple Music 3.4.0 для Android Android версии 5.0 и выше 26 окт 2020 iOS 14.1 и iPadOS 14.1
В этом обновлении нет опубликованных записей CVE.iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 20 окт 2020 watchOS 7.0.3
В этом обновлении нет опубликованных записей CVE.Apple Watch серии 3 19 окт. 2020 г.
watchOS 7.0.2
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 3 и новее 12 окт. 2020 tvOS 14.0.2
В этом обновлении нет опубликованных записей CVE.Apple TV 4K и Apple TV HD 05 окт 2020 macOS 10.14.6 Дополнительное обновление macOS Мохаве 01 окт 2020 iCloud для Windows 7.21 Windows 7 и более поздние версии 24 сен 2020 iCloud для Windows 11.4 Windows 10 и более поздние версии через Microsoft Store 24 сен 2020 macOS Catalina 10.15.7, обновление для системы безопасности 2020-005 High Sierra, обновление для системы безопасности 2020-005 Mojave macOS High Sierra 10.13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.6 24 сен 2020 iOS 14.0.1 и iPadOS 14.0. 1
В этом обновлении нет опубликованных записей CVE.iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch (7-го поколения) 24 сен 2020 watchOS 7.0.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 3 и новее 24 сен 2020 tvOS 14.0.1
В этом обновлении нет опубликованных записей CVE.Apple TV 4K и Apple TV HD 24 сен 2020 Сафари 14.0 macOS Каталина и macOS Мохаве 16 сен 2020 ТВОС 14.0 Apple TV 4K и Apple TV HD 16 сен 2020 watchOS 7.0 Apple Watch Series 3 и новее 16 сен 2020 iOS 14.0 и iPadOS 14.0 iPhone 6s и новее, iPod touch 7-го поколения, iPad Air 2 и новее, iPad mini 4 и новее 16 сен 2020 iTunes для Windows 12. 10.9
Windows 7 и более поздние версии 16 сен 2020 Xcode 12.0 macOS Catalina 10.15.4 и более поздние версии 16 сен 2020 iOS 13.7
В этом обновлении нет опубликованных записей CVE.iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 01 Сен 2020 iOS 13.6.1
: В этом обновлении нет опубликованных записей CVE.iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 12 авг 2020 macOS Catalina 10.15.6 Дополнительное обновление
В этом обновлении нет опубликованных записей CVE.macOS Каталина 10.15.6 12 авг 2020 iCloud для Windows 11.3 Windows 10 и более поздние версии через Microsoft Store 10 авг 2020 iCloud для Windows 7.20 Windows 7 и более поздние версии 10 авг 2020 iTunes 12. 10.8 для Windows
Windows 7 и более поздние версии 30 июл 2020 Сафари 13.1.2 macOS Mojave и macOS High Sierra, а также включены в macOS Catalina 15 июля 2020 г. iOS 12.4.8
В этом обновлении нет опубликованных записей CVE.iPhone 5s, iPhone 6 и 6 Plus, iPad Air, iPad mini 2 и 3, iPod touch (6-го поколения) 15 июля 2020 г. watchOS 5.3.8
В этом обновлении нет опубликованных записей CVE.Apple Watch серии 1, 2, 3 и 4 15 июля 2020 г. Xcode 11.6
В этом обновлении нет опубликованных записей CVE.macOS Мохаве 10.15.2 и более поздних версий 15 июля 2020 г. iOS 13.6 и iPadOS 13.6 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 15 июля 2020 г. твОС 13.4.8 Apple TV 4K и Apple TV HD 15 июля 2020 г. watchOS 6.2.8 Apple Watch Series 1 и новее 15 июля 2020 г. macOS Catalina 10.15.6, обновление безопасности 2020-004 Mojave, обновление безопасности 2020-004 High Sierra macOS High Sierra 10.13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.5 15 июля 2020 г. macOS Catalina 10.15.5 Дополнительное обновление, обновление безопасности 2020-003 High Sierra macOS High Sierra 10.13.6, macOS Catalina 10.15.5 01 июн 2020 твОС 13.4.6 Apple TV 4K и Apple TV HD 01 июн 2020 watchOS 6.2.6 Apple Watch Series 1 и новее 01 июн 2020 iOS 13.5.1 и iPadOS 13.5.1 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 01 июн 2020 macOS Catalina 10.15.5, обновление безопасности 2020-003 Mojave, обновление безопасности 2020-003 High Sierra macOS High Sierra 10. 13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.4
26 мая 2020 г. Помощник по миграции Windows 2.2.0.0 (версия 1A11) macOS Каталина 26 мая 2020 г. Сафари 13.1.1 macOS Mojave и macOS High Sierra и включены в macOS Catalina 26 мая 2020 г. iCloud для Windows 11.2 Windows 10 и более поздние версии через Microsoft Store 26 мая 2020 г. iCloud для Windows 7.19 Windows 7 и более поздние версии 26 мая 2020 г. iTunes 12.10.7 для Windows Windows 7 и более поздние версии 21 мая 2020 г. iOS 13.5 и iPadOS 13.5 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 20 мая 2020 г. iOS 12.4.7 iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch 6-го поколения 20 мая 2020 г. ТВОС 13.4.5 Apple TV 4K и Apple TV HD 20 мая 2020 г. Xcode 11.5 macOS Catalina 10.15.2 и более поздние версии 20 мая 2020 г. watchOS 5.3.7 Apple Watch Series 1, Apple Watch Series 2, Apple Watch Series 3 и Apple Watch Series 4 при сопряжении с iPhone с установленной iOS 12 18 мая 2020 г. watchOS 6.2.5 Apple Watch Series 1 и новее 18 мая 2020 г. iOS 13.4.1
В этом обновлении нет опубликованных записей CVE.iPhone SE (2-го поколения) 23 апр 2020 watchOS 6.2.1
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 1 и 2
Apple Watch Series 3 и новее20 апр 2020
08 апр 2020Xcode 11.4.1 macOS Catalina 10.15.2 и более поздние версии 15 апр 2020 macOS Catalina 10. 15.4 Дополнительное обновление
В этом обновлении нет опубликованных записей CVE.macOS Каталина 10.15.4 08 апр 2020 iOS 13.4.1 и iPadOS 13.4.1
В этом обновлении нет опубликованных записей CVE.iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 07 апр 2020 iCloud для Windows 7.18 Windows 7 и более поздние версии 25 мар 2020 iCloud для Windows 10.9.3 Windows 10 и более поздние версии через Microsoft Store 25 мар 2020 iTunes 12.10.5 для Windows Windows 7 и более поздние версии 24 мар 2020 iOS 13.4 и iPadOS 13.4 iPhone 6s и новее, iPad Air 2 и новее, iPad mini 4 и новее и iPod touch 7-го поколения 24 мар 2020 watchOS 5.3.6
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 1, Apple Watch Series 2, Apple Watch Series 3 и Apple Watch Series 4 при сопряжении с iPhone с установленной iOS 12 24 мар 2020 iOS 12.4.6
В этом обновлении нет опубликованных записей CVE.iPhone 5s, iPhone 6, iPhone 6 Plus, iPad Air, iPad mini 2, iPad mini 3 и iPod touch 6-го поколения 24 марта 2020 г. Сафари 13.1 macOS Mojave и macOS High Sierra, а также включены в macOS Catalina 24 мар 2020 watchOS 6.2 Apple Watch Series 1 и новее 24 мар 2020 ТВОС 13.4 Apple TV 4K и Apple TV HD 24 мар 2020 macOS Catalina 10.15.4, обновление безопасности 2020-002 Mojave, обновление безопасности 2020-002 High Sierra macOS High Sierra 10.13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.3 24 мар 2020 Xcode 11. 4
macOS Catalina 10.15.2 и более поздние версии 24 мар 2020 watchOS 6.1.3
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 1 и новее 18 фев 2020 watchOS 5.3.5
В этом обновлении нет опубликованных записей CVE.Apple Watch Series 1, Apple Watch Series 2, Apple Watch Series 3 и Apple Watch Series 4 при сопряжении с iPhone с установленной iOS 12 18 фев 2020 iCloud для Windows 10.9.2 Windows 10 и более поздние версии через Microsoft Store 29 января 2020 г. iTunes 12.10.4 для Windows Windows 7 и более поздние версии 28 января 2020 г. твОС 13.3.1 Apple TV 4K и Apple TV HD 28 января 2020 г. Сафари 13.0.5 macOS Mojave и macOS High Sierra и включены в macOS Catalina 28 января 2020 г.

 Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 1 , положителен (больше нуля).
Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 1 , положителен (больше нуля). 2 Решение x 2 -4x-5 = 0 путем заполнения квадрата.
2 Решение x 2 -4x-5 = 0 путем заполнения квадрата.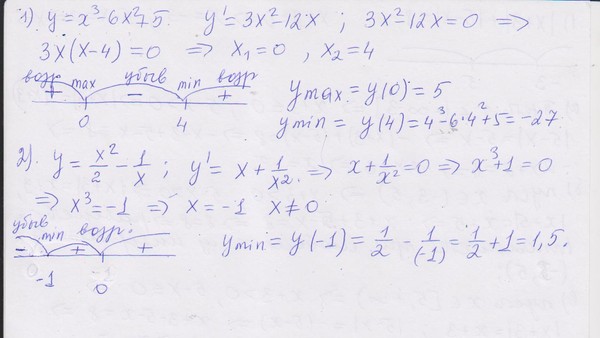
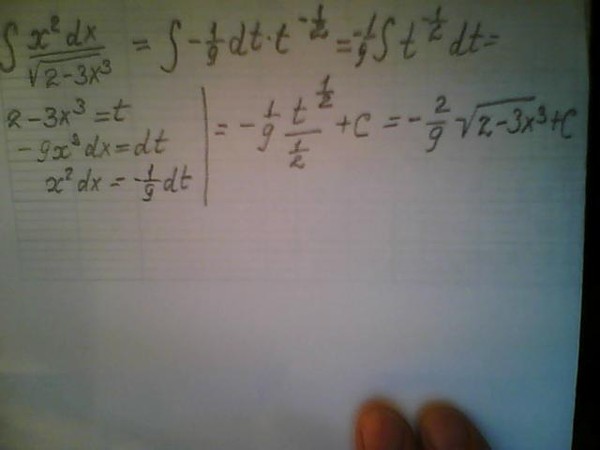 B 2 -4AC =
B 2 -4AC = 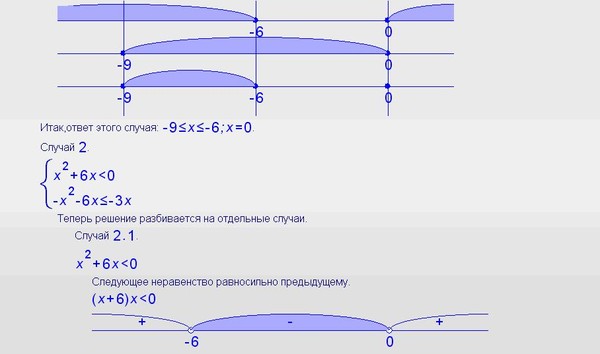


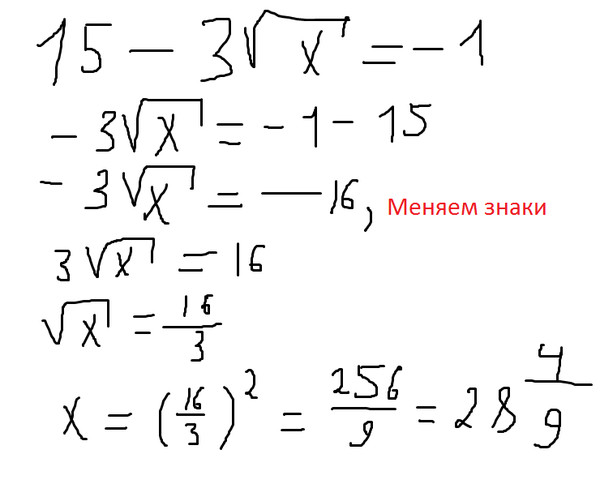

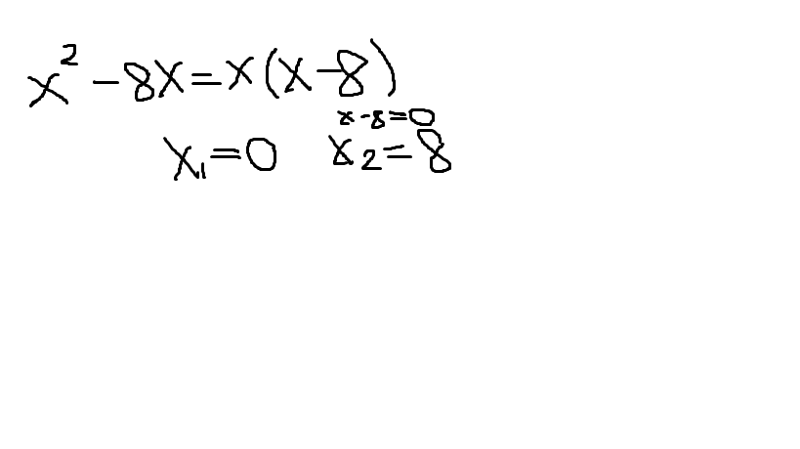 Вам может понравиться этот метод.
Вам может понравиться этот метод.


 ..
.. 9
(871)
9
(871) Разложите эти выражения по одному, и у вас останется:
Разложите эти выражения по одному, и у вас останется: Вы должны знать, как корни многочлена, равные нулю, связаны с факторами многочлена, и это отношение приводит к другой полиномиальной теореме.
Вы должны знать, как корни многочлена, равные нулю, связаны с факторами многочлена, и это отношение приводит к другой полиномиальной теореме.

 Правило знаков Декарта может помочь вам сузить круг возможных вариантов, но давайте исходить из того, что −1 сработает!
Правило знаков Декарта может помочь вам сузить круг возможных вариантов, но давайте исходить из того, что −1 сработает! 9
(90)
9
(90)
 7
7 6
6 5.1
5.1 


 4.1
4.1  2.1 и iPadOS 15.2.1
2.1 и iPadOS 15.2.1 3
3 0.1 (Рекомендации включают содержимое безопасности macOS Monterey 12.0 и macOS Monterey 12.0.1)
0.1 (Рекомендации включают содержимое безопасности macOS Monterey 12.0 и macOS Monterey 12.0.1) 
 2021 г.
2021 г. 1
1 6
6
 4
4 2.3
2.3  2, обновление для системы безопасности 2021-001 Catalina, обновление для системы безопасности 2021-001 Mojave
2, обновление для системы безопасности 2021-001 Catalina, обновление для системы безопасности 2021-001 Mojave

 6
6 15.7, обновление macOS Catalina 10.15.7
15.7, обновление macOS Catalina 10.15.7 2020 г.
2020 г. 1
1  10.9
10.9 10.8 для Windows
10.8 для Windows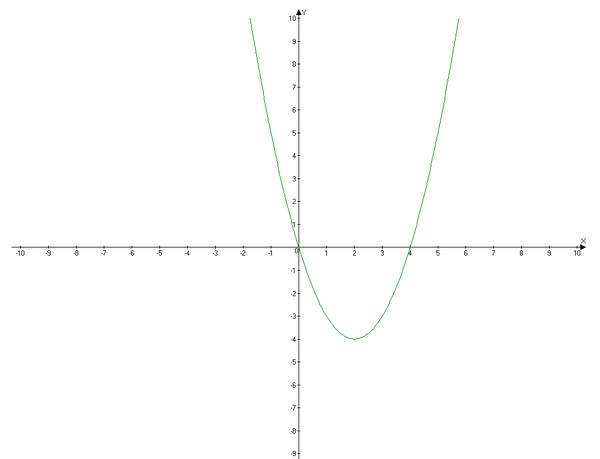
 13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.4
13.6, macOS Mojave 10.14.6, macOS Catalina 10.15.4
 15.4 Дополнительное обновление
15.4 Дополнительное обновление 
 4
4