Формулы Маклорена и Тейлора
Многочлен Тейлора и остаточный член
Пусть задана функция f(x), которая некоторое число раз дифференцируется в точке x0. Найдем многочлен n-й степени вида
Для которого выполняются равенства
Для того, чтобы вычислить коэффициенты многочлена, найдем его производные и рассчитаем их значения в точке х0.
Таким образом, коэффициенты имеют вид:
А многочлен называемый многочленом Тейлора:
Разность между функцией и многочленом носит название остаточного члена.
Формула Тейлора
Формула Тейлора в общем виде:
Формула Маклорена
Формула Маклорена это упрощенное представление формулы Тейлора при х0=0
Пример 1
Разложить в ряд Тейлора функцию в точке x0 = 1.
\[y(x)=x^{2} +2x-3\]Решение.
- Найдем первую производную в точке 1 \[y'(x)=\left(x^{2} +2x-3\right)^{{‘} } =2x+2\] \[y'(1)=2x+2=2\cdot 1+2=4\]
- Найдем вторую производную в точке 1 \[y»(x)=\left(2x+2\right)^{{‘} } =2\] \[y»(1)=2\]
- Найдем третью производную \[y»'(x)=2’=0\]
- Таким образом \[\begin{array}{l} {y^{(n)} (x)=0} \\ {y^{(n)} (1)=0} \end{array}\] \[y(1)=1^{2} +2\cdot 1-3=0\]
- Ряд Тейлора будет иметь вид \[y(x)=0+\frac{0}{1!} (x-2)+\frac{2}{2!} (x-2)^{3} +\frac{4}{3!} (x-2)^{3} +0+…\] \[=(x-2)+\frac{2}{3} (x-2)^{2} \]
Пример 2
Разложить в ряд Маклорена функцию в точке а = 0.
\[y=e^{2x} \]Решение.
- Найдем первую производную в точке 0 \[y'(x)=\left(e^{2x} \right)^{{‘} } =2e^{2x} \] \[y'(0)=2e^{2x} =2e^{2\cdot 0} =2\]
- Найдем вторую производную в точке 0 \[y»(x)=\left(2e^{2x} \right)^{{‘} } =2\cdot 2e^{2x} =4e^{2x} \] \[y»(0)=4e^{0} =4\]
- Найдем третью производную \[y»'(x)=\left(4e^{2x} \right)^{{‘} } =4\cdot 2e^{2x} =8e^{2x} \] \[y»'(0)=8e^{0} =8\]
- Таким образом \[\begin{array}{l} {y^{(n)} (x)=2^{n} e^{2x} } \\ {y^{(n)} (0)=2^{n} } \end{array}\]
- Ряд Маклорена будет иметь вид \[y(x)=e^{kx} =1+\frac{2}{1!} x+\frac{4}{2!} x^{2} +\frac{8}{3!} x^{3} +…+\frac{2^{n} }{n!} x^{n} \]
Пример 3
Разложить по степеням (х — 1) функцию
\[y=2x^{3} +x^{2} -3x+5\]Решение.
- Найдем первую производную в точке 1 \[y'(x)=6x^{2} +2x-3\] \[y'(1)=6\cdot 1+2\cdot 1-3=5\]
- Найдем вторую производную в точке 1 \[y»(x)=\left(6x^{2} +2x-3\right)^{{‘} } =12x+2\] \[y»(1)=12\cdot 1+2=14\]
- Найдем третью производную в точке 1 \[y»'(x)=\left(12x+2\right)^{{‘} } =12\] \[y»'(1)=12\]
- Найдем 4 производную в точке 1 \[y^{(4)} (x)=12’=0\] \[y^{(4)} (0)=0\]
- Распишем ряд Тейлора \[y(x)=5+\frac{0}{1!} (x-1)+\frac{12}{2!} (x-1)^{3} +\frac{14}{3!} (x-1)^{3} +\frac{5}{4!} (x-1)^{4} \] \[y(x)=5+6(x-1)^{3} +\frac{7}{3} (x-1)^{3} +\frac{5}{24} (x-1)^{4} \]
Значит производная функции равна нулю при n больше или равно числу 4.
\[y(1)=2+1-3+5=5\]spravochnick.ru
Формулы Тейлора и Маклорена

Доказательство.
Так как Tn (x0 )= a0 и Tn (x0 )= f (x0 ), то a0 = f (x0 ). Вычислим производную от многочлена Тейлора
Tn ‘ (x)= a1 + a2 2 (x − x0 )+ a3 3 (x − x0 )2 +…
и подставим в это равенство x = x0 . Получим Tn′(x0 )= a1 .
Поскольку из определения многочлена Тейлора следует, что должно быть выполнено условие Tn′(x0 )= f ′(x0 ), то
a1 = f ‘ (x0 ).
Вычислим вторую производную от многочлена Тейлора
Tn »(x)= 2 a2 + a3
Подставив в это равенство x = x0 , Тейлора справедливо Tn′′(x0 )= f ′′(x0 )
a2
3 2 (x − x0 )+ a4 4 3 (x − x0 )2 +…
получим, что Tn′′(x0 )= 2 a2 . Так как для многочлена , то 2a2 = f ′′(x0 ), откуда следует, что
= f »(x0 )= f »(x0 ).
2 2!
Вычислим третью производную от многочлена Тейлора
|
| ′′′ | 2 + a4 4 3 2 (x − x0 )+… | |||||
|
| Tn (x)= a3 3 | ||||||
и подставим в нее | x = x0 . Получим | ′′′ | 2 a3 . Так как должно быть выполнено | |||||
Tn | (x0 )= 3 | |||||||
′′′ | ′′′ |
| ′′′ |
|
|
|
|
|
условие Tn (x0 )= f | (x0 ), то 3 2 a3 = f | (x0 ), откуда следует, что | ||||||
|
| a3 = | f ′′′(x0 ) | = |
| f ′′′(x0 ) | . | |
|
|
|
| 3! | ||||
|
|
| 3 2 |
| ||||
Последовательно | дифференцируя | n раз | многочлен Тейлора и подставляя в | |||||
вычисленную производную x = x0 , получим формулу для коэффициента an при любом
значении n : |
|
|
| f ‘(n)(x | ) |
|
|
|
|
|
|
|
| ||
|
| an = |
| 0 | . |
| |
|
|
| n! |
|
| ||
|
|
|
|
|
|
| |
|
|
| |||||
Пусть функция | f (x) | n раз дифференцируема в некоторой окрестности Uδ(x0 ) точки | |||||
x0 и пусть Tn | (x) – | ее многочлен | Тейлора в точке x0 . | Если обозначить | |||
Rn (x)= f (x)−Tn (x), то функцию f (x) в окрестности Uδ(x0 ) точки x0 | можно представить | ||||||
формулой: |
|
|
| f (x)=Tn (x)+ Rn (x) |
| ||
|
|
|
| (1) | |||
или
f (x)= f (x0 )+ f ‘1!(x0 ) (x − x0 )+ f »2!(x0 ) (x − x0 )2 + … + f (nn)(!x0 )(x − x0 )n + Rn (x). (2)
Определение 1
Формула (1) или (2) называются формулами Тейлора для функции f (x) в точке x0 , а выражение Rn (x) – остаточным членом формулы Тейлора.
Теорема.
lim Rn (x)= 0
x→x0
Доказательство
очевидно, так как f (x0 )=Tn (x0 ), а функция f (x) так же, как и ее многочлен Тейлора,
непрерывны. Тогда
34
studfiles.net
§4. Разложение по формуле Маклорена некоторых элементарных функций
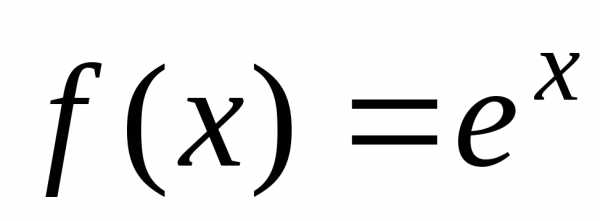 .
.Поскольку и , то формула Маклорена имеет вид
где: 1)
2)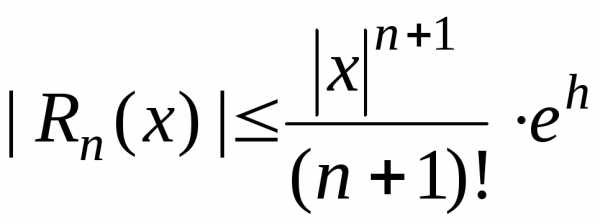 ,
для любого промежутка
,
для любого промежутка 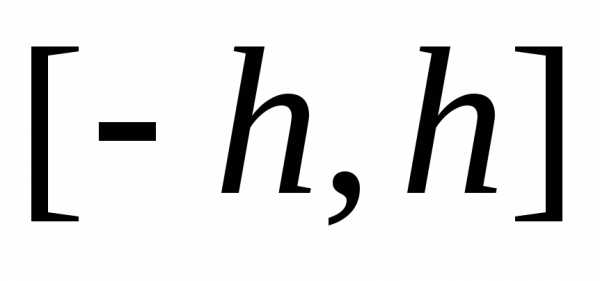 (очевидно, что ).
(очевидно, что ).
II. .
Известно, чтоТогда:
Условия теоремы
из §3 выполнены на всей оси с  Формула
Маклорена имеет вид
Формула
Маклорена имеет вид
где: 1)
2) .
На первый
взгляд написанные формы для 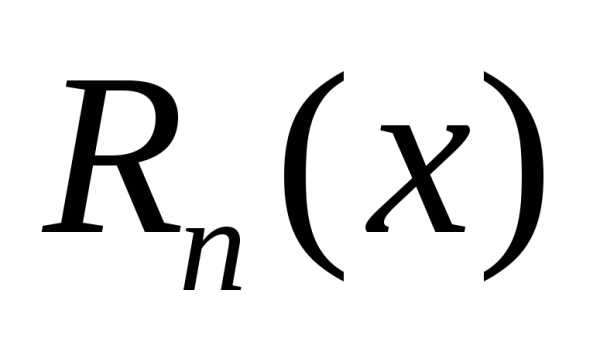 отличаются от общих результатов. Но
надо не забывать, что, вообще говоря, в
разложении для
отличаются от общих результатов. Но
надо не забывать, что, вообще говоря, в
разложении для 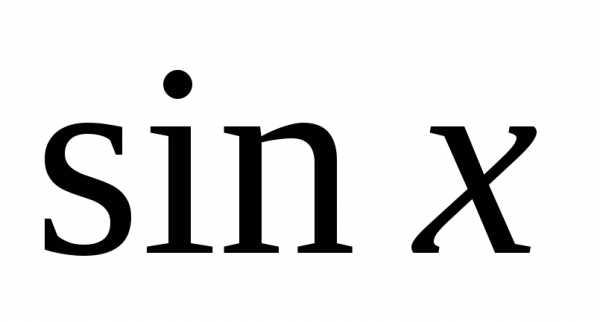
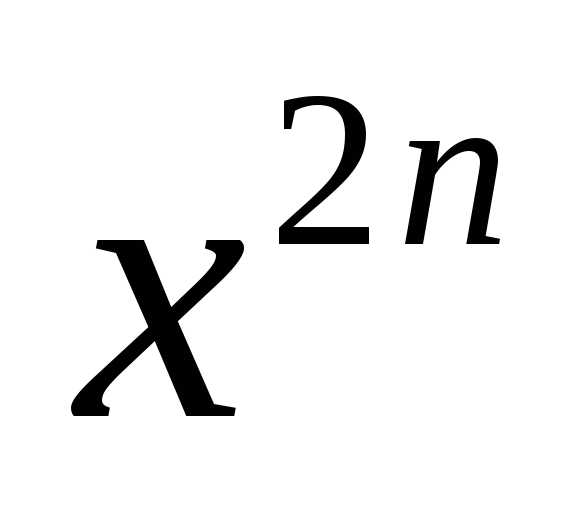 ,
только коэффициент при этой степени
равен 0.
,
только коэффициент при этой степени
равен 0.III. .
Аналогично предыдущему нетрудно получить
где: 1)
2).
IV. .
Прежде всего, имеем . Теперь можно использовать формулу дифференцирования степенной функции:
При Формула Маклорена имеет вид (с учётом того, что ):
где: 1)
2)
Отметим, что для
оценки остаточного члена для требуется форма 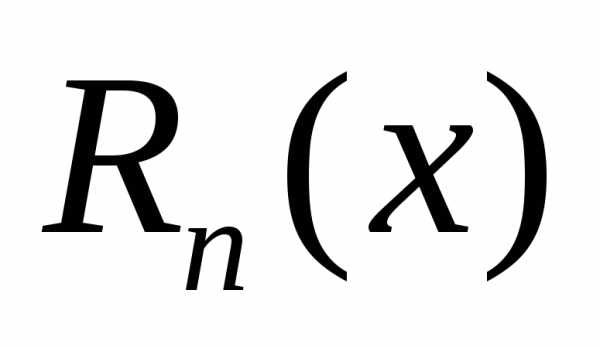 ,
отличная от формы Пеано и Лагранжа.
Кроме того, пользоваться разложением
,
отличная от формы Пеано и Лагранжа.
Кроме того, пользоваться разложением 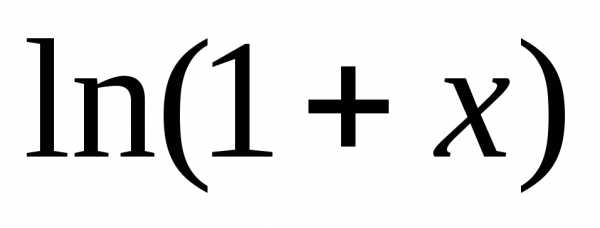
 : только для
таких значений.
: только для
таких значений.V. .
Поскольку
то
Формула Маклорена для этой функции имеет вид:
Здесь для остаточного
члена имеем: Как и в случае
логарифмической функции для оценки  требуется форма, отличная от Пеано и
Лагранжа. Более подробно об этом мы
будем говорить в третьем семестре в
теме «Степенные ряды». Отметим только,
что написанным разложением в приближённых
вычислениях можно пользоваться лишь
для .
требуется форма, отличная от Пеано и
Лагранжа. Более подробно об этом мы
будем говорить в третьем семестре в
теме «Степенные ряды». Отметим только,
что написанным разложением в приближённых
вычислениях можно пользоваться лишь
для .
VI.
Другие функции. Пользуясь известными разложениями,
можно, не вычисляя производных,
непосредственно писать разложения с
остаточным членом в форме Пеано и для
более сложных функций. При этом все
степени х,
до назначенной включительно, учитываем
точно, а более высокие степени будем
сразу включать в 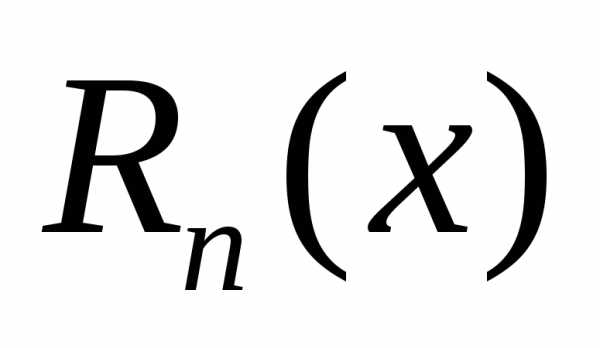 (не выписывая их).
(не выписывая их).
Пример
1. Написать
разложении функции до 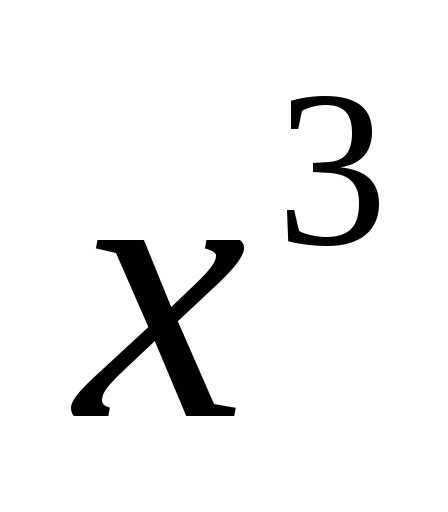 .
.
В силу I имеем:
где остаточный член
, так как . Далее, в силу II имеем: . Таким образом
После упрощения получим искомое разложение
Пример
2. Написать
разложение функции
до члена с 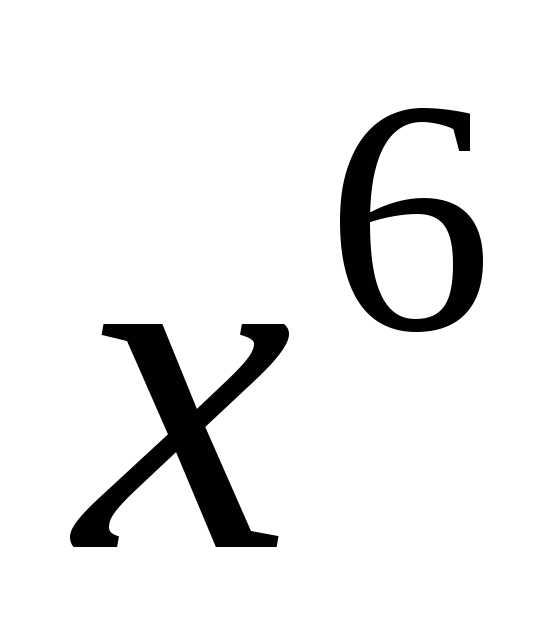 .
.
Согласно IV,
.
Необходимое
разложение для  (см. III)
выпишем в нескольких вариантах:
(см. III)
выпишем в нескольких вариантах:
.
Учитывая, кроме всего, и ~–0,5х2, х→ 0, получим:
После приведения подобных членов будем иметь:
.
§5. Приложения формулы Маклорена
I Вычисление пределов
В §11 темы «Введение
в математический анализ» были приведены
т.н. асимптотические формулы (ещё говорят
«асимптотические оценки») такие, как:
(при 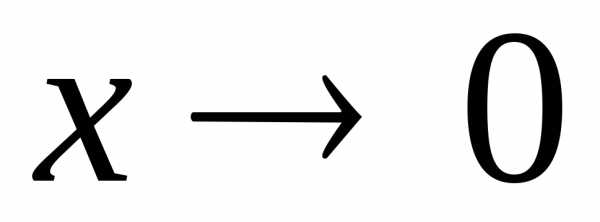 )
и т.п. Фактически они являются частными
случаями формул Маклорена для
соответствующих функций. Для вычисления
простых пределов тех формул было
достаточно. Однако, при работе со сложными
пределами требуются формулы Маклорена
более высокого порядка. Например, предел
)
и т.п. Фактически они являются частными
случаями формул Маклорена для
соответствующих функций. Для вычисления
простых пределов тех формул было
достаточно. Однако, при работе со сложными
пределами требуются формулы Маклорена
более высокого порядка. Например, предел
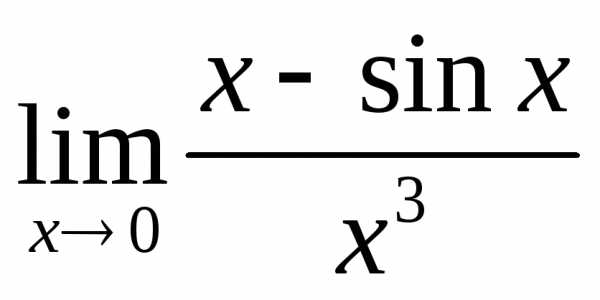
при помощи формулы вычислить невозможно, ибо
Если же возьмём
для 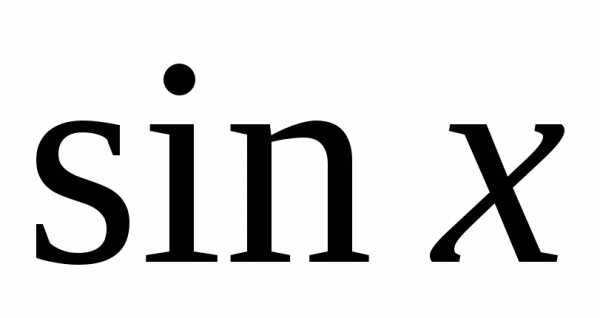 формулу Маклорена
третьего порядка ,
легко получим
формулу Маклорена
третьего порядка ,
легко получим
Рассмотрим более сложные примеры.
Пример 1. Вычислить предел
Для вычисления используем такие формулы:
, где
Имеем:
.
Пример 2. Часто студенты считают, что при
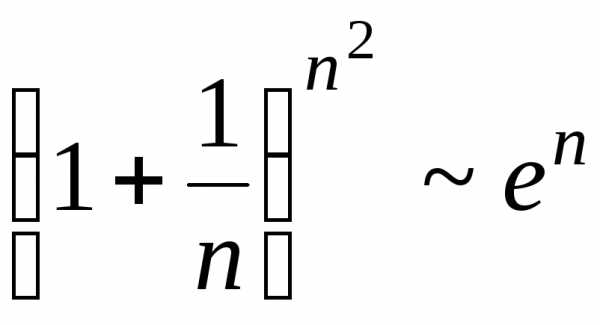
Докажем по определению, что это не так.
Действительно,
Вычислим отдельно
предел показателя степени, используя
формулу Маклорена с  при:
при:
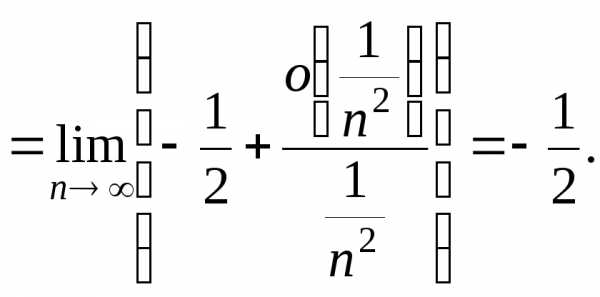
Используя
непрерывность показательной функции,
можем записать:  .
Полученный
предел отличен от 1, это и означает, что
предполагаемая эквивалентность неверна.
.
Полученный
предел отличен от 1, это и означает, что
предполагаемая эквивалентность неверна.
studfiles.net
Применение формул Тейлора и Маклорена
4.f (x)= ln(1 + x).
f (0)= ln1 = 0 . Поскольку |
|
| (n) |
|
|
|
|
|
|
|
|
|
|
|
|
| n−1 (n −1)! |
|
|
|
|
|
| (n) |
|
|
| n−1 |
|
| |||||||||||||||||||||
f |
|
|
|
| (x)= (− | 1) |
|
|
|
|
|
| , то f |
| (0)= (−1) | (n −1)! . Тогда | |||||||||||||||||||||||||||||||||||
|
|
|
| (x +1)n+1 |
| ||||||||||||||||||||||||||||||||||||||||||||||
формулу Маклорена для функции f (x)= ln(1 + x) можно записать в виде |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
| ln(x +1)= x − | 1! |
| x2 + | 2! | x3 |
|
|
| − | 3! |
|
| x4 +… + (−1)n−1 |
| (n −1)! | xn | + ϑ(xn ), или | |||||||||||||||||||||||||||||||||
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| 3! |
|
|
|
|
|
|
|
| 4 ! |
|
|
|
|
|
|
|
|
|
|
|
|
| n! |
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
| ln(x +1)= x − | x2 |
| + |
| x3 | − |
| x4 |
| −… +(−1)n−1 | xn | + ϑ(xn ). |
|
| |||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
|
| |||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
Пример 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Представьте функцию | f (x)= e−x2 |
|
| формулой Маклорена. |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Формула |
| Маклорена |
|
|
|
|
|
|
| для |
|
|
| функции |
|
|
|
| f (x)= ex | имеет | вид | ||||||||||||||||||||||||||||||
ex =1 + | x | + | x2 | + | x3 | +… + | xn | + ϑ(xn ). | Чтобы получить формулу Маклорена для заданной | ||||||||||||||||||||||||||||||||||||||||||
| 2! |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
1! | 3! |
|
|
|
|
| n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
функции, нужно x заменить на − x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||
|
|
|
|
|
|
|
| 2 |
|
|
|
| x2 |
|
|
|
|
| x4 |
|
|
|
|
|
| x6 |
|
|
| x2n |
|
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
| e−x |
|
|
| =1 − |
|
|
|
|
| + |
|
|
|
|
| − |
|
|
| +… + (−1)n |
|
| + ϑ(x2n ). |
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 1! |
|
|
|
| 2! |
| 3! |
| n! |
|
|
| ||||||||||||||||||||||||||||
Пример 2 |
|
|
|
|
|
|
|
| f (x)= ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
Представьте функцию | формулой Тейлора в точке x0 =1. |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x =1 + y и ln x = ln(1 + y). |
|
| ln(1 + y) | ||||||||||||||||||
Сделаем | замену | y = x −1, | тогда | Функцию | |||||||||||||||||||||||||||||||||||||||||||||||
представим формулой Маклорена. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| + ϑ(xn ). |
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
| ln(y +1)= y − | y 2 |
| + | y3 |
| − | y 4 |
| +… + (−1)n−1 | y n |
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
| 3 |
|
|
| 4 |
|
|
|
|
|
|
|
|
| n |
|
|
|
|
|
| |||||||||
Заменяя в | последней |
| формуле |
|
| y = x −1 , | получим |
| формулу Тейлора | для | функции | ||||||||||||||||||||||||||||||||||||||||
f (x)= ln x | в точке x0 =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
ln x = (x −1)− (x −21)2 + (x −31)3 − (x −41)4 +… + (−1)n−1 (x −n1)n + ϑ(xn ).
Пример 1 |
|
|
|
Вычислить предел, используя формулу Маклорена |
| ||
lim | e−x2 | −sin(x2 )− cos 2x | . |
| x3 sin x | ||
x→0 |
|
| |
Решение
Представим следующие функции формулой Маклорена
e−x2 =1 − | x2 | + | x4 |
| − | x6 | +ϑ(x6 ), | |||
|
|
|
|
| ||||||
1! | 2! |
|
|
| 3! |
| ||||
sin x = x − | x3 | + | x5 | + ϑ(x5 ), | ||||||
|
| |||||||||
|
| 3! |
| 5! |
|
| ||||
|
| 36 |
|
|
|
|
| |||
studfiles.net
Формула Маклорена для основных элементарных функций
lim Rn (x)= lim (f (x)−Tn (x))= f (x0 )−Tn (x0 )= 0 . | |
x→x0 | x→x0 |
ЗАМЕЧАНИЕ 1
Можно доказать, что остаточный член Rn (x) при x → x0 является бесконечно малой более высокого порядка, чем (x − x0 )n . Это записывается в следующем виде:
Rn (x)= ϑ((x − x0 )n ). Подобная форма записи остаточного члена формулы Тейлора называется остаточным членом в форме Пеано.
Используя форму Пеано для остаточного члена, можно записать формулу Тейлора в следующем виде.
f (x)= f (x0 )+ |
| f ‘(x0 ) | (x − x0 )+ | f »(x0 ) | (x − x0 )2 +… … + | f ‘(n)(x0 ) | (x − x0 )n +ϑ((x − x0 )n ). | |||||||
| 1! | 2! |
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
| n! | ||||
Определение 2 | f (x) | n раз дифференцируема в некоторой окрестности Uδ(0) точки | ||||||||||||
Пусть функция | ||||||||||||||
x = 0 . Формула |
|
| f ‘(0) |
|
| f »(0) |
| f (n)(0) | xn +ϑ(xn ), | |||||
f (x)= f | (0)+ |
| x + | x2 +… + | ||||||||||
|
|
| ||||||||||||
|
|
| 1! |
| 2! |
| n! | |||||||
называется формулой Маклорена.
ЗАМЕЧАНИЕ 2
Из определения ясно, что формула Маклорена получится из формулы Тейлора, если положить x0 = 0 .
ЗАМЕЧАНИЕ 3 |
|
|
|
|
|
|
|
|
| ||
Можно |
|
| доказать, | что | остаточный член | формулы | Тейлора имеет | вид: | |||
|
| f | (n+1)(θ) |
| n+1 |
|
|
|
| ||
R (x) | = |
|
|
| (x − x ) | , где x < θ < x . | Такая форма | записи остаточного | члена | ||
(n +1)! | |||||||||||
n |
|
| 0 | 0 |
|
|
| ||||
|
|
|
|
|
|
|
| ||||
называется остаточным членом в форме Лагранжа.
1. | f (x)= ex . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| ′ |
|
| (n) |
| x |
| x x2 x3 |
| xn | n |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| = f |
| (0)=1 , то e |
| =1 + 1! + 2! + 3! +… + n! + ϑ(x |
| ). | |||||||||||
| Поскольку f (0)= f (0)=… |
|
|
| ||||||||||||||
2. | f (x)= sin x . f (0)= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Так как (sin x)(n) = sin(x + | πn | ), | то все производные четного порядка в точке | x0 равны | |||||||||||||
| 2 | |||||||||||||||||
нулю, а производные нечетного порядка равны ±1 , причем знаки чередуются. Поскольку
′ | ′ |
|
|
|
|
|
|
|
|
|
| |||
(sin x) | =1 > 0 , то есть перед первым членом в формуле знак +. | |||||||||||||
= cos x , то f (0)= cos 0 | ||||||||||||||
Учитывая все это формулу Маклорена для заданной функции можно записать в виде: | ||||||||||||||
|
| x | x3 | x5 |
|
| x2n−1 | |||||||
| sin x = |
| − |
| + |
| −… + (− | 1)n+1 |
|
| + ϑ(x2n−1 ); | |||
| 1! | 3! | 5! | (2n −1)! | ||||||||||
3. f (x)= cos x |
|
|
|
|
| ), |
|
|
|
| ||||
f (0)=1. Поскольку (cos x)(n) = cos(x + | πn | то | f (2n+1)(0)= 0 , f (2n)(0)= ±1 для любых | |||||||||||
| ||||||||||||||
|
|
|
|
|
| 2 |
|
|
|
|
| |||
значений n . При этом вторая производная f | ′′ |
|
|
| ||||||||||
(0)= −cos0 = −1 . Значит, все производные | ||||||||||||||
порядка 2n равны –1, а все производные порядка 4n равны 1. Формула Маклорена для функции f (x)= cos x имеет вид:
| x2 | x4 | x6 |
| x2n | |||
cos x =1 − |
| + |
| − |
| +… + (−1)n |
| + ϑ(x2n ). |
2! | 4! | 6! | (2n)! | |||||
|
|
|
|
|
| 35 |
|
|
studfiles.net
Тема формулы тейлора и маклорена
Лекция 15
§1. Формула Тейлора для многочлена. Бином Ньютона
Напомним формулу для вычисления производных (любого порядка) степенной функции с натуральным показателем степени:
С помощью этой формулы установим связь между коэффициентами многочлена пой степени
(1)
и производными самого многочлена в нуле. Запишем многочлен в виде
Первое слагаемое
правой части после k–кратного
дифференцирования обратится в ноль, а
второе – в 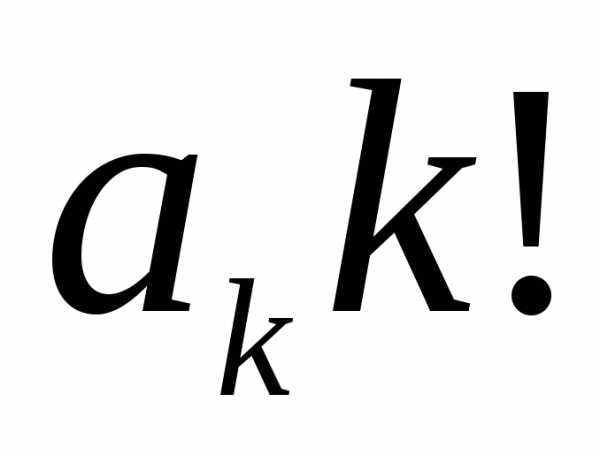 .
Для третьего слагаемого имеем:
.
Для третьего слагаемого имеем:
В этой сумме все
показатели степени  .
Чтобы эта сумма обратилась в ноль,
достаточно положить
.
Чтобы эта сумма обратилась в ноль,
достаточно положить  Итак, получим связь:
Итак, получим связь:
Отсюда вытекает формула, выражающая коэффициенты многочлена через производные самого многочлена:
(2)
Теперь многочлен (1) можно записать в форме
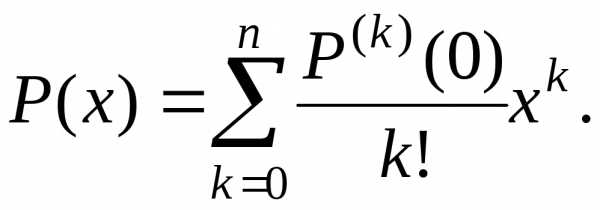
Напомним, что производная нулевого порядка – это сама функция.
Иногда
требуется многочлен (1) записать не по
степеням
,
а по степеням двучленаНетрудно убедиться, что в этом случае
коэффициенты вычисляются по формуле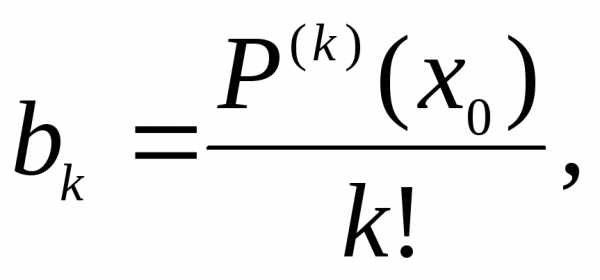 а сам многочлен можно записать в виде
а сам многочлен можно записать в виде
Это и есть формула Тейлора для многочлена.
Из формулы (2) для коэффициентов многочлена (1) можно вывести два важных следствия.
Следствие 1. Рассмотрим два многочлена
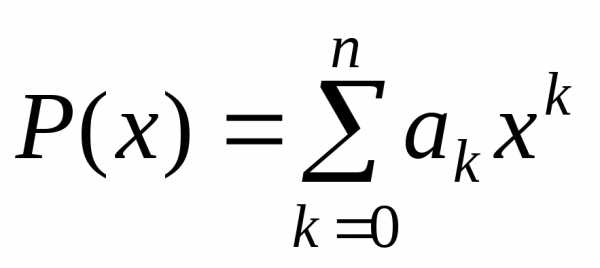 и
и 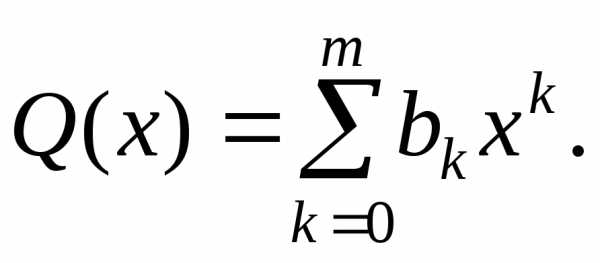
Если
то иоткуда получим: а) степени многочленов
равные –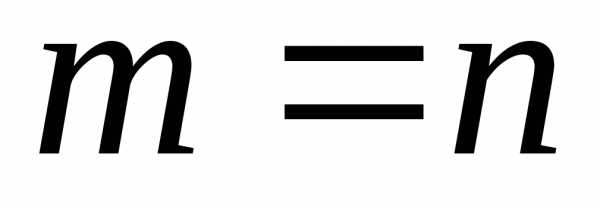 ;
б) коэффициенты при одинаковых степенях
переменной равные –
;
б) коэффициенты при одинаковых степенях
переменной равные –
Следствие
2. Рассмотрим
многочлен, представляющий собой  степень бинома
степень бинома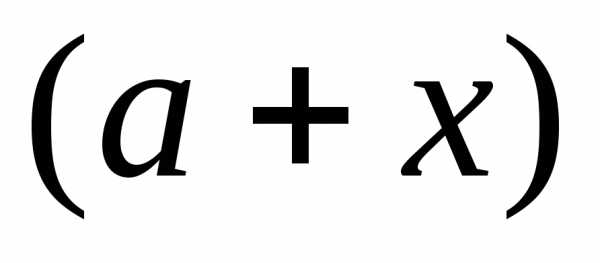 и запишем его в стандартной форме (1):
и запишем его в стандартной форме (1):
Коэффициенты вычислим по формуле (2):
Итак, мы получили т.н. формулу бинома Ньютона:
Числа обозначают 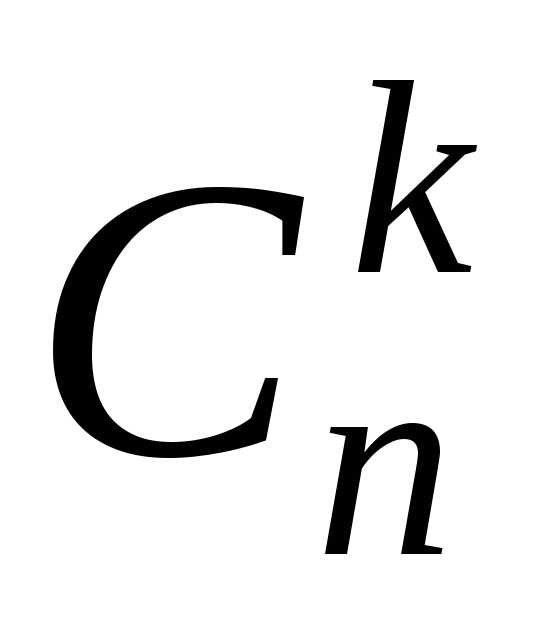 и называют
биномиальными коэффициентами. Так как
и называют
биномиальными коэффициентами. Так как 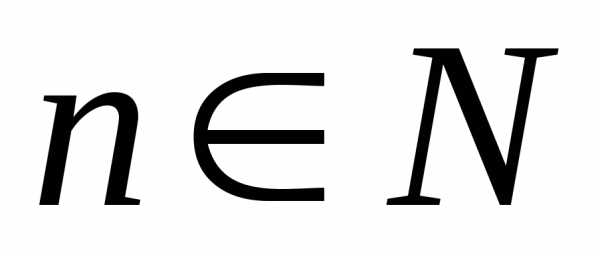 ,
можно использовать компактную запись
этих чисел:
,
можно использовать компактную запись
этих чисел:
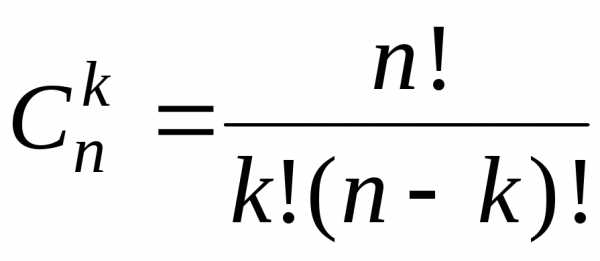
Это число возникают
в задачах комбинаторики, где они
называются «числом сочетаний из 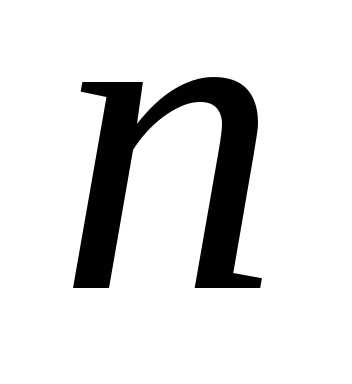 по
по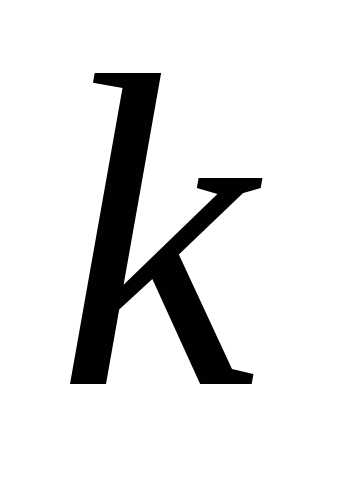 »
и дают ответ на вопрос: «Сколькими
способами можно выбрать
»
и дают ответ на вопрос: «Сколькими
способами можно выбрать предметов из
предметов из предметов, если не важен порядок выбора?»
предметов, если не важен порядок выбора?»
Пример. Запишем многочлен
по степеням .
В соответствии с формулой Тейлора имеем:
.
В соответствии с формулой Тейлора имеем:
Здесь:
Итак,
§2. Формула Тейлора для произвольной функции
I Определения
Рассмотрим
функцию 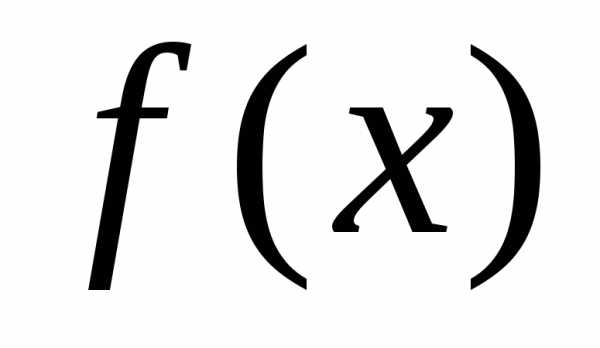 ,
которая имеет в точке
,
которая имеет в точке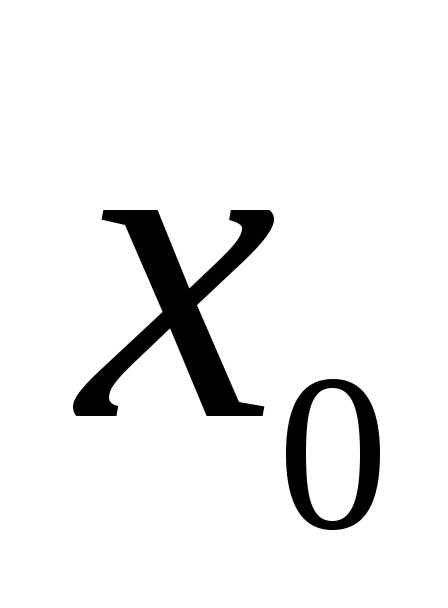 производные всех порядков доп-го
включительно. Составим для этой функции
многочлен
.(1)
производные всех порядков доп-го
включительно. Составим для этой функции
многочлен
.(1)
Из результатов
предыдущего параграфа следует, что
коэффициент при 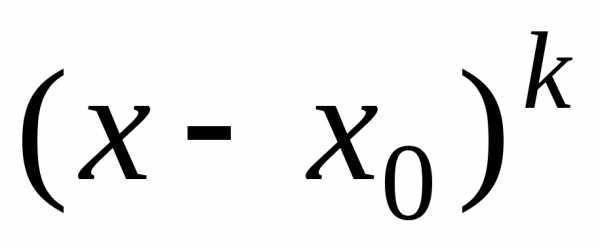 ,
т.е.
,
т.е. 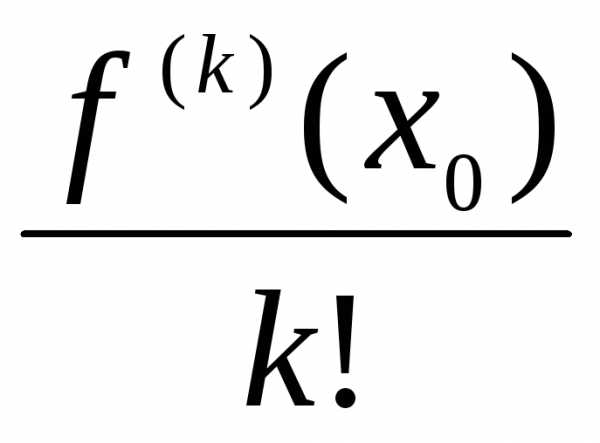 ,
должен равняться
,
должен равняться  .
Таким образом, многочлен (1) удовлетворяет
соотношениям:
.
Таким образом, многочлен (1) удовлетворяет
соотношениям:
Поскольку функция  не многочлен, то уже нельзя ожидать
равенства.
Однако, из-за совпадения производных
естественно ожидать, что.
Поэтому особый интерес приобретает
изучение разности
не многочлен, то уже нельзя ожидать
равенства.
Однако, из-за совпадения производных
естественно ожидать, что.
Поэтому особый интерес приобретает
изучение разности
Для производных этой функции справедливы соотношения:
(2)
Для последнего,
очевидно, требуется, чтобы у функции 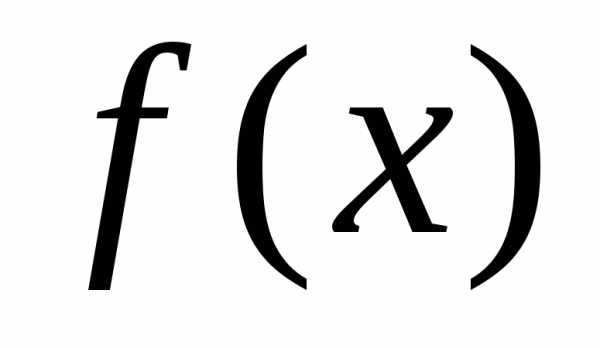 существовала производная
существовала производная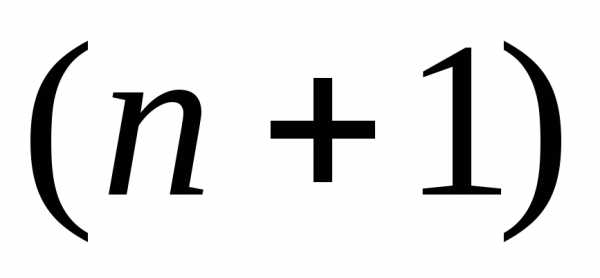 -го
порядка.
-го
порядка.
Принята следующая терминология:
1) многочлен
(1):
– многочлен Тейлора порядка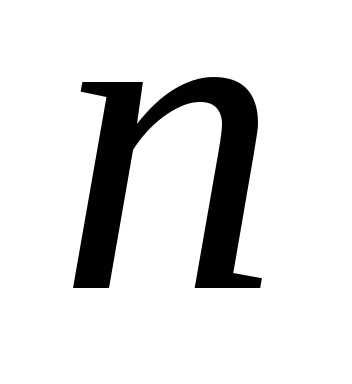 для функции
для функции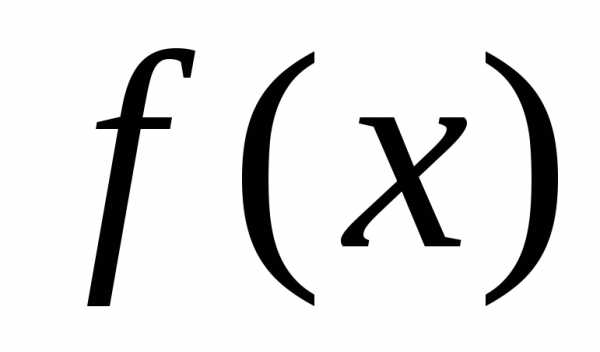 ;
;
2) формула
– формулаТейлора
порядка 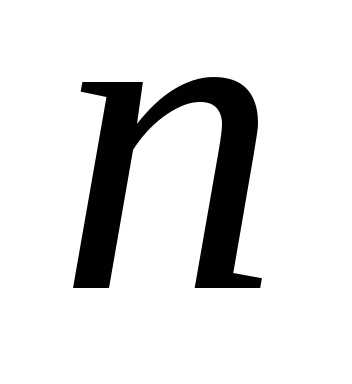 для функции
для функции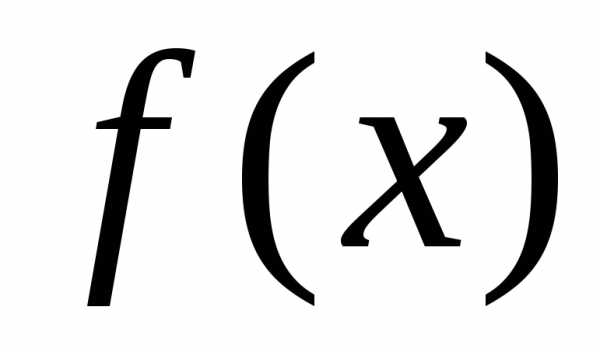 или разложение по формуле Тейлора
функции
или разложение по формуле Тейлора
функции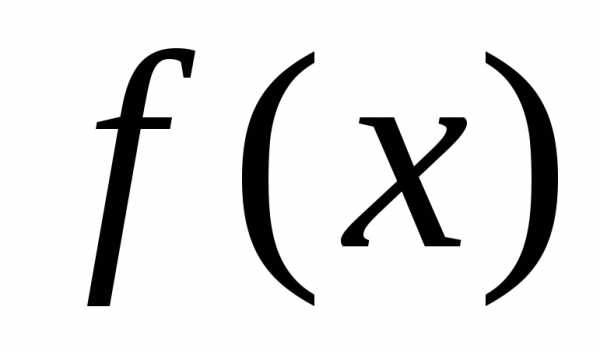 ;
;
3) разность – остаточный член формулы Тейлора. Для разных целей имеются различные формы остаточного члена. Формулы Тейлора и различают по этим формам. Мы рассмотрим лишь 2 формы остаточного члена.
studfiles.net
4.5 Ряды Тейлора и Маклорена
Формула Тейлора.
Наиболее простой функцией среди элементарных является многочлен. Он легко дифференцируется и интегрируется. Значения многочлена вычисляются так же значительно легче, чем других функций. В связи с этим встает вопрос, нельзя ли другие, более сложные функции заменить многочленами, не допуская при этом больших погрешностей. Этот вопрос положительно решен по отношению к некоторым функциям с помощью, так называемой формулы Тейлора.
Предположим, что функция f(x)имеет все производные до(n+1)-го порядка включительно, в некотором промежутке, содержащем точкух=а.
Найдем многочлен 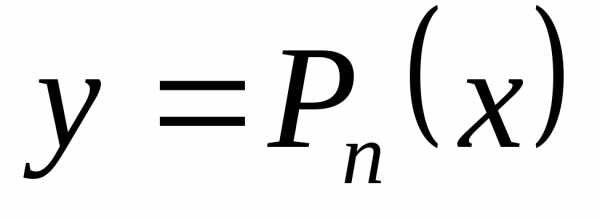 степени не вышеn,
значение которого в точкех=аравняется значению функцииf(x)в этой точке, а значения его производных
доn-го порядка в точкех=аравняются значениям соответствующих
производных от функцииf(x)в этой точке, т.е. удовлетворяют условиям:
степени не вышеn,
значение которого в точкех=аравняется значению функцииf(x)в этой точке, а значения его производных
доn-го порядка в точкех=аравняются значениям соответствующих
производных от функцииf(x)в этой точке, т.е. удовлетворяют условиям:
(4.5.1)
Будем искать этот многочлен в виде
(4.5.2)
Задача – определить коэффициенты .
Продифференцируем
многочлен  nраз
nраз
Подставим в формулу (4.5.2) и формулы (4.5.3) значение х=а, получим, используя условие (4.5.1)
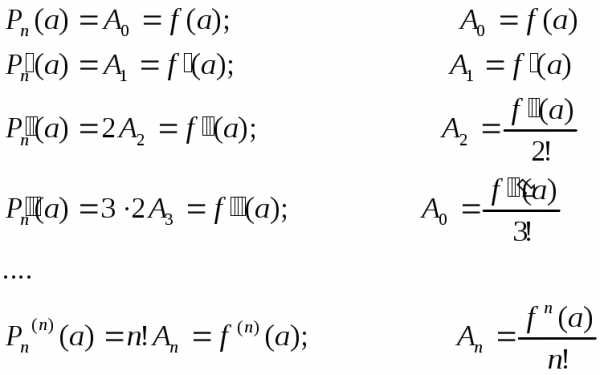
Получим искомый полином
Обозначим разность
значений данной функции 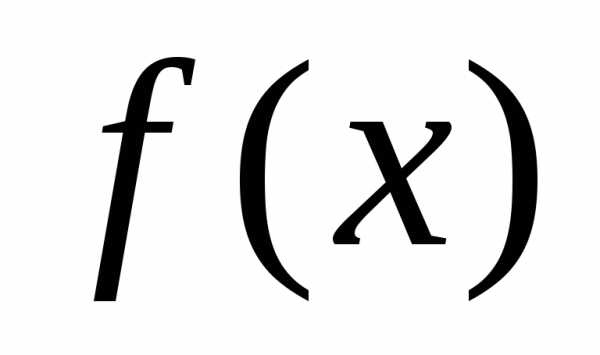 и построенного многочлена
и построенного многочлена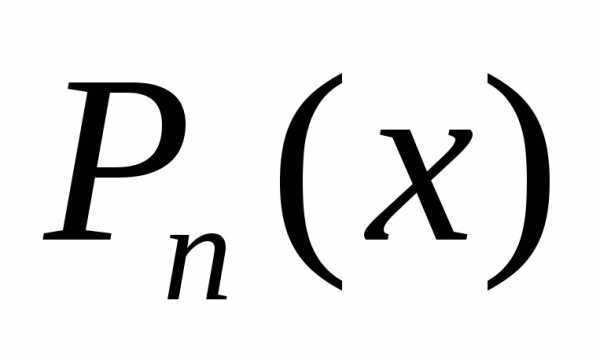 ,
т.е..
,
т.е..
Получаем или
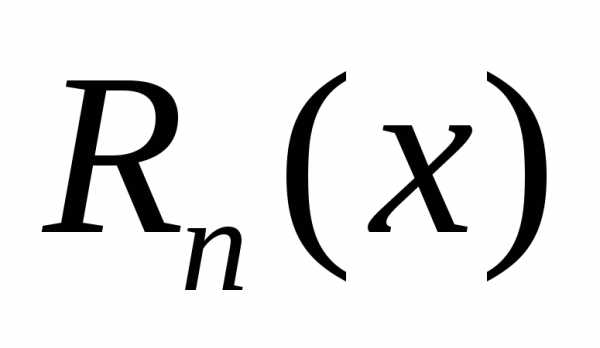 — ошибка, которую
допускаем, заменяя данную функцию
— ошибка, которую
допускаем, заменяя данную функцию 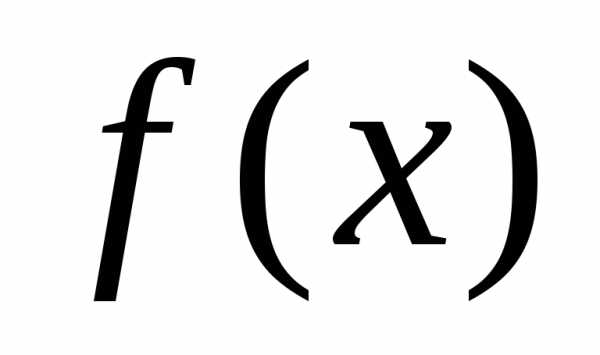 многочленом.
многочленом.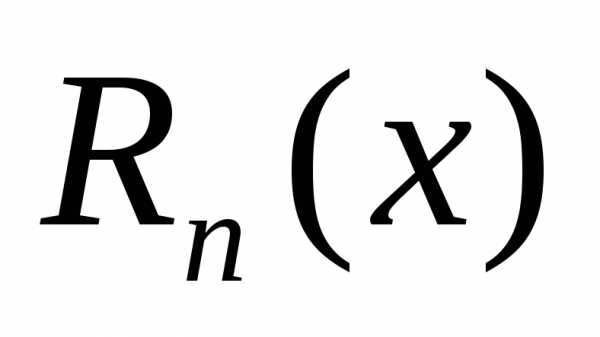 называетсяостаточным членом. Для
тех значенийх, при которых величина
называетсяостаточным членом. Для
тех значенийх, при которых величина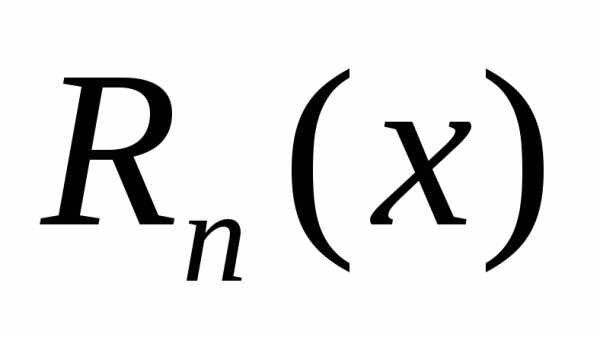 мала по сравнению с величиной
мала по сравнению с величиной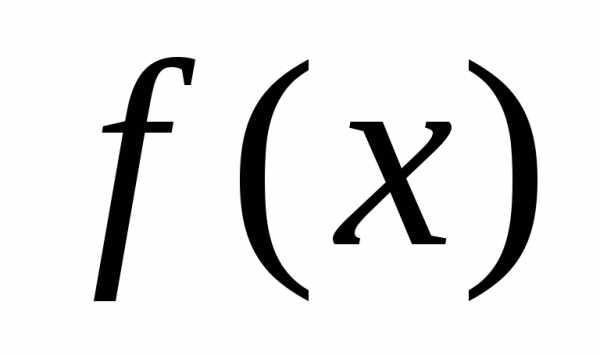 ,
многочлен дает удовлетворительное
“сближение” значений
,
многочлен дает удовлетворительное
“сближение” значений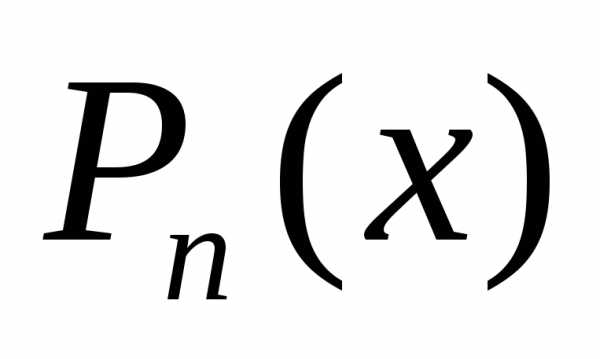 и
и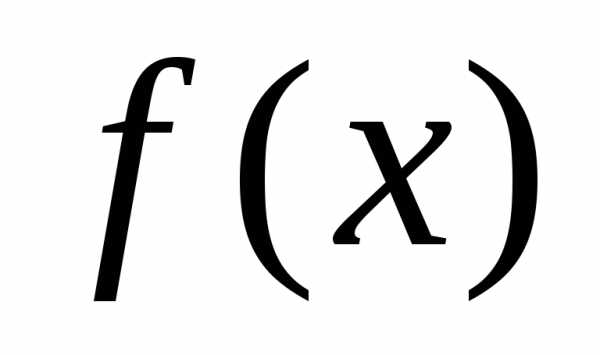 .
Т.о., имеется возможность заменить
функциюy=f(x) многочленом
.
Т.о., имеется возможность заменить
функциюy=f(x) многочленом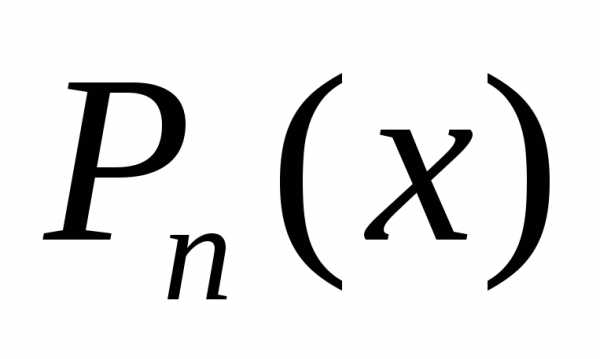 с соответствующей степенью точности,
равной значению остаточного члена
с соответствующей степенью точности,
равной значению остаточного члена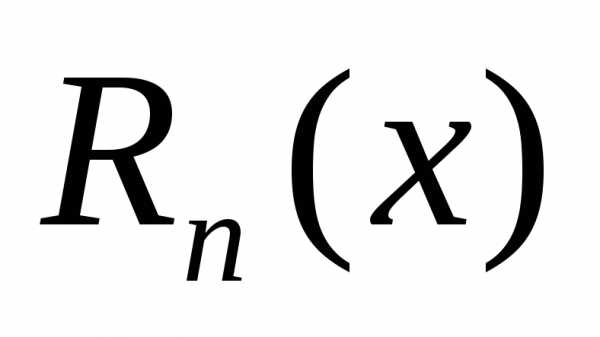 .
.
В полном курсе математического анализа доказывается, что остаточный член можно записать в форме Лагранжа:
В итоге получаем формулу Тейлора для функции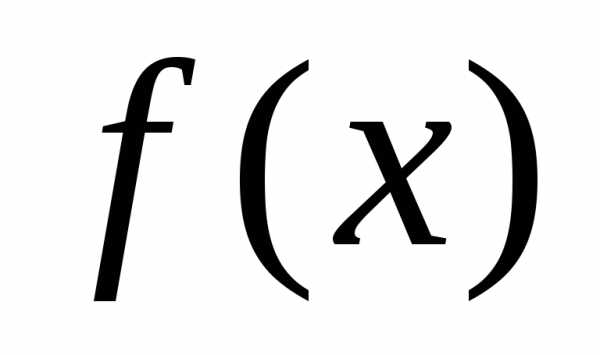
Если в формуле Тейлора положить a=0,то получаем частный случай формулы Тейлора –формулу Маклорена:
Обе формулы представляют собой степенные ряды, которые называются рядом Тейлора и рядом Маклорена.
Ряд Тейлора можно
формально построить для любой бесконечно
дифференцируемой функции в окрестности
точки а,но отсюда ещё не следует,
что он будет сходиться к данной функции.
Ряд может оказаться расходящимся или
сходящимся, но не к функции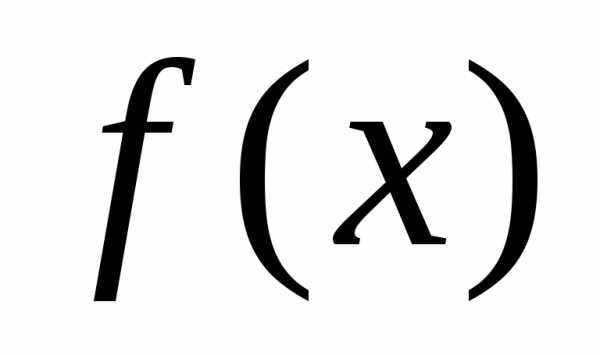 .
.
Теорема 1.Для
того чтобы ряд Тейлора, функции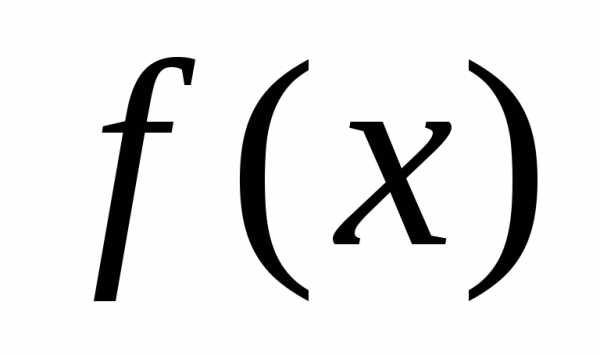 ,
сходился к самой функции в точкех,необходимо и достаточно, чтобы в этой
точке остаточный член формулы Тейлора
стремился к нулю при,
т.е. чтобы
,
сходился к самой функции в точкех,необходимо и достаточно, чтобы в этой
точке остаточный член формулы Тейлора
стремился к нулю при,
т.е. чтобы
На практике пользуются ещё одной теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.
Теорема 2.Если
модули всех производных функции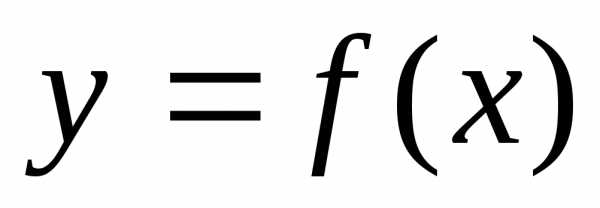 ограничены в окрестности точких=аодним и тем же числом
ограничены в окрестности точких=аодним и тем же числом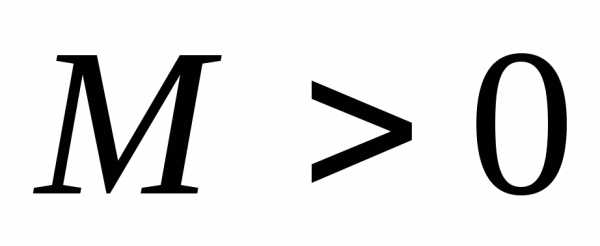 ,
то для любогох из этой окрестности
ряд Тейлора функции
,
то для любогох из этой окрестности
ряд Тейлора функции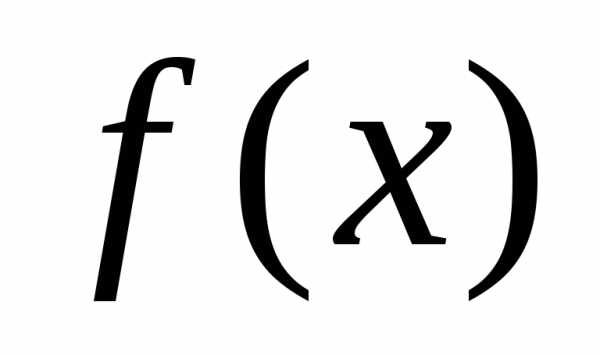 сходится к функции
сходится к функции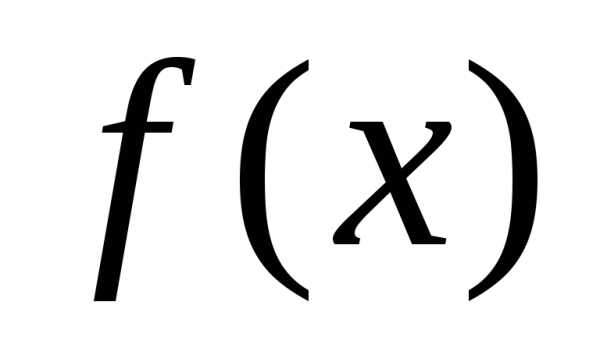 ,
т.е. имеет место разложение
,
т.е. имеет место разложение
4.6 Разложение некоторых элементарных функций в ряд Маклорена
Для разложения
функции 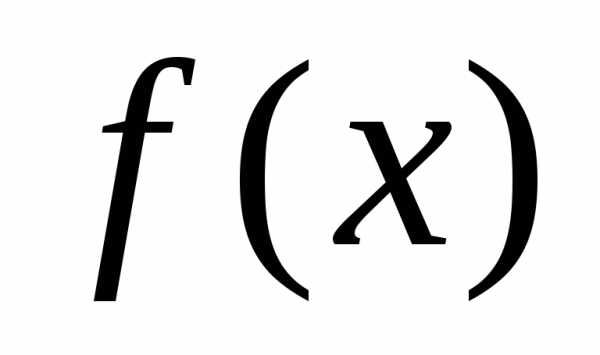 в ряд Маклорена
в ряд Маклорена
нужно:
найти производные
 ,
, и т.д.;
и т.д.;вычислить значение производных в точке х=0;
написать ряд для заданной функции, найти его интервал сходимости;
найти интервал, в котором остаточный член ряда Маклорена при. Если такой интервал существует, то в нем функция
 и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Выведем формулу
разложения в ряд Маклорена для функции 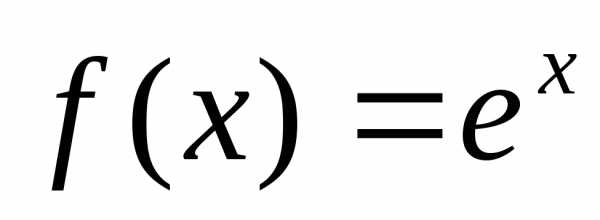 .
.
1)
2) при х=0
3)
4) Находим радиус сходимости
т.е. ряд сходится
в интервале 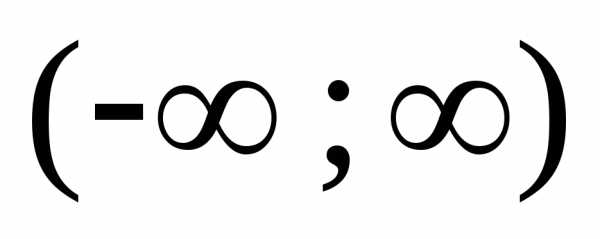
Для всех имеемт.е. все производные в этом интервале ограничены одним и тем же числом
 ,
следовательно, по теореме 2
,
следовательно, по теореме 2
Т.о.
Пример: вычислить число е, взяв первые пять членов ряда и оценить ошибку
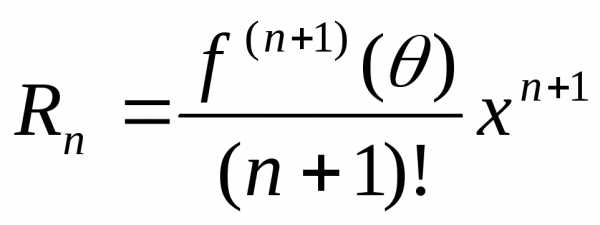
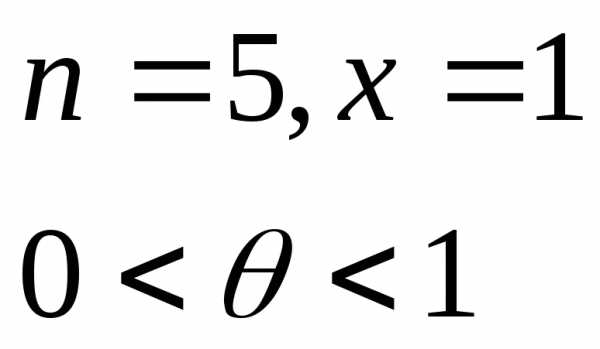
Пример: Вычислить 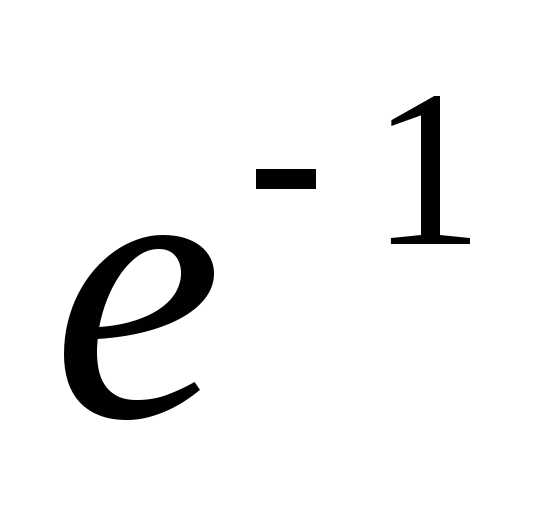 с
точностью 0,01.
с
точностью 0,01.
Четвертое слагаемое 0,0083 меньше 0,01, поэтому для заданной точности достаточно сложить первые четыре члена ряда.
— число, которое показывает калькулятор.
Разложение в ряд
Маклорена функции 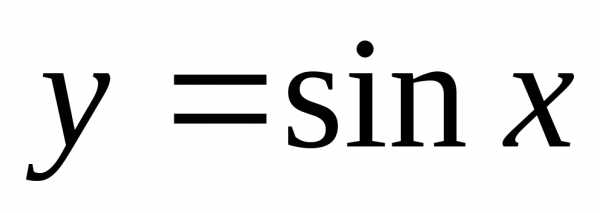 в точкех=0
в точкех=0
1)
2) значение функции и производных в нуле
3)
4) интервал сходимости
5) любая производная функции по модулю не превосходит 1
следовательно
Имеет место разложение
Разложение для функции .
Воспользуемся свойством 3 степенных рядов.
Продифференцируем
почленно ряд для 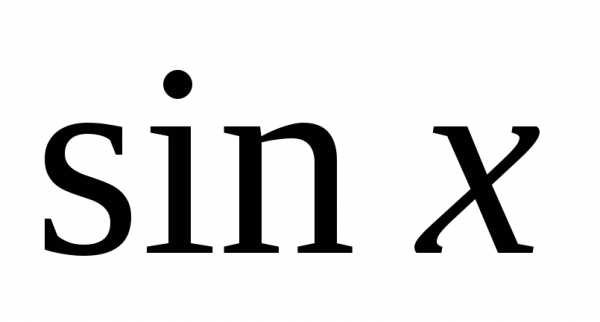 ,
получим
,
получим
Таблица разложения в ряд Маклорена некоторых элементарных функций.
1)
2)
3)
4)
(биноминальный ряд)
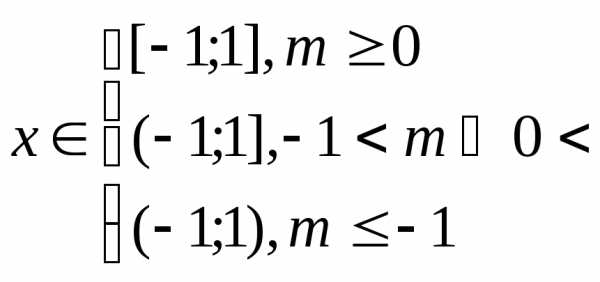
5)
6)
7)
8)
9)
10)
Примеры:
1) пользуясь
таблицей получить разложение для функции  .
Воспользуемся биноминальным рядом
.
Воспользуемся биноминальным рядом
2) написать ряд Маклорена для функции
Воспользовавшись
4-м свойством степенных рядов, проинтегрируем
ряд для функции  ,
получим:
,
получим:
Можно показать,
что ряд сходится и при 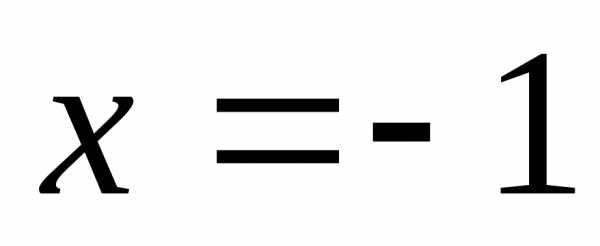 и
и 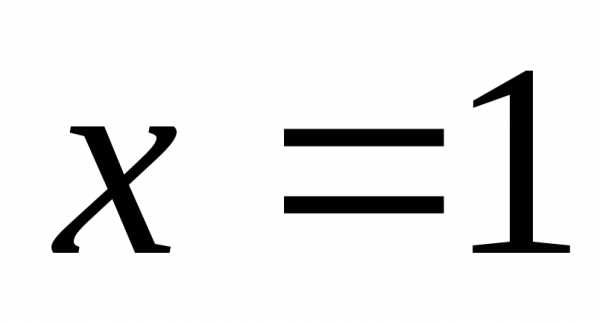
При 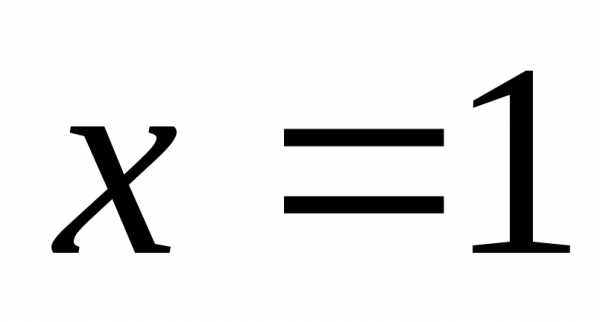
 — лейбницевский ряд, сходится.
— лейбницевский ряд, сходится.
При 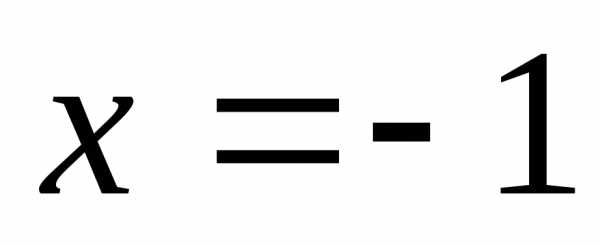
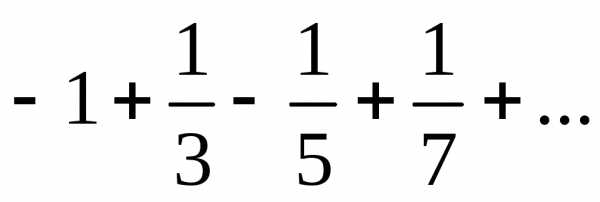 — лейбницевский ряд , сходится .
— лейбницевский ряд , сходится .
Таким образом ряд
для функции
сходится
для всех .
.
studfiles.net

 ,
, и т.д.;
и т.д.; и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.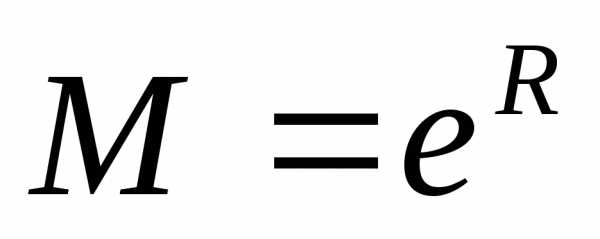 ,
следовательно, по теореме 2
,
следовательно, по теореме 2