Углы при параллельных прямых
Автор Сергей Валерьевич
Вторник, Ноябрь 24, 2015
Как известно, соответствующий раздел в школьном курсе геометрии изучается уже в 7 классе. Однако, для многих школьников этот материал оказывается трудным для запоминания. В результате на экзамене, будь то ЕГЭ или дополнительное вступительное испытание по математике в вузе, бедному сдающему приходится в муках вспоминать, что же он изучал по этой теме в далеком 7 классе. К сожалению, зачастую безуспешно. Решим эту проблему раз и навсегда! Ниже приведен основный справочный материал по данной важнейшей теме школьного курсе геометрии от репетитора по математике и физике.
Накрест лежащие прямые при параллельных прямых
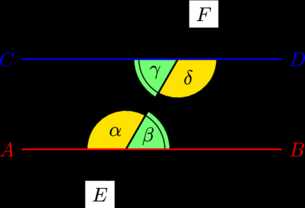
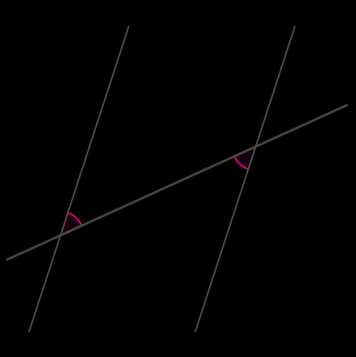
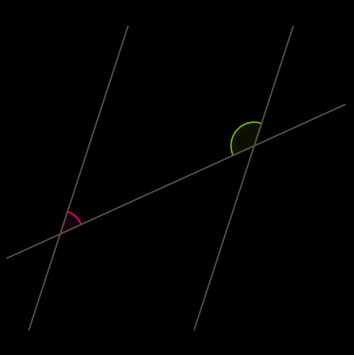
На рисунке углы и , а также и являются накрест лежащими при прямых , и секущей . Если прямая параллельна прямой , то и (свойство параллельных прямых). Верно и обратное. Если или , то прямая параллельна прямой (
Соответственные углы при параллельных прямых
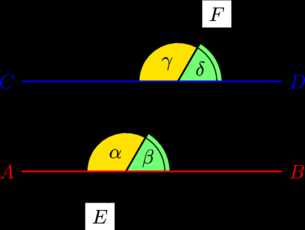
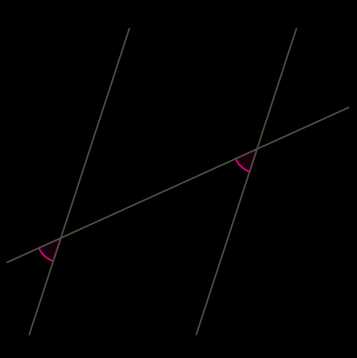
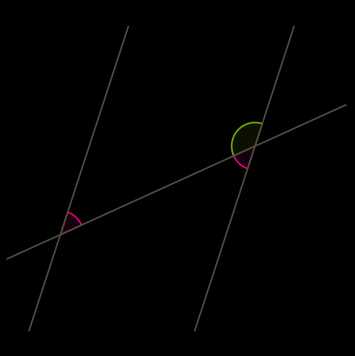
На рисунке углы и , а также и являются соответственными при прямых , и секущей . Если прямая параллельна прямой , то
yourtutor.info
1. Определение и доказательства признаков параллельности прямых в плоскости

Две прямые, лежащие на одной плоскости, либо имеют только одну общую точку, либо не имеют ни одной общей точки.
В первом случае говорят, что прямые пересекаются, во втором случае — прямые не пересекаются.
На плоскости две прямые \(a\) и \(b\), которые не пересекаются, называются параллельными и обозначаются a∥b.
Обрати внимание!
Если рассмотреть прямые, которые не лежат в одной плоскости, то возможна ситуация, что прямые не пересекаются, но они и не параллельны.
Один из признаков параллельности прямых на плоскости гласит:
1. признак. Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны.
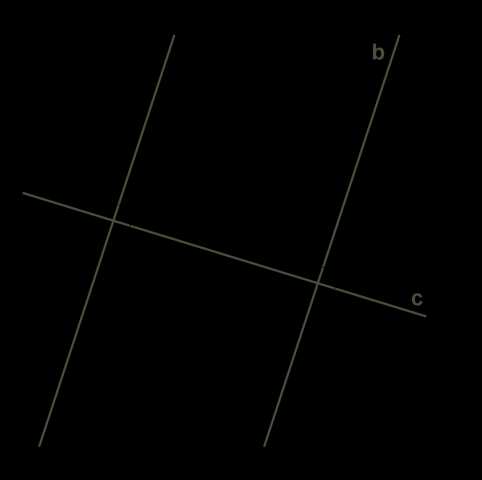
Этот признак легко доказать, если вспомнить, что к прямой в плоскости из любой точки можно провести только один перпендикуляр.
Допустим, что прямые, перпендикулярные одной и той же прямой, не параллельны, то есть имеют общую точку.
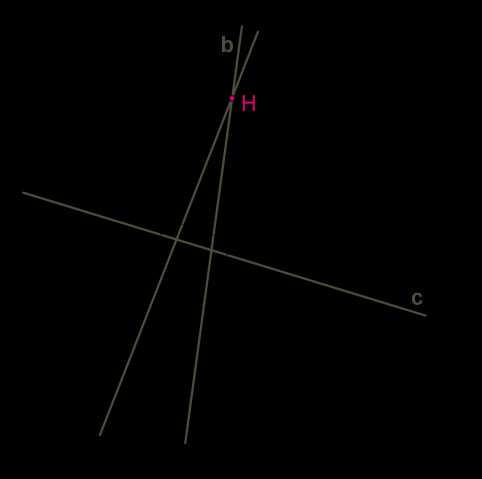
Получается противоречие — из одной точки \(H\) к прямой \(c\) проведены два перпендикуляра. Такое невозможно, поэтому две прямые на плоскости, перпендикулярные одной и той же прямой, параллельны.
Для рассмотрения других признаков надо ознакомиться с некоторыми видами углов:
1) вспомним, что нам известны названия и свойства углов, которые образуют две пересекающиеся прямые.
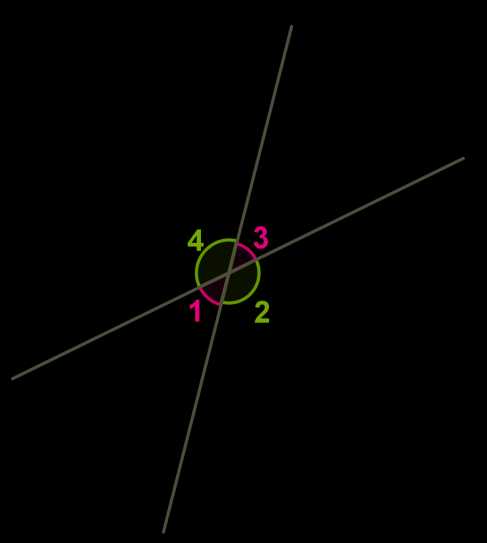
Вертикальные углы равны: ∡1=∡3;∡2=∡4.
Сумма смежных углов 1800:∡1+∡2=∡2+∡3=∡3+∡4=∡4+∡1=1800.
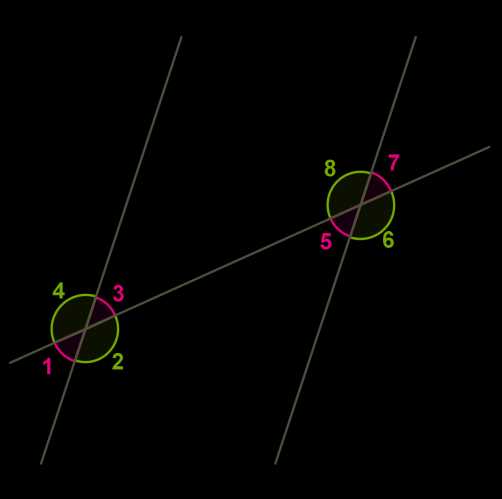
2) Если две прямые пересекает третья прямая, то углы называются так:
накрест лежащие углы: ∡3 и ∡5;∡2 и ∡8;
соответственные углы: ∡1 и ∡5;∡4 и ∡8;∡2 и ∡6;∡3 и ∡7;
односторонние углы: ∡3и∡8;∡2и∡5.
Эти углы помогут определить параллельность прямых \(a\) и \(b\). Итак, другой признак параллельности прямых на плоскости гласит:
2. признак. Если при пересечении двух прямых третьей секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна \(180°\) — то прямые параллельны.
Докажем этот признак.
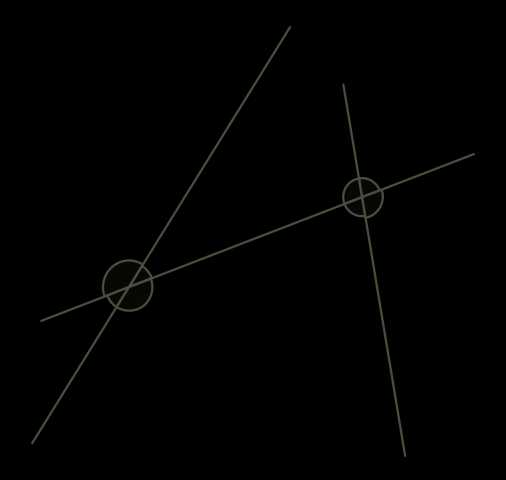
Сначала докажем: если прямые \(a\) и \(b\) пересекает прямая \(c\), и накрест лежащие углы равны, то прямые \(a\) и \(b\) параллельны.
Например, если ∡3=∡5, то a∥b.
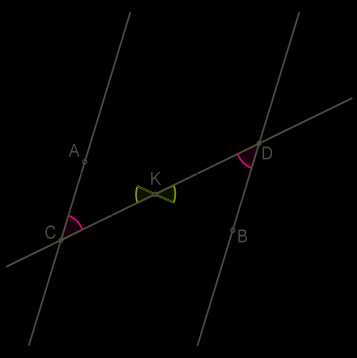
1) Отметим точки \(C\) и \(D\), в которых прямые \(a\) и \(b\) пересекает прямая \(c\). Через серединную точку \(K\) этого отрезка проведём перпендикуляр \(AB\) к прямой \(a\).
2) ∡CKA \(=\) ∡DKB как вертикальные углы, ∡3 \(=\) ∡5 \(=\) α, \(CK = KD\) — значит, ΔCKA \(=\) ΔDKB по признаку о стороне и двум прилежащим к ней углам.
3) Очевидно, если ΔCKA прямоугольный, то и ΔDKB прямоугольный, и \(AB\) перпендикулярен к прямой \(b\).
4) Согласно первому доказанному признаку прямые, перпендикулярные одной и той же прямой, параллельны.
5) В случае, когда равны соответственные углы, имеем в виду, что вертикальные углы равны, и доказываем, как в пунктах 1) — 4).
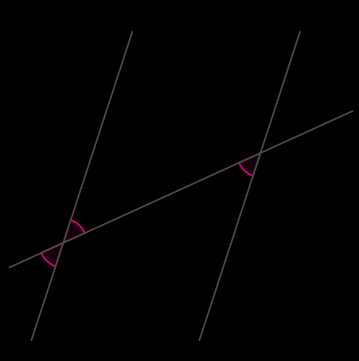
6) В случае, когда сумма односторонних углов равна 180°, имеем в виду, что сумма смежных углов тоже равна \(180°\), и используем в доказательстве пункты 1) — 4).
3. Признак параллельных прямых действует и как свойство параллельных прямых.
При пересечении двух параллельных прямых третьей секущей:
— накрест лежащие углы равны,
— соответственные углы равны,
— сумма односторонних углов равна \(180°\).
О других свойствах параллельных прямых — в следующем пункте теории.
www.yaklass.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.
Углы, образующиеся при пересечении двух прямых третьей прямой
Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Замечание. Два отрезка называются параллельными, если они лежат на параллельных прямых.
Признаки параллельности двух прямых
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180° |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° |
Следствие
| Рисунок | Признак параллельности |
| Две прямые, перпендикулярные к третьей прямой, параллельны |
Признак параллельности: Две прямые, перпендикулярные к третьей прямой, параллельны |
Переход свойства параллельности прямых
| Рисунок | Признак параллельности |
| Если прямая a параллельна прямой b, а прямая b параллельна прямой c, то прямая a параллельна прямой c |
Признак параллельности: Если прямая a параллельна прямой b, |
Задача. Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
Решение. Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Признаки параллельности прямых | Треугольники
Признаки параллельности прямых:
1) Если внутренние накрест лежащие углы равны, то прямые параллельны.
2) Если соответственные углы равны, то прямые параллельны.
3) Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.
4) Если две прямые параллельны третьей прямой, то они параллельны между собой.
5) Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.
Виды углов
www.treugolniki.ru
