1, 2, 3, 4 степень с примерами
Раковая опухоль — это новообразование злокачественного характера, которое постоянно размножается и быстро растет, выделяя при этом большое количество продуктов жизнедеятельности, и прорастая в здоровые клетки.
Сама жизнь ракового образования разделена на несколько этапов, именно от номера этапа обычно и зависит ее размер, степень повреждения близлежащих тканей, а также характер и тип лечения от онколога.
В основном пациенты боятся 4 степени рака, когда рак начинает метастазировать по всему телу. Но на самом деле и первая стадия не дает 100 % гарантии выздоровления. Все это связано как с видом заболевания, так и со многими факторами, которые влияют на саму опухоль.
Конечно, терапия на начальной стадии дает более положительный результат, чем на других этапах. Рассмотрим все стадии рака и различные классификации, которые помогают определить врачам свойства образования.
Рак молочной железы
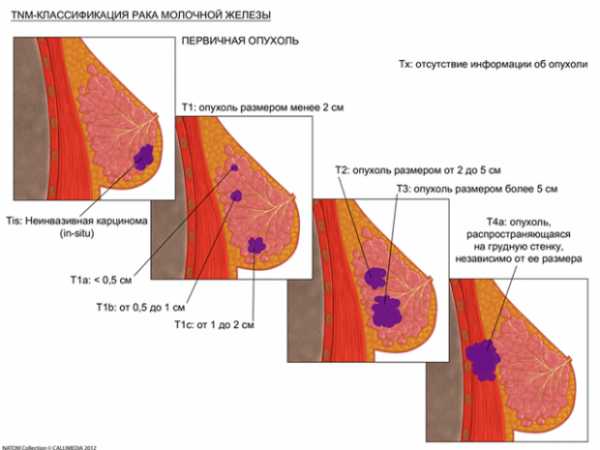
Классификация по системе TNM
TNM система определения ракового злокачественного заболевания — это ныне существующая классификация онкологических заболеваний, которая принята национальным комитетом здравоохранения для классификации этапов развития и роста раковой опухоли, по ней более точно определяют образ самого злокачественного образования.
Данная система была разработана Пьером Денуа в 1952 году. С процессом развитии онкологии сама система ежегодно улучшалась и эволюционировала. На данный момент имеет актуальность публикация 2009-го года. В ней собраны стандарты и четкая классификация онкологических заболеваний.
Мы начнем рассматривать саму систему, отталкиваясь от трех компонентов:
T — сокращенно от латинского слова Tumor — опухоль. Данный показатель отражает размер, распространенность, прорастание самого рака вглубь близ лежащих тканей и локализацию опухоли. Каждая опухоль имеет букву и цифру, определяющую градацию и размер рака — от T0 до T4.
N — идет от латинского слова Nodus — узел. Когда раковая опухоль вырастает, она начинает позже накладываться и воздействовать на ближайшие лимфатические узлы. Именно это и показывает данная буква. Если у нас стоит N0 — то раковая опухоль еще не захватывает лимфатические узлы, N3 — уже идет максимальное поражение лимфоузлов.
M — идет от греческого слова Metastasis. Наличие метастазов в другие органы. Как и в предыдущих случаях, цифра будет определять градацию распространенности злокачественных клеток в другие органы. M0 — говорит о том, что раковое образование не дает метастазов. M1 — есть метастазирование на ближайшие органы. Но тут нужно уточнить маленькую деталь, обычно после M пишут название самого органа, куда идет метастазирование. К примеру, M(Mar) — раковое новообразование начало метастазирование в костный мозг, а M(Ski) — метастазы распространяются в кожу.
| Символы | Название органа |
| Oth | Остальные органы |
| Pul | Легкие |
| Ski | Кожа |
| Oss | Кости |
| Adr | Надпочечники |
| Hep | Печень |
| Per | Брюшина |
| Bra | Головной мозг |
| Ple | Плевра |
| Lym | Лимфатическая система |
| Mar | Костный мозг |
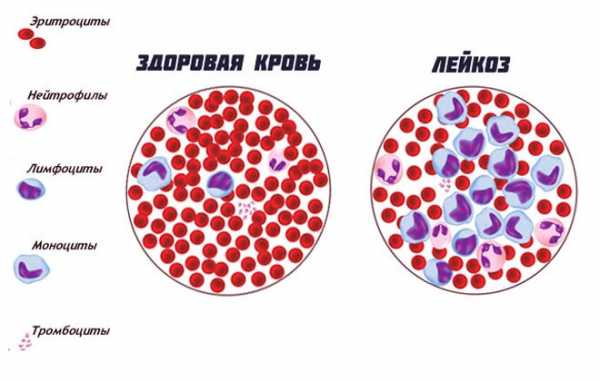
Рак крови — лейкемия
Дополнительные символы
Помимо использования основных букв TNM используется еще дополнительная маркировка. Она помогает показать, когда именно была обнаружена опухоль.
| Символ | Расшифровка |
| c | Использовались неинвазивные методы диагностики при выяснении стадии рака. |
| p | Стадия была обнаружена и установлена при хирургическом вмешательстве. |
| m | Обнаружено сразу несколько опухолей. |
| y | Определяет опухоль после терапии. |
| r | Оценка рецидивных опухолей (повторяющихся) |
| a | Классификация опухоли после вскрытия человека. |
Рак легкого
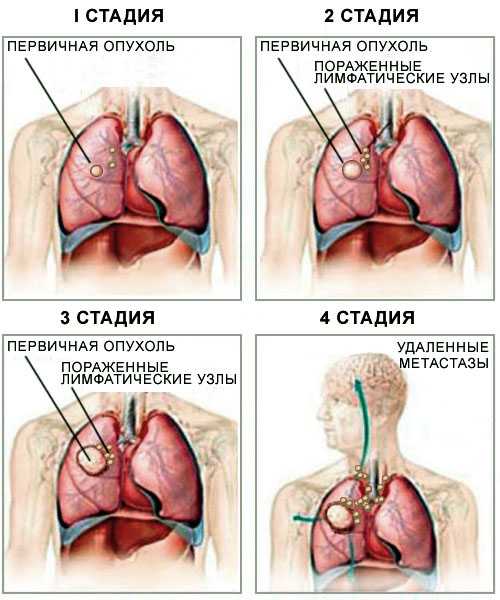
Гистологические стадии рака
TNM на данный момент самая подробная классификация, но помимо нее используются и другие. Обычно используется основной символ G, который показывает насколько агрессивна опухоль. Также указывает и на активность опухоли, и ее скорость роста.
| Символ | Расшифровка |
| GX | Нет данных для определения дифференцирования опухоли |
| G1 | Высокодифференцированный рак — неагрессивная и медленная карцинома g2. |
| G2 | Средне — дифференцированная опухоль — Средняя скорость раковых процессов. |
| G3 | Низкодифференцированная опухоль — довольно агрессивная аденокарцинома с высоким темпом роста тканей. |
| G4 | Недифференцированная опухоль — сверх-агрессивная опухоль |
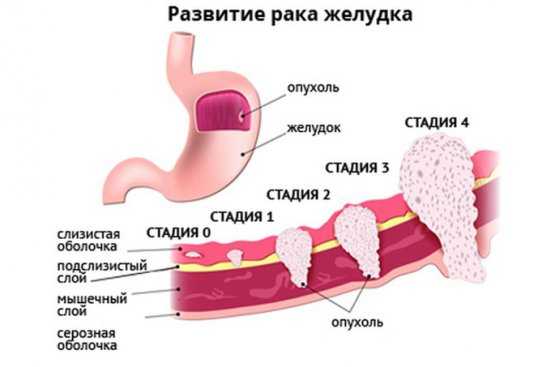
Стадии рака желудка
ПРИМЕЧАНИЕ! В последнее время стали объединять 3 и 4 цифру. Для некоторых онкологических заболеваний используется фраза или термины «высокой или низкой степенью агрессивности». В раке предстательной железы иногда используют пятую стадию или G5.
Обычно гистологическую классификацию используют непосредственно для прогноза роста и времени для больной онкологии. Чем выше агрессивность опухоли, тем, понятное дело, меньше осталось времени на лечение.
Система TNM наоборот дает больше информации насчет размера и степени погруженности раковых тканей в соседние, а также распространенность самой опухоли. От этого будет зависеть вид и тип лечения. Например, при обширном метастазировании, нет смысла использовать хирургическое вмешательство и обычно лечат радиотерапией, химиотерапией и медикаментами.
Стадии рака матки
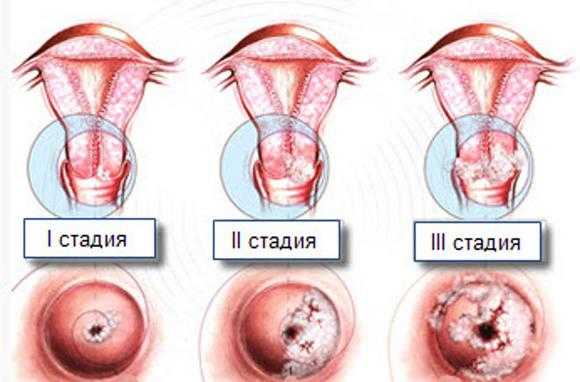
Классификация рака по стадиям
Есть так называемая классическая классификация, которая дает информацию непосредственно пациенту. Это 1, 2, 3 и 4 стадия. Но обычно для врачей используется эта же классификация непосредственно в комплексе с системой TNM, чтобы более точно определить характер опухоли на каждой стадии. Рассмотрим таблицу:
| Стадия | Размер опухоли | Поражение лимфатических узлов | Распространенность метастаз |
| 1 | T1 | N0 | M0 |
| 2 | T0-1 | N1 | M0 |
| T2 | N0 | M0 | |
| T2 | N1 | M0 | |
| 3 | T3 | N0 | M0 |
| T3 | N1 | M0 | |
| T-любая | N2 | M0 | |
| 4 | T-любая | N-любая | M1 |
| T4 | N-любая | M-любая |
Обычно стадию обозначают от 0 до 4. Нулевую стадию используют врачи для обозначения предракового состояния или злокачественной опухоли. Плюс используют буквы, которые еще более детально дают информацию. Рассмотрим 4 стадии развития рака.
0 Стадия
Обычно больше обозначают неинвазивную опухоль, когда она является больше не злокачественной, а доброкачественной. При этом сами клетки не злокачественные, но есть риск, что эти ткани могут перерасти в рак. Правда при обнаружении данного состояния шанс вылечиться всегда положительный. Можно сказать, что это начальная стадия рака.
1 Стадия — ранний рак
Рак 1 стадии классифицируется тем, что образуются первые сгустки и узелки, но которые не вылезают за границу самого органа. Нет поражения лимфатических узлов, а также внешние признаки очень малозаметны. Некоторые типы опухолей можно обнаружить на начальной стадии только с помощью анализов на онкомаркеры. Первая стадия рака имеет наиболее высокий шанс вылечиться. Выживаемость — 80 %.
2 Стадия
Рак во второй степени уже имеет размеры побольше, а также прорастает в ближайшие ткани и в конце уже затрагивает лимфатические узлы. Некоторые органы на этом этапе начинают уже давать сигнал в виде симптомов, правда в основном они похожи на обычные болезни и воспаления. Выживаемость — 60 %.
3 Стадия
Рак 3 степени уже глубоко прорастает в органе и задевает все ближайшие лимфатические узлы. При этом может задевать и ближайшие органы. Правда удаленные метастазы еще не распространены, так что еще есть шанс на лечение. Третья стадия рака уже агрессивно проявляется относительно симптомов. При лечении третьей степени используют более жесткие методы терапии: от хирургии до радиационного облучения, при этом состояние пациента сильно ухудшается. Выживаемость — 30 %.
4 последняя стадия
Четвертая стадия рака уже имеет огромные размеры, при этом могут возникать внутренние кровотечения, так как сама патология растет быстрее чем кровеносные сосуды. Метастазы уже по крови распространены и воздействуют на любые органы. Это самая опасная стадия, когда шанс летального исхода в разы увеличивается. Вылечиться от рака в четвертой стадии практически невозможно. Но при правильном лечении есть шанс продлить жизнь на несколько лет. Выживаемость — меньше 5 %.
Сколько живут пациенты с раком?
Тут все зависит от характера самой болезни, и когда ее диагностировали. Чем раньше начали лечить недуг, тем больше шансов на выздоровление и тем дольше проживет сам пациент. Понятно дело, что на 3 и 4 стадии шанс сильно падает.
Излечим рак или нет? Тут все зависит от самого лечения, а также от типа опухоли. Есть много онкологических заболеваний, которые уже никак не лечатся на 4 стадии.
Какие есть методы лечения рака? В основном все зависит от вида онкологии, а также от стадии. В основном применяют:
- Хирургия
- Радиотерапия
- Химиотерапия
- Медикаменты
Как врач до операции определяет стадию? Для этого есть совокупность различных методов обследования: МРТ, УЗИ, КТ, биопсия, анализы на опухолевые маркеры и т.д.
Какие причины возникновения и симптомы рака? Про симптомы вы можете более подробно почитать в этой статье. А причины до сих пор точно не известны. Но ученые выделяют ряд некоторых факторов, которые влияют на шанс появление опухоли:
- Плохая экология.
- Генетика.
- Курение и алкоголь
- Работа с химическими реагентами
- Плохое питание
- Ожирение
- Низкая подвижность и сидячая работа
oncoved.ru
Уравнение четвёртой степени — Википедия. Что такое Уравнение четвёртой степени
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:
- f(x)=ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).
Так как f(x){\displaystyle f(x)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0{\displaystyle a>0}, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если a<0{\displaystyle a<0}, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум
Теорема Виета для уравнения четвёртой степени
Корни уравнения четвёртой степени x1,x2,x3,x4{\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами a,b,c,d,e{\displaystyle a,\,b,\,c,\,d,\,e} следующим образом:
- x1+x2+x3+x4=−ba,{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}
- x1x2+x1x3+x1x4+x2x3+x2x4+x3x4=ca,{\displaystyle x_{1}\,x_{2}+x_{1}\,x_{3}+x_{1}\,x_{4}+x_{2}\,x_{3}+x_{2}\,x_{4}+x_{3}\,x_{4}={\frac {c}{a}},}
- x1x2x3+x1x2x4+x1x3x4+x2x3x4=−da,{\displaystyle x_{1}\,x_{2}\,x_{3}+x_{1}\,x_{2}\,x_{4}+x_{1}\,x_{3}\,x_{4}+x_{2}\,x_{3}\,x_{4}=-{\frac {d}{a}},}
- x1x2x3x4=ea.{\displaystyle x_{1}\,x_{2}\,x_{3}\,x_{4}={\frac {e}{a}}.}
История
Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.
Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»[2].
То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема. [3]
Решения
Через резольвенту
Решение уравнения четвёртой степени
- x4+px2+qx+r=0{\displaystyle x^{4}+px^{2}+qx+r=0}
сводится к решению кубической резольвенты
- y3−2py2+(p2−4r)y+q2=0{\displaystyle y^{3}-2py^{2}+(p^{2}-4r)y+q^{2}=0}
Корни резольвенты y1,y2,y3{\displaystyle y_{1},y_{2},y_{3}} связаны с корнями исходного уравнения x1,x2,x3,x4{\displaystyle x_{1},x_{2},x_{3},x_{4}} (которые и нужно найти) следующими соотношениями:
- y1=(x1+x2)(x3+x4){\displaystyle y_{1}=(x_{1}+x_{2})(x_{3}+x_{4})}
- y2=(x1+x3)(x2+x4){\displaystyle y_{2}=(x_{1}+x_{3})(x_{2}+x_{4})}
- y3=(x1+x4)(x2+x3){\displaystyle y_{3}=(x_{1}+x_{4})(x_{2}+x_{3})}
Корни резольвенты могут быть решены по формуле Кардано. Три формулы соотношений между yi{\displaystyle y_{i}} и xi{\displaystyle x_{i}} вместе с исходным уравнением дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.
Решение Декарта — Эйлера
В уравнении четвёртой степени
- ax4+bx3+cx2+dx+e=0,a≠0{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0}
сделаем подстановку x=y−b4a{\displaystyle x=y-{\frac {b}{4a}}}, получим уравнение в следующем виде (оно называется «неполным»):
- y4+py2+qy+r=0,{\displaystyle y^{4}+py^{2}+qy+r=0,}
где
- p=8ac−3b28a2,{\displaystyle p={\frac {8ac-3b^{2}}{8a^{2}}},}
- q=8a2d+b3−4abc8a3,{\displaystyle q={\frac {8a^{2}d+b^{3}-4abc}{8a^{3}}},}
- r=16ab2c−64a2bd−3b4+256a3e256a4.{\displaystyle r={\frac {16ab^{2}c-64a^{2}bd-3b^{4}+256a^{3}e}{256a^{4}}}.}
Корни y1,y2,y3,y4{\displaystyle y_{1},\,y_{2},\,y_{3},\,y_{4}} такого уравнения равны одному из следующих выражений:
- ±z1{\displaystyle \pm {\sqrt {z_{1}}}} ±z2{\displaystyle \pm {\sqrt {z_{2}}}} ±z3,{\displaystyle \pm {\sqrt {z_{3}}},}
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
- (±z1)(±z2)(±z3)=−q8,{\displaystyle (\pm {\sqrt {z_{1}}})(\pm {\sqrt {z_{2}}})(\pm {\sqrt {z_{3}}})=-{\frac {q}{8}},}
причём z1,z2,z3{\displaystyle z_{1},\,z_{2},\,z_{3}} — это корни кубического уравнения
- z3+p2z2+p2−4r16z−q264=0.{\displaystyle z^{3}+{\frac {p}{2}}z^{2}+{\frac {p^{2}-4r}{16}}z-{\frac {q^{2}}{64}}=0.}
Решение Феррари
Решение уравнения четвёртой степени вида x4+ax3+bx2+cx+d=0{\displaystyle x^{4}+ax^{3}+bx^{2}+cx+d=0} может быть найдено по методу Феррари. Если y1{\displaystyle y_{1}} — произвольный корень кубического уравнения
| y3−by2+(ac−4d)y−a2d+4bd−c2=0,{\displaystyle y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0,} | (2) |
(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений
- x2+a2x+y12=±(a24−b+y1)x2+(a2y1−c)x+y124−d{\displaystyle x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}}
где подкоренное выражение в правой части является полным квадратом.
Биквадратное уравнение
Биквадратное уравнение[4] — уравнение четвёртой степени вида ax4+bx2+c=0{\displaystyle ax^{4}+bx^{2}+c=0}, где a,b,c{\displaystyle a,b,c} — заданные комплексные числа и a≠0{\displaystyle a\not =0}. Подстановкой y=x2;y⩾0{\displaystyle y=x^{2};y\geqslant 0} оно сводится к квадратному уравнению относительно y{\displaystyle y}.
Четыре его корня находятся по формуле
- x1,2,3,4=±−b±b2−4ac2a.{\displaystyle x_{1,2,3,4}=\pm {\sqrt {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.}
Возвратные уравнения четвёртой степени
Возвратное уравнение четвёртой степени является также относительно легко решаемым: для ax4+bx3+cx2+bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0} такого, что a≠0{\displaystyle a\neq 0}, решение находится приведением к виду:
- a(x2+1×2)+b(x+1x)+c=0{\displaystyle a\left(x^{2}+{1 \over x^{2}}\right)+b\left(x+{1 \over x}\right)+c=0},
После замены t=x+1x{\displaystyle t={x+{1 \over x}}} ищется решение квадратного уравнения at2+bt+c−2a=0{\displaystyle at^{2}+bt+c-2a=0}, а затем — квадратного уравнения x2−tx+1=0{\displaystyle x^{2}-tx+1=0}.
Примечания
- ↑ Ferrari biography
- ↑ «Великое искусство» (Ars magna, 1545)
- ↑ Стюарт, Ян. Теория Галуа, издание третье (Chapman & Hall/CRC Mathematics, 2004) (англ.)
- ↑ В литературе до середины XX века биквадратным также могли называть уравнение четвёртой степени общего вида
Литература
Ссылки
wiki.sc
сколько живут с ней, как проходит лечение
Онкология
25.10.2018
Люди, которые столкнулись с онкологией, задаются очевидным вопросом, рак 4 стадии – сколько можно прожить с таким заболеванием, насколько опасными могут быть последствия?
Данный этап является опасным, победить заболевание на этой стадии оказывается невозможным. Единственное, что могут сделать врачи, так это назначить препараты, способные улучшить состояние жизни и снять боль.
Как умирают при раке?
Если имеется в виду последняя стадия рака, то при данном заболевании человек умирает в определенной последовательности. С ним происходит ряд вещей, которые на самом деле можно считать первыми предпосылками приближающейся смерти.
Многие больные сталкивается с такой неприятной вещью, как передагония. При наличии у больного такой фазы заболевания наблюдается нарушение в работе центральной нервной системы, угнетение эмоциональной и физической активности, кожа приобретает синюшный цвет, становится бледной, наблюдается значительное понижение артериального давления.
Если обратиться к врачу своевременно, начать прием необходимых медикаментозных препаратов, то такое состояние может продолжаться долгое время.
Агония. При последней стадии у больного наблюдается агония, которая является последней перед смертью. На этом этапе жизни у человека больного онкологией наблюдается разбалансирование функций, важных для жизни. В результате чего ткани организма насыщаются кислородом неравномерно.
В конечном итоге, при продолжительном кислородном голодании у больного наблюдается остановка циркуляции крови и дыхания, что приводит к летальному исходу. При наличии агонии на фоне рака последней стадии, смерть наступает спустя три часа.
Клиническая гибель. Рак 4 степени способен стать причиной возникновения у больного клинической смерти. В данный период у больного останавливаются все функции в организме, по сути можно считать, что человек умер. Во время клинической смерти наблюдаются минимальные обменные действия в клетках человека.
Если при наличии других заболеваний, принято считать, что при клинической смерти можно спасти больного в течении 5-9 минут, то 4 я стадия рака делает процесс кончины неизбежным. Вернуть больного в этом случае является невозможным.
Фиксированная смерть. Процесс, во время которого наблюдается полная остановка жизнедеятельности тканей мозга головы. В дальнейшем такой процесс начинает переходить на весь организм. На этом жизнь человека, у которого 4 стадия рака прекращается.
Признаки приближения смерти
Если у больного была диагностирована 4 стадия рака, сколько живут при ней? Такой вопрос интересует всех людей, страдающих от онкологии. В данном случае имеется несколько признаков, свидетельствующих о приближении смерти. Нужно отметить, что в зависимости от вида и локализации рака, возникнуть они могут в самый разный период жизни.
Когда количество жизни неумолимо сокращается, у больного наблюдается уменьшение количества потребляемой в сутки пищи. По мере того, как наблюдается развитие раковой кахексии и слабости в мышцах в целом, у человека наблюдается уменьшение необходимости в воде и еде.
Если у человека диагностирована четвертая стадия рака, при этом он отказывается от пищи, то это говорит о том, что наступила термальная стадия болезни. При наличии такого проявления болезни, рекомендуется нанимать для пациента сиделку, с целью того, чтобы помогать человеку каждый день справляться с развивающимся недугом.
Перед наступлением смерти, многие больные хотят провести последние минуты в окружении своих родных. Даже в том случае, если у онкольного наступило коматозное состояние, то врачи советуют находиться в данный период возле него, не переставая с ним общаться.
Есть информация, что даже в этот период человек способен не только слышать, но и воспринимать слова. Поэтому если больной умирает, рекомендуется обязательно остаться возле него.
Нарушение глубины и регулярности дыхания. При последней стадии рака, перед наступлением агонии. Причиной такого явления становится то, что метаболические процессы постепенно угнетаются, в организме начинает уменьшаться потребность в получаемом кислороде. Если у больного имеется рак легких, то при наличии жидкости в этом органе могут наблюдаться различные шумы при выдохе и вдохе. В данный период жизни, рекомендуется оставаться возле больного, так как может наблюдаться промежуточное апноэ.
При четвертой степени и наличии такого состояния, с целью облегчения общего самочувствия, нередко врач рекомендует использовать кислородную подушку, с помощью которой кислород начинает поступать в ткани легких. Во время ухода за больным при таком проявлении рака, рекомендуется периодически смачивать ротовую полость и губы простой водой.
В том случае, если наступает летальный исход, то у больного на коже начинают выступать капли холодного пота, кожа становится холодной. В большинстве случаев, причиной наступления клинической смерти при онкологии, становится именно остановка дыхания, во время которой к тканям головного мозга перестает поступать кислород.
Готовность к кончине психологически. Если есть рак 4 степени, то в этот период человек четко понимает, что летальный исход является неизбежным. В большинстве случаев, при наличии такого заболевания пациент уже морально подготовлен к приближающейся кончине. Жить на данном этапе заболевания становится крайне сложно, перед наступлением стадии агонии, больной большую часть своего времени проводит во сне. Кроме этого, при данном состоянии нередко наблюдается апатия ко всему и отстраненность.
Нередко 4 степень рака сопровождается беспамятным состоянием и психозом. Человек проживший свою жизнь, на данном периоде может сильно измениться. Родственникам необходимо быть готовым к большим сложностям. Также необходимо понимать, что при наличии последней стадии рака, у человека наблюдаются сильные боли.
Если есть рак последняя стадия, человек испытывает сильнейшие болезненные ощущения. В таком случае медики могут назначить уколы морфия, который способен временно облегчить состояние.
Когда прожить остается уже несколько дней, обезболивающие препараты уже могут не давать необходимого результата. Снять болезненные ощущения становится невозможно.
Больному с 4 стадией рака необходимо создать идеальные условия для проживания последних суток. Можно включить расслабляющую тихую мелодию, поговорить о прошедшей жизни, почитать его любимые книги. Главное в этом случае, дать понять человеку, что вы его любите, будете оставаться с ним до последней минуты жизни.
На вопрос: сколько живут с раком 4 стадии сложно дать однозначный ответ, зачастую этот период составляет всего несколько месяцев. Если у человека была диагностирована последняя стадия онкологии, рекомендуется приложить максимум усилий, чтобы последние дни его жизни были самыми лучшими, прошли в спокойной домашней обстановке, в окружении близких и дорогих ему людей. Берегите свое здоровье, не допускайте развития рака четвертой стадии.
wmedik.ru
как посчитать число в степени 1/4
Это корень 4 степени из числа. Надо подобрать такое число, 4-я степень которого дает данноедва раза извлеки корень квадратный (тот, который самый простой и даже на телефонном калькуляторе есть).
есть формула…. здесь её не напишешь. . в общем будет число под корнем четвертой степени
Запустите на своем компьютере Excel. В ячейку А1 введите число, которое вы хотите возвести в степень. Дальше выберите любую другую ячейку, которая вам больше всего по душе (кроме конечно А1). Выделить — это значит щелкнуть левой кнопкой мышки на понравившейся вам ячейке. Нажмите клавишу F2. В ячейке появится курсор. Наберите латинскими буквами следующую формулу =A1^(1/4) и нажмите Enter. Вы получите ответ на ваш вопрос. Вводя в ячейку А1 любые числа вы будете получать значение кореня 4-й степени из этого числа. Абсолютно уверен, что вы не будете вводить в ячейку А1 отрицательные числа. ВУ А ЛЯ как говорят у них. Удачи и успехов!!!это означает корень четвёртой степени из данного числа, можно на калькуляторе, а какого числа?
touch.otvet.mail.ru
