Формула медианы равнобедренного треугольника: Все формулы высоты, медианы, биссектрисы равнобедренного треугольника

Геометрия: свойства треугольника — intmag24.ru

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

На рисунке: Треугольник ABC;
A, B, C – вершины треугольника ABC;
AB, AC, BC – стороны треугольника ABC;
∠BAC, ∠ABC, ∠ACB – углы треугольника ABC.

Содержание

1. Виды треугольников
2. Свойства сторон треугольника
3. Свойства углов треугольника
4. Свойства высоты треугольника
5. Свойства медианы треугольника
6. Свойства биссектрисы треугольника
7. Средняя линия треугольника
8. Равнобедренный треугольник
9. Равносторонний треугольник
10. Прямоугольный треугольник
11. Треугольник и окружность
12. Основные формулы
13. Теорема Чевы
14. Теорема Менелая

Виды треугольников

1. Треугольник называется остроугольным, если все его углы острые.
2. Треугольник называется тупоугольным, если один из его углов тупой.
3. Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
4. Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
5. Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
6. Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны. Основные признаки равенства треугольников: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам.

    

Свойства сторон треугольника

• Сумма любых двух сторон треугольника больше его третьей стороны.
  На рисунке: b+c>a, a+c>b, a+b>c.
• Длина каждой стороны треугольника больше разности  длин двух других сторон. На рисунке: |a-b| <c, |a-c|<b, |b-c|<a.

Свойства углов треугольника

• Сумма углов треугольника равна 180°:
• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.

Свойства высоты треугольника

Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны. На рисунке: BD – высота треугольника ABC.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. На рисунке: H – ортоцентр треугольника ABC.

Свойства медианы треугольника

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (AM).
— Она делит треугольник на два равновеликих (с равными площадями) треугольника.
— Три медианы треугольника делят его на шесть равновеликих треугольников. Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины треугольника. На рисунке: AG/GA1=BG/GB1=CG/GC1=2/1.

Формула медианы:

Свойства биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. На рисунке: AL – биссектриса треугольника ABC.

Свойство биссектрисы треугольника: Отношение отрезков, на которые биссектриса делит сторону треугольника, равно отношению прилежащих к этим отрезкам сторон треугольника. На рисунке: BL/CL=AB/AC. 

Биссектрисы треугольника пересекаются в одной точке. Эта точка равноудалена от всех сторон треугольника и является центром окружности, вписанной в треугольник.

Формула нахождения длины биссектрисы:

Средняя линия треугольника

Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника. 
На рисунке: MN – средняя линия треугольника ABC.

Средняя линия треугольника параллельна третьей стороне треугольника и равна её половине.
На рисунке: MN||AC,MN=AC/2.

Средние линии разбивают треугольник на четыре равных треугольника, подобных исходному с коэффициентом 1/2. Треугольник из средних линий называется срединным треугольником.
На рисунке: MNP – срединный треугольник треугольника ABC.

 

Равнобедренный треугольник

Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

На рисунке:
△ABC равнобедренный;
AC – основание,
AB, BC – боковые стороны.

Свойства равнобедренного треугольника:

• В равнобедренном треугольнике углы при основании равны.
  На рисунке: ∠BAC=∠BCA
• В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
  На рисунке: AD=DC, ∠ABD=∠CBD, BD⊥AC.

Признаки равнобедренного треугольника:

• Если два угла треугольника равны, то этот треугольник равнобедренный. На рисунке: ∠BAC=∠CAB⇒AB=BC.
• Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, BD⊥AC ⇒ AB=BC.
• Если в треугольнике медиана и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, ∠ABD=∠CBD ⇒ AB=BC.
• Если в треугольнике высота и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: BD⊥AC, ∠ABD=∠CBD ⇒ AB=BC.

Равносторонний треугольник

• Все стороны равностороннего треугольника равны.
• Все углы равностороннего треугольника равны 60°.
• Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.

Прямоугольный треугольник

Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой. 

На рисунке: △ABC прямоугольный; AC, BC – катеты, AB – гипотенуза.

Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
На рисунке: ∠C=90∘,CM – медиана △ABC⇒AM=BM=CM.

Высота, проведённая к гипотенузе, делит прямоугольный треугольник на два треугольника подобных друг другу и исходному треугольнику.  На рисунке: △ACH∽△CBH∽△ABC.

В прямоугольном треугольнике катет, лежащий напротив угла в 30∘, равен половине гипотенузы.
На рисунке: если ∠A=30∘⇔BC=AB/2.

Основные метрические соотношения в прямоугольном треугольнике:
Пусть в треугольнике ABC ∠C=90∘, a=BC, b=AC – катеты, c=AB – гипотенуза, h=CH – высота к гипотенузе, a1=BH, b1=AH – проекции катетов на гипотенузу. Тогда:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы:  Радиус r окружности, вписанной в прямоугольный треугольник, может быть вычислен по формуле:  r=(a+b−c)/2, где a и b – катеты треугольника, c – его гипотенуза.

Калькулятор для прямоугольного треугольника поможет вычислить все его характеристики: стороны, углы, периметр и площадь, радиус вписанной и описанной окружности.

Треугольник и окружность

Около любого треугольника можно описать окружность, и только одну. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Радиус описанной окружности треугольника ABC может быть вычислен по формулам: где a, b и c – длины сторон треугольника ABC, S – его площадь.

В любой треугольник можно вписать окружность, и только одну. Центром вписанной окружности треугольника является точка пересечения биссектрис треугольника. 

Пусть a, b и c – длины сторон треугольника ABC и p=(a+b+c)/2 – его полупериметр. Тогда
— длины отрезков касательных из вершин A, B, C до точек касания вписанной окружности со сторонами треугольника равны p−a, p−b, p−c соответственно.

Радиус r вписанной окружности треугольника может быть вычислен по формуле: где a, b и c – длины сторон треугольника, p=(a+b+c)/2 – его полупериметр, S – площадь треугольника.

Основные формулы:

Периметр: P=a+b+c

Площадь по стороне и высоте: площадь треугольника равна половине произведения стороны треугольника на высоту, проведённую к этой стороне.

Площадь по сторонам и углу между ними: площадь треугольника равна половине произведения двух его сторон на синус угла между ними.  или половине произведения катетов:

Площадь по формуле Герона (где p=(a+b+c)/2 – полупериметр, a, b, c – стороны треугольника):

Площадь  по трем сторонам и радиусу вписанной окружности (где p=(a+b+c)/2 – полупериметр треугольника, r — радиус вписанной окружности):   Площадь  по трем сторонам и радиусу описанной окружности:

Стороны прямоугольного треугольника (Теорема Пифагора):

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ  — угол между сторонами и r — радиус вписанной окружности, R — радиус описанной окружности

Для нахождения характеристик простого, равнобедренного или равностороннего треугольника, воспользуйтесь калькулятором для треугольника.

Чтобы вычислить все характеристики прямоугольного треугольника, воспользуйтесь калькулятором для прямоугольного треугольника.

Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие.

Теорема Чевы

Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Прямые AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда:

Теорема Менелая

Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Точки A1, B1 и C1 лежат на одной прямой тогда и только тогда, когда:

 

Свойство медианы треугольника

• Бугрышева Татьяна Николаевна, учитель математики

org/BreadcrumbList»> Разделы: Математика

---

Цели урока:

1. Обучающие — познакомить ребят с дополнительными соотношениями между элементами треугольника, повторить сопутствующий материал.
2. Развивающие — формирование умений анализировать, сравнивать , делать выводы, самостоятельно открывать блок новых знаний.
3. Воспитывающие — формирование навыков коммуникативности , умение быть внимательным, уметь представить свою работу.

Ход урока

1. Оргмомент. Учитель приветствует ребят, настраивает на работу, приглашает к сотрудничеству и совместному творчеству.

2. Актуализация знаний.

Вопросы к классу:

1. Что называется параллелограммом?
2. Свойства, признаки параллелограмма.
3. О диагоналях параллелограмма.
4. Что называется медианой треугольника? Что вы знаете о медианах?
5. Какой треугольник называется равнобедренным?

3. Самостоятельная работа. (1 ученик работает на переносной доске, проектор на экране высвечивает таблицу возможных ответов)

Номер \ N	1	2	3	4
A	12	40	6	8 и 16
B	3	12	3	4 и 20
C	4	8	10	4 и 8
Оценка:

СР- медиана, СР=6 см, СО — ? .

ABCD – параллелограмм , АВ= 2 ВС= 4 Найти сумму квадратов длин диагоналей параллелограмма

ABCD – параллелограмм АВ = 2 АD = 3 A = 300 SABCD — ?

PABCD =24 см. AB — ? BC — ?

Проверка: на проекторе пошаговое открытие правильных ответов, работавший у доски представляет свое решение, класс обсуждает решение. Исправляются неточности и ошибки ( если они есть), отвечавший сразу получает оценку, при необходимости ему можно задать дополнительные вопросы. Ребята, работавшие на местах, ставят себе оценку сами.

Задание. Учитель обращает внимание класса на задачу:

Дано треугольник АВС АВ = 5 см ВС = 6 см АС = 4 см АМ = МС Найти : ВМ

Ребята начинают искать способы ее решения и высказывают мысль о том, что хорошо бы иметь формулу, дающую связь между длиной медианы треугольника и ее сторонами.

4. Постановка проблемы.

Учитель предлагает ребятам еще раз сформулировать возникшую у них проблему. Тема урока все еще не формулируется.

5. Открытие учениками новых знаний.

Учитель: давайте рассмотрим треугольник со сторонами a,b,c и медианой m _a, проведенной из вершины А.

1.) Продолжим медиану AD на расстояние DE=DA. 2.) Соединим т. В и т. Е, т.Е и т. С. Чем является полученный четырехугольник? Почему? 3.) Теперь используем теорему о том, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

АЕ² + ВС² = АВ² + ВЕ² + ЕС² + АС²

АЕ² +

АЕ²

АЕ =

m_a =

Ученики говорят о том, что нашли связь между длиной медианы треугольника и длинами его сторон. Формулируем теорему:

Длина медианы треугольника выражается формулой m_a=, где a, b, c –

длины сторон треугольника.

Учитель: Сможем ли мы теперь решить пропущенную задачу? Совместное решение.

Учитель: Давайте попробуем решить несколько заданий с помощью открытого нами свойства медианы треугольника. Можете ли вы, ребята, сейчас сформулировать тему нашего урока? Из предложенных вариантов выбирают самый удачный и записывают его.

6.Задача.

В равнобедренном треугольнике с боковой стороной, равной 4 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3 см.

Дано: теругольник АВС – равнобедренный АВ= ВС= 4 см AF=3 см Найти: АС

Выберите правильный рисунок.

Решение: по свойству медианы треугольника AF =

АС= см.

Ответ: см.

7. Задача.

Основание равнобедренного треугольника равно 4 см, а медиана боковой стороны равна 5 см. Найти длину каждой из боковых сторон.

Дано: треугольник АВС – равнобедренный. АВ = ВС АС=4 см. AF=5 см Найти: АВ, ВС.

Решение: Пусть АВ = ВС= х (см) , тогда по свойству медианы треугольника имеем:

AF=, х=6.

Ответ: 6 см.

8. Итог урока.

Ребята, что нового вы узнали сегодня на уроке, все ли вам понятно? Можно поинтересоваться мнением учеников по структуре урока, какие моменты были особенно трудными.

9. Домашнее задание.

1. Записать теорему в тетрадь- памятку.

2. Придумать и решить задачу, где будут известны длины трех сторон треугольника, а найти надо его медиану.

Удачной работы! Спасибо за урок!

Список литературы:

1. Л.С. Атанасян, В.Ф. Бутузов, и др.”Геометрия 7-9” .
2. М.И.Сканави “Сборник задач по математике, для поступающих во ВТУЗы ”.

6.03.2008

Уравнения равнобедренного треугольника Калькулятор формул

Изменить уравнение
Выберите, чтобы найти другое неизвестное

Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов

Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.

	Периметр
	Полупериметр
	Зона
	Зона
	Основание
	Высота
	Биссектриса угла стороны a
	Биссектриса угла стороны b
	Биссектриса стороны c
	Медиана стороны a
	Среда n стороны b
	Медиана стороны c
	Высота стороны a
	Высота стороны b
	Высота стороны c
	Радиус описанной окружности
	Радиус вписанной окружности

Закон косинусов

9001 7

	длина стороны a
угол А

---

Равносторонний треугольник:
Все три стороны имеют одинаковую длину
Все три угла равны 60 градусов метр Полупериметр Площадь Высота Медиана Биссектриса угла 9001 8 Радиус описанной окружности Радиус вписанной окружности

---

Прямоугольный треугольник:
Один угол равен 90 градусам

Уравнения прямоугольного треугольника

9 0016

	Теорема Пифагора
	Периметр
	Полупериметр
	Площадь
	Высота
	Высота b
	Высота c
	Биссектриса угла a
	Биссектриса угла b
	Биссектриса угла c
	Медиана a
	Медиана b
	Медиана c
	Радиус вписанной окружности
	Радиус описанной окружности

---

Равнобедренный треугольник:
Две стороны имеют одинаковую длину
Два угла равны

Равнобедренный треугольник Equ

	Периметр
	Полупериметр
	Площадь
	Высота сторон a и c
	Высота стороны b
	Медиана сторон a и c
	Медиана стороны b
	Угол Bi сектор сторон a и c
	Биссектриса угла стороны b
	Радиус описанной окружности
	Радиус вписанной окружности

Где

900 17 = 9 0017 b 900 16 90 017 =

P	Периметр
s	=	Полупериметр
a	=	Длина стороны a
=	Длина стороны b
c	=	Длина стороны сторона c
h	=	Высота
м	=	Медиана
А	=	Уголок А
B	=	Уголок B
C	=	Уголок C
t	Биссектриса угла
R	=	Радиус описанной окружности
r	=	Радиус вписанной окружности

---

Справочник — Книги: 1) Макс А.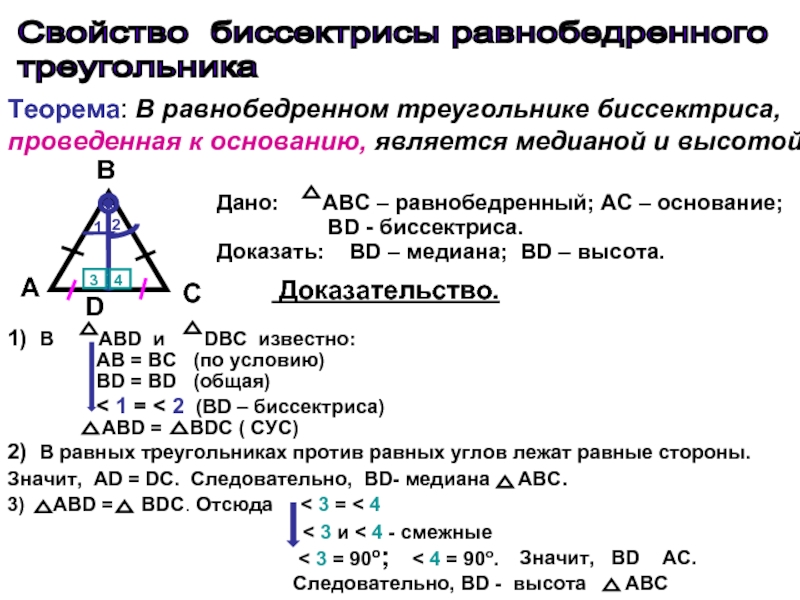 Собель и Норберт Лернер. 1991. Предварительная математика. Прентис Холл. 4-е изд.

Прямоугольный равнобедренный треугольник и длина медианы

Чтобы показать или доказать, что медиана прямоугольного равнобедренного треугольника равна половине гипотенузы, начните с прямоугольного треугольника, а затем проведите медиану (показана красным в треугольнике ниже)

Сначала покажите, что треугольник ABD и треугольник ADC конгруэнтны. Если мы сможем это показать, то сможем заключить, что угол BAD и угол DAC равны и каждый равен 45 градусам.

Это также будет означать, что угол BDA = 90 градусов.

Следовательно, мы можем использовать теорему Пифагора для треугольников ABC и треугольников ABD.

Как показать, что показанный выше прямоугольный равнобедренный треугольник (ABC) имеет два конгруэнтных треугольника (ABD и ADC)

Покажем, что треугольник ABD и треугольник ADC конгруэнтны по SSS. Это означает, что нам нужно найти три равные стороны, и все готово.

Мы уже знаем, что отрезок AB = отрезку AC, так как треугольник ABC равнобедренный.

Поскольку отрезок AD является медианой отрезка BC, отрезок BD = отрезку DC.

Наконец, отрезок AD является общей стороной, а значит, равен у обоих треугольников.

Мы нашли 3 равные стороны, поэтому треугольник ABD и треугольник ADC равны. Поскольку треугольник ABD и треугольник ADC равны, мы можем сделать вышеупомянутое.

Теперь воспользуемся теоремой Пифагора для треугольника ABC, треугольника и треугольника ABD. Теперь основное внимание будет уделено длинам сторон.

Для треугольника ABC,

x ² = y ² + y ²

x ² = 2y ^{2 9050 5}

Разделите обе части уравнения на 2

y ² = (x ² ) / 2

Для треугольника ABD, y ² = z ² + (x/2) ² 90 006

Замена (x ² ) / 2 для у ²

Получаем:

(х ² ) / 2 = z ² + (х/2) ²

(х ² ) / 2 = г ² + (x ² ) / 4

Вычесть (x ² ) / 4 из обеих частей уравнения

(x ² ) / 2 — (x ² ) / 4 = z ² + (х ² ) / 4 — (х ² ) / 4

(х ² ) / 2 — (х ² ) / 4 = г ²

(2x ² ) / 4 — (x ² ) / 4 = z ²

(x ² ) / 4 = г ²

х/2 = г ( Готово!)

Узнайте гораздо больше, чем прямоугольный равнобедренный треугольник.