Формула нахождения длины вектора: примеры и решения, формулы и теоремы

Содержание

Вычисление длины (модуля) вектора в EXCEL. Примеры и описание

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a _x и a _y , то длину вектора можно найти по формуле

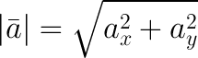
В случае вектора в пространстве добавляется третья координата

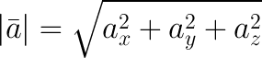
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки

B8:B9 , см. файл примера ).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .

2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

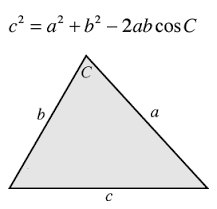
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL

4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.

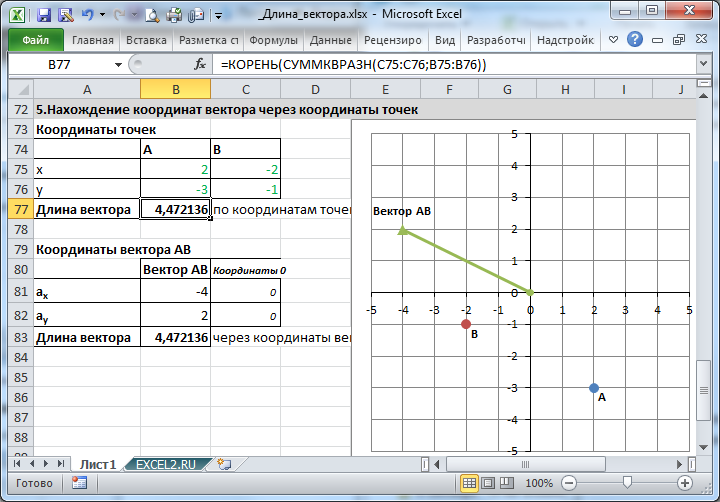
Формулы векторов

1. Координаты вектора

Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала:

2. Длина или модуль вектора

Если вектор , то его длина равна корню квадратному из суммы квадратов координат:

3. Сумма векторов

Если векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых:

4. Умножение вектора на число

Чтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число:

5. Скалярное произведение векторов

Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:

6. Векторное произведение векторов

Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле:

7. Смешанное произведение векторов

Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов:

Замечание. Обычно такой определитель вычисляется методом треугольников.

8. Угол между векторами

Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей:

9. Проекция вектора на вектор

Проекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора :

Понравился сайт? Расскажи друзьям!

Как найти длину вектора? — Студопедия

Если дан вектор плоскости 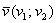, то его длина вычисляется по формуле .

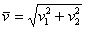Если дан вектор пространства 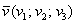, то его длина вычисляется по формуле .

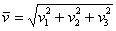Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.

Пример 5

Даны точки 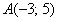и

. Найти длину вектора

Я взял те же точки, что и в Примере 3.

Решение: Сначала найдём вектор :

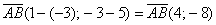
По формуле 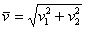вычислим длину вектора: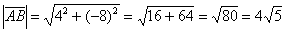

Ответ: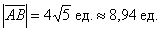

Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3-х знаков после запятой.

Выполним чертеж к задаче: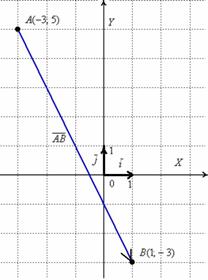

В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.

А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка 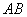равна длине вектора . Так же очевидно, что длина вектора 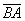будет такой же. По итогу: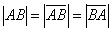

Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки 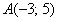и . Найти длину отрезка .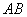

Вместо применения формулы 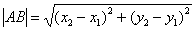, поступаем так:
1) Находим вектор .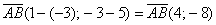
2) А теперь ссылаемся на то, что длина отрезка 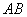равна длине вектора :

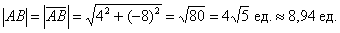
Этот способ широко практикуется в ходе решений задач аналитической геометрии.

Вышесказанное справедливо и для пространственного случая

Для тренировки:

Пример 6

а) Даны точк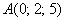и и 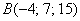. Найти длину вектора .
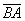б) Даны векторы 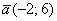, , 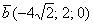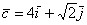и 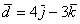. Найти их длины.

Решения и ответы в конце урока.

[Зачет 70] Определение ортонормированного базиса и прямоугольной декартовой системы координат (ПДСК). Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками.

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками.

Нахождение длины вектора по координатам.

Длину вектора будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА. Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Рассмотрим пример.

Найдите длину вектора , заданного в декартовой системе координат. Сразу применяем формулу для нахождения длины вектора по координатам :
. Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве. В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, . Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Рассмотрим решения примеров.

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов , и угол между ними (или косинус угла), а требуется найти длину вектора или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Итак, для нахождения длины вектора по координатам используем формулы
или ,
по координатам точек начала и конца вектора —
или ,
в некоторых случаях к результату приводит теорема косинусов.

Расстояние между двумя точкамиA1(x1;y1) и A2(x2;y2) в прямоугольной системе координат выражается формулой:

Порядок точек не играет роли. Расстояние считается положительным. поэтому корень берется с одним знаком (плюс).

Расстояние между двумя точками

Длина вектора, онлайн калькулятор

Наш онлайн калькулятор позволяет найти длину вектора всего за пару кликов. Для нахождения длины вектора заданного координатами или по точкам — выберите размерность и способ задания вектора, введите все координаты и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет подробно расписан, это поможет вам понять решение и закрепить пройденный материал.

Введите данные для вычисления длины вектора

Размерность вектора:

2 3

Форма представления вектора:

координатами точками

Формула :

Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Определение координат вектора заданного координатами его начальной и конечной точки.

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y ; B_z — A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; … ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ — A₁ ; B₂ — A₂ ; … ; B_n — A_n}

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3 — 1; 1 — 4} = {2; -3}.

Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB_x = B_x — A_x => B_x = AB_x + A_x => B_x = 5 + 3 = 8
AB_y = B_y — A_y => B_y = AB_y + A_y => B_y = 1 + (-4) = -3

Ответ: B(8; -3).

Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).

Решение:

AB_x = B_x — A_x => A_x = B_x — AB_x => A_x = 3 — 5 = -2
AB_y = B_y — A_y => A_y = B_y — AB_y => A_y = -4 — 1 = -5

Ответ: A(-2; -5).

Примеры для пространственных задач

Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.

Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3
AB_z = B_z — A_z   =>   B_z = AB_z + A_z   =>   B_z = 2 + 3 = 5

Ответ: B(8; -3; 5).

Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5
AB_z = B_z — A_z   =>   A_z = B_z — AB_z   =>   A_z = 1 — 4 = -3

Ответ: A(-2; -5; -3).

Примеры для n -мерного пространства

Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.

Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).

Решение:

AB₁ = B₁ — A₁   =>   B₁ = AB₁ + A₁   =>   B₁ = 5 + 3 = 8
AB₂ = B₂ — A₂   =>   B₂ = AB₂ + A₂   =>   B₂ = 1 + (-4) = -3
AB₃ = B₃ — A₃   =>   B₃ = AB₃ + A₃   =>   B₃ = 2 + 3 = 5
AB₄ = B₄ — A₄   =>   B₄ = AB₄ + A₄   =>   B₄ = 1 + 2 = 3

Ответ: B(8; -3; 5; 3).

Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).

Решение:

AB₁ = B₁ — A₁   =>   A₁ = B₁ — AB₁   =>   A₁ = 3 — 5 = -2
AB₂ = B₂ — A₂   =>   A₂ = B₂ — AB₂   =>   A₂ = -4 — 1 = -5
AB₃ = B₃ — A₃   =>   A₃ = B₃ — AB₃   =>   A₃ = 1 — 4 = -3
AB₄ = B₄ — A₄   =>   A₄ = B₄ — AB₄   =>   A₄ = 8 — 5 = 3

Ответ: A(-2; -5; -3; 3).

Сумма векторов, длина вектора

Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Понятие вектора

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.

Обозначение векторов

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Сумма векторов

Суммой двух векторов АВ и ВС будет являться вектор АС.
Записывается как АВ+ВС=АС.

Это правило называется – правилом треугольника.

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b, или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *

Правило параллелограмма

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили вектор противоположный вектору b, и нашли разность.

Координаты вектора

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть, координаты вектора представляют собой пару чисел.

Если

И координаты векторов имеют вид:

То c₁= a₁+ b₁ c₂= a₂+ b₂

Если

То c₁= a₁– b₁ c₂= a₂– b₂

Модуль вектора

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

Найдём вектор, который будет являться результатом АО–ВО:

АО–ВО=АО+(–ВО)=АВ

То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.

Ответ: 8

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ+AD.

100

Найдём вектор, который будет являться суммой векторов AD и AB. Вектор BC равен вектору AD. Значит AB+AD=AB+BC=AC

Длина вектора AC это длина диагонали ромба АС, она равна 16.

Ответ: 16

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО+ВО.

101

Найдём вектор, который будет являться суммой векторов АО и ВО. Вектор ВО равен вектору OD, значит

102

Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

103

По теореме Пифагора:

104

Ответ: 10

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО–ВО.

101

Найдём вектор, который будет являться результатом АО–ВО:

110

Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:

111

По теореме Пифагора:

112

Ответ: 10

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ–АС.

120

Найдём результат разности векторов:

121

Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

Ответ: 3

121

27663. Найдите длину вектора а(6;8).

131

Посмотреть решение

27664. Найдите квадрат длины вектора АВ.

132

Посмотреть решение

27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС.

133

Посмотреть решение

27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD.

134

Посмотреть решение

27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD.

134

Посмотреть решение

27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО.

135

Посмотреть решение

27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ.

136

Посмотреть решение

27715. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–AD.

137

Посмотреть решение

27716. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–АС.

139

Посмотреть решение

Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ+АС.

120

Посмотреть решение

В будущем мы продолжим рассматривать задачи с векторами, не пропустите! Задания будут связаны с координатами векторов, скалярным произведением.

На этом всё. Успеха вам!

С уважением, Александр

Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!

P.S: Буду благодарен, если расскажете о статье в социальных сетях.

13.3: Длина и кривизна дуги

Цели обучения

Определите длину пути частицы в пространстве с помощью функции длины дуги.
Объясните значение кривизны кривой в пространстве и сформулируйте ее формулу.
Опишите значение нормального и бинормального векторов кривой в пространстве.

В этом разделе мы изучаем формулы, относящиеся к кривым как в двух, так и в трех измерениях, и видим, как они связаны с различными свойствами одной и той же кривой.Например, предположим, что вектор-функция описывает движение частицы в пространстве. Мы хотели бы определить, как далеко прошла частица за заданный интервал времени, который можно описать длиной дуги пути, по которому она следует. Или предположим, что векторная функция описывает дорогу, которую мы строим, и мы хотим определить, насколько круто изгибается дорога в данной точке. Это описывается кривизной функции в этой точке. В этом разделе мы исследуем каждую из этих концепций.{b} _ {a} \ | \ vecs r ′ (t) \ | dt. \ label {Arc3D} \ end {align} \]

Эти две формулы очень похожи; они отличаются только тем, что пространственная кривая имеет три составляющие функции вместо двух. Обратите внимание, что формулы определены для гладких кривых: кривых, где вектор-функция \ (\ vecs r (t) \) дифференцируема с ненулевой производной. Условие гладкости гарантирует, что кривая не имеет изгибов (или углов), которые могут сделать формулу проблематичной.

Пример \ (\ PageIndex {1} \): определение длины дуги

Рассчитайте длину дуги для каждой из следующих векторных функций:

\ (\ vecs r (t) = (3t − 2) \, \ hat {\ mathbf {i}} + (4t + 5) \, \ hat {\ mathbf {j}}, \ quad 1≤t≤ 5 \)
\ (\ vecs r (t) = ⟨t \ cos t, t \ sin t, 2t⟩, 0≤t≤2 \ pi \)

Решение

Используя уравнение \ ref {Arc2D}, \ (\ vecs r ′ (t) = 3 \, \ hat {\ mathbf {i}} + 4 \, \ hat {\ mathbf {j}} \), поэтому

\ [\ begin {align *} s & = \ int ^ {b} _ {a} \ | \ vecs r ′ (t) \ | dt \\ [4pt] & = \ int ^ {5} _ {1 } \ sqrt {3 ^ 2 + 4 ^ 2} dt \\ [4pt] & = \ int ^ {5} _ {1} 5 dt = 5t \ big | ^ {5} _ {1} = 20.{3/2}) ≈37,785 \) шт.

Вернемся к спирали, представленной ранее в этой главе. Векторную функцию, описывающую спираль, можно записать в виде

\ [\ vecs r (t) = R \ cos \ left (\ dfrac {2πNt} {h} \ right) \, \ hat {\ mathbf {i}} + R \ sin \ left (\ dfrac {2πNt} {h} \ right) \, \ hat {\ mathbf {j}} + t \, \ hat {\ mathbf {k}}, 0≤t≤h, \ nonumber \]

, где \ (R \) представляет радиус спирали, \ (h \) представляет высоту (расстояние между двумя последовательными витками), а спираль совершает \ (N \) витков.2}. \ End {align *} \]

Это дает формулу для длины провода, необходимой для образования спирали с \ (N \) витками, имеющими радиус \ (R \) и высоту \ (h \).

Параметризация длины дуги

Теперь у нас есть формула для длины дуги кривой, определяемой векторной функцией. Давайте сделаем еще один шаг и рассмотрим, что такое функция длины дуги .

Если вектор-функция представляет положение частицы в пространстве как функцию времени, то функция длины дуги измеряет, как далеко эта частица перемещается как функция времени.2} ди. \ label {arclength3} \]

Если кривая двухмерная, то под квадратным корнем внутри интеграла появляются только два члена. Причина использования независимой переменной и состоит в том, чтобы различать время и переменную интегрирования. Поскольку \ (s (t) \) измеряет пройденное расстояние как функцию времени, \ (s ′ (t) \) измеряет скорость частицы в любой момент времени. Поскольку у нас есть формула для \ (s (t) \) в уравнении \ ref {arclength3}, мы можем дифференцировать обе части уравнения:

\ [\ begin {align *} s ′ (t) & = \ dfrac {d} {dt} \ bigg [\ int ^ {t} _ {a} \ sqrt {(f ′ (u)) ^ 2+ (g ′ (u)) ^ 2+ (h ′ (u)) ^ 2} du \ bigg] \\ [4pt] & = \ dfrac {d} {dt} \ bigg [\ int ^ {t} _ { a} ‖ \ vecs r ′ (u) ‖du \ bigg] \\ [4pt] & = \ | \ vecs r ′ (t) \ |.{t} _ {a} ‖ \ vecs r ′ (u) ‖ \, du \]

Кроме того,

\ [\ dfrac {ds} {dt} = ‖ \ vecs r ′ (t) ‖> 0. \ nonumber \]

Если \ (‖ \ vecs r ′ (t) ‖ = 1 \) для всех \ (t≥a \), то параметр \ (t \) представляет длину дуги от начальной точки в \ (t = a \ ).

Полезное применение этой теоремы — найти альтернативную параметризацию данной кривой, называемую параметризацией длины дуги . Напомним, что любую векторную функцию можно повторно параметризовать с помощью замены переменных.Например, если у нас есть функция \ (\ vecs r (t) = ⟨3 \ cos t, 3 \ sin t⟩, 0≤t≤2π \), которая параметризует круг радиуса 3, мы можем изменить параметр с \ (t \) to \ (4t \), получив новую параметризацию \ (\ vecs r (t) = ⟨3 \ cos 4t, 3 \ sin 4t⟩ \). Новая параметризация по-прежнему определяет круг радиуса 3, но теперь нам нужно использовать только значения \ (0≤t≤π / 2 \), чтобы пройти круг один раз.

Предположим, что мы нашли функцию длины дуги \ (s (t) \) и можем решить эту функцию для \ (t \) как функцию \ (s \) . Затем мы можем повторно параметризовать исходную функцию \ (\ vecs r (t) \), подставив выражение для \ (t \) обратно в \ (\ vecs r (t) \). Векторнозначная функция теперь записывается в терминах параметра \ (s \) . Поскольку переменная \ (s \) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \ (\ vecs r (t) \). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное по кривой, начиная с \ (s = 0 \), теперь равно параметру \ (s \).Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.

Пример \ (\ PageIndex {2} \): поиск параметризации длины дуги

Найдите параметризацию длины дуги для каждой из следующих кривых:

\ (\ vecs r (t) = 4 \ cos t \, \ hat {\ mathbf {i}} + 4 \ sin t \, \ hat {\ mathbf {j}}, \ quad t≥0 \)
\ (\ vecs r (t) = ⟨t + 3,2t − 4,2t⟩, \ quad t≥3 \)

Решение

Сначала мы находим функцию длины дуги, используя уравнение \ ref {arclength3}:
\ [\ begin {align *} s (t) & = \ int_a ^ t ‖ \ vecs r ′ (u) ‖ \, du \\ [4pt] & = \ int_0 ^ t ‖⟨ − 4 \ sin u, 4 \ cos u⟩‖ \, du \\ [4pt] & = \ int_0 ^ t \ sqrt {(- 4 \ sin u) ^ 2 + (4 \ cos u) ^ 2} \, du \\ [4pt] & = \ int_0 ^ t \ sqrt {16 \ sin ^ 2 u + 16 \ cos ^ 2 u} \, du \\ [4pt] & = \ int_0 ^ t 4 \, du = 4t, \ end {align *} \]
, который дает соотношение между длиной дуги \ (s \) и параметром \ (t \) как \ (s = 4t; \), то есть \ (t = s / 4 \).Затем мы заменяем переменную \ (t \) в исходной функции \ (\ vecs r (t) = 4 \ cos t \, \ hat {\ mathbf {i}} + 4 \ sin t \, \ hat {\ mathbf {j}} \) с выражением \ (s / 4 \), чтобы получить
\ [\ vecs r (s) = 4 \ cos \ left (\ frac {s} {4} \ right) \, \ hat {\ mathbf {i}} + 4 \ sin \ left (\ frac {s} {4} \ right) \, \ hat {\ mathbf {j}}. \ nonumber \]
Это параметризация длины дуги для \ (\ vecs r (t) \). Поскольку исходное ограничение на \ (t \) было задано как \ (t≥0 \), ограничение на s становится \ (s / 4≥0 \) или \ (s≥0 \).t 3 \, du \\ [4pt] & = 3t — 9. \ end {align *} \]
Следовательно, связь между длиной дуги \ (s \) и параметром \ (t \) равна \ (s = 3t − 9 \), поэтому \ (t = \ frac {s} {3} +3 \). Подставляя это в исходную функцию \ (\ vecs r (t) = ⟨t + 3,2t − 4,2t⟩ \), получаем
\ [\ vecs r (s) = ⟨\ left (\ frac {s} {3} +3 \ right) +3, \, 2 \ left (\ frac {s} {3} +3 \ right) — 4, \, 2 \ left (\ frac {s} {3} +3 \ right)⟩ = ⟨\ frac {s} {3} +6, \ frac {2s} {3} +2, \ frac {2s } {3} + 6⟩. \ Nonumber \]
Это параметризация длины дуги \ (\ vecs r (t) \).Первоначальное ограничение на параметр \ (t \) было \ (t≥3 \), поэтому ограничение на \ (s \) равно \ ((s / 3) + 3≥3 \) или \ (s≥0 \).

Упражнение \ (\ PageIndex {2} \)

Найдите функцию длины дуги для спирали

\ [\ vecs r (t) = ⟨3 \ cos t, 3 \ sin t, 4t⟩, \ quad t≥0. \ nonumber \]

Затем используйте взаимосвязь между длиной дуги и параметром \ (t \), чтобы найти параметризацию длины дуги для \ (\ vecs r (t) \).

Подсказка

Начните с поиска функции длины дуги.

Ответ

\ (s = 5t \) или \ (t = s / 5 \). Подставляя это в \ (\ vecs r (t) = ⟨3 \ cos t, 3 \ sin t, 4t⟩ \), получаем

\ [\ vecs r (s) = ⟨3 \ cos \ left (\ frac {s} {5} \ right), 3 \ sin \ left (\ frac {s} {5} \ right), \ frac { 4s} {5}⟩, \ quad s≥0 \ nonumber \]

Кривизна

Кривизна — важный аспект, связанный с длиной дуги. Концепция кривизны позволяет определить, насколько круто поворачивает плавная кривая.Круг имеет постоянную кривизну. Чем меньше радиус круга, тем больше кривизна.

Представьте, что вы едете по дороге. Предположим, дорога лежит по дуге большого круга. В этом случае вам почти не придется крутить руль, чтобы оставаться на дороге. Теперь предположим, что радиус меньше. В этом случае вам потребуется более крутой поворот, чтобы оставаться на дороге. В случае кривой, отличной от окружности, часто бывает полезно сначала вписать окружность в кривую в данной точке так, чтобы она касалась кривой в этой точке и «обнимала» кривую как можно ближе в точке. окрестность точки (рис. \ (\ PageIndex {1} \)).Кривизна графика в этой точке затем определяется как такая же, как кривизна вписанной окружности.

Рисунок \ (\ PageIndex {1} \): график представляет кривизну функции \ (y = f (x). \) Чем круче поворот графика, тем больше кривизна и тем меньше радиус вписанный круг.

Определение: кривизна

Пусть \ (C \) будет гладкой кривой на плоскости или в пространстве, заданном как \ (\ vecs r (s) \), где \ (s \) — параметр длины дуги. Кривизна \ (κ \) в точке \ (s \) равна

\ [κ = \ bigg {\ |} \ dfrac {d \ vecs {T}} {ds} \ bigg {\ |} = ‖ \ vecs T ′ (s) ‖.\]

Посетите это видео, чтобы получить дополнительную информацию о кривизне пространственной кривой.

Формула для определения кривизны не очень полезна с точки зрения расчета. В частности, напомним, что \ (\ vecs T (t) \) представляет единичный касательный вектор к заданной векторнозначной функции \ (\ vecs r (t) \), а формула для \ (\ vecs T (t) \) равно

\ [\ vecs T (t) = \ frac {\ vecs r ′ (t)} {∥ \ vecs r ′ (t) ∥}. \]

Чтобы использовать формулу для кривизны, сначала необходимо выразить \ (\ vecs r (t) \) через параметр длины дуги \ (s \), затем найти единичный касательный вектор \ (\ vecs T ( s) \) для функции \ (\ vecs r (s) \), затем возьмем производную от \ (\ vecs T (s) \) по \ (s \).Это утомительный процесс. К счастью, есть эквивалентные формулы для кривизны.

Теорема: альтернативные формулы кривизны

Если \ (C \) — гладкая кривая, заданная формулой \ (\ vecs r (t) \), то кривизна \ (κ \) кривой \ (C \) в точке \ (t \) равна

\ [κ = \ dfrac {‖ \ vecs T ′ (t) ‖} {‖ \ vecs r ′ (t) ‖}. \ label {EqK2} \]

Если \ (C \) — трехмерная кривая, то кривизна может быть задана формулой

\ [κ = \ dfrac {‖ \ vecs r ′ (t) × \ vecs r ′ ′ (t) ‖} {‖ \ vecs r ′ (t) ‖ ^ 3}.{3/2}}. \ Label {EqK4} \]

Проба

Первая формула следует непосредственно из цепного правила:

\ [\ dfrac {d \ vecs {T}} {dt} = \ dfrac {d \ vecs {T}} {ds} \ dfrac {ds} {dt}, \ nonumber \]

где \ (s \) — длина дуги вдоль кривой \ (C \). Разделив обе стороны на \ (ds / dt \) и взяв величину обеих сторон, получим

\ [\ bigg {\ |} \ dfrac {d \ vecs {T}} {ds} \ bigg {\ |} = \ left \ lVert \ frac {\ vecs T ′ (t)} {\ dfrac {ds} {dt}} \ right \ rVert. \ nonumber \]

Так как \ (ds / dt = ‖ \ vecs r ′ (t) ‖ \), это дает формулу кривизны \ (κ \) кривой \ (C \) в терминах любой параметризации \ (C \ ):

\ [κ = \ dfrac {‖ \ vecs T ′ (t) ‖} {‖ \ vecs r ′ (t) ‖}.3}. \ Nonumber \]

Это доказывает \ (\ ref {EqK3} \). Чтобы доказать \ (\ ref {EqK4} \), мы начнем с предположения, что кривая \ (C \) определяется функцией \ (y = f (x) \). Затем мы можем определить \ (\ vecs r (t) = x \, \ hat {\ mathbf {i}} + f (x) \, \ hat {\ mathbf {j}} + 0 \, \ hat {\ mathbf {к}} \). Используя предыдущую формулу кривизны:

\ [\ begin {align *} \ vecs r ′ (t) & = \, \ hat {\ mathbf {i}} + f ′ (x) \, \ hat {\ mathbf {j}} \\ [4pt ] \ vecs r ″ (t) & = f ″ (x) \, \ hat {\ mathbf {j}} \\ [4pt] \ vecs r ′ (t) × \ vecs r ″ (t) & = \ begin {vmatrix} \ hat {\ mathbf {i}} & \ hat {\ mathbf {j}} & \ hat {\ mathbf {k}} \\ 1 & f ′ (x) & 0 \\ 0 & f ″ ( x) & 0 \ end {vmatrix} = f ″ (x) \, \ hat {\ mathbf {k}}.3

Модуль 24 — Векторы — Урок 1

В этом уроке вы научитесь определять векторы на TI-89 и выполнять три типа умножения векторов. Будут обсуждены единичные векторы, и будут идентифицированы два формата, используемых для обозначения векторов.

Определение векторов

Величины, которые имеют как величину, так и направление, называются векторами и часто представлены направленными отрезками линий, как показано ниже.

Показанный вектор имеет начальную точку на O и конечную точку на P .

Представление векторов с помощью скобок

Векторы могут быть представлены на TI-89, задав координаты кончика стрелки. Например, вектор, идущий от начала координат к точке (3, 2), представлен на TI-89 с обозначением [3, 2].Обратите внимание на использование скобок вместо скобок для обозначения того, что величина является вектором.

Выполнить NewProb
Сохраните вектор [3, 2] в переменной a на вашем TI-89.

Вам нужно ввести «запятую» между компонентами при вводе вектора на TI-89, но калькулятор не отображает его, когда он отображает векторы.Этот факт проиллюстрирован на снимке экрана выше.

Определение единичных векторов i и j

Вектор i имеет длину одну единицу и указывает вдоль положительной оси x , а вектор j имеет длину одну единицу и указывает вдоль положительной оси y .Поскольку векторы i и j имеют длину равную единице, они называются единичными векторами. И i , и j показаны ниже вместе с вектором [3, 2].

Представление векторов с использованием i и j

В другом обозначении для представления вектора используются единичные векторы i и j . Вектор [3, 2] также можно записать как

a = 3 i + 2 j

Обратите внимание, что a , i и j выделены жирным шрифтом, что означает, что они являются векторами.

Нахождение длины вектора

Длина или величина любого вектора a = [x, y] равна

Длина a = [3, 2] равна единицы.

Векторное умножение

Есть три типа умножения, в которых используются векторы.Два типа создают вектор, а оставшийся тип дает действительное число. Каждый тип умножения обсуждается ниже.

Скалярное умножение векторов

Пусть c представляет собой

Скаляр — это действительное число.У него есть величина, но нет направления.

скаляр и a представляют вектор, скалярное кратное c a — вектор, длина которого равна | c | умноженное на длину a и направление такое же, как a , если c положительное, и направление, противоположное a , если c отрицательное.

Координаты c a находятся путем умножения каждой координаты a на c .

c a = c [ a ₁, a ₂] = [ ca  ₁, ca  ₂]

Сохраните вектор [3, -1] в переменной a на вашем калькуляторе и умножьте вектор на скаляр 2.
Умножьте вектор [2, -5] на скаляр 3, не сохраняя вектор в переменной.

Использование команды unitV

Вектор, который указывает в том же направлении, что и a , и имеет величину, равную единице, можно найти с помощью команды unitV .

Определите единичный вектор, который указывает в том же направлении, что и a = [3, 2].

Откройте меню Math, нажав
Откройте подменю Матрица, выбрав 4: Матрица и нажав
Прокрутите до L: Vector ops

Откройте подменю векторной операции, нажав

Пункт меню «1: unitV (» должен быть выделен.

Нажмите чтобы вставить его в строку редактирования
Введите unitV (a)

Каждый компонент a был умножен на величину, обратную величине a , чтобы создать единичный вектор, который указывает в том же направлении, что и a . Обратите внимание, что дроби были

Рационализация (знаменатель): дробь рационализируется путем записи ее в виде эквивалентной дроби без радикалов в знаменателе.

рационализировать.

Нахождение скалярных произведений векторов

Второй тип умножения называется скалярным произведением .Скалярное произведение двух векторов [ a ₁, a ₂] и [ b ₁, b ₂] определяется как a ₁ · b ₁ + a ₂ · b ₂.
Скалярное произведение a и b можно найти с помощью команды dotP , которая находится в меню Math Matrix: Vector ops.

Сохраните вектор -2 i + 5 j в b

Вычислите скалярное произведение a · b .

Откройте подменю Матрица в меню Математика.
Откройте подменю: Vector ops подменю Matrix.

Вставьте dotP (в строку редактирования
Введите dotP (a, b)

Скалярное произведение a · b равно 4.

Обратите внимание, что результатом скалярного произведения двух векторов является действительное число , а не вектор. Скалярное произведение равно произведению величины a , величины b и косинуса угла между a и b .
Если это угол между a и b

Точечные произведения широко используются в физике.Например, они используются для расчета работы, выполняемой силой, действующей на объект.

Проецирование одного вектора на другой вектор

Проекцию можно рассматривать как тень одного вектора на другом. Когда два вектора имеют одинаковую начальную точку, проекция b на a параллельна a и имеет длину тени b .На схеме ниже показана проекция b на a , записанная как proj _a b и показанная более темным вектором.

Проекции и точечные произведения

Величина проекции b на a , | proj _a b | также называется компонентом из b вдоль a , и она равна | b | соз ,Обратите внимание, что компонент b вдоль a равен a · b / | а |.

Поиск формулы для точечных произведений на вашем калькуляторе

Формула для нахождения скалярного произведения двух векторов [ a ₁, a ₂] и [ b ₁, b ₂] может быть получена на TI-89.

Введите dotP ([a1, a2], [b1, b2])

24.1.1 Напишите формулу для нахождения скалярного произведения двух векторов. Щелкните здесь, чтобы получить ответ.

Определение перекрестных продуктов

Третий тип умножения называется перекрестным произведением и используется в геометрии и во многих ситуациях в физике и технике.Перекрестное произведение a x b двух трехмерных векторов — это вектор, который на перпендикулярен как a , так и b . Если — угол между a и b , тогда длина a x b определяется как

Перекрестное произведение определяется только для 3-мерных векторов, но TI-89 вычисляет перекрестное произведение 2-мерных векторов, рассматривая их как 3-мерные векторы с 0 в качестве третьего компонента.

Поиск перекрестных продуктов

Перекрестное произведение можно вычислить с помощью команды crossP , которая находится в меню операций Math Matrix Vector.

Найдите векторное произведение a x b ранее определенных векторов a = [3, 2] и b = [-2, 5].

[3, 2, 0] x [-2, 5, 0] = [0, 0, 19] = 0 i + 0 j + 19 k

Результатом перекрестного произведения является вектор , который имеет три компонента, что означает, что это трехмерный вектор.Единичный вектор k указывает вдоль положительной оси z. Вектор 0 i + 0 j + 19 k направлен вверх вдоль положительной оси z и имеет длину 19.

Перекрестное произведение двух векторов a и b всегда перпендикулярно каждому из двух векторов. Его величина равна величине a , умноженной на величину компонента b , которая перпендикулярна a .

24.1.2 Найдите векторное произведение трехмерных векторов a = 2 i + j — 4 k и b = — i — 2 j + k . Опишите связь между a , b и их перекрестным произведением. Щелкните здесь, чтобы проверить свой ответ.

Величина векторного определения, формулы и задачи

- Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  000 NC Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT Exemplar Class
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  0004
  000300030004
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000
  000 Microology
  000
  000 Microology
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000 PBS4000
  000300030002 Примеры калькуляторов химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел. для класса 12
  CBSE — вопросник за предыдущий год
  CBSE — вопросник за предыдущий год, класс 10
  CBSE — за предыдущий год — вопросник, класс 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  Решения HC Verma, класс 12, физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Заметки CBSE
  , класс
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  CBSE
  Примечания к редакции класса 10 CBSE
  Примечания к редакции класса 11 CBSE 9000 4
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по науке класса 9 CBSE
  Дополнительные вопросы по математике для класса 10
  Дополнительные вопросы по науке, класс 10 по CBSE
  CBSE, класс
  , класс 3
  , класс 4
  , класс 5
  , класс 6
  , класс 7
  , класс 8
  , класс 9 Класс 10
  Класс 11
  Класс 12
  Учебные решения
  Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для класса 11 по физике
  Решения NCERT для класса 11 Химия
  Решения для биологии класса 11
  Решения NCERT для математики класса 11
  9 0003 NCERT Solutions Class 11 Accountancy
  NCERT Solutions Class 11 Business Studies
  NCERT Solutions Class 11 Economics
  NCERT Solutions Class 11 Statistics
  NCERT Solutions Class 11 Commerce
  NCERT Solutions For Class 12
  NCERT Solutions For Класс 12 по физике
  Решения NCERT для химии класса 12
  Решения NCERT для класса 12 по биологии
  Решения NCERT для класса 12 по математике
  Решения NCERT Класс 12 Бухгалтерия
  Решения NCERT, класс 12, бизнес-исследования
  Решения NCERT, класс 12 Экономика
  NCERT Solutions Class 12 Accountancy Part 1
  NCERT Solutions Class 12 Accountancy Part 2
  NCERT Solutions Class 12 Micro-Economics
  NCERT Solutions Class 12 Commerce
  NCERT Solutions Class 12 Macro-Economics
  NCERT Solutions For Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для математики класса 6
  Решения NCERT для науки класса 6
  Решения NCERT для социальных наук класса 6
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для класса 7 Наука
  Решения NCERT для класса 7 по социальным наукам
  Решения NCERT для класса 7 Английский
  Решения NCERT для класса 8
  Решения NCERT для класса 8 Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для социальных наук 8 класса
  Решение NCERT ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для социальных наук класса 9
  Решения NCERT для математики класса 9
  Решения NCERT для математики класса 9 Глава 1
  Решения NCERT для Математика класса 9 Глава 2
  Решения NCERT для математики класса 9 Глава 3
  Решения NCERT для математики класса 9 Глава 4
  Решения NCERT
  для математики класса 9 Глава 5
  Решения NCERT для математики класса 9 Глава 6
  Решения NCERT для Математика класса 9 Глава 7
  Решения NCERT для математики класса 9 Глава 8
  Решения NCERT
  для математики класса 9 Глава 9
  Решения NCERT
  для математики класса 9 Глава 10
  Решения NCERT для математики класса 9 Глава 11
  Решения NCERT для Математика класса 9 Глава 12
  Решения NCERT для математики класса 9 Глава 13
  Решения
  NCERT для математики класса 9 Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки класса 9
  Решения NCERT для науки класса 9 Глава 1
  Решения NCERT для науки класса 9 Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для Науки Класса 9 Глава 4
  Решения NCERT для Науки Класса 9 Глава 5
  Решения NCERT для Науки Класса 9 Глава 6
  Решения NCERT для Науки Класса 9 Глава 7
  Решения NCERT для Класса 9 Наука Глава 8
  Решения NCERT для Науки Класса 9 Глава 9
  Решения NCERT для Науки Класса 9 Глава 10
  Решения NCERT для Науки Класса 9 Глава 12
  Решения NCERT для Науки Класса 9 Глава 11
  Решения NCERT для Класса 9 Наука Глава 13
  Решения NCERT для класса 9 Наука Глава 14
  Решения NCERT для класса 9 по науке Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 по социальным наукам
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  Решения NCERT для математики класса 10 Глава 3
  Решения NCERT для математики класса 10 Глава 4
  Решения NCERT для математики класса 10 Глава 5
  Решения NCERT для математики класса 10 Глава 6
  Решения NCERT для математики класса 10 Глава 7
  Решения NCERT для математики класса 10 Глава 8
  Решения NCERT для математики класса 10 Глава 9
  Решения NCERT
  для математики класса 10 Глава 10
  Решения
  NCERT для математики класса 10 Глава 11
  Решения NCERT для математики класса 10 Глава 12
  Решения NCERT для математики класса 10 Глава 13
  NCERT Sol Решения NCERT для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки класса 10
  Решения NCERT для науки класса 10 Глава 1
  Решения NCERT для науки класса 10 Глава 2
  Решения NCERT для науки класса 10, глава 3
  Решения NCERT для науки класса 10, глава 4
  Решения NCERT для науки класса 10, глава 5
  Решения NCERT для науки класса 10, глава 6
  Решения NCERT для науки класса 10, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки класса 10 Глава 9
  Решения NCERT для науки класса 10 Глава 10
  Решения NCERT для науки класса 10 Глава 11
  Решения NCERT для науки класса 10 Глава 12
  Решения NCERT для науки 10 класса Глава 13
  Решения NCERT для науки 10 класса Глава 14
  Решения NCERT для науки 10 класса Глава 15
  Решения NCERT для науки 10 класса Глава 16
  Учебный план NCERT
  NCERT
  Commerce
  Class 11 Commerce Syllabus
  ancy Account
  Программа бизнес-исследований 11 класса
  Учебная программа по экономике 11 класса
  Учебная программа по коммерции 12 класса
  Учебная программа по бухгалтерии 12 класса
  Учебная программа по бизнесу 12 класса
  Учебная программа по экономике
  9000 9000
  Образцы коммерческих документов класса 11
  Образцы коммерческих документов класса 12
  TS Grewal Solutions
  ,
  Вывод формулы проекции вектора с решенными примерами
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
  КОНКУРСНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  000 NC Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT Exemplar Class
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  0004
  000300030004
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000
  000 Microology
  000
  000 Microology
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000 PBS4000
  000300030002 Примеры калькуляторов химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел. для класса 12
  CBSE — вопросник за предыдущий год
  CBSE — вопросник за предыдущий год, класс 10
  CBSE — за предыдущий год — вопросник, класс 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  Решения HC Verma, класс 12, физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Заметки CBSE
  , класс
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  CBSE
  Примечания к редакции класса 10 CBSE
  Примечания к редакции класса 11 CBSE 9000 4
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по науке класса 9 CBSE
  Дополнительные вопросы по математике для класса 10
  Дополнительные вопросы по науке, класс 10 по CBSE
  CBSE, класс
  , класс 3
  , класс 4
  , класс 5
  , класс 6
  , класс 7
  , класс 8
  , класс 9 Класс 10
  Класс 11
  Класс 12
  Учебные решения
  Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для класса 11 по физике
  Решения NCERT для класса 11 Che
  ,
  No related posts.

Вычисление длины (модуля) вектора в EXCEL. Примеры и описание

1. Вычисление длины вектора по его координатам

2. Нахождение длины вектора через координаты точек

3. Нахождение длины вектора по теореме косинусов

4. Нахождение длины вектора через координаты точек треугольника

5. Нахождение координат вектора через координаты точек

Формулы векторов

1. Координаты вектора

2. Длина или модуль вектора

3. Сумма векторов

4. Умножение вектора на число

5. Скалярное произведение векторов

6. Векторное произведение векторов

7. Смешанное произведение векторов

8. Угол между векторами

9. Проекция вектора на вектор

Как найти длину вектора? — Студопедия

Нахождение длины вектора по координатам.

Длина вектора, онлайн калькулятор

Определение координат вектора заданного координатами его начальной и конечной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

Формула определения координат вектора для пространственных задач

Формула определения координат вектора для n -мерного пространства

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Примеры для пространственных задач

Примеры для n -мерного пространства

Сумма векторов, длина вектора

13.3: Длина и кривизна дуги

Параметризация длины дуги

Кривизна

Модуль 24 — Векторы — Урок 1

Величина векторного определения, формулы и задачи

Вывод формулы проекции вектора с решенными примерами

Добавить комментарий Отменить ответ