Формула синуса квадрат – Синус в квадрате, формула и примеры

Содержание

Чему равен синус квадрат альфа, косинус квадрат альфа и тангенс квадрат альфа?

синус квадрата альфа= 2синус альфа умноженое на косинус альфа. косинус квадрата альфа = 2 косинус квадрат минус 1 тангенс квадрата альфа= 2тангенс альфа деленое на 1 минус тангенс квадрата альфа

по отдельности или это всё перемножается?

синус квадрат альфа равен 1-косинус квадрат альфа, косинус квадрат альфа равен=1-синус квадрат альфа

чему равен минус синус квадрат альфа?

touch.otvet.mail.ru

Полная таблица всех тригонометрических формул приведения

ГЛАВНАЯ
- расчеты
- мониторинг
- консалтинг
ОБЪЕКТЫ
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
ОНЛАЙН
- сосуды и аппараты
- трубопроводы
- прочие
- математика
МАТЕРИАЛЫ
- статьи
- презентации
- отчеты
- log-files
- прочие
ЛИТЕРАТУРА
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие

Карта сайта

Искать…

cae-cube.ru

Гиперболические функции свойства графики формулы

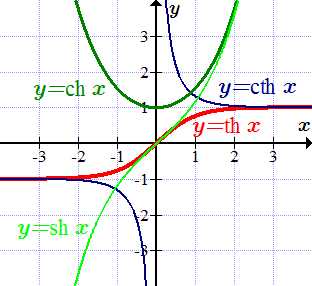
Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.

Определения гиперболических функций, их области определений и значений

sh x — гиперболический синус

, –∞ < x < +∞; –∞ < y < +∞.

ch x — гиперболический косинус

, –∞ < x < +∞; 1 ≤ y < +∞.

th x — гиперболический тангенс

, –∞ < x < +∞; – 1 < y < +1.

cth x — гиперболический котангенс

, x ≠ 0; y < –1 или y > +1.

Графики гиперболических функций

График гиперболического синуса y = sh x

График гиперболического косинуса y = ch x

График гиперболического тангенса y = th x

График гиперболического котангенса y = cth x

Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i² = –1.

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.

Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.

Разность квадратов

ch² x – sh² x = 1.

Формулы суммы и разности аргументов

sh(x &pm; y) = sh x ch y &pm; ch x sh y,
ch(x &pm; y) = ch x ch y &pm; sh x sh y,
,
,

sh 2x = 2 sh x ch x ,
ch 2x = ch² x + sh² x = 2 ch² x – 1 = 1 + 2 sh² x,
.

Формулы произведений гиперболического синуса и косинуса

,
,
,

,
,
.

Формулы суммы и разности гиперболических функций

,
,
,
,
.

Связь гиперболического синуса и косинуса с тангенсом и котангенсом

, ,
, .

Производные

Интегралы от sh x, ch x, th x, cth x

,
,
.

Разложения в ряды

sh x

ch x

th x

cth x

Обратные функции

Ареасинус

При – ∞ < x < ∞ и – ∞ < y < ∞ имеют место формулы:
,
.

Ареакосинус

При 1 ≤ x < ∞ и 0 ≤ y < ∞ имеют место формулы:
,
.

Вторая ветвь ареакосинуса расположена при 1 ≤ x < ∞ и – ∞ < y ≤ 0 :
.

Ареатангенс

При – 1 < x < 1 и – ∞ < y < ∞ имеют место формулы:
,
.

Ареакотангенс

При – ∞ < x < – 1 или 1 < x < ∞ и y ≠ 0 имеют место формулы:
,
.

Автор: Олег Одинцов. Опубликовано: 27-07-2014

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

1cov-edu.ru

как вывести забытую тригонометрическую формулу?

На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

Основное тригонометрическое тождество: sin²a+cos²a = 1
Определение тангенса:
Определение котангенса:
Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
Формула косинуса суммы: cos(a+b) = cosacosb—sinasinb

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb—cosasinb
Косинус разности: cos(a-b) = cosacos(-b)—sinasin(-b) = cosacosb+sinasinb

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
Косинус двойного угла: cos2a = cos(a+a) = cosacosa—sinasina = cos²a—sin²a

Аналогично получаются и формулы других кратных углов:

Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos²a—sin²a)sina = 2sinacos²a+sinacos²a—sin³a = 3sinacos²a—sin³a = 3sina(1-sin²a)-sin³a = 3sina-4sin³a
Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa—sin2asina = (cos²a—sin²a)cosa-(2sinacosa)sina = cos³a-sin²acosa-2sin²acosa = cos³a-3sin²acosa = cos³a-3(1-cos²a)cosa = 4cos³a-3cosa

Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол — острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sina = 3,а cosa = 4.
(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin²a+cos²a = 1 и разделим его на cos²a. Получим:

Связь тангенса и косинуса:

Так что решением этой задачи будет:

(Т.к. угол острый, при извлечении корня берётся знак +)

Аналогично получаем связь котангенса и синуса:

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:

Сразу выводится и

Формула тангенса двойного угла:

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:
cos2a = cos²a—sin²a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos²a—sin²a+cos²a+sin²a
2cos²a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:

Косинус половинного угла:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим:
cos2a-1 = cos²a—sin²a—cos²a—sin²a
2sin²a = 1-cos2a

Cинус половинного угла:

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y. Тогда
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

Представление суммы синусов в виде произведения:

Сразу же можно вывести

Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

www.intelmath.narod.ru

Квадрат — косинус — Большая Энциклопедия Нефти и Газа, статья, страница 1

Квадрат — косинус

Cтраница 1

Квадрат косинуса быстро меняется на интервалах Дг, малых по сравнению с рассматриваемыми расстояниями. [1]

Квадраты косинусов всегда положительные. Знаменатели в выражениях (1.16) и (1.18) также положительные, а в выражении (1.17) отрицательные. [2]

Среднее значение квадрата косинуса равно половине. [3]

В квадратичном члене представим квадрат косинуса в виде cos2 ( Фд — Ф5) [ 1 cos 2 ( Ф — Ф5) ] / 2, откуда видно, что этому члену, с одной стороны, соответствует косинусоидальная решетка двойной пространственной частоты, обусловливающая появление пучка второго порядка дифракции, с другой стороны, — постоянная составляющая, вносящая вклад в пучок нулевого порядка. В го-лографической схеме Лейта и Упатниекса нелинейность, которая выражается только квадратичным членом, так мала, что не проявится при реконструкции. [4]

Интенсивность излучения будет пропорциональна квадрату косинуса угла между направлениями колебаний и излучения. [5]

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат его синуса. [6]

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат его синуса. [7]

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла. [8]

Косинус двойного аргумента равен разности квадратов косинуса и синуса данного аргумента. [9]

Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине. [10]

Косинус двойного угла равен разности квадратов косинуса и синуса данного угла. [11]

Косинус двойного аргумента равен разности квадратов косинуса и синуса данного аргумента. [12]

Косинус двойного угла равен разности квадратов косинуса и синуса данного угла. [13]

В табл. 2.3 приведены средние значения квадратов косинусов углов рассеяния и ориентации для различных предельных значений параметров Л и Л, характеризующих входной и выходной каналы. [15]

Страницы: 1 2 3 4