Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
| Формулы для стороны, периметра и площади правильного n – угольника |
| Формулы для стороны, периметра и площади правильного треугольника |
| Формулы для стороны, периметра и площади правильного шестиугольника |
| Формулы для стороны, периметра и площади квадрата |
Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.
Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.
Замечание 1. В любой правильный многоугольник можно вписать окружность.
В любой правильный многоугольник можно вписать окружность.
Замечание 2. Около любого правильного многоугольника можно описать окружность.
Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Используемые обозначения
| Число вершин правильного многоугольника | Сторона правильного многоугольника | Радиус вписанной окружности | Радиус описанной окружности | Периметр | Площадь |
| n | a | r | R | P | S |
| Число вершин правильного многоугольника | n |
| Сторона правильного многоугольника | a |
| Радиус вписанной окружности | r |
| Радиус описанной окружности | R |
| Периметр | P |
| Площадь | S |
Формулы для стороны, периметра и площади правильного
n – угольника| Величина | Рисунок | Формула | Описание |
| Периметр | P = an | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Площадь | Выражение площади через сторону | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного n – угольника |
Выражение периметра через сторону P = an Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного n – угольника |
Выражение площади через сторону и радиус вписанной окружности Выражение площади через сторону Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного n – угольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного треугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 3a | Выражение периметра через сторону | |
| Площадь | Посмотреть вывод формулы | Выражение площади через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного треугольника |
Выражение периметра через сторону P = 3a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного треугольника |
Выражение площади через сторону Посмотреть вывод формулы Выражение площади через сторону и радиус вписанной окружности Выражение площади через радиус вписанной окружности Посмотреть вывод формулы Выражение площади через радиус описанной окружности Посмотреть вывод формулы |
| Формулы для стороны правильного треугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного шестиугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 6a | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону | ||
| Площадь | S = 3ar | Выражение площади через сторону и радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | a = R | Выражение стороны через радиус описанной окружности | |
| Периметр | P = 6R | Выражение периметра через радиус описанной окружности | |
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного шестиугольника |
Выражение периметра через сторону P = 6a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности P = 6R |
| Формулы для площади правильного шестиугольника |
Выражение площади через сторон Выражение площади через сторону и радиус вписанной окружности S = 3ar Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного шестиугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности a = R |
Формулы для стороны, периметра и площади квадрата
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 4a | Выражение периметра через сторону | |
| Площадь | S = a2 | Выражение площади через сторону | |
| Сторона | a = 2r | Выражение стороны через радиус вписанной окружности | |
| Периметр | P = 8r | Выражение периметра через радиус вписанной окружности | |
| Площадь | S = 4r2 | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | S = 2R2 | Выражение площади через радиус описанной окружности |
| Формулы для периметра квадрата |
Выражение периметра через сторону P = 4a Выражение периметра через радиус вписанной окружности P = 8r Выражение периметра через радиус описанной окружности |
| Формулы для площади квадрата |
Выражение площади через сторону S = a2 Выражение площади через радиус вписанной окружности S = 4r2 Выражение площади через радиус описанной окружности S = 2R2 |
| Формулы для стороны квадрата |
Выражение стороны через радиус вписанной окружности a = 2r Выражение стороны через радиус описанной окружности |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
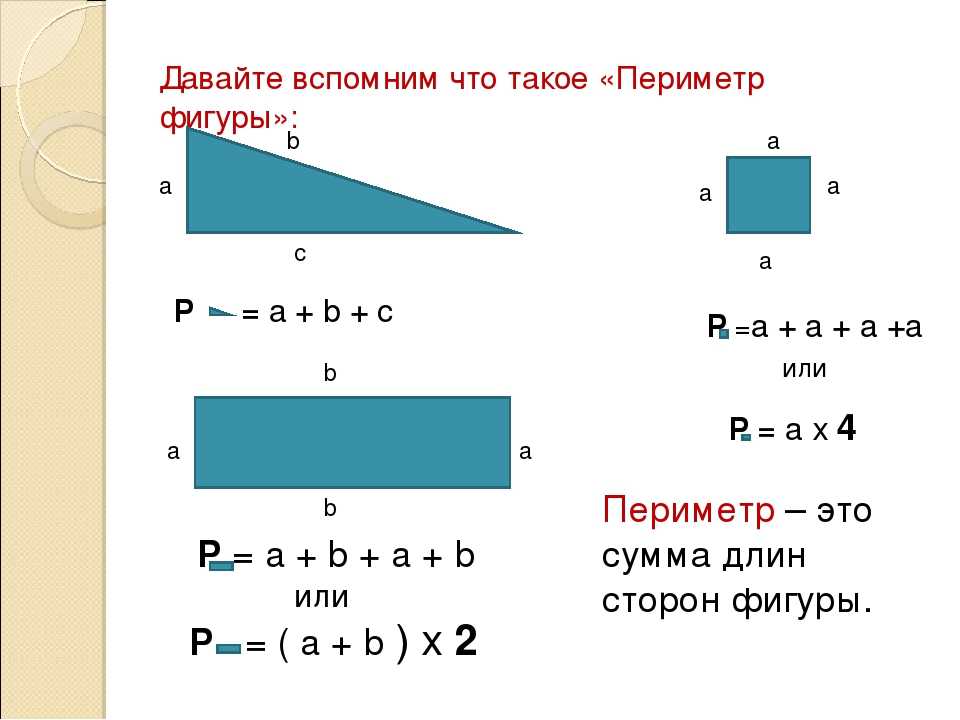
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Каждой ваше пожертвование увеличивает количество полезной и интересной информации на сайте Easy-Math.ru!
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле \({\color{red} P=2\cdot (a+b)}\) , площадь – по формуле \({\color{red} S=a\cdot b}\) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
\({\color{red} a + b = 24 : 2 = 12}\) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной \({\color{red} 12 : 2 = 6}\) см.
Тогда площадь этого квадрата равна
\({\color{red}S_{k}=6\cdot 6=36}\) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
\({\color{red} S–S _{k}=36-32=4}\) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной.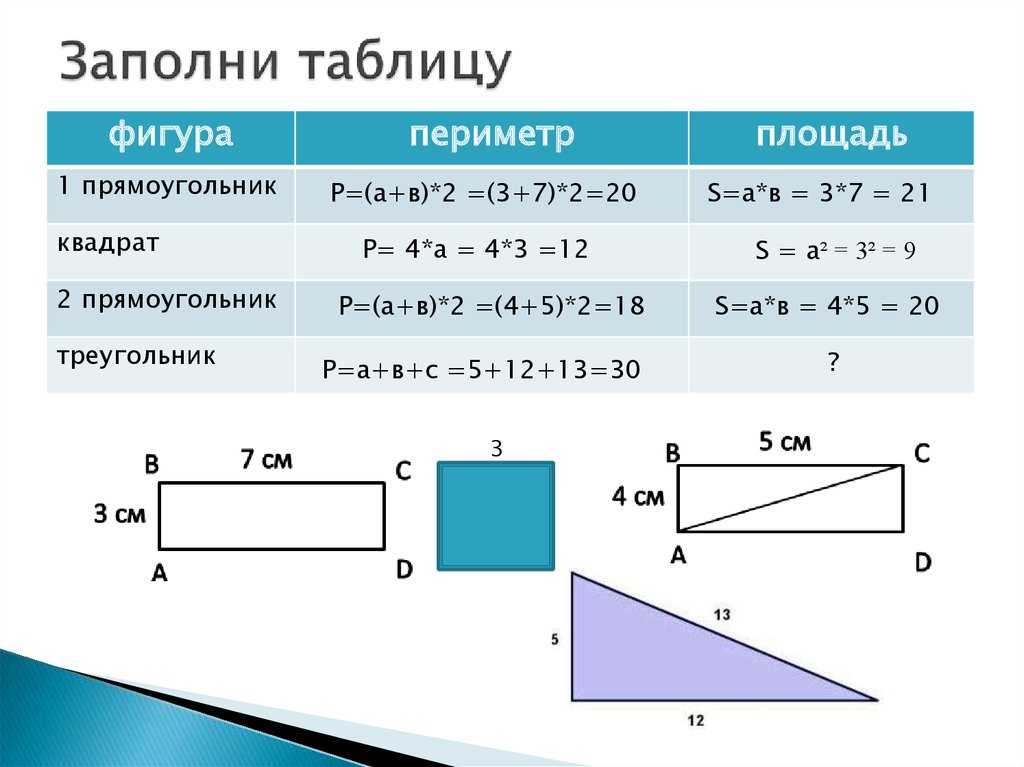 То есть, ширину уменьшить, а длину увеличить на одно и то же число.
То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
\({\color{red} a=6-2=4}\) см
а длина:
\({\color{red} b=6+2=8}\) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
\({\color{red} P=2\cdot (4+8)=2\cdot 12=24}\) см
\({\color{red} S=4\cdot 8=32}\) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
\({\color{red} a+b=46:2=23}\) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица.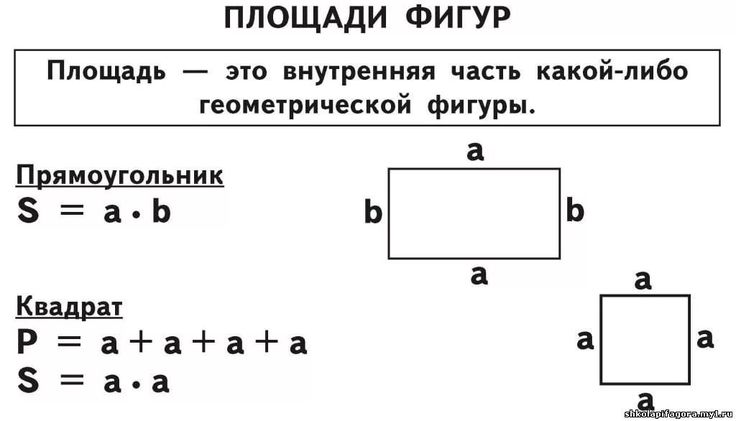 Это прямоугольник со сторонами 11 и 12, т.к. \({\color{red} 23=11+12}\).
Это прямоугольник со сторонами 11 и 12, т.к. \({\color{red} 23=11+12}\).
Площадь такого прямоугольника равна:
\({\color{red}S_{2}=11\cdot 12=132}\) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
\({\color{red}S_{2}-S=132-126=6}\) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
\({\color{red} a=11-2=9}\) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
\({\color{red} b=12+2=14}\) см.
Проведем проверку:
\({\color{red} P=2\cdot (9+14)=2\cdot 23=46}\) см.
\({\color{red}S=9\cdot 14=126}\) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.5 / 5. Количество оценок: 4
Оценок пока нет. Поставьте оценку первым.
Вам также пригодится:
Определение стоимости по площади или периметру – Математика 3-го класса
Бывают случаи, когда вам нужно покрыть площадь или пространство тканью или плиткой.
Или, может быть, вы хотите выровнять периметр таким материалом, как дерево.
Проекты, требующие материалов, например, покраска стены или строительство забора, стоят денег.
Так что важно планировать заранее и видеть, как много денег вам нужно, чтобы закончить свой проект.
👉 Это называется найти стоимость вашего проекта.
Давайте узнаем, как определить стоимость покрытия или облицовки формы на нескольких примерах. 😺
Пример 1: Ограждение катка
Джек хочет построить ограждение вокруг катка. Каток 20 метра длина и 40 метра ширина .Стоимость материалов для перил $ 10 . 00 на счетчик . Сколько стоит установка перил вокруг катка?
Перила будут огибать каток.
Итак, нам нужно найти его периметр!
К найти периметр пространства, прибавить длину всех сторон.
Чертеж модель каток поможет нам разобраться.
Длина катка 20 метров. Его ширина составляет 40 метров.
Помните: Противоположные стороны в прямоугольнике имеют одинаковую длину.
Таким образом, наше уравнение:
20 + 20 + 40 + 40 = 120
👉 Периметр катка состоит из 120 (или 120 м) .
До знать общая стоимость до строка a периметр с материалом, умножить периметр на стоимость метра.
120 м × 10 долл. США = 1 200 долл. США
Общая стоимость ограждения катка составляет 1 200 долл. США . ✅
Пример 2. Покрытие выставочного стенда художественной бумагой
Покрытие выставочного стенда художественной бумагой Дисплейный стенд имеет размеры 8 футов высоты и 5 футов 4 9003 ширины. Стоит $ 2 на квадратный фут , чтобы покрыть его художественной бумагой. Какова общая стоимость покрытия всей выставочной доски художественной бумагой?
Чтобы найти площадь фигуры , умножить ширину на высоту.
Нарисуем доску.
Теперь умножаем длину на на ширину :
8 x 5 = 40
0003 футов (или 40 футов²) .
Чтобы узнать общая стоимость до покрытие и площадь , умножьте площадь на стоимость единицы площади.
🖐 Пауза на мгновение. Прочитайте ключевой момент выше еще раз 👆. Это важно.
40 футов² x 2 доллара США за фут² = 80 долларов США
Общая стоимость покрытия всего картона художественной бумагой составляет 80 долларов США . ✅
Отличная работа! 🎉
А теперь попробуйте потренироваться.
Периметр сектора — математика GCSE
Введение
Как найти периметр сектора
Периметр рабочего листа сектора
Как решать задачи с периметром сектора
Распространенные заблуждения
Похожие уроки
Практика периметр сектора вопросы
Периметр сектора Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как найти периметр сектора
Периметр рабочего листа сектора
Как решать задачи на периметр сектора
Распространенные заблуждения
Похожие уроки
Практика периметр сектора вопросы
Периметр сектора вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о вычислении 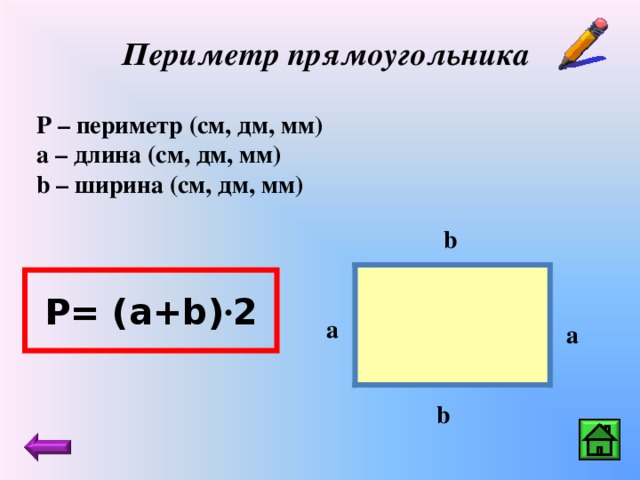
Существуют также рабочие листы по периметру сектора, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое периметр сектора?
Периметр сектора — это расстояние вокруг сектора.
Мы можем вычислить периметр сектора, сложив длины двух радиусов и длину дуги сектора.
Напр.
Вычислите периметр нижнего сектора с точностью до 1 знака после запятой: 9o и r = 8 , поэтому
\begin{aligned} \text { Длина дуги }&=\frac{115}{360} \times 2 \times \pi \times 8 \\\\ &=16.05702912 \ldots \ end{aligned}
Чтобы вычислить периметр сектора, нам нужно добавить длину дуги к длинам двух радиусов:
Формула периметра сектора:
\begin{align} \text { Периметр сектора }&= \text{Длина дуги + радиус + радиус}\\\\ &=16.05702912 + 8 + 8\\\\ &=32.05702912\ldots\\\\ &=32,1 \;см\; (1.д.п) \end{выровнено}
Каков периметр сектора?
Как найти периметр сектора
Чтобы найти периметр сектора:
- Найдите длину диаметра/радиуса.

- Найдите величину угла, образующего дугу сектора.
- Найдите длину дуги сектора.
- Сложите длину дуги и два радиуса.
- Четко сформулируйте свой ответ .
Объясните, как найти периметр сектора
Периметр рабочего листа сектора
Получите бесплатный периметр рабочего листа сектора из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксПериметр рабочего листа сектора
Получите бесплатный периметр рабочего листа сектора из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры периметра сектора
Пример 1: расчет периметра сектора (квадранта)
Расчет периметра сектора сектора.
Дайте ответ с точностью до 3 знаков после запятой.
- Найдите длину диаметра/радиуса.
Радиус = 6 см
2 Найдите величину угла, образующего дугу сектора.
Угол = 9о . Обозначается символом прямого угла.
3 Найдите длину дуги сектора.
\text{Длина дуги} = \frac{\theta}{360} \times 2\times\pi \times r
\begin{align} &=\frac{90}{360} \times 2\ times\pi \times 6 \\\\ &=3\pi \end{aligned}
4 Сложите длину дуги и два радиуса.
Длина дуги: 3\pi \; см
Радиус: 6 \; см
\text{Суммарный периметр сектора } = 3\pi + 6 +6 \; см
\text{Суммарный периметр сектора } = 3\pi + 12 \; см
5 Четко сформулируйте свой ответ.
На вопрос предлагается округлить ответ до 3 знаков после запятой
\text{Периметр сектора} = 3\pi + 12 \; см
\text{Длина дуги} = 21,424777..см
\text{Длина дуги} = 21,425 \; см
Помните, что периметр сектора является мерой расстояния, поэтому единицы измерения не возводятся в квадрат.
Пример 2: расчет периметра сектора (полукруга) 9о . Это потому, что показанная форма представляет собой полукруг. Следовательно, угол прямой равен 180 градусов.
Найдите длину дуги сектора.
\text{Длина дуги} = \frac{\theta}{360} \times \pi\times d
\begin{align} &=\frac{180}{360} \times \pi\times 24 \\\\ &=12\pi \end{aligned}
Сложите длину дуги и два радиуса.
Длина дуги: 12\pi \; см
Диаметр: 24 \; см
Радиус: 12 \; см
\text{Суммарный периметр сектора } = 12\pi + 12 +12 \; см
\text{Суммарный периметр сектора } = 12\pi + 24 \; см
Четко сформулируйте свой ответ.
На вопрос предлагается дать ответ в единицах числа пи
\text{Периметр сектора } = 12\pi + 24 \; см
Этот ответ выражен в пи
Пример 3: вычислить периметр сектора (с заданным углом) 9o
Найти длину дуги сектора.
\text{Длина дуги} = \frac{\theta}{360} \times 2\times\pi \times r
\begin{aligned} &=\frac{117}{360} \times 2\times\pi \times 5.5 \\\\ &=\frac{143}{40} \pi \end{aligned}
Сложите длину дуги и два радиуса.
Длина дуги: \frac{143}{40} \pi \; см
Радиус 5,5 \; см
\text{Суммарный периметр сектора } = \frac{143}{40} \pi + 5,5 +5,5 \; см
\text{Суммарный периметр сектора } = \frac{143}{40} \pi + 11 \; см
Четко сформулируйте свой ответ.
В вопросе предлагается округлить ответ до трех значащих цифр
\text{Периметр сектора } = \frac{143}{40} \pi + 11 \; см
\text{Периметр сектора} = 22,2311…см
\text{Периметр сектора} = 22,2 \; см
Пример 4: расчет периметра сектора (угол не указан)
Вычислить периметр сектора сектора AOB ниже;
Длина радиуса (ОВ) 9см.
Длина хорды (АВ) 10см.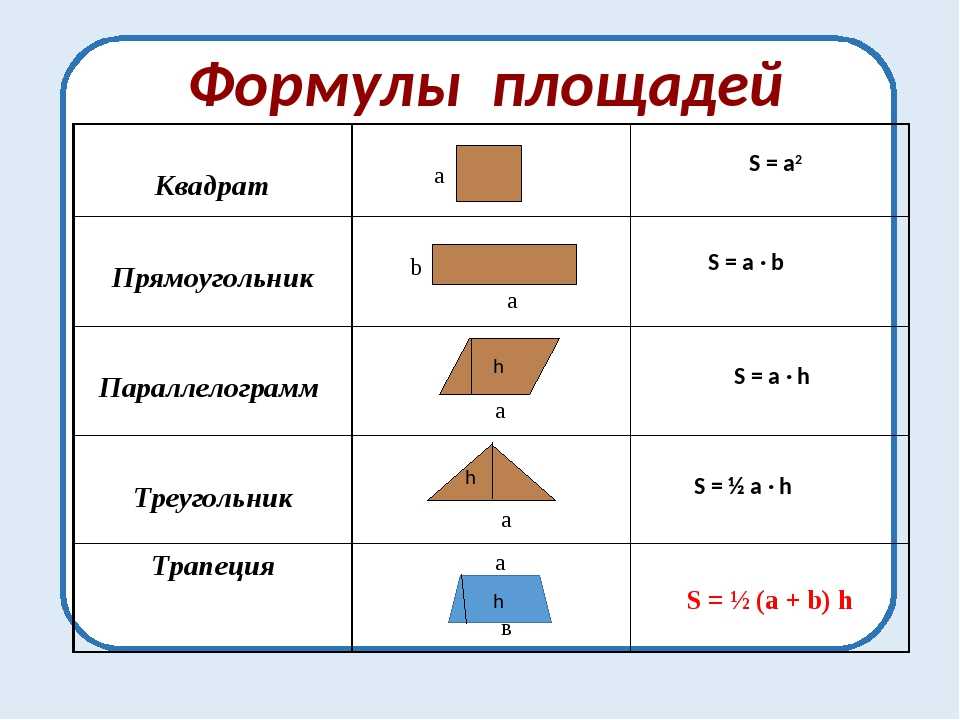
Дайте ответ с точностью до 1 знака после запятой.
Найдите длину диаметра/радиуса.
Радиус = 19\; см
Найдите величину угла, образующего дугу сектора.
В этом примере угол сектора не задан, его нужно сначала вычислить. 9о .
Найдите длину дуги сектора.
Поскольку вы знаете радиус, вы можете использовать формулу, в которой «r» является переменной.
\text{Длина дуги} = \frac{\theta}{360} \times 2\times\pi \times r
\begin{aligned} &=\frac{63.5}{360} \times 2 \times\pi \times 9 \\\\ &=21.057… \end{aligned}
Сложите длину дуги и два радиуса.
Длина дуги: 21,057 \; см Обратите внимание, как вы округляете это число до более чем окончательного Это делается для того, чтобы избежать ошибок округления.
Радиус 19 \; см
\text{Суммарный периметр сектора} = 21,057 + 19 + 19 \; см
\text{Суммарный периметр сектора} = 59,057 \; см
Четко сформулируйте свой ответ.
В вопросе вам предлагалось округлить ответ до 1 знака после запятой.
\text{Длина дуги} = 59,057 \; см
\text{Длина дуги} = 59,1 \; см
Как решать задачи на периметр сектора
Иногда вам могут дать периметр сектора и попросить найти свойство окружности, например радиус.
В этом случае вам необходимо «обратить» процесс.
- Четко укажите, какие свойства вам известны, а какие нет.
- Составьте уравнение для периметра сектора и подставьте известное значение. 9o
Периметр сектора = \; 20 см
Длина дуги = \; \frac{125}{360} \times 2\times\pi \times x
Длина дуги = \; \frac{25x}{36} \times\piСоставьте уравнение для периметра сектора и подставьте в него известное значение.

Периметр сектора = длина дуги + радиус + радиус
\begin{align} 20&=\frac{25}{36} \pi x+x+x \hspace{2.6cm} \text{ Подставить значения } \\\\ 20&=\frac{25}{36} \pi x+2 x \hspace{3cm} \text{Упростить} x+x \end{align}Решите уравнение, чтобы найти неизвестное свойство.
\begin{align} 20&=\frac{25}{36} \pi x+2 x \hspace{3cm} \text{Упрощение} x+x \\\\ 20&=x\left(\frac {25}{36} \pi+2\right) \hspace{2.5cm} \text{Взять } x \text{ out как множитель} \\\\ 20&=x(4.18166) \\\\ 20 \div 4.18166&=x \hspace{4.3cm} \text{Сделать } x \text{ темой}\\\\ 4.783 \ldots&=x \end{align}
Четко сформулируйте свой ответ.
На вопрос предлагается дать ответ с точностью до 2 знаков после запятой
x=4,783…
x=4,78Пример 6: нахождение угла сектора по периметру сектора
Сектор ниже имеет периметр 62 см и радиус 18 см.

Вычислите длину x.
Дайте вам ответ с точностью до 2 знаков после запятой.
Четко укажите, какие свойства вам известны, а какие нет.
Радиус = \; 18 9o
Периметр сектора = \; 62 см
\begin{aligned} \text { Длина дуги }&=\frac{x}{360} \times 2 \times \pi \times 18 \\\\ \text { Длина дуги }&= \frac{ 1}{10} \pi x \end{aligned}Составьте уравнение для периметра сектора и подставьте в него известное вам значение.
Периметр сектора = длина дуги + радиус + радиус
\begin{align} 62&=\frac{1}{10} \pi x+18+18 \hspace{2.3cm} \text{ Подставьте значения } \\\\ 62&=\frac{1}{10} \pi x+36 \hspace{3cm} \text{Упрощение} \\\\ 26&=\frac{1}{10} \pi x \end{выровнено}Решите уравнение, чтобы найти неизвестное свойство.
\begin{align} 26&=\frac{1}{10} \pi x \\\\ 26 \div \frac{\pi}{10}&=x \hspace{4.
 8cm} \text{ Сделайте } x \text{ темой}\\\\ 82.76057&=x \end{aligned}
8cm} \text{ Сделайте } x \text{ темой}\\\\ 82.76057&=x \end{aligned}Четко сформулируйте свой ответ.
В вопросе предлагается дать ответ с точностью до 2 знаков после запятой
x=82,76057…
x=82,76Распространенные заблуждения
- Нахождение длины дуги, а не периметра сектора
Вы должны помнить, что периметр сектора равен сумме длины дуги и двух радиусов.
- Единицы
Помните, что периметр — это длина, поэтому единицы измерения не будут возведены в квадрат или куб. Квадратные единицы относятся к площади, а кубические – к объему.
Периметр сектора – это часть нашей серии уроков, посвященных пересмотру кругов, секторов и дуг. Возможно, вам будет полезно начать с урока по основным кругам, секторам и дугам, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам.
 Другие уроки в этой серии включают в себя:
Другие уроки в этой серии включают в себя:- .
Практический периметр сектора вопросы
Окружность
Сектор
Малая дуга
Сектор с углом 360º представляет собой полный круг.
Следовательно, периметр сектора равен всей длине внешней стороны круга, которая называется окружностью. 92
7\pi +8 \; см
Общий периметр сектора = Длина дуги + радиус + радиус
Общий периметр сектора = 7\pi + 4 +4 \; см
Суммарный периметр сектора = 7\pi + 8 \; см
Суммарный периметр сектора = 29,9911 \; см
Суммарный периметр сектора = 30,0 \; см
Периметр сектора вопросы GCSE 9о.
Рассчитайте периметр сектора, дайте ваш ответ правильный к 3 значащим рисункам
(4 оценки)
Покажите ответ
\ FRAC {1500 {150 {150 {150 {150 {150 {150 ram {150 {150 ram {150 {150 {150 ram {150 ram {150 ram {150 ram {150 ram {150 ram {150 ram {150 ram {150 ram {150.
 \ times \ pi \ times 13 \ Quad or \ Quad 34.0339
\ times \ pi \ times 13 \ Quad or \ Quad 34.0339(1)
«34.0339” + 13 + 13(1)
699959
60.0339
6
60.0339
169
60.0339
169
60.0339
60.0339 616.
60,0 9oВычислите периметр сектора, дайте правильный ответ до 3-х значащих цифр.
(4 балла)
Показать ответ
\ FRAC {290} {360} \ Times 2 \ Times \ PI \ Times 6.5 \ Quad или Quad 32.899
(1)
69999959
(1)
6699999959
(1)
6699999999
(1) 9000 4
999999999
(1) 9000 4 9000
9999
. «32,899» + 13 + 13
(1)
58,899(1)
58,9oВычислите периметр сектора, ответьте правильно до двух значащих цифр.

(4 marks)
Show answer
\frac{60}{360} \times 2\times\pi \times 4.9 \quad or \quad 5.1312
(1)
«5,1312» + 4,9 + 4,9(1)
14,9312(1)
14,93(1)
4. Ниже показан сектор круга с периметром сектора 60 см и радиусом 10 см
Найдите величину угла, обозначенного x.
Дайте правильный ответ до 3-х значащих цифр.
(5 баллов)
Показать ответ
Правильная попытка составить уравнение для периметра сектора
60}{3=\frac жирныйсимвол{\pi} \times 10 + 20(1)
Попытка решить уравнение относительно x 2)
229,18(1)
229(1)
имеет сектор по периметру 5 см.


 Стоимость материалов для перил $ 10 . 00 на счетчик . Сколько стоит установка перил вокруг катка?
Стоимость материалов для перил $ 10 . 00 на счетчик . Сколько стоит установка перил вокруг катка?

 8cm} \text{ Сделайте } x \text{ темой}\\\\ 82.76057&=x \end{aligned}
8cm} \text{ Сделайте } x \text{ темой}\\\\ 82.76057&=x \end{aligned}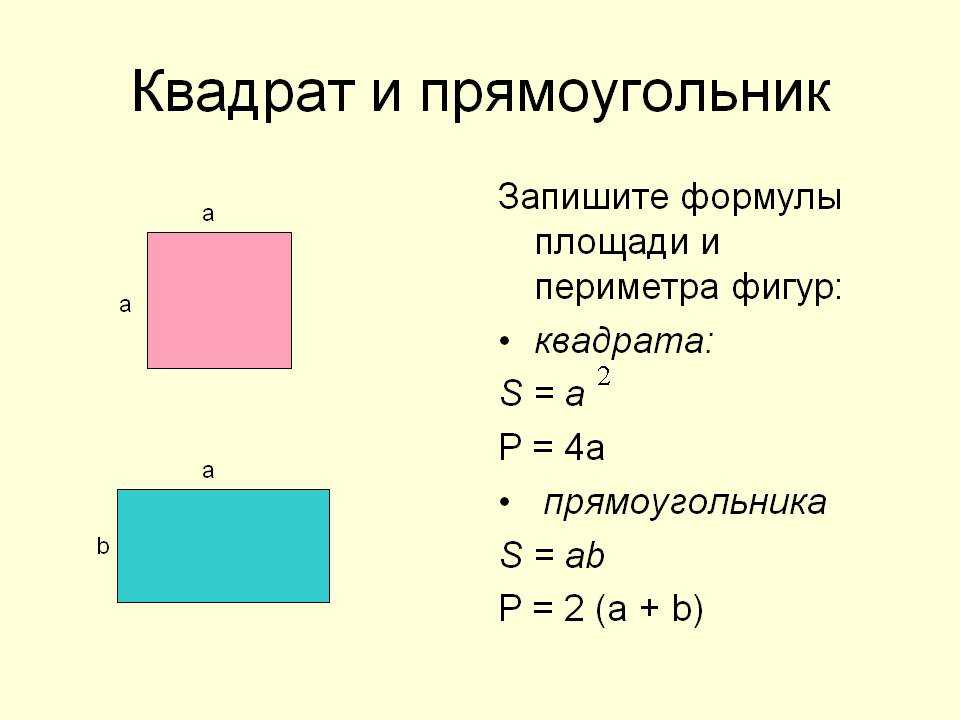 Другие уроки в этой серии включают в себя:
Другие уроки в этой серии включают в себя: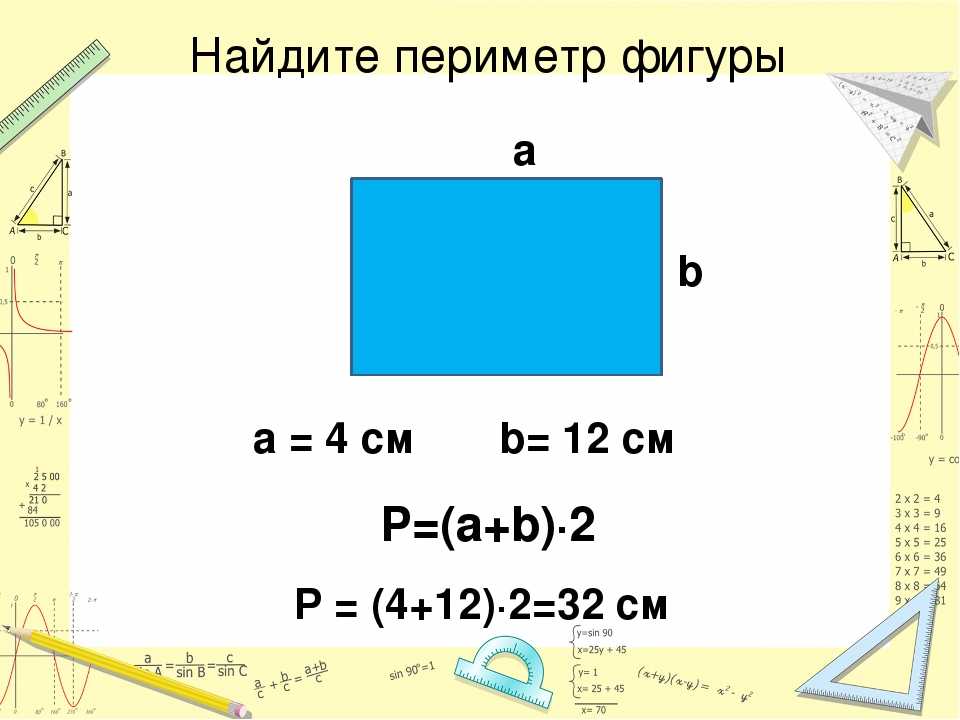 \ times \ pi \ times 13 \ Quad or \ Quad 34.0339
\ times \ pi \ times 13 \ Quad or \ Quad 34.0339
