Периметр прямого треугольника: Как найти периметр треугольника 🔺 формула нахождения

Находим периметр треугольника различными способами :: SYL.ru

Необычно изогнутые формы: тенденции в декорировании ванных комнат

Для зимних вечеров: рецепт традиционного напитка «Лондонский туман»

Прощаяющая душа: признаки здоровых отношений в паре

Перловка превращается в десерт. Готовим аппетитное блюдо

Аллегрова рассказала о чертах характера и счастье в личной жизни

Дисциплина: 6 важных привычек, которые облегчат жизнь вашим детям

Фарш из индейки: ошибки при его использовании в приготовлении разных блюд

Капуста не испортится. Как хранить соленье а холодильнике

Лосось стимулирует выработку серотонина: продукты, которые помогают детям спать

Румяные и нежные. Готовим выпечку как в школьной столовой

Автор Нина Даниленко April 20, 2015

Периметр любого треугольника – это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех сторон этого многоугольника.

Вычисление по данным значениям длины сторон

Когда известны их значения, то сделать это несложно. Обозначив эти параметры буквами m, n, k, а периметр буквой P, получим формулу для вычисления: P = m+n+k. Задание: Известно, что треугольник имеет стороны длиной 13,5 дециметров, 12,1 дециметров и 4,2 дециметра. Узнать периметр. Решаем: Если стороны данного многоугольника — a = 13,5 дм, b = 12,1 дм, c = 4,2 дм, то P = 29,8 дм. Ответ: P = 29,8 дм.

Периметр треугольника, который имеет две равные стороны

Такой треугольник называется равнобедренным. Если эти равные стороны имеют длину a сантиметров, а третья сторона – b сантиметров, то периметр легко узнать: P =b+2a. Задание: треугольник имеет две стороны по 10 дециметров, основание 12 дециметров. Найти P. Решение: Пусть боковая сторона a = c = 10 дм, основание b = 12 дм. Сумма сторон P = 10 дм + 12 дм + 10 дм = 32 дм. Ответ: P = 32 дециметра.

Периметр равностороннего треугольника

Если все три стороны треугольника имеют равное количество единиц измерения, он называется равносторонним. Еще одно название – правильный. Периметр правильного треугольника находят при помощи формулы: P = a+a+a = 3·a. Задача: Имеем равносторонний треугольный земельный участок. Одна сторона равна 6 метрам. Найти длину забора, которым можно обнести этот участок. Решение: Если сторона этого многоугольника a= 6м, то длина забора P = 3·6 = 18 (м). Ответ: P = 18 м.

Треугольник, у которого есть угол 90°

Его называют прямоугольным.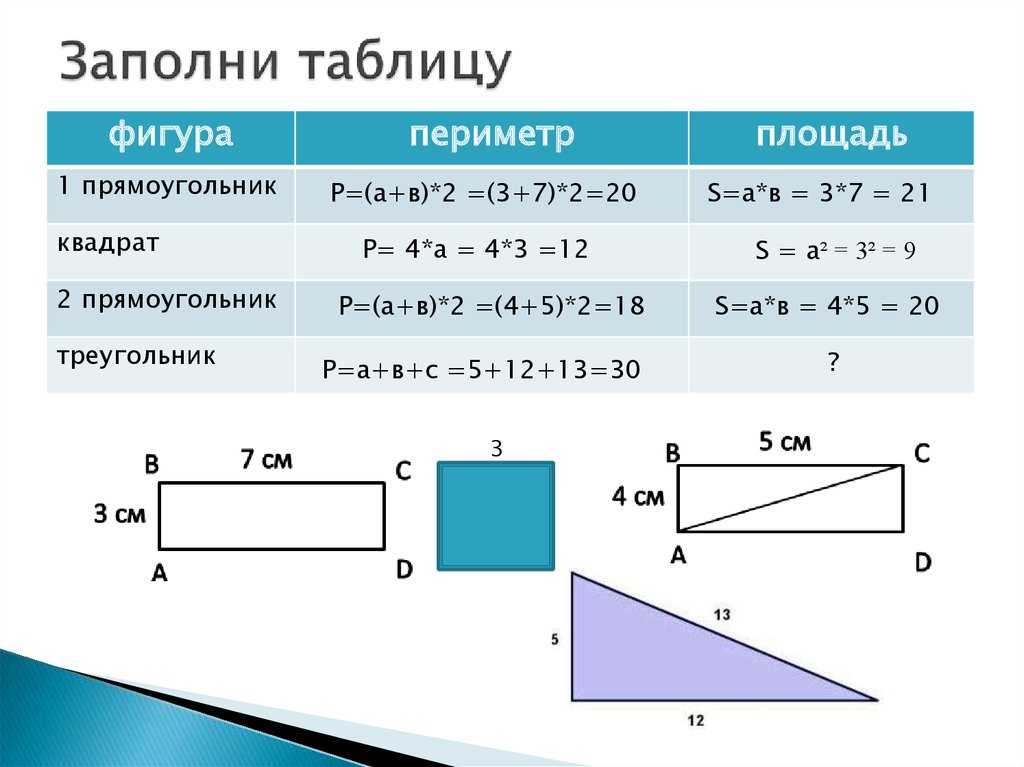 Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c² = a² + b². Катеты a = √ (c² – b²) и b = √ (c² – а²). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,3² + 6,2²) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,3² + 6,2²) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c² – b²) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов – 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (12² – 8²) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А – 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол – 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого – на синус и для второго – на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). Значит периметр этого многоугольника равен P = 9,1 + 7 + 5,8 = 21,9 (см). Или P = 9,1·(1 + 0,77 + 0,64) = 21,9 (см). Ответ: P = 21,9 сантиметров.

Произвольный треугольник, одна из сторон которого неизвестна

Если мы имеем значения двух сторон a и c, и угла между этими сторонами γ, третью находим теоремой косинусов: b ² = с² + a ² – 2 ас cos β, где β – угол, лежащий между сторонами а и с. Затем находим периметр. Задание: Δ АВС имеет отрезок АВ длиной 15 дм, отрезок АС, длина которго 30,5 дм. Значение угла между этими сторонами 35 градусов. Вычислить сумму сторон Δ АВС. Решение: Теоремой косинусов вычислим длину третей стороны.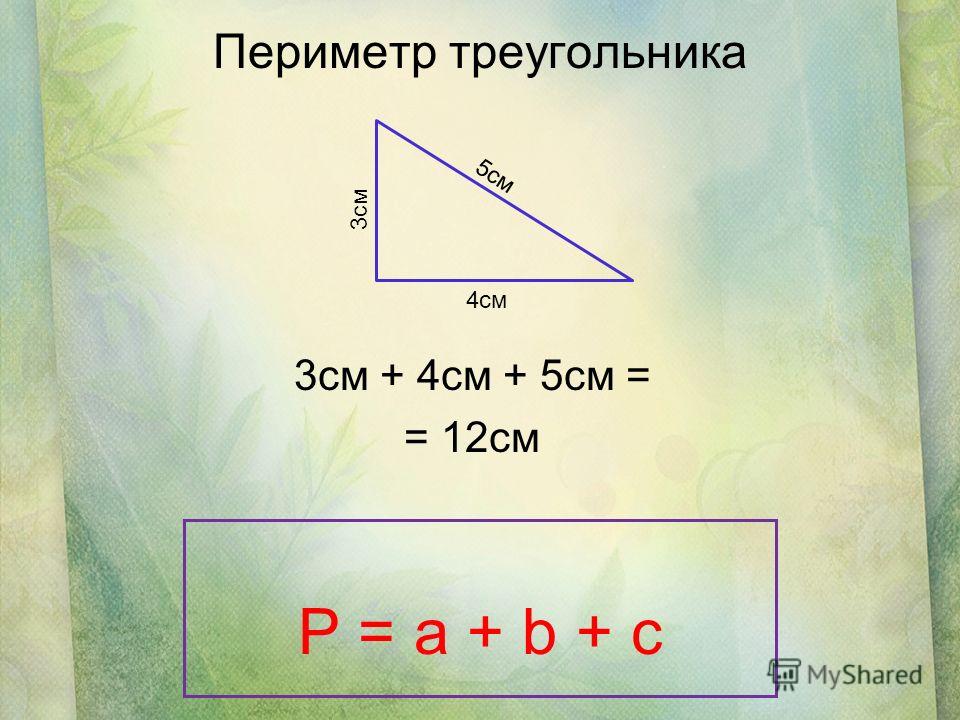 BC² = 30,5² + 15² — 2·30,5·15·0,82 = 930,25 + 225 – 750,3 = 404,95. BC = 20,1 см. P = 30,5 + 15 + 20,1 = 65,6 (дм).Имеем: P = 65,6 дм.

Сумма сторон произвольного треугольника, у которого длины двух сторон неизвестны

Когда знаем длину только одного отрезка и значение двух углов, можно узнать длину двух неизвестных сторон, пользуясь теоремой синусов: «в треугольнике стороны всегда пропорциональны значениям синусов противоположных углов». Откуда b = (a* sin β)/ sin a. Аналогично c = (a sin γ): sin a. Периметр в таком случае будет P = а + (а sin β)/ sin a + (a sin γ)/ sin a. Задание: Имеем Δ ABC. В нем длина стороны BC 8,5 мм, значение угла C – 47°, а угла B – 35 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим длины сторон BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α= 47°, ∟B = β = 35°, ∟ C = γ = 180° – (47° + 35°) = 180° – 82° = 98°. Из соотношений, полученных из теоремы синусов, находим катеты AC = b = (8,5·0,57): 0,73= 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм).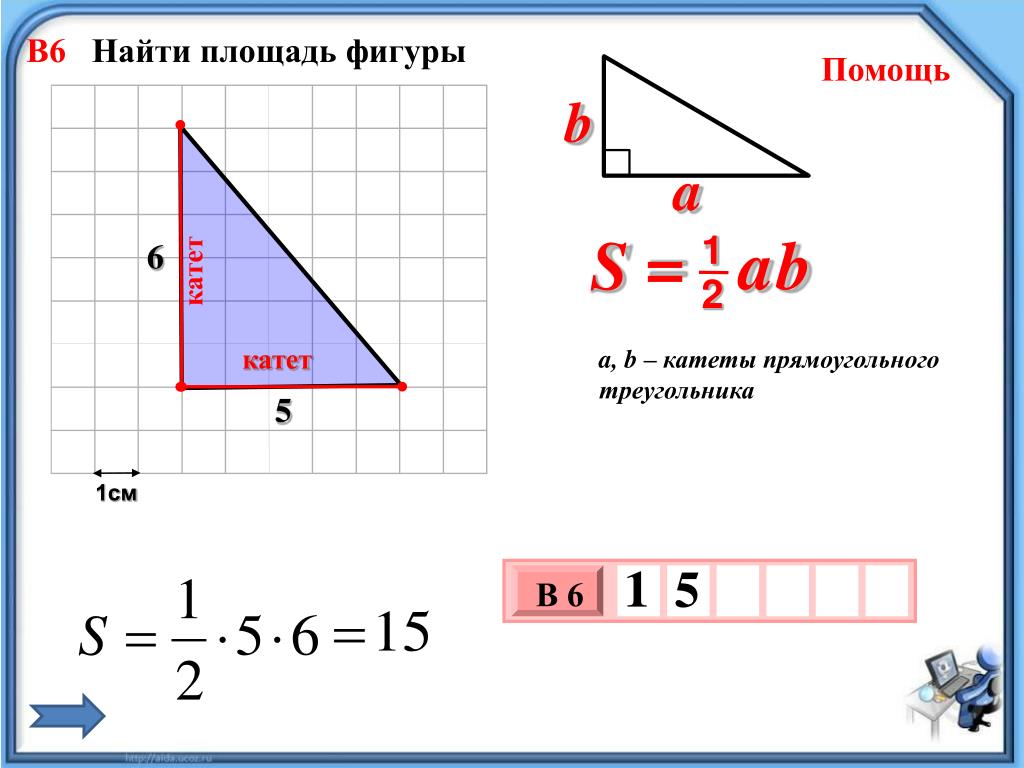 Отсюда сумма сторон этого многоугольника равна P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Ответ: P = 23,5 мм. В случае, когда есть только длина одного отрезка и значения двух прилежащих углов, сначала вычисляем угол, противоположный известной стороне. Все углы этой фигуры в сумме имеют 180 градусов. Поэтому ∟A = 180° — (∟B + ∟C). Дальше находим неизвестные отрезки, используя теорему синусов. Задание: Имеем Δ ABC. Он имеет отрезок BC, равный 10 см. Значение угла B равно 48 градусов, угол C равен 56 градусов. Найти сумму сторон Δ ABC. Решение: Сначала найдем значение угла A, противолежащего стороне BC. ∟A = 180° – (48° + 56°) = 76°. Теперь с теоремой синусов вычислим длину стороны AC = 10·0,74: 0,97 = 7,6 (см). AB = BC* sin C/ sin A = 8,6. Периметр треугольника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.

Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него

Иногда из условия задачи не известна ни одна сторона. Зато есть значение площади треугольника и радиуса окружности, вписанной в него. Эти величины связаны: S = r p. Зная значение площади треугольника, радиуса r, можем найти полупериметр p. Находим p = S: r. Задача: Участок имеет площадь 24 м², радиус r равен 3 м. Найти количество деревьев, которое нужно высадить равномерно по линии, ограждающей этот участок, если между двумя соседними должно быть расстояние 2 метра. Решение: Сумму сторон данной фигуры находим так: P = 2 · 24: 3 = 16 (м). Затем делим на два. 16:2= 8. Итого: 8 деревьев.

Сумма сторон треугольника в декартовых координатах

Вершины Δ АВС имеют координаты: A (x₁; y₁), B (x₂; y₂), C(x₃ ; y₃). Найдем квадраты каждой из сторон AB² = (x₁ — x₂)² + (y₁ — y₂)²; ВС²= (x₂ — x₃)² + (y₂ — y₃)²; АС² = (x₁ — x₃)² + (y₁ — y₃)².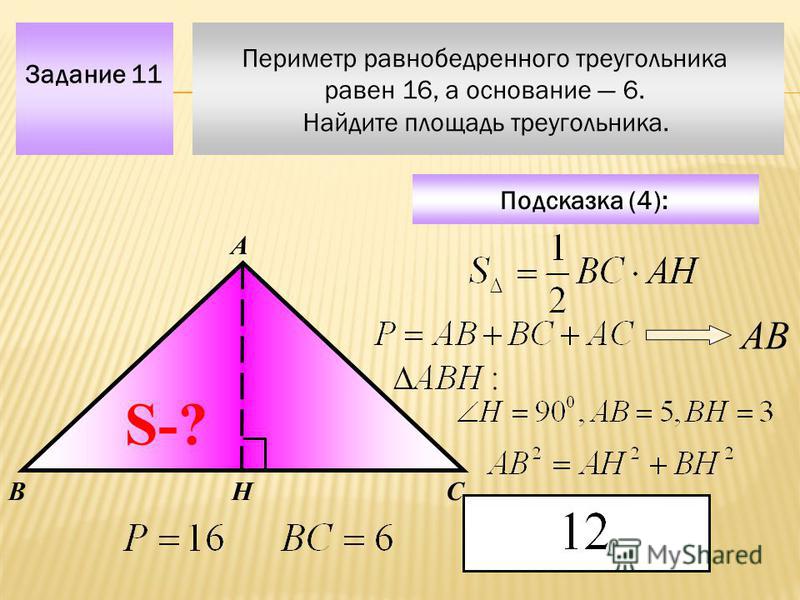 Чтобы найти периметр, достаточно сложить все отрезки. Задание: Координаты вершин Δ ABC: B (3; 0), A (1; -3), C (2; 5). Найти сумму сторон этой фигуры. Решение: поставив значения соответствующих координат в формулу периметра, получим P = √(4 + 9) + √(1 + 25) + √(1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 + 8,0 = 16,6. Имеем: P = 16,6. Если фигура находится не на плоскости, а в пространстве, то каждая из вершин имеет три координаты. Поэтому формула суммы сторон будет иметь еще одно слагаемое.

Векторный метод

Если фигура задана координатами вершин, периметр можно вычислить, используя векторный метод. Вектор – отрезок, имеющий направление. Его модуль (длина) обозначается символом ǀᾱǀ. Расстояние между точками – это и есть длина соответствующего вектора, или модуль вектора. Рассмотрим треугольник, лежащий на плоскости. Если вершины имеют координаты А (х

1; у₁), М(х₂; у₂), Т (х₃; у₃), то длину каждой из сторон находим по формулам: ǀАМǀ = √ ((х₁ – х₂)² + (у₁ – у₂)²), ǀМТǀ = √ ((х₂ – х₃)² + (у₂ – у₃)²), ǀАТǀ = √ ((х₁ – х₃)² + (у₁ – у₃)²). Периметр треугольника получим, сложив длины векторов. Аналогично находят сумму сторон треугольника в пространстве.

Похожие статьи

• Как найти длину окружности: через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
• Периметр квадрата и прямоугольника. Способы определения и примеры решения.
• Медиана треугольника: формула и свойства
• Как найти гипотенузу: 4 способа поиска ответа
• Признаки, составляющие элементы и свойства равнобедренного треугольника
• Как узнать площадь многоугольника?
• Как формулируется и доказывается теорема косинусов?

Также читайте

Онлайн тест по Математике по теме Периметр прямоугольного треугольника

Школьная программа занимается изучением геометрических фигур и нахождением их различных показателей в 4 классе.

Тест, проверяющий уровень знаний, а также подготовки по изученной тематике, состоит из 5 практических заданий. Очень удобно, что вначале теста есть ссылка на необходимый материал, который нужно усвоить перед его прохождением. В статье очень подробно рассказана вся информация с практическими примерами.

При ответе на первый вопрос теста необходимо знать составляющие для расчета периметра прямоугольного треугольника. Второе задание проверяет знание специализированной формулы для вычисления длины.

Третье упражнение — это практика. Есть числовые показатели катета и угла при гипотенузе. Нужно вычислить периметр. Четвертое — заключается в расчете длины прямоугольного треугольника, если известен катет и гипотенуза.

Последний заключительный пример также проверяет умение вычислить необходимую величину, когда известны катет и острый угол.

После ответов на все предложенные тестом задания программа показывает результат прохождения. Указывается количество правильных ответов. Это отличный инструмент контроля.

Тест очень удобен тем, что покажет уровень подготовки. При этом проверяет как теорию, так и ее применение на практике. И если остаются какие-либо пробелы и не до конца изученные моменты, их можно изучить, повторить еще раз.

---

---

Пройти тест онлайн

1. Имея какие данные, можно посчитать периметр прямоугольного треугольника?

Катет и гипотенузу


Гипотенузу и угол


Катет и угол


Все варианты верны

2. Назовите специализированную формулу периметра для прямоугольных треугольников

Половина произведения катетов


Половина основания на высоту


Утроенное произведение катетов


Такой формулы нет

3.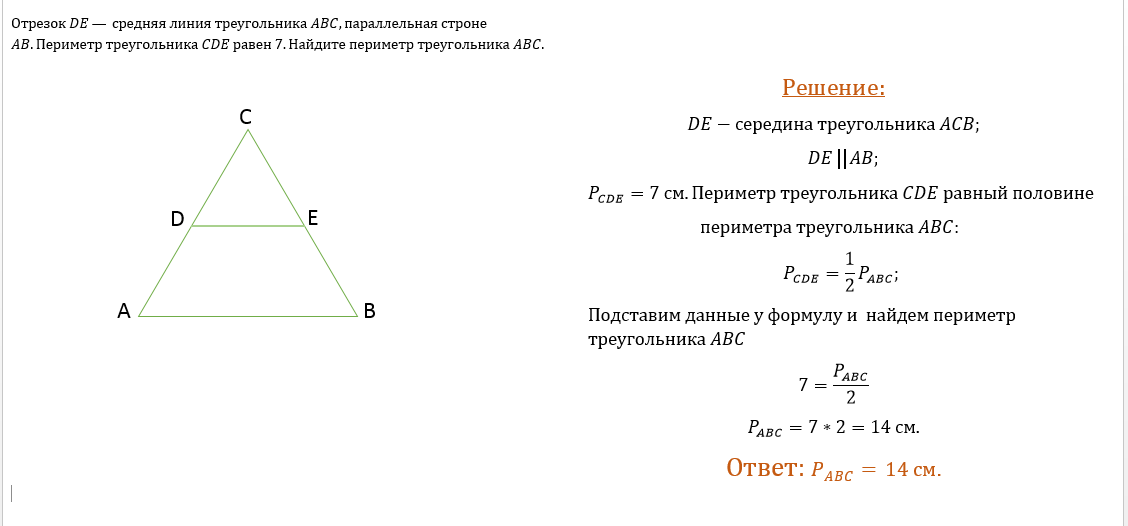 Чему равен периметр прямоугольного треугольника, если катет равен 5, а угол при гипотенузе 91?

7


8


9


Данные некорректны

4. Как посчитать периметр прямоугольного треугольника, зная катет и гипотенузу?

Найти второй катет через теорему Пифагора и сложить стороны


Найти все углы


Воспользоваться тригонометрической функцией для нахождения второго катета и сложить стороны


Данные некорректны

5. Как посчитать периметр прямоугольного треугольника, зная катет и острый угол??

Найти второй катет через теорему Пифагора и сложить стороны


Найти все углы


Воспользоваться тригонометрической функцией для нахождения второго катета и сложить стороны


Данные некорректны

---

---

Ещё никто не оставил комментария, вы будете первым.

Написать комментарий

Другие тесты

Как найти периметр прямоугольного треугольника

Обновлено 24 апреля 2017 г.

Автор: Jon Zamboni

Периметр фигуры — это длина по внешней стороне этой фигуры. Поскольку внешняя сторона треугольника состоит из трех линий, вы можете найти его периметр, сложив длины этих линий. Если вы знаете длины только двух сторон прямоугольного треугольника, вы можете использовать теорему Пифагора, чтобы найти длину третьей стороны.

Добавление сторон для нахождения периметра

Треугольник имеет три стороны: a, b и c. Чтобы найти периметр, P, сложите длины этих сторон:

P = a + b + c

Допустим, у вас есть прямоугольный треугольник, три стороны которого равны 3 дюймам, 4 дюймам и 5 дюймам. Чтобы найти периметр, сложите 3, 4 и 5.

P = 3 + 4 + 5 P = 12

Итак, ваш треугольник имеет периметр 12 дюймов.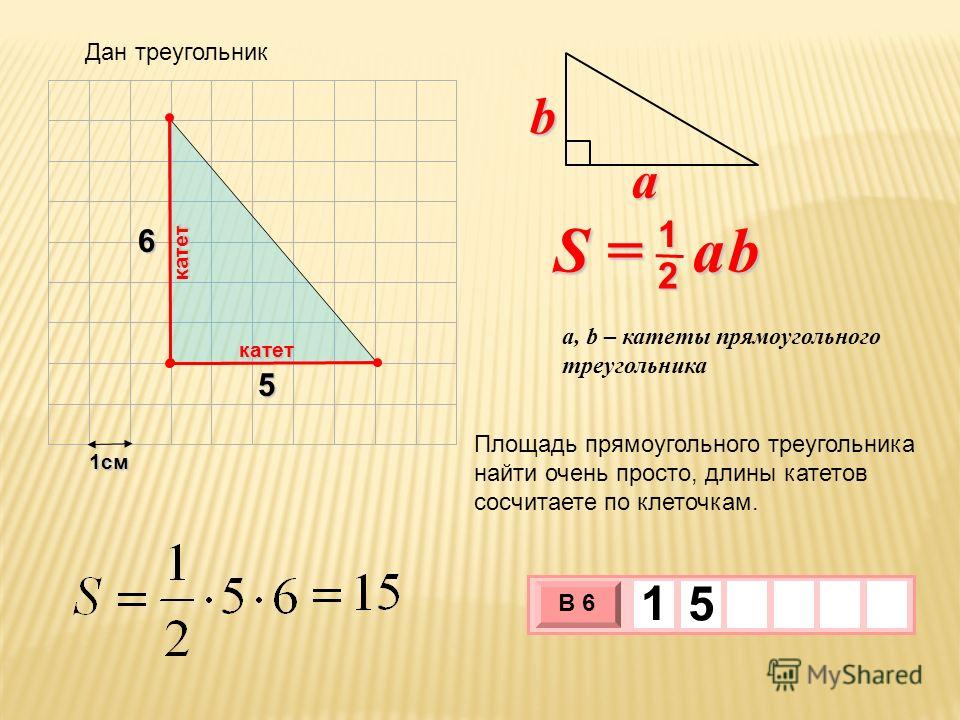

Теорема Пифагора

92 равно c, а квадратный корень из 25 равен 5. Теперь вы знаете, что длина стороны c равна 5 дюймам, поэтому вы можете найти периметр, суммировав длины трех сторон.

P = 3 дюйма + 4 дюйма + 5 дюймов = 12 дюймов

Итак, периметр этого треугольника равен 12 дюймам.

Теорема для нахождения других сторон

Вы также можете использовать теорему Пифагора, чтобы найти длину стороны треугольника , если вы знаете длину другой стороны и гипотенузу. В этом случае квадрат неизвестного катета равен квадрату гипотенузы минус квадрат известного катета: 92 равно 144, что означает, что b равно квадратному корню из 144. Квадратный корень из 144 равен 12, поэтому длина ноги b составляет 12 дюймов. Теперь вы можете сложить стороны, чтобы найти периметр:

P = 9 дюймов + 15 дюймов + 12 дюймов = 36 дюймов

Таким образом, треугольник имеет периметр 36 дюймов.

Как найти периметр прямоугольного треугольника?

Периметр геометрической фигуры равен общей длине ее границы. В этом пошаговом руководстве вы узнаете, как найти периметр прямоугольного треугольника.

Периметр прямоугольного треугольника равен сумме длин всех трех сторон, включая гипотенузу, высоту и основание.

Связанные темы

• Как решать задачи по теореме Пифагора?

Пошаговое руководство по   нахождению периметра прямоугольного треугольника

Периметр прямоугольного треугольника равен сумме его сторон. Например, если \(a, b\) и \(c\) являются сторонами прямоугольного треугольника, его периметр будет равен: \((a + b + c)\). Теперь, когда треугольник прямоугольный, мы можем сказать, что его периметр равен сумме длин двух сторон и гипотенузы.

См. рисунок ниже, на котором показан прямоугольный треугольник со сторонами \(a, b\) и \(c\), где \(c\) — гипотенуза, а \(a, b\) — стороны, которые вместе образуют угол \(90°\). Три стороны можно назвать следующим образом: \(a =\) высота, \(b =\) основание и \(c =\) гипотенуза.

Как найти периметр прямоугольного треугольника?

Периметр прямоугольного треугольника можно найти несколькими способами. Для этого мы должны проверить параметры в соответствии с заданными условиями. Давайте посмотрим на разные методы.

Способ 1:

Зная длины всех сторон прямоугольного треугольника, достаточно сложить их длины. Например, если заданы стороны \(p, q,\) и \(r\), то:

Периметр \(\color{blue}{= p + q + r}\)

Это метод возможен только в том случае, если известны измерения всех сторон.

Метод 2:

Если длины сторон не указаны, но прямоугольный треугольник нарисован в масштабе, мы используем линейку для измерения сторон и складываем размеры каждой стороны. Периметр прямоугольного треугольника равен:

Периметр \(\color{blue}{= сумма\:всех\:сторон\:измерено\:по\:линейке\:линейке}\)

Метод 3:  

Когда даны обе стороны прямоугольного треугольника, мы сначала находим недостающую сторону, используя теорему Пифагора, а затем вычисляем периметр прямоугольного треугольника.