Формула нахождения периметра параллелограмма: Как найти периметр параллелограмма? Ответ на webmath.ru

Как узнать периметр параллелограмма?

Как узнать периметр параллелограмма?

Формула периметра параллелограмма: 1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).

Что делает диагональ в параллелограмме?

Любая диагональ параллелограмма делит его на два равных треугольника.

Как найти диагональ в прямоугольной трапеции?

Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее большего основания и боковой стороны, которая перпендикулярна основаниям.

Как найти диагональ равнобедренной трапеции?

Диагонали равнобедренной трапеции

1. Формула длины диагонали через стороны: d1 = √с2 + ab.
2. Формулы длины диагонали по теореме косинусов: d1 = √a2 + c2 — 2ac cos α d1 = √b2 + c2 — 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию: d1 = √h3 + m2
4. Формула длины диагонали через высоту и основания:

Как пересекаются диагонали трапеции?

Диагонали трапеции обладают такими свойствами Отрезок, соединяющий середины диагоналей, лежит на средней линии и равен половине разности диагоналей. 2}} S=2a+bc2−(2(a−b)(a−b)2+c2−d2)2 , где a, b — основания трапеции, c, d — боковые стороны трапеции.

Что называется равнобедренной трапецией?

Виды трапеций Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой или равнобочной трапецией). Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Какое соотношение имеется между углами при основании равнобедренной трапеции?

Углы В равнобедренной трапеции углы при основаниях попарно равны. … Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.

Как найти высоту в равнобедренной трапеции?

Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Чему равна сумма всех углов в равнобедренной трапеции?

Сумма всех углов трапеции равна 360°. Так как трапеция равнобедренная, то углы, прилежащие к каждому основанию, равны между собой. Так как 360°-148°=212°, то углы, составляющие сумму 148° равны между собой, они и будут меньшими, так как их сумма меньше. Ответ: меньший угол трапеции равен 74°.

Сколько оснований у трапеции?

Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами.

Как описать окружность вокруг трапеции?

Трапеция вписана в окружность

1. Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. …
2. При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла.

Почему нельзя описать окружность около ромба?

Однозначно НЕТ. Описать окружность вокруг ромба можно лишь в том случае, если все его углы равны 90 градусам. Разберемся почему. Фигуру можно вписать в окружность, только если сумма ее углов, которые лежат напротив друг друга, равна 180 градусов (согласно свойству вписанного в окружность четырехугольника).

В каком случае можно описать окружность вокруг четырехугольника?

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Что является центром описанной около треугольника окружности?

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника. … Таким образом, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Кроме того, точка пересечения серединных перпендикуляров равноудалена от вершин треугольника.

Как построить центр описанной окружности?

Построение описанной окружности треугольника

1. Чтобы вокруг треугольника описать окружность необходимо найти центр этой окружности. Шаг 1. В треугольнике к двум сторонам построить серединные перпендикуляры. …
2. Шаг 2. Точку пересечения этих перпендикуляров обозначить буквой О. …
3. Шаг 3. Таким образом нужно построить окружность с центром в точке О и радиусом ОА (ОВ или ОС).

Что такое окружность описанная около треугольника что является центром этой окружности как расположение центра описанной окружности зависит от вида треугольника?

Ответ: Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. \circ. Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей Трапеция, вписанная в окружность – равнобокая

Когда около треугольника можно описать окружность?

Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности. Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника. … Для остроугольного треугольника центр окружности находится в треугольнике.

§ Периметр. Как найти периметр прямоугольника, квадрата и треугольника

Содержание материала

1. Формула периметра многоугольника
2. Видео
3. Площадь квадрата
4. Перевод единиц измерения объёма
5. Формула периметра параллелограмма
6. Примеры нахождения периметра

Формула периметра многоугольника

Общая формула периметра многоугольника

P=a+b+c+d+e+.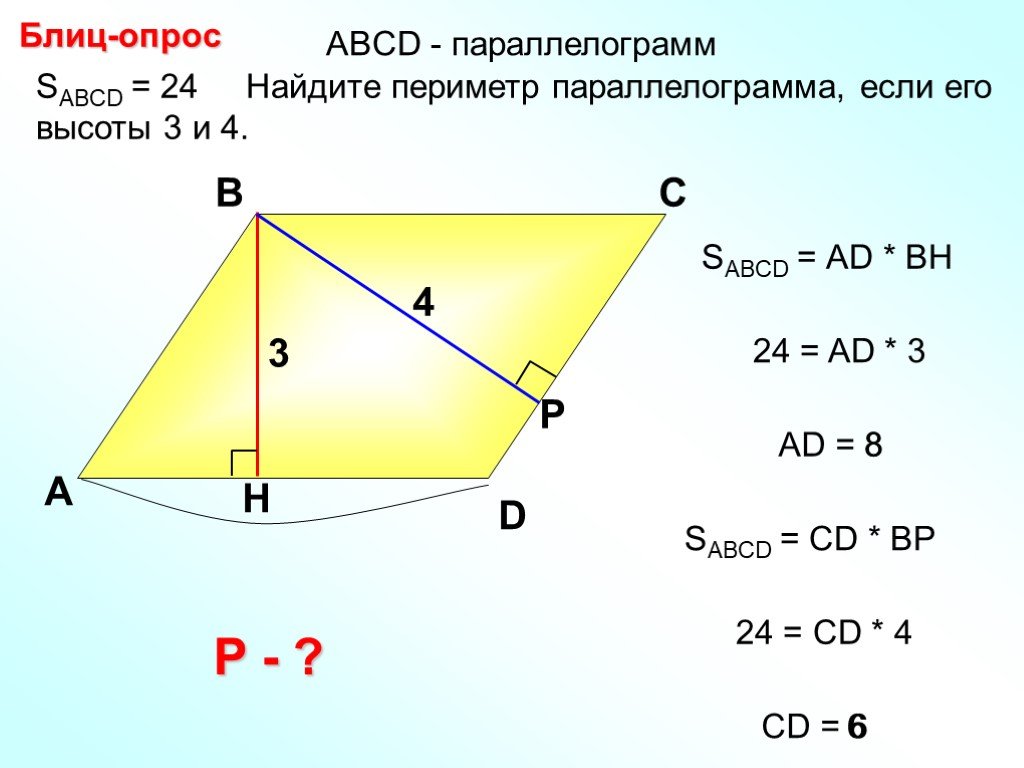 ..P=a+b+c+d+e+…P=a+b+c+d+e+…,

Читайте также: Мультяшный голос в Adobe Audition

где a,b,c,d,e,…a, b, c, d, e,…a,b,c,d,e,… — длины сторон многоугольника.

Частным случаем многоугольника является так называемый правильный многоугольник.

Определение правильного многоугольника

Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.

Читайте также: Как пишется, К ВСЕМ или КО ВСЕМ? «к всем изделиям прилагается….»???

Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.

Периметр правильного многоугольника

P=n⋅aP=n\cdot aP=n⋅a

aaa — длина стороны многоугольника; nnn — количество сторон многоугольника.

Читайте также: Как нарисовать и сделать аватарку для Инстаграма

Разберем задачи на нахождение периметра правильного и неправильного многоугольников.

Задача 1

Найти периметр правильного шестиугольника со стороной 10 см.

Решение

a=10a=10a=1 n=6n=6n=6

Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aaa численное значение:

P=n⋅a=6⋅10=60P=n\cdot a=6\cdot 10=60P=n⋅a=6⋅1=6 см.

Читайте также: Как научиться пить в меру алкоголь и вовремя остановится

Ответ: P=60P=60P=6 см.

Задача 2

Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.

Решение

a=6a=6a=6 b=5b=5b=5 c=2c=2c=2 d=3d=3d=3 e=1e=1e=1

В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:

Читайте также: Как правильно прозванивать мультиметром, тестром или прозвонкой

P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.

Ответ: P=17P=17P=17 см.

Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!

Видео

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³  = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

Формула периметра параллелограмма

Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу

P = 2(a + b )

где P — периметр параллелограмма, a, b — длины сторон параллелограмма. Смотрите также онлайн калькулятор для расчета периметра параллелограмма

Примеры нахождения периметра

Пример 1 Найдем периметр квадрата с длиной стороны 5 см.

P_квадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см.

Пример 2 Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см.

P_{прямоуг.} = 6 + 8 + 6 + 8 = (6 + 8) ⋅ 2 = 28 см.

Пример 3 Найдем периметр шестиугольника ниже.

P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28.

Теги

треугольникарадиусокружностьпрямоугольныйматематикатрапециистатьесвойствагеометрическоедверомбаквадратныйпараллелепипедкругдробичетыребуквойравностороннийгеометриясайтовимеетпоказатьтаблицаработыугломсуммукмсторонукласс

По какой формуле найти периметр параллелограмма?

Последняя обновленная дата: 15 марта 2023 г.

•

Общее представление: 219K

•

Просмотры сегодня: 1,98K

Ответ

Проверено

219K+ виды

HINT: . двумерная фигура как сумма длин всех ее сторон. Чтобы вывести формулу периметра параллелограмма, нам нужно сначала рассмотреть параллелограмм ABCD и сложить все его стороны. Тогда, используя свойства параллелограмма, мы сможем приравнять длины противоположных сторон и, следовательно, получить требуемую формулу через длины смежных сторон.

Полный пошаговый ответ:
Мы знаем, что периметр двумерной фигуры равен сумме длин всех сторон фигуры. Давайте рассмотрим параллелограмм ABCD, как показано на диаграмме ниже.

Из приведенного выше рисунка видно, что длины равны
$\begin{align}
  & \Rightarrow AB=a……\left( i \right) \\
 & \Rightarrow BC= b……\влево( ii \вправо) \\
 & \Стрелка вправо CD=c……\влево( iii \вправо) \\
 & \Rightarrow DA=d……\left( iv \right) \\
\end{align}$
Поскольку периметр двумерного изображения равен сумме длин фигуры, периметр параллелограмма ABCD будет равен
$\Rightarrow P=AB+BC+CD+DA$
Подставляя уравнения (i), (ii), (iii) и (iv) в приведенное выше уравнение, мы получаем
$ \Rightarrow P=a+b+c+d. …..\left( v \right)$
Теперь из свойств параллелограмма мы знаем, что противоположные стороны параллельны и равны по длине. Из приведенного выше рисунка для параллелограмма ABCD видно, что стороны AB и CD противоположны друг другу. Итак, мы можем написать
$\Rightarrow AB=CD$
Составляя уравнения (i) и (iii), мы можем написать
\[\begin{align}
  & \Rightarrow a=c \\
 & \Rightarrow c=a…. ..\left( vi \right) \\
\end{align}\]
Также, поскольку BC и DA противоположны, мы можем написать
$\Rightarrow BC=DA$
Составляя уравнения (i) и (iii ) мы можем написать
\[\begin{align}
  & \Rightarrow b=d \\
 & \Rightarrow d=b……\left( vii \right) \\
\end{align}\ ]
Теперь, наконец, мы можем подставить уравнения (vi) и (vii) в уравнение (v), и мы получим
$\begin{align}
  & \Стрелка вправо P=a+b+a+b \\
 & \Стрелка вправо P=2a+2b \\
 & \Стрелка вправо P=2\влево( a+b \вправо) \ \
\end{align}$
Отсюда формула для периметра параллелограмма $2\left( a+b \right)$, где a и b — длины смежных сторон.

Примечание: Формула для периметра параллелограмма, которая получается как $2\left( a+b \right)$ аналогична для периметра прямоугольника. Это потому, что прямоугольник — это всего лишь тип параллелограмма. Вместо периметра квадрата и ромба мы можем подставить $b=a$, чтобы получить $4a$, так как все стороны в них имеют одинаковую длину.

периметр параллелограмма

Сложение и вычитание целых чисел

В этом разделе мы обсудим периметр параллелограмма и площадь параллелограмма.

Формулы являются следующими:

• Периметр = 2L + 2W
• Область = базовая x высота
• База = площадь/высота
• высота = область

. :

1) Длина параллелограмма 25 см, а ширина 20 см. Найдите периметр.
Решение:
Периметр = 2 (Д + Ш)
⇒ = 2 (25 + 20)
⇒ = 2 х 45
∴ Периметр = 90 см.
_________________________________________________________________
2) Найдите периметр и площадь параллелограмма с основанием 5 см, шириной 3 см и высотой 4,2 см.
Решение:
Площадь = основание x высота
Площадь = 5 x 4,2
Площадь = 21 см

2
Периметр = 2l + 2w
= 2(5) + 2(3)
= 10 + 6 Периметр = 10 + 6 16 см.
_________________________________________________________________
3) Найдите высоту параллелограмма, площадь которого 2,25 кв.м, а основание 25 дм.
Решение:
Площадь параллелограмма = 2,25 кв.м
1 дм = 0,1 м
Итак, 25 дм = 25 x 0,1
Основание параллелограмма = 2,5 м
Высота параллелограмма = Площадь / Основание
= 2,25/2,5
Высота = 0,9 м
________________________________________________________________
4) Две стороны параллелограмма ABCD равны 6см и 4см. Высота, соответствующая базовому компакт-диску, составляет 3 см, как показано на рис. Найдите
(i) площадь параллелограмма (ii) высота, соответствующая основанию AD.