Формула нахождения площади трапеции равнобедренной: Все формулы площади трапеции — найти онлайн

Площадь трапеции формула. Как найти площадь равнобедренной трапеции

Площадь трапеции формула. Как найти площадь равнобедренной трапеции

Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.

Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:

Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :

Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:

Допустим, дана трапеция с основаниями a = 3 см, b = 7 см и боковыми сторонами c = 5 см, d = 4 см. найдем площадь фигуры:

Площадь равнобокой трапеции

Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:

Помните, что диагонали равнобокой трапеции равны между собой!

То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.

Площадь криволинейной трапеции

Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.

Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:

Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:

Здесь F(a) – это значение первообразной функции f(x) в точке a , F(b) – значение этой же функции f(x) в точке b .

Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x ={-8}, слева прямой x ={-10} и осью OX снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:

Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:

Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.

Что нужно знать про трапецию?

Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.

В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.

Формулы площади трапеции

Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.

Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .

Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.

Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними:

S= 1/2d 1 d 2 *sinα .

Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .

Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.

Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α.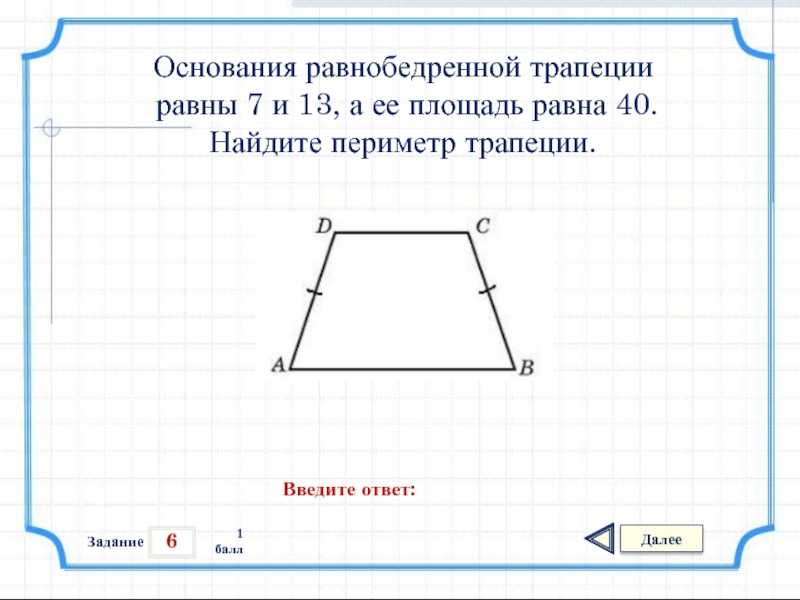

Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.

Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .

Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .

Формула площади криволинейной трапеции

Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x.

Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.

Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.

Примеры задач

Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.

Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.

Решение: Постройте трапецию АМРС.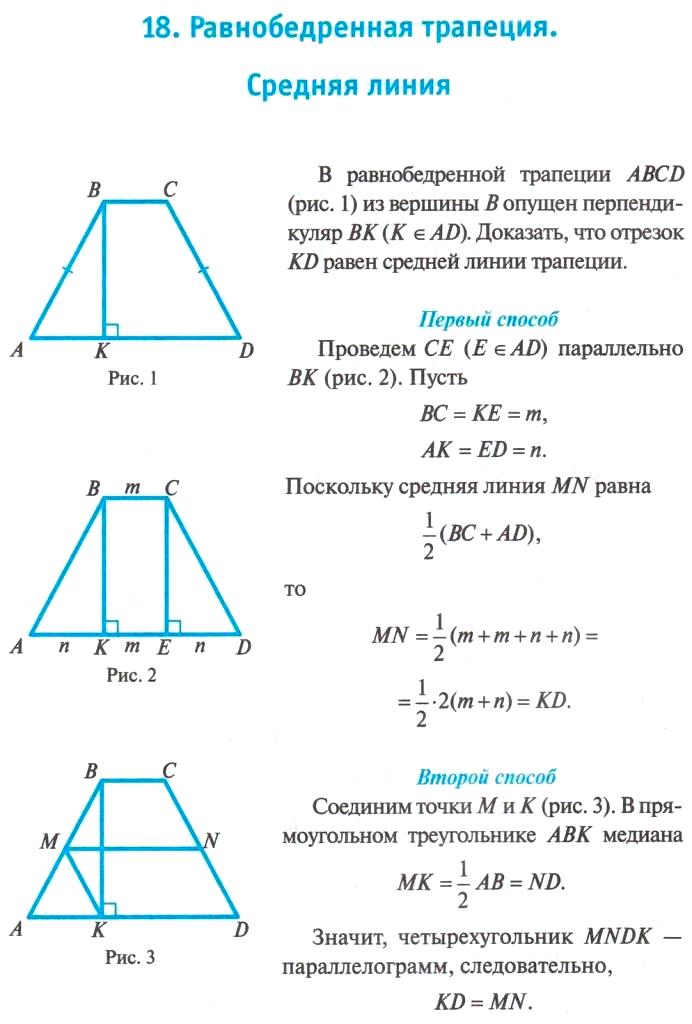 Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.

Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.

Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .

Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.

Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .

Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.

Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.

Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).

Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).

Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.

Таким образом, ОЕ = х = √(5а 2 + b 2)/6.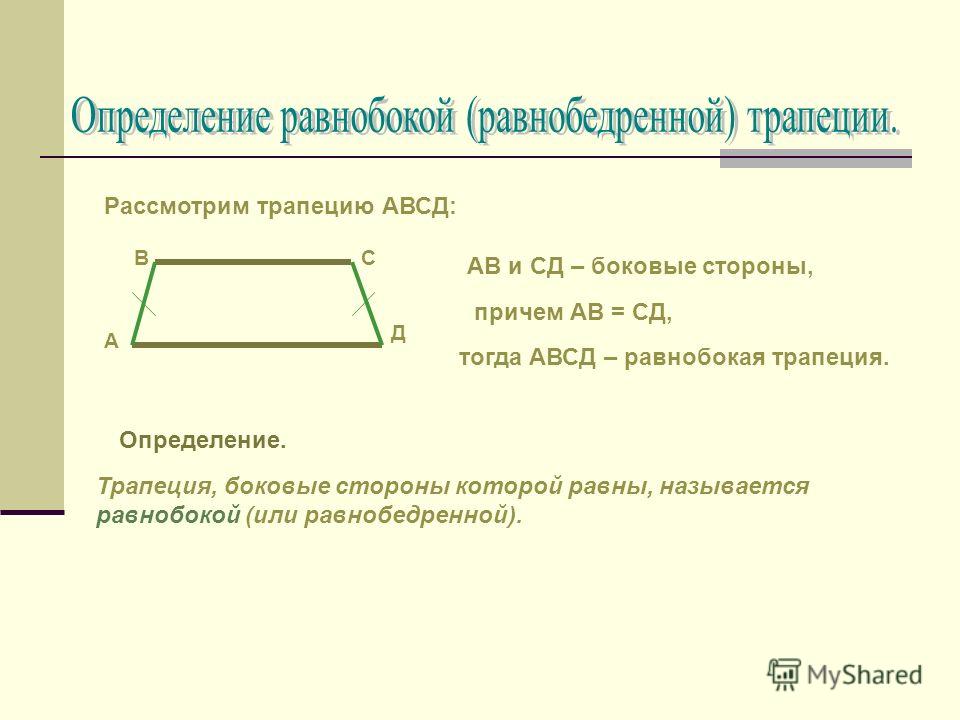

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции.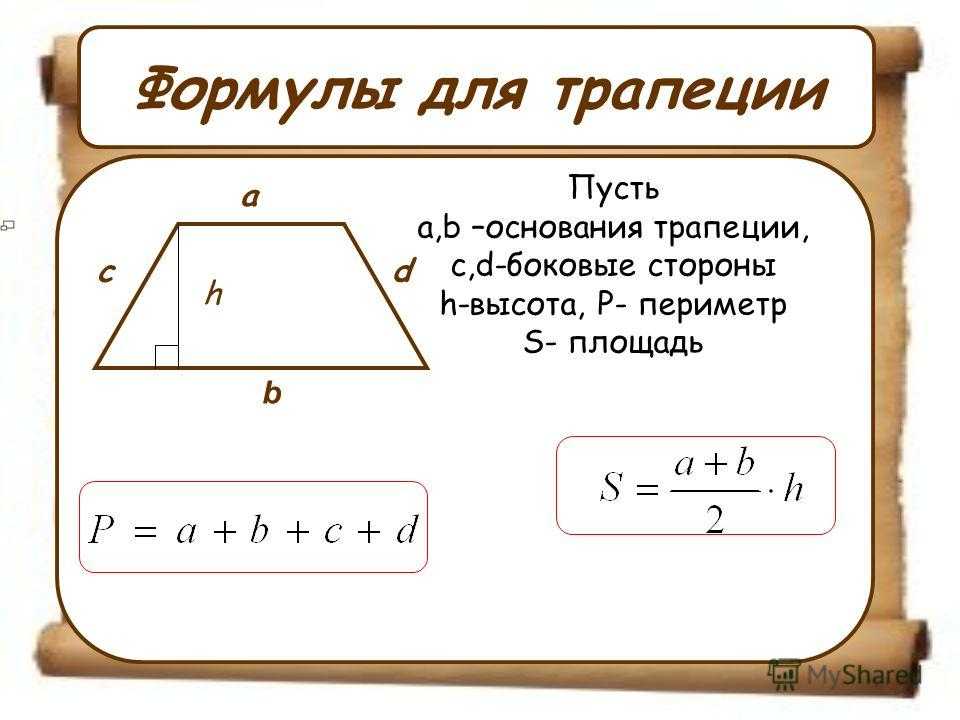 Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

1. Средняя линия трапеции равна полусумме оснований и параллельна им.
   
2. У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
   
3. Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
   
4. Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
   
5. Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
   
6. Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
   
7. Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
   

Как найти площадь трапеции .

Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:

где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.

Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.

Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.

В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.

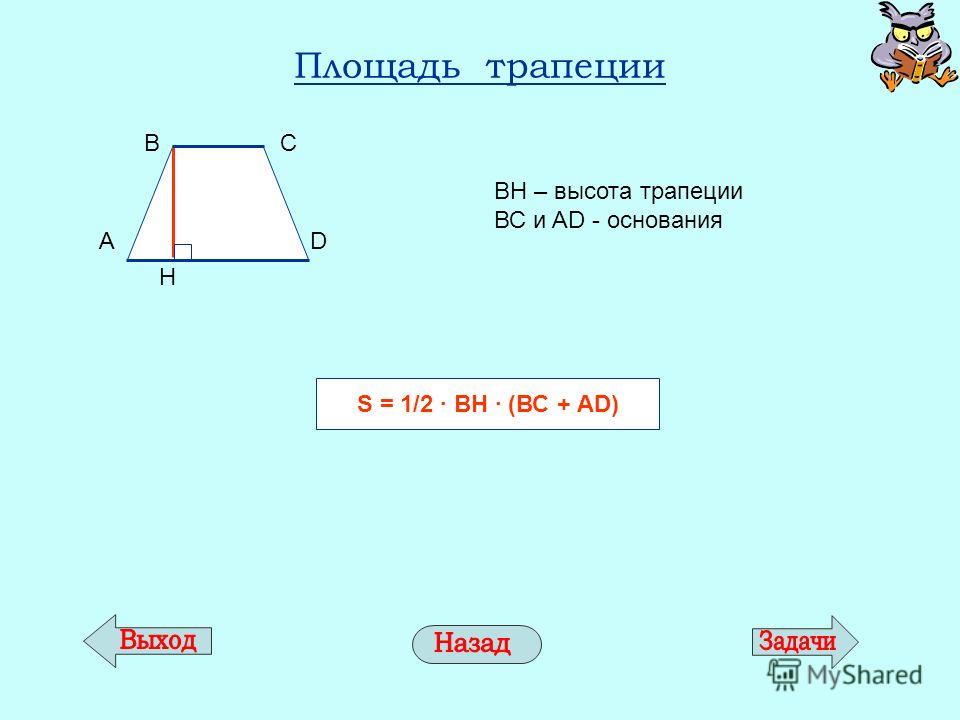
Площадь трапеции

Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:

S = ½ * (a+b) * h

т.е. взять полусумму оснований, умноженную на высоту.

Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда

Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d.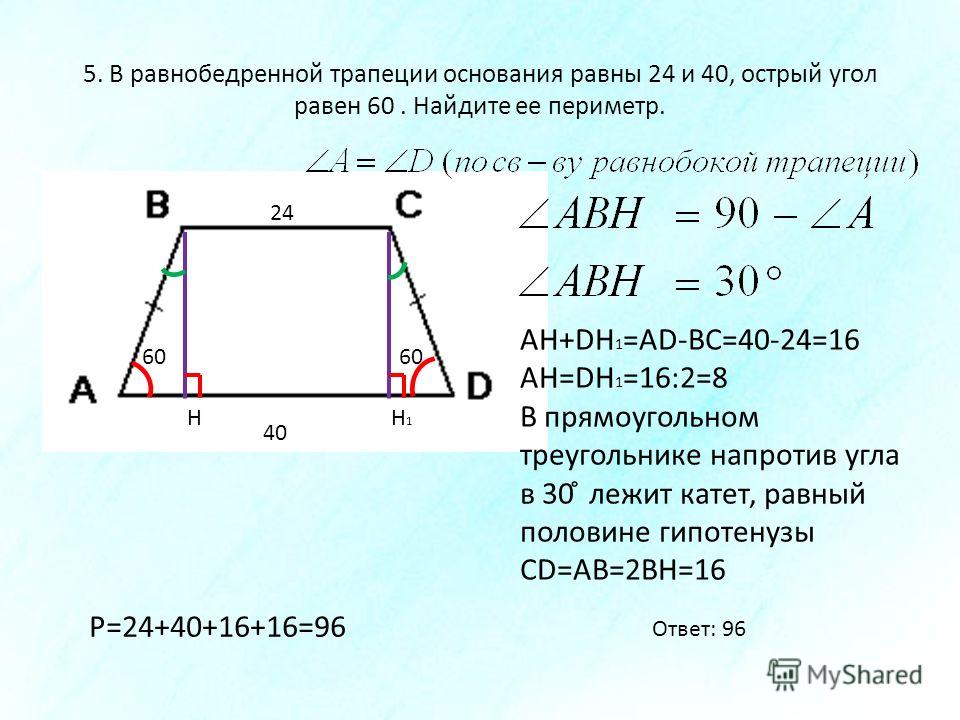 Тогда площадь отыщется по формуле:

Если известны длины диагоналей и угол между ними, то площадь ищется так:

S = ½ * d1 * d2 * sin α

где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.

При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:

S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))

Площадь равнобедренной трапеции

Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.

Найти площадь равнобедренной трапеции можно несколькими способами.

• Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:

• Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:

S = c * sin α * (a + c * cos α)

где а — верхнее основание, с — боковая сторона.

• Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:

S = c * sin α * (b – c * cos α)

• Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:

S = ½ * (b2 – a2) * tg α

• Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:

S = ½ * d2 * sin α

• Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.

Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:

S = m * c * sin α

Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.

Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:

S = 4r2 / sin α

Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):

Зная основания и угол, площадь равнобедренной трапеции вычисляется так:

S = a * b / sin α

(эта и последующие формулы верны только для трапеций с вписанной окружностью).

Через основания и радиус окружности площадь ищется так:

Если известны только основания, то площадь считается по формуле:

Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:

Площадь прямоугольной трапеции

Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.

Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.

Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.

• Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:

S = (a + b) * h / 2

В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:

S = (a + b) * c / 2

• Другой способ рассчитать площадь — перемножить длину средней линии на высоту:

или на длину боковой перпендикулярной стороны:

• Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:

S = ½ * d1 * d2 * sin α

Если диагонали перпендикулярны, то формула упрощается до:

S = ½ * d1 * d2

• Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:

S = (2r + c) * r

• Если в трапецию вписана окружность, то площадь вычисляется так же:

где m — длина средней линии.

Площадь криволинейной трапеции

Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.

Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:

Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.

Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:

Следующее важное понятие.

Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?

Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:

*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии.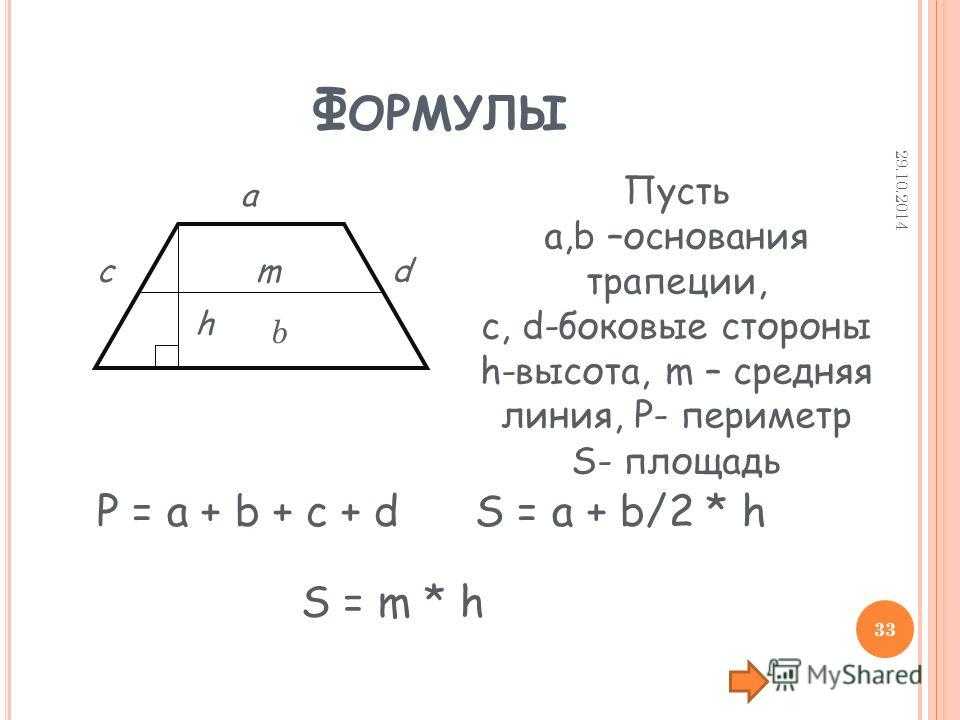 Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

Посмотреть ещё одно объяснение

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:

Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.

Теперь рассмотрим треугольник:

*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Площадь трапеции формула:

Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.

То есть, получается, что она равна произведению средней линии и высоты:

Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:

То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:

Но дело тут не в записи, конечно, а в понимании.

Скачать (посмотреть) материал статьи в формате *pdf

На этом всё. Успеха вам!

С уважением, Александр.

Площадь трапеции

На данной странице вы можете ознакомиться со всеми формулами для нахождения площади трапеции, как обычной, так и равнобедренной или неправильной. Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.

Площадь трапеции по высоте и двум основаниям

Формула нахождения площади трапеции по высоте и двум основаниям:

$S = \frac{a + b}{2} \cdot h$,

$S$ — площадь трапеции, где

$a$ — малое основание трапеции,

$b$ — большее основание трапеции,

$h$ — высота трапеции.

Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:

$S = m \cdot h$, где

$S$ — площадь трапеции,

$m$ — средняя линия,

$h$ — высота трапеции.

Ну а сейчас рассмотрим на примере, как найти площадь трапеции по высоте и средней линии. Быстро и без лишних действий самостоятельно найдем возможные ошибки в своем решении с помощью данного калькулятора и сверим с ним ответы.

Пример 1

Дано: высота $h = 7$ см, средняя линия $m = 8$ см.

Найти: площадь трапеции $S$.

Решение:

$S = 8 \cdot 7 = 56$

Площадь трапеции по четырём сторонам

Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:

$S = \frac{a + b}{2} \cdot \sqrt{c^2 — (\frac{(b — a)^2 + c^2 — d^2}{2 \cdot (b — a)})^2}$, где

$S$ — площадь трапеции,

$a$ — малое основание,

$b$ — большее основание,

$c, d$ — боковые стороны. 2 \cdot \sin (α)$, где

$S$ — площадь трапеции,

$D$ — диагональ трапеции,

$α$ — угол между диагоналями.

Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:

$S = m \cdot c \cdot \sin (α)$, где

$S$ — площадь трапеции,

$m$ — средняя линия трапеции,

$c$ — боковая сторона,

$α$ — угол при основании.

Чтобы проверить правильность своего решения и ответа или найти какие-либо ошибки в действиях необходимо решить пример данной задачи. Для наглядности выполним пример задачи на нахождение равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании.

Пример 2

Дано: средняя линия $m = 8$ см, боковая сторона $c = 10$ см, угол при основании $α = 30°$.

Найти: площадь трапеции $S$.

Решение:

$S = 8 \cdot 10 \cdot \sin (30) = 80 \cdot \frac12 = 40$ см$^2$. 2}{\sin (α)}$, где

$S$ — площадь трапеции,

$R$ — радиус вписанной окружности,

$α$ — угол между сторонами.

Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности

Формула нахождения площади равнобедренной трапеции через два ее основания и радиус вписанной окружности:

$S = r \cdot (a + b)$, где

$S$ — площадь трапеции,

$r$ — радиус вписанной окружности,

$a$ — малое основание,

$b$ — большее основание

Площадь равнобедренной трапеции через ее основания и угол при большем основании

Формула нахождения площади равнобедренной трапеции через ее основания и угол при большем основании:

$S = \frac {d \cdot b} {\sin (α)}$, где

$S$ — площадь трапеции,

$d$ — малое основание,

$b$ — большее основание,

$α$ — угол при большем основании.

Площадь равнобедренной трапеции через основания и среднюю линию

Формула нахождения площади равнобедренной трапеции через основания и среднюю линию:

$S = m \cdot \sqrt {a \cdot b}$, где

$S$ — площадь трапеции,

$m$ — средняя линия,

$a$ — малое основание,

$b$ — большее основание.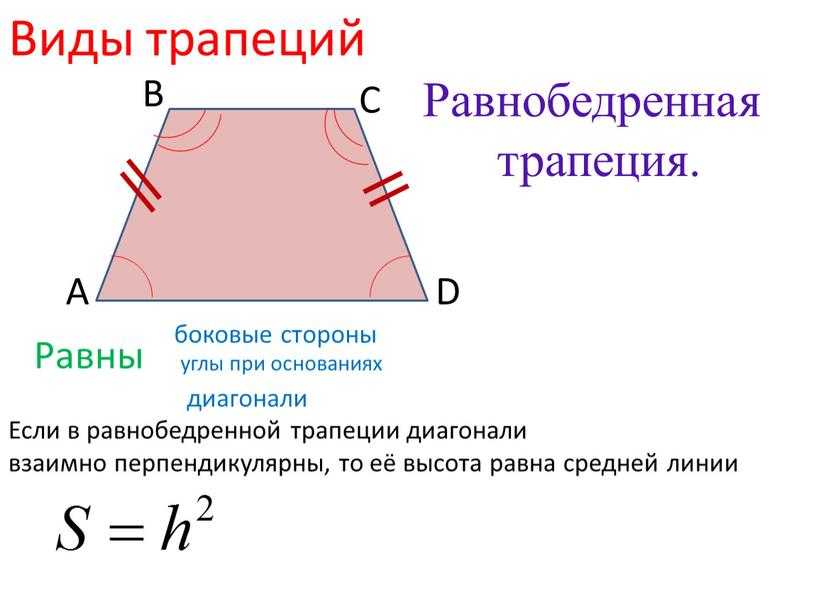 2$

формула расчета, как по 4 сторонам, формула

Содержание:

• Что такое площадь трапеции
  • Способы нахождения площади
• Формулы для вычисления площади равнобедренной и неправильной трапеций
  • По длине оснований и высоте
  • Через длины всех сторон (Формула Герона)
  • Через диагонали и угол между ними
  • Через радиус вписанной окружности
  • Через среднюю линию, боковую сторону и угол при основании
• Примеры решения задач

Содержание

• Что такое площадь трапеции
  • Способы нахождения площади
• Формулы для вычисления площади равнобедренной и неправильной трапеций
  • По длине оснований и высоте
  • Через длины всех сторон (Формула Герона)
  • Через диагонали и угол между ними
  • Через радиус вписанной окружности
  • Через среднюю линию, боковую сторону и угол при основании
• Примеры решения задач

Что такое площадь трапеции

Трапеция — четырехугольник, две стороны которого, называемые основаниями, параллельны друг другу, а две другие стороны — нет.

Вычисление площади трапеции входит в раздел геометрии, который называется планиметрия и занимается фигурами на плоскости.

Площадь трапеции, как и любой другой геометрической фигуры — это часть плоскости, ограниченная периметром и измеряемая в квадратных единицах.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В формулах основания обозначаются буквами a и b, боковые стороны — с и d.

Способы нахождения площади

Существует более двадцати способов вычисления площади трапеции. Выбор способа расчета зависит от известных данных, которые можно подставить в формулу, и от типа самой трапеции: она может быть равнобедренной (равнобокой) или прямоугольной, тогда задача упростится.

Например, если трапеция равнобедренная, вычислить длину ее сторон можно, разбив ее на прямоугольник и два прямоугольных треугольника. {2}}.\)

Существует более простая формула, известная, как формула Герона. Для облегчения ее запоминания вводится р, полусумма всех четырех сторон:

\(p = \frac{1}{2} (a+b+c+d).\)

Формула Герона выглядит так: \(S = \frac{a + b}{\left|a\;-\;b\right|} \times \sqrt{(p — a) (p — b) (p — a — c) (p — a — d)}.\)

Через диагонали и угол между ними

\(S = \frac{1}{2}\times d_{1} \times d_{2} \times \sin\alpha.\)

Здесь \(d_{1}\) и \(d_{2}\) — диагонали, а \(\alpha\) — угол, образованный ими.

Через радиус вписанной окружности

Примечание

Вписать окружность в трапецию можно только тогда, когда сумма ее оснований равна сумме боковых сторон.

Площадь любой трапеции можно найти через радиус вписанной окружности, зная длину оснований:

\(S = (a + b) \times r. {2}\).

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Как найти площадь трапеции

Все ресурсы по математике для средней школы

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

Справка по математике для старших классов » Геометрия » Плоская геометрия » Четырехугольники » Трапеции » Как найти площадь трапеции

Найдите площадь следующей трапеции:

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади трапеции:

Где – длина одного основания, – длина другого основания, а  – высота.

Чтобы найти высоту трапеции, используйте тройку Пифагора:

Подставив наши значения, мы получим:

Сообщить об ошибке:0005

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте формулу для треугольников, чтобы найти длину основания и высоту.

Формула:

Где  – длина стороны, противоположной .

Начиная со стороны, если бы мы создали треугольник, длина основания и высота были бы равны.

Создавая еще один треугольник слева, находим высоту, длину основания и сторону.

 

Формула площади трапеции:

Где – длина одного основания,  – длина другого основания, а   – высота.

Plugging in our values, we get:

Report an Error

Determine the area of ​​the following trapezoid:

Possible Answers:

Correct answer:

Объяснение:

Формула площади трапеции:

,

где – длина одного основания,               это длина другого основания, а        это длина высоты.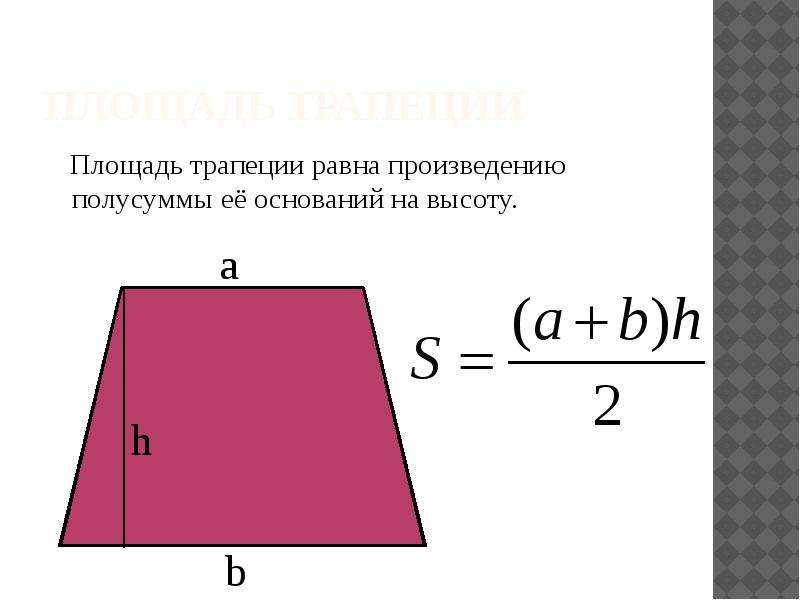

Подключение наших значений, мы получаем:

Отчет о ошибке

Найдите площадь следующего трапеции:

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади трапеции:

,

где — длина одного основания, — длина другого основания, — длина высоты.

Используйте теорему Пифагоре, чтобы найти высоту трапеции:

Подключение в наших значениях, мы получаем:

Отчет о ошибке

Найти область следующего трапезоида. :

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади трапеции:

.

Используйте теорему Pythagorean, чтобы найти длину высоты:

Подключение в наших значениях, мы получаем:

. Отчет о ошибке

:

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади трапеции:

,

, где – основание трапеции, а – высота трапеции.

Используйте формулу для треугольника, чтобы найти длину основания и высоту:

Используйте формулу для треугольника, чтобы найти длину основания и высоту:

Подставляем наши значения , получаем:

Сообщить об ошибке

Какова площадь этой правильной трапеции?

Возможные ответы:

20

26

45

32

Правильный ответ:

32

Пояснение:

Чтобы решить этот вопрос, вы должны разделить трапецию на прямоугольник и два прямоугольных треугольника.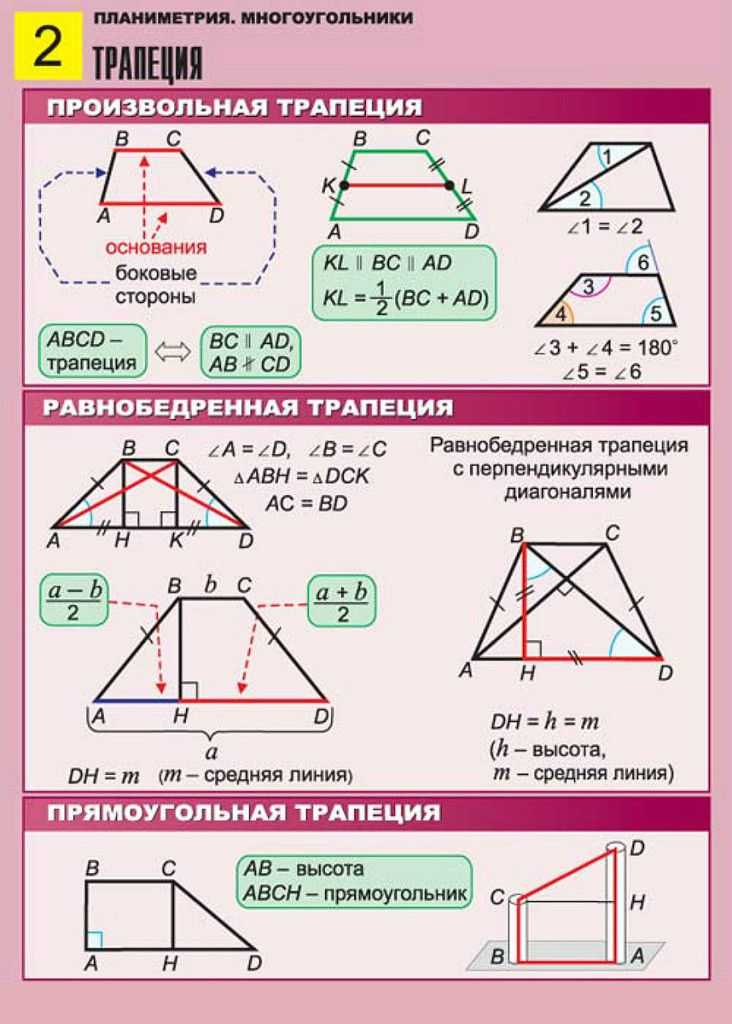 Используя теорему Пифагора, вы вычислите высоту треугольника, которая равна 4. Размеры прямоугольника равны 5 и 4, следовательно, площадь будет равна 20. Основание треугольника равно 3, а высота треугольника равна 4. Площадь одного треугольника равна 6. Следовательно, общая площадь будет 20+6+6=32. Если вы забудете разделить фигуру на прямоугольник и ДВА треугольника или добавите размеры трапеции, вы можете получить ответ 26.

 

Сообщить об ошибке

Какова площадь трапеции выше, если a = 2, b = 6 и h = 4?

Возможные ответы:

8

64

16

32

24

Правильный ответ:

16

Объяснение:

Площадь трапеции = ½(a+b)*h

= ½ (2+6) * 4

= ½ (8) * 4

= 4 * 4 = 16

Сообщить об ошибке

Трапеция имеет основание длиной 4, другое основание длиной s и высоту длиной s . Длина стороны квадрата s . Чему равно число s , если площадь трапеции равна площади квадрата?

Возможные ответы:

Правильный ответ:

Пояснение:

В общем, формула площади трапеции: (1/2)( а + b )( h ), где а и b — длины оснований, а h — длина высоты. Таким образом, мы можем записать площадь трапеции, данной в задаче, следующим образом:

площадь трапеции = (1/2)(4 + s )( s )

Аналогично, площадь квадрата с длина сторон a равна a ² . Таким образом, площадь квадрата, данного в задаче, равна с ² .

Теперь мы можем положить площадь трапеции равной площади квадрата и найти s .

(1/2)(4 + s )( s ) = s ²

Умножьте обе части на 2, чтобы исключить 1/2.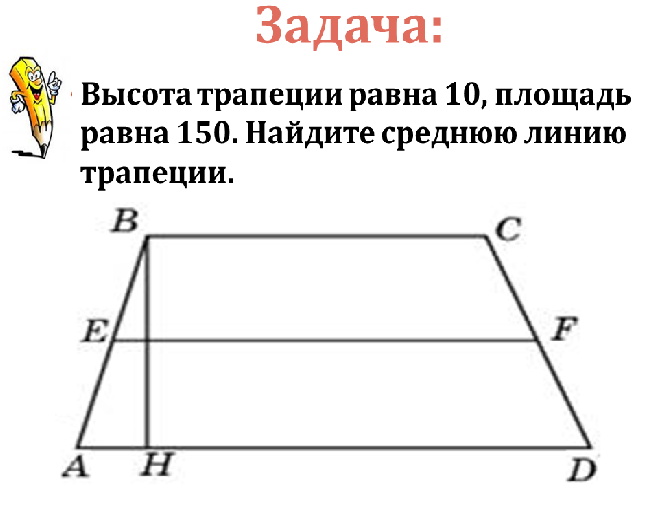

(4 + s )( s ) = 2 s ²

Распределите s слева.

4 с + с ² = 2 s ²

Вычесть s ² с обеих сторон.

4 s = s ²

Поскольку s должно быть положительным числом, мы можем разделить обе части на s .

4 = s

Это означает, что значение s должно быть 4.

Ответ: 4.

Сообщить об ошибке

сторона 10 дюймов

Какова площадь равнобедренной трапеции?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти площадь равнобедренной трапеции, нужно усреднить основания и умножить на высоту.

Среднее значение оснований прямое:

 

Чтобы найти высоту, вы должны нарисовать высоту. Это создает прямоугольный треугольник, в котором один из катетов также является высотой трапеции. Вы можете распознать тройку Пифагора (6-8-10) и легко определить высоту как 8. В противном случае используйте .

Умножьте среднее значение баз (12) на высоту (8), чтобы получить площадь 96.

Отчет о ошибке

Обратите внимание на авторские права

ВСЕ школа

4

. 8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept

Как найти площадь трапеции

Как найти площадь трапеции

Чтобы найти площадь трапеции:

1. Добавьте длины двух параллельных сторон.
2. Умножьте это на расстояние между параллельными сторонами.
3. Разделите это на 2.

Например, найти площадь трапеции с параллельными сторонами 6 м и 10 м, расстояние между которыми 4 м.

1. Сложите параллельные стороны: 6 + 10 = 16.
2. Умножьте это на расстояние между ними: 16 × 4 = 64,
3. Разделить на 2: 64 ÷ 2 = 32.

Итак, площадь равна 32 м ² .

В качестве альтернативы площадь трапеции можно найти по формуле Площадь = ¹ / ₂ (a+b)h, где a и b — параллельные стороны трапеции, а h — расстояние между ними.

a = 6 и b = 10, а h = 4.

Площадь = ¹ / ₂ (a+b)h становится площадью = ¹ / ₂ ×(6+10)×4.

Получается Площадь = ¹ / ₂ × 16 × 4, что равно 32 м ² .

Формула площади трапеции

Формула площади трапеции: Площадь = ^h / ₂ (a+b), где a и b — длины двух параллельных сторон, а h — расстояние между ними. Например, если у трапеции параллельные стороны 5 м и 7 м, а расстояние между ними 4 м, то a = 5, b = 7 и h = 4. Формула площади принимает вид ⁴ / ₂ (5+7), что равно 24 м ² .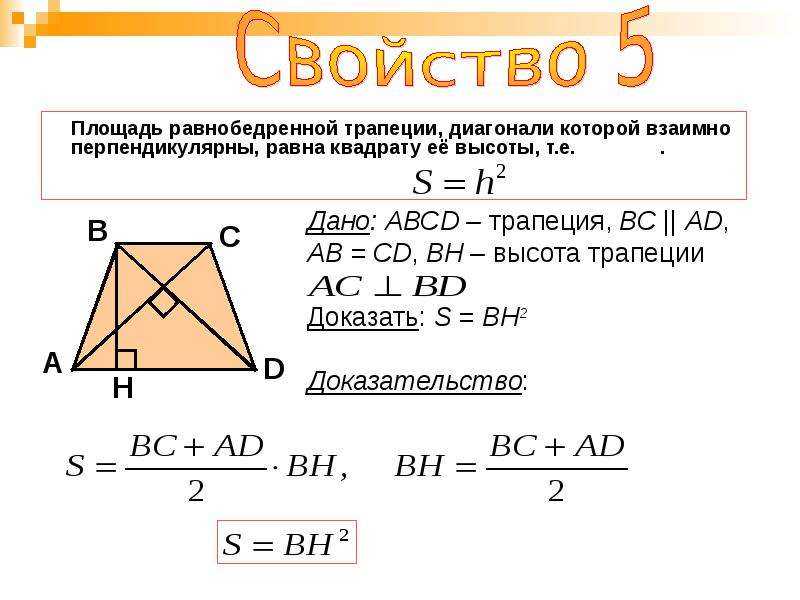

Не имеет значения, какая из двух параллельных сторон помечена как a и b .

Формула площади трапеции также может быть записана как Площадь = ^(a+b) / ₂ h.

Его также можно записать как Площадь = ¹ / ₂ h(a+b) или Площадь = ¹ / ₂ (a+b)h.

Все эти формулы являются просто перестановками одной и той же формулы и дадут один и тот же ответ.

Площадь прямоугольной трапеции

Чтобы найти площадь прямоугольной трапеции, используйте формулу Площадь = ¹ / ₂ h(a+b), где a и b — две параллельные стороны, а h — расстояние между ними.

Например, вычислите площадь следующей прямоугольной трапеции.

Две параллельные стороны равны 5 м и 9 м, поэтому a = 5 и b = 9. Неважно, какая сторона равна a, а какая — b.

Расстояние между параллельными сторонами равно 2 м, значит, h = 2.

Чтобы найти площадь, подставьте значения h = 2, a = 5 и b = 9 в Area = ¹ / ₂ h(a+b).

Площадь = ¹ / ₂ h(a+b) становится Площадь = ¹ / ₂ × 2 × (5 + 9)

Получается Площадь = ¹ / ₂ × 2 × 14, что равно 14 м ² .

Площадь равнобедренной трапеции

У равнобедренной трапеции диагональные стороны имеют одинаковую длину. Эти длины диагональных сторон не влияют на площадь. Чтобы найти площадь равнобедренной трапеции, используйте формулу Площадь = ¹ / ₂ h(a+b), где a и b — длины двух параллельных сторон, а h — расстояние между ними.

Вот, например, равнобедренная трапеция. Его диагональные стороны имеют одинаковый размер, и он симметричен относительно своей середины.

Длины двух параллельных сторон равны 4 м и 8 м. Таким образом, a = 4 и b = 8. Неважно, какая сторона равна a, а какая b из этих двух значений.

Расстояние между параллельными сторонами равно 3 м. Итак, ч = 3.

Подставляем значения h = 3, a = 4 и b = 8 в формулу Площадь = ¹ / ₂ h(a+b).

Получается Площадь = ¹ / ₂ × 3 × (4 + 8), которая становится Площадью = ¹ / ₂ × 3 × 12.

12 легче разделить пополам, чем 3, поэтому мы разделим 12 пополам, чтобы получить 6.

Площадь = 3 × 6, что равно 18 см ² .

Площадь измеряется в см ² , потому что стороны трапеции измеряются в см.

Площадь неправильной трапеции

Площадь неправильной трапеции находится обычным способом, используя площадь = ¹ / ₂ h(a+b). a и b — две параллельные стороны, h — расстояние между ними. Неважно, какой длины диагональные стороны неправильной трапеции, поскольку они не влияют на площадь.

Например, найдите площадь неправильной трапеции, изображенной на рисунке.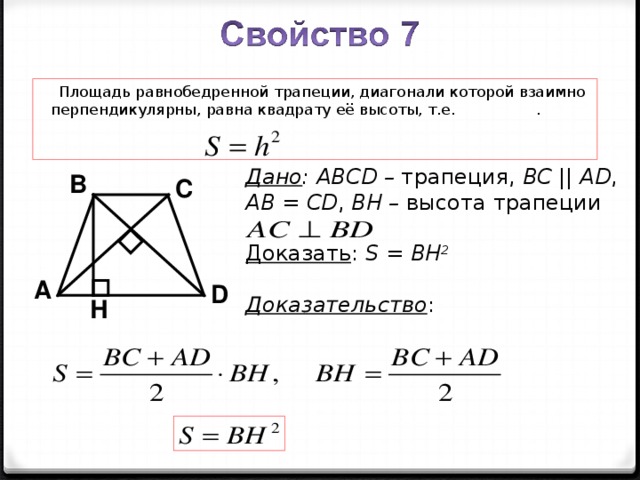

Две параллельные стороны равны 6 м и 10 м. Таким образом, a = 6 и b = 10. Неважно, какие стороны равны a и b, лишь бы они были параллельны.

Расстояние между параллельными сторонами равно 4 м, значит, h = 4.

Площадь неправильной трапеции находится по формуле Площадь = ¹ / ₂ h(a+b).

Подставляя в h = 4, a = 6 и b = 10, получаем Площадь = ¹ / ₂ × 4 × (6 + 10).

Получается Площадь = ¹ / ₂ × 4 × 16. Половина 16 равна 8, а 8 × 4 = 32. Площадь равна 32 м ² .

Площадь трапеции без высоты

Если высота трапеции не указана, ее необходимо вычислить по теореме Пифагора. Для этого представьте себе прямоугольный треугольник, образованный на одной стороне трапеции, где диагональной стороной является гипотенуза. Возведите гипотенузу в квадрат, вычтите основание треугольника в квадрате, а затем извлеките из него корень, чтобы найти высоту трапеции. Затем площадь можно найти, используя A = ¹ / ₂ h(a+b).

Вот пример вычисления площади трапеции без знания высоты.

Первый шаг — создать прямоугольный треугольник на одной стороне трапеции. Гипотенуза треугольника — диагональная сторона трапеции, в данном случае она равна 5 м.

Затем найдите основание треугольника, которое представляет собой разницу между длинами верхней и нижней сторон трапеции. 7 – 3 = 4, значит, основание треугольника равно 4 м.

Следующим шагом является использование теоремы Пифагора для определения высоты треугольника. Это будет равно высоте трапеции. 92}$$, где h — высота, c — диагональная сторона треугольника, а b — основание треугольника.

5 ² – 4 ² = 9 и тогда квадратный корень из 9 равен 3. Высота равна 3.

Теперь площадь трапеции можно найти, используя Площадь = ¹ / ₂ h(a+b).

h — высота трапеции, b — основание трапеции и a — верхняя сторона трапеции.

Площадь = ¹ / ₂ × 3 × (3 + 7) = 15 ² .

Доказательство формулы площади трапеции

Трапецию высотой «h» и длинами параллельных сторон «a» и «b» можно составить из треугольника и прямоугольника вместе взятых. Площадь прямоугольника равна ah, а площадь треугольника равна ¹ / ₂ h(b-a). Сложение площадей треугольника и прямоугольника доказывает формулу площади трапеции: Площадь = ¹ / _{2 905:15 ч(а+б).}

Доказательство площади трапеции показано ниже.

Трапеция имеет высоту «h», основание «b» и длину вершины «a». Его можно разделить на две отдельные формы, прямоугольник и треугольник.

Площадь прямоугольника равна длине × ширине, то есть a × h или ah. Мы называем это Область 1, A ₁ .

Площадь треугольника равна ¹ / ₂ × основание × высота. Длина основания треугольника равна большей стороне трапеции, за вычетом меньшей стороны b-a. Площадь треугольника, А ₂ = ¹ / ₂ з(б-а).

Прибавляем площадь прямоугольника к площади треугольника, чтобы найти площадь трапеции.

Площадь = А ₁ + А ₂ .

Площадь = ah + ¹ / ₂ h(b-a).

Разлагая второе слагаемое, получаем:

Площадь = ah + ¹ / ₂ bh – ¹ / ₂ ah.

Вычитание ¹ / ₂ ах из ах получаем:

Площадь = ¹ / ₂ а.ч. + ¹ / ₂ га.ч.

Разложив на множители ¹ / ₂ и h, мы получим конечную площадь трапеции:

Площадь = ¹ / ₂ h(a + b).

Вот альтернативное доказательство площади трапеции, в котором мы складываем две трапеции вместе, чтобы сформировать прямоугольник.

Две одинаковые трапеции с высотой «h», основанием «b» и верхней стороной «a» можно сложить вместе, чтобы получился прямоугольник. Этот прямоугольник имеет высоту «h» и длину основания «a+b». Площадь прямоугольника равна основанию × высоте, то есть h × (a+b). Площадь каждой отдельной трапеции составляет половину этой площади, то есть ¹ / ₂ ч(а+б).

Площадь прямоугольника равна основанию × высоте. Мы видим, что высота прямоугольника равна высоте каждой трапеции, а основание прямоугольника состоит из основания трапеции и верхней стороны трапеции вместе взятых. Основание прямоугольника равно a+b.

Площадь прямоугольника равна h(a+b), однако каждая трапеция составляет половину общей площади прямоугольника, потому что их две. Разделим площадь прямоугольника пополам, чтобы получить площадь трапеции.

Площадь = ¹ / ₂ h(a+b).

Равнобедренная трапеция

• Равнобедренная трапеция (двумерная фигура) — это трапеция только с одной парой параллельных ребер и с одинаковыми углами при основании.
• Острый угол меньше 90°.
• Окружность — это окружность, проходящая через все вершины двумерной фигуры.
• Диагональ — это несмежная линия, идущая от одной вершины к другой.
• Тупой угол больше 90°.
• a и c являются основаниями
• б и д ножки
• а ∥ в
• а ≠ в
• б = д
• ∠A и ∠D < 90°
• ∠B и ∠C > 90°
• ∠А = ∠Д
• ∠В = ∠С
• ∠А + ∠В = 180°
• ∠C + ∠D = 180°
• ∠А + ∠С = 180°
• ∠B + ∠D = 180°
• 2 диагонали 92}{2\;\left(\frac{a \;-\; c}{2}\right)\;b} }\)    \(\large{  y =  180° — x  }\)   

  Где:

  \(\large{x}\) = острый угол

  \(\large{y}\) = тупой угол

  \(\large{a, b, c, d}\ ) = ребро

  \(\large{ h }\) = высота

   

  Площадь равнобедренной трапеции формулы

  \(\large{  A_{area} =  \frac {h}{2} \ ; \слева(с + а \справа)  }\)
  \(\large{  A_{площадь} =  h  \left(  \frac  {c \;+\; a}  {2 }  \right)  }\)
  \(\large{  A_{площадь} =  mc \; sin \; x  }\)
  \(\large{  A_{площадь} =  mc \; sin \; y  }\)

  Где:

  \(\large{A_{площадь}}\) = площадь

  \(\large{м}\) = центральная медиана
  

  \(\large{ a, b, c, г }\) = ребро

  \(\large{ h }\) = высота

   

  Окружность равнобедренной трапеции формулы

  \(\large{  R =  \frac{ b\;D’\;c  }{  4 \ ;\sqrt  {  s \; \left( s \;-\; b \right) \; \left( s \;-\; D’ \right)  \left( s \;-\; c \right)   } }   }\)          \(\large{ s =  \frac  {b \;+\; D’ \;+\; c} {2}    }\)
  \(\large{  R =  \frac  { b\; D’ \;a  }     {  4 \;\sqrt  { s \; \left( s \;-\; b \right) \; \left( s \;-\; D’ \right) \left( s \;-\; a \right)   }  }    }\)          \(\large{  s =  \frac  {b \;+\; D’ \;+ \; а} {2}    }\)  92  \;+\; в\;а   }   }\)

  Где:

  \(\large{D’}\) = диагональ

  \(\large{a, b, c, d}\) = ребро

  \(\large{h}\) = высота

   

  Расстояние от центроида равнобедренной трапеции формулы

  \(\large{  C_x =  \frac{ a }{ 2 }    }\)
  \(\large{  C_y =  \frac{ h }{ 3}  \;  \left(     \frac { 2\;c \;+\; a } { c \;+\; a }  \right)    } \)

  Где:

  \(\large{C}\) = расстояние от центра тяжести

  \(\large{a, b, c, d}\) = край

  \(\large{h}\ ) = высота.

  No related posts.