градиент, дивергенция и ротор MathCAD 12 руководство
- Дифференцирование
- 3.1. Аналитическое дифференцирование
- 3.1.1. Аналитическое дифференцирование функции
- 3.1.2. Вычисление производной функции в точке
- 3.1.3. Определение функций пользователя через оператор дифференцирования
- 3.1.4. Дифференцирование при помощи меню
- 3.2. Численное дифференцирование
- 3.2.1. Дифференцирование в точке
- 3.2.2. Об алгоритме дифференцирования
- 3.3. Производные высших порядков
- 3.4. Частные производные
- 3.4.1. Частные производные
- 3.4.2. Примеры: градиент, дивергенция и ротор
- 3.4.3. Пример: якобиан
- 3.5. Разложение функции в ряд Тейлора
- 3.5.1. Разложение в ряд при помощи меню
- 3.5.2. Оператор разложения в ряд
Завершим разговор о частных производных несколькими примерами векторного анализа, которые нередко встречаются в вычислительной практике.
Листинг 3.14. Вычисление градиента функции двух переменных
Рис. 3.9. Модельная функция двух переменных (продолжение листинга 3.14)
Рис. 3.10. Векторное поле градиента функции двух переменных (продолжение листинга 3.14)
Как можно убедиться, сравнив графики на рис.
3.9 и 3.10, математический смысл градиента состоит в задании в каждой точке (х,у) направления на
плоскости, в котором функция f (х,у) растет наиболее быстро. Абсолютное значение градиента (т. е. длина вектора в каждой точке) определяет локальную скорость изменения
f (x,y). Из сопоставления графи ков ясно, что в центре показанной на них области
(х,у) сама функция f (х,у) меняется медленно (соответственно, значения ее градиента являются малыми), а в углах — быстро (там значения градиента максимальны).
Очень важно заметить, что градиент является не скалярной, а векторной функцией переменных х,у, поскольку фактически представляет собой комбинацию двух функций, задающих соответствующие проекции (горизонтальную и вертикальную) вектора в каждой точке. До сих пор в данной главе мы рассматривали дифференцирование скалярных функций, однако в математике часто приходится иметь дело и с вычислением производных векторных функций. Рассмотрим эти действия на примере операции поиска дивергенции (листинг 3.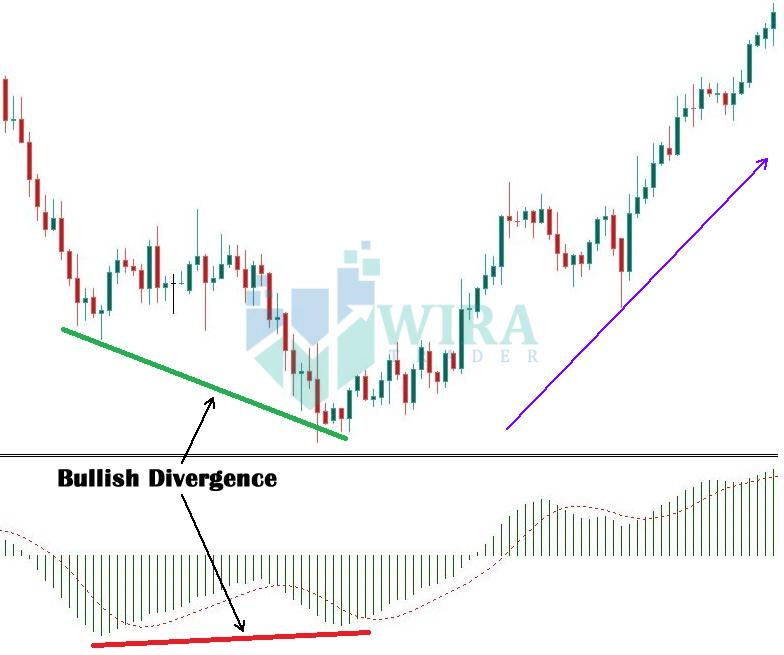
Листинг 3.15. Вычисление дивергенции векторной функции
Если, как принято в математике, обозначить оператор взятия градиента символом V, то дивергенцию вектор-функции можно формально определить как скалярное произведение
Vf, а еще одну распространенную операцию векторного анализа — ротор (или, по-другому, вихрь или завихренность) — как векторное произведение Vxf. Рис. 3.11 иллюстрирует пример векторной функции f (х,у) (определяемой в первой строке листинга) и вычисление ее дивергенции (которое производится аналитически в третьей строке). Обратите внимание, что в качестве исходной вектор-функции взят результат предыдущих расчетов, показанный (в форме векторного поля) на рис. 3.10. Строки кода в верхней части рис. 3.11 нужны для подготовки графика вычисленной дивергенции (в виде трехмерной поверхности и линий уровня, соответственно сверху и снизу).
Точно такую же структуру имеют расчеты ротора той же векторной функции f (х,у) в листинге 3.16, причем определение операции взятия ротора приводится в его второй строке (как и в случае дивергенции для листинга 3.15).
Читателю, знакомому с векторным анализом, предлагается догадаться самому, почему в рассматриваемом примере (листинги 3.14—3.16) ротор получается тождественно равным нулю (последняя строка листинга 3.16).
Рис. 3.11. График дивергенции векторной функции (продолжение листинга 3.15)
Листинг 3.16. Вычисление ротора векторной функции
В заключение разговора о векторном анализе функций подчеркнем, что примеры в листингах 3.14—3.16 относились к функциям двух переменных, т. е. описывали двумерный случай. Еще два листинга — 3.17 и 3.18 — показывают, как действуют перечисленные операции векторного анализа в трехмерном (пространственном) случае.
ПРИМЕЧАНИЕ
В электронной книге Resource Center (Центр ресурсов), поставляемой вместе с Mathcad, вы найдете дополнительные примеры вычисления градиента, дивергенции и ротора, относящихся к трехмерному случаю.
Листинг 3.17. Градиент функции трех переменных
Листинг 3.18. Дивергенция и ротор в трехмерном пространстве
Нравится
Твитнуть
Секреты градиента, расхождения и скручивания
1. Понимание основных понятий
1. Направленная производная: Производная в определенном направлении в точке функциональной области.
2. Градиент: Вектор (вектор), указывающий, что производная по направлению функции в этой точке принимает максимальное значение вдоль этого направления.
3. ФлюсВ движении жидкости определенное количество свойства, которое протекает через единицу площади в единицу времени, является физической величиной, которая представляет силу переноса определенного количества свойства.
4. Тираж: Вектор интегрируется по замкнутой кривой. Например, любая замкнутая кривая берется в поле потока, а интеграл скорости вдоль линии замкнутой кривой называется петлей скорости замкнутой кривой.
Точно так же, как метод расчета силы на работу, петлю скорости визуально называют работой скорости скорости вокруг замкнутой кривой.
5. Дивергенция(Дивергенция) может использоваться для характеристики степени дивергенции векторного поля в различных точках пространства. Физически смысл дивергенции — это активность поля. Когда div F> 0, это означает, что точка имеет положительный источник потока (расходящийся источник), когда div F <0 означает, что точка имеет отрицательный источник поглощенного потока (отверстие или сток), когда div F = 0, это означает, что Точка пассивная.
6. ЗавитокЭто векторный оператор в векторном анализе, который может указывать степень вращения, вызванного трехмерным векторным полем, на микроэлементы вблизи определенной точки. Этот вектор обеспечивает свойства поворота векторного поля в этой точке. Направление вектора скручивания представляет собой ось вращения обстоятельства с наибольшей степенью вращения векторного поля вокруг этой точки, а направление его вращения с вектором соответствует правилу правой руки.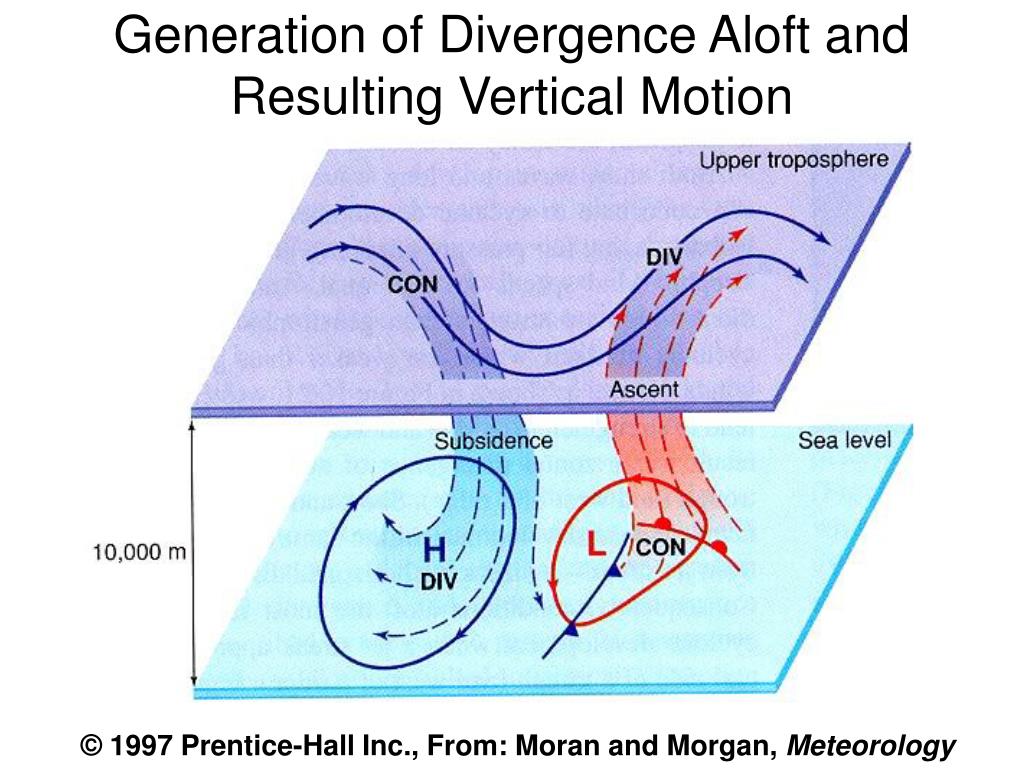
Размер вектора скручивания представляет собой отношение величины вращения вокруг этой оси вращения к площади бункера, окруженной траекторией вращения.
7. Понимание расхождения
Дивергенция не равна нулю, указывая, что поле является активным полем,Электрическое поле активноНет вращения,Пассивное магнитное полеЕсть вращение. Электрическое поле создается благодаря наличию разделенного заряда, поэтому он активен, но магнитное поле еще не нашло магнитного монополя, поэтому оно пассивно.
8. Понимание скручиваемости
Как говорится, есть картинки и правда, давайте поговорим, посмотрев на картинки!
Насколько я понимаю, он будет «вращаться» из-за неравномерных сил. Как и в примере с потоком воды на первом изображении, поток воды имеет одинаковый размер в вертикальной верхней и нижней плоскостях, поэтому слева нет вихря. Вихрь возникает с правой стороны, потому что сила неравномерна. В вертикальной верхней и нижней плоскостях, чем дальше вниз, тем меньше сила, поэтому создается вихрь.
2. Природа и связь градиента, расхождения и скручивания
1. Объект функции, объект операции и результат
градиент
Цель: скалярное поле
Объект: скаляр
Результат операции: вектор (вектор)
дивергенция
Цель: векторное поле
Объект: вектор
Результат операции: скаляр
Curl
Цель: векторное поле
Объект: вектор
Результат операции: вектор
1. Градиент направлен против скалярного поля (потенциального поля) и измеряет направление изменения скалярного поля. Градиент 0 указывает, что потенциальное поле является эквипотенциальным полем. Результатом является вектор.
2. Для векторного поля расходимость измеряет напряженность поля в единичном объеме векторного поля. Расхождение 0 указывает на то, что у этого поля нет источника. Результатом является скаляр.
3. Спин против векторного поля, измеряя спин векторного поля. Завиток 0 указывает, что это поле является консервативным полем (невращающееся поле) .
Консервативное поле должно быть градиентным полем скалярного поля. Результатом является вектор.
2. Иллюстрация Вращение градиента любого скалярного поля равно 0
Как показано ниже, электрическое поле внутри конденсатора представляет собой градиент. Для каждой вертикальной плоскости потенциал равен. Итак, это похоже на пример потока воды сейчас: сила равна вверх и вниз, так что скручивание равно нулю.
3. Решение расходимости и скручивания в электромагнитном поле
В любой точке электромагнитного поля
(1) (E · E) Расходимость напряженности электрического поля == отношение объемной плотности свободного заряда в этой точке к диэлектрической проницаемости.
(2) (▽ xE) Сгиб напряженности электрического поля == отрицательное значение скорости изменения силы магнитной индукции в этой точке.
(3) (▽ · B) Расходимость магнитной индукции == везде равна нулю.
(4) (▽ xB) Завиток магнитной индукции == произведение плотности тока и проницаемости в этой точке.
(5) (▽ · D) Расхождение электрического смещения == объемная плотность свободного заряда в этой точке.
(6) (▽ xH) Завиток напряженности магнитного поля == векторная сумма плотности тока проводимости и плотности тока смещения в этой точке.
Комментарий:
E — вектор напряженности электрического поля
B — вектор интенсивности магнитной индукции
D — вектор электрического смещения (также называемый интенсивностью электрической индукции), должен быть вектор электрической проводимости E = D +?
H — вектор напряженности магнитного поля H = B +?
Внутренняя ссылка:
D=εE
B=μH
Все заглавные буквы являются векторными
4. Классификация поля
Векторное поле A, поле количества u
▽ называется оператор Гамильтона—· ▽ = ▽ 2 = △
△ называется оператором Лапласа.
1. Вращение градиента ▽ × ▽ u = 0
Вращение поля градиента равно 0, поэтому поле градиента является консервативным полем (без поля вращения, потенциальное поле).
Например, гравитационное поле.
2. Дивергенция скручиваемости ▽ · (▽ × A) = 0
Дивергенция поля скручивания равна 0, поэтому поле скручивания является пассивным. Например, магнитное поле, само магнитное поле является полем скручивания других полей.
В частности, однородное поле является консервативным полем, а само магнитное поле имеет завиток. Следовательно, абсолютно однородное магнитное поле невозможно.
Оператор Лапласа △Это частичное x, частичное y, частичное z; оператор Лапласа — это дифференциальный оператор второго порядка в n-мерном евклидовом пространстве, определяемый как дивергенция.
Формула Стокса является обобщением формулы Грина. Формула Грина выражает связь между двойным интегралом на замкнутой области плоскости и интегралом кривой на граничной кривой. Формула Стокса связывает поверхностный интеграл на поверхности с интегралом кривой вдоль граничной кривой.
|
⇐ ПредыдущаяСтр 8 из 8 Ротор Ротор векторного поля характеризует степень отличия исследуемо го поля от однородного. Дивергенция Значение дивиргенции равно плотности источников рассматривае- мого поля в заданной точке пространства. Дивиргенциювекторного поля Авычисляют путем дифференци-рования его проекций по определенным правилам: 67. Оператор Лапласа Опера́тор Лапла́са (лапласиа́н, оператор дельта) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом . Функции он ставит в соответствие функцию в n-мерном пространстве. Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции: , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом , то есть в виде скалярного произведения оператора набла на себя. В произвольных ортогональных криволинейных координатах в трехмерном пространстве : где — коэффициенты Ламе. Цилиндрические координаты В цилиндрических координатах вне прямой : Сферические координаты В сферических координатах вне начала отсчёта (в трёхмерном пространстве): или В случае если в n-мерном пространстве: В декартовой системе координат оператор запишется: 68. Скалярное поле. Поверхности и линии уровня. Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. При мер скалярных полей дает поле температур, электростатическое поле. Задание скалярного поля осуществляется заданием скалярной функции точки М
Если в пространстве введена декартова СК xyz, то
Геометрической характеристикой скалярного поля служат поверхности уровня – геометрическое место точек, в которых скалярная функция поля принимает одно и то же значение.
В случае поля температур, создаваемого в однородной и изотропной среде точечным источником тепла, поверхности уровня будут сферами с центром в источнике (центрально-симметричное поле). В случае бесконечно равномерно нагретой нити поверхностями уровня (изотермическими поверхностями) будут круговые цилиндры, ось которых совпадает с нитью
69. Производная по направлению. Ее физический смысл В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Связь с градиентом Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления: Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении. Определение Для случая трёхмерного пространства градиентом скалярной функции координат , , называется векторная функция с компонентами Или, использовав для единичных векторов по осям прямоугольных декартовых координат : Если — функция переменных , то её градиентом называется -мерный вектор компоненты которого равны частным производным по всем её аргументам. Пример Например, градиент функции будет представлять собой: Для характеристики величины и направления скорости измене- ния скалярного поля в пространстве вводят градиент этого поля где — коэффициенты Ламэ по координатам , яв- ляющиеся коэффициентами пропорциональности между диффе- ренциалами обобщенных координат и бесконечно малыми ребра- ми элементарного параллелепипеда в выбранной (•) пространства Коэффициенты Ламэ для наиболее употребительных СК:
Оператор Гамильтона В декартовой системе координат оператор ∇ записывается:
Свойства оператора набла Этот оператор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется. Если умножить вектор на скаляр , то получится вектор , который представляет собой градиент функции . Если вектор скалярно умножить на вектор , получится скаляр , то есть дивергенция вектора . Если умножить на векторно, то получится ротор вектора : · Замечание: как и для обозначения скалярного и векторного произведения вообще, в случае их применения с оператором набла, наряду с использоваными выше, часто используются эквивалентные им альтернативные обозначения, так, например, вместо нередко пишут , а вместо пишут ; это касается и формул, приводимых ниже. Соответственно, скалярное произведение есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также . В декартовых координатах оператор Лапласа определяется следующим образом: . Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. То есть производная выражения, зависящего от двух полей, есть сумма выражений, в каждом из которых дифференцированию подвергается только одно поле. Для удобства обозначения того, на какие поля действует набла, принято считать, что в произведении полей и операторов каждый оператор действует на выражение, стоящее справа от него, и не действует на всё, что стоит слева. Если требуется, чтобы оператор действовал на поле, стоящее слева, это поле каким-то образом отмечают, например, ставя над буквой стрелочку: Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться. Операторы второго порядка Так как существуют различные способы перемножения векторов и скаляров, с помощью оператора набла можно записать различные виды дифференцирования. Комбинирование скалярных и векторных произведений даёт 7 различных вариантов производных второго порядка: Для достаточно гладких полей (дважды непрерывно дифференцируемых) эти операторы не независимы. Два всегда совпадают: Три оставшихся связаны соотношением: Еще одно может быть выражено через тензорное произведение векторов:
⇐ Предыдущая12345678 Читайте также: |
Поверхность уровня данного поля определяется уравнением
Например:
Два из них всегда равны нулю:Дивергенция, градиент и завиток — многомерное исчисление
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по многомерным вычислениям
14 практических тестов Вопрос дня Карточки Learn by Concept
Справка по многомерному исчислению » Тройная интеграция поверхности » Расхождение, градиент и изгиб
Вычислите изгиб для следующего векторного поля.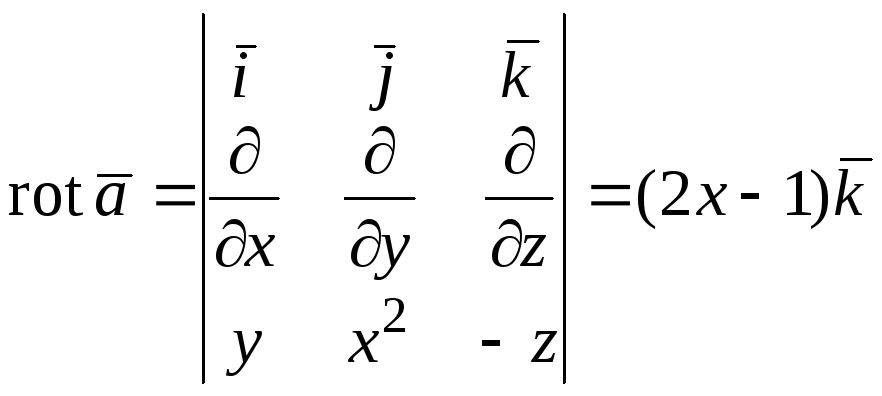
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы рассчитать завиток, нам нужно вспомнить формулу.
где , и соответствуют компонентам данного векторного поля:
Теперь давайте применим это к нашей ситуации.
Таким образом, завиток равен
Сообщить об ошибке
Вычислить , где .
Возможные ответы:
Правильный ответ:
Пояснение:
Все, что нам нужно сделать, это вычислить частные производные и сложить их вместе.
Сообщить об ошибке
Рассчитать завиток для следующего векторного поля.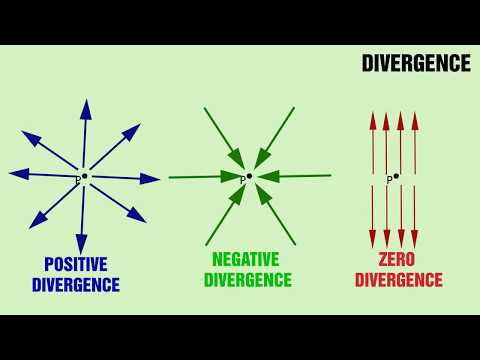
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы рассчитать завиток, нам нужно вспомнить формулу.
где , и соответствуют компонентам данного векторного поля:
Теперь давайте применим это к нашей ситуации.
Таким образом, завиток равен
Сообщить об ошибке
,8
Возможные ответы:
Правильный ответ:
Пояснение:
Все, что нам нужно сделать, это вычислить частные производные и сложить их вместе.
Сообщить об ошибке. Университет Хьюстона, бакалавр наук, инженер-механик.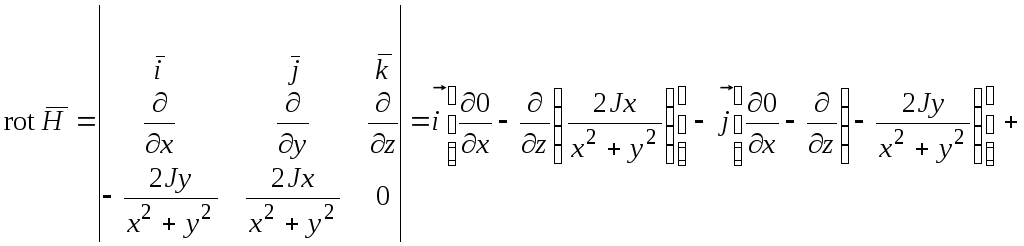
..
View Репетиторы по многомерному исчислению
Томас
Сертифицированный репетитор
Дартмутский колледж, бакалавр искусств, биохимии и молекулярной биологии. Колумбийский университет в городе Нью-Йорк, магистр …
Просмотреть преподаватели многомерного исчисления
Алонсо
Сертифицированный преподаватель
Государственный университет Трумэна, бакалавр наук, специальность математика, дополнительная статистика.
Все ресурсы по вычислениям с несколькими переменными
14 практических тестов Вопрос дня Карточки Учитесь по концепции
Понимание градиента и дивергенции | Стрела Времени
Мне нужно было написать это давным-давно, когда я понял внутреннюю работу этого материала. Но хорошо, я считаю, что никогда не поздно научить чему-то . Итак, начнем…
Я не знал об этих вещах до недавнего времени…
Я выучил векторное исчисление наизусть во втором семестре, когда я ничего не делал, но все время жаловался на дрянную систему, которая у нас в школе.
колледж. (хм, мою историю всегда можно пропустить)
Приходилось глотать такие вещи, как роторность, дивергенция, градиент, теоремы Гаусса и Стокса и т.д. и без потерь блевать на экзаменах. В то время я даже не подозревал об изяществе этих операций и не понимал работы векторов (вещей, определяющих симметрию и придающих гениальное прикосновение к физическим законам).
Когда я впервые изучил электромагнетизм, я не мог понять физического значения уравнений Максвелла (я гик, который любит собирать знания, при условии, что я действительно способен понять их физическое значение вполне удовлетворительно ). Более того, будучи потрясающим любителем физики, я всегда изучал вещи (что бы это ни было!) концептуально.
К сожалению, на этот раз я не могу. С тех пор это начало глючить внутри меня. Пришлось потерпеть несколько месяцев.
Ну, слава богу, ненадолго. Я думаю, вы уже знаете, что я был занят онлайн-курсами edX. В моем курсе бакалавриата у меня есть предмет под названием «аэродинамика», который является неотъемлемой частью (например, близкой к сердцу) аэронавтики.
Но, к несчастью, у нас есть беспощадный преподаватель (эх, таких видов у нас минимум два в семестр), который нещадно копирует пасту из работы Дж. Д. Андерсона.
Итак, я подумал о том, чтобы пройти курс edX по аэродинамике (знав некоторые основы). Когда я присоединился к edX, было уже слишком поздно, чтобы пропустить курс. Следующим курсом была аэродинамика летательных аппаратов. Примечательно, что он предоставлен Массачусетсом.
Насколько я знаю, Массачусетский технологический институт является враждебно настроенным оценщиком во всем edX. Допускается не более 2 представлений, студенты должны получить более высокие оценки (например, 70%), чтобы пройти курс и получить сертификат, домашние задания и экзаменационные вопросы будут крутой как АД!!! Такое часто бывает с их стандартом МООК (Это не разглагольствования! Таких людей всегда надо ценить за их работу)
Это хорошо. Мне нравится решать проблемы. Итак, я прошел сложный курс. Но вскоре я был поражен в первом лекционном видео, когда инструктор написал операции расхождения и завитка, говоря: «это исходное распределение — мы все это знаем…» и продолжил.
Да кого я обманываю? Это точно не вводный курс.
Пока оптимист держал меня за спину, я начал изучать векторное исчисление. Мне пришлось несколько раз взорвать себе мозг, чтобы понять концепции. Я пытался понять эти операции на примерах потоков жидкости, таких как источник, сток и т. д., но вскоре обнаружил, что увлекаюсь уравнениями Максвелла. У меня уже есть некоторые знания об этом, просто я не мог понять дифференциальные формы. В любом случае, это не заняло много времени. Электромагнетизм помог мне понять эти векторные операции, что в конечном итоге привело меня к пониманию гидродинамики.
Ура! Я наконец-то был счастлив! Это был один из приятных моментов, которые у меня были. Проблема векторного исчисления заняла у меня некоторое время, чтобы решить. Но каким-то образом я понял. А позже Фейнман помог мне закрепить неясные, частично заполненные понятия.
Теперь, когда у вас хватило терпения прочитать мое прошлое, давайте попробуем интерпретировать некоторые магические операции, выполняемые с помощью простого оператора перевернутой дельты (называемого «набла» или его официальное название « Del »).
–
Начнем «разбираться» (понятие полей)…
Действительно ли мы понимаем математику? Меня это часто глючит. На самом деле мои сокурсники просто запоминают формулы и процедуры решения конкретной задачи, и они говорят мне, что понимают задачу, которую они только что «решили». Я всегда представлял себе обучение как «сбор знаний для развития творческого мышления».
Есть отличная цитата Поля Дирака. Он говорит,
«Я считаю, что я понимаю математическое уравнение, когда я могу предсказать свойства его решений, не решая его на самом деле».
Может быть, нам всем следует перестать говорить, что мы «понимаем» математическое уравнение, просто решая его. Итак, сегодня я запланировал дать определение каждой операции (или теореме) на основе ее физического значения.
Окей, мы всегда начинаем векторное исчисление с понятия полей , которое, конечно же, является одним из самых абстрактных понятий, которые когда-либо определялись, представлялись и часто использовались в физике (насколько мне известно).
Честно говоря, мы до сих пор не знаем, существует ли на самом деле что-то настолько безумное, как поле! Но по нашему опыту, основанному на разнообразных экспериментах, проведенных до сих пор, все, что мы можем сказать, это то, что есть некая «вещь», которая согласуется с нашей теоретической концепцией полей. Итак, мы продолжаем верить, что это действительно существует!
Существует два вида полей: скалярное поле и векторное поле.
Скалярное поле:
Это позволит вам легко изобразить поле. Скалярное поле — это область в пространстве, где каждая точка связана со значением (скаляром). Например, температура в вашей комнате может быть скалярным полем. Может быть где-то в углу, рядом с розеткой кондиционера и т.д. Но на самом деле дело не в константе. Это очень похоже на эту симуляцию из htwins (включите «температуру» и попробуйте изменить возмущение, чтобы визуализировать поле).
Аналогичным образом это можно представить для потенциалов (потенциал есть не что иное, как скалярная функция положения, показывающая количество работы, необходимой для перемещения чего-либо в поле против силы) в других полях, таких как электромагнитное или гравитационное поле.
.
Векторное поле:
Материал в этом поле имеет направление в дополнение к значению, связанному с каждой точкой. Примеры включают скорость частиц (профиль скорости) в ветре, типичный поток жидкости и т. д.
Сбоку изображение потока жидкости в трубопроводе, демонстрирующее вязкость, что сила сдвига изменяется в зависимости от градиента скорости перпендикулярно потоку.
Проще говоря, из-за вязкости скорость частиц жидкости равна нулю на границе жидкости и трубы и максимальна вблизи центра трубы.
Векторное поле обычно изображается набором стрелок, указывающих в направлении поля, длина которых пропорциональна величине поля (указывающей напряженность поля). Мы также рисуем линии поля, чтобы визуализировать поля (в основном для электрических и магнитных вещей, и да! гидродинамики тоже…) таким образом, чтобы эти стрелки были касательными к линиям поля.
С той же темой линий поля мы также рисуем контуры (которые представляют собой линии одинаковой величины чего-то, в основном изопотенциалы).
Ах! Вы бы видели карту мира. Горы, реки — контурные линии, обозначающие области одинаковой высоты. Контуры более элегантны, чем линии поля, потому что в дополнение к линиям они также представляют интенсивность поля в каждой точке.
Вот пример подъема потока над круглым цилиндром. Изолинии (здесь они называются по-другому, они называются линиями тока) обозначают изопотенциалы скорости.
Хорошо, это разные способы изображения полей. Но они не всегда хорошо держатся. В любом случае, я оставлю это исследование в качестве упражнения для вас!
Градиент означает, как поле изменяется в пространстве…
Теперь, что мы имеем в виду, когда мы дифференцируем/интегрируем что-то по отношению к чему-то?
Дифференциация дает знание об изменении чего-либо по отношению к чему-либо. А интеграция дает обратное. Он экстраполирует конкретное изменение (мы только что получили) на весь предел, тем самым давая среднее значение функции по интегральному пределу.
Если мы хотим узнать, как определенная функция изменяется по отношению, скажем, ко времени, мы берем частную производную функции, потому что нам нужно только то, как функция изменяется со временем, и чтобы ее не беспокоили никакие другие задействованные параметры.
Что, если мы хотим узнать, как конкретное поле изменяется по отношению к пробелу ? Градиент делает свое дело. Он показывает, как соответствующие компоненты определенного поля изменяются в зависимости от размеров пространства.
Возьмем двухмерный случай, так как его довольно легко визуализировать…
Мы знаем, что функция (подобная функции поля) состоит из компонентов поля в разных измерениях. На данный момент мы смотрим только на размеры пространства.
Скалярное поле определяется его интенсивностью. В поле, показанном сбоку, плотность поля равна нулю в центре и увеличивается квадратично по мере удаления от центра.
Мы можем создать векторное поле для этого скалярного поля. Конечно, мы используем функцию градиента. дает изменение вдоль направлений x, y (т.е.) и .
Это потому что магический оператор. Он фиксирует изменение функции по каждому пространственному измерению.
Скажем, мы находимся на каком-то месте в нашей области.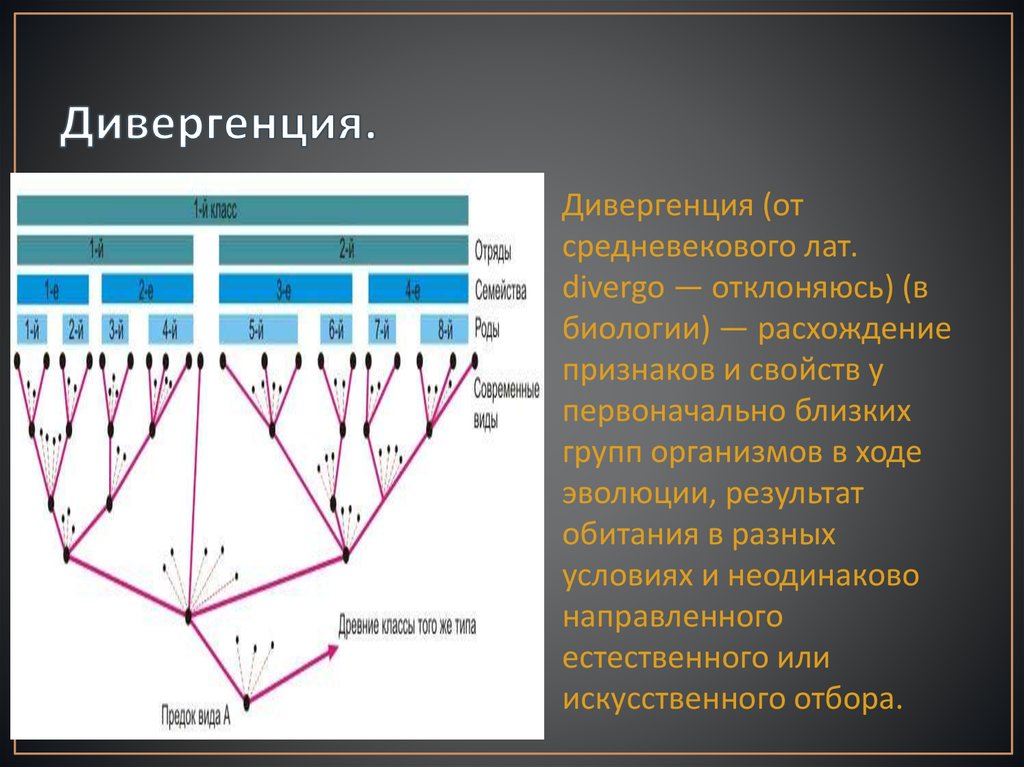
Что дает градиент, так это направление, вдоль которого происходит максимальное изменение области.
Итак, с нашей позиции мы смотрим вокруг, ищем направление, вдоль которого есть максимальное изменение (используя результат нашего градиента), и мы можем начать двигаться в этом направлении. Ух ты! Это прекрасный способ построить траекторию, вдоль которой интенсивность поля всегда увеличивается по мере нашего движения.
Итак, что произойдет, когда мы достигнем места с максимальной интенсивностью поля? Простой. Градиент становится равным нулю. Для скалярного поля, подобного показанному выше, на самом деле нет максимум . Поле продолжает увеличиваться в сторону . Неважно, этого достаточно для нашего обсуждения.
Таким образом, градиент помогает преобразовать скалярное поле в векторное поле. Ну, его также можно использовать для анализа векторного поля. Но тема остается прежней.
Дивергенция (вход или выход?)…
Я помню, как давно объяснял о потоке, когда писал о переменном токе.
Точнее, это просто течение чего-то через поверхность, перпендикулярную потоку. Обычно это произведение среднего нормального компонента «чего-то» и площади, через которую оно протекает.
Например, электрический поток. Это напряженность электрического поля на определенной площади (разумеется, на замкнутой поверхности). Другими словами, количество силовых линий, пересекающих замкнутую поверхность. Или давайте упростим жизнь.
Допустим, у вас есть гипотетический мешок для воды. И давайте создадим этот сценарий с неконсервативным полем (т.е.) источник воды каким-то образом хранится внутри мешка. Теперь в сумке пробита дырка, так что она занимает одного процента от (просто упомянем, что она маленькая, не имеет отношения к нашему анализу) всей площади сумки.
Вода с некоторой скоростью вытекает из отверстия. Что нам нужно, так это что-то, чтобы измерить чистый исходящий поток. Мы берем нормальную составляющую и делаем математику (т.е.) умножаем ее на площадь отверстия.
Теперь внимательно посмотрите на юниты. Мы получаем . В нашем примере это поток. Он дает объем воды, вытекающей из мешка каждую секунду.
Теперь приступим к дивергенции. Скажем, мы «хлопаем» этим мешком с водой. Теперь мы хотим знать, как течет вода, выходит ли она наружу или внутрь. Что ж, это легко. Она всегда будет вытекать, что верно в нашем простейшем примере с мешком для воды.
После того, как шарик лопнет, все частицы (пока нам не нужны атомы или молекулы!) в потоке имеют скорость, направленную наружу, как показано ниже (помните, что внутри есть точечный источник — в отсутствие какого-либо возмущение, частицы выбрасываются наружу в виде сферических волновых фронтов). И заметьте! Это течение идеальной (невязкой, несжимаемой и т. д.) жидкости.
Воображаемая сфера просто указывает на область, перпендикулярную «стрелкам»…
Что произойдет, если мы добавим несколько усложнений? Скажем, в этом гипотетическом мешке есть ряд источников (дающих воду) и стоков (высасывающих воду).
А теперь мы в замешательстве. Мы хотим знать, является ли чистый поток воды (после сложения и вычитания всего) исходящим или поступающим.
Эта операция расхождения дает результат. Это мера потока чего-то из/в поле. Поток жидкости задается векторным полем. И дивергенция выполняет работу по добавлению/вычитанию сил источников/стоков, тем самым она предсказывает «исходящий» поток (через определенную область).
Давайте посмотрим поближе…
Теперь мы переходим к теореме. В нашем примере давайте возьмем точечный источник, который мы использовали выше, и поместим его внутрь трубы. Это какая-то произвольная часть трубки (исходник здесь не показан). И я не думаю, что есть другая замена Фейнману для объяснения этой теоремы. Итак, позвольте мне сплагиатить его вывод.
Предположим, что эти линии являются линиями тока, а стрелки имеют постоянную величину (удлинение стрелок происходит только из-за проекции 3D)
Для нашего удобства предположим бесконечно малый куб со стороной в поле течения.
Но так как это может создать некоторую путаницу, мы будем использовать , и в качестве длины куба в соответствующих направлениях (и мы используем правую систему координат). Всякий раз, когда мы используем площадь в векторном анализе, мы выбираем ее направление с помощью единичного вектора нормали, выступающего из поверхности. В нашем случае он выходит за пределы куба со всех сторон.
Выберем две поверхности вдоль оси x (где присутствуют красные точки) и предположим, что вектор напряженности поля на этих двух поверхностях равен . Нам нужен поток векторного поля через эти две поверхности. Вспомним наше определение потока. Это не просто продукт. Когда мы играем с векторами, мы используем скалярное произведение (которое связано с нахождением вклада параметра в отношении его ориентации). Перекрестное произведение связано с вращением, и мы обсудим его, когда будем играть с «завитком» (возможно, в следующий раз).
Поток через первую поверхность будет
, а через другую
.
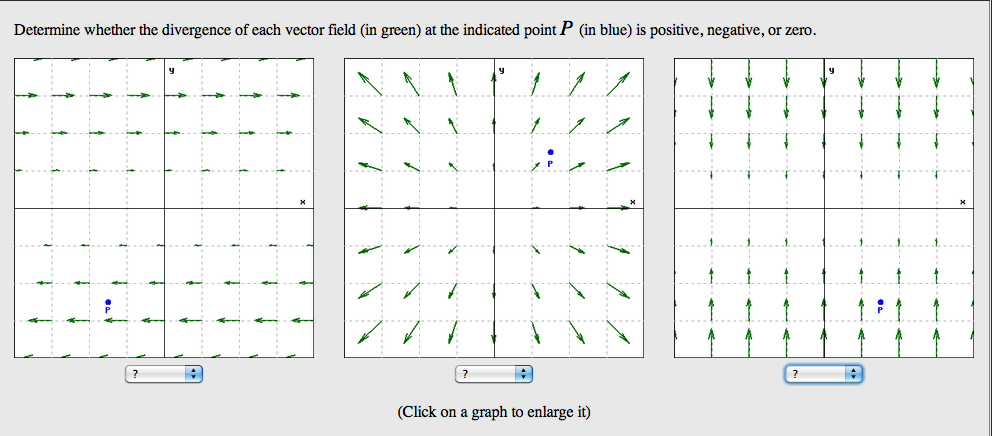
Направление меняется, да. Но НЕТ! величина не будет прежней! Мы занимаемся вычислениями здесь. Мы должны учитывать, меняет ли что-то поток между кубами.
Итак, оба потока различаются примерно в раз …
Так как интеграл есть сумма двух частей, мы можем сложить оба потока. Следовательно, общий поток в направлении x будет составлять в сумме
Теперь мы выходим из трубы и смотрим (макроскопически) общий поток от всех граней куба, который представляет собой сумму вкладов потоков от всех граней. И мы получаем что-то другое.
Посмотрите внимательно. Это скалярное произведение нашего оператора на вектор поля. И наш общий поток — это скалярное произведение вектора интенсивности потока с единичным вектором нормали, умноженное на площадь выбранной поверхности (это то, что мы определили и написали все это время).
Для бесконечно малого куба мы написали . Для произвольного объема это объемный интеграл функции.
Итак, левая и правая стороны становятся…
И вот! Это теорема Гаусса о дивергенции, очень полезная теорема для дифференциального исчисления векторных полей. Мы только что нашли применение дивергенции. Обратите внимание на поверхностный интеграл. Она обведена (гм, кружок должен заключать в себе оба интеграла, мой плохой! ), потому что выбранная поверхность должна быть замкнутой. Если бы он был открыт, мы не смогли бы оценить объем. Я думаю, вы знаете о дифференциации и интеграции.
Нравится:
Нравится Загрузка…
Tagged: Образование, Поля, Векторное исчисление, Векторы
Точные последовательности | расхождение, градиент, завиток
Пару дней назад, ближе к концу поста, я упомянул точные последовательности. Этот термин означает не то, что вы могли бы разумно подумать. Это не значит точно в том смысле, что не является приблизительным.
Это означает, что то, что получается на одном шаге, точно такое же, что и обнуляется на следующем шаге.
То есть образ каждой функции является в точности ядром следующей функции в последовательности [1].
Градиент и завиток
Например, пусть f будет градиентом, а g — завитком. Тогда следующая последовательность является точной
, если A — набор гладких функций от ℝ³ до ℝ, а B и C — набор гладких функций от ℝ³ до ℝ³.
Это говорит о том, что образ f , векторных полей, являющихся градиентом чего-либо, является ядром g , векторных полей с нулевым завихрением. Другими словами, градиентные векторные поля являются безвихревыми, а все безвихревые векторные поля являются градиентом некоторой потенциальной функции.
To show that
image f = kernel g
we have to show two things:
image f ⊂ kernel g
and
image f ⊃ kernel g
Как это часто бывает, первое проще второго.
Распространенной домашней задачей [2] является показать, что ротор дивергенции равен нулю, т.е.
∇×(∇φ) = 0
0348 F с ∇ × F = 0 существует потенциал φ такой, что F = ∇φ. Легче показать, что образ первой функции является частью ядра следующей, чем показать, что ядром первой является в точности ядро следующей, потому что последняя требует доказательства существования чего-либо.
Короткие точные последовательности
Короткие точные последовательности — это точные последовательности следующего вида. (Это называется коротким, потому что точные последовательности часто длиннее.)
На стрелке от 0 до нет метки A , потому что есть только одна функция от 0 до любого места. Также нет метки на стрелке от C до 0, потому что есть только одна функция, которая ведет из любого места в 0 [3].
Нуль слева означает, что функция f является однозначной (инъективной). Его изображение — это только один элемент, поэтому ядро и — это только один элемент.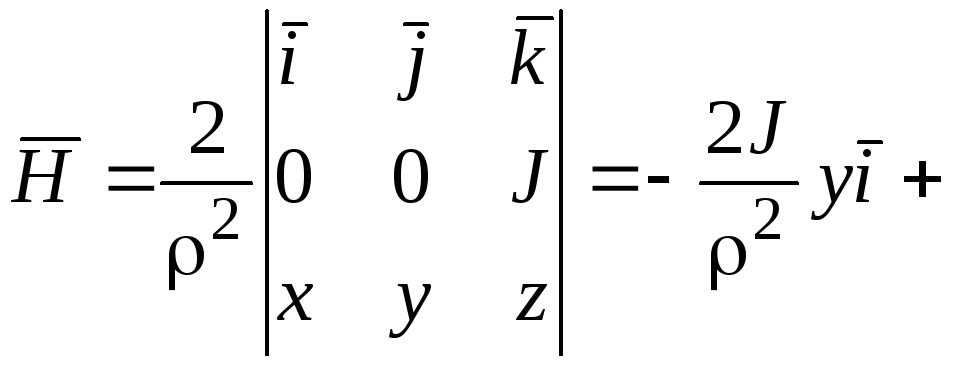
Точно так же ноль справа означает, что функция г на (сюръективное). Ядром последней стрелки является все в C , поэтому образ g должен быть всем в C .
Например, пусть B — группа, а φ — гомоморфизм B в другую группу. Пусть A будет ядром φ и пусть f будет отображением включения из ядра в B . Пусть г будет частным отображением, принимающим C = B / А . Тогда так называемая «теорема о первом групповом гомоморфизме» утверждает, что приведенная выше последовательность точна.
Div, grad, curl и все такое
Название этого раздела — дань уважения превосходной небольшой книжке Х. М. Шей.
Выше мы сказали, что ротор градиента равен нулю и что все векторные поля с нулевым ротором являются градиентами. Верно также и то, что дивергенция завитка равна нулю, и что векторное поле имеет нулевую дивергенцию, если оно представляет собой завиток чего-либо.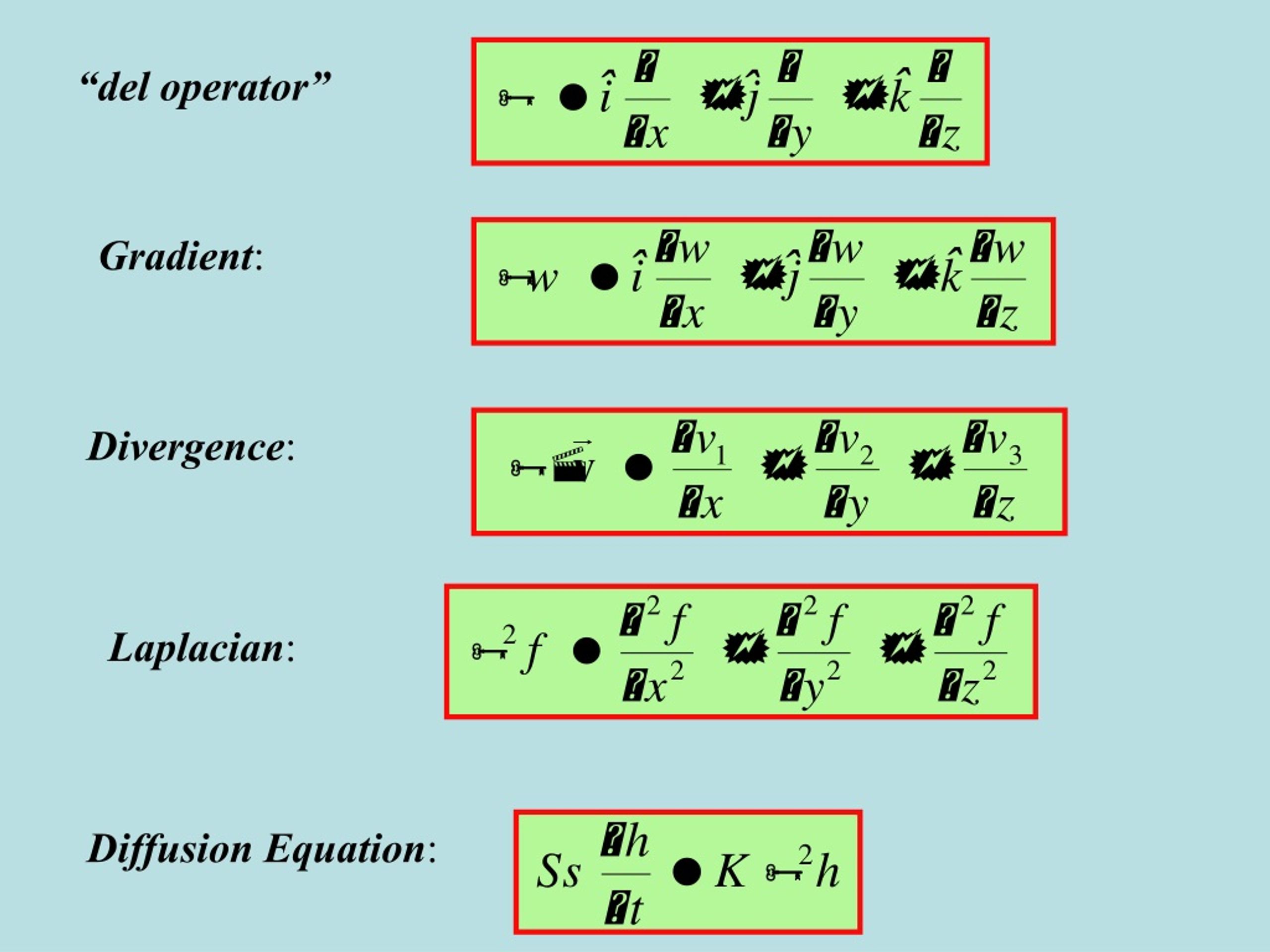
То есть для векторного поля F ,
∇ · (∇ × F ) = 0
и если ∇ · G = 0 для векторного поля G , то существует векторное поле
× F 90
Это означает, что мы можем расширить наш пример до
, если тщательно определим A .
Обсуждение в этом разделе оправдывает только обозначенные стрелки. Нам нужно выровнять две немаркированные стрелки на концах.
Нуль слева требует, чтобы градиент был один к одному. Но в целом градиент равен , а не один к одному: функции, отличающиеся на константу, имеют одинаковый градиент. Но если мы определим A как набор i интегрируемых функций на ℝ³, тогда градиент будет взаимно однозначным. Требование существования интеграла функции по ℝ³ означает, что функции должны в конечном итоге приближаться к нулю во всех направлениях.
Нуль справа требует, чтобы каждая гладкая функция на ℝ³ была дивергенцией чего-либо.
Это просто. Дана функция φ от ℝ³ до ℝ, пусть F — векторное поле, первый компонент которого в точке ( x , y , z) является интегралом от φ от начала координат до ( x , 0, 0), а второй и третий компоненты равны 0. Тогда расхождение F равно φ.
Длинные точные последовательности
Точная последовательность в предыдущем разделе длиннее короткой точной последовательности, и на практике встречаются более длинные точные последовательности. Точная последовательность может быть бесконечной в одном или обоих направлениях. Например, последовательность Майера-Виеториса, основополагающий инструмент гомологии, бесконечна слева и оканчивается 0 на правом конце.
Похожие сообщения
- Поиск диаграмм: четыре, пять и девять лемм
- Следующие области математики, которые необходимо применить
- Как связаны области математики
[1] Термин «ноль» здесь перегружен. Это может быть целое число 0, начало векторного пространства, ядро группы и т.