Дробное число в дробную степень
|
|
|
|||||||||||||||||||||
Частное решение.
Угол между ними.
Как посчитать число в большой степени
Мы разобрались, что вообще из себя представляет степень числа.
Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень – это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a .
Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите – 2 в степень 4 .
Решение
Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности.
Разберем пример.
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1
0 0 – не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 2 в степень – 3 .
Решение
Используя определение выше, запишем: 2 – 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень – 2 .
Решение
Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1 , 43 ) – 2 = 10000 20449
Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 – 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2
После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью.
Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 .
(2⋅24) ≡ 436(mod541)
.
Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.
Какие подходы задействованы для вычисления:
б) откуда взялось деление с остатком?
в) не понял суть знака «тождественно равно» (вики прочитал, но разницы от обычного знака равенства не уяснил)
- Вопрос задан более года назад
- 602 просмотра
Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование – формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.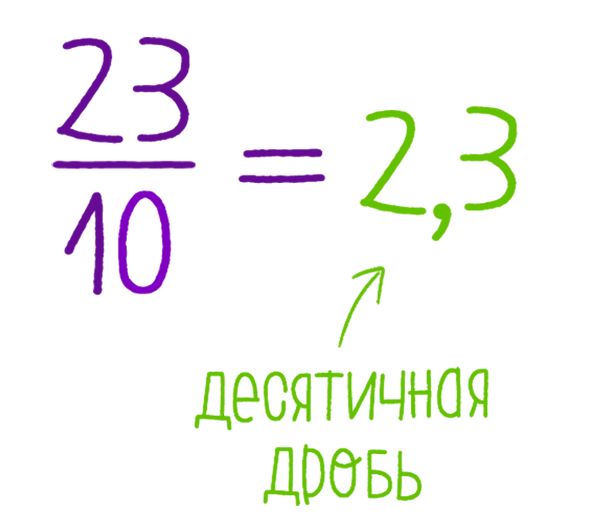
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат – 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.
Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».
Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.
Как возвести число в степень.
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:
Возведение в степень
А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.
5 3 = 5 x 5 x 5 = 125
Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.
Как возводить в отрицательную степень.
При возведении в отрицательную степень необходимо использовать простое правило:
как возводить в отрицательную степень
Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т.
е. в положительной степени. Таким образом, чтобы найти значение
2 -3
Дробная степень числа калькулятор. Инженерный калькулятор
Включает такую нужную для многих функцию, как калькулятор степеней. С его помощью выполнить возведение числа в степень проще простого, задайте выражение — получите результат. Калькулятор производит возведение в степень онлайн , как и любые другие функции, прямо на нашем сайте.
Как возвести число в степень в калькуляторе?
Возведение в степень — это действие умножения числа самого на себя n раз, где число x y — степень, x — основание степени, y=n — показатель степени. Чтобы возвести в степень на калькуляторе, используйте соответствующие кнопки на панели управления. Если вам нужна более подробная информация по работе с цифровой панелью калькулятора, перейдите на страницу .
Функция возведения в степень в калькуляторе представлена пятью кнопками: возведение в квадрат, возведение в куб, возведение в n степень произвольного числа, возведение в степень основания равного 10-ти и возведение в степень экспоненты.
Пример, как найти степень числа 10:
Экспонента в степени
Нажав на кнопку, увидите в строке запись exp(). Чтобы посчитать число е в степени, нужно возвести число Эйлера в степень e x = exp(x). Кому интересно знать, чему равно число е: его значение 2.71828182845905.
Пример, как возвести е в степень:
Возведение в дробную степень
Допустим, нас интересует дробная степень числа x y1/y2 . Так как возведение в степень — действие, обратное к извлечению корня, расчёт сводится к нахождению корня степени y2 из числа x в степени y1. Если значение y2 чётное, то дробную степень можно вычислить только при положительном основании, так как корень отрицательного числа не существует и калькулятор в подобной ситуации выдаст вам ошибку!
При возведении в дробную степень не забывайте закрывать основание в скобки, иначе знаменатель дроби в показателе степени уйдет в знаменатель основания!
Этот пример показывает, как возвести в дробную степень на калькуляторе:
Наш онлайн калькулятор позволяет возвести как в положительную, так и в отрицательную степень.
При отрицательном значении показателя, основание должно принять вид (1/x), другими словами, числитель и знаменатель основания степени должны поменяться местами и только после этого можно начинать возведение. Калькулятор позволяет возвести число в отрицательную степень автоматически, опуская все промежуточные преобразования и выдавая сразу окончательный ответ.
При возведении в отрицательную степень всевозможных функций, в том числе тригонометрических, онлайн калькулятор автоматически учитывает их четность/нечетность по правилу знаков.
Этот пример показывает, как возвести в отрицательную степень на калькуляторе:
Дробное число в степени калькулятор тоже рассчитает.
Возведение дроби в степень с помощью калькулятора:
Возведение корня в степень с помощью калькулятора:
Все функции нашего бесплатного калькулятора собраны в одном разделе.
Возведение в степень онлайн was last modified: Март 3rd, 2016 by Admin
- 02.
12.2015Датчик температуры кулера (вентилятора) начинает работать когда температура повышается до заданного значения и выключается при ее понижении. Питание на кулер подается через реле (12В, 200 Ом). Датчиком температуры служит термистор с отрицательным температурным коэффициентом. Операционный усилитель LM311 используется в качестве компаратора. При повешении температуры сопротивление термистора уменьшается, соответственно падает напряжение на …
- 06.04.2015
Микросхема К1182ГГ3Р является интегральной схемой высоковольтного полумостового автогенератора. Она изготовлена по уникальной биполярной технологии, разработанной для класса ИС, ориентированных на применение в сети переменного тока до 240В. ИС преобразует постоянное напряжение (в частности, выпрямленное сетевое напряжение) в высокочастотное напряжение 30-50 кГц и позволяет создавать гальванически развязанные вторичные источники питания мощностью до 12 Вт. Номиналы элементов для входного напряжения сети 220В …
- 14. 07.2015
Как известно напряжение бортовой сети автомобиля находится в пределах от 12 до 14,4В, что вводит ограничение по мощности используемых усилителей ЗЧ. Для увеличения выходной мощности усилителя необходимо использовать преобразователь напряжения. Микросхема TDA1562Q позволяет легко решить эту проблему. Выходная мощность усилителя на TDA1562Q 18Вт (14,4В Rн=4 Ом), при увеличении мощности усилитель переходит в …
- 23.09.2014
Автомат работает с 7-ю лампочками и создает эффект световой линии, которая сначала постепенно вырастает из центральной светящейся точки, а затем гаснет, постепенно, от центра к краям. Автомат управляет лампочками 15Вт 220В. Схема состоит из мультивибратора, задающего периодичность пульсации, трех линий задержки и четырех выходных тиристоров. Периодичность повторений пульсаций зависит он …
12.2015
07.2015Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов.
Приведем примеры таких выражений:
\(5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\(xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)
Сумму одночленов называют многочленом.
3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто
встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.
Калькулятор степеней
Возвести в степень
Возведений в степень: 20880
Что такое натуральная степень числа?
Число p называют n -ой степенью числа a , если p равно числу a , умноженному само на себя n раз: p = a n = a·.
..·a
n — называется показателем степени , а число a — основанием степени .
Как возвести число в натуральную степень?
Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:
Пример 1 . Возвести число три в четвёртую степень. То есть необходимо вычислить 3 4
Решение : как было сказано выше, 3 4 = 3·3·3·3 = 81 .
Ответ : 3 4 = 81 .
Пример 2 . Возвести число пять в пятую степень. То есть необходимо вычислить 5 5
Решение : аналогично, 5 5 = 5·5·5·5·5 = 3125 .
Ответ : 5 5 = 3125 .
Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.
Что такое отрицательная степень числа?
Отрицательная степень -n числа a — это единица, поделённая на a в степени n: a -n = .
При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.
Как возвести число в целую отрицательную степень?
Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.
Пример 1 . Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2 -4
Решение : как было сказано выше, 2 -4 = = = 0.0625 .
Ответ : 2 -4 = 0.0625 .
Инструкция
Примечание: π записывается как pi ; корень квадратный как sqrt() .
Шаг 1. В ячейки запишите число и степень.
Шаг 2. Нажмите кнопку “Возвести”.
Шаг 3. Получите результат.
Вводить можно любое число. Если в водите десятичную дробь, тогда нужно употреблять точку (2.56), а если обыкновенную дробь, тогда вводится знак “/” (2/3).
Как возвести число в степень
Возведение числа в степень – это умножение заданного числа само на себя столько раз, в какой степени оно находится.
Рассмотрим на простом примере. Нам надо возвести в степень 3 цифру 7. Пример записывается так: . В ашем примере цифра 7 – это основание, а 3 – степень. Значит умножаем: 7 * 7 * 7 = 343.
Кроме того, можно возводить числа и в отрицательную степень. Для этого вспомним правило: . Всё довольно-таки просто, нужно поделить “1” на основание в указанной степени, но без знака минус. Таким образом наш пример примет другое выражение, если степень будет “-3”. Итак, возводим . Получается: = или 0,002 (1 поделили на 343).
Дробные показатели — Алгебра II
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по алгебре II
10 диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 Следующая →
Алгебра II Помощь » Математические отношения и основные графики » Экспоненты » Понимание экспонентов » Дробные показатели
Упростите выражение:
Возможные ответы:
Правильный ответ:
Объяснение:
Помните, что показатели степени дроби аналогичны радикалам.
Быстрее всего было бы выразить термины в виде показателей и искать возможности для отмены.
В любом случае нам нужно умножить на два члена.
Сообщить об ошибке
Преобразование экспоненты в радикальное представление.
Возможные ответы:
Правильный ответ:
Объяснение:
Помните, что показатели степени в знаменателе относятся к корню члена, а показатели степени в числителе можно трактовать как обычно.
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Запишите произведение в радикальной форме
Возможные ответы:
Правильный ответ: 3
Объяснение: Эта задача основана на ключевых знаниях о том, что умножение членов с показателями степени требует сложения показателей степени. Таким образом, наш окончательный ответ. Сообщить об ошибке Оцените следующее выражение: Возможные ответы: Правильный ответ: Объяснение: или Отчет о ошибке Упрощение: Возможные ответы: Правильный ответ: Правильный ответ: Правильный ответ: .0003 Объяснение: Имейте в виду, что при делении показателей степени с одинаковым основанием вам потребуется вычесть показатель степени, находящийся в знаменателе, из показателя степени, находящегося в числителе. Чтобы найти показатель степени для , вычтите показатель степени знаменателя из показателя степени числителя. Чтобы найти показатель степени для , вычтите показатель степени знаменателя из показателя степени числителя. Поскольку показатель степени отрицательный, вам нужно будет поставить в знаменателе, чтобы сделать его положительным. Итак, Сообщить об ошибке Найдите значение . Возможные ответы: Правильный ответ: Объяснение: , когда у вас есть число или значение с дробным показателем, или Итак, Сообщение о ошибке Найдите значение .0196 Правильный ответ: Explanation: When you have a number or value with a fractional exponent, or So then, Report an Error Simplify: Possible Answers: Правильный ответ: Объяснение: Когда показатели степени возводятся в другую степень, вам нужно будет перемножить показатели вместе. Когда у вас есть число или значение с дробным показателем, или SO, Отчет о ошибке . Отчет . Правильный ответ: Объяснение: Один из способов решить эту проблему — разделить дробь. Перепишите дробный показатель следующим образом: Значение в половинной степени равно квадратному корню из этого значения. Подставьте это значение обратно в . Отчет о ошибке ← Предыдущий 1 2 3 4 5 6 7 Next → Уведомление об авторских правах View Algebra 2 Tutors Destin 8889898. Scerpification Scerpification. Посмотреть репетиторов по алгебре 2 Элисон Университет Сент-Томас, бакалавр искусств, биологии, общие. Посмотреть Алгебра 2 Репетиторы Сьюзен Колледж Хоуп, бакалавр искусств, химия. Медицинский факультет государственного университета Уэйна, доктор медицинских наук, биомедицинские науки. 10 диагностических тестов
630 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Следовательно, мы можем переписать выражение так:
Сертифицированный Scervifive
Сертифицированный репетитор
Университет Миннесоты, бакалавр наук, сестринское дело (RN).
Сертифицированный репетитор Все ресурсы по алгебре II
Возведение дроби в степень. Онлайн калькулятор.
0 АС +/- ÷ 7 8 9 × 4 5 6 — 1 2 3 + 0 00 , =
Этот калькулятор может возвести любую дробь в положительную, отрицательную и дробную степени и даст подробное решение.
Если дробь не имеет целочисленной части, оставьте это поле пустым, если дробь отрицательна, установите ее знак с помощью кнопки (+/-). Чтобы написать дробную степень, используйте знак «/», например 3/5 или -3/5.Правила возведения дроби в степень
Чтобы возвести дробь в степень n, нужно возвести числитель и знаменатель дроби в степень n. Например,
Чтобы возвести дробь в степень -n с отрицательным показателем, нужно поменять местами числитель и знаменатель дроби и заменить знак степени на противоположный. Затем нужно возвести числитель и знаменатель дроби в степень. Например,
Чтобы возвести дробь в степень с дробным показателем, необходимо числитель и знаменатель дроби представить в виде подкоренного числа, возведенного в степень, равную числителю степени, и записать знаменатель дроби мощность как индекс корня. Например,
Чтобы возвести дробь в степень с отрицательным дробным показателем, необходимо поменять местами числитель и знаменатель дроби, при этом знак степени меняется на противоположный.
Тогда числитель и знаменатель дроби представляют в виде подкоренного числа, возведенного в степень, равную числителю степени, а знаменатель степени записывают в виде индекса корня. Например,
| You may also find the following calculators helpful | |
| Fraction Calculators | |
| Simplifying Fractions Calculator | |
| Improper to Mixed Fraction Calculator | |
| Mixed Fraction to Improper Calculator | |
| Fractions Calculator With Пошаговое решение | |
| Возведение дроби в степень. Онлайн калькулятор. | |
| Калькулятор десятичной дроби | |
| Fraction to Decimal Calculator | |
| Compare Fractions Calculator | |
| Common Denominator Calculator | |
| Trigonometers Calculators | |
| Sine Calculator | |
| Cosine Calculator | |
| Tangent Calculator | |
| Расчет котангенса | |
| Расчет секанса | |
| Cosecant Calculator | |
| Arcsine Calculator | |
| Arccosine Calculator | |
| Arctangent Calculator | |
| Arccotangent Calculator | |
| Arcsecant Calculator | |
| Arccosecant Calculator | |
| Numeral Systems Calculators | |
| Калькулятор римских цифр | |
| Римские цифры От 1 до 3999 | |
| Калькулятор систем счисления | |
Двоичный калькулятор. Сложение, вычитание, умножение и деление двоичных чисел. | |
| Calculators (Number theory) | |
| Mathematical Expressions Calculator | |
| Calculator Parentheses | |
| Prime Factorization Calculator | |
| Gcd and Lcm Calculator With Steps | |
| Gcd and Lcm calculator using Euclidean алгоритм | |
| Калькулятор Gcd и Lcm для любого количества чисел | |
| Разбить число на его значение | |
| Разделить число на отношение. Онлайн -калькулятор с шагами | |
| Процентный калькулятор с шагами | |
| Научная нотация к калькулятору для десятичного преобразования | |
| Учительная нотация | |
| FACTIFIC NOTATATION | |
| FACTIFIC Notation | |
| FACTIRICALATATURT | |
| .0511 | Logarithm Calculator |
| Quadratic Equations Calculator With Steps | |
| Remainder Calculator | |
| Root Calculator | |
| Decimal Period Calculator | |
| Big Number Calculator | |
| Rounding Numbers Calculator | |
| Калькулятор свойств корней и показателей | |
| Калькулятор комплексных чисел | |
| Area Calculators | |
| Area of a Square Calculator | |
| Area of a Rectangle Calculator | |
| Combinatorics Calculators | |
| Permutations of N Elements Calculator | |
| Combinations of N Elements by M Calculator | |
| Перестановки N элементов с помощью М-калькулятора | |
| Математические тренажеры | |
| Дополнительный математический тренажер | |
| Subtraction Math Trainer | |
| Multiplication Math Trainer | |
| Division Math Trainer | |
| Multiplication Table Math Trainer | |
| Online Preschool Counting Trainer | |
| Online Preschool Mindfulness Trainer | |
Online Addition Тренажер по математике отдела умножения вычитания. Найдите правильный ответ. | |
| Онлайн-тренажер числовых выражений | |
| Linear Algebra and Analytical Geometers Calculators | |
| Matrix Addition and Subtraction Calculator | |
| Matrix Multiplication Calculator | |
| Matrix Transpose Calculator | |
| Matrix Determinant Calculator | |
| Inverse Matrix Calculator | |
| Длина сегмента линии. Онлайн-калькулятор расстояния между точками. | |
| Калькулятор векторных координат по двум точкам | |
| Калькулятор векторного модуля (длины) | |
| Калькулятор векторного сложения и вычитания | |
| Калькулятор векторного скалярного произведения. Используя длину векторов и косинус угла между векторами. | |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. | |
Калькулятор векторного произведения. Используя векторные координаты. | |
| Векторный калькулятор тройного произведения | |
| Vector Multiplication by Number Calculator | |
| Angle Between Vectors Calculator | |
| Vector Collinearity Check Calculator | |
| Vector Coplanarity Calculator | |
| Converters | |
| Length Converter | |
| Speed Converter | |
| Преобразователь ускорения | |
| Калькуляторы физики | |
Механика | |
| Speed Time Distance Calculator | |
| Acceleration Speed Distance Calculator | |
| Displacement Time Calculator | |
| Time Calculator | |
| Newton’s Second Law Calculator | |
| Gravitational Force Calculator | |
| Momentum Калькулятор | |
| Калькулятор импульсов | |
| Калькулятор веса объекта | |
Optics | |
| Light Reflection and Refraction Calculator | |
Electricity and Magnetism | |
| Ohm’s Law Calculator | |
| Coulomb’s Law Calculator | |
| Electric Field Strength Calculator | |
| Point Калькулятор электрического заряда Q | |
| Калькулятор силы, действующей на заряд | |
| Distance From Charge Calculator | |
| Potential Charge Energy Calculator | |
| Electric Field Potential Calculator | |
| Conductor and Sphere Capacitance Calculator | |
Capacitors | |
| Калькулятор емкости параллельных пластинчатых, цилиндрических и сферических конденсаторов | |
| Калькулятор напряженности электрического поля в пластинчато-параллельных, цилиндрических и сферических конденсаторах | |
| Voltage (Potential Difference) of Parallel Plate, Cylindrical and Spherical Capacitors Calculator | |
| Distance Between Plates in Parallel Plate Capacitor Calculator | |
| Plate Area in Parallel Plate Capacitor Calculator | |
| Energy Stored in Charged Capacitor Калькулятор | |
| Калькулятор энергии, запасенной в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах | |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов | |
| Астрономические калькуляторы | |
| Вес объекта на других планетах | |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках | |
| Генераторы | |
| Генератор случайных чисел | |
| Генератор паролей |
Дробные степени: правила и расчеты
Знаете ли вы, что степени или степени могут быть не целыми числами, а дробями? Да, показатели степени также существуют в виде дробей, и мы будем обсуждать их здесь.
В этой статье мы увидим, что такое дробные степени, что такое отрицательные дробные степени, их правила и примеры применения.
Что такое показатель степени дроби?
Дробные степени или показатели степени дроби представляют собой выражения, составленные из дробей и имеющие форму x а/б .
Нам больше знакомы целые показатели степени в форме x a . Поскольку x питается от a , это означает, что x умножается само на себя a раз. Однако, когда дробь является степенью или показателем степени, вы можете найти корень этого выражения. Это означает, что для дробного показателя степени, такого как x 1/a , вам необходимо найти a корень x ;
.
Решите для .
Решение
Найдите
Решение
Какова дробная степень числа в десятичной форме?
Степень дроби в десятичной форме — это показатель степени, представляющий собой дробь, представленную в виде десятичной дроби. Встречается в форме;
,
, где a и b — две цифры, разделенные десятичной точкой. Теперь они могут быть перевыражены, чтобы стать;
Помните, что a и b — это цифры, образующие десятичное число ab . Например, учитывая десятичное число 3,2, где a и b будут 3 и 2 соответственно. Давайте посмотрим на пример, чтобы прояснить это лучше.
Решить для .
Раствор
Напомним, что;
Затем;
Вспоминая, что тогда мы имеем
В заключение,
Что такое отрицательные дробные степени?
Отрицательные дробные степени возникают, когда выражение было преобразовано в отрицательную дробь.
Это отображается в форме x – a/b . Когда это происходит, обратное выражение получает дробь. Тогда это становится
.
Это соответствует правилу отрицательных показателей степени , которое гласит, что
.
Отрицательные дробные степени входят в число правил дробных полномочий, которые будут обсуждаться ниже.
Правила дробных степеней
Применение этих правил позволит вам легко решать задачи с дробными показателями. Однако, прежде чем перейти к правилам, обратите внимание, что дробные степени определяются формой
, а также
Зная это определение, следует применять следующие правила.
Rule 1: When the base for instance x is powered by a negative fraction for example , find the b root of x and power by a , затем найти обратную величину результата.
Решить .
Раствор
Применяя правило 1,
Правило 2: Когда основание представляет собой дробь, например, , и питается от отрицательной дроби, например, b , найдите
6 b и мощность .Решить
Решить
Применив правило 2,
Правило 3: Если произведение двух или более дробных степеней в этом случае и , имеют одно и то же основание в этом случае x , то найдите ab корень из x и степень в виде суммы б и а .
Решить .
Решение
Применяя правило 3,
Правило 4: Когда произведение двух или более дробных степеней в этом случае и , имеют в этом случае одно и то же основание x , затем найдите ab корень из x и возведите в степень сумму bm и
.
Решение
SOL UTTION
, применяя Правило 4,
Правило 5: , когда у него есть двойная уединка, и в этом рамке. в данном случае x , затем найдите ab корень x и возведите в степень разность b и a .
Решение
Решение
, применив Правило 5,
Правило 6: , когда к цитату двух фракционных Powers в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае, и в этом случае. x , затем найдите ab корень из x и мощность по разнице bm и и .
Решить .
Решение
, применив правило 6,
Правило 7: , когда продукт двух дробных способностей имеет разные основания в этом случае x и . степени в этом случае, то найти корень из ху .
Решить .
Solution
By applying rule 7,
Rule 8: When the quotient of two fractional powers have different bases in this case x and y , but with the same полномочия в этом случае, то найти корень .
Решить .
Решение
Применяя правило 8,
Решите следующее;
а.
б.
г.
Раствор
а.
Первое, что нужно сделать, это посмотреть, можно ли преобразовать число в экспоненциальную форму (индексы).
Обратите внимание;
Поэтому;
Напомним, что;
Затем;
б.
Напомним, что;
Затем;
в.
Первое, что нужно сделать, это посмотреть, можно ли преобразовать число в экспоненциальную форму (индексы).
Поэтому;
Напомним, что;
Затем;
или вы можете решить прямо с этой точки;
Биномиальное разложение для дробных степеней
Как выполняется биномиальное разложение для дробных степеней?
Биномиальное разложение для дробных степеней выполняется простым применением формулы
, где n — степень или показатель степени.
Решите первые 4 члена .
Решение
Убедитесь, что вы разложили на множители или повторно выразили выражение с показателем степени, чтобы оно соответствовало форме;
.
Итак, ваш план состоит в том, чтобы преобразовать (8 + 2 года) в (1 + год). Для этого разложите 8 + 2y на 8. У вас получится
. Пусть
Подставим в уравнение
Вспоминая, что у нас тогда есть
Напомним, что
Кроме того, нас интересуют только первые 4 члена, поэтому;
Замените реальное значение на как;
Поэтому;
И так
Дополнительные примеры вычисления дробных степеней
Еще несколько примеров помогут вам лучше понять дробные степени.
Если кубический корень из числа возведен в квадрат и результат равен 4. Найдите число.
Решение
Пусть неизвестное число будет y.