Формула вычисления объема в литрах. Как посчитать объем
Инструкция
Если тело имеет форму прямоугольного параллелепипеда (это может быть спичечный коробок , книга, кубик и т.п.), то его объем находится по формуле: V=abc, где a — высота тела, b — его ширина, c — длина. Величины снимаются при помощи обычной линейки или измерительной ленты. Пусть дан спичечный коробок, чтобы рассчитать его объем необходимо измерить его параметры: a=2см, b=4см, c=5 см, значит, объем коробка равен 4см*2см*5см=40 см в кубе.
Если же у тела форма, отличная от параллелепипеда, неправильная форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III веке до нашей эры. Для этого нужно налить воды в измерительный сосуд, запомнить сколько в нем воды (V1), далее опустить туда тело и измерить сколько воды стало (V2), объемом предмета будет являтся разница:V2-V1. Следует внимательно изучить сосуд, в каких единицах он измеряет воду, скорее всего в миллилитрах или литрах, значит и объем тела тоже будет в той же величине.
Пример: пусть надо измерить объем камня. Налить в мензурку 50 мл воды. После опускания камня в воду в мензурке стало 60 мл воды, значит объем данного камня равен 60-50=10мл.
В случае когда известны масса и плотность тела, объем тела рссчитывается по формуле: V=m/p, где m-масса, p-плотность. Считать по формуле нужно только тогда, когда масса тела известна в килограммах, а плотность — в килограммах, деленных на кубический метр; или масса — в граммах, а плотность — в граммах на кубический см, тогда объем в первом случае будет измерен в кубических метрах, а во втором — в кубических сантиметрах. Плотность тела — величина табличная, имеются специальные таблицы плотностей различных веществ.
Пример: пусть надо найти объем железного гвоздика, масса которого 7,8 г. В таблице плотностей найти железо — его плотность 7,8 г/кубический см. Тогда объем равен 7,8 (г) разделить на 7,8 (г/кубический см) равно 1 кубический сантиметр.
Рассчитать объем куба
может понадобиться не только при решении математических задач. Например, вам необходимо знать, сколько кирпичей находится в упаковке кубической формы или сколько жидкого или сухого вещества поместится в контейнер. Для этого, конечно, потребуется выяснить еще несколько параметров, но прежде всего необходимо рассчитать объем куба .Вам понадобится
- Вспомнить определение и свойства куба
- Измерительный прибор
Инструкция
Вспомните, что такое куб. Это правильный гексаэдр — геометрическое тело, каждая грань которого представляет собой квадрат. Поскольку все стороны куба одинаков — то и грани его равны между собой, равно как и ребра. То есть для определения объема вам необходимо знать размер всего одной грани.
Вспомните, чему равен объем параллелепипеда. Он равен площади основания, умноженной на высоту. Но у куба длина, ширина и высота равны между собой. Куб можно поставить на любую грань, все равно площадь основания быдет той же самой, что и в первоначальном положении. Обозначьте ребро
Вычислите объем, умножив площадь основания а2 на высоту, которая в данном случае также равна а. Соответственно, объем V будет равен размеру ребра куба , возведенному в третью степень. V=a3.
Если вам необходимо рассчитать количество вещества, которым предполагается заполнить контейнер кубической формы, то необходимо знать плотность этого вещества. Это количество будет равно плотности, умноженной на объем куба . А для того, чтобы рассчитать, например, количество кирпичей в контейнере кубической формы, необходимо вычислить объем каждого кирпича, после чего разделить объем контейнера на объем кирпича.
Обратите внимание
В некоторых случаях необходимо найти не объем, а площадь стен — например, при расчете количества стекла для аквариума. Поскольку все грани куба одинаковы, площадь складывается из площадей 6 граней, то есть выражается формулой S=6a2
Полезный совет
Старайтесь практические измерения проводить по возможности точно. Пользоваться можно линейкой, рулеткой, штанген-циркулем. Главное, чтобы деления соответствовали стандартам.
Метр в кубе , кубический метр или кубометр — стандартная единица измерения объема. В этих единицах рассчитывается объем помещений, а также расход воды и газа. В них же нередко указывается количество некоторых стройматериалов, например, досок. В кубические метры также переводят остальные, внесистемные единицы измерения объема — литры, кубические дециметры и сантиметры.
Вам понадобится
- — калькулятор;
- — таблица плотности веществ;
- — компьютер.
Инструкция
Чтобы рассчитать количество кубометров, если объем известен, но задан в дольных, кратных или внесистемных единицах, то умножьте его на нужный коэффициент. Например, чтобы рассчитать количество метров в
Как посчитать объем коробки имеющую четыре стороны, которую обычно называют прямоугольной коробкой. Перед тем как посчитать объем коробки, необходимо перевести размеры все сторон, коим является длина, ширина и высота в метры. Далее объем данной коробки получается умножением длины на ширину и на высоту (ДхШхВ). Таким образом, вы получаете объем в кубических метрах.
Вычисление объёмного веса прямоугольных коробок:
ОВ=(X×Y×Z)/5000
X — длина, Y — высота, Z — ширина.
electricianprof.ru
Вычисление формулы объема и площади в Excel
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Как рассчитать объем и площадь в Excel
В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.
В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.
В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.14). Поэтому значения ячеек A2 и A3 немного отличаются.
Вычисление арифметических формул в Excel
Допустим нам нужно в Excel вычислить формулу:
Чтобы получить результат вычисления ее нужно просто записать в одну строку: =(125*(3+4,5)^2)/(12-3,7).
Данная формула содержит 5 арифметических действий: суммирование, вычитание, умножение, деление и поднесение к степени (^). Если мы записываем все в одно строку, то нужно соблюдать правила арифметической последовательности. Для этого нужно использовать скобки.
Формула для вычисления объема сферы в Excel
Например, нам нужно регулярно вычислить объемы сфер с разными радиусами.
Формула вычисления объема сферы выгладит так:
Предыдущие примеры плохо подходят для решения данной задачи, так как они не используют переменных значений в формулах, а только константы. Из-за этого при смене радиуса нужно переписывать формулу. Но Excel позволяет нам использовать эффективное решение:
- В ячейку B2 запишем формулу вычисления объема сферы в одну строку: =(4/3)*ПИ()*A2^3 (A2 – это ссылка на ячейку).
- В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.
exceltable.com
7.3 Вычисление объема тела
а) Вычисление объема тела по известным площадям параллельных сечений.
П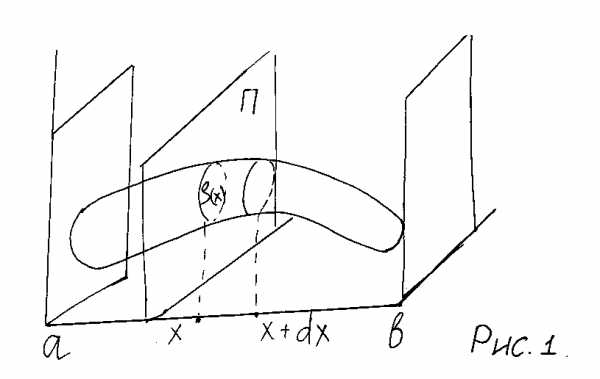 усть
требуется найти объем тела V при известной
площади S сечений этого тела относительно
плоскости, перпендикулярной некоторой
оси, например, ох;.
Применим метод 2.
усть
требуется найти объем тела V при известной
площади S сечений этого тела относительно
плоскости, перпендикулярной некоторой
оси, например, ох;.
Применим метод 2.
Через произвольную точку 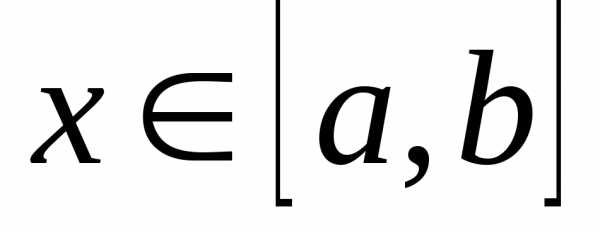 проведем плоскость
проведем плоскость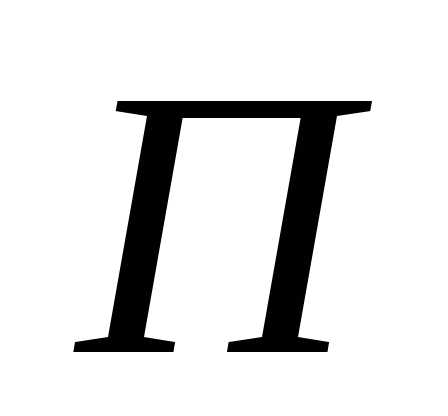 ,
перпендикулярную оси ох. Обозначим
через
,
перпендикулярную оси ох. Обозначим
через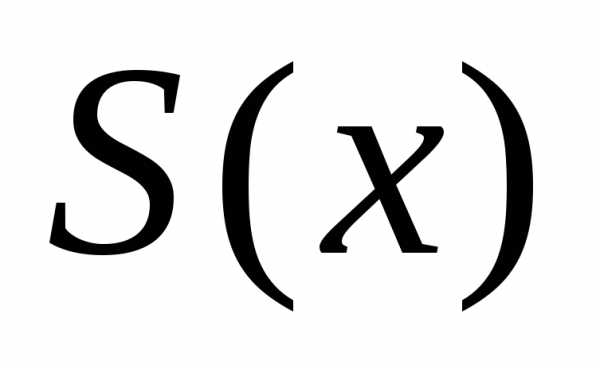 площадь
сечения тела этой плоскостью.
площадь
сечения тела этой плоскостью.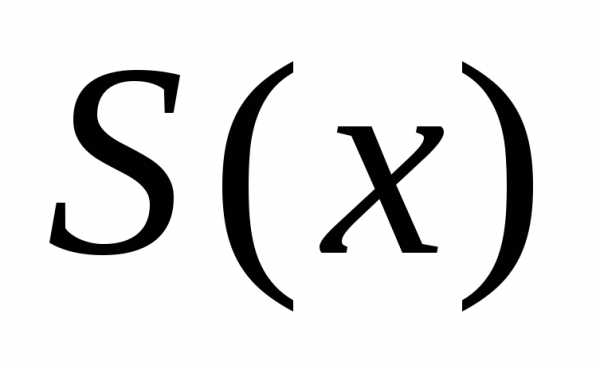 считаем известной и изменяющейся
непрерывно при изменении
считаем известной и изменяющейся
непрерывно при изменении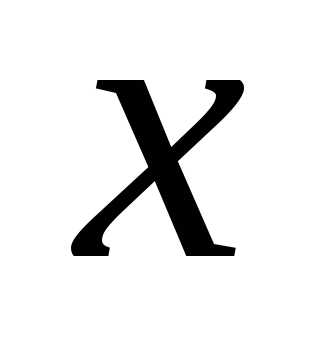 .
Через
.
Через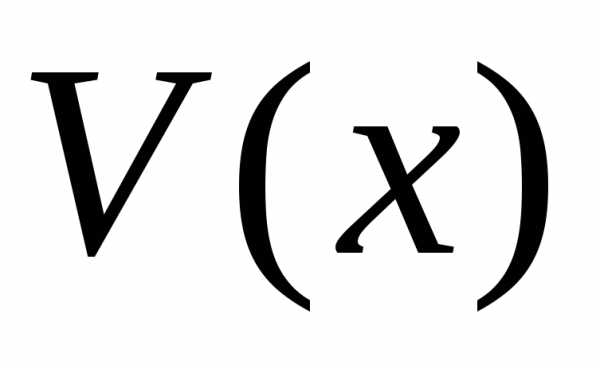 обозначим объем части тела, лежащие
левее плоскости
обозначим объем части тела, лежащие
левее плоскости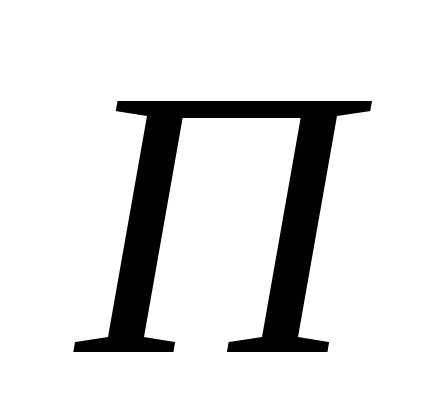 .
Будем считать, что на отрезке
.
Будем считать, что на отрезке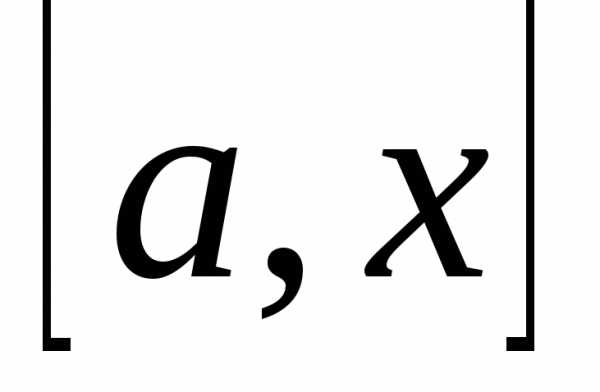 величина
величина есть функция от
есть функция от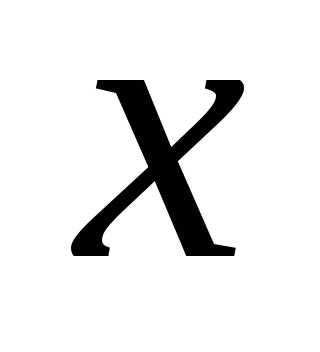 ,
т.е..
Теперь найдем дифференциал функции
,
т.е..
Теперь найдем дифференциал функции .
Он представляет собой слой тела,
заключенного между параллельными
плоскостями, пересекающими ось
.
Он представляет собой слой тела,
заключенного между параллельными
плоскостями, пересекающими ось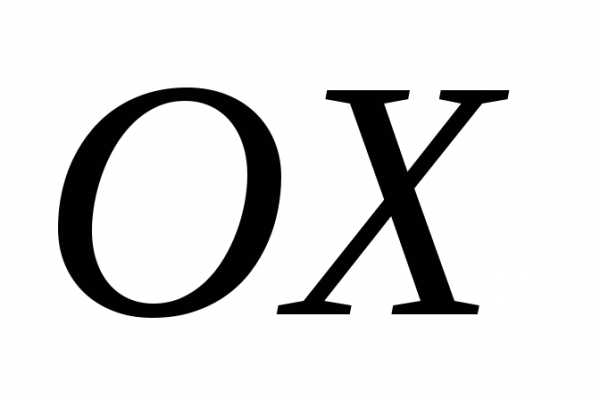 в точках
в точках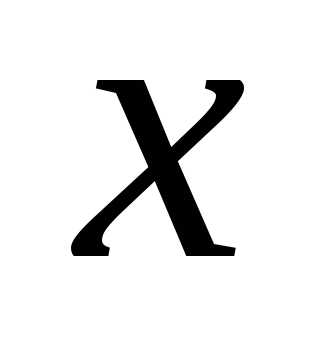 и
и ,
который можно приближено принять за
цилиндр с основанием
,
который можно приближено принять за
цилиндр с основанием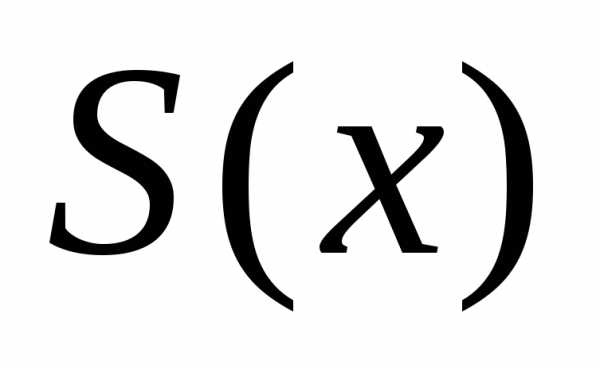 и высотой
и высотой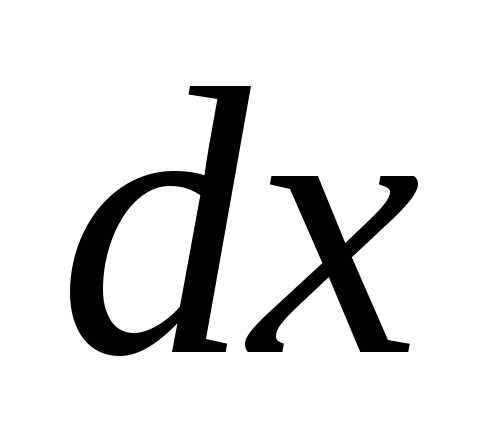 (рис.1).
поэтому дифференциал объема.
Тогда для нахождения полного объема
это соотношение надо проинтегрировать
в пределах от
(рис.1).
поэтому дифференциал объема.
Тогда для нахождения полного объема
это соотношение надо проинтегрировать
в пределах от до
до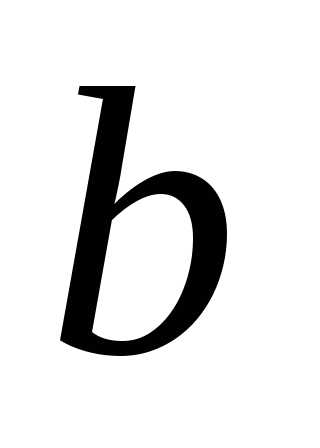 .
.
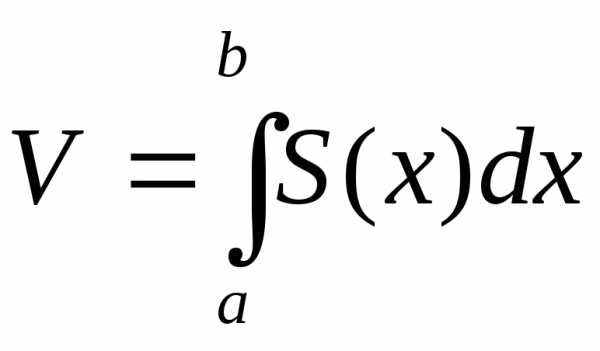 —
полученная формула называется формулой
объема тела по площади параллельных
сечений.
—
полученная формула называется формулой
объема тела по площади параллельных
сечений.
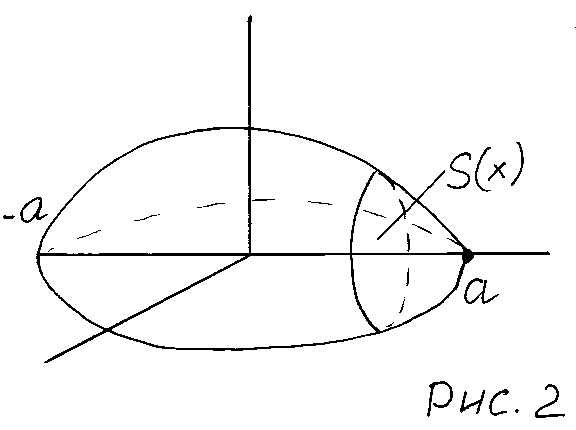
Пример: Найти объем эллипсоида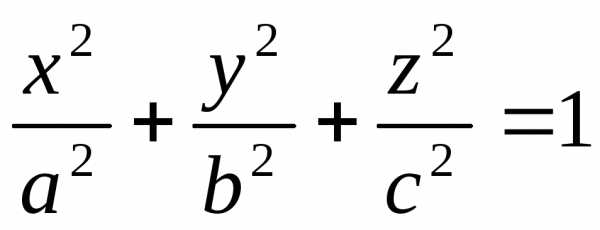 .
Если эллипсоид рассечен плоскостью,
параллельной плоскости
.
Если эллипсоид рассечен плоскостью,
параллельной плоскости и на расстоянии
и на расстоянии от нееполучим эллипс (см. рис. 2).
от нееполучим эллипс (см. рис. 2).
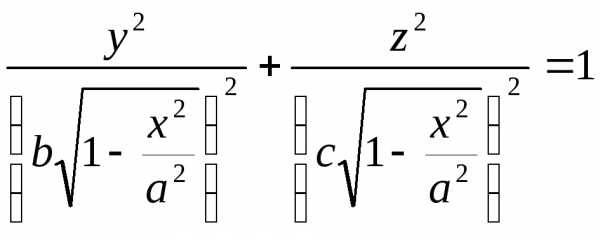
 .
.
Площадь этого эллипса равна . Поэтому объем эллипсоида
б) Объем тела вращения
П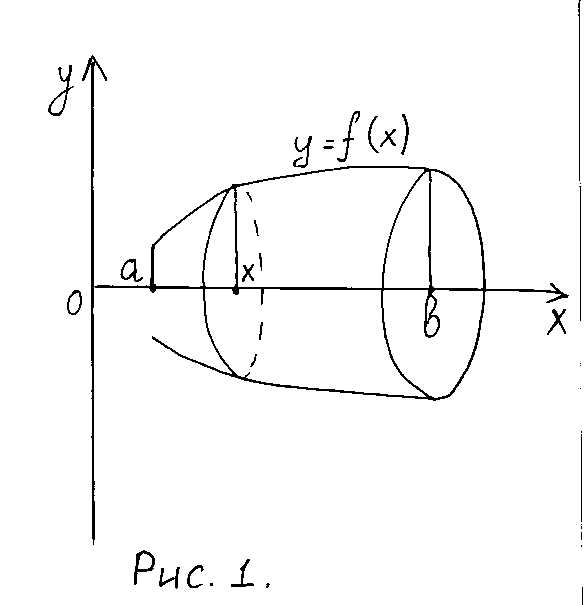 усть
вокруг оси
усть
вокруг оси вращается криволинейная трапеция,
ограниченная непрерывной линиейотрезкоми прямыми
вращается криволинейная трапеция,
ограниченная непрерывной линиейотрезкоми прямыми и
и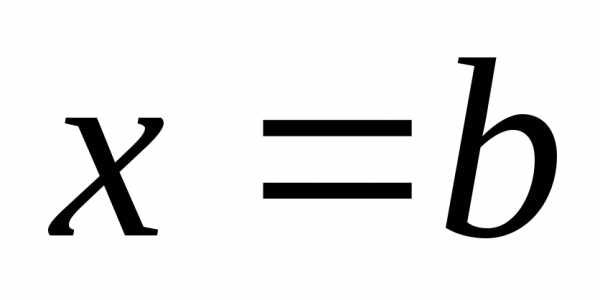 .
Полученная от вращения фигура, называется
телом вращения. Сечение этого тела —
плоскостью, перпендикулярной оси
.
Полученная от вращения фигура, называется
телом вращения. Сечение этого тела —
плоскостью, перпендикулярной оси ,
проведенной через произвольную точку,
есть круг радиуса
,
проведенной через произвольную точку,
есть круг радиуса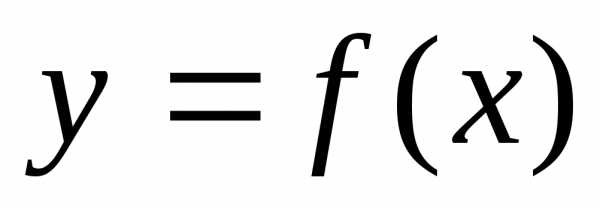 .
Следовательно,.
Поскольку- выражение для объема тела вращения
вокруг оси
.
Следовательно,.
Поскольку- выражение для объема тела вращения
вокруг оси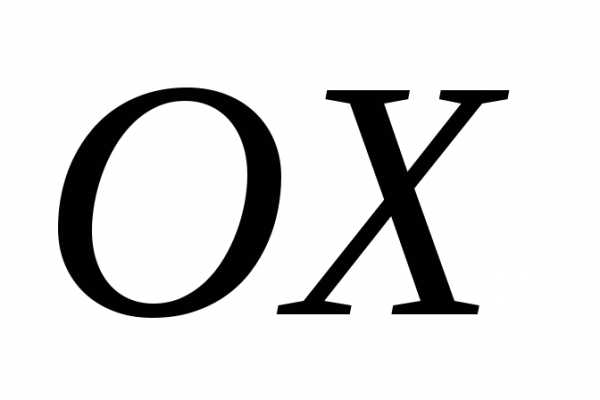 .
Если криволинейная трапеция ограничена
графиком непрерывной функциии прямымипри условии
.
Если криволинейная трапеция ограничена
графиком непрерывной функциии прямымипри условии ,
то для объема тела, образованного
вращением этой трапеции относительно
оси
,
то для объема тела, образованного
вращением этой трапеции относительно
оси ,
по аналогии с полученным выше можно
записать:
,
по аналогии с полученным выше можно
записать:
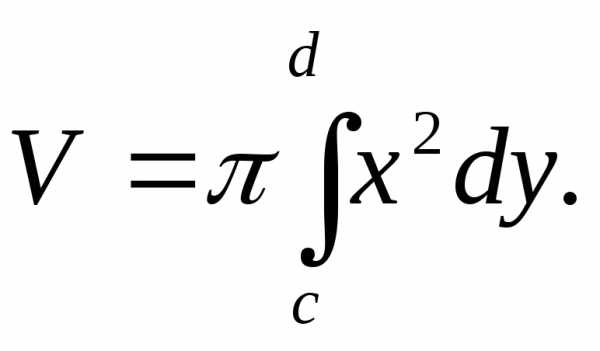
в) Вычисление координат центра тяжести плоской фигуры
П усть
дана материальная плоская фигура
(пластина), ограниченная кривойи прямыми(рис. 2). Будем считать, что плотность
пластины
усть
дана материальная плоская фигура
(пластина), ограниченная кривойи прямыми(рис. 2). Будем считать, что плотность
пластины есть величина
есть величина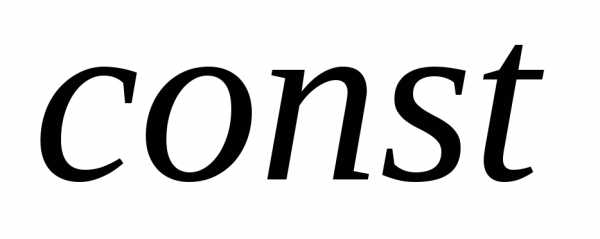 .
Тогда масса всей пластины
.
Тогда масса всей пластины ,
т.е.
,
т.е.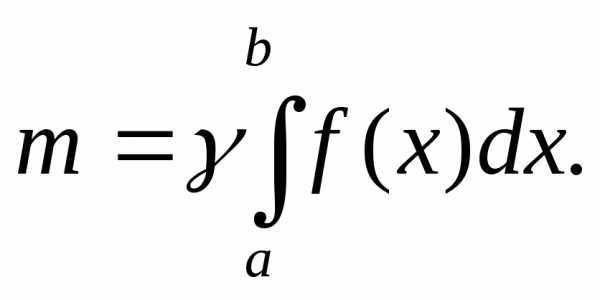 Выделим элементарный участок пластины
в виде бесконечно малой узкой вертикальной
полосы и будем считать его прямоугольником.
Его масса равна
Выделим элементарный участок пластины
в виде бесконечно малой узкой вертикальной
полосы и будем считать его прямоугольником.
Его масса равна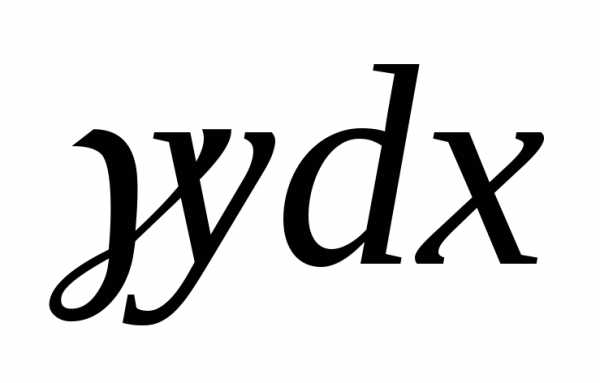 .
Центр тяжести прямоугольника лежит на
пересечении диагоналей прямоугольника.
Это точка
.
Центр тяжести прямоугольника лежит на
пересечении диагоналей прямоугольника.
Это точка стоит от оси
стоит от оси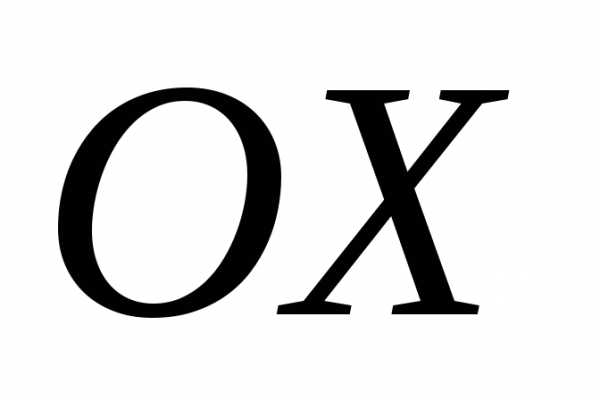 на расстоянии
на расстоянии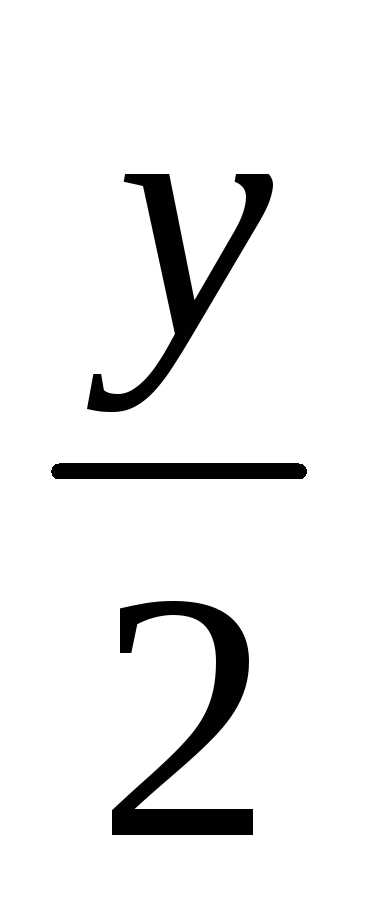 ,
а от оси
,
а от оси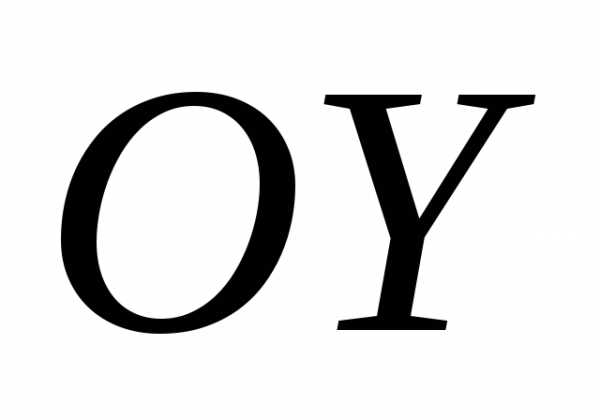 на расстоянии
на расстоянии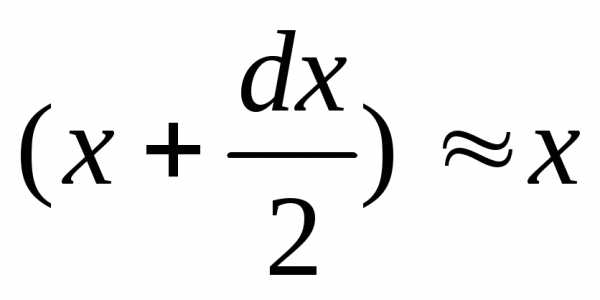 .
Тогда для элементарных статистических
моментов относительно осей
.
Тогда для элементарных статистических
моментов относительно осей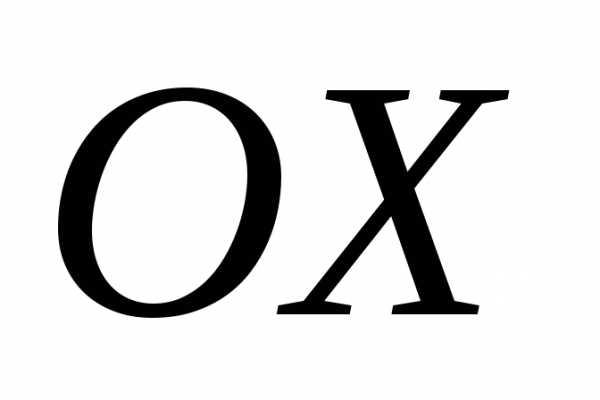 и
и получим следующие соотношения:и.
Отсюда
получим следующие соотношения:и.
Отсюда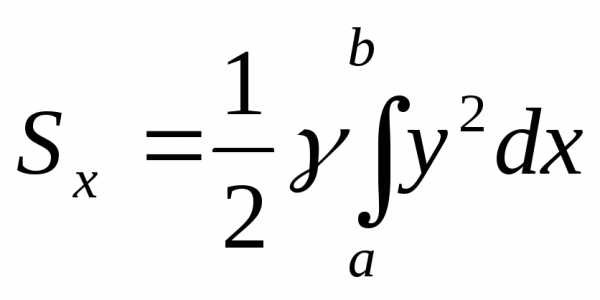 ;
;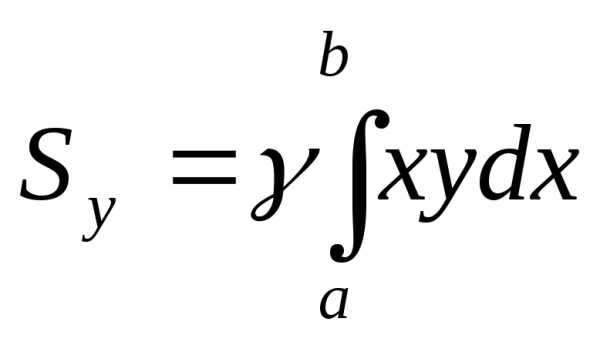 .
Если обозначим координаты центра тяжести
плоской фигуры
.
Если обозначим координаты центра тяжести
плоской фигуры то получим, что
то получим, что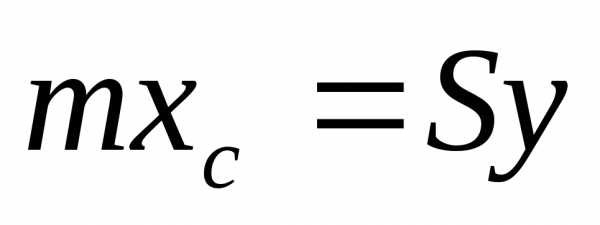 ;
;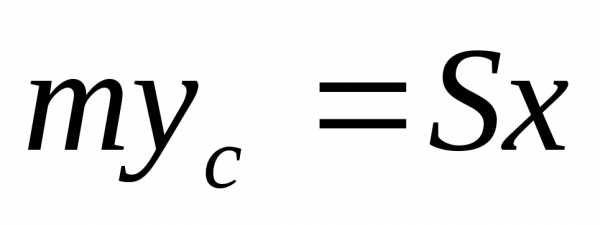 ,
т.е.
,
т.е.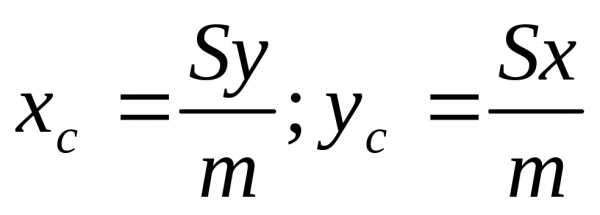 или
или и
и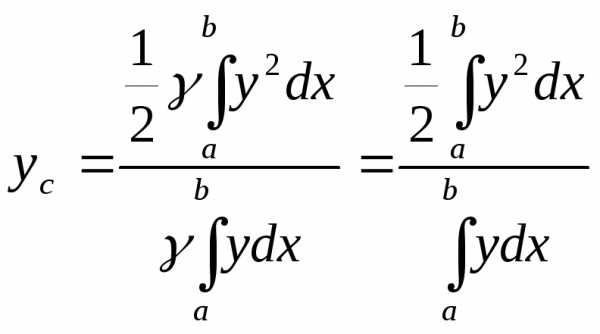 .
.
8. Приближенное вычисление определенного интеграла
Пусть требуется найти определенный
интеграл 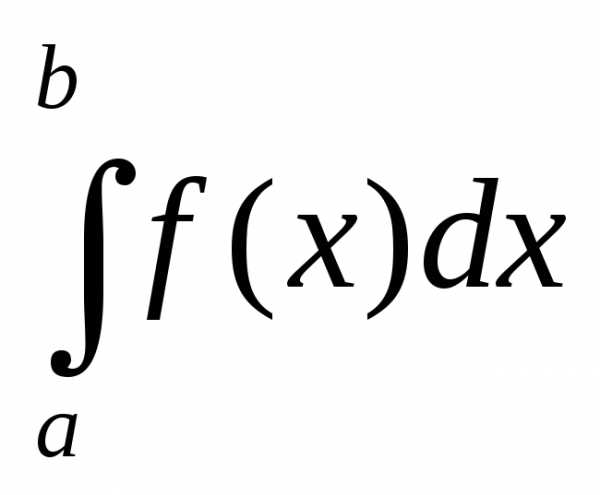 от непрерывной функции
от непрерывной функции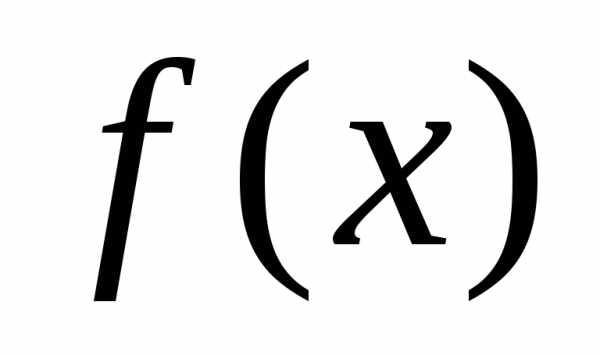 .
Если можно найти первообразнуюфункции
.
Если можно найти первообразнуюфункции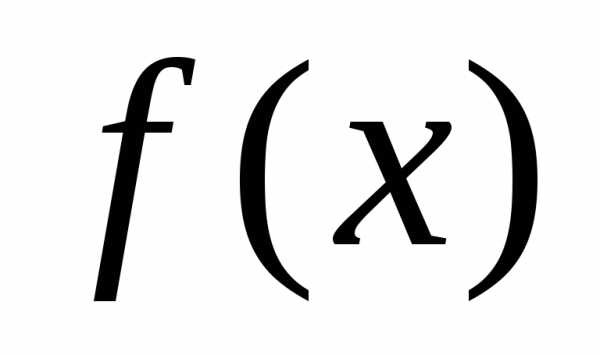 ,
то интеграл находится по формуле
Ньютона-Лейбница:
,
то интеграл находится по формуле
Ньютона-Лейбница:
. Но поиск первообразной функции иногда весьма сложен, кроме того не для всякой функции первообразная выражается через элементарные функции. В этих и других случаях прибегают к приближенным формулам, с помощью которых интеграл находится с любой степенью сложности.
8.1. Формулы прямоугольников
П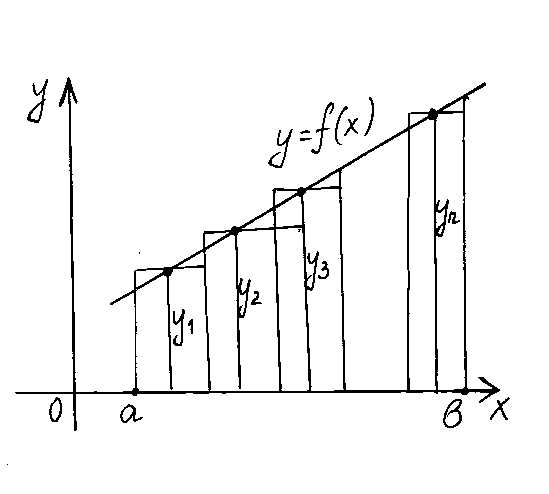 усть
на отрезкезадана непрерывная функция
усть
на отрезкезадана непрерывная функция .
Требуется вычислить
.
Требуется вычислить интеграл
интеграл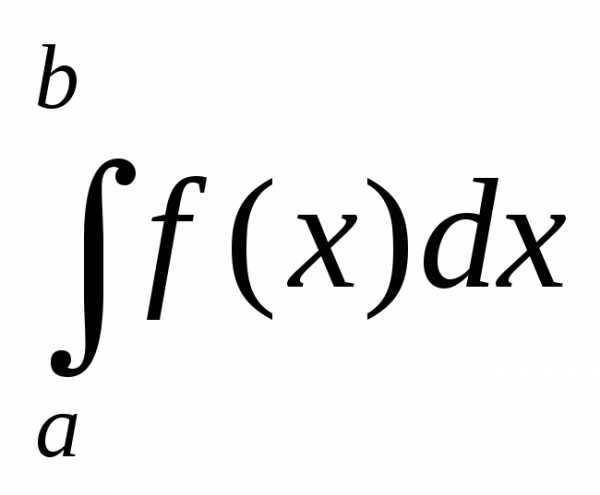 численно равный площади соответствующей
трапеции. Разобьем основание этой
трапеции, т.е. отрезок
численно равный площади соответствующей
трапеции. Разобьем основание этой
трапеции, т.е. отрезок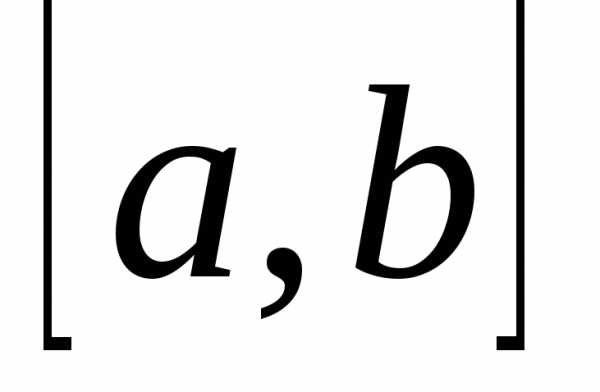
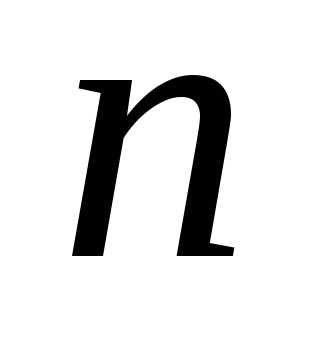 равных частей длиныс помощью точек.
Можно записать, что.
В середине каждого отрезка
равных частей длиныс помощью точек.
Можно записать, что.
В середине каждого отрезка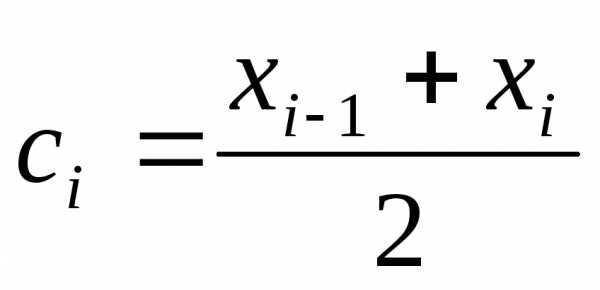 .
Построим ординату
.
Построим ординату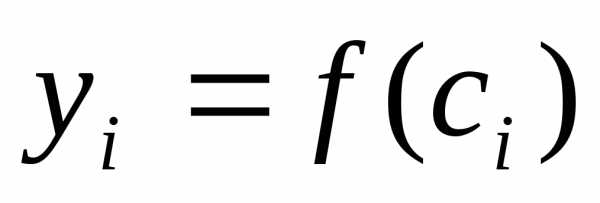 графика функции
графика функции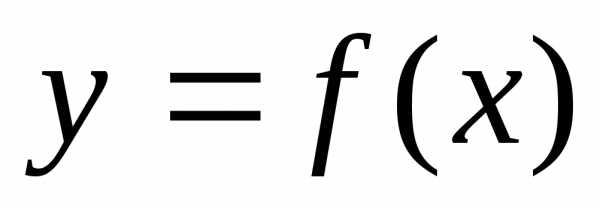 .
Приняв эту ординату за высоту, построим
прямоугольник с площадью
.
Приняв эту ординату за высоту, построим
прямоугольник с площадью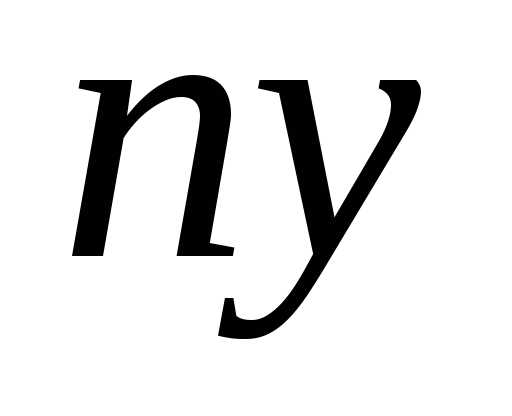 .
Тогда сумма площадей всех прямоугольников
даст площадь фигуры, представляющую
собой приближенное значение искомого
определенного интеграла:.
Эта формула и называется формулой
прямоугольников. Абсолютная погрешность
оценивается с помощью следующего
соотношения
.
Тогда сумма площадей всех прямоугольников
даст площадь фигуры, представляющую
собой приближенное значение искомого
определенного интеграла:.
Эта формула и называется формулой
прямоугольников. Абсолютная погрешность
оценивается с помощью следующего
соотношения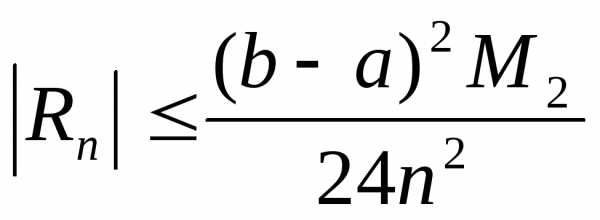 ,
где
,
где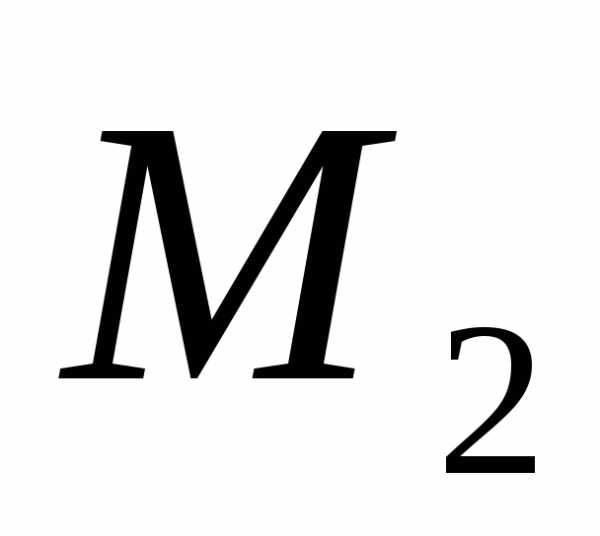
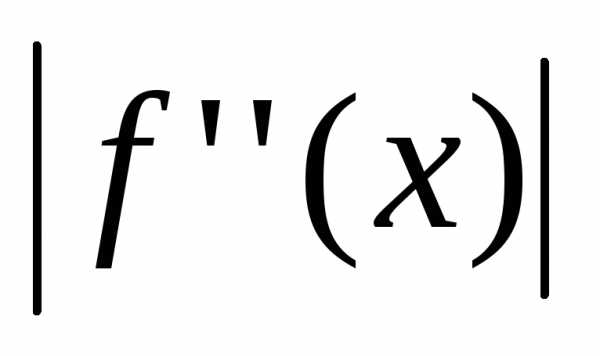 на отрезке
на отрезке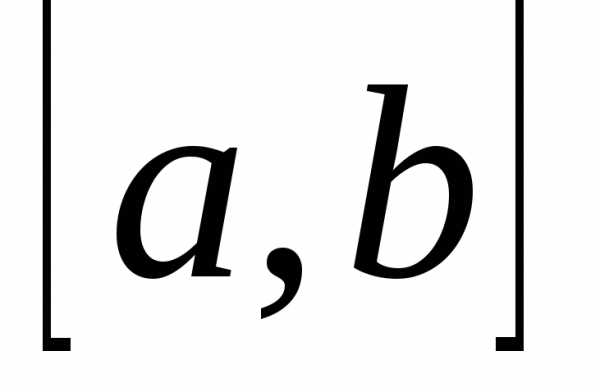 .
.studfiles.net
Ответы@Mail.Ru: Нахождение объема(формула) Очень нужно!Помогите!
произведение площади основания на высоту
<a rel=»nofollow» href=»http://www.dink.ru/ref/vol.php» target=»_blank»>http://www.dink.ru/ref/vol.php</a>V=m/p масса делить на плотность вещества
объем любого тела равна тройному интегралу от некоторого элемента объема dv в рассматриваемых координатах по некоторой области D. для прямоугольных координат dv = dx * dy * dz
V (объём) = масса/ плотность, V (объём) = длина * высота * ширина
спасибо я тоже искал
Алена, спасибо
V=m/p масса делить на плотность вещества
touch.otvet.mail.ru
